Основы технической диагностики. Лекция №7. Модель протяженного объекта

1. МОДЕЛЬ ПРОТЯЖЕННОГО ОБЪЕКТА

ОСНОВЫ ТЕХНИЧЕСКОЙ
ДИАГНОСТИКИ
Лекция №7
МОДЕЛЬ ПРОТЯЖЕННОГО
ОБЪЕКТА

2.

Предисловие
• Рассмотрим такую модель на примере опоры контактной
сети.
• Состояние опоры контактной сети, как несущей
конструкции зависит от состояния бетона и арматуры.
• В работах по диагностике опора контактной сети
рассматривается как объект, имеющий сосредоточенные
параметры - и по бетону и по арматуре.

3.

• Например, арматура характеризуется
единственным параметром - степенью
коррозии.
• Это объясняется тем, что часто
используемые на практике СД
контролируют не прямые, а косвенные
параметры.
• В действительности несущая способность
опоры определяется пространством
состояний с большим числом фазовых
координат.

4. Основных причин большой размерности пространства состояний три:

• опора имеет конечные (отличные от нуля)
геометрические размеры и, следовательно, непостоянную
по протяженности прочность (под протяженностью в
общем случае понимается три измерения);
• нагрузки, включая климатические, по протяженности
опоры также неодинаковы;
• степень и скорость коррозии арматуры под действием
токов, и бетона по протяженности различны.

5. Рассмотрим последовательно все три составляющих.

• Несущий момент опоры
по длине не одинаков.
• При принятой конусности
опор величина несущего
момента на уровне пяты
консоли составляет 50% от
момента на уровне условного
обреза фундамента.

6. Для опоры с предварительно напряженной арматурой имеются дополнительные факторы:

• не все стержни арматуры в зависимости от
конструкции опоры доходят до торцевых частей.
• из-за конического сечения опоры число
стержней арматуры, приходящееся на единицу
объема железобетона, в верхней части опоры
выше, чем в нижней.
• Это приводит к тому, что бетон в верхней
части опоры более напряжен, чем в нижней.

7. Неравномерность нагрузки по протяженности опоры складывается из трех составляющих:

• Неравномерный по длине опоры момент.
• Неравномерная загрузка кольцевого сечения
опоры при изгибающих моментах в сторону пути.
• В поперечном сечении опоры разные по глубине
залегания слои материала несут неодинаковую
нагрузку.
7

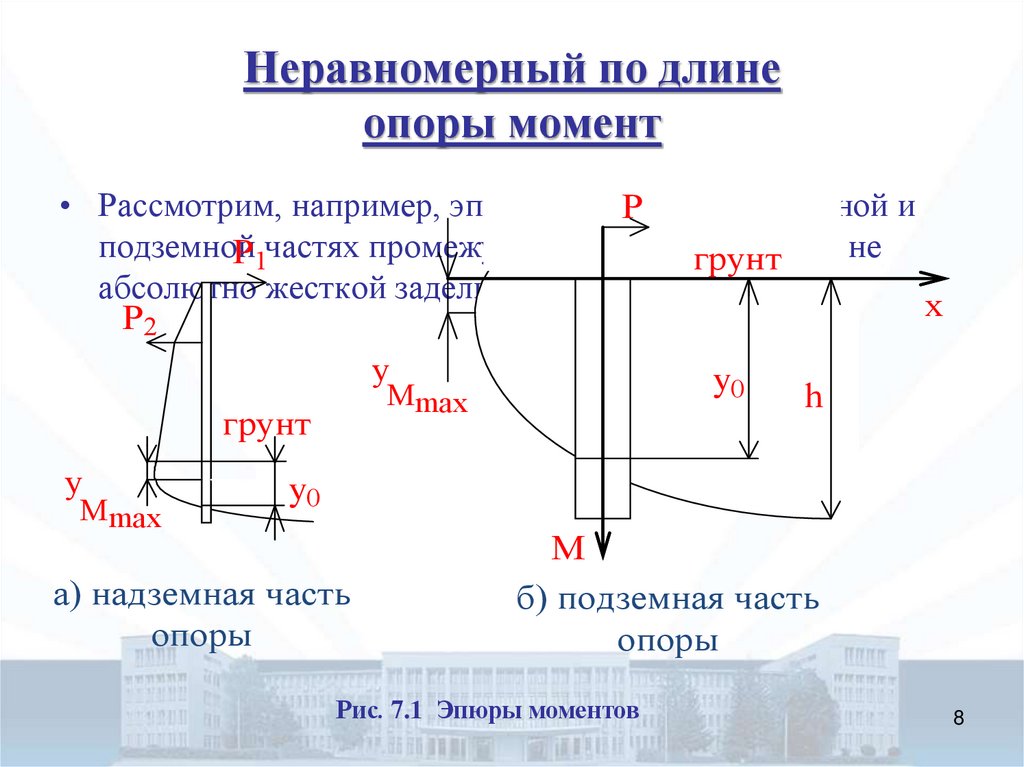
8. Неравномерный по длине опоры момент

• Рассмотрим, например, эпюры моментов
в надземной и
Р
подземной
с учетом не
P1частях промежуточной опорыгрунт
абсолютно жесткой заделки в грунт (Рис. 11.1)
x
P2
y
y0
Mmax
h
грунт
y
Mmax
y0
а) надземная часть
опоры
M
б) подземная часть
опоры
Рис. 7.1 Эпюры моментов
8

9. Примечание

• Направление эпюры моментов меняется на глубине y0.
Величина y0 зависит от заглубления опоры h и свойств
грунта.
• Например, при заглублении h = 3,5 м, для некоторых
грунтов y0 =2,5 м.
• При этом максимальный изгибающий момент будет
находиться на глубине около 0,5 м.
• Практически величина yMmax зависит от характера и
состояния грунта.
• Например, в скальном грунте или при промерзании
грунта эта величина стремится к нулю.
• Картина значительно изменяется при наличии лежней
9

10.

10

11.

11

12.

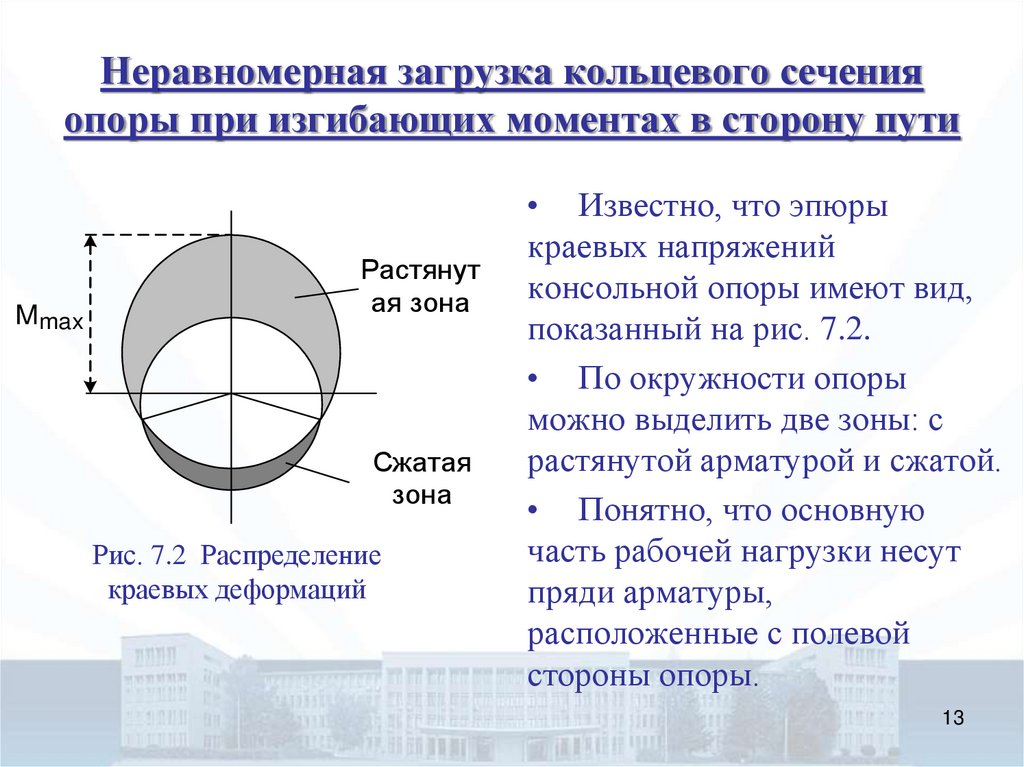
12

13. Неравномерная загрузка кольцевого сечения опоры при изгибающих моментах в сторону пути

Mmax
Растянут
ая зона
Сжатая
зона
Рис. 7.2 Распределение
краевых деформаций
• Известно, что эпюры
краевых напряжений
консольной опоры имеют вид,
показанный на рис. 7.2.
• По окружности опоры
можно выделить две зоны: с
растянутой арматурой и сжатой.
• Понятно, что основную
часть рабочей нагрузки несут
пряди арматуры,
расположенные с полевой
стороны опоры.
13

14. В поперечном сечении опоры разные по глубине залегания слои материала несут неодинаковую нагрузку

• Неравномерность коррозии опоры по длине
очевидна и не вызывает никаких сомнений.
• Интенсивно корродирует арматура,
расположенная лишь в подземной части.
• Однако и в подземной части по глубине степень
коррозии неравномерна.
• Из опыта эксплуатации известно, что наиболее
часто коррозионные повреждения встречаются на
глубине 0,2 ... 0,6 м.
14

15. Причины

• Прежде всего, это неравномерная
проводимость и увлажненность грунта,
имеющие закономерные изменения с
ростом глубины.
• Из влияющих факторов можно назвать
уносы с подвижного состава.
15

16. Пример

• На Южно-Уральской железной дороге в результате
экспериментальных исследований было обнаружено, что
верхняя часть грунта 0,1 ... 0,2 м (щебень, балласт) в
сухую погоду имеет весьма малую проводимость и
поэтому коррозия арматуры здесь маловероятна.
• Далее, на глубине 0,3 ... 0,7 м (этот слой был верхним в
период работы участка на паровой тяге) на
подавляющем большинстве участков грунт имеет
характерный темный цвет, что подтверждает гипотезу
о значительном содержании в нем угольной и тормозной
пыли, а также топочных уносов паровозов.
16

17. Пример

• На этом уровне из-за высокой проводимости грунта,
как правило, и наблюдается повышенная интенсивность
коррозии арматуры.
• Подобный эффект создают соли и удобрения,
перевозимые по железной дороге.
• Менее очевидным является факт неравномерности
коррозии по окружности поверхности опоры.
• Разность потенциалов грунта и арматуры также
непостоянна по протяженности опоры.
17

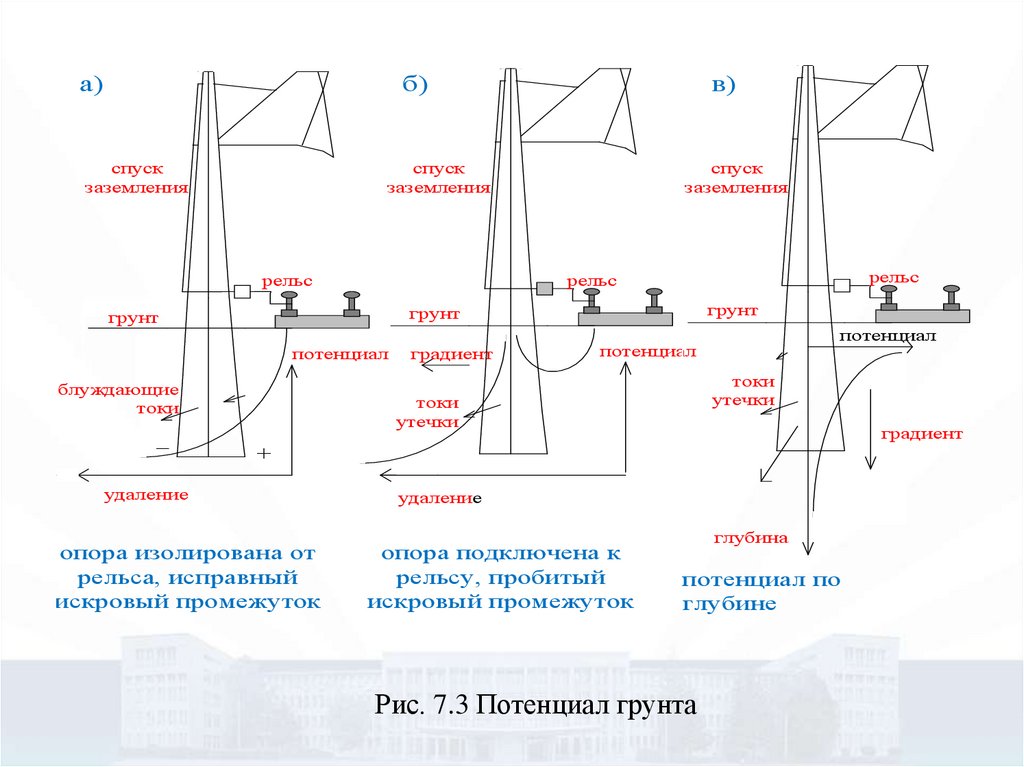
18.

Рассмотрим сначала горизонтальную
плоскость, расположенную на некоторой глубине
залегания
Здесь возможны два крайних случая:
• опора изолирована от рельса, исправный искровой
промежуток (Рис. 7.3, а);
• опора подключена к
промежуток (Рис. 7.3, б).
рельсу,
пробитый
искровой

19.

а)
б)
спуск
заземления
спуск
заземления
рельс
спуск
заземления
рельс
рельс
грунт
грунт
грунт
потенциал
блуждающие
токи
–-
в)
градиент
потенциал
потенциал
токи
утечки
токи
утечки
градиент
+
удаление
опора изолирована от
рельса, исправный
искровый промежуток
удаление
опора подключена к
рельсу, пробитый
искровый промежуток
глубина
потенциал по
глубине
Рис. 7.3 Потенциал грунта

20.

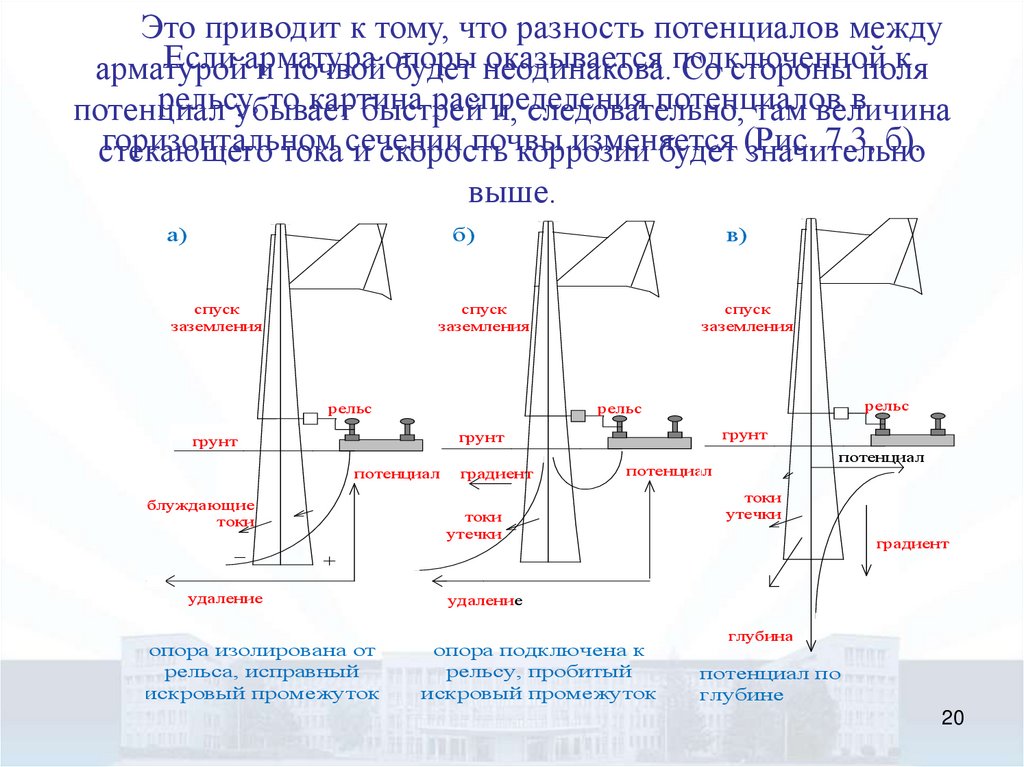
Это приводит к тому, что разность потенциалов между
Если арматура
оказывается подключенной
к
арматурой
и почвойопоры
будет неодинакова.
Со стороны поля
рельсу,
то картина
распределения
потенциалов
в
потенциал
убывает
быстрей
и, следовательно,
там величина
горизонтальном
почвы
изменяется
7.3, б).
стекающего
тока сечении
и скорость
коррозии
будет (Рис.
значительно
выше.
а)
б)
спуск
заземления
спуск
заземления
рельс
спуск
заземления
рельс
рельс
грунт
грунт
грунт
потенциал
блуждающие
токи
–-
в)
градиент
потенциал
потенциал
токи
утечки
токи
утечки
градиент
+
удаление
опора изолирована от
рельса, исправный
искровый промежуток
удаление
опора подключена к
рельсу, пробитый
искровый промежуток
глубина
потенциал по
глубине
20

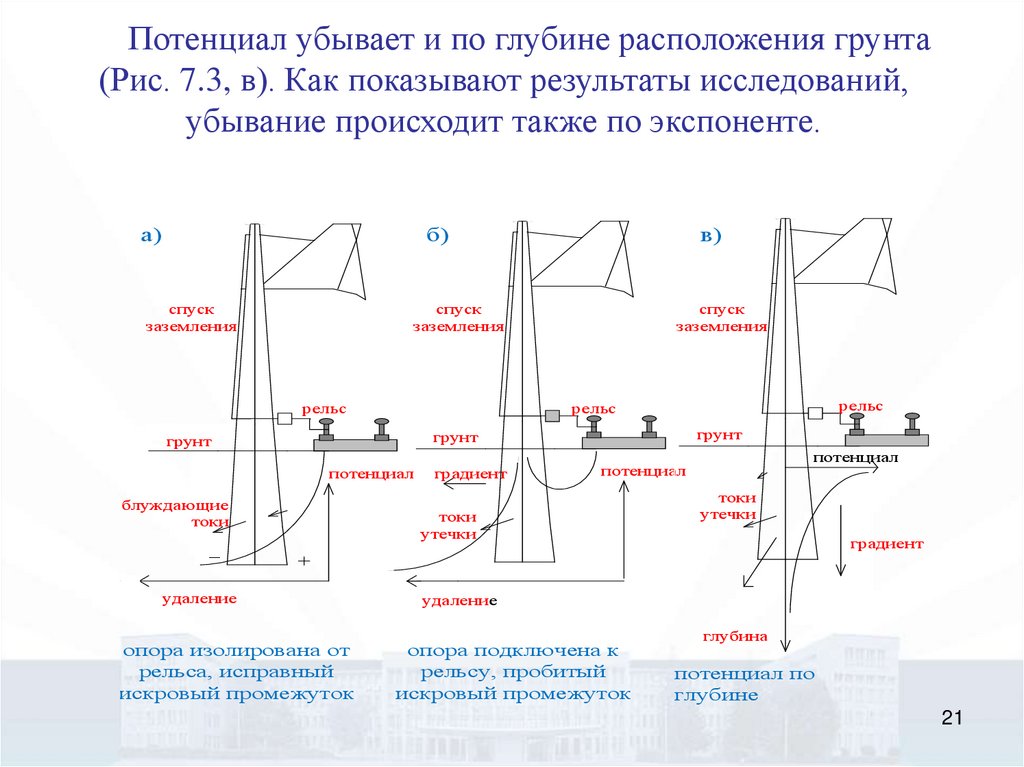
21.

Потенциал убывает и по глубине расположения грунта
(Рис. 7.3, в). Как показывают результаты исследований,
убывание происходит также по экспоненте.
а)
б)
спуск
заземления
спуск
заземления
рельс
спуск
заземления
рельс
рельс
грунт
грунт
грунт
потенциал
блуждающие
токи
–-
в)
градиент
потенциал
потенциал
токи
утечки
токи
утечки
градиент
+
удаление
опора изолирована от
рельса, исправный
искровый промежуток
удаление
опора подключена к
рельсу, пробитый
искровый промежуток
глубина
потенциал по
глубине
21

22.

Это подтверждается и на демонтированных опорах –
5 ... 10 см концевой арматуры полностью
прокорродировало.
Хотя коррозия на глубине 3 ... 4 м не представляет
особой опасности, подобный эффект может влиять и на
верхние части опоры.

23.

• Все выше указанное требует учета в модели опоры
пространственной протяженности.
• В общем виде модель опоры, как ОД, может быть
представлена записью
Z = Ψ(M, X, Y, Z, А, В, t),
(4.9)
где М - момент от внешних сил;
X,Y,Z - пространственные координаты;
А,В - параметры арматуры и бетона.
Требуемая зависимость может быть представлена
в аналитической или табличной форме.

24.

Другим следствием является требование к СД
определять не только степень коррозии арматуры в
опоре, но, прежде всего, место и размеры
коррозионных повреждений.
Например, наиболее информативной для
промежуточных опор будет определение степени
коррозии арматуры в подземной части с внешней
стороны опоры на глубине 0,3 … 0,6 м.

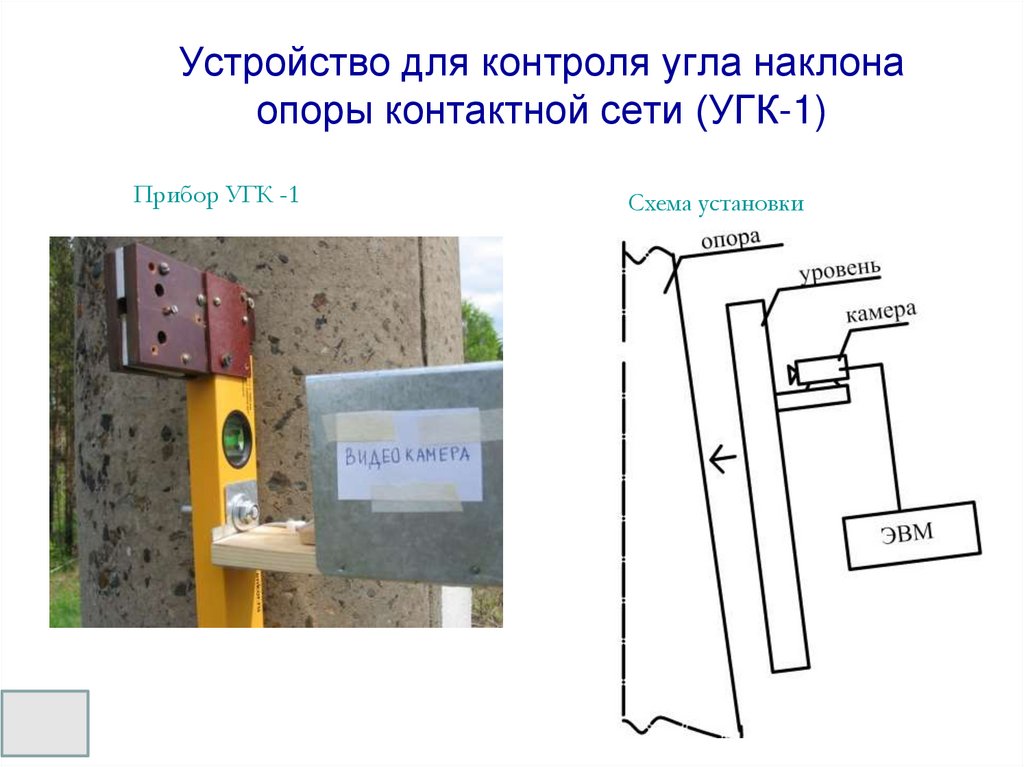
25. Устройство для контроля угла наклона опоры контактной сети (УГК-1)

Прибор УГК -1
Схема установки

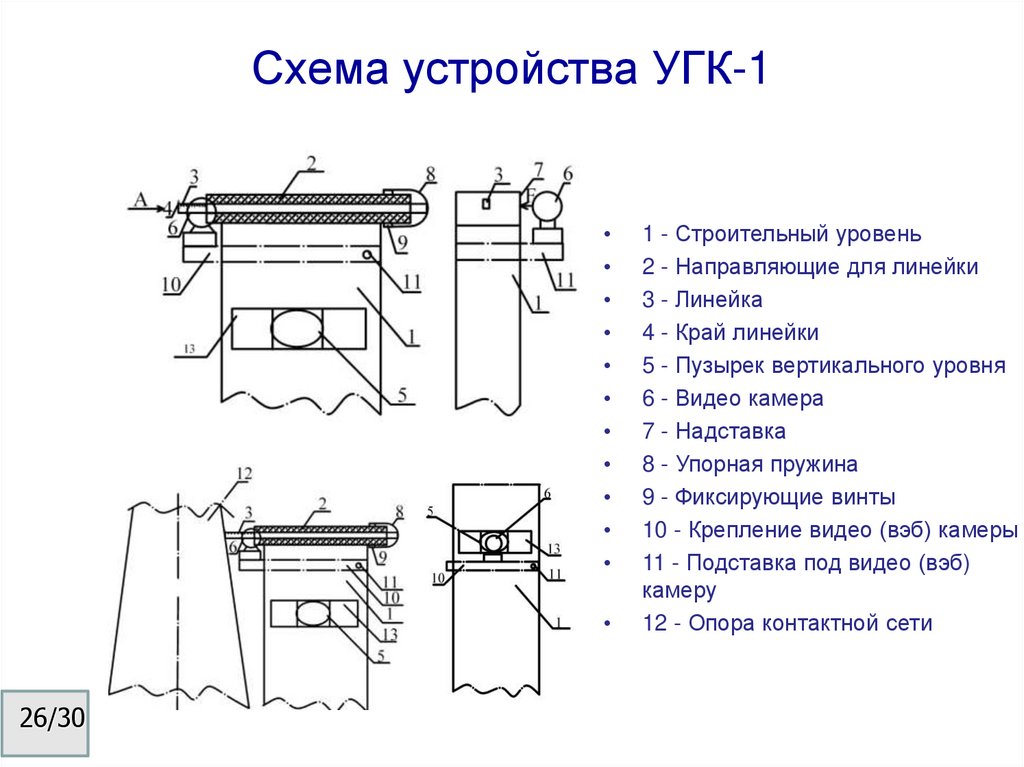
26. Схема устройства УГК-1

26/30
1 - Строительный уровень
2 - Направляющие для линейки
3 - Линейка
4 - Край линейки
5 - Пузырек вертикального уровня
6 - Видео камера
7 - Надставка
8 - Упорная пружина
9 - Фиксирующие винты
10 - Крепление видео (вэб) камеры
11 - Подставка под видео (вэб)
камеру
12 - Опора контактной сети

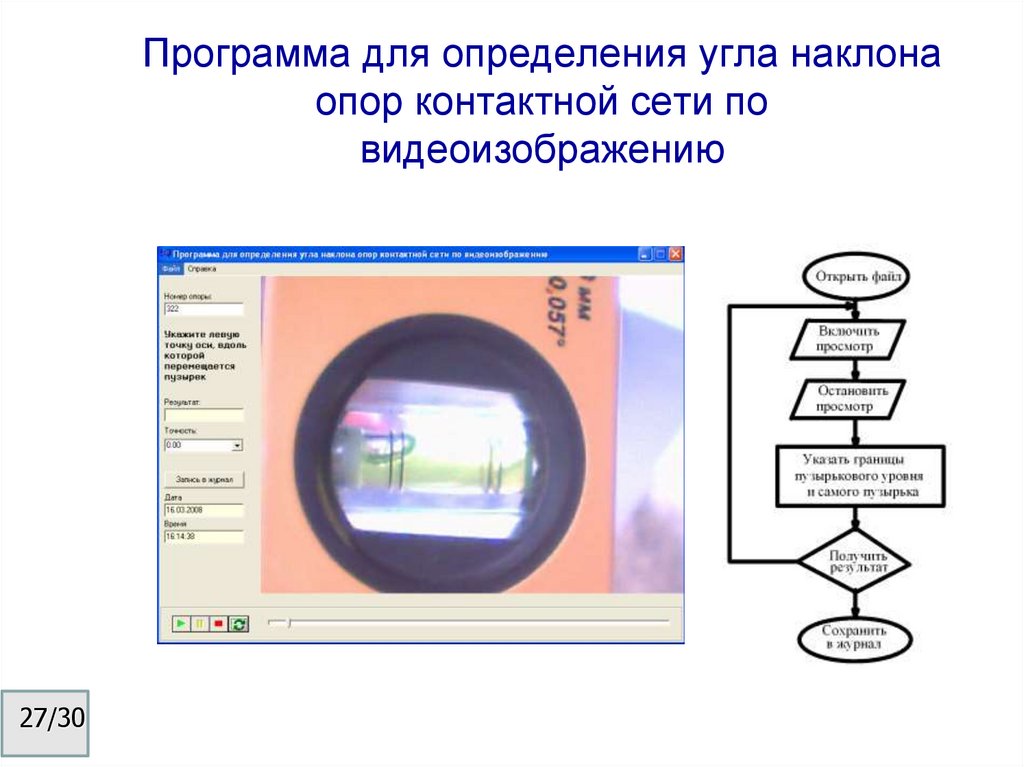
27. Программа для определения угла наклона опор контактной сети по видеоизображению

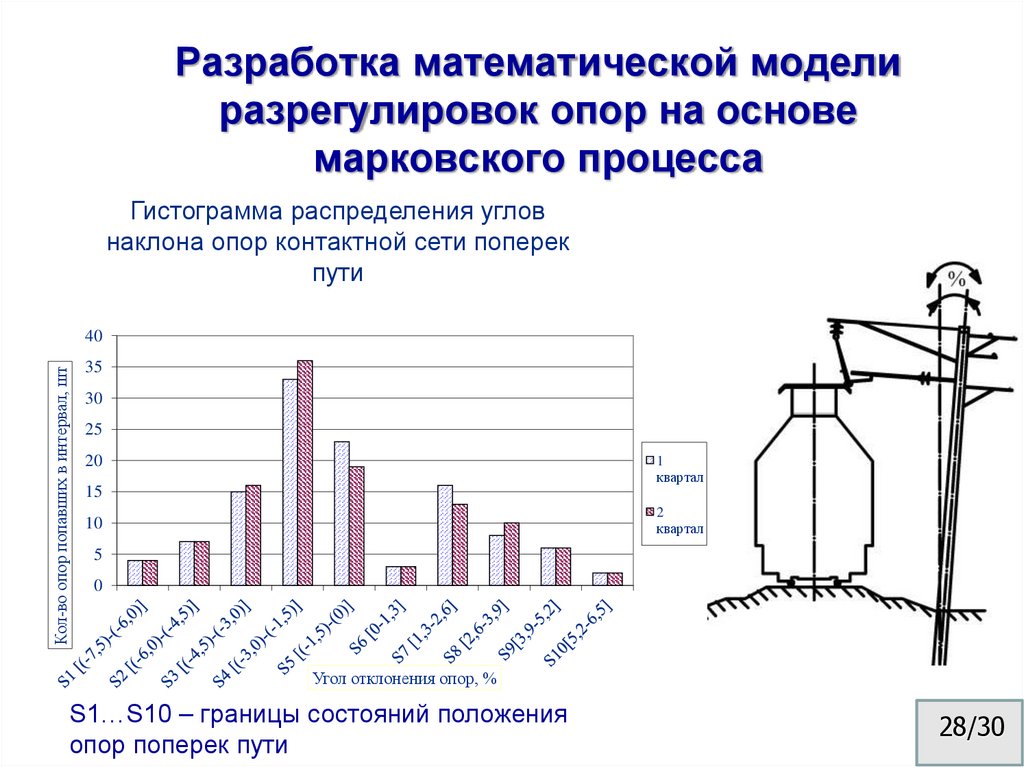
27/30

28. Разработка математической модели разрегулировок опор на основе марковского процесса

Гистограмма распределения углов
наклона опор контактной сети поперек
пути
Кол-во опор попавших в интервал, шт
40
35
30
25
20
1
квартал
15
2
квартал
10
5
0
Угол отклонения опор, %
S1…S10 – границы состояний положения
опор поперек пути
28/30

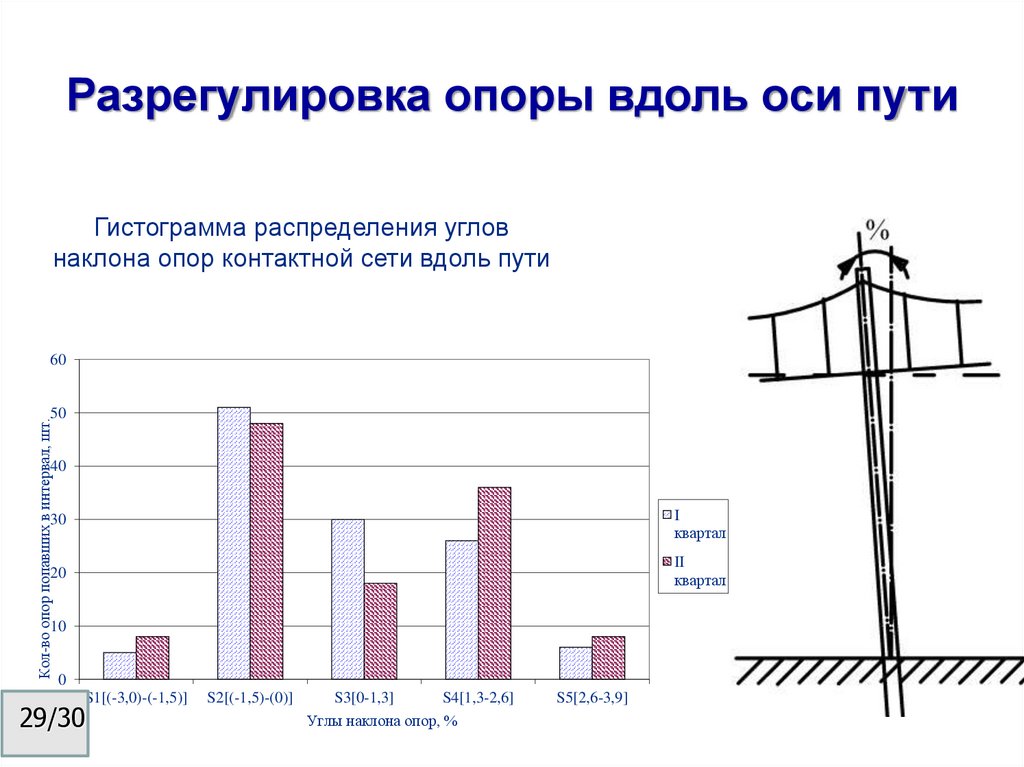
29. Разрегулировка опоры вдоль оси пути

Гистограмма распределения углов
наклона опор контактной сети вдоль пути
60
Кол-во опор попавших в интервал, шт.
50
40
30
I
квартал
20
II
квартал
10
0
S1[(-3,0)-(-1,5)]
29/30
S2[(-1,5)-(0)]
S3[0-1,3]
S4[1,3-2,6]
Углы наклона опор, %
S5[2,6-3,9]

30.

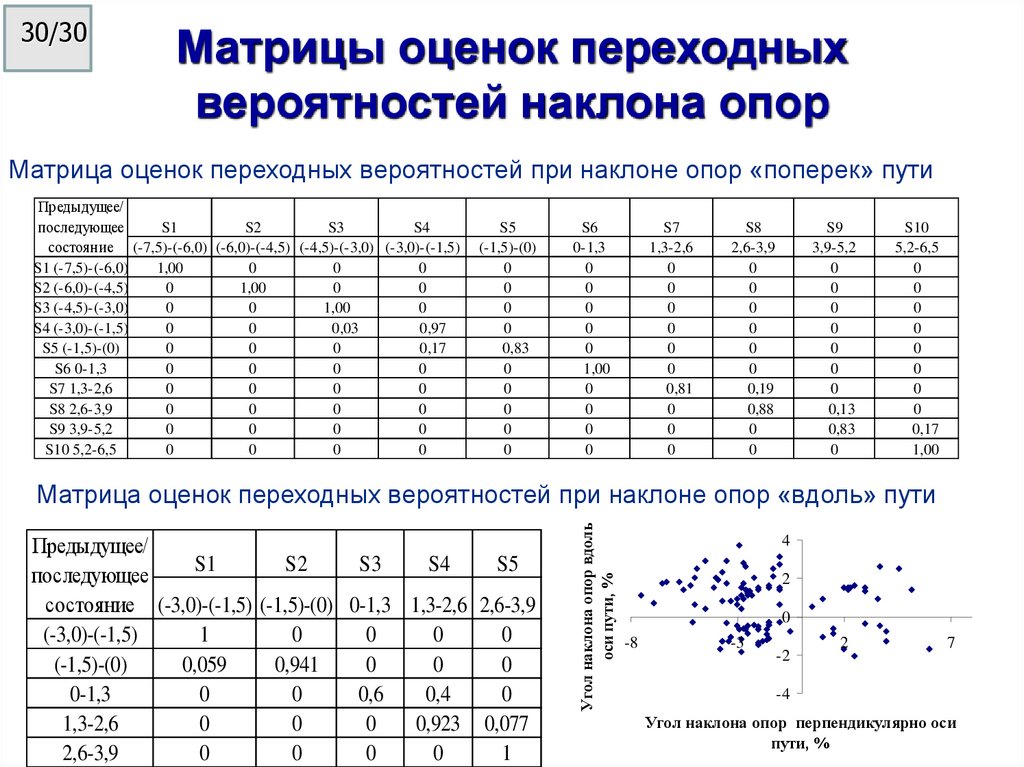
30/30
Матрицы оценок переходных
вероятностей наклона опор
Матрица оценок переходных вероятностей при наклоне опор «поперек» пути
Предыдущее/
последующее
S1
S2
S3
S4
состояние (-7,5)-(-6,0) (-6,0)-(-4,5) (-4,5)-(-3,0) (-3,0)-(-1,5)
S1 (-7,5)-(-6,0)
1,00
0
0
0
S2 (-6,0)-(-4,5)
0
1,00
0
0
S3 (-4,5)-(-3,0)
0
0
1,00
0
S4 (-3,0)-(-1,5)
0
0
0,03
0,97
S5 (-1,5)-(0)
0
0
0
0,17
S6 0-1,3
0
0
0
0
S7 1,3-2,6
0
0
0
0
S8 2,6-3,9
0
0
0
0
S9 3,9-5,2
0
0
0
0
S10 5,2-6,5
0
0
0
0
S5
(-1,5)-(0)
0
0
0
0
0,83
0
0
0
0
0
S6
0-1,3
0
0
0
0
0
1,00
0
0
0
0
S7
1,3-2,6
0
0
0
0
0
0
0,81
0
0
0
S8
2,6-3,9
0
0
0
0
0
0
0,19
0,88
0
0
S9
3,9-5,2
0
0
0
0
0
0
0
0,13
0,83
0
S10
5,2-6,5
0
0
0
0
0
0
0
0
0,17
1,00
Предыдущее/
S1
S2
S3
S4
S5
последующее
состояние (-3,0)-(-1,5) (-1,5)-(0) 0-1,3 1,3-2,6 2,6-3,9
(-3,0)-(-1,5)
1
0
0
0
0
(-1,5)-(0)
0,059
0,941
0
0
0
0-1,3
0
0
0,6
0,4
0
1,3-2,6
0
0
0
0,923 0,077
2,6-3,9
0
0
0
0
1
Угол наклона опор вдоль
оси пути, %
Матрица оценок переходных вероятностей при наклоне опор «вдоль» пути
4
2
0
-8
-3
-2
2
7
-4
Угол наклона опор перпендикулярно оси
пути, %

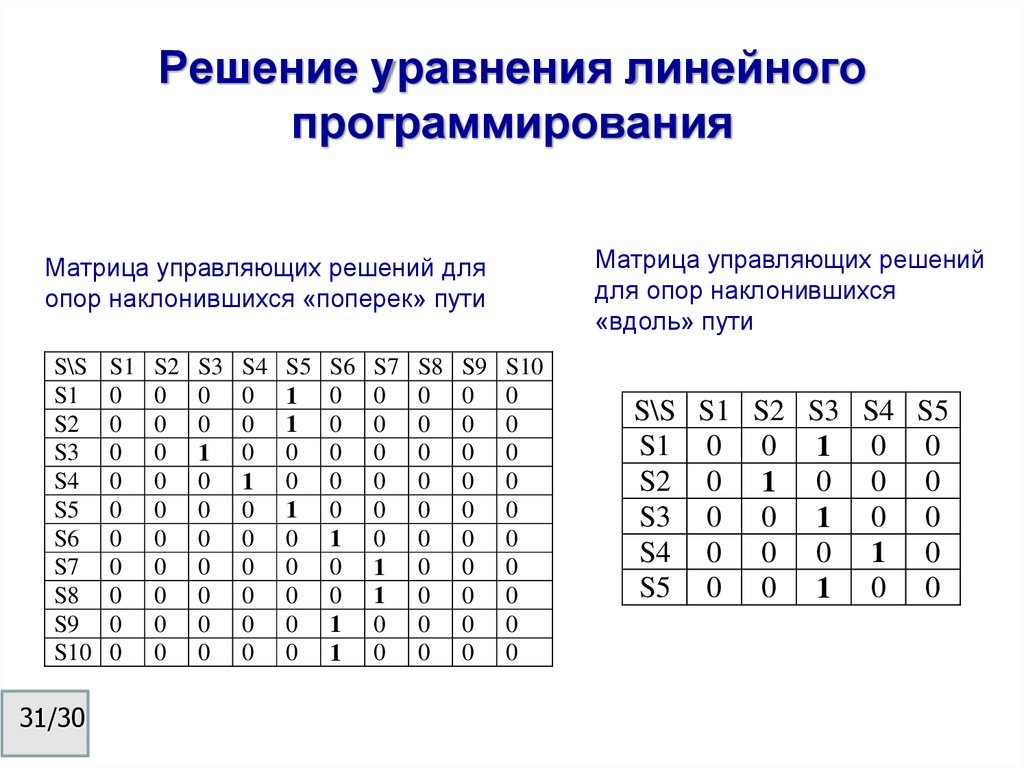
31. Решение уравнения линейного программирования

Матрица управляющих решений
для опор наклонившихся
«вдоль» пути
Матрица управляющих решений для
опор наклонившихся «поперек» пути
S\S
S1
S2
S3
S4
S5
S6
S7
S8
S9
S10
31/30
S1
0
0
0
0
0
0
0
0
0
0
S2
0
0
0
0
0
0
0
0
0
0
S3
0
0
1
0
0
0
0
0
0
0
S4
0
0
0
1
0
0
0
0
0
0
S5
1
1
0
0
1
0
0
0
0
0
S6
0
0
0
0
0
1
0
0
1
1
S7
0
0
0
0
0
0
1
1
0
0
S8
0
0
0
0
0
0
0
0
0
0
S9
0
0
0
0
0
0
0
0
0
0
S10
0
0
0
0
0
0
0
0
0
0
S\S S1 S2 S3 S4 S5
S1 0 0 1 0 0
S2 0 1 0 0 0
S3 0 0 1 0 0
S4 0 0 0 1 0
S5 0 0 1 0 0

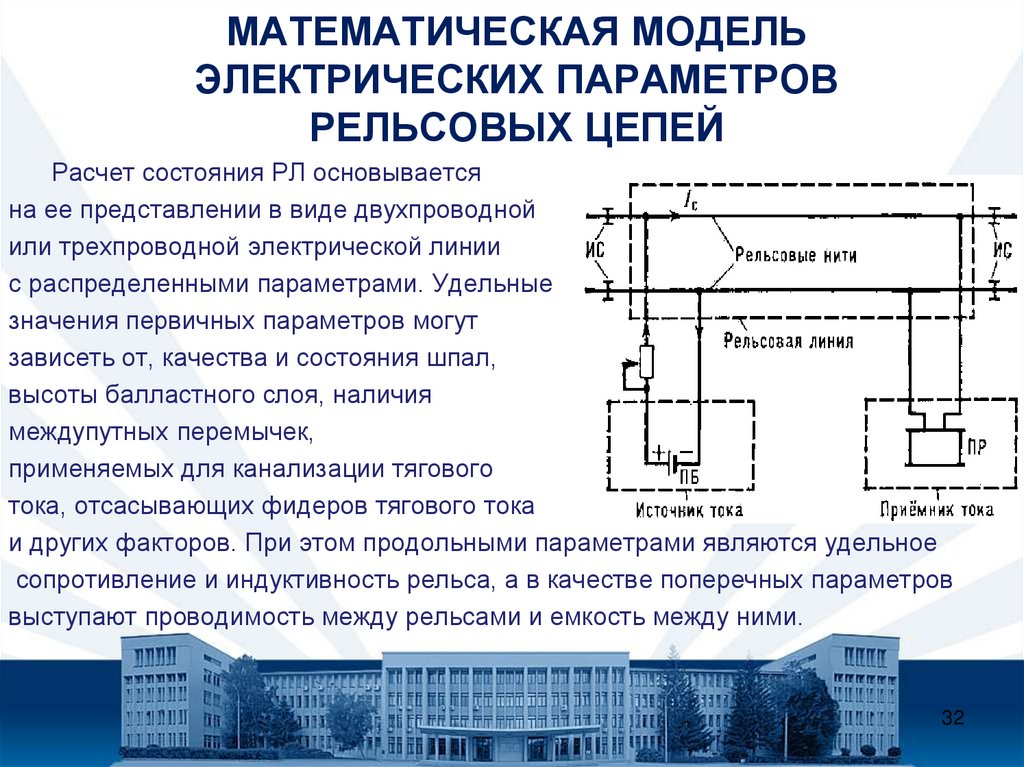
32. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ЭЛЕКТРИЧЕСКИХ ПАРАМЕТРОВ РЕЛЬСОВЫХ ЦЕПЕЙ

Расчет состояния РЛ основывается
на ее представлении в виде двухпроводной
или трехпроводной электрической линии
с распределенными параметрами. Удельные
значения первичных параметров могут
зависеть от, качества и состояния шпал,
высоты балластного слоя, наличия
междупутных перемычек,
применяемых для канализации тягового
тока, отсасывающих фидеров тягового тока
и других факторов. При этом продольными параметрами являются удельное
сопротивление и индуктивность рельса, а в качестве поперечных параметров
выступают проводимость между рельсами и емкость между ними.
32

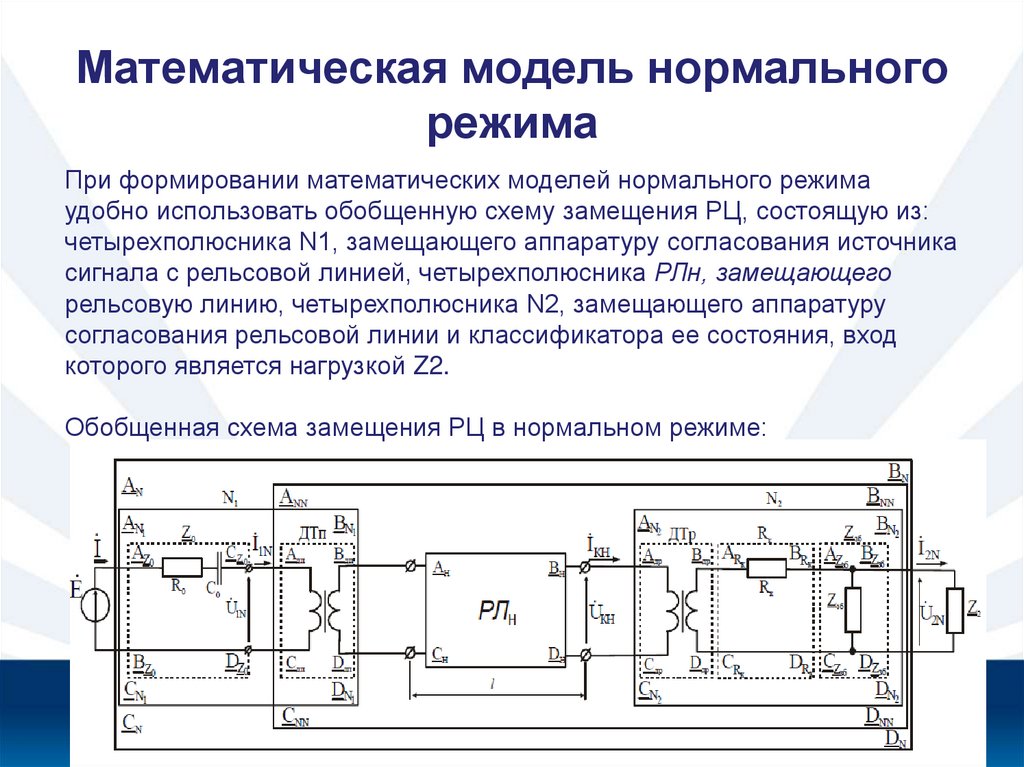
33. Математическая модель нормального режима

При формировании математических моделей нормального режима
удобно использовать обобщенную схему замещения РЦ, состоящую из:
четырехполюсника N1, замещающего аппаратуру согласования источника
сигнала с рельсовой линией, четырехполюсника РЛн, замещающего
рельсовую линию, четырехполюсника N2, замещающего аппаратуру
согласования рельсовой линии и классификатора ее состояния, вход
которого является нагрузкой Z2.
Обобщенная схема замещения РЦ в нормальном режиме:
33

34.

В расчетах всех классов состояний коэффициенты четырехполюсников
N1 и N2, определяемые с учетом схемы и параметров элементов
представленных в работе [3], остаются неизменными, и их параметры
являются константами.
Коэффициенты четырехполюсника N1 определяются как произведение
двух матриц
где AДП , BДП , CДП , DДП - коэффициенты дроссель трансформатора
питающего конца РЦ ДТп, которые представлены в [3], Zo комплексное
сопротивление ограничителя, образованного активным сопротивлением
ограничителя R0 и емкостью C0.
34

35.

Коэффициенты четырехполюсника N2 определяются
где AДр , BДр ,CДр ,DДр - коэффициенты дроссель трансформатора
релейного конца РЦ ДТр, которые представлены в работе [3], Rк –
сопротивление кабеля между дроссель – трансформатором ДТр и нагрузкой
Z2, Zзб - комплексное сопротивление защитного блока ЗБФ.
Матрица коэффициентов обобщенного четырехполюсника РЦ имеет
Вид
35

36.

• С учетом уравнений выше, коэффициенты матрицы принимают вид
• Связь напряжения U вх и тока Iвх на входе каждого из
четырехполюсников N1, РЛН, N2, NN с напряжением U вых и током Iвых
на их выходах удобно выразить с помощью уравнений следующего
вида
36

37.

Для обобщенного четырехполюсника рельсовой цепи для класса образов
нормального режима уравнения имеют вид
где E и I - напряжение и ток на входе обобщенного четырехполюсника
N,U2N и I2N - напряжение и ток на нагрузке обобщенного
четырехполюсника N.
Z2 - комплексное сопротивление нагрузки (входной импеданс
классификатора состояний), подключенного к выходу четырехполюсника
N, получим уравнение, описывающее напряжение и его фазу на нагрузке
РЦ, для класса образов нормального режима
37

38.

Связь напряжения U1N и тока I1N на входе четырехполюсника NN с
напряжением U 2N и током I2N на его выходе описывается системой
уравнений вида
38

39.

Из системы уравнений выше,напряжение U& 1N и ток &I1N на входе
рельсовой линии, находящейся в классе образов нормального режима,
определятся следующими выражениями.
Уравнения являются математическими моделями информативных
признаков нормального режима
39