Модель принятия решений. Модель объекта

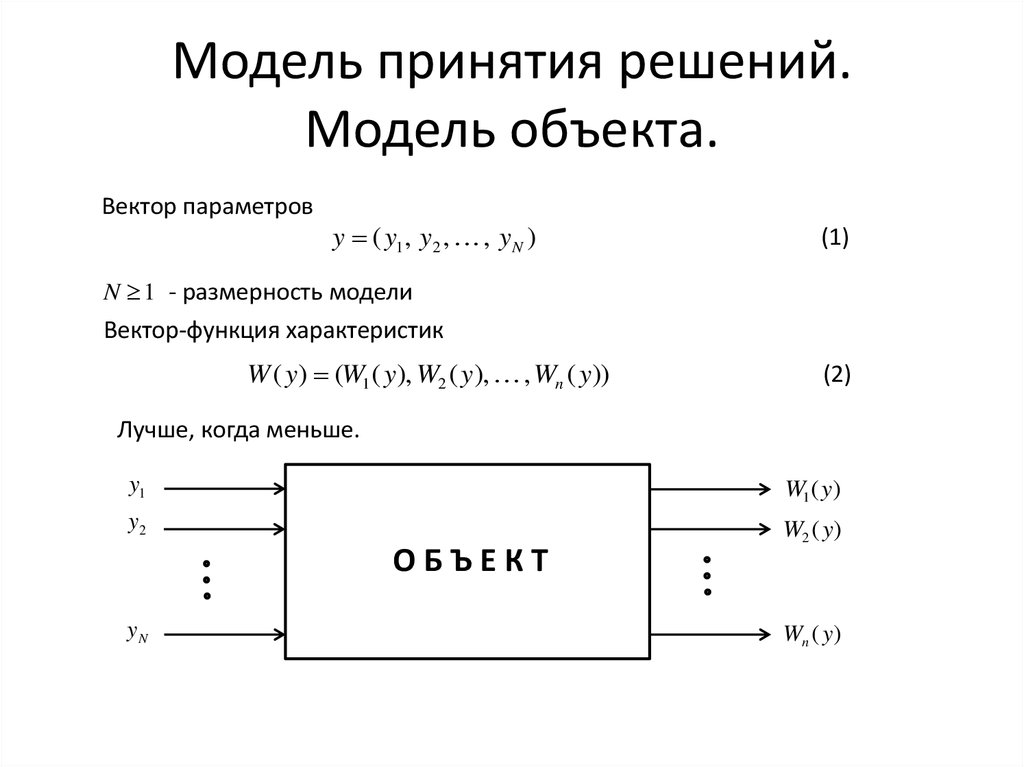
1. Модель принятия решений. Модель объекта.

Вектор параметров
y ( y1 , y2 , , y N )
(1)
N 1 - размерность модели
Вектор-функция характеристик
W ( y) (W1 ( y), W2 ( y), , Wn ( y))
(2)
Лучше, когда меньше.
y1
W1 ( y)
y2
W2 ( y)
ОБЪЕКТ
yN
Wn ( y )

2. Модель принятия решений. Координатные ограничения.

Координаты вектора y ( y1 , y2 , , y N ) изменяются в заданных
пределах, определяемых векторами начала и конца
a (a1 , a2 , , aN ),
где
ai , bi , 1 i N ,
b (b1 , b2 , , bN ),
(3)
- константы, причем , возможно
ai и / или bi
Гиперпараллелепипед возможных значений вектора
y
D { y R N : ai yi bi ,1 i N }
(4)

3. Модель принятия решений. Функциональные ограничения.

Задается множество индексов
G { j1 , , jm } {1, 2, , n}
(5)
qi ,1 i m.
Для характеристик W ji ( y ) с номерами ji G ставится условие
непревышения соответствующих допусков qi , т.е. вводятся
и набор допусков
функциональные ограничения
W ji ( y ) qi , ji G.
Определение. Вектор y D, удовлетворяющий неравенствам (6),
называется допустимым вектором (допустимой точкой).
(6)

4. Модель принятия решений. Функциональные ограничения.

Введем обозначения
Тогда
g i ( y ) W ji ( y ) qi , 1 i m,
(7)
gi ( y) 0, 1 i m.
(8)
Допустимая область
Q { y D : gi ( y) 0, 1 i m}.
Если
m 0
, то Q D .
(9)

5. Модель принятия решений. Частичная вычислимость.

Введем семейство вложенных множеств
Q1 D, Qi 1 { y Qi : gi ( y) 0}
(10)
Очевидно, что
Qm 1 Q и Qm 1 Qm Q2 Q1 D .
Определение. Ограничения (7) называются полностью вычислимыми,
если все функции
множестве
gi ( y), 1 i m, определены и вычислимы в
D.
Определение. Ограничения (7) называются частично-вычислимыми,
если каждая функция
gi ( y), 1 i m, определена и вычислима в
соответствующем множестве
Qi .

6. Модель принятия решений. Векторный критерий эффективности.

Зададим множество индексов
F {i1 , i2 , , ik } {1, 2, , n}
(11)
и введем вектор-функцию
f ( y) ( f1 ( y), , f k ( y)),
(12)
где
f s ( y ) Wis ( y ), is F .
(13)
Вектор-функция (12) называется векторным критерием эффективности.
В модели с частичной вычислимостью все частные критерии f s ( y),1 s k ,
могут быть определены только в области Qm 1 Q.
В общем случае допускается
G F .

7. Модель принятия решений. Оптимальность решения.

Решение оптимизационной задачи
f ( y ) min, y Q,
(14)
принимается в качестве оптимального решения в рамках сформированной
модели.

8. Модель принятия решений. Консервная банка.

r
h
y ( r , h)
r 0, h 0
V r 2h
S 2 r 2 2 rh
L 4 r h
V const
V
r2
S 2 r 2 2V / r
h
L 4 r V / r 2

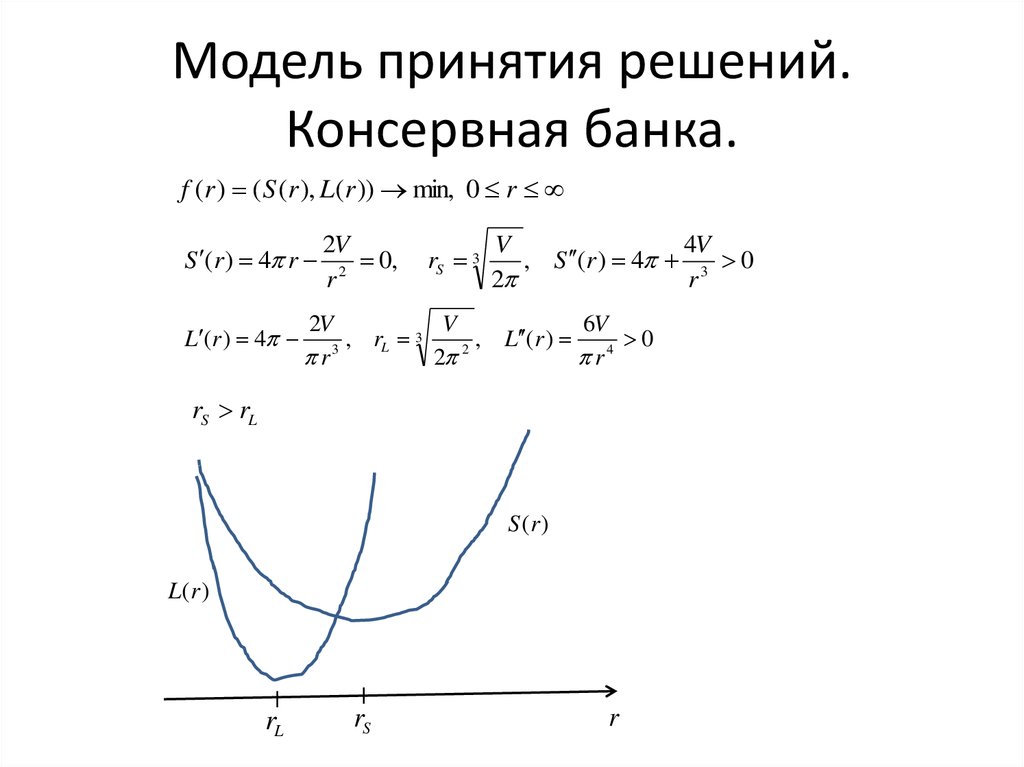
9. Модель принятия решений. Консервная банка.

f (r ) ( S (r ), L(r )) min, 0 r
S (r ) 4 r
L (r ) 4
2V
0,
r2
rS 3
V
4V
, S (r ) 4 3 0
2
r
2V
V
6V
3
,
r
,
L
(
r
)
0
L
3
2
4
r
2
r
rS rL
S (r )
L(r )
rL
rS
r

10. Модель принятия решений. Оптимальное решение

f ( y) min, y Q R N
f ( y) ( f1 ( y), , f k ( y)),
Q { y D : gi ( y) 0, 1 i m}.
D { y R N : ai yi bi ,1 i N }
Что является оптимальным решением в случае противоречивости
частных критериев?

11. Модель принятия решений. Оптимальное решение

Определение 1. Точка x Q доминирует точку y Q ( x y ) , если
i,1 i k ,
f i ( x) f i ( y )
(сильное доминирование).
Определение 2. Точка x Q доминирует точку y Q ( x y ) , если
i,1 i k , f i ( x) f i ( y)
и существует номер j , 1 j k , такой, что f j ( x) f j ( y )
(слабое доминирование).

12. Модель принятия решений. Паретовское оптимальное решение.

*
*
Определение 3. Точка y Q и соответствующий ей вектор f ( y )
называются эффективными (неулучшаемыми, оптимальными по Парето),
Если y Q из условий
f i ( y ) f i ( y * ), 1 i k ,
следует, что
f ( y) f ( y* ) .
y * оптимальна по Парето, если ее нельзя улучшить в Q ни по одному
частному критерию.
Оптимальное решение – множество P всех паретовских точек.

13. Модель принятия решений. Слейтеровское оптимальное решение.

~
Определение 4. Точка y Q называется слабо эффективной (оптимальной
по Слейтеру, слейтеровской точкой), если не существует x Q такой, что
f i ( x) f i ( ~
y ), 1 i k ,
(т.е. не существует доминатора в смысле Определения 1).
Оптимальное решение – множество S всех слейтеровских точек.
Очевидно, что P S .

14. Метод главного критерия

f ( y ) min, y Q R N
f ( y ) ( f1 ( y ), f 2 ( y ), , f k ( y ))
Q1* { y1* Q : f1 ( y1* ) min f1 ( y)}
y Q
Q2* { y2* Q1* : f 2 ( y2* ) min* f 2 ( y )}
y Q1
. . . . .
Qk* { yk* Qk* 1 : f k ( yk* ) min* f k ( y )}
y Qk 1

15. Метод сверток. Линейная свертка.

f ( y ) min, y Q R N
f ( y ) ( f1 ( y ), f 2 ( y ), , f k ( y ))
k
Вектор весов
( 1 , , k ), i 0, 1 i k , i 1
k
Линейная свертка
( y ) i f i ( y )
i 1
Рассмотрим задачу
( y ) min, y Q
i 1

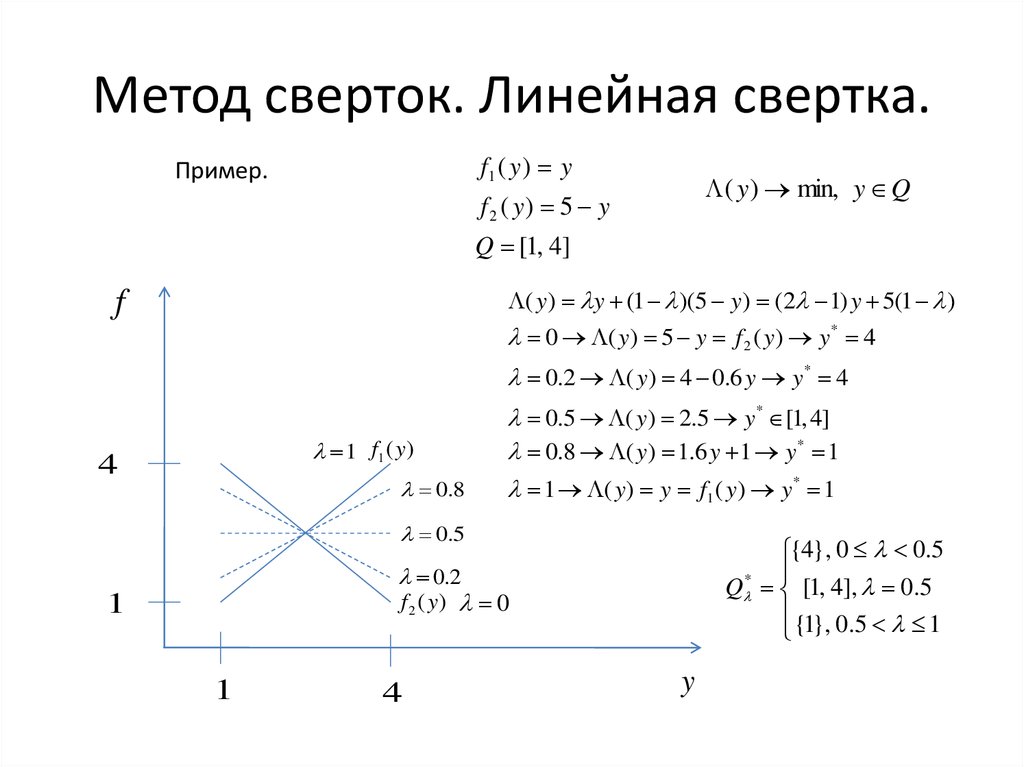
16. Метод сверток. Линейная свертка.

f1 ( y ) y
Пример.
( y ) min, y Q
f 2 ( y) 5 y
Q [1, 4]
( y ) y (1 )(5 y ) (2 1) y 5(1 )
f
0 ( y ) 5 y f 2 ( y ) y * 4
0.2 ( y) 4 0.6 y y* 4
1 f1 ( y)
4
0.8
0.5 ( y) 2.5 y* [1, 4]
0.8 ( y) 1.6 y 1 y* 1
1 ( y) y f1 ( y) y* 1
0.5
{4}, 0 0.5
Q * [1, 4], 0.5
{1}, 0.5 1
0.2
f 2 ( y) 0
1
1
4
y

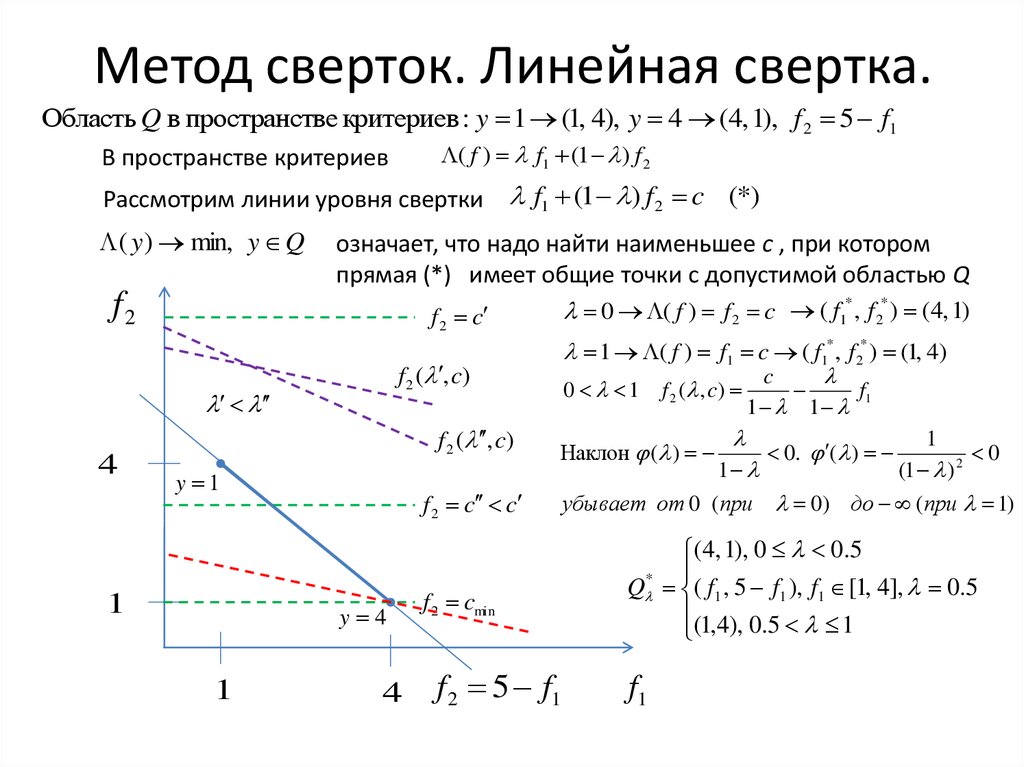
17. Метод сверток. Линейная свертка.

Область Q в пространстве критериев : y 1 (1, 4), y 4 (4, 1), f 2 5 f1
( f ) f1 (1 ) f 2
В пространстве критериев
Рассмотрим линии уровня свертки f1 (1 ) f 2 c (*)
( y ) min, y Q
f2
означает, что надо найти наименьшее c , при котором
прямая (*) имеет общие точки с допустимой областью Q
0 ( f ) f 2 c ( f1* , f 2* ) (4, 1)
f 2 c
f 2 ( , c)
4
f 2 ( , c)
y 1
1
0 1
4
f 2 ( , c )
f 2 cmin
f 2 5 f1
c
f1
1 1
1
0
1
(1 ) 2
убывает от 0 (при 0) до (при 1)
Наклон ( )
f 2 c c
y 4
1
1 ( f ) f1 c ( f1* , f 2* ) (1, 4)
0. ( )
(4, 1), 0 0.5
Q * ( f1 , 5 f1 ), f1 [1, 4], 0.5
(1,4), 0.5 1
f1

18. Метод сверток. Линейная свертка.

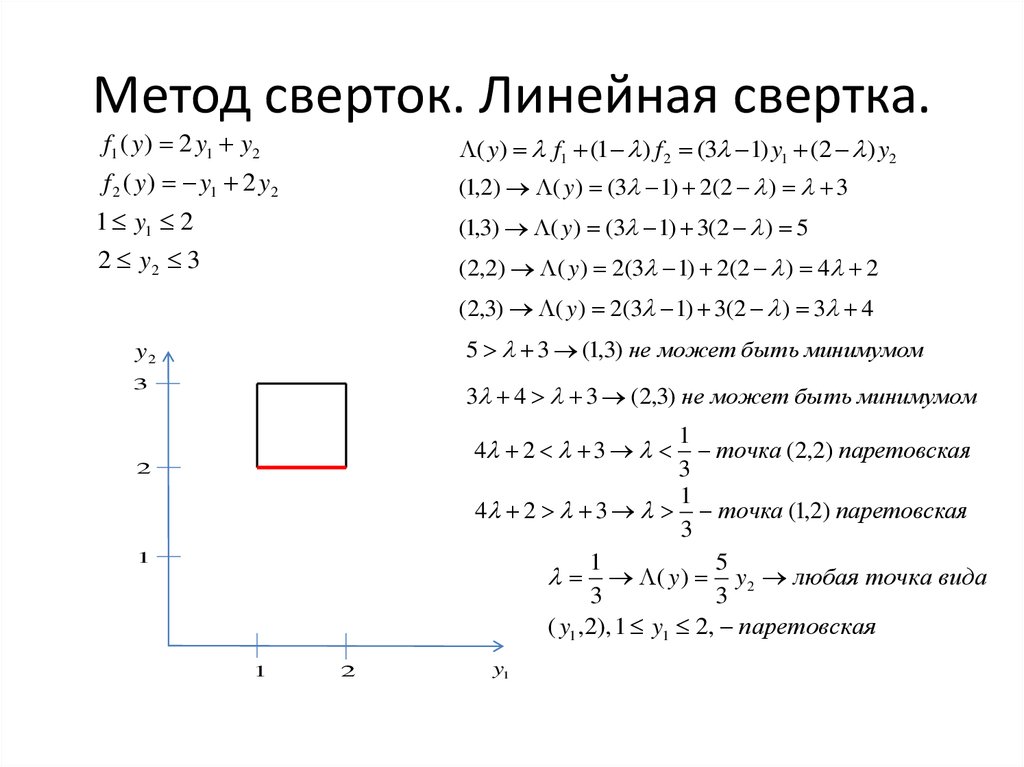
f1 ( y ) 2 y1 y2
( y) f1 (1 ) f 2 (3 1) y1 (2 ) y2
f 2 ( y ) y1 2 y2
(1,2) ( y ) (3 1) 2(2 ) 3
1 y1 2
(1,3) ( y ) (3 1) 3(2 ) 5
2 y2 3
(2,2) ( y ) 2(3 1) 2(2 ) 4 2
(2,3) ( y ) 2(3 1) 3(2 ) 3 4
5 3 (1,3) не может быть минимумом
y2
3
3 4 3 (2,3) не может быть минимумом
1
точка (2,2) паретовская
3
1
4 2 3 точка (1,2) паретовская
3
1
5
( y ) y2 любая точка вида
3
3
( y1 ,2), 1 y1 2, паретовская
4 2 3
2
1
1
2
y1

19. Метод сверток. Линейная свертка.

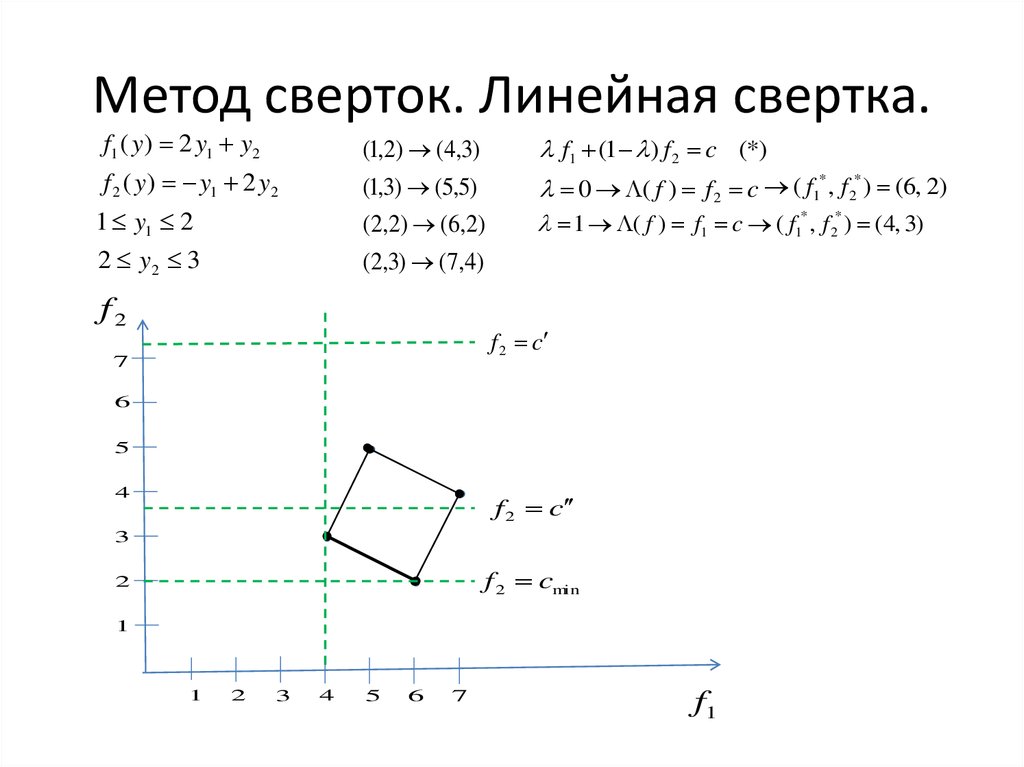
f1 ( y ) 2 y1 y2
(1,2) (4,3)
f 2 ( y ) y1 2 y2
f1 (1 ) f 2 c (*)
(1,3) (5,5)
0 ( f ) f 2 c ( f1 , f 2 ) (6, 2)
1 ( f ) f1 c ( f1* , f 2* ) (4, 3)
*
1 y1 2
(2,2) (6,2)
2 y2 3
(2,3) (7,4)
f2
f 2 c
7
6
5
4
f 2 c
3
f 2 cmin
2
1
1
2
3
4
5
6
7
f1
*

20. Метод сверток. Линейная свертка.

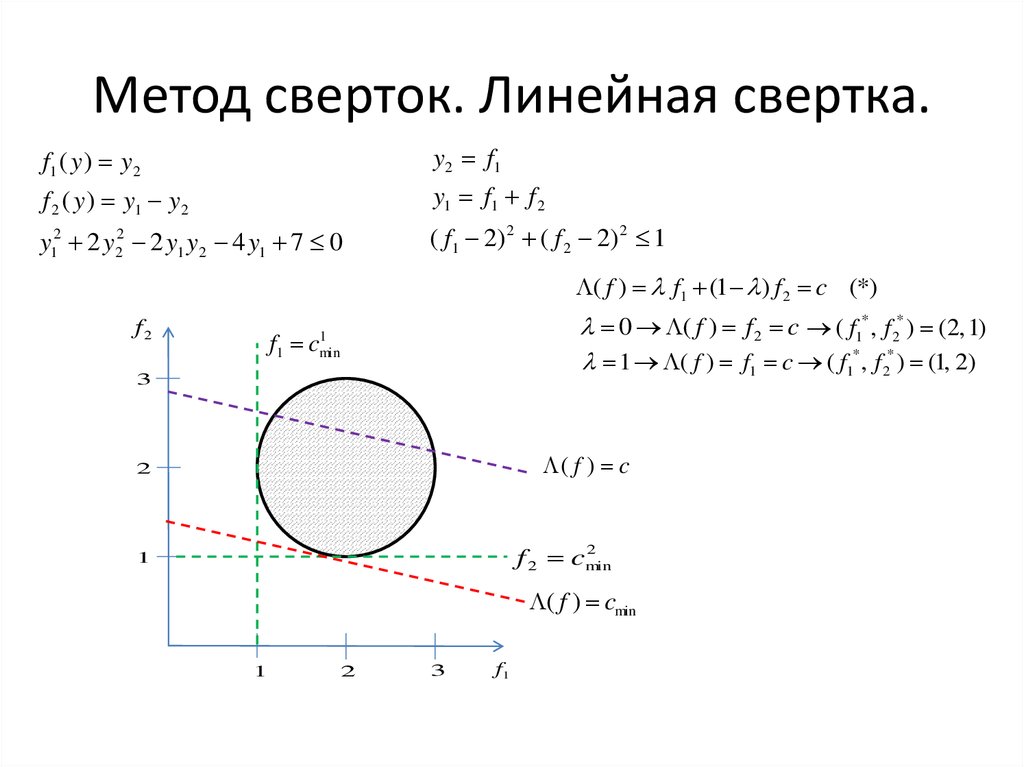
y2 f1
f1 ( y ) y2
f 2 ( y ) y1 y2
y1 f1 f 2
y12 2 y22 2 y1 y2 4 y1 7 0
( f1 2) 2 ( f 2 2) 2 1
( f ) f1 (1 ) f 2 c (*)
f2
0 ( f ) f 2 c ( f1* , f 2* ) (2, 1)
1 ( f ) f1 c ( f1* , f 2* ) (1, 2)
f1 c
1
min
3
( f ) c
2
2
f 2 cm
in
1
( f ) cmin
1
2
3
f1

21. Метод сверток. Линейная свертка.

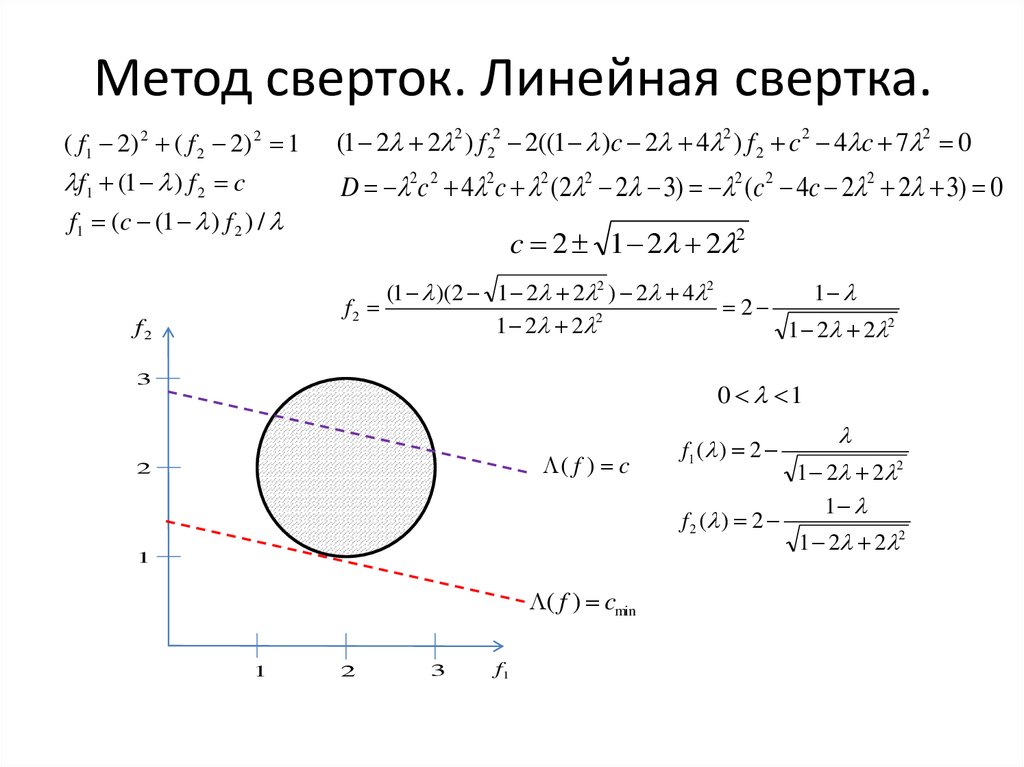
( f1 2) 2 ( f 2 2) 2 1
(1 2 2 2 ) f 22 2((1 )c 2 4 2 ) f 2 c 2 4 c 7 2 0
f1 (1 ) f 2 c
f1 (c (1 ) f 2 ) /
D 2c 2 4 2c 2 (2 2 2 3) 2 (c 2 4c 2 2 2 3) 0
c 2 1 2 2 2
(1 )( 2 1 2 2 2 ) 2 4 2
1
f2
2
1 2 2 2
1 2 2 2
f2
3
0 1
( f ) c
2
f1 ( ) 2
f 2 ( ) 2
1
( f ) cmin
1
2
3
f1
1 2 2 2
1
1 2 2 2

22. Метод сверток. Свертка Гермейера.

f ( y ) min, y Q R N
f ( y ) ( f1 ( y ), f 2 ( y ), , f k ( y ))
k
Вектор весов ( 1 , , k ), i 0, 1 i k , i 1
i 1
Свертка Гермейера ( y ) max i f i ( y )
1 i k
Пусть fi ( y) 0, 1 i k , y Q.
Решение y* ( ) задачи
( y) min, y Q,
является слейтеровским решением
многокритериальной задачи

23. Геометрическая интерпретация свертки Гермейера.

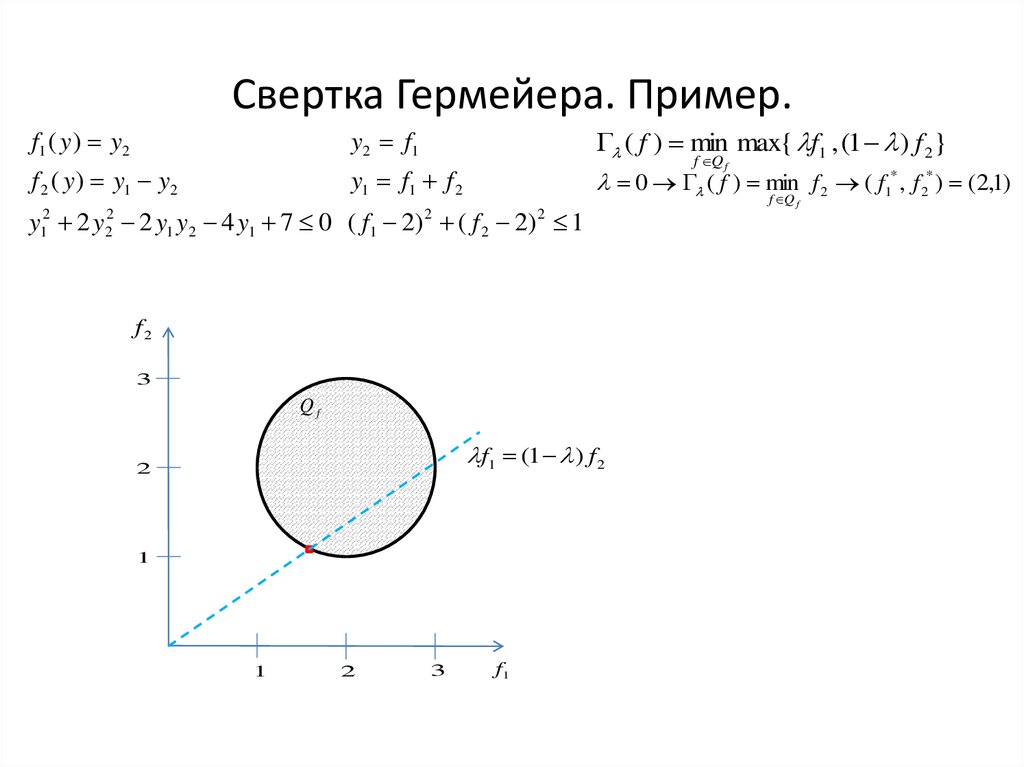
24. Свертка Гермейера. Пример.

f1 ( y ) y2
y2 f1
( f ) min max{ f1 , (1 ) f 2 }
f 2 ( y ) y1 y2
y1 f1 f 2
0 ( f ) min f 2 ( f1* , f 2* ) (2,1)
f Q f
y 2 y 2 y1 y2 4 y1 7 0 ( f1 2) ( f 2 2) 1
2
1
2
2
2
2
f2
3
Qf
f1 (1 ) f 2
2
1
1
2
3
f1
f Q f

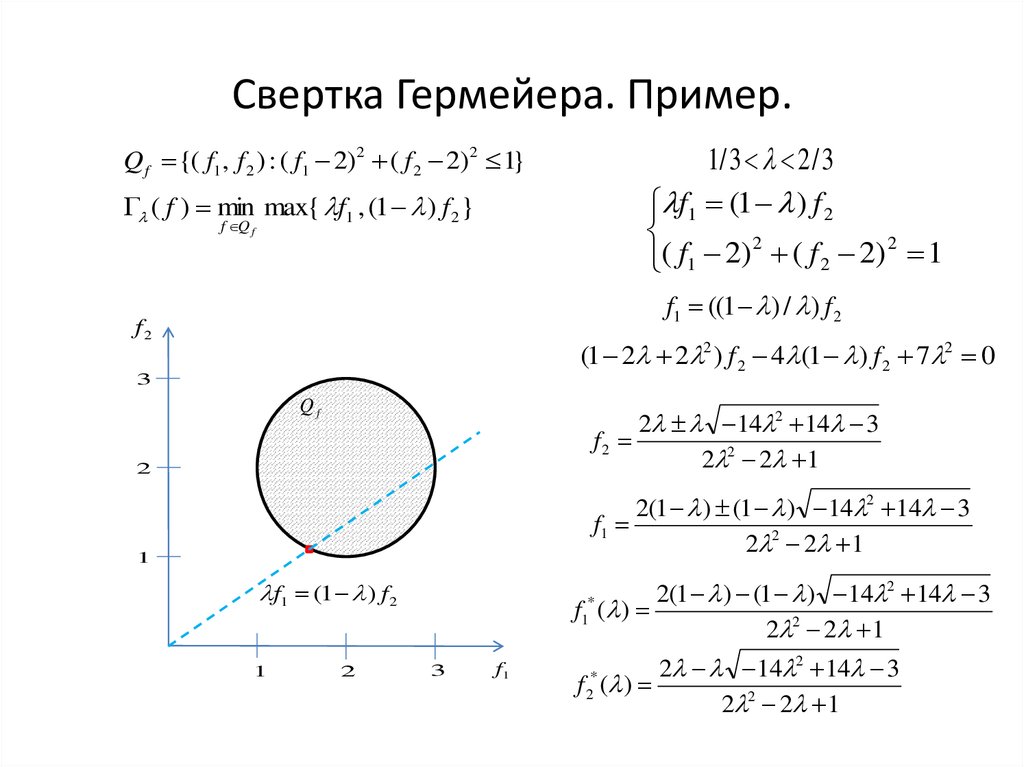
25. Свертка Гермейера. Пример.

1/ 3 2 / 3
f1 (1 ) f 2
2
2
(
f
2
)
(
f
2
)
1
2
1
Q f {( f1 , f 2 ) : ( f1 2)2 ( f 2 2)2 1}
( f ) min max{ f1 , (1 ) f 2 }
f Q f
f1 ((1 ) / ) f 2
f2
(1 2 2 2 ) f 2 4 (1 ) f 2 7 2 0
3
Qf
2 14 2 14 3
f2
2 2 2 1
2
2(1 ) (1 ) 14 2 14 3
f1
2 2 2 1
1
2(1 ) (1 ) 14 2 14 3
f ( )
2 2 2 1
f1 (1 ) f 2
1
2
*
1
3
f1
2 14 2 14 3
f ( )
2 2 2 1
*
2

26. Метод уступок

f ( y ) min, y Q R N
f ( y ) ( f1 ( y ), f 2 ( y ), , f k ( y ))
Упорядочиваем по важности
f1 f 2 f k
f1* min{ f1 ( y) : y Q}
1 0 : f * ( 1 ) min{ f 2 ( y) : y Q, f1 ( y) f1* 1}
2

27. Метод уступок

2 0 : f 3* ( 1 , 2 ) min{ f 3 ( y) : y Q, f1 ( y) f1* 1 ,
f 2 ( y) f 2* ( 1 ) 2 }
.
.
.
.
.
k 1 0 : f k* ( 1 , k 1 ) min{ f k ( y ) : y Q, f1 ( y ) f1* 1 ,
f 2 ( y ) f 2* ( 1 ) 2 ,
. . . . .
f k 1 ( y ) f k* 1 ( 1 , k 2 ) k 1}
y k* - глобальный минимум последней задачи –
Точка
паретовская.

28. Многокритериальные задачи. Примеры.

f1 ( y ) y 2 4 y 5
f 2 ( y) y 1
1 y 4
____________________________________________________________
f1 ( y ) ( y 2 ) 2 1
f 2 ( y ) 2 y 2 8 y 12
1 y 3

29. Многокритериальные задачи. Примеры.

f1 ( y ) 2 y1 y2
f 2 ( y ) y1 2 y2
1 y1 2
2 y2 3