Похожие презентации:
Текстовые задачи по математике
1. Текстовые задачи
2. Определение
Текстовая задача - описание некоторой проблемы илипроблемной ситуации на естественном языке с
требованием дать количественную характеристику того
или иного компонента этой ситуации.
3. Определения
Под моделью (франц. мodèle от лат. мodulus —«мера, аналог, образец») понимается упрощенное
представление о реальном объекте, процессе или
явлении, которое отражает его существенные
свойства.
Процесс построения моделей называется
моделированием, а исходный объект называется при
этом прототипом или оригиналом.
4. Виды моделей
эвристические,графические,
математические модели,
комбинации моделей.
5. Виды моделей
Эвристическое моделирование - анализ содержания задачи,выведения следствий, преобразований, которые могут
привести к отысканию нужного метода решения задачи.
Графическое моделирование предполагает использование при
решении текстовых задач графиков, чертежей, графов и т.д.
Математическое моделирование основывается на
представлении оригинала посредством совокупности
взаимосвязанных математических и формально-логических
выражений. При решении текстовых задач применяются
численные модели, представляющие собой уравнения и
неравенства, системы уравнений и неравенств,
устанавливающие взаимосвязи между значениями величин.
6. Этапы решения задачи
1.2.
3.
4.
Анализ задачи
Поиск плана решения
Решение задачи
Проверка.
7. В процессе решения задачи выделяются три этапа математического моделирования:
I этап - перевод условий задачи на математическийязык (выделяются необходимые для решения данные и
искомые и математическими способами описываются
связи между ними);
II этап - внутримодельное решение (т.е. нахождение
значения выражения, выполнение действий, решение
уравнения);
III этап - интерпретация, т.е. перевод полученного
решения на тот язык, на котором была сформулирована
исходная задача.
8. Методы решения задач
арифметический,алгебраический,
геометрический,
графический,
практический,
логический и др.
9. Арифметический метод
Два мотоциклиста выехали из двух населенныхпунктов навстречу друг другу. Первый ехал со
скоростью 45 км/ч и через 2 ч встретил второго.
Второй мотоциклист ехал до встречи 3 ч. Какова
скорость второго мотоциклиста, если расстояние
между населенными пунктами 216 км?
10.
Два мотоциклиста выехали из двух населенных пунктов навстречу друг другу.Первый ехал со скоростью 45 км/ч и через 2 ч встретил второго. Второй
мотоциклист ехал до встречи 3 ч. Какова скорость второго мотоциклиста, если
расстояние между населенными пунктами 216 км?
1.
2.
3.
45*2=90 (км)
216-90=126 (км)
126:3=42 (км/ч)
11. Алгебраический метод
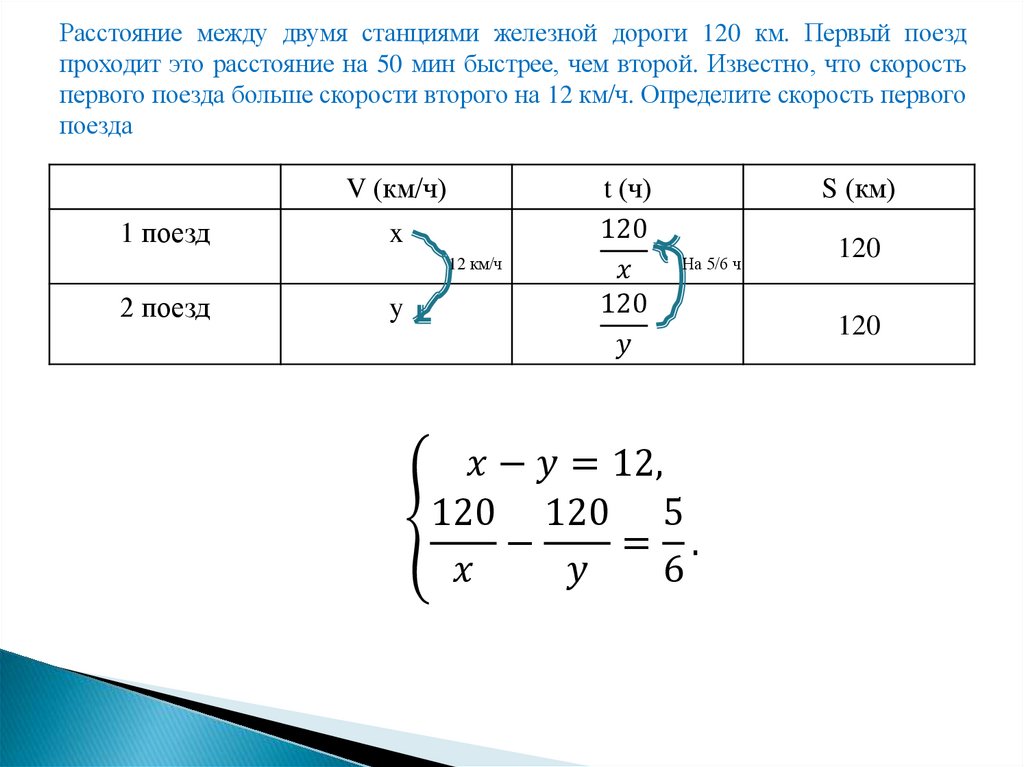
Расстояние между двумя станциями железной дороги120 км. Первый поезд проходит это расстояние на 50
мин быстрее, чем второй. Известно, что скорость
первого поезда больше скорости второго на 12 км/ч.
Определите скорость первого поезда
12.
Расстояние между двумя станциями железной дороги 120 км. Первый поездпроходит это расстояние на 50 мин быстрее, чем второй. Известно, что скорость
первого поезда больше скорости второго на 12 км/ч. Определите скорость первого
поезда
V (км/ч)
1 поезд
x
12 км/ч
2 поезд
y
t (ч)
120













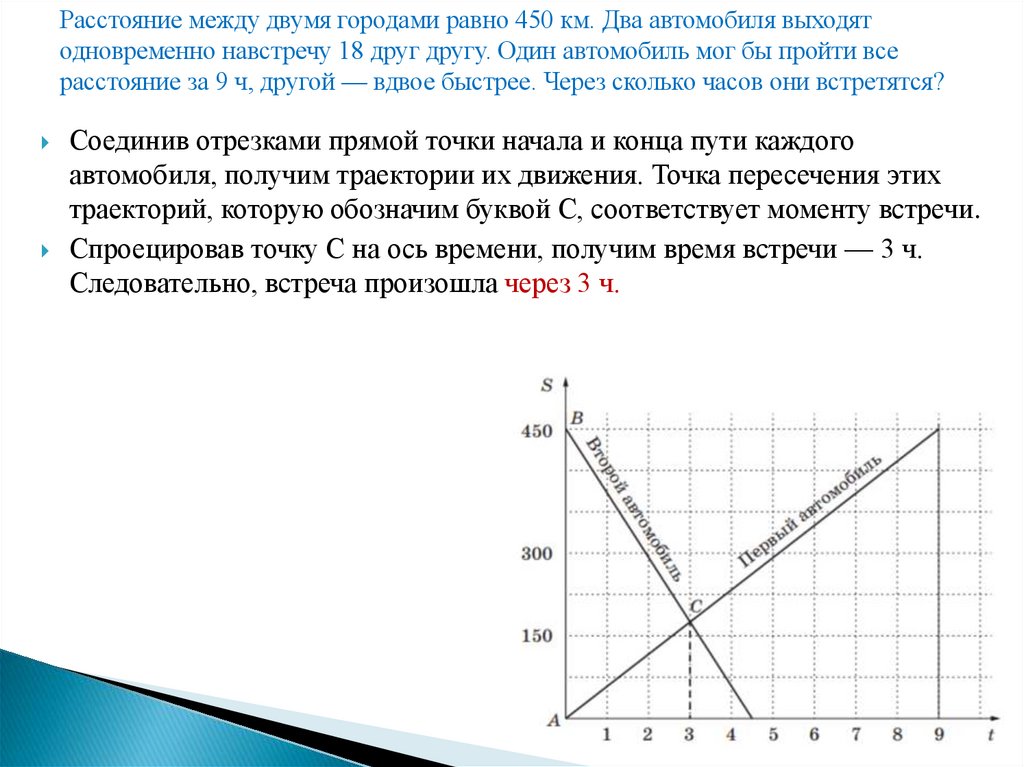

















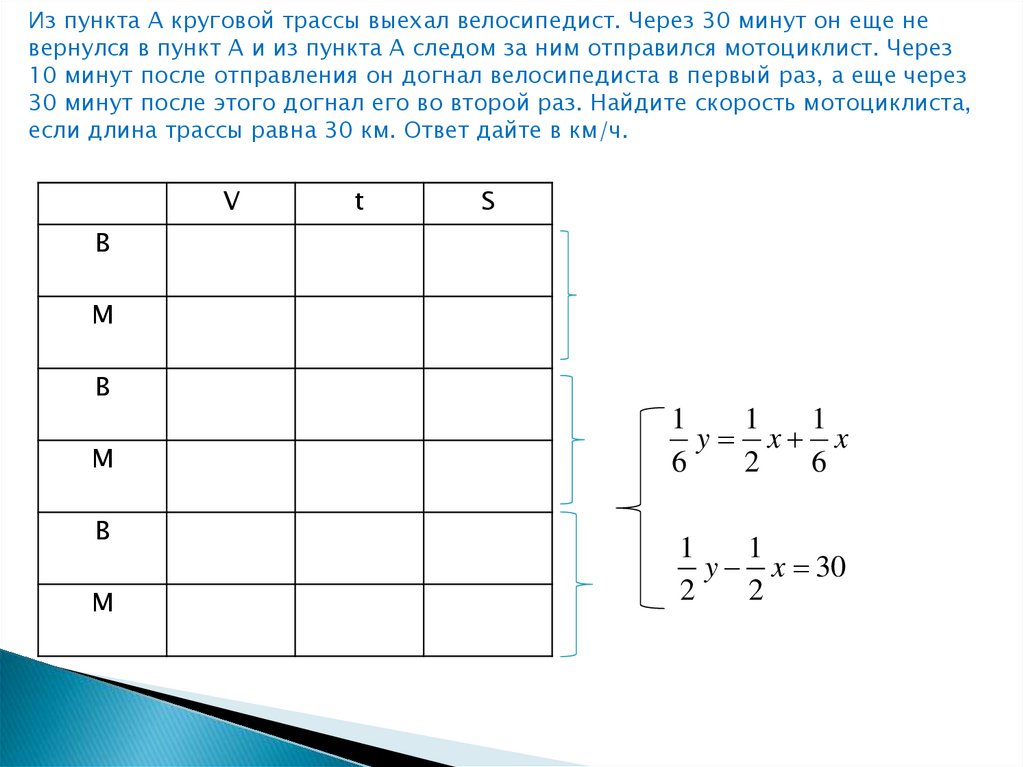








 Математика
Математика








