Решение систем ОДУ средствами Python

1.  «Решение систем ОДУ средствами Python»

«Решение систем ОДУ
средствами Python»
ВЫПОЛНИЛ:
ИЗМАЙЛОВ В.Д., МОАИСМ -О-24/1

2. Назначение и функциональные возможности программного средства

Python — это текстовый язык программирования, который
можно использовать различными способами, например, для
создания текстовых редакторов или веб-браузеров.

3. Основные свойства

Основные свойства и возможности Python
Python интерпретируемый язык программирования – код на нем выполняется
построчно, в режиме реального времени. Это свойство позволяет быстро исправлять
и проверять код без необходимости компиляции.
Python является языком с динамической типизацией, то есть тип переменной
определяется автоматически, во время выполнения кода. Это упрощает процесс
программирования и делает его гибким при работе с данными различного типа.
Python поддерживает объектно-ориентированное программирование (ООП), что
позволяет разрабатывать код в виде объектов, которые взаимодействуют друг с
другом. Это делает код более модульным и повторно используемым.
Python поддерживает также императивное, функциональное и аспектноориентированное программирование. Таким образом, разработчики имеют
возможность выбирать нужный подход для решения конкретной задачи.

4. ОДУ

Обыкновенные дифференциальные уравнения (ОДУ).
Они содержат функцию от одной независимой переменной.
ОДУ первого порядка в общем виде можно записать так:
y'(x) = f(x)g(x),где fx и g(x) — функции от переменной x.
Для решения обыкновенных дифференциальных уравнений (ОДУ) в Python используются
библиотеки SciPy и SymPy.
SciPy предоставляет функции для численного решения ОДУ, включая методы Эйлера и РунгеКутты.
SymPy позволяет проводить аналитическое решение, давая решение в виде математического
выражения.

5. Примеры решения задач

Пример 1. ОДУ 1 порядка: dy/dt = -2y

6. Примеры решения задач

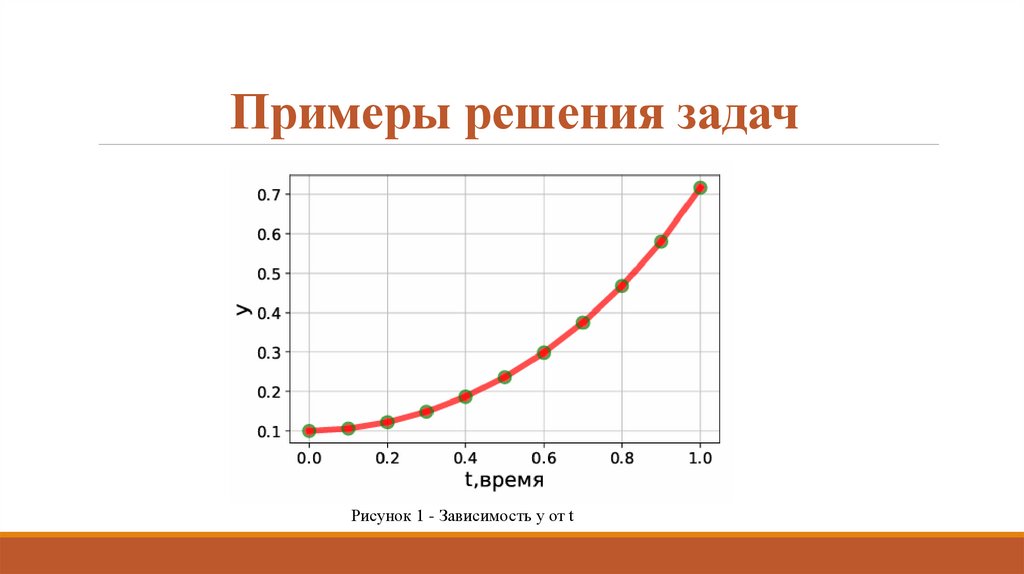
Пример 2. y′ = y2 +t с
начальным условием y(0)
= 0.1 на интервале t ∈
[0,1]

7. Примеры решения задач

Рисунок 1 - Зависимость y от t

8. Примеры решения задач

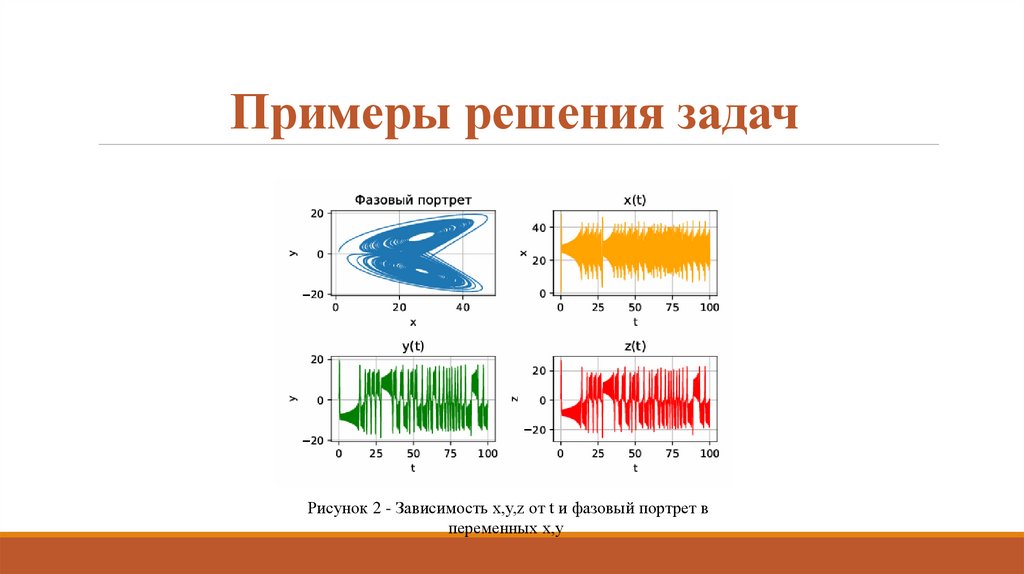
Пример 3. Решение
системы ОДУ

9. Примеры решения задач

Рисунок 2 - Зависимость x,y,z от t и фазовый портрет в
переменных x,y

10. Примеры решения задач

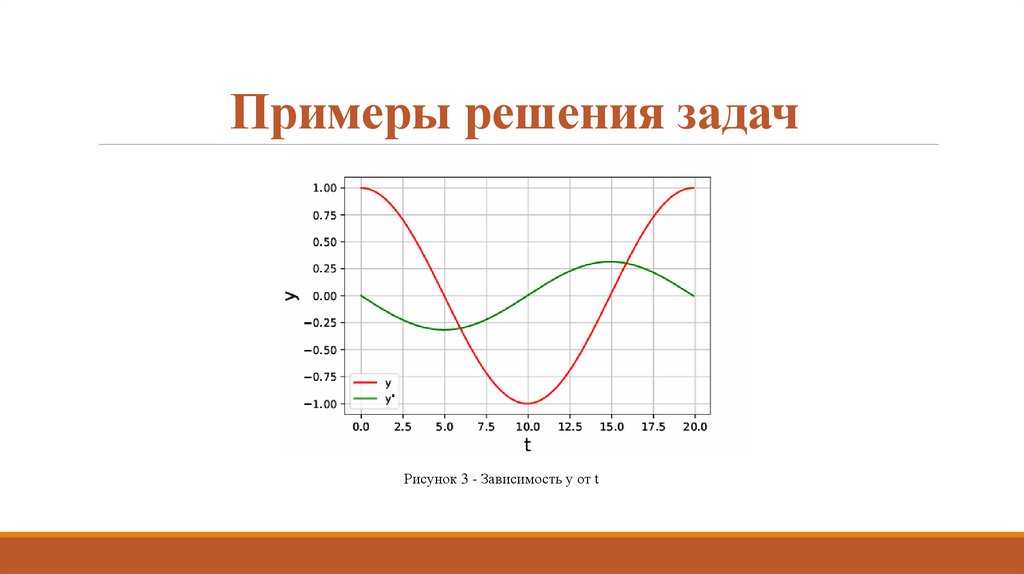
Пример 4. Решение ОДУ 2 порядка
Для t∈[0,20]
После замены:

11. Примеры решения задач

Рисунок 3 - Зависимость y от t

12. Примеры решения задач

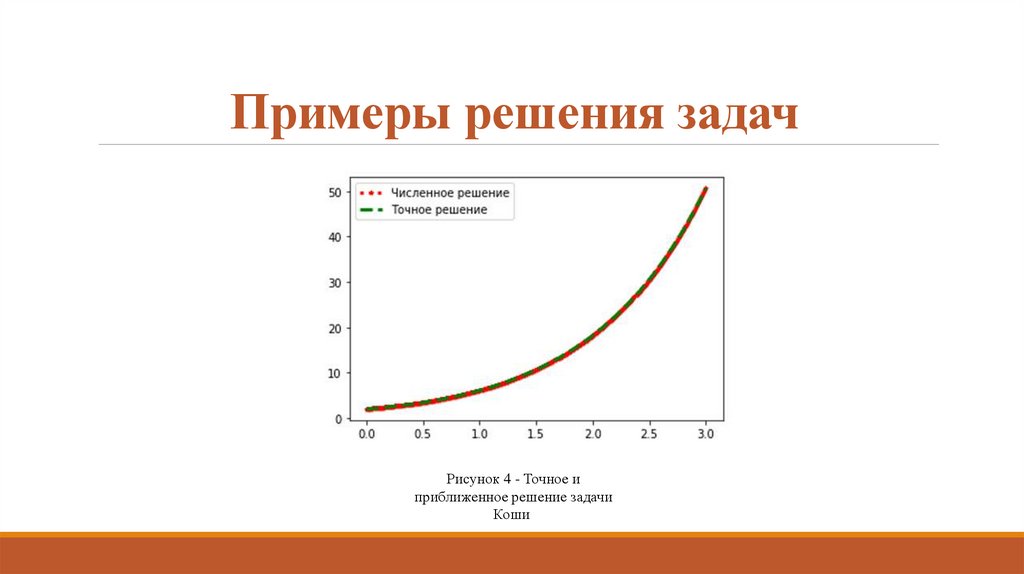
Пример 5. Задача Коши
для ОДУ 1 порядка

13. Примеры решения задач

Рисунок 4 - Точное и
приближенное решение задачи
Коши

14. Примеры решения задач

Пример 6. Решение
примера 5 с
использованием функции
solve_ivp ()

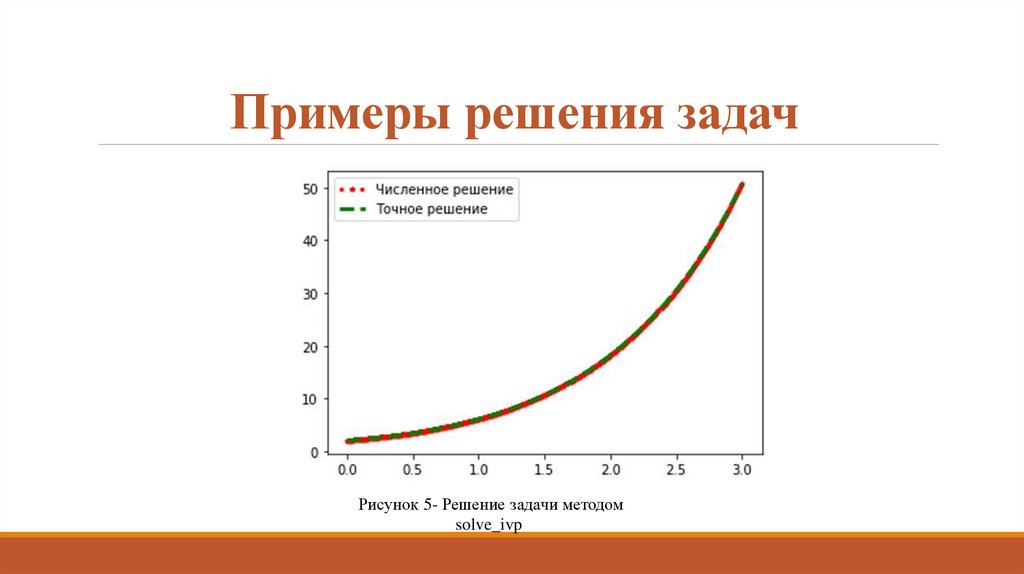
15. Примеры решения задач

Рисунок 5- Решение задачи методом
solve_ivp

16. Примеры решения задач

Пример 7. Решить задачу Коши для
системы двух дифференциальных
уравнений 1 порядка методом Эйлера

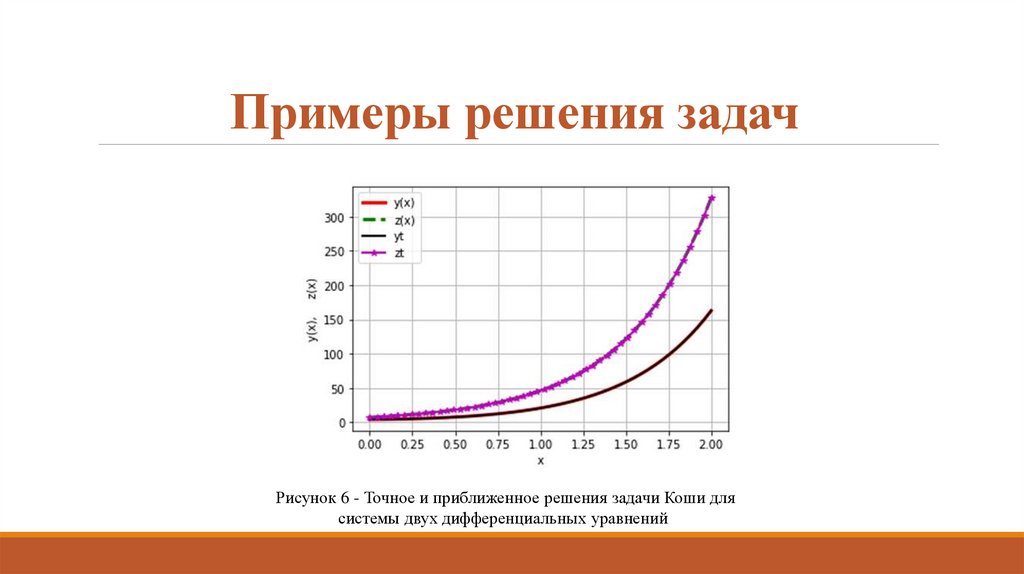
17. Примеры решения задач

Рисунок 6 - Точное и приближенное решения задачи Коши для
системы двух дифференциальных уравнений

18. СПАСИБО ЗА ВНИМАНИЕ!