Задачи нелинейного программирования. Методы и инструментальные средства их решения

1. Задачи нелинейного программирования. Методы и инструментальные средства их решения

Лекция 8
1

2. План лекции

I Общая постановка задачи НЛП.
II Геометрическая интерпретация решения двумерной
задачи НЛП.
III Классическая задача на условный экстремум
IV Численные методы решения задач НЛП
V Обзор стандартных пакетов прикладных программ
для решения задач НЛП.
2

3. Постановка задачи нелинейного программирования

Целевая функция
f x1, x 2 ,...x n min
(1)
Система ограничений
g1 x1, x 2 ,...x n 0
g x , x ,...x 0
2 1 2
n
( 2)
....
g m x1, x 2 ,...x n 0
x X, X R n
(3)
x* arg min f x1, x 2 ,...x n (4)
x D
3

4. Геометрическая интерпретация решения двумерной задачи НЛП

Алгоритм
1. Находят область допустимых решений (ограничения
2-3)
2. Строят характерные линии уровня целевой функции 1
3. Находят точку области допустимых решений через
которую проходят линии наименьшего уровня
(наивысшего уровня) или устанавливают
неразрешимость задачи, в случае неограниченности
целевой функции снизу (сверху)
4

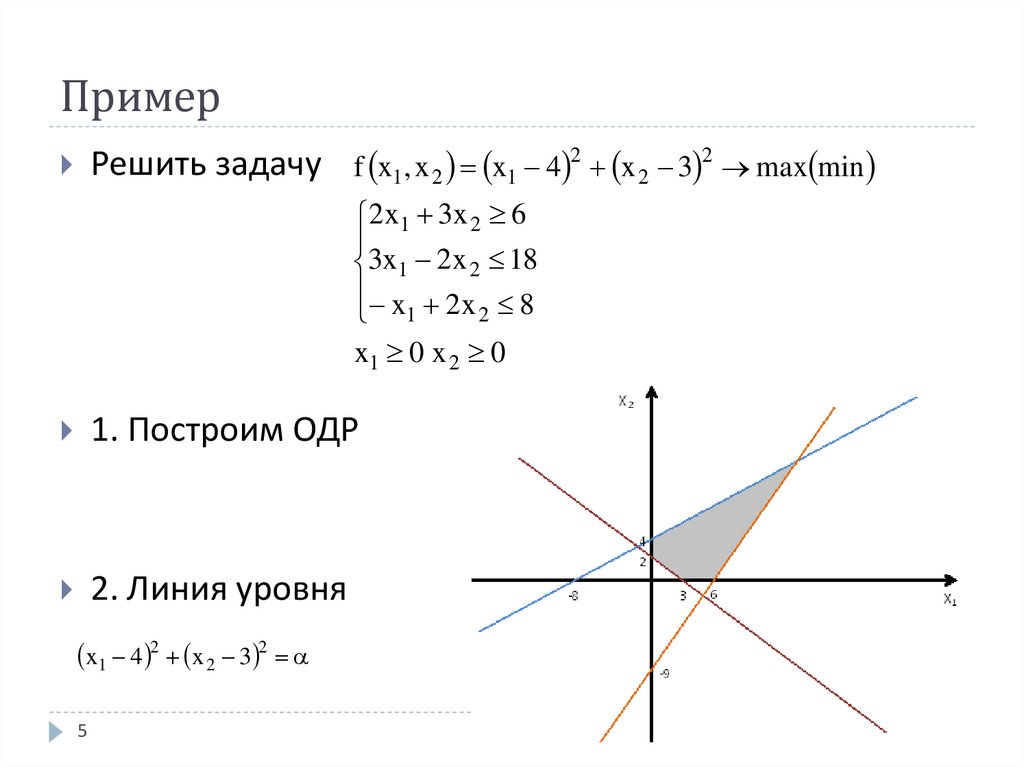
5. Пример

Решить задачу f x1, x 2 x1 4 2 x 2 3 2 max min
2 x1 3x 2 6
3x1 2 x 2 18
x 2 x 8
2
1
x1 0 x 2 0
1. Построим ОДР
2. Линия уровня
x1 4 2 x 2 3 2
5

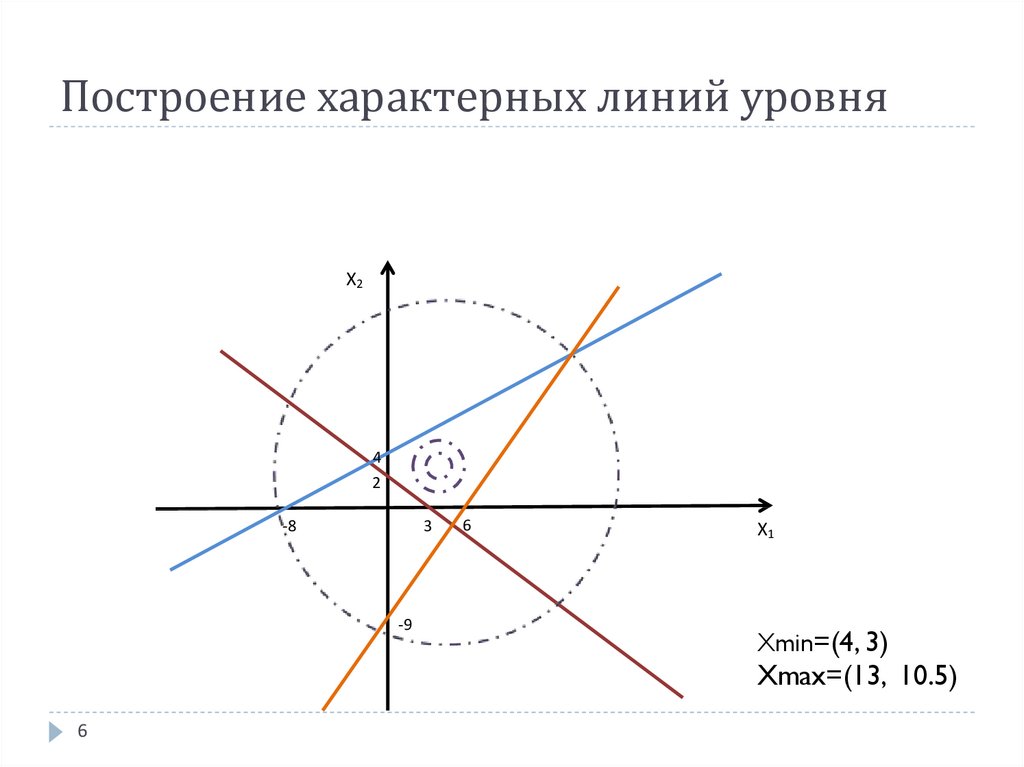
6. Построение характерных линий уровня

X2
4
2
-8
3
-9
6
X1
Xmin=(4, 3)
Xmax=(13, 10.5)
6

7. Выводы

Решение задачи НЛП может находится как внутри
допустимой области, так и на её границе
Решение задачи НЛП может быть затруднено
наличием глобальных и локальных экстремумов
целевой функции
В теории НЛП выделяют класс задач, обладающих
некоторыми свойствами, которые позволяют
разработать аналитический аппарат их решения
7

8. Постановка классической задачи на условный экстремум

Целевая функция
f x1, x 2 ,...x n min
(5)
Система ограничений
g i x1,...x n 0 i 1, m (6)
x Rn
8

9. Метод множителей Лагранжа

Идея метода: решение задачи на условный экстремум
сводится к нахождению безусловного экстремума
функции с большим количеством неизвестных.
Обобщенная функция Лагранжа
m
L x , y0 , y y0 f x yi g i x min (7)
i 1
Классическая (регулярная) функция Лагранжа
m
L x , y f x yi g i x (8)
i 1
Градиент функции Лагранжа
Матрица Гёссе L xx x, y
9
m
L x x , y f x y i g i x
i 1

10. Обоснование метода

Теорема условие локальной оптимальности задачи (5-6)
Пусть функции f(x) и gi(x) i=1..m непрерывно
дифференцируемые в некоторой окрестности
точки
x*. Если x*
* *
*
локальное решение задачи (5,6) то y0 y* y1 y2 ... ym
неравные 0 одновременно и такие, что L x x*, y * 0
Если градиенты ограничений в точке x* линейно независимы,
y*0 0
то
Замечание 1: условие теоремы означает, что градиенты f x * , gi x *
линейно независимы
Замечание 2: если градиенты ограничений в т. x* линейно
независимы, то из решения системы получим стационарную
точку задачи (5, 6)
L x , y 0
x
(8)
g i x 0 i 1, m
10

11. Обоснование метода

Теорема 2 Достаточное условие экстремума
11
Пусть функции f(x) и gi(x) i=1..m дважды непрерывно
дифференцируемые в точке x* и x* является допустимым
решением задачи (удовлетворяет условиям 6). Пусть
выполняется необходимое условие и матрица Гёссе по
переменной х функции Лагранжа является
положительноопредленной (отрицательноопределенной
для max), тогда точка x* является локальным решением
задачи (5,6).

12. Обзор численных методов

Требование: задачи выпуклого НЛП
Метод условного градиента
Метод проекции градиента
Методы штрафных функций
12

13. Пакеты прикладных программ для решения задач НЛП

MS Excel надстройка «Поиск решения»
ППП MathCAD (встроенная функция)
ППП MathLab
Система Mathematica
Отдельные модули в специализированных
программных средствах
Разработка собственных программных средств
13