Похожие презентации:
Экстремум функции двух переменных. Условный экстремум. Метод множителей Лагранжа. Метод наименьших квадратов
1.
Лекция 15Экстремум функции двух переменных.
Условный экстремум. Метод множителей
Лагранжа. Метод наименьших квадратов
2.
Экстремум функции двух переменныхКак и в случае функции одной переменной, функция z=f(x,y) имеет узловые,
определяющие график функции, точки.
Определим точки экстремума для функции двух переменных.
Точка М(х0,у0) называется точкой
максимума (минимума) функции z=f(x,y),
если существует окрестность точки М,
такая что для всех точек (х,у) из этой
окрестности выполняется неравенство:
f ( x0 , y0 ) f ( x, y )
f ( x0 , y0 ) f ( x, y )
3.
Экстремумимеет
локальный
характер,
поскольку
рассматривается максимальное и минимальное значение
функции в достаточно малой окрестности точки М(х0,у0).
Сформулируем аналог теоремы Ферма для функции двух
переменных:
Пусть
точка
(х0,у0)
является
точкой
дифференцируемой функции z=f(x,y).
Тогда частные производные в этой точке
f x ( x0 , y0 )
f y ( x0 , y0 )
равны нулю:
f x ( x0 , y0 ) 0
f y ( x0 , y0 ) 0
экстремума
4.
Пусть точка М(х0,у0) – точка максимума.Зафиксируем одну из переменных, например, у:
у=у0
Тогда получим функцию одной переменной
z1=f(х,у0)
которая будет иметь максимум при х=х0.
Согласно теореме Ферма
z1 ( x0 ) f x ( x, y0 ) 0
Аналогично можно доказать, что
f y ( x0 , y ) 0
5.
Точки, в которых выполняются условияэкстремума функции z=f(x,y), т.е.
z x 0
z y 0
называются критическими или
стационарными.
6.
Необходимое условие экстремумасформулировать иначе:
можно
В точках максимума или минимума
дифференцируемой функции градиент этой
функции равен нулю:
z 0
7.
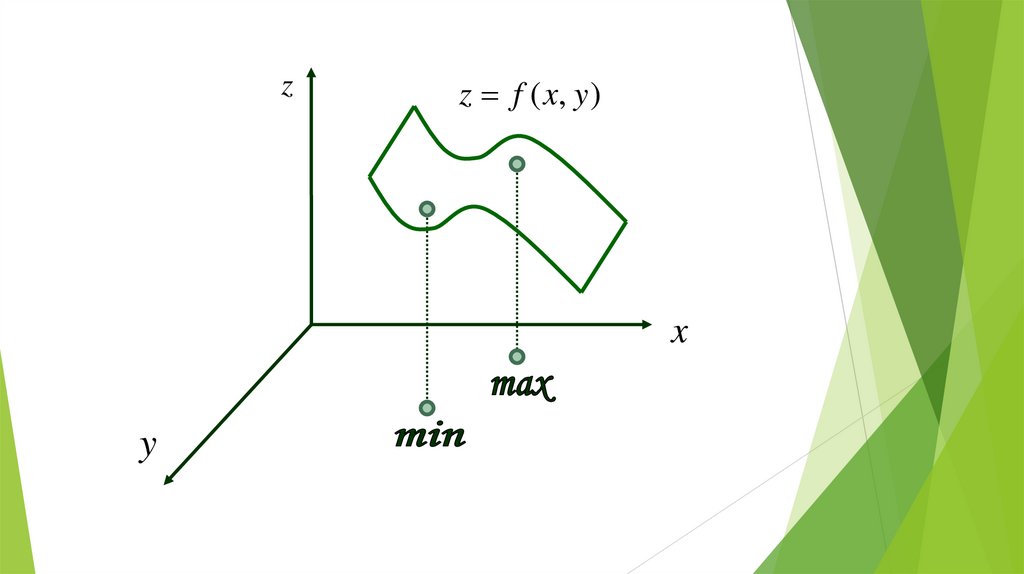
zz f ( x, y )
x
y
8.
Пусть функция z=f(x,y)Определена
в
некоторой
окрестности
критической точки (х0,у0), в которой
f x ( x0 , y0 ) 0
f y ( x0 , y0 ) 0
9.
Имеет в этой точке непрерывныечастные производные второго
порядка:
( xy ) A
f xx
f xy ( xy ) f yx ( xy ) B
( xy ) C
f yy
10.
Тогда, если A C B 2 0то в данной точке функция
имеет экстремум, причем
если А>0, то минимум
если А<0, то максимум
если
то функция экстремума не имеет,
если A C B 2 0
то
вопрос
остается
открытым.
11.
Найти экстремум функцииz x y 3 xy
3
z
z x
3x 2 3 y
x
3x 2 3 y 0
2
3 y 3 x 0
3
z
z y
3 y 2 3 x
y
x1 0 x2 1
y1 0 y2 1
12.
z6 y
2
y
2
z
6x
2
x
2
z
z
3
x y y x
2
2
Экстремума нет.
13.
Экстремум есть.Т.к. А<0, то это будет максимум.
14.
Условный экстремум.Метод множителей Лагранжа
Метод множителей Лагранжа
Рассмотрим
частный случай общей задачи нелинейного
программирования, предполагая, что система ограничений
содержит только уравнения:
F F x1, ..., x n max min
g i x1 , ..., x n bi i 1, m
Полагаем, что все функции непрерывны вместе со своими первыми
частными производными
15.
Для решения задачи построимфункцию Лагранжа
m
L x1 , ..., x n , 1 , ..., m F x1 , ..., x n i bi g i x1 , ..., x n
i 1
- называются множителями Лагранжа
i 1, m
i
16.
Определим частные производныеL
j 1, n
xj
L
i 1, m
i
Приравняем их к нулю. В результате получим систему уравнений
относительно n+m переменных.
g
m
F
L
i
0, j 1, n
i
xj
xj
i 1
xj
L
0, i 1, m
,
...,
x1
g
b
x
i
n
i
j
17.
Всякое решение системы уравнений определяет точку в которой может иметь местоэкстремум функции F
18.
Решение задачи методом Лагранжа включаетследующие этапы:
1.
Составляют функцию Лагранжа.
2.
Находят частные производные от функции Лагранжа по
переменным и приравнивают их нулю.
3.
Решают систему уравнений и находят все точки, в которых
целевая функция F может иметь экстремум.
4.
Среди найденных точек находят такие, в которых целевая
функция F достигает максимального (минимального)
значения
19.
ПримерПо плану производства продукции предприятию необходимо
изготовить 180 изделий.
Эти изделия могут быть изготовлены двумя технологическими
способами.
При производстве
изделий I способом затраты равны 4x1+x12
При изготовлении
изделий II способом они составляют 8x2+x22
Определить, сколько изделий каждым из способов следует
изготовить, чтобы общие затраты на производство продукции были
минимальными
20.
Решение.Составим математическую модель задачи.
F 4 x x 8 x x min
2
1
1
2
2
x1 x 2 180
x1 0,
x 2 0,
2
21.
Составим функцию ЛагранжаL x1 , x 2 ,
2
2
4
8
x
x
x
x
1
1
2
2
180 x1 x 2
Вычислим частные производные функции L и приравняем их нулю.
L 4 2
0
x
1
x1
L
8 2 x2 0
x2
L 180
0
x
x
1
2
22.
Решая данную систему, получим* 91
x1
* 89
x2
В этой точке может быть экстремум целевой функции F. Используя вторые
частные производные, можно показать, что в данной точке функция F имеет
условный минимум
F min 17278
Если предприятие изготовит 91 изделие I способом и 89 изделий II
способом, то общие затраты будут минимальными и составят 17278
руб
23.
Метод множителей Лагранжа может быть применен и для случая, когда система ограничений задачинелинейного программирования содержит только неравенства
F F
,
...,
x n max min
x1
g i x1, ..., x n bi
i 1, m
24.
1.Решение такой задачи находится
в 2 этапа:
Находят
стационарные точки безусловного экстремума целевой функции F
Для этого определяют частные производные функции F и приравнивают их к нулю.
В результате получают систему n уравнений относительно n переменных.
25.
F 0x1
F 0
x
n
Из всех решений системы
выбираем только те точки ,
которые удовлетворяют системе
строгих неравенств:
g i x1 , ..., x n bi
i 1, m
26.
2.Находят точки условного экстремума целевой функции F при условиях
g i x1, ..., x n bi
i 1, m
Для этого строят функцию Лагранжа
m
L x1 , , x n , 1 , , m F x1 , , x n i
b
i g i x1 , , x n
i 1
Находят частные производные от функции Лагранжа и приравнивают их
нулю.
Решают систему n+m уравнений относительно n+m переменных
27.
В результате, на 1 и 2 этапе находится множество точек, в которых целевая функция F может иметьэкстремальные значения.
Для определения максимального (минимального) значения целевой функции F необходимо вычислить
значения этой функции в полученных точках
28.
Пример. Найти минимальное имаксимальное значение функции
F x1 2 x 2 3
2
При условиях
x x 52
2
1
2
2
2
29.
РешениеОпределим точки безусловного экстремума целевой функции F, лежащие внутри области.
Для этого найдем частные производные функции F и приравняем их к нулю.
F 2 x 2 0
1
x
1
F
2
3
x
0
2
x
2
30.
получим* 2
x1
F 2,3 0
* 3
x2
Так как 22+32=13<52, следовательно, точка А(2,3)
лежит внутри области.
31.
Строим функцию Лагранжа для случая, когда ограничение имеет видx x
2
1
L x1 , x 2 ,
2
2
52
x 2 x 3
2
1
2
2
2
2
52 x1 x 2
32.
Вычислим частные производные функции L по и приравняем их к нулю.L 2 x 2 2
1
x1 0
x
1
L
2
3
2 x2 0
x
2
x2
L 52 2 2 0
x1 x 2
33.
Первое уравнение системы домножим на x2 , второе уравнениеx1 . В результате получим:
x 2 x1 2
3
x
x
1 2
x1 x 2
x1 x 2
Решая систему
2
3
x 2 x1
x1 x 2
2 x 2 3 x1
2
2
x1 x 2 52
2 x 2 3 x1
34.
получаем два решения – две точки B(4, 6) и C(-4, -6), в которых целевая функция F может иметьэкстремумы
F 4, 6 13,
F 4, 6 117.
Таким образом, минимальное значение
целевой функции
максимальное значение
достигается в точке
0
F min
A(2, 3),
F max 117
в точке C(-4,
-6)
35.
Нахождение наибольшего и наименьшегозначений функции на компакте
Пусть функция
u = f(x1, x2, ... , xm) : Rm → R
непрерывна на ограниченном замкнутом множестве G ⊂ Rm (на компакте)
и дифференцируема во всех внутренних точках этого множества.
Напомним, что для функции, непрерывной на компакте, существуют на
этом компакте точки, в которых функция принимает наибольшее и
наименьшее значения. Эти точки могут быть внутренними и граничными.
Поэтому следует действовать по такой схеме:
⮚ найти стационарные точки внутри области G и вычислить значения
функции в этих точках;
⮚ исследовать функцию на границе области (здесь решается задача на
условный экстремум);
⮚ сравнить значения функции в стационарных точках и на границе,
выбрать среди них наибольшее и наименьшее.
36.
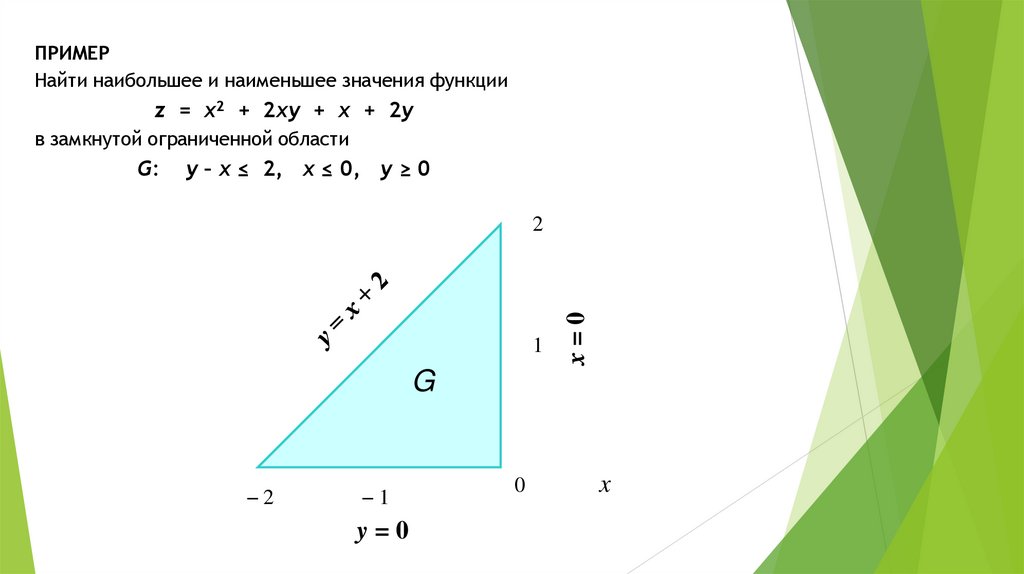
ПРИМЕРНайти наибольшее и наименьшее значения функции
z = x2 + 2xy + x + 2y
в замкнутой ограниченной области
y – x ≤ 2, x ≤ 0, y ≥ 0
2
1
x=0
G:
G
–2
–1
y=0
0
x
37.
⮚ Найдем стационарные точки функции.zx = 2x + 2y + 1; zy = 2x + 2.
Точка М1(–1, 1/2)∈G, z(–1,1/2) = 0.
⮚ Исследуем функцию на границе области.
▪ y = 0.
Задача сводится к нахождению наибольшего и наименьшего значений
на отрезке [– 2, 0] функции одной переменной
f ( x ) = z ( x, 0) = x2 + x.
Сначала найдем ее стационарные точки.
f ´ (x ) = 2x + 1 = 0 ⇒ x = – 1/2 ∈ [– 2, 0]. f (– 1/2) = – 1/4.
На концах отрезка f (– 2) = 2, f (0) = 0.
Следовательно, z(–1/2, 0) = – 1/4, z(–2, 0) = 2; z(0, 0) = 0.
38.
▪ x = 0.Исследуем на наибольшее и наименьшее значение на отрезке [0, 2]
функцию
g ( y ) = z (0, y) = 2y.
Эта функция не имеет стационарных точек.
На конце отрезка g (2) = 4. Следовательно, z (0, 2) = 4.
▪ y = x + 2.
Исследуем на наибольшее и наименьшее значение на [– 2, 0] функцию
ϕ ( x) = z ( x, x + 2) = x2 + 2x(x + 2) + x + 2(x + 2) = 3 x2 + 7 x + 4.
ϕ ´ ( x) = 6x + 7 = 0 ⇒ x = – 7/6 ∈ [– 2, 0], ϕ (– 7/6) = – 1/12.
Следовательно, z(–7/6, 5/6) = – 1/12.
39.
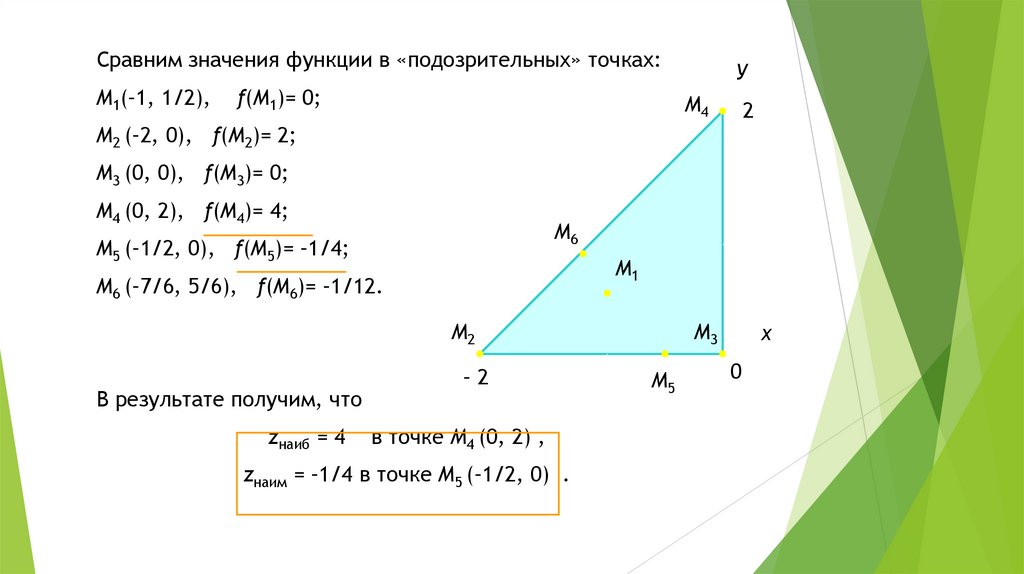
⮚ Сравним значения функции в «подозрительных» точках:М1(–1, 1/2),
f(М1)= 0;
y
M4
2
М2 (–2, 0), f(М2)= 2;
М3 (0, 0), f(М3)= 0;
М4 (0, 2), f(М4)= 4;
M6
М5 (–1/2, 0), f(М5)= –1/4;
M1
М6 (–7/6, 5/6), f(М6)= –1/12.
M2
В результате получим, что
zнаиб = 4
–2
в точке М4 (0, 2) ,
zнаим = –1/4 в точке М5 (–1/2, 0) .
M3
M5
x
0
40.
Метод наименьших квадратовМетод наименьших квадратов-математический метод,
применяемый для решения различных задач,
основанный на минимизации суммы квадратов
отклонений некоторых функций от искомых
переменных.
МНК является одним из базовых методов
регрессионного анализа для оценки неизвестных
параметров регрессионных моделей по выборочным
данным.
Применяется также для приближённого
представления заданной функции другими (более
простыми) функциями и оказывается полезным при
обработке наблюдений.
41.
42.
Плюсы и минусы данного метода+ он приводит к сравнительно простому математическому способу
определения параметров а, b, с, … искомого функционала;
+ он дает довольно веское теоретическое обоснование с
вероятностной точки зрения.
- основным недостатком МНК является чувствительность оценок к
резким выбросам, которые встречаются в исходных данных.
43.
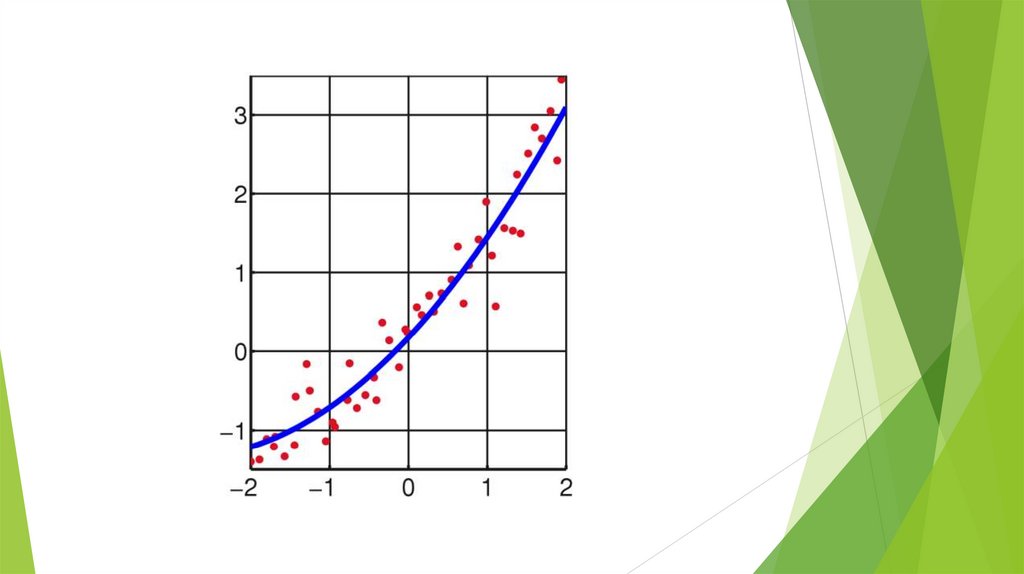
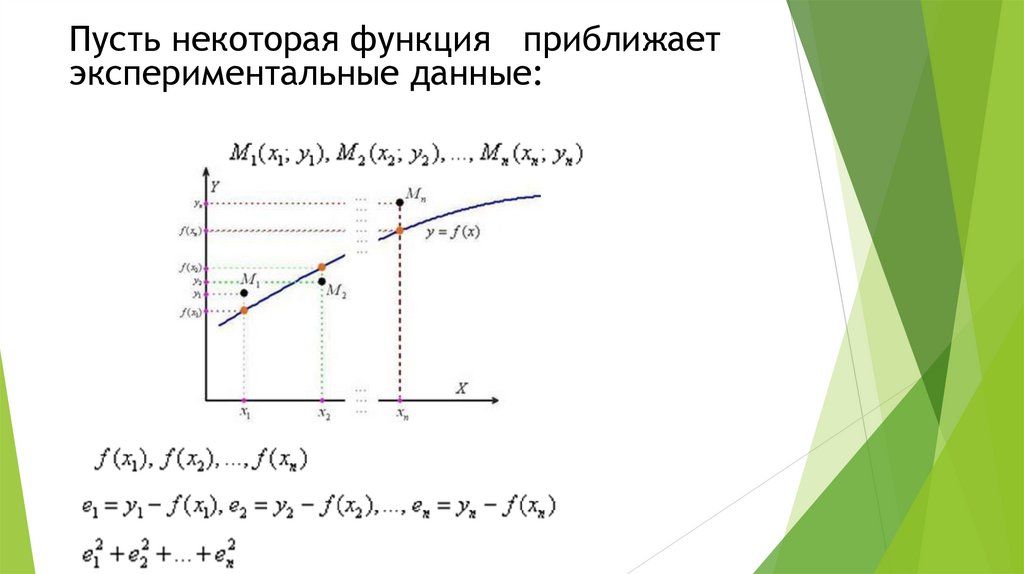
Пусть некоторая функция приближаетэкспериментальные данные:
44.
Иными словами, задача состоит внахождении таких коэффициентов a и
b – чтобы сумма квадратов отклонений
была наименьшей.
45.
Вывод формул для нахождениякоэффициентов
46.
Из необходимых условийэкстремума следует:
47.
Алгоритм МНК:1)
Находим суммы
2)
Составляем систему уравнений с определённым кол-вом
неизвестных.
3)
Решаем систему. (метод Крамера)
4)
В результате получаем стационарную точку S (искомые
коэффициенты a;b)
5)
Вычисляем сумму квадратов отклонений между эмпирическими и
теоретическими значениями.
48.
Коэффициенты a, b оптимальной функции y=ax+b найдём какрешение системы:
49.
.50.
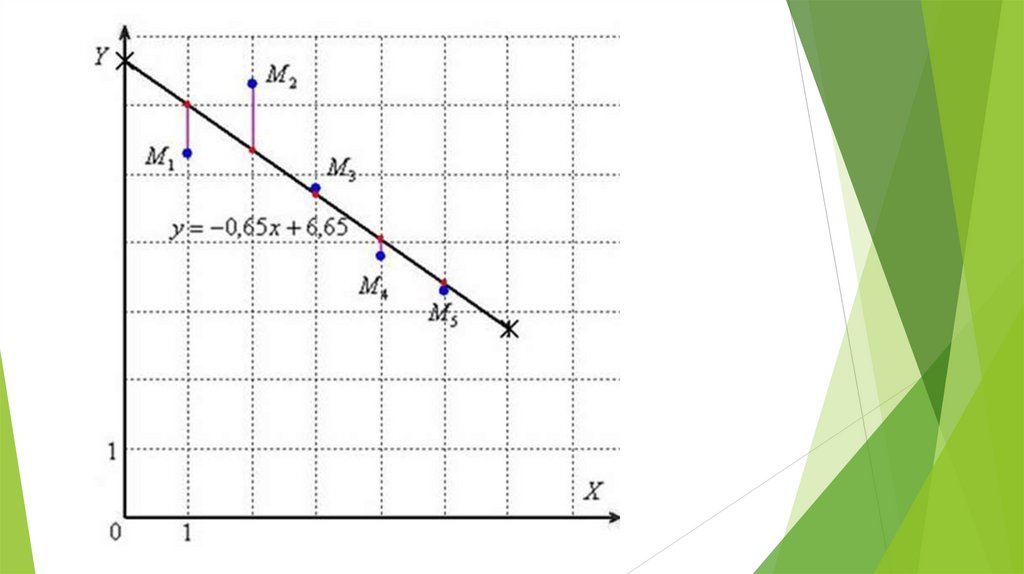
Проверка:Таким образом, искомая аппроксимирующая функция:
Для построения графика аппроксимирующей функции
найдём два её значения:
и выполним чертёж:


















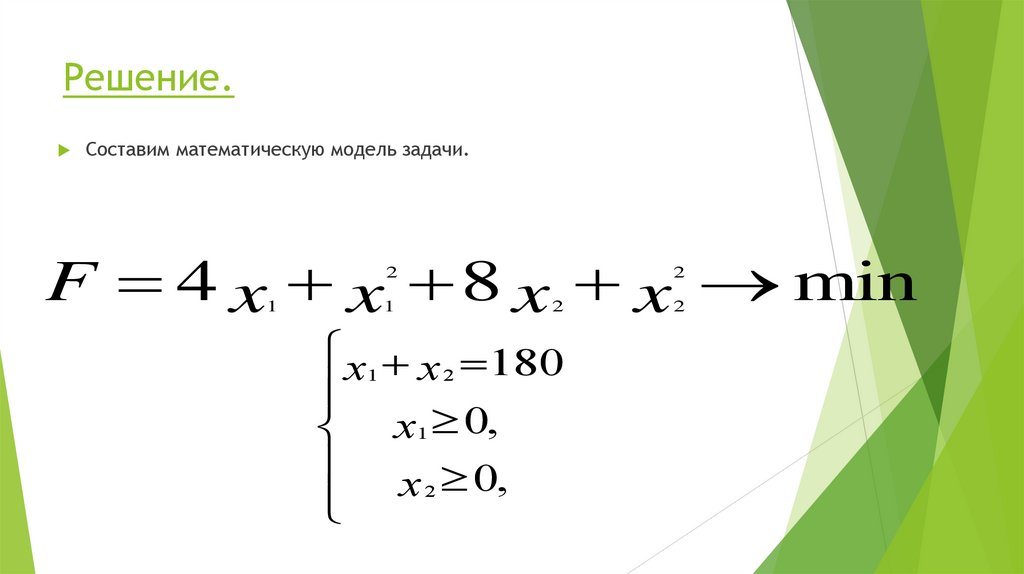



























 Математика
Математика








