Похожие презентации:
Условный экстремум. Метод Лагранжа. Лекция 2
1. Здравствуйте!
Лекция №202.
Условный экстремум. Метод ЛагранжаВ жизни всегда приходится подчиняться каким-то ограничениям,
наложенным на нас природой, обществом, финансами и т.д.
Математически эта ситуация формализуется как задача нахождения
экстремума некоторой функции п переменных при наличии
ограничений. Эти ограничения могут иметь самый разнообразный
вид, но ниже будет рассмотрена лишь простейшая ситуация, когда
задача выглядит так: найти максимум или минимум функции
f ( x1 , x 2 , ..., x n ) extr
при наличии ограничений на переменные x1 , x 2 , ..., x n вида
F1 ( x1 , x 2 , ..., x n ) 0 ,
F ( x , x , ..., x ) 0 ,
2 1 2
n
...
Fm ( x1 , x 2 , ..., x n ) 0.
Наличие ограничений (условий) дает и имя этой задачи: она
называется задачей на условный экстремум.
3.
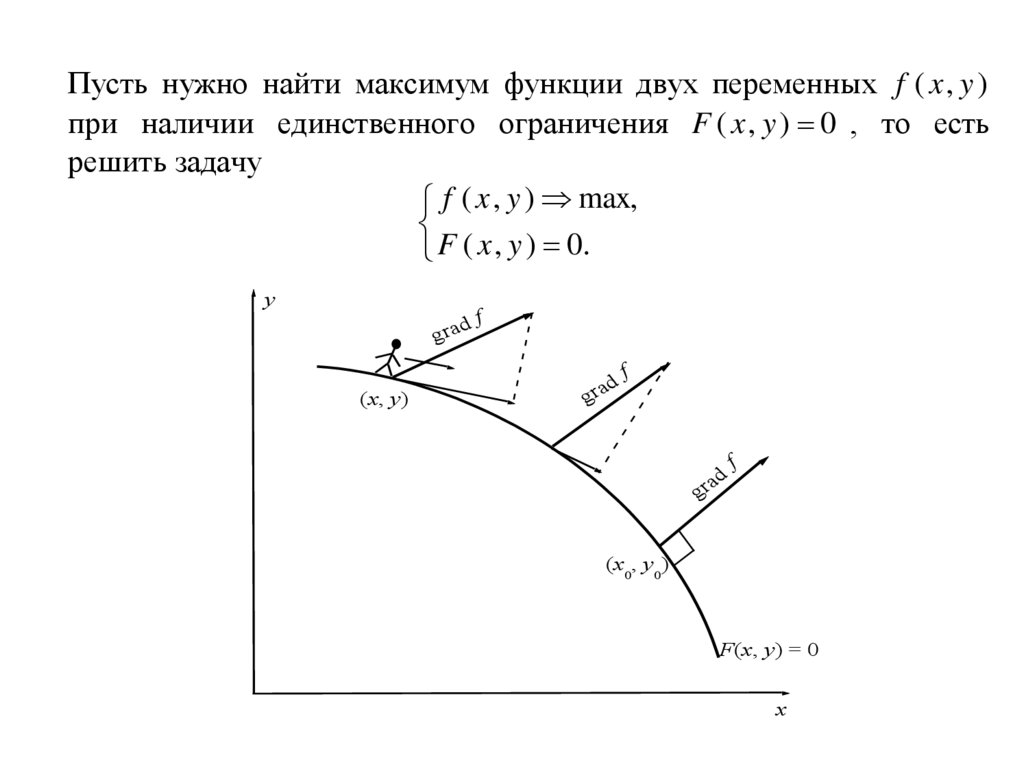
Пусть нужно найти максимум функции двух переменных f ( x , y )при наличии единственного ограничения F ( x , y ) 0 , то есть
решить задачу
f ( x , y ) max,
F ( x , y ) 0.
y
f
d
a
r
g
(x, y)
d
gra
f
d
gra
f
(x0, y0)
F(x, y) = 0
x
4.
Если мы желаем увеличить f ( x , y ) , мы должны двигаться покривой в том направлении, куда указывает проекция градиента.
До каких же пор наше движение будет приводить к увеличению
f ( x , y ) ? Очевидно, что это увеличение окончится тогда, когда
производная по направлению касательной будет равна нулю. Это
произойдет тогда, когда grad f будет перпендикулярен касательной,
то есть будет параллелен нормали к кривой.
F F
,
Но вектор нормали N
. Условие, что grad f
x y
коллинеарен нормали, приводит к условию
f x f y
.
F x F y
5.
Обозначая это отношение через , придем к системе уравненийF
f
x x 0 ,
f
F
0,
y
y
F ( x , y ) 0.
В этой системе три уравнения, неизвестных также три – это х, у и .
Так что, решив эту систему, мы получим точку, «подозрительную»
на экстремум. Значение можно выбросить.
6.
В общем случае рассуждения выглядят следующим образом: пустьнадо решить задачу
f ( x1 , x 2 , ..., x n ) extr ,
F1 ( x1 , x 2 , ..., x n ) 0 ,
F ( x , x , ..., x ) 0 ,
2 1 2
n
...
Fm ( x1 , x 2 , ..., x n ) 0.
Направление возрастания функции f ( x ) указывает вектор
grad f . С другой стороны, условие Fi ( x1 , x 2 , ..., x n ) 0 вырезает из
нашего п-мерного пространства некоторую гиперповерхность
размерности п 1. Вектор нормали к этой гиперповерхности имеет
вид
Fi Fi
Fi
Ni
,
, ...,
.
x n
x1 x 2
7.
Рассмотрим линейное многообразие, образованное этими векторами,то есть совокупность векторов
вида
N 1 N 1 2 N 2 ... m N m .
Тогда точки, «подозрительные на экстремум, должны определяться
тем условием, что вектор градиента принадлежит этому
многообразию, то есть 1 , 2 , ..., m такие, что
grad f 1 N 1 2 N 2 ... m N m .
В компонентах это выглядит так:
Fm
F1
F2
f
...
0,
1
2
m
x
x1
x1
x1
1
f F1 F2 ... Fm 0 ,
1
2
m
(4)
x 2
x 2
x 2
x 2
...
f
Fm
F1
F2
1
2
... m
0.
x n
x n
x n
x n
8.
Добавляя сюда ограничения задачиF1 ( x1 , x 2 , ..., x n ) 0 ,
F ( x , x , ..., x ) 0 ,
2 1 2
n
(5)
...
Fm ( x1 , x 2 , ..., x n ) 0 ,
мы получим систему из п т уравнений относительно п т
неизвестных x1 , x 2 , ..., x n , 1 , 2 , ..., m , решая которую и найдем
возможные точки экстремума.
9.
Формально это выглядит так: составляется так называемая функцияЛагранжа
L f ( x ) 1 F1 ( x ) 2 F2 ( x ) ... m Fm ( x ) .
Появляющиеся здесь сомножители 1 , 2 , ..., m называются
неопределенными множителями Лагранжа. Система уравнений,
определяющая возможные точки экстремума, выглядит так
L 0 , i 1, n ,
x
i
L
0 , j 1, m .
j
Уравнения L x i 0 дают систему (4), уравнения L j 0
систему (5).









 Математика
Математика








