Voľná metóda, priečelná poloha. Lineárna perspektíva 3

1.

Lineárna perspektíva 3
Voľná metóda, priečelná poloha
8. GL_RP na prednášku 17.4. a cvičenie 22. 4. – 24. 4.

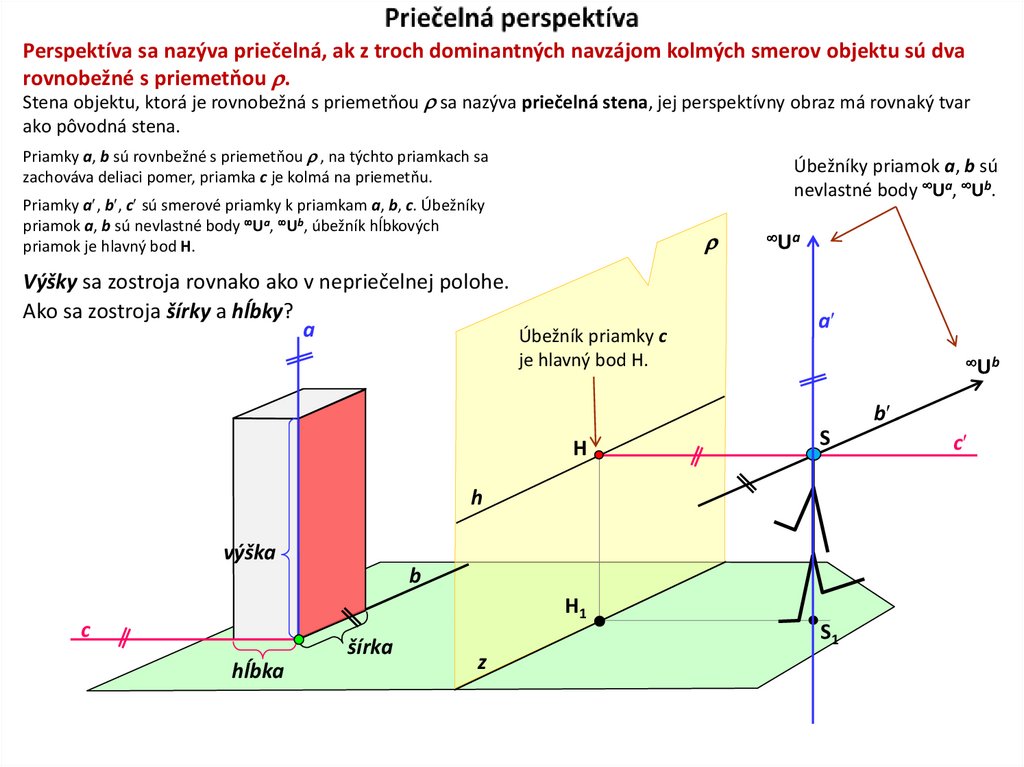
2. Priečelná perspektíva

Perspektíva sa nazýva priečelná, ak z troch dominantných navzájom kolmých smerov objektu sú dva
rovnobežné s priemetňou .
Stena objektu, ktorá je rovnobežná s priemetňou sa nazýva priečelná stena, jej perspektívny obraz má rovnaký tvar
ako pôvodná stena.
Priamky a, b sú rovnbežné s priemetňou , na týchto priamkach sa
zachováva deliaci pomer, priamka c je kolmá na priemetňu.
Úbežníky priamok a, b sú
nevlastné body Ua, Ub.
Priamky a , b , c sú smerové priamky k priamkam a, b, c. Úbežníky
priamok a, b sú nevlastné body Ua, Ub, úbežník hĺbkových
priamok je hlavný bod H.
Výšky sa zostroja rovnako ako v nepriečelnej polohe.
Ako sa zostroja šírky a hĺbky?
a
Úbežník priamky c
Ua
a
je hlavný bod H.
Ub
b
H
S
h
výška
b
H1
c
šírka
hĺbka
z
S1
c

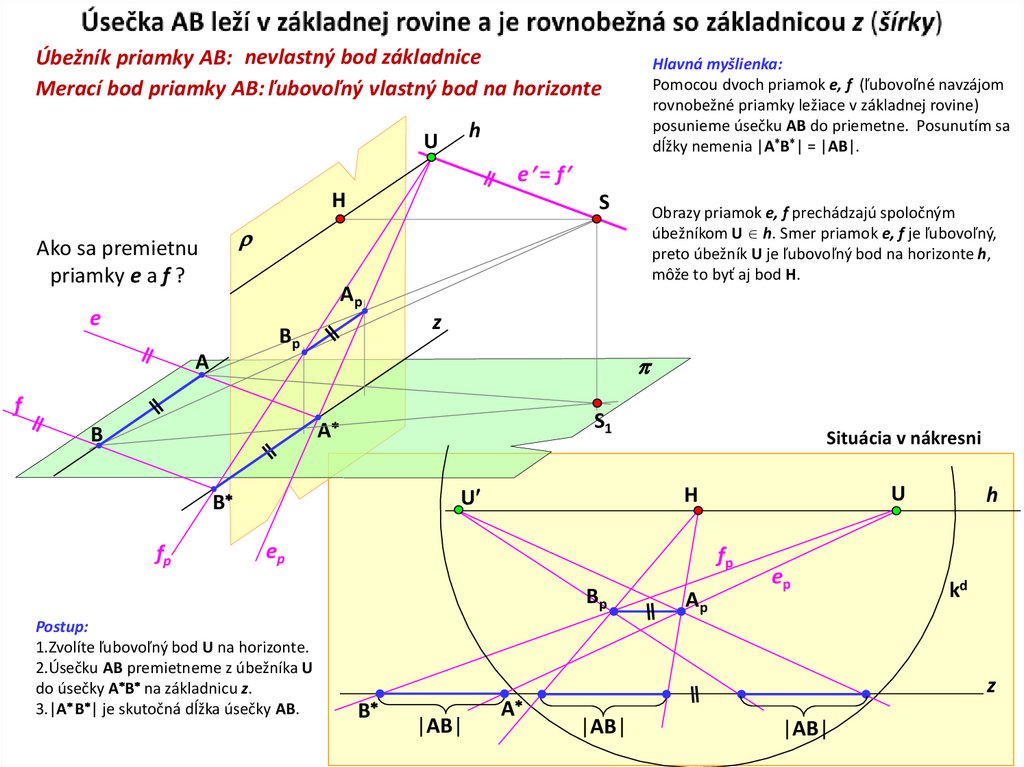
3. Úsečka AB leží v základnej rovine a je rovnobežná so základnicou z (šírky)

Úbežník priamky AB: nevlastný bod základnice
Merací bod priamky AB: ľubovoľný vlastný bod na horizonte
Hlavná myšlienka:
Pomocou dvoch priamok e, f (ľubovoľné navzájom
rovnobežné priamky ležiace v základnej rovine)
posunieme úsečku AB do priemetne. Posunutím sa
dĺžky nemenia |A*B*| = |AB|.
h
U
e = f
H
S
Ako sa premietnu
priamky e a f ?
Ap
e
z
Bp
A
f
S1
A
B
Situácia v nákresni
ep
fp
Bp
Postup:
1.Zvolíte ľubovoľný bod U na horizonte.
2.Úsečku AB premietneme z úbežníka U
do úsečky A B na základnicu z.
3.|A B | je skutočná dĺžka úsečky AB.
U
H
U
B
fp
Obrazy priamok e, f prechádzajú spoločným
úbežníkom U h. Smer priamok e, f je ľubovoľný,
preto úbežník U je ľubovoľný bod na horizonte h,
môže to byť aj bod H.
B
|AB|
A
Ap
ep
h
kd
z
|AB|
|AB|

4.

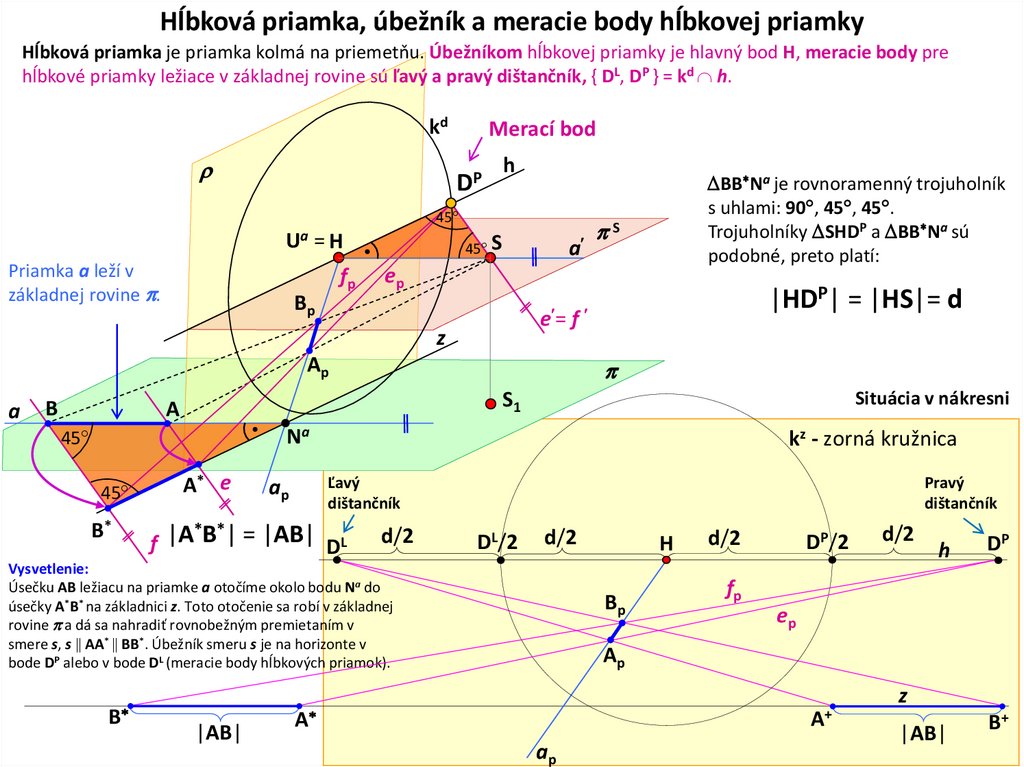
Hĺbková priamka, úbežník a meracie body hĺbkovej priamky
Hĺbková priamka je priamka kolmá na priemetňu. Úbežníkom hĺbkovej priamky je hlavný bod H, meracie body pre
hĺbkové priamky ležiace v základnej rovine sú ľavý a pravý dištančník, { DL, DP } = kd h.
kd
Merací bod
DP
h
45
Ua = H
Priamka a leží v
základnej rovine .
fp
45 S
a
Bp
|HDP| = |HS|= d
e = f
Ap
B
S
ep
z
a
BB Na je rovnoramenný trojuholník
s uhlami: 90 , 45 , 45 .
Trojuholníky SHDP a BB Na sú
podobné, preto platí:
Situácia v nákresni
S1
A
Na
45
45
B*
A* e
kz - zorná kružnica
Pravý
dištančník
Ľavý
dištančník
ap
* *
f |A B | = |AB| DL
d/2
DL/2
d/2
Vysvetlenie:
Úsečku AB ležiacu na priamke a otočíme okolo bodu Na do
úsečky A*B* na základnici z. Toto otočenie sa robí v základnej
rovine a dá sa nahradiť rovnobežným premietaním v
smere s, s AA* BB*. Úbežník smeru s je na horizonte v
bode DP alebo v bode DL (meracie body hĺbkových priamok).
B
|AB|
H
Bp
d/2
DP/2
d/2
h
DP
|AB|
B+
fp
ep
Ap
A
A+
ap
z

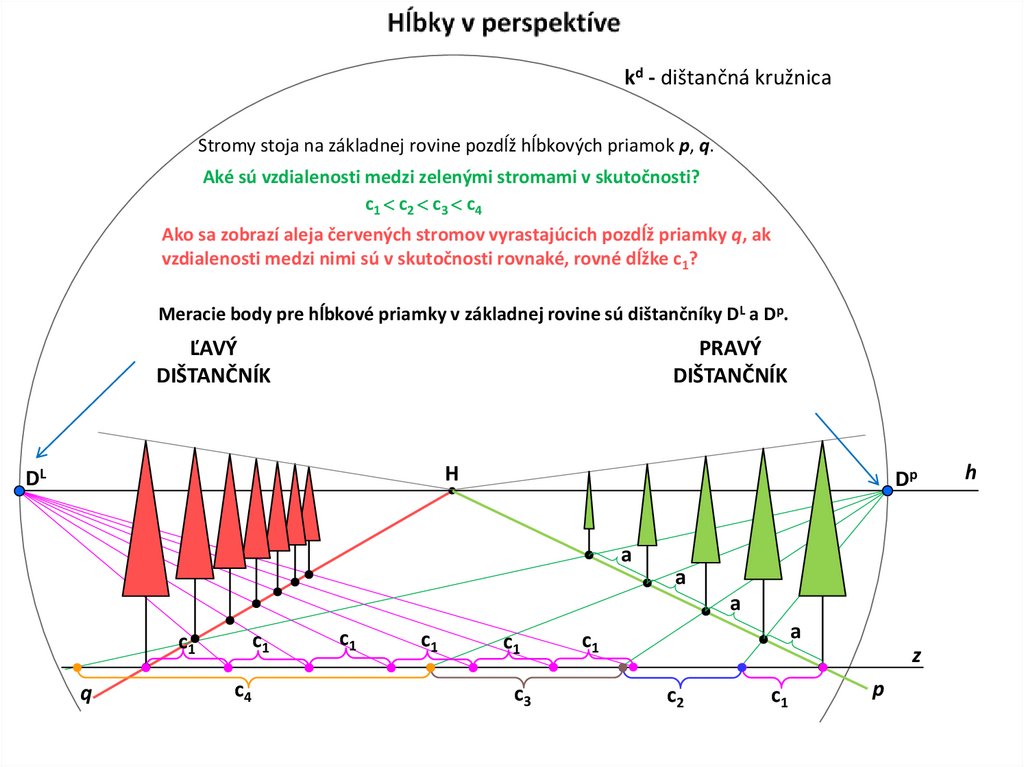
5. Hĺbky v perspektíve

kd - dištančná kružnica
Stromy stoja na základnej rovine pozdĺž hĺbkových priamok p, q.
Aké sú vzdialenosti medzi zelenými stromami v skutočnosti?
c1 c2 c3 c4
Ako sa zobrazí aleja červených stromov vyrastajúcich pozdĺž priamky q, ak
vzdialenosti medzi nimi sú v skutočnosti rovnaké, rovné dĺžke c1?
Meracie body pre hĺbkové priamky v základnej rovine sú dištančníky DL a Dp.
ĽAVÝ
DIŠTANČNÍK
PRAVÝ
DIŠTANČNÍK
H
DL
Dp
a
a
a
c1
c1
q
c4
c1
c1
c1
c3
a
c1
z
c2
c1
p
h

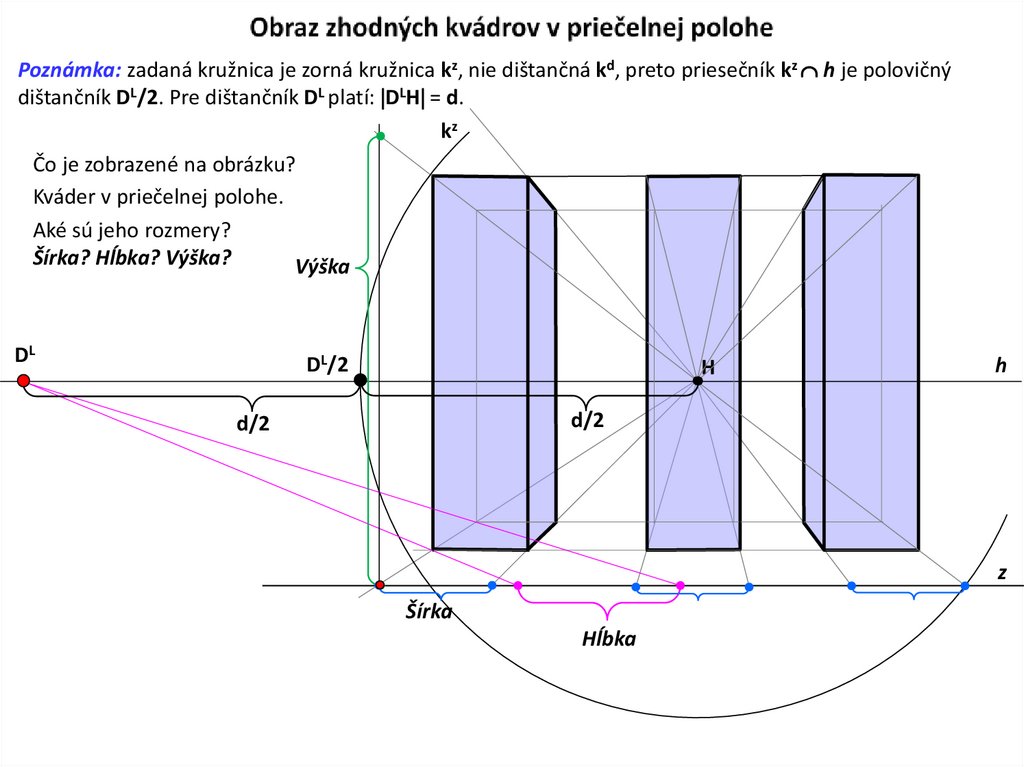
6. Obraz zhodných kvádrov v priečelnej polohe

Poznámka: zadaná kružnica je zorná kružnica kz, nie dištančná kd, preto priesečník kz h je polovičný
dištančník DL/2. Pre dištančník DL platí: DLH = d.
kz
Čo je zobrazené na obrázku?
Kváder v priečelnej polohe.
Aké sú jeho rozmery?
Šírka? Hĺbka? Výška?
Výška
DL
DL/2
H
h
d/2
d/2
z
Šírka
Hĺbka

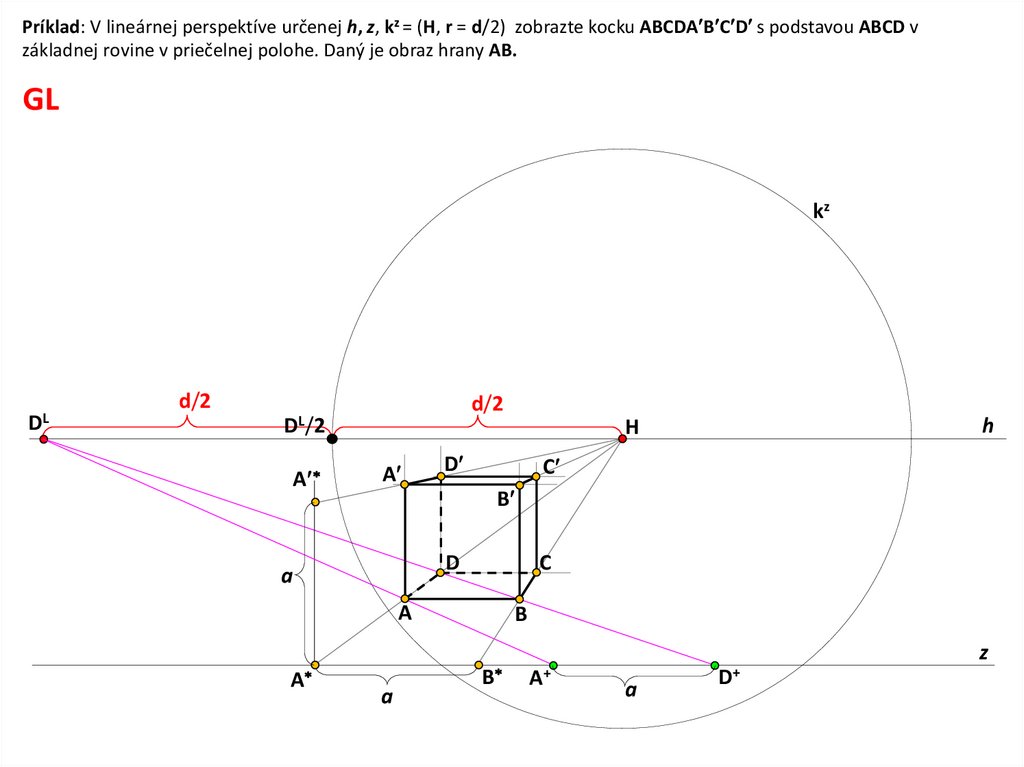
7.

Príklad: V lineárnej perspektíve určenej h, z, kz = (H, r = d/2) zobrazte kocku ABCDA B C D s podstavou ABCD v
základnej rovine v priečelnej polohe. Daný je obraz hrany AB.
GL
kz
DL
d/2
d/2
DL/2
A
A
D
C
B
D
a
C
A
A
h
H
a
B
B
z
A+
a
D+

8.

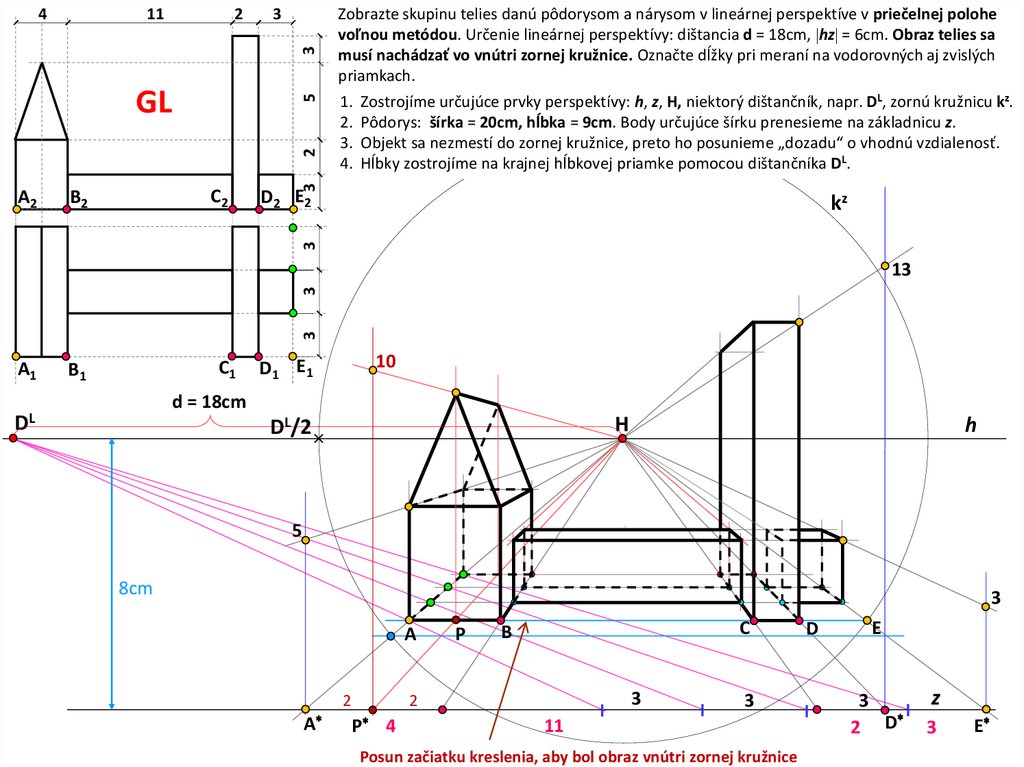
11
2
3
3
4
C2
B2
D2 E2
kz
3
A2
1. Zostrojíme určujúce prvky perspektívy: h, z, H, niektorý dištančník, napr. DL, zornú kružnicu kz.
2. Pôdorys: šírka = 20cm, hĺbka = 9cm. Body určujúce šírku prenesieme na základnicu z.
3. Objekt sa nezmestí do zornej kružnice, preto ho posunieme „dozadu“ o vhodnú vzdialenosť.
4. Hĺbky zostrojíme na krajnej hĺbkovej priamke pomocou dištančníka DL.
3
2
5
GL
Zobrazte skupinu telies danú pôdorysom a nárysom v lineárnej perspektíve v priečelnej polohe
voľnou metódou. Určenie lineárnej perspektívy: dištancia d = 18cm, hz = 6cm. Obraz telies sa
musí nachádzať vo vnútri zornej kružnice. Označte dĺžky pri meraní na vodorovných aj zvislých
priamkach.
3
3
13
A1
C1
B1
10
D1 E1
d = 18cm
DL
H
DL/2
h
5
8cm
3
A
A
P
C
B
3
2
2
P 4
3
11
Posun začiatku kreslenia, aby bol obraz vnútri zornej kružnice
D
E
3
2 D
z
3
E

9.

Plochy technickej praxe
Literatúra: e-skriptá
http://www.math.sk/skriptaDG2/1/
http://www.math.sk/skriptaDG2/2/

10.

Plocha je množina bodov v priestore, ktorá vznikne spojitým pohybom čiary u, ktorá nie je
dráhou tohto pohybu, pričom tvar čiary u sa počas pohybu môže meniť.
Čiara u sa nazýva tvoriaca čiara.
vA
u
vB
v
A
B
M
Každý bod krivky u sa pohybuje po nejakej krivke v.
Na ploche sú dve sústavy kriviek: u – krivky a v – krivky. Každým regulárnym bodom plochy
prechádza práve jedna krivka z každej sústavy.
Tereňová
10

11.

1. Matematické – poznáme analytické vyjadrenie
2. Empirické - topografické a grafické plochy
3. Geometrické – poznáme geometrické vzťahy
Matematické - plochy, ktoré môžeme vyjadriť analyticky (rovnicou alebo systémom rovníc):
1. Parametricky
2. explicitne
3. implicitne
x r. cos u. cos v
z r 2 x2 y2
x2 y2 z 2 r 2 0
y r. cos u. sin v
z r. sin u
r 0, u , v 0, 2
Príklad: guľová plocha so stredom [0,0,0] a polomerom r
Empirické plochy
- plochy, ktoré sú určené systémom bodov
alebo kriviek, príkladom sú topografické plochy.
Geometrické plochy
- plochy, ktoré sú určené geometrickými
vlastnosťami určujúcich prvkov a tvoriacich čiar
a spôsobom ich vytvárania.
1.
2.
3.
4.
5.
6.
Rotačné
Skrutkové
Priamkové
Klinové
Translačné
...............

12.

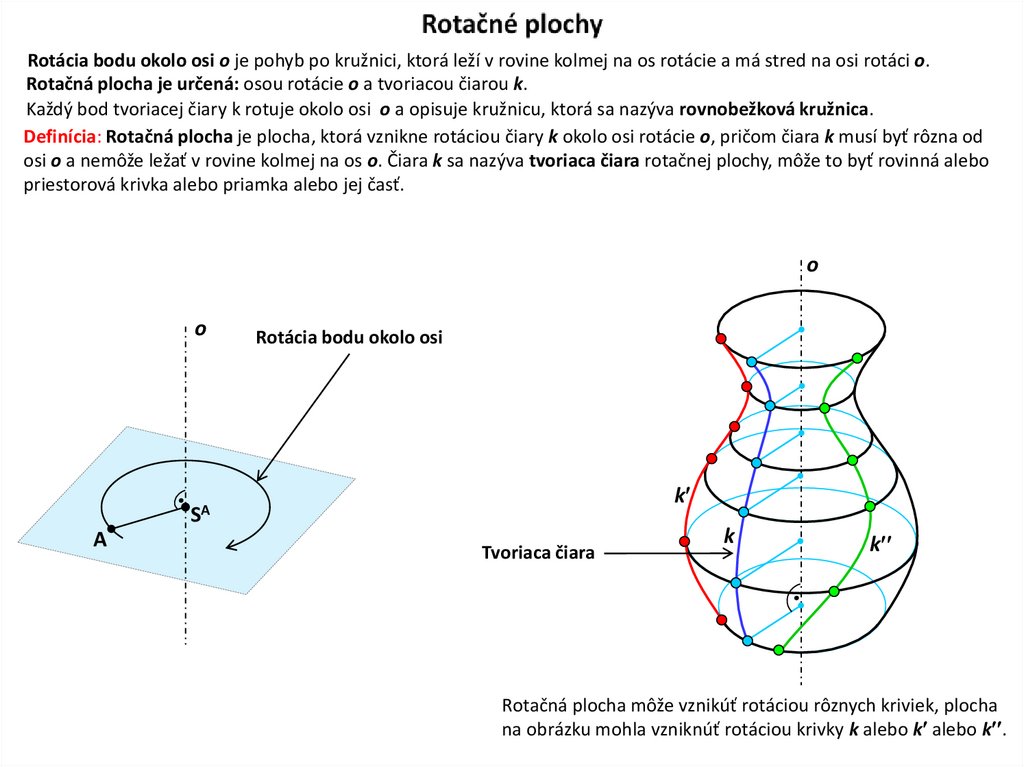
Rotačné plochy

13. Rotačné plochy

Rotácia bodu okolo osi o je pohyb po kružnici, ktorá leží v rovine kolmej na os rotácie a má stred na osi rotáci o.
Rotačná plocha je určená: osou rotácie o a tvoriacou čiarou k.
Každý bod tvoriacej čiary k rotuje okolo osi o a opisuje kružnicu, ktorá sa nazýva rovnobežková kružnica.
Definícia: Rotačná plocha je plocha, ktorá vznikne rotáciou čiary k okolo osi rotácie o, pričom čiara k musí byť rôzna od
osi o a nemôže ležať v rovine kolmej na os o. Čiara k sa nazýva tvoriaca čiara rotačnej plochy, môže to byť rovinná alebo
priestorová krivka alebo priamka alebo jej časť.
o
o
Rotácia bodu okolo osi
k
SA
A
Tvoriaca čiara
k
k
Rotačná plocha môže vznikúť rotáciou rôznych kriviek, plocha
na obrázku mohla vzniknúť rotáciou krivky k alebo k alebo k .

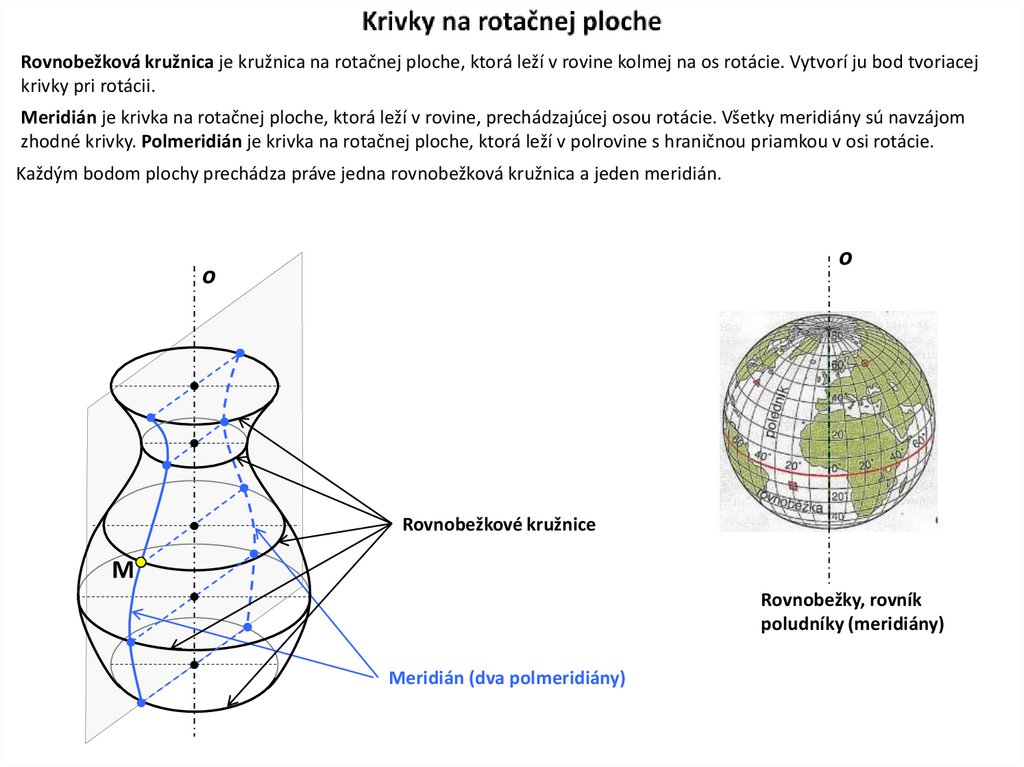
14. Krivky na rotačnej ploche

Rovnobežková kružnica je kružnica na rotačnej ploche, ktorá leží v rovine kolmej na os rotácie. Vytvorí ju bod tvoriacej
krivky pri rotácii.
Meridián je krivka na rotačnej ploche, ktorá leží v rovine, prechádzajúcej osou rotácie. Všetky meridiány sú navzájom
zhodné krivky. Polmeridián je krivka na rotačnej ploche, ktorá leží v polrovine s hraničnou priamkou v osi rotácie.
Každým bodom plochy prechádza práve jedna rovnobežková kružnica a jeden meridián.
o
o
Rovnobežkové kružnice
M
Rovnobežky, rovník
poludníky (meridiány)
Meridián (dva polmeridiány)

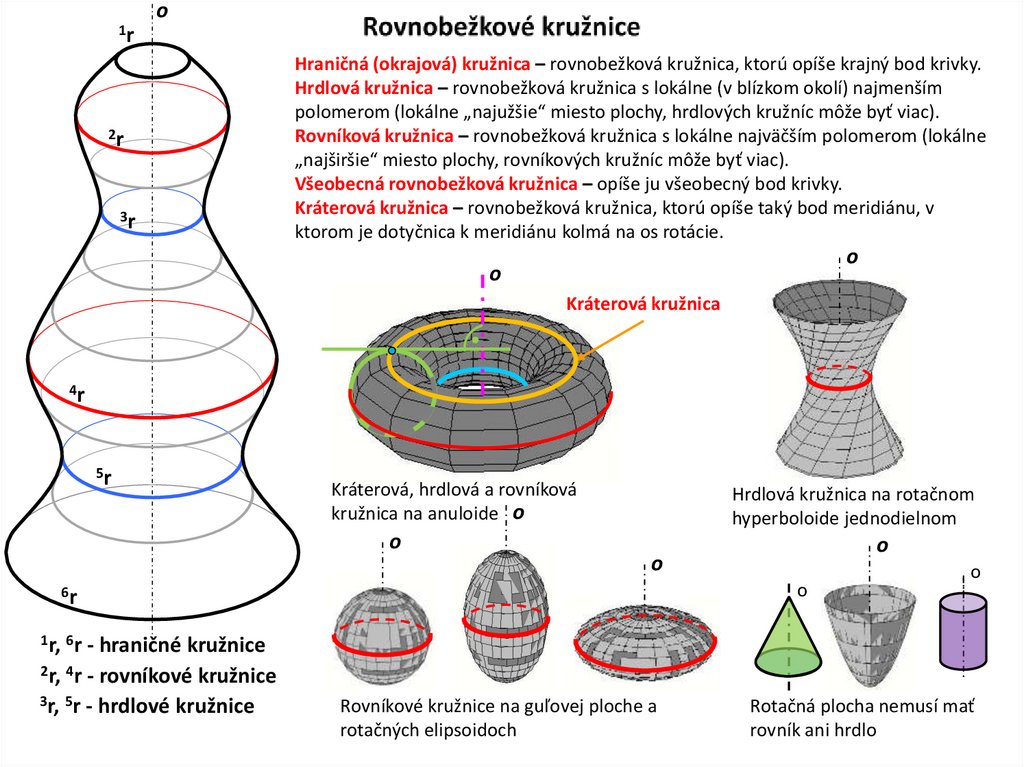
15. Rovnobežkové kružnice

o
1r
2r
3r
Hraničná (okrajová) kružnica – rovnobežková kružnica, ktorú opíše krajný bod krivky.
Hrdlová kružnica – rovnobežková kružnica s lokálne (v blízkom okolí) najmenším
polomerom (lokálne „najužšie“ miesto plochy, hrdlových kružníc môže byť viac).
Rovníková kružnica – rovnobežková kružnica s lokálne najväčším polomerom (lokálne
„najširšie“ miesto plochy, rovníkových kružníc môže byť viac).
Všeobecná rovnobežková kružnica – opíše ju všeobecný bod krivky.
Kráterová kružnica – rovnobežková kružnica, ktorú opíše taký bod meridiánu, v
ktorom je dotyčnica k meridiánu kolmá na os rotácie.
o
o
Kráterová kružnica
4r
5r
Kráterová, hrdlová a rovníková
kružnica na anuloide o
o
Hrdlová kružnica na rotačnom
hyperboloide jednodielnom
o
o
o
6r
o
1r, 6r - hraničné kružnice
2r, 4r - rovníkové kružnice
3r, 5r - hrdlové kružnice
Rovníkové kružnice na guľovej ploche a
rotačných elipsoidoch
Rotačná plocha nemusí mať
rovník ani hrdlo

16.

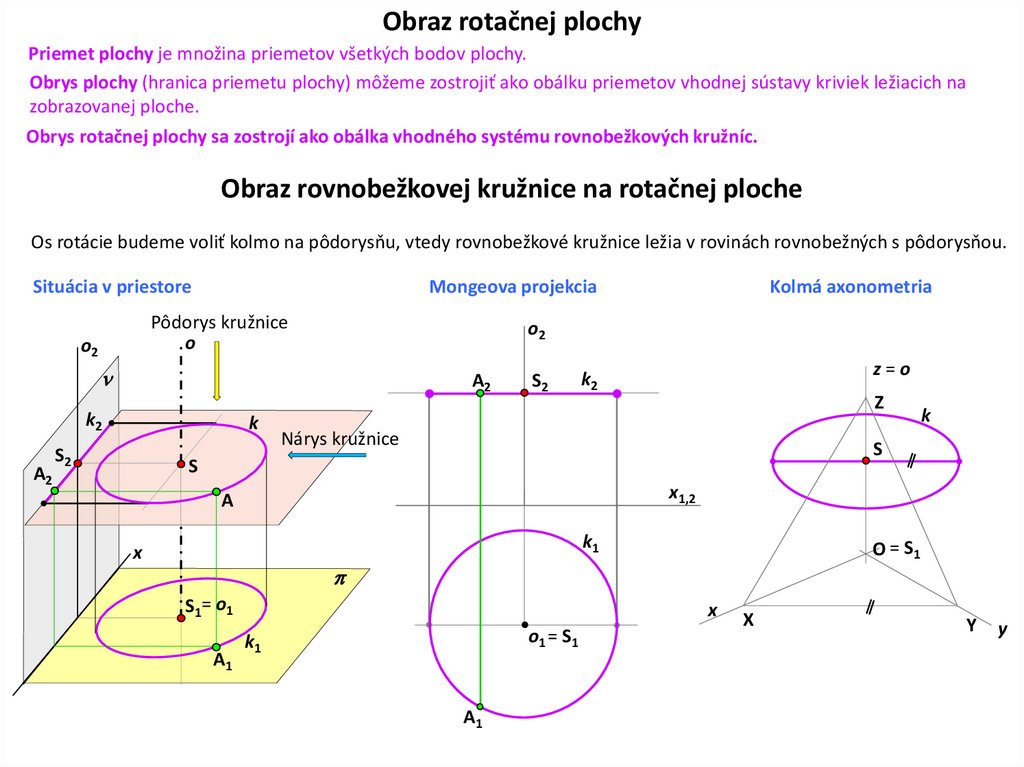
Obraz rotačnej plochy
Priemet plochy je množina priemetov všetkých bodov plochy.
Obrys plochy (hranica priemetu plochy) môžeme zostrojiť ako obálku priemetov vhodnej sústavy kriviek ležiacich na
zobrazovanej ploche.
Obrys rotačnej plochy sa zostrojí ako obálka vhodného systému rovnobežkových kružníc.
Obraz rovnobežkovej kružnice na rotačnej ploche
Os rotácie budeme voliť kolmo na pôdorysňu, vtedy rovnobežkové kružnice ležia v rovinách rovnobežných s pôdorysňou.
Situácia v priestore
Mongeova projekcia
Pôdorys kružnice
o
o2
o2
A2
k2
A2
k
S2
Kolmá axonometria
S2
z=o
k2
Z
Nárys kružnice
k
S
S
x1,2
A
k1
x
O = S1
S1= o1
A1
x
o1 = S1
k1
A1
X
Y
y

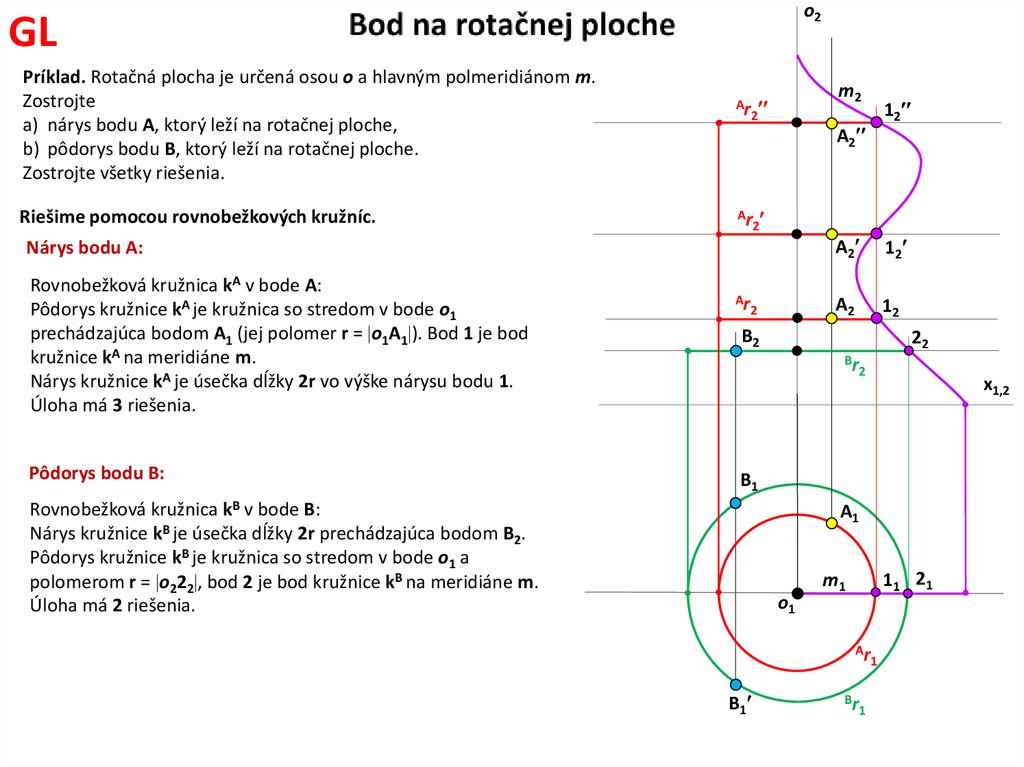
17. Bod na rotačnej ploche

o2
GL
Príklad. Rotačná plocha je určená osou o a hlavným polmeridiánom m.
Zostrojte
a) nárys bodu A, ktorý leží na rotačnej ploche,
b) pôdorys bodu B, ktorý leží na rotačnej ploche.
Zostrojte všetky riešenia.
Riešime pomocou rovnobežkových kružníc.
m2
Ar
2
A2
Ar
2
Nárys bodu A:
Rovnobežková kružnica kA v bode A:
Pôdorys kružnice kA je kružnica so stredom v bode o1
prechádzajúca bodom A1 (jej polomer r = o1A1 ). Bod 1 je bod
kružnice kA na meridiáne m.
Nárys kružnice kA je úsečka dĺžky 2r vo výške nárysu bodu 1.
Úloha má 3 riešenia.
Pôdorys bodu B:
Ar
2
12
A2
12
A2
12
B2
22
Br
2
x1,2
B1
Rovnobežková kružnica kB v bode B:
Nárys kružnice kB je úsečka dĺžky 2r prechádzajúca bodom B2.
Pôdorys kružnice kB je kružnica so stredom v bode o1 a
polomerom r = o222 , bod 2 je bod kružnice kB na meridiáne m.
Úloha má 2 riešenia.
A1
o1
11 21
m1
Ar
1
B1
Br
1

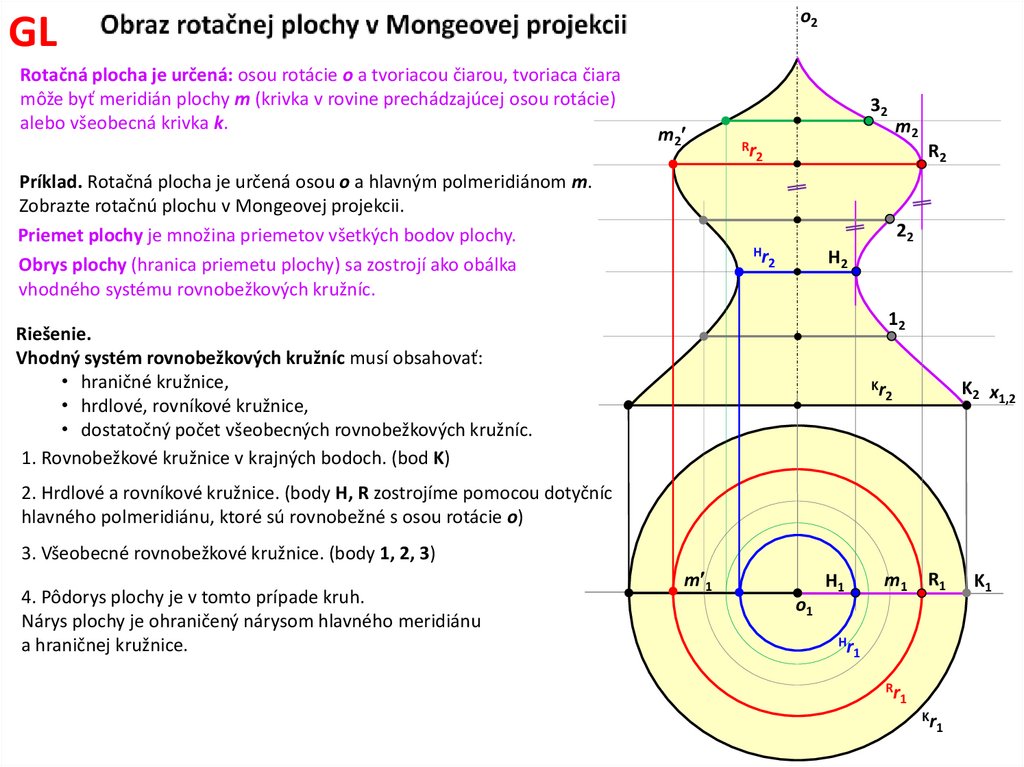
18. Obraz rotačnej plochy v Mongeovej projekcii

o2
GL
Rotačná plocha je určená: osou rotácie o a tvoriacou čiarou, tvoriaca čiara
môže byť meridián plochy m (krivka v rovine prechádzajúcej osou rotácie)
alebo všeobecná krivka k.
32
m2
Príklad. Rotačná plocha je určená osou o a hlavným polmeridiánom m.
Zobrazte rotačnú plochu v Mongeovej projekcii.
Priemet plochy je množina priemetov všetkých bodov plochy.
Obrys plochy (hranica priemetu plochy) sa zostrojí ako obálka
vhodného systému rovnobežkových kružníc.
m2
Rr
2
R2
22
Hr
2
H2
12
Riešenie.
Vhodný systém rovnobežkových kružníc musí obsahovať:
• hraničné kružnice,
• hrdlové, rovníkové kružnice,
• dostatočný počet všeobecných rovnobežkových kružníc.
1. Rovnobežkové kružnice v krajných bodoch. (bod K)
K2 x1,2
Kr
2
2. Hrdlové a rovníkové kružnice. (body H, R zostrojíme pomocou dotyčníc
hlavného polmeridiánu, ktoré sú rovnobežné s osou rotácie o)
3. Všeobecné rovnobežkové kružnice. (body 1, 2, 3)
4. Pôdorys plochy je v tomto prípade kruh.
Nárys plochy je ohraničený nárysom hlavného meridiánu
a hraničnej kružnice.
m 1
H1
m1
R1
o1
Hr
1
Rr
1
Kr
1
K1

19.

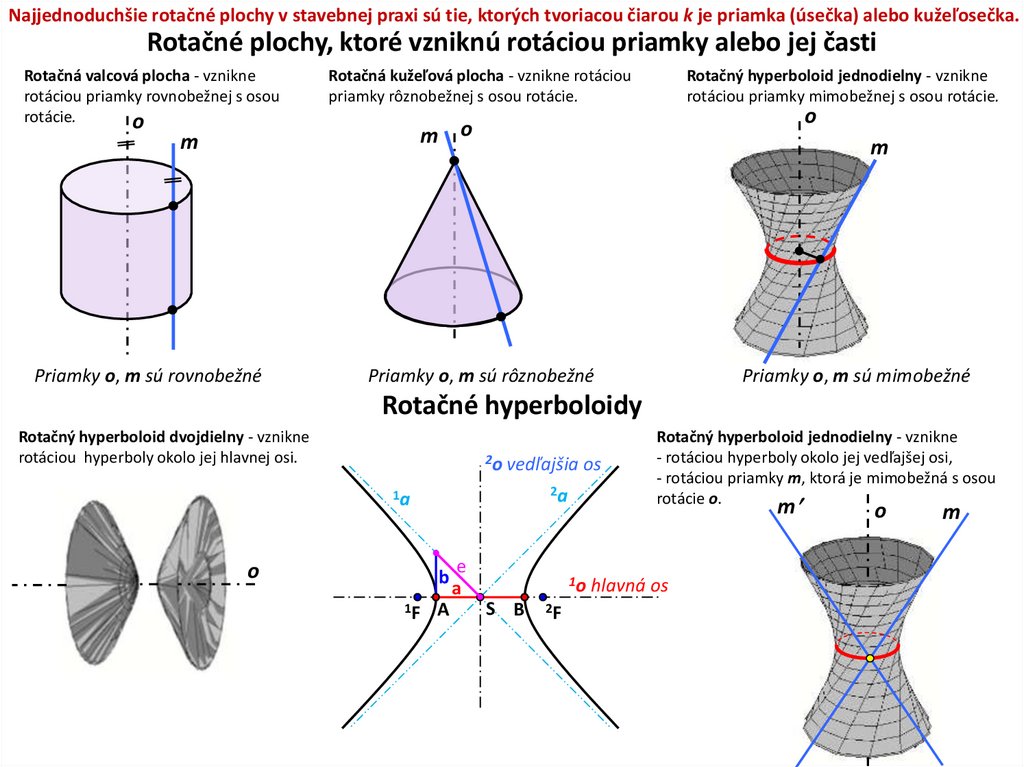
Najjednoduchšie rotačné plochy v stavebnej praxi sú tie, ktorých tvoriacou čiarou k je priamka (úsečka) alebo kužeľosečka.
Rotačné plochy, ktoré vzniknú rotáciou priamky alebo jej časti
Rotačná valcová plocha - vznikne
rotáciou priamky rovnobežnej s osou
rotácie.
o
Rotačná kužeľová plocha - vznikne rotáciou
priamky rôznobežnej s osou rotácie.
o
m o
m
Priamky o, m sú rovnobežné
Rotačný hyperboloid jednodielny - vznikne
rotáciou priamky mimobežnej s osou rotácie.
m
Priamky o, m sú rôznobežné
Priamky o, m súhttp://www.root.cz/
mimobežné
Rotačné hyperboloidy
Rotačný hyperboloid dvojdielny - vznikne
rotáciou hyperboly okolo jej hlavnej osi.
2o vedľajšia os
2a
1a
o
b
1F
A
e
a
Rotačný hyperboloid jednodielny - vznikne
- rotáciou hyperboly okolo jej vedľajšej osi,
- rotáciou priamky m, ktorá je mimobežná s osou
rotácie o.
m
1o hlavná os
S B
2F
o
m

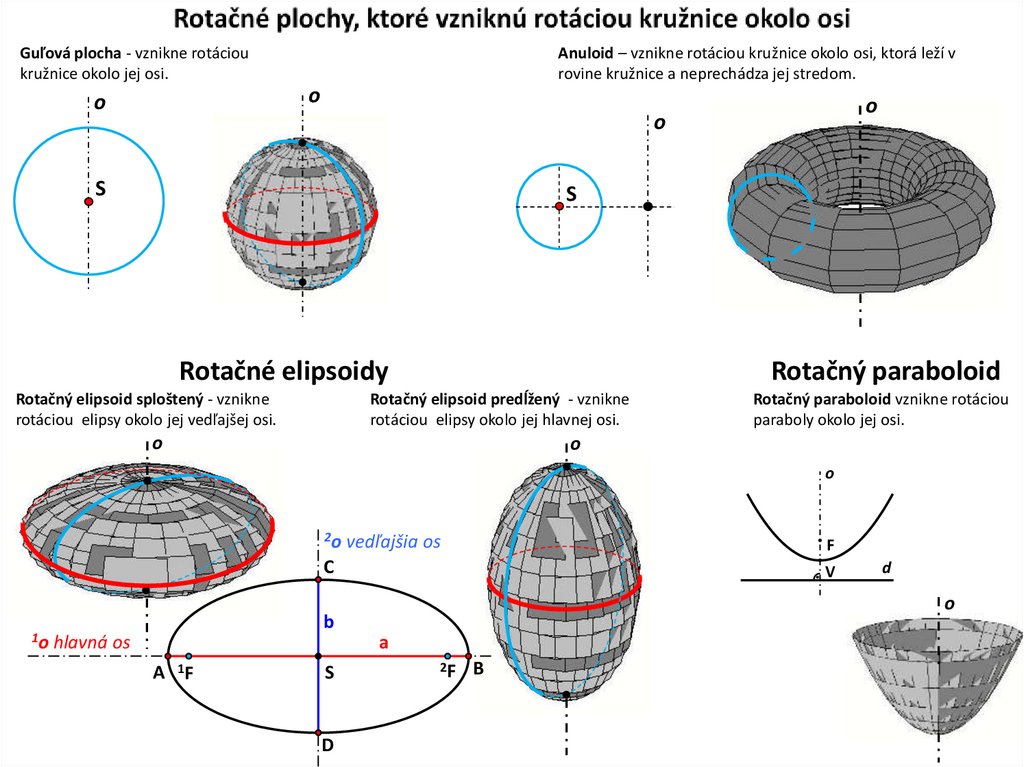
20. Rotačné plochy, ktoré vzniknú rotáciou kružnice okolo osi

Guľová plocha - vznikne rotáciou
kružnice okolo jej osi.
Anuloid – vznikne rotáciou kružnice okolo osi, ktorá leží v
rovine kružnice a neprechádza jej stredom.
o
o
o
o
S
S
Rotačné elipsoidy
Rotačný elipsoid sploštený - vznikne
rotáciou elipsy okolo jej vedľajšej osi.
Rotačný paraboloid
Rotačný elipsoid predĺžený - vznikne
rotáciou elipsy okolo jej hlavnej osi.
o
Rotačný paraboloid vznikne rotáciou
paraboly okolo jej osi.
o
o
2o vedľajšia os
F
C
V
o
b
1o hlavná os
a
A 1F
S
D
d
2F
B