История развития ДМ. Задачи Принцип Дирихле Основные правила комбинаторики Выборки. Комбинаторные числа

1.

История развития ДМ. Задачи
Принцип Дирихле
Основные правила комбинаторики
Выборки. Комбинаторные числа
Метод включений и исключений
Бином Ньютона. Полиномиальная формула
Рекуррентные соотношения
Производящие функции

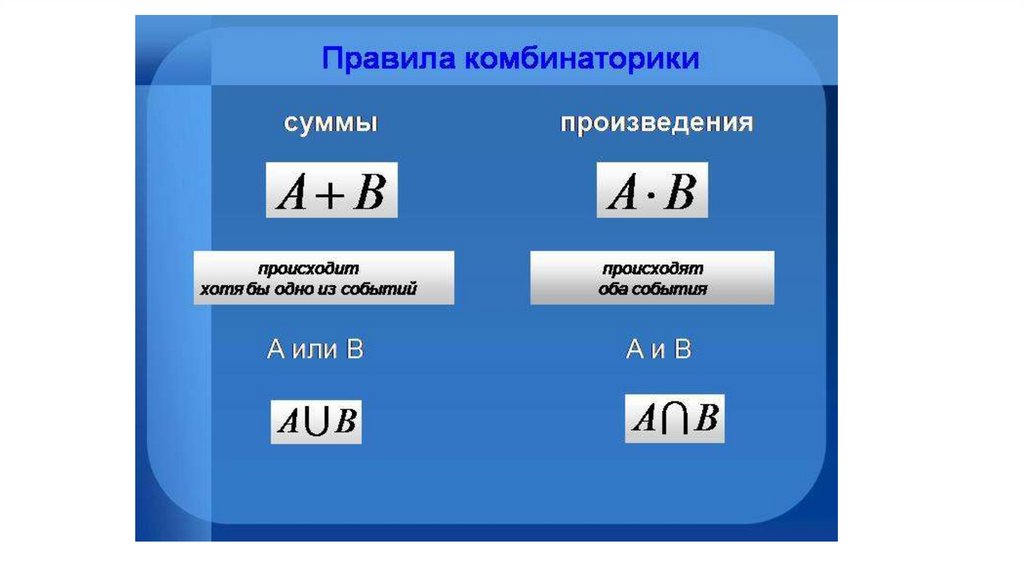
2. ОСНОВНЫЕ ПРАВИЛА КОМБИНАТОРИКИ

ПРАВИЛО СУММЫ
И ПРАВИЛО ПРОИЗВЕДЕНИЯ

3.

Определение.
Семейство множеств A1, A2, …, Ak
называется разбиением множества S, если
S = A1 A2 … Ak,
Ai P(S)
и Ai Aj = при i j.

4.

Теорема (правило суммы). Если S — конечное
множество, семейство множеств A1, A2, …, Ak является
разбиением множества S, т.е. S = A1 A2 … Ak,
Ai P(S) и Ai Aj = при i j, то справедливо
равенство |S| = |A1| + |A2| + … + |Ak|.

5.

При решении текстовых комбинаторных задач правило суммы
используют в следующей формулировке.
Правило суммы. Если некоторый объект A можно выбрать m
способами, а объект B — n способами, то выбор «либо A, либо B» можно
осуществить m + n способами.
Правило суммы в этой формулировке можно обобщить на случаи,
когда число объектов больше двух.

6.

«Тут уж не до рассуждений, тут выбор: либо одно, либо
другое.»
Фёдор Достоевский
«Преступление и наказание»

7.

При решении комбинаторных задач все изучаемые
комбинации разбивают на несколько классов, причем
каждая комбинация входит в один и только один класс,
тогда общее число комбинаций равно сумме чисел
комбинаций во всех классах.

8.

«О, как мучителен порой бывает
выбор меж двух зол!»
Александр Пушкин «Евгений
Онегин»

9.

10.

Пример 1 (правило суммы). В классе
учится 17 мальчиков и 19 девочек. Сколькими
способами
можно
назначить
одного
дежурного?
Решение
Дежурным
можно
назначить
либо
мальчика, либо девочку. Дежурным может
быть назначен либо любой из 17 мальчиков,
либо любая из 19 девочек.
По правилу суммы получаем, что одного
дежурного можно назначить 17 + 19 = 36
способами.

11.

Теорема (правило произведения).
Для конечных множеств A1, A2,
справедливо равенство
…,
|A1 х A2 х … х Ak| = = |A1| ∙ |A2| ∙ … ∙ |Ak|.
Ak

12.

При решении комбинаторных задач правило произведения
используют в следующей формулировке.
Правило произведения. Если некоторый объект A можно
выбрать m способами и если после каждого такого выбора
объект B можно выбрать n способами, то выбор пары «A и B»
можно осуществить m ∙ n способами.
Правило произведения в этой формулировке можно
обобщить на случаи, когда число объектов больше двух.

13.

«Выбор всегда труден, особенно когда
речь идёт о будущем.»
Иван Тургенев «Отцы и дети»

14.

15.

Пример 3 (правило произведения). В
чемпионате страны по шахматам участвует 17
человек.
Разыгрываются
медали:
золотая,
серебряная и бронзовая. Сколькими способами
они могут быть распределены?
Решение
Золотая медаль может быть получена любым
из 17 участников. Если золотая медаль получена
уже каким-либо участником, то на серебряную
медаль остается 16 претендентов. Аналогично,
если и золотая и серебряная медали уже
распределены, то на бронзовую медаль остается
15 претендентов.
По правилу произведения получаем, что
медали
могут
быть
распределены
17 · 16 · 15 = 4080 способами.

16.

17.

«Сумма полученных сведений и произведение
размышлений позволили Мастеру сделать
вывод, который оказался верным.»
Михаил Булгаков «Мастер и Маргарита»

18.

Пример 5 (правило произведения). Шесть человек
обменялись рукопожатиями друг с другом. Сколько
было сделано рукопожатий?

19.

Пример 5 (правило произведения). Шесть человек
обменялись рукопожатиями друг с другом. Сколько
было сделано рукопожатий?
Решение
Первого человека для рукопожатия можно выбрать
шестью способами, а второго — пятью. Однако если
поменять местами первого и второго человека, то
получим то же самое рукопожатие, поэтому после
применения правила произведения получившееся число
рукопожатий нужно разделить на 2:
(6 5) : 2 = 15.

20.

Пример 6 (правило произведения). Сколько пятибуквенных
слов можно составить из 33 букв, если допускаются
повторения, но никакие две соседние буквы не должны
совпадать (т. е. такие слова, как «пресс» и «ссора», не
допускаются)? Под словом здесь понимается любая
последовательность из пяти букв без пробелов.

21.

Пример 6 (правило произведения). Сколько пятибуквенных
слов можно составить из 33 букв, если допускаются
повторения, но никакие две соседние буквы не должны
совпадать (т. е. такие слова, как «пресс» и «ссора», не
допускаются)? Под словом здесь понимается любая
последовательность из пяти букв без пробелов.
Решение
На первом месте можно написать любую из 33 букв, а на
каждом из следующих мест — любую из 32 (исключается
предшествующая буква). По правилу произведения получаем,
что число слов равно: 33 32 32 32 32 = 33 324.

22.

Пример 7 (правило произведения). Сколькими
способами можно переставлять буквы в слове
«Карелия» так, чтобы не менялся порядок гласных
букв?

23.

Пример 7 (правило произведения). Сколькими способами можно
переставлять буквы в слове «Карелия» так, чтобы не менялся порядок
гласных букв?
Решение
Выпишем буквы «а», «е», «и», «я» в данном порядке. Тогда для
буквы «к» имеется 5 мест: _а_е_и_я_. После того как выписана буква
«к», имеется 6 мест для буквы «р», например, _а_е_к_и_я_, и далее
после того как выписана буква «р», имеется 7 мест для буквы «л»,
например, _р_а_е_к_и_я_.
По правилу произведения получаем, что число способов
перестановки букв равно: 5 6 7 = 210.

24.

1. Фёдор Достоевский, «Преступление и наказание»:
2. «Сумма усилий и произведение мыслей привели его
к этому решению, которое казалось неизбежным.»
3. Лев Толстой, «Война и мир»:
4. «Пьер понял, что сумма знаний и произведение
опыта дают возможность предугадать исход
событий.»
1. Иван Тургенев, «Отцы и дети»:
2. «Он видел, что сумма всех стараний и
произведение усилий не приводят к желаемому
результату.»
3. Александр Пушкин, «Евгений Онегин»:
4. «Сумма впечатлений и произведение чувств
рождали в душе Татьяны смутные ожидания.»

25.

Пример 9 (правило произведения). Имеется 3 курицы,
4 утки и 2 гуся. Сколько существует комбинаций для
выбора нескольких птиц так, чтобы среди выбранных
были и куры, и утки, и гуси?

26.

Пример
9
(правило
произведения).
Имеется
3
курицы,
4 утки и 2 гуся. Сколько существует комбинаций для выбора нескольких птиц
так, чтобы среди выбранных были и куры, и утки, и гуси?
Решение
Каждая из трех куриц может либо попасть в число отобранных, либо нет.
Поэтому по правилу произведения получаем, что число способов отбора кур
равно 2 2 2 = 23 = 8. Однако при этом надо отбросить один способ, при
котором ни одна из кур не попадет в число отобранных, поэтому число
способов отбора кур, удовлетворяющих условию задачи, равно 23 – 1 = 7.
Аналогично получаем, что число способов отбора уток равно 24 – 1 = 15,
а гусей — 22 – 1 = 3.
По правилу произведения получаем, что количество комбинаций для
выбора нескольких птиц так, чтобы среди выбранных были и куры, и утки, и
гуси, равно 7 15 3 = 315.

27.

Пример 12 (правило
суммы и правило
произведения).
Сколькими способами
из 28 костей домино
можно выбрать две
кости так, чтобы их
можно было приложить
друг к другу?

28.

Пример 12 (правило суммы и правило произведения). Сколькими способами из 28
костей домино можно выбрать две кости так, чтобы их можно было приложить друг к другу?
Решение
Первую кость можно выбрать 28 способами. При этом в 7 случаях выбранная кость —
«дубль»: «0 : 0», «1 : 1», «2 : 2», «3 : 3», «4 : 4», «5 : 5», «6 : 6», а в 21 случае — кость с разным
числом очков.
Если первая кость «дубль», то вторую кость можно выбрать 6 способами. Например, если
на первом шаге выбрана кость «1 : 1», то на втором шаге можно выбрать «0 : 1», «2 : 1»,
«3 : 1», «4 : 1», «5 : 1», «6 : 1».
Если же первая кость с разным числом очков, то вторую кость можно выбрать 12
способами. Например, если на первом шаге выбрана кость «3 : 5», то на втором шаге можно
выбрать «0 : 3», «1 : 3», «2 : 3», «3 : 3», «3 : 4», «3 : 6», «0 : 5», «1 : 5», «2 : 5», «4 : 5», «5 : 5»,
«5 : 6».
Разобьем все способы выбора на два класса: если первая кость «дубль», то относим этот
способ выбора к первому классу, а если первая кость с разным числом очков, то — ко второму.
По правилу произведения получаем, что в первом классе 7 · 6 = 42 способа выбора двух
костей домино, которые можно приложить друг к другу, а во втором классе — 21 · 12 = 252.
По правилу суммы общее число способов выбора двух костей домино равно сумме
способов выбора в обоих классах: 42 + 252 = 294.
Если не учитывать порядок, в котором выбирались кости, то способов выбора в два раза
меньше — 294 : 2 = 147.