Приложения дифференциального исчисления 15. Исследование функций с помощью производных (выпуклость, точки перегиба)

1. Приложения дифференциального исчисления

15. Исследование функций с
помощью производных
(выпуклость, точки перегиба)

2. Выпуклость графика функции (кривой)

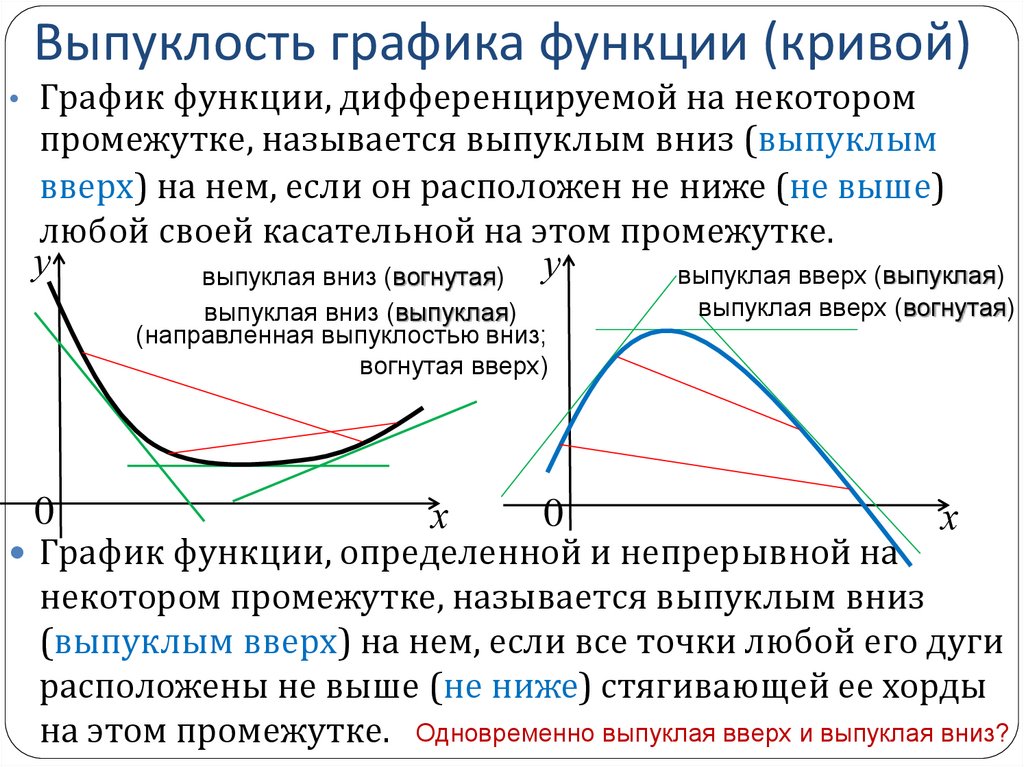
• График функции, дифференцируемой на некотором
промежутке, называется выпуклым вниз (выпуклым
вверх) на нем, если он расположен не ниже (не выше)
любой своей касательной на этом промежутке.
у
0
выпуклая вниз (вогнутая) у
выпуклая вниз (выпуклая)
(направленная выпуклостью вниз;
вогнутая вверх)
х
0
выпуклая вверх (выпуклая)
выпуклая вверх (вогнутая)
График функции, определенной и непрерывной на
х
некотором промежутке, называется выпуклым вниз
(выпуклым вверх) на нем, если все точки любой его дуги
расположены не выше (не ниже) стягивающей ее хорды
на этом промежутке. Одновременно выпуклая вверх и выпуклая вниз?

3. Выпуклость функции

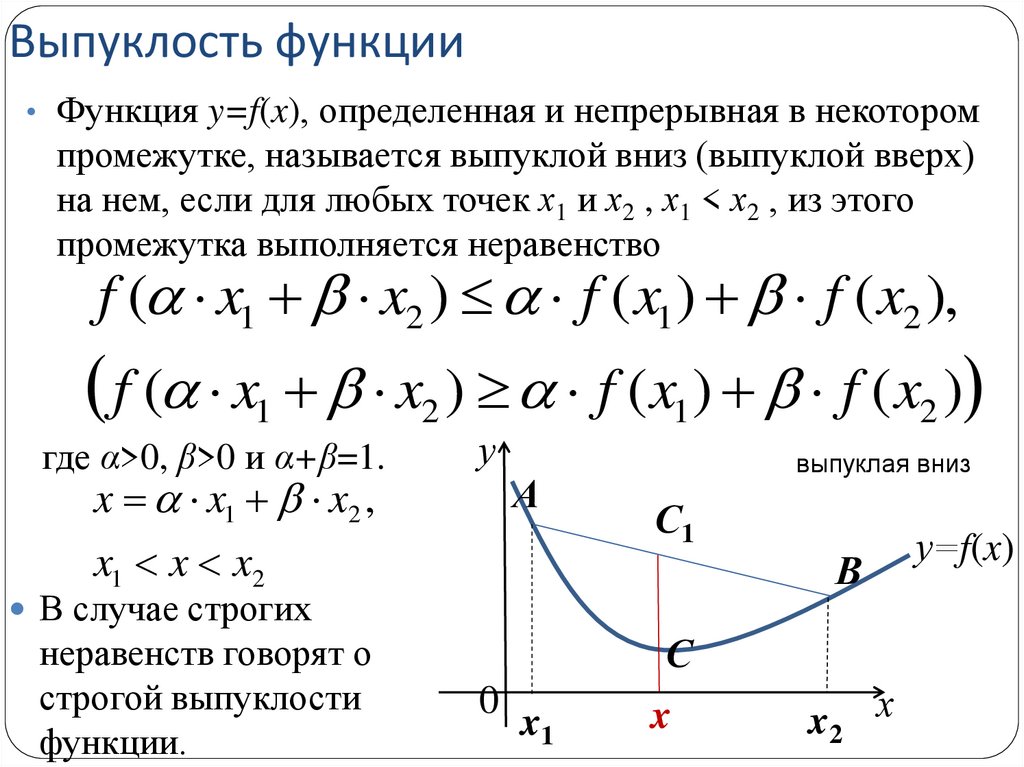
• Функция y=f(x), определенная и непрерывная в некотором
промежутке, называется выпуклой вниз (выпуклой вверх)
на нем, если для любых точек х1 и х2 , х1 < х2 , из этого
промежутка выполняется неравенство
f ( x1 x2 ) f ( x1 ) f ( x2 ),
f ( x1 x2 ) f ( x1 ) f ( x2 )
где α>0, β>0 и α+β=1.
x x1 x2 ,
у
А
x1 x x2
выпуклая вниз
С1
В
В случае строгих
неравенств говорят о
строгой выпуклости
функции.
С
0
x1
x
x2 х
у=f(x)

4. Направление выпуклости

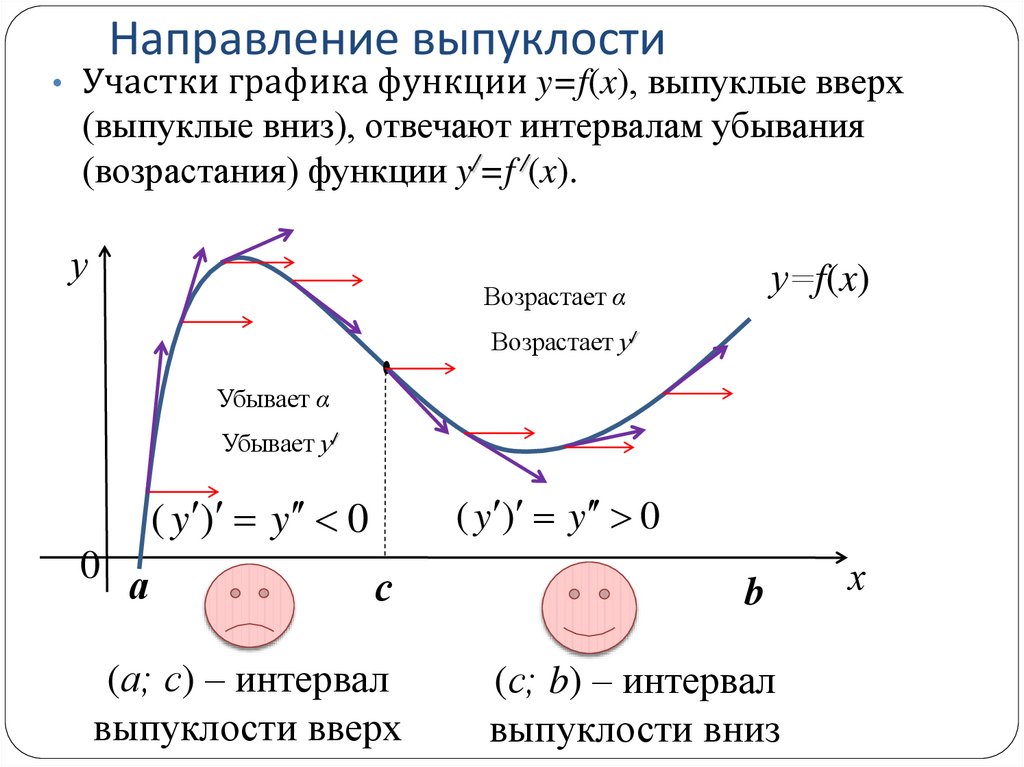
• Участки графика функции y=f(x), выпуклые вверх
(выпуклые вниз), отвечают интервалам убывания
(возрастания) функции y/=f /(x).
у
у=f(x)
Возрастает α
Возрастает у/
Убывает α
Убывает у/
( y ) y 0
( y ) y 0
0
а
с
b
(а; с) – интервал
выпуклости вверх
(с; b) – интервал
выпуклости вниз
х

5. Достаточный признак строгой выпуклости графика функции

Пусть функция y=f(x) определена и непрерывна
вместе со своей производной первого порядка на
интервале (a; b) и имеет на нем конечную
производную второго порядка.
Если во всех точках интервала (a; b) производная
второго порядка отрицательная (f //(x) < 0 ), то функция
y=f(x) (и её график) в этом интервале строго выпукла
вверх, а если же f //(x) > 0, то функции в этом
интервале строго выпукла вниз.
Для выпуклости функции на интервале (a; b)
необходимо и достаточно, чтобы на этом интервале
выполнялось неравенство y 0 ( y 0)

6. Точки перегиба

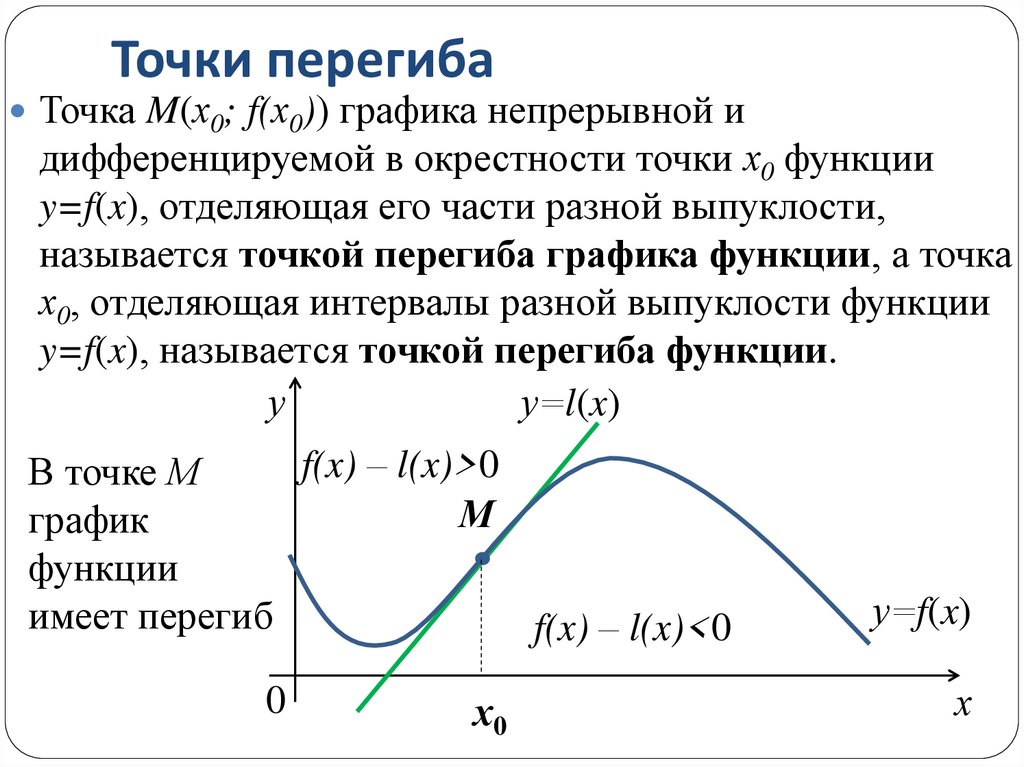
Точка M(х0; f(х0)) графика непрерывной и
дифференцируемой в окрестности точки х0 функции
y=f(x), отделяющая его части разной выпуклости,
называется точкой перегиба графика функции, а точка
х0, отделяющая интервалы разной выпуклости функции
y=f(x), называется точкой перегиба функции.
у=l(x)
у
f(x) – l(x)>0
В точке М
М
график
функции
имеет перегиб
f(x) – l(x)<0
0
х0
у=f(x)
х

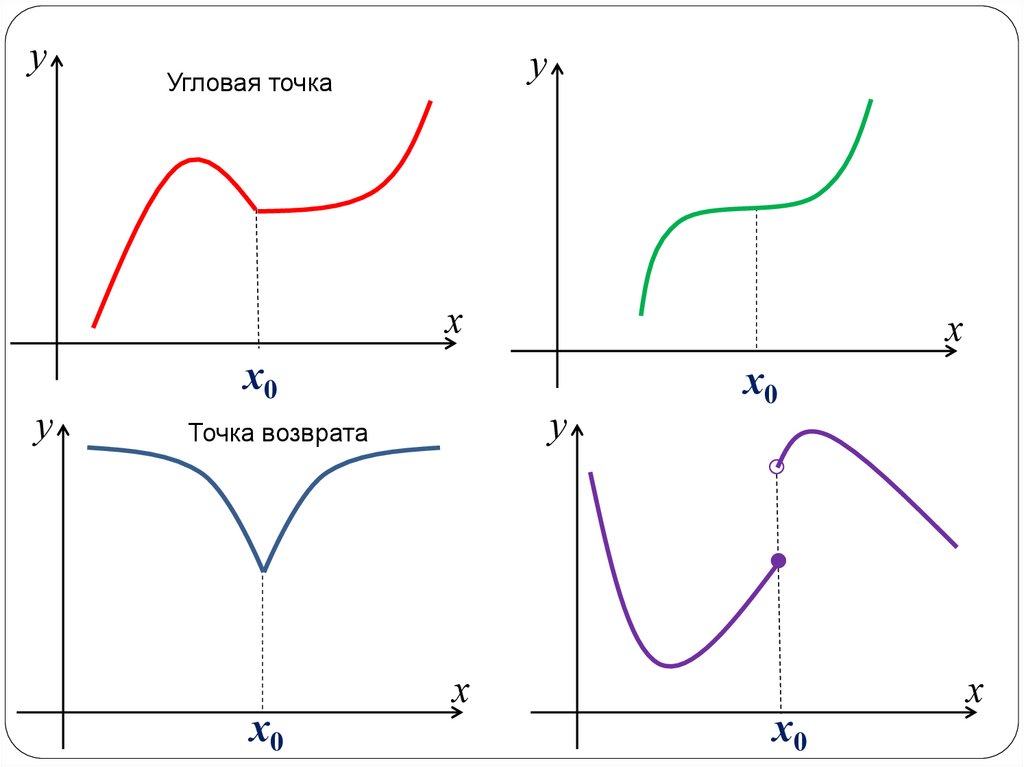
7.

у
у
Угловая точка
х
у
х0
у
Точка возврата
х0
х
х
х0
х0
х

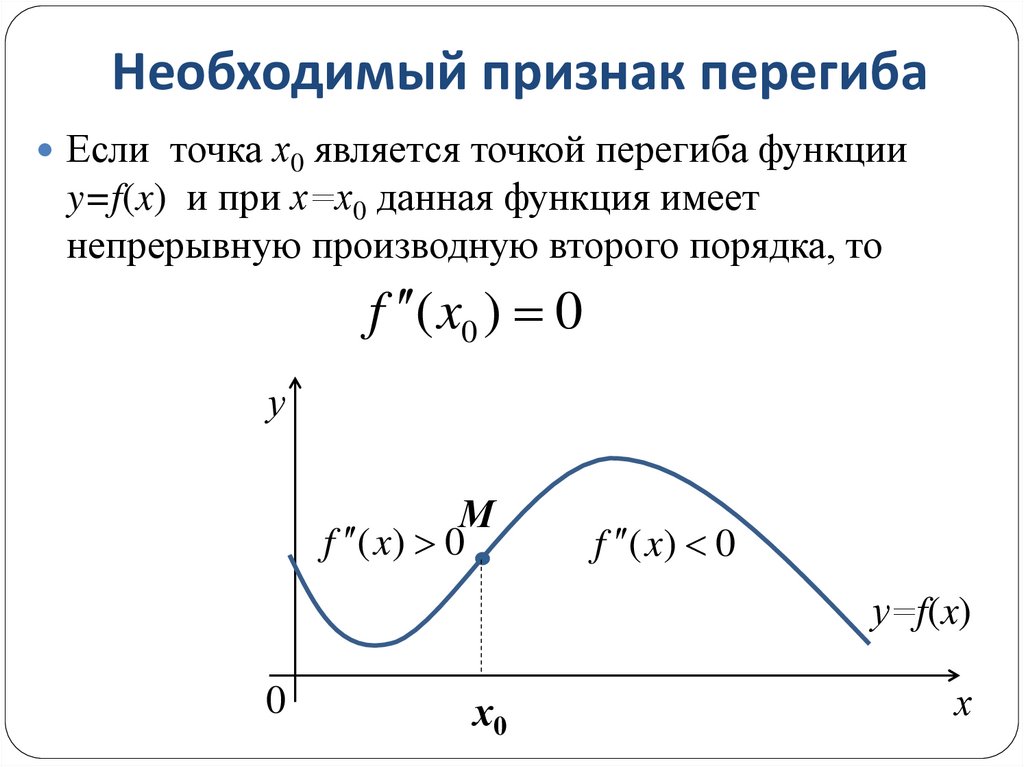
8. Необходимый признак перегиба

Если точка х0 является точкой перегиба функции
y=f(x) и при х=х0 данная функция имеет
непрерывную производную второго порядка, то
f ( x0 ) 0
у
М
f ( x) 0
f ( x) 0
у=f(x)
0
х0
х

9. Достаточный признак существования точек перегиба

Если производная второго порядка точке в x0 не
существует, равна бесконечности или равна нулю и
при переходе через эту точку вторая производная
меняет знак (слева и справа в окрестности точки х0),
то точка x0 есть точка перегиба функции.