Задачи. Риски

1. «Задачи. Риски»

канд. экон. наук
Юлия Валериевна Сухина

2. Оптимальность по Парето

Множество объектов, не имеющих предпочтения друг
перед другом одновременно по всем частным критериям,
называется множеством Парето. Множество Парето
называют также множеством неулучшаемых решений,
эффективных решений, переговорным множеством,
областью компромисса.
Объекты, входящие в множество Парето, называются
оптимальными по Парето.
Варианты, которые не доминируются любыми другими
вариантами, называются эффективными. Это означает, что
не существует такого варианта в допустимой области их
значений, что по всем, за исключением одного, показателям
данный вариант не хуже, и по одному показателю он является
наилучшим.

3. Оптимальность по Парето

Все альтернативы паретовского (эффективного)
множества являются несравнимыми.
Улучшение по одному из показателей выбранной
альтернативы ведет к ухудшению другого показателя
относительно
остальных
альтернатив
этого
множества.
Применение данного принципа позволяет
существенно снизить размерность решаемой задачи,
уменьшив число сравниваемых вариантов.
Рассмотрим случай сравнения альтернатив по
двум критериям К1 и К2.

4. Оптимальность по Парето

Предложен графический способ определения эффективных
альтернатив для следующих ситуаций в зависимости от того,
какие критерии применяются для оценки:
1. При увеличении показателей К1 и К2 эффективность
принятого решения увеличивается. Такими показателями
могут быть: прибыль, чистый доход, индекс доходности,
внутренняя норма доходности и т.д.
2. Увеличение эффективности принятого решения при
увеличении показателя К1 и снижении показателя К2.
Подобная ситуация возникает, например, при оценке
эффективности проектов по показателям внутренняя норма
доходности и срок окупаемости, интегральный эффект и
капитальные вложения.
3. Эффективность принимаемого решения повышается при
снижении показателей К1 и К2. В этом случае в качестве
показателей могут рассматриваться срок окупаемости,
себестоимость продукции, капитальные вложения и т.д.

5. Оптимальность по Парето

Пример 1. Определить эффективные альтернативы (проекты)
по двум критериям, которые стремятся к максимуму. Исходные
данные по семи инвестиционным проектам П1, П2, …, П7
представлены в табл. 1.

6. Оптимальность по Парето

Решение
На рис. 1 представлено множество точек,
характеризующих сравниваемые альтернативы
(проекты) по двум показателям.
Наиболее эффективным с позиции критерия К1
является шестой проект П6, а с позиций второго
критерия К2 – проект П1.
Через точки П1 и П6, расположенные ближе
всего к осям, проводим прямые параллельные осям
координат (в результате получаем прямоугольник
ABCD). Варианты, не попавшие в данный
прямоугольник (П2 и П4), исключаются из
рассмотрения.

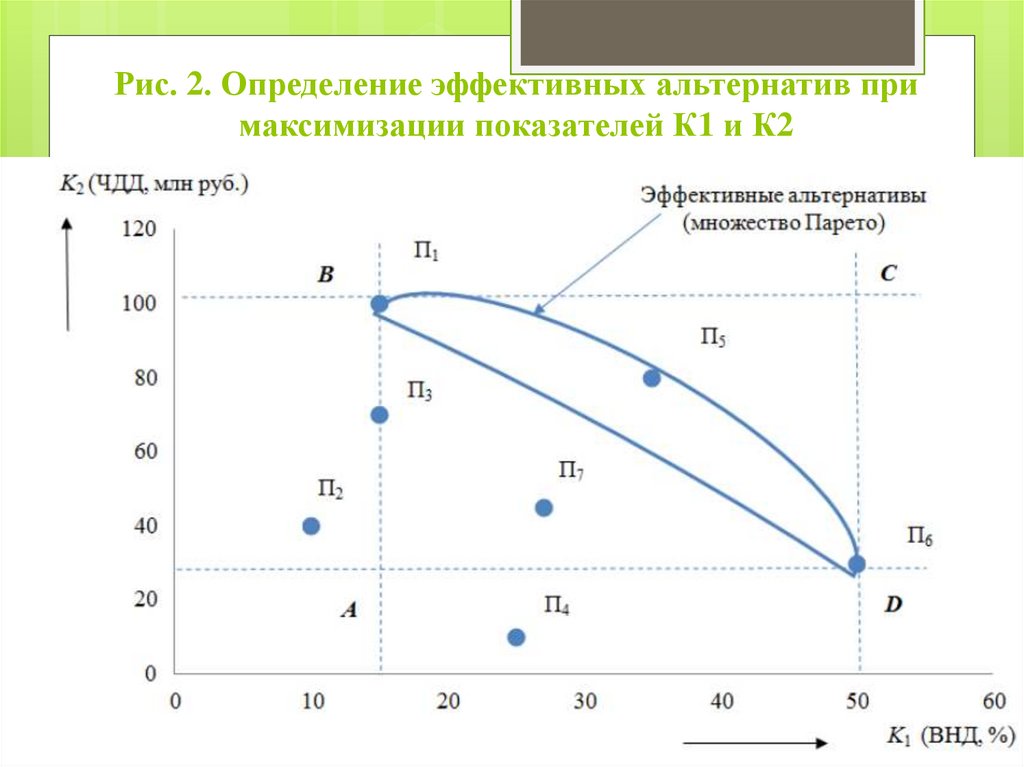
7. Рис. 2. Определение эффективных альтернатив при максимизации показателей К1 и К2

8. Оптимальность по Парето

В качестве вариантов, подлежащих сравнению,
рассматриваются проекты П1, П3, П5, П6 и П7.
В результате их сравнения проекты П3 и П7
исключаются из рассмотрения, так как уступают
вариантам П1 и П5 соответственно по обоим
показателям (П1 и П3 имеют одинаковые значения
показателя К1), но проект П5 характеризуется
большим значением показателя К2.
Таким образом, в множестве эффективных
решений остаются проекты П1, П5 и П6. Эти
варианты являются несравнимыми.

9. Оптимальность по Парето

Пример 2. Определить эффективные альтернативы
(проекты) по двум критериям, один из которых стремиться к
максимуму, а другой к минимуму. Исходные данные по семи
инвестиционным проектам представлены в табл. 2.
Исходные данные для определения эффективных
альтернатив
К1
min и К2
max

10. Оптимальность по Парето

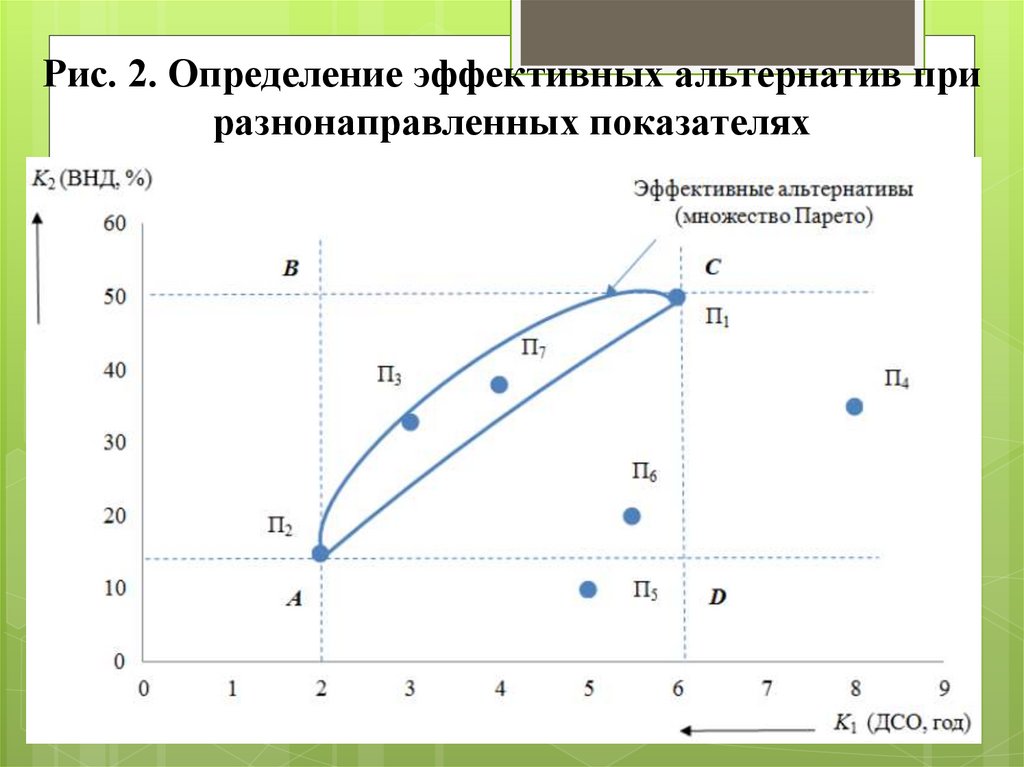
В данной ситуации по показателю К1 лучшим
является проект П2, а по показателю К2 – проект П1
(рис. 2). Используя подход, описанный в предыдущем
примере, формируем прямоугольник ABCD. Проекты,
не вошедшие в данный прямоугольник, исключаются из
рассмотрения как неэффективные (проекты П4 и П5).
Варианты П1, П2, П3, П6 и П7, принадлежащие
прямоугольнику ABCD, подлежат сравнению. При этом
варианты П3 и П7 доминируют над вариантом П6,
поэтому проект П6 следует признать неэффективным.
Оставшиеся варианты проектов П1, П2, П3 и П7 –
несравнимы по показателям К1 и К2.

11. Рис. 2. Определение эффективных альтернатив при разнонаправленных показателях

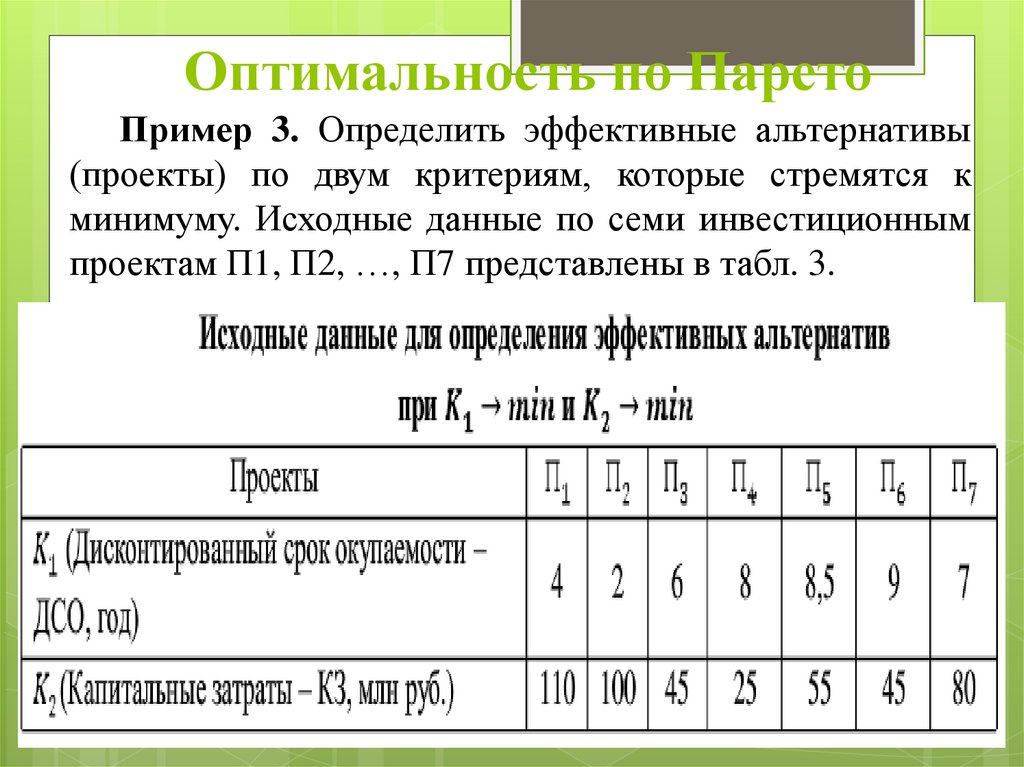
12. Оптимальность по Парето

Пример 3. Определить эффективные альтернативы
(проекты) по двум критериям, которые стремятся к
минимуму. Исходные данные по семи инвестиционным
проектам П1, П2, …, П7 представлены в табл. 3.

13. Оптимальность по Парето

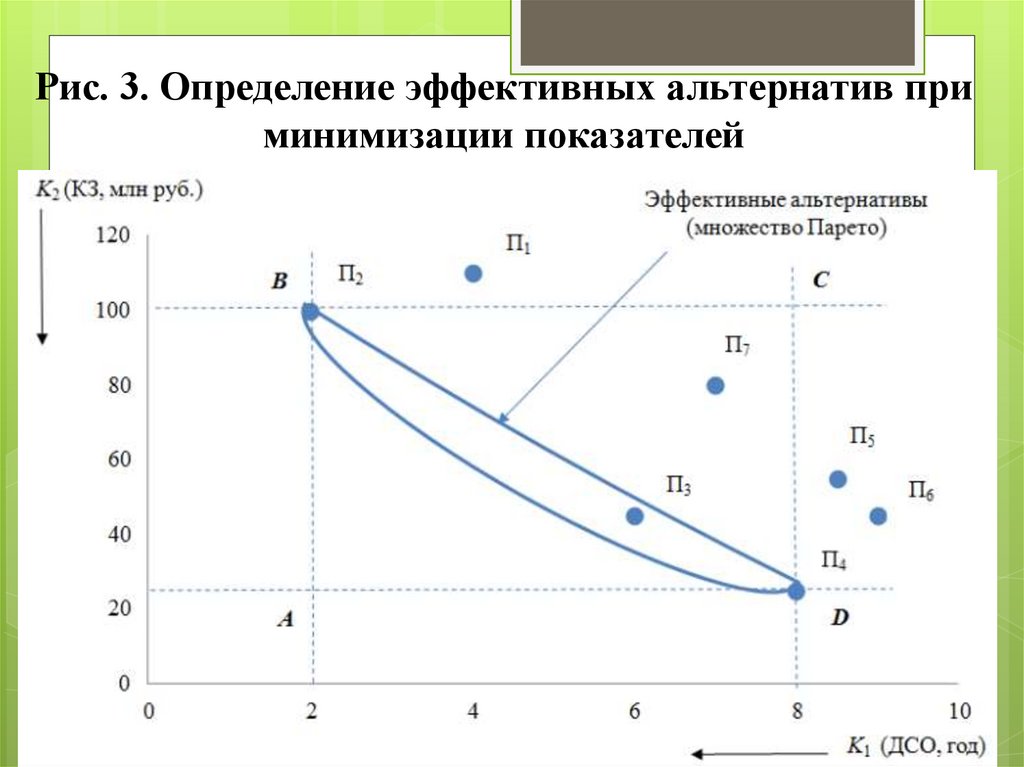
Решение
Наиболее целесообразным с позиции критерия К1
является проект П2, а с позиций второго критерия К2 –
проект П4 (рис. 3).
Через точки П2 и П4 проводим прямые параллельные
осям координат и получаем прямоугольник ABCD.
Варианты, не попавшие в данный прямоугольник (П1, П5
и П6), исключаются из рассмотрения. Сравнению
подлежат варианты П2, П3, П4 и П7. Вариант П7
исключается из рассмотрения, так как уступает варианту
П3 по обоим показателям К1 и К2.
Оставшиеся варианты П2, П3, П4 несравнимы, потому
что характеризуются показателями, один из которых
«лучше», а другой – «хуже» сравниваемых вариантов.

14. Рис. 3. Определение эффективных альтернатив при минимизации показателей