Похожие презентации:
Оценка качества работы классификаторов
1. Оценка качества работы классификаторов
Материалы статьи.Автор: Владимир Вежневец
2. Основные понятия
Задача классификации заключается вразбиении множества объектов на классы
(категории) по определенному критерию.
Объекты в пределах одного класса считаются
эквивалентными с точки зрения критерия
разбиения.
Классы часто бывают неизвестны заранее и
могут формироваться динамически.
3.
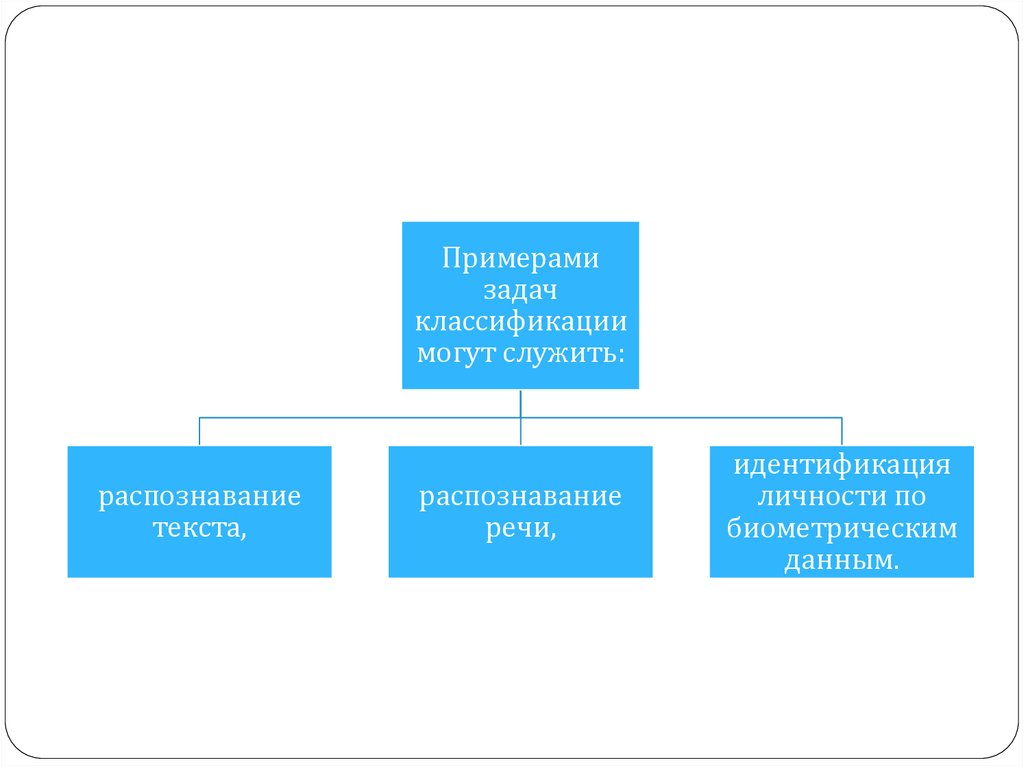
Примерамизадач
классификации
могут служить:
распознавание
текста,
распознавание
речи,
идентификация
личности по
биометрическим
данным.
4. Рассмотрим упрощенную задачу
Пусть количество классов равняется двум.Цель задачи: автоматическое обнаружение
некоторого события.
Пример задачи - обнаружение присутствия
лица человека на изображении.
5.
Объект представлен векторомпризнаков (числовых
характеристик) объекта.
Каждый элемент вектора
признаков несет информацию о
некотором свойстве объекта.
6. Классификатор
Классификаторомназовем функцию,
которая по вектору
признаков объекта
выносит решение,
какому именно
классу он
принадлежит:
7.
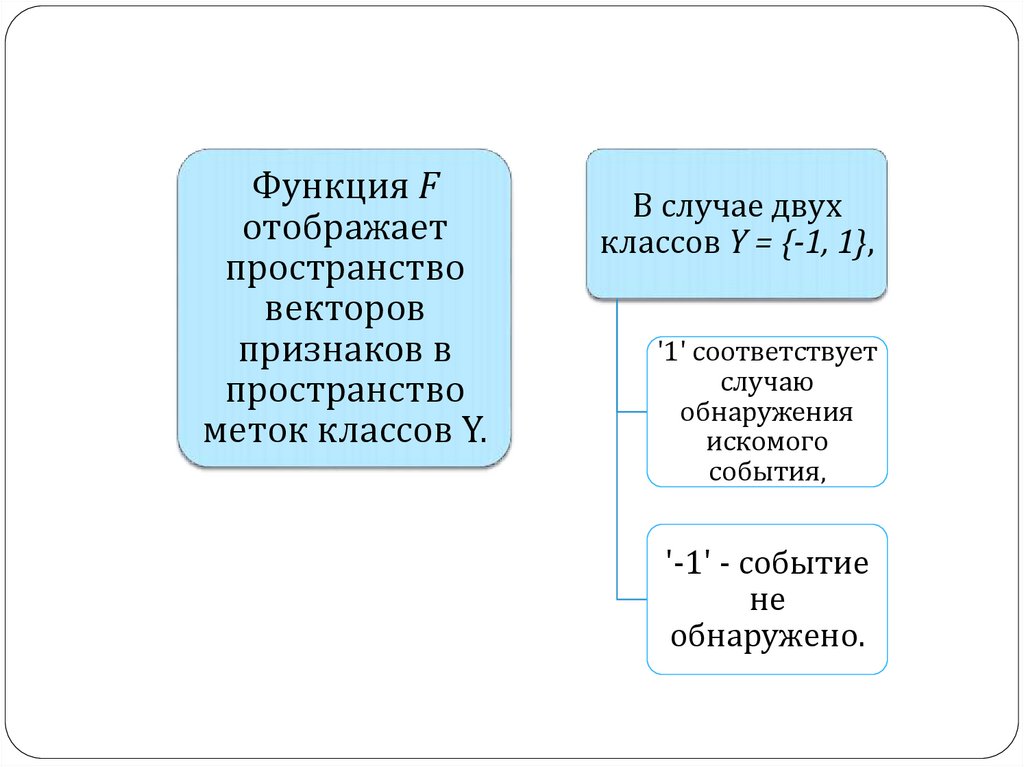
Функция Fотображает
пространство
векторов
признаков в
пространство
меток классов Y.
В случае двух
классов Y = {-1, 1},
'1' соответствует
случаю
обнаружения
искомого
события,
'-1' - событие
не
обнаружено.
8. Обучение с учителем
Для обучения классификатора нам доступеннекоторый набора векторов {x} , для которых
известна их истинная принадлежность к одному
из классов.
Для обучения классификатора используется только
часть данных, которая называется тренировочным
набором.
После того как обучение классификатора на
тренировочном наборе завершено, необходимо
оценить качество получившегося
классификатора.
9.
Целью тренировки классификатора являетсяувеличение вероятности верной
классификации данных, в момент тренировки
недоступных (unseen data).
Раз так - оценка качества классификации
тренировочных данных не является
адекватной мерой для оценки работы
классификатора на новых, в процессе
тренировки не использованных, данных.
10. Переобучение
При тренировке классификаторов существуетопасность того, что классификатор будет
слишком хорошо подогнан под тренировочные
данные, что может привести к плохим
результатам на новых (unseen) данных.
Эта проблема называется <перетренировкой>
или <переобучением> классификатора.
11. Переобучение может быть не обнаружено
Принятие решения о качествеполучившегося классификатора
на основании проверки на
тренировочных данных может
привести к тому, что
переобучение (если оно
присутствует) может не быть
обнаружено.
12. Альтернатива:
оценка производительностина тестовом наборе наборе данных,
размеченных по классам, но
не использовавшимся в
процессе тренировки.
13. Экспериментальная оценка
Обычно оценкапроизводительности производится
экспериментально, поскольку для
аналитической оценки требуется
построить формальную
спецификацию задачи, а многие из
задач распознавания существенно
неформальны
14.
Экспериментальная оценка обычноизмеряет производительность
классификатора.
Под производительностью в данном
случае понимается его способность
принимать верные решения
(вероятность верной классификации).
15. Базовые характеристики
16.
Базовыми характеристиками качестваклассификации являются уровни ошибок
первого и второго рода (error rates).
Ошибка второго рода Ошибка первого рода "ложное обнаружение"
это "ложный пропуск"
(false positive), когда
(false negative), когда
при отсутствии
интересующее нас
события ошибочно
событие ошибочно не
выносится решение о
обнаруживается.
его присутствии.
17.
Пусть количество объектов втестовом наборе равно N,
• Np количество "положительных" (c меткой '1')
объектов,
• Nn -количество объектов "отрицательных"
(с меткой '-1').
N=Np+Nn.
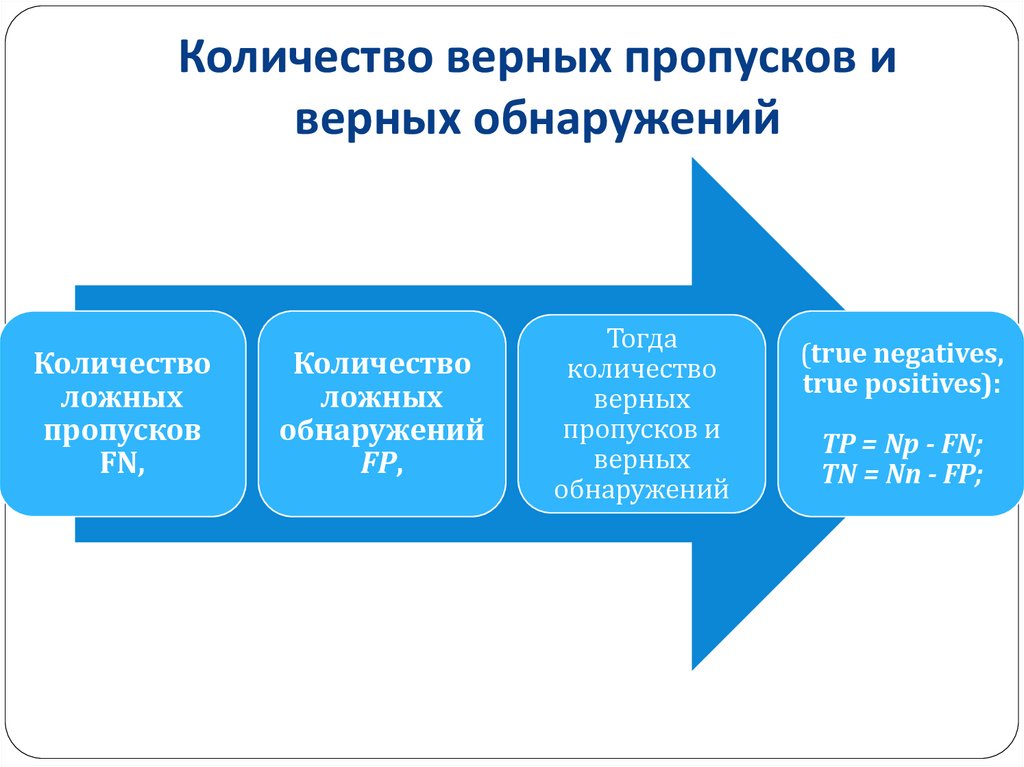
18. Количество верных пропусков и верных обнаружений
Количестволожных
пропусков
FN,
Количество
ложных
обнаружений
FP,
Тогда
количество
верных
пропусков и
верных
обнаружений
(true negatives,
true positives):
TP = Np - FN;
TN = Nn - FP;
19. Нормированные уровни ошибок первого и второго рода
nFN=FN / Np * 100%;nFP = FP / Nn * 100%;
nTN=TN / Nn * 100%;
nTP = TP / Np * 100%;
20.
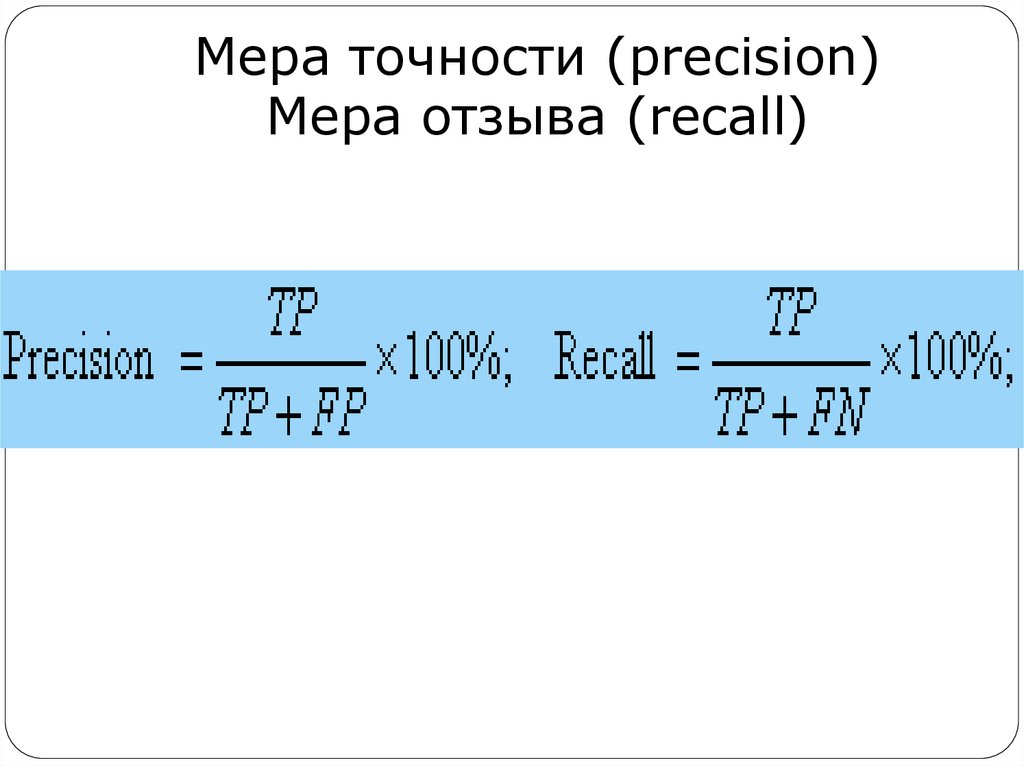
21. Мера точности (precision) Мера отзыва (recall)
22.
Отзыв измеряет долю верногораспознавания относительно всех
объектов интересующего нас класса,
совпадает с nTP.
Точность измеряет долю верных
обнаружений среди всех
обнаруженных объектов.
23. ROC-кривая
24.
Классификатор можетсодержать некоторые
дополнительные параметры,
позволяющие уже после
проведенного обучения
варьировать соотношение
верных и ложных обнаружений.
25. Модельный пример
Предположим, поставлена задачанаучиться отличать баскетболистов от
футболистов исключительно по росту.
Известно, что обычно в баскетбол
играют спортсмены высокого роста, но
далеко не всегда.
Также известно, что футболисты обычно
ниже баскетболистов, хотя и среди них
встречаются достаточно высокие люди.
26. Вектор признаков состоит только из одного компонента h (роста).
Рассмотрим классификатор, производящий решениена основе близости этого признака к среднему
значению на тренировочной выборке спортсменов.
В процессе тренировки вычисляется среднее
значение роста для обоих классов Hb, Hf. Пусть Hb > Hf.
Тогда требуется выбрать величину порога Hb >= T >=
Hf, по которому мы будем принимать решение.
27.
Чем ближе будет эта величина к Hb, темменьше вероятность ложного обнаружения
баскетболиста (ошибки второго рода).
В то же время, чем она ближе к Hf тем меньше
вероятность ошибочного пропуска
баскетболиста (ошибки первого рода).
Выбор величины T влияет на соотношение nFP
и nTP.
28.
Такие соотношения выражаются ROC-кривойметода (receiver operator characteristic - ROC
curve).
Английское название пришло из области
обработки сигналов.
Кривая выражает соотношение уровня верных
(nTP) и ложных обнаружений (nFP).
29.
Такие соотношения выражаются ROC-кривойметода (receiver operator characteristic - ROC
curve).
Английское название пришло из области
обработки сигналов.
Кривая выражает соотношение уровня верных
(nTP) и ложных обнаружений (nFP).
30.
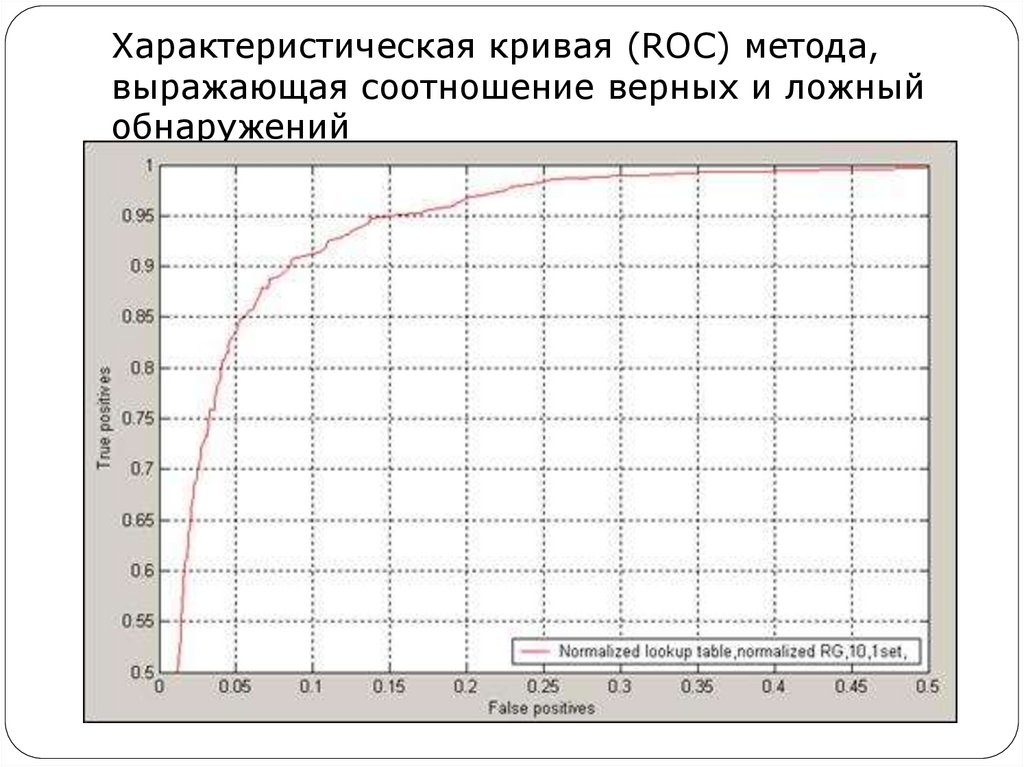
Рисунок демонстрирует кривую ROCдля метода распознавания цвета кожи,
основанного на нормированной
таблице частот.
Построение кривой ROC обычно
производится путем варьирования
параметров классификатора и
фиксации получающихся nTP и nFP.
31. Характеристическая кривая (ROC) метода, выражающая соотношение верных и ложный обнаружений
32. Способы разделения данных на тренировочный и тестовый наборы
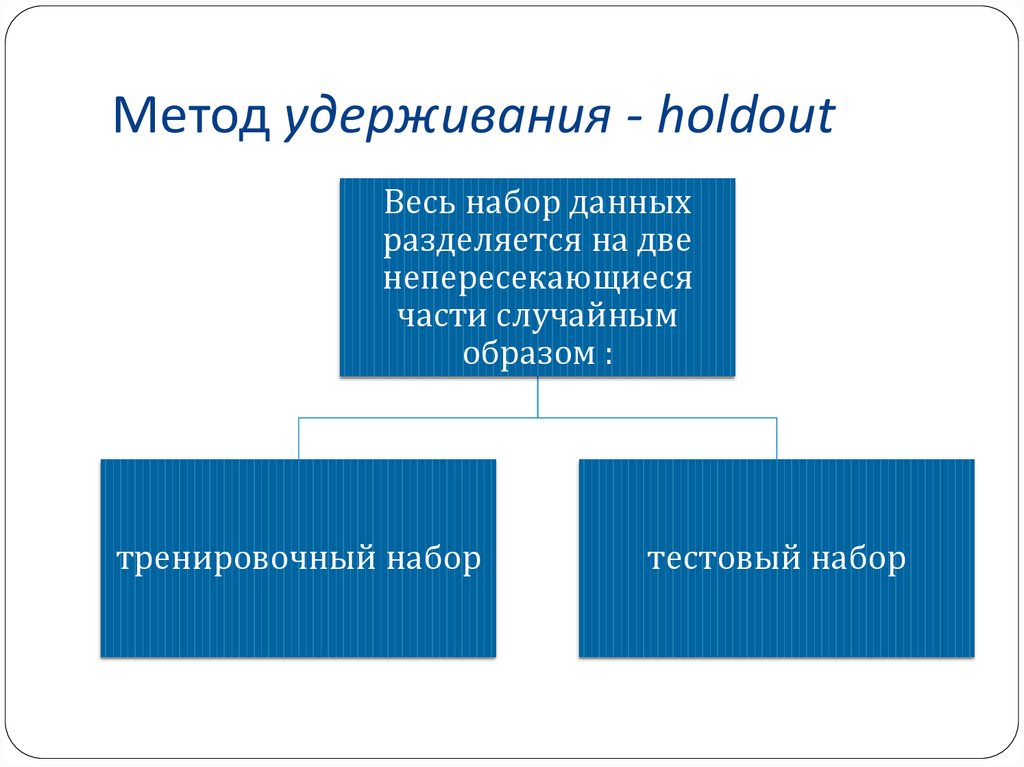
33. Метод удерживания (Holdout)
В случае, когда объем данныхдоступных для тренировки и
проверки классификатора
достаточно велик, часть
данных можно попридержать
до тестирования, и не
использовать для тренировки.
34. Метод удерживания - holdout
Весь набор данныхразделяется на две
непересекающиеся
части случайным
образом :
тренировочный набор
тестовый набор
35.
Обучение производится на тренировочном,проверка на тестовом наборах.
Обычно, для тестирования отводится от 1/10 до
1/3 всего доступного набора данных.
Для увеличения надежности подобная процедура
удержания части данных производится несколько
раз, и результат усредняется (repeated holdout).
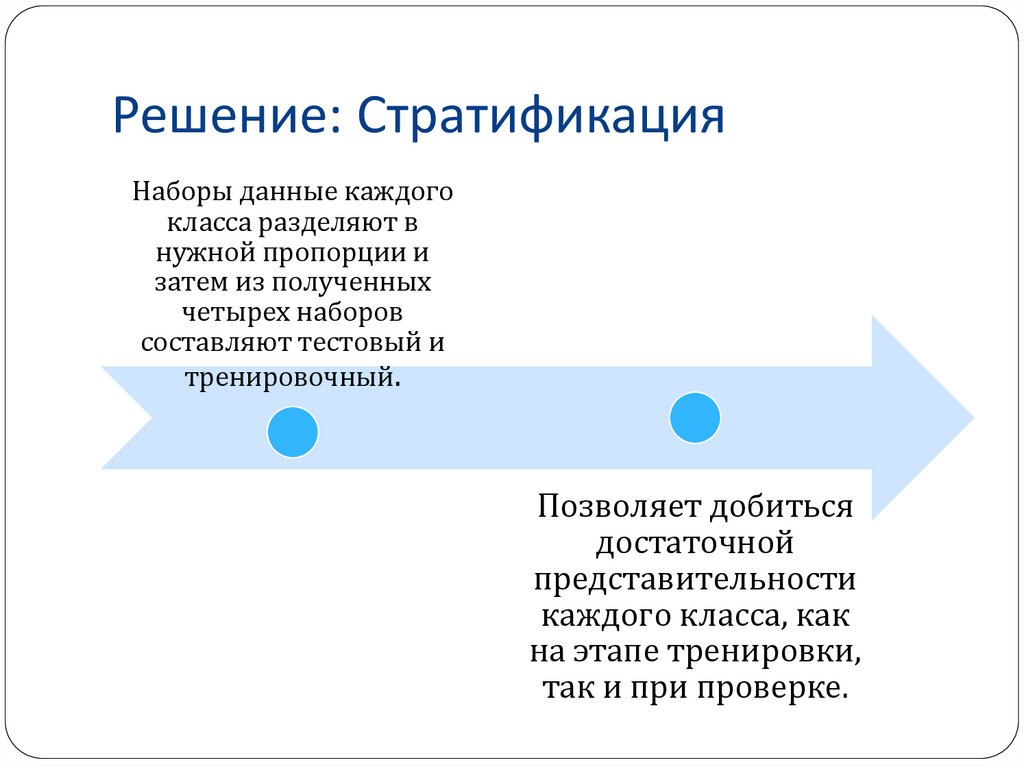
36. Стратификация (Stratification)
Если один классдоминирует над
другим, то при
случайном
разделении
данных на
тренировочный/те
стовый наборы
может возникнуть
неприятная
ситуация.
В тренировочный
(или тестовый)
набор может
попасть слишком
мало экземпляров
второго класса
(теоретически вообще ни одного).
37. Решение: Стратификация
Наборы данные каждогокласса разделяют в
нужной пропорции и
затем из полученных
четырех наборов
составляют тестовый и
тренировочный.
Позволяет добиться
достаточной
представительности
каждого класса, как
на этапе тренировки,
так и при проверке.
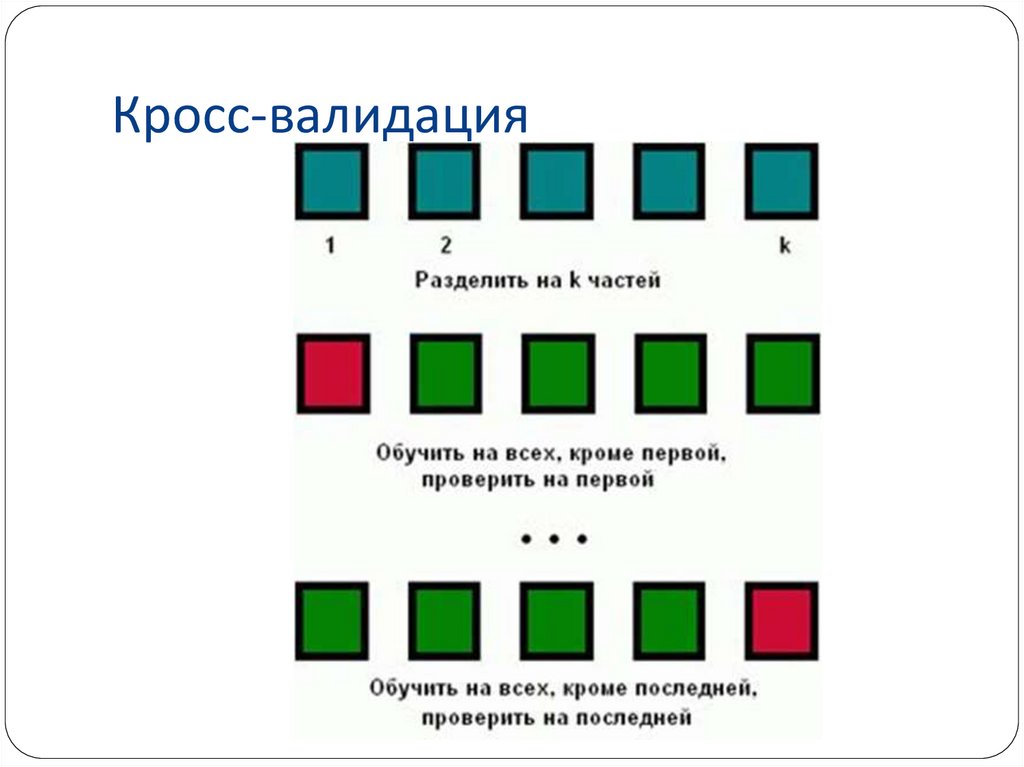
38. Перекрестная проверка (Cross-validation)
Для избежания пересечения тестовых наборов,(возможно при использовании метода Repeated
holdout), используется метод cross-validation.
Он заключается в разделении всего набора
данных на k подмножеств (иногда с учетом
стратификации).
Затем k раз производится тренировка по k-1
наборам и проверка по одному оставшемуся
39. Кросс-валидация
40.
Результаты, полученные на каждой из k итераций,усредняются для получения финального результата.
10 итераций обычно оказывается достаточно,
поэтому k обычно принимается равным 10
(tenfold cross-validation).
Для точной оценки уровня ошибок иногда
производится десятикратная перекрестная
проверка (ten tenfold cross validation).
41. Вариант метода
Вариантом перекрестной проверки является проверка <безодного> - leave-one-out. Фактически он является
перекрестной проверкой для случае k равному N
(количество данных).
Этот вариант часто используется для проверки гипотез. К
плюсам метода стоит отнести тренировку по максимуму
данных, отсутствие случайности, которая присутствует при
использовании holdout и перекрестной проверки.
Минусами являются невозможность стратификации, а также
очень высокая вычислительная сложность.
42. Самонастройка (Bootstrap)
В том случае, когда набор доступных данныхневелик, для повышения надежности
приходится использовать другие методики
проверки классификаторов.
Одной из таких методик является
самонастройка (bootstrap), алгоритм
которой можно записать так:
43. Для набора из N объектов повторить N раз следующую процедуру:
Cоставить тренировочный набор из случайновыбранных N элементов (элементы могут
входить в тренировочный набор несколько раз!)
Провести тренировку на этом наборе
Проверить на остальных данных, в набор не
попавших.
44. Самонастройка '0.632 bootstrap'
Самонастройка считается наилучшимспособом оценки классификации при
очень маленьких наборов данных.
Самонастройку также иногда называют
'0.632 bootstrap'.
0.632 - это ожидаемая доля всех
доступных данных, использованных для
тренировки хотя бы на одном из шагов:
45.
46.
Как видно из формул, приросте N вероятность
использования каждого
из векторов данных (хотя
бы в одной из итераций)
стремится к 63.2%.
47. Сравнение классификаторов
48. Прямое сравнение
Простейшим способом сравнения двухклассификаторов является сравнение
их уровней ошибок (error rates) и
выбора наиболее подходящего.
В случае, если классификатор содержит
свободный параметр, позволяющий
регулировать соотношение nTP и nFP целесообразно сравнивать ROC кривые.
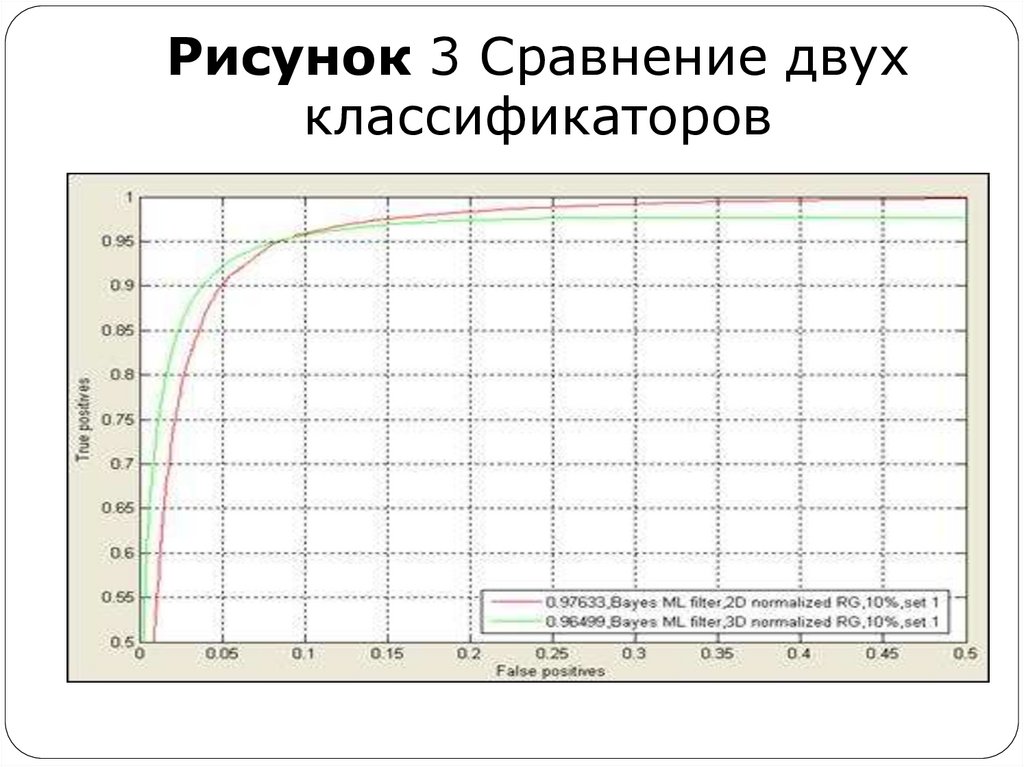
49.
На Рис. показано сравнение двухклассификаторов.
Можно увидеть что второй (график зеленого цвета)
показывает больший уровень верных обнаружений
при уровне ложных обнаружений менее 8%.
В зависимости от того, какой уровень ложного
обнаружения является допустимым можно выбрать
из этих двух классификаторов оптимальный.
50. Рисунок 3 Сравнение двух классификаторов
51.
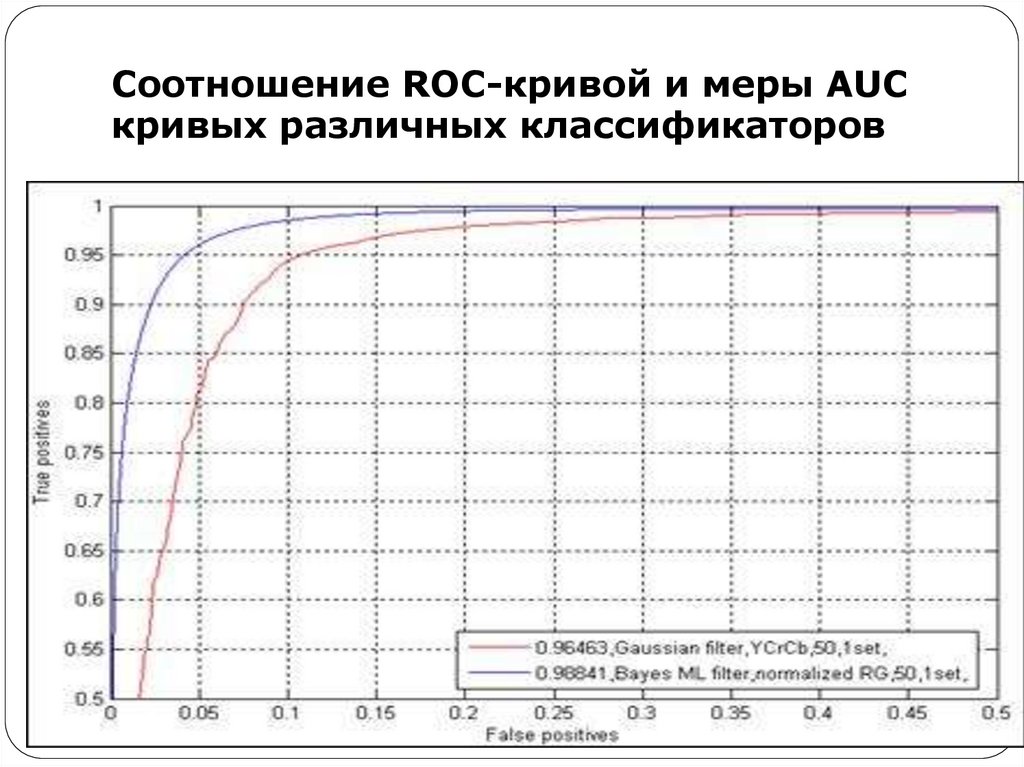
Более компактная мера (не несущая, впрочем,всей информации о соотношении верных и
ложных обнаружений) - это площадь под ROC
кривой (area under curve - AUC).
Для случая заметного превосходства одного
классификатора над другим (см. Рисунок 4) AUC
позволяет уверенно сравнить две кривые ROC и
выбрать лучший.
52. Соотношение ROC-кривой и меры AUC кривых различных классификаторов
53.
Красный график - AUC =0.96463, синий - AUC = 0.98841.
54.
Однако не во всех случаях AUC дает верноепредставление о том, какой из
классификаторов лучше.
Например, на Рисунок 3 AUC для первого
классификатора (красный график) больше, чем для
второго, в то время как первый классификатор
уступает второму при уровне ложных обнаружений
менее 8%.
В таких случаях без анализа самих кривых не
обойтись.
55. Статистические тесты
Уровни ошибок, рассчитываемые понекоторому количеству испытаний, по сути,
сами являются случайными величинами.
Для повышения надежности оценки они
усредняются (repeated holdout, cross-validation,
leave one out).
Фактически это означает, что производится
оценка математического ожидания этих
случайных величин.
56.
Прямое сравнение полученных оценок матожидания уровняошибок может дать неверные результаты, поскольку не
учитывает <надежность> полученных оценок.
Для проверки различия средних значений в статистике
приняты различные тесты, в частности t-тест (тест
Стьюдента) сравнения средних [5].
Данный тест дает ответ на вопрос - действительно ли имеет
место значимое различие между средними, или оно
объясняется статистическими колебаниями.
57. Парный двухвыборочный t-тест
Для двух классификаторов,тренированных и проверяемых на
одних и тех же данных (например,
на одном и том же разделении при
перекрестной проверке)
применяется более точный
парный двухвыборочный t-тест
[6].
58.
Проверка наличия статистического различияматожиданий уровней ошибок производится
следующим образом.
Пусть для оценки качества распознавания
применяется перекрестная проверка с k
подмножествами.
На каждой итерации i=1..k; вычисляется уровень
ошибок для первого и второго классификаторов
Xi, Yi (для одного и того же набора).
59. Для вынесения решения о статистически значимом отличии этих величин вычисляются следующие величины:
60.
Данное распределение t имеет k-1 степеньсвободы.
Для того чтобы принять (или отвергнуть)
гипотезу о статистически значимом различии
средних нужно сравнить полученное значение t
с таблицей распределения Cтьюдента для k-1
степеней свободы.
61.
В случае если вычисленное значение не превышаеттабличное, вероятность существенного различия не
выше указанного в таблице (таблица составляется
для определенного уровня значимости), в
противном случае - выше.
Если гипотеза о существовании различия
подтверждается с высокой вероятностью, то
проверить, какой конкретный классификатор
лучше, можно с помощью простых методов проверки
из предыдущего раздела.
62. Заключение
63.
Выбрать способ разделения на тренировочный и тестовыйнаборы
Провести испытания для всех классификаторов на общих
наборах, вычислить характеристики производительности
методов;
Проверить на наличие статистического различия между
полученными величинами;
Выбрать классификатор c наилучшими характеристиками;
64.
Выбор оптимального классификатора производитсяисходя из требований к задаче. Для каждого конкретного
случая можно выбирать что важнее - уменьшить уровень
ошибок первого или второго родов.
После того, как из набора имеющихся классификаторов
был выбран наилучший, перед его использованием для
распознавания новых данных имеет смысл провести его
тренировку на всем имеющемся наборе исходных данных
с известной разметкой по классам.
65. литература
Vezhnevets V., Sazonov V., Andreeva A., "A Survey on Pixel-Based Skin Color Detection Techniques". Proc.Graphicon-2003, pp. 85-92, Moscow, Russia, September 2003.
[2] "Метод главных компонент," Цифровая библиотека лаборатории компьютерной
графики и мультимедиа ВМиК МГУ, http://library.graphicon.ru/catalog/19.
[3] "Линейный дискриминантный анализ," Цифровая библиотека лаборатории
компьютерной графики и мультимедиа ВМиК МГУ,
http://library.graphicon.ru/catalog/184.
[4] "Факторный анализ," Цифровая библиотека лаборатории компьютерной графики
и мультимедиа ВМиК МГУ, http://library.graphicon.ru/catalog/217.
[5] "Основные статистики и таблицы," Электронный учебник StatSoft,
http://www.statsoft.ru/home/textbook/modules/stbasic.html




































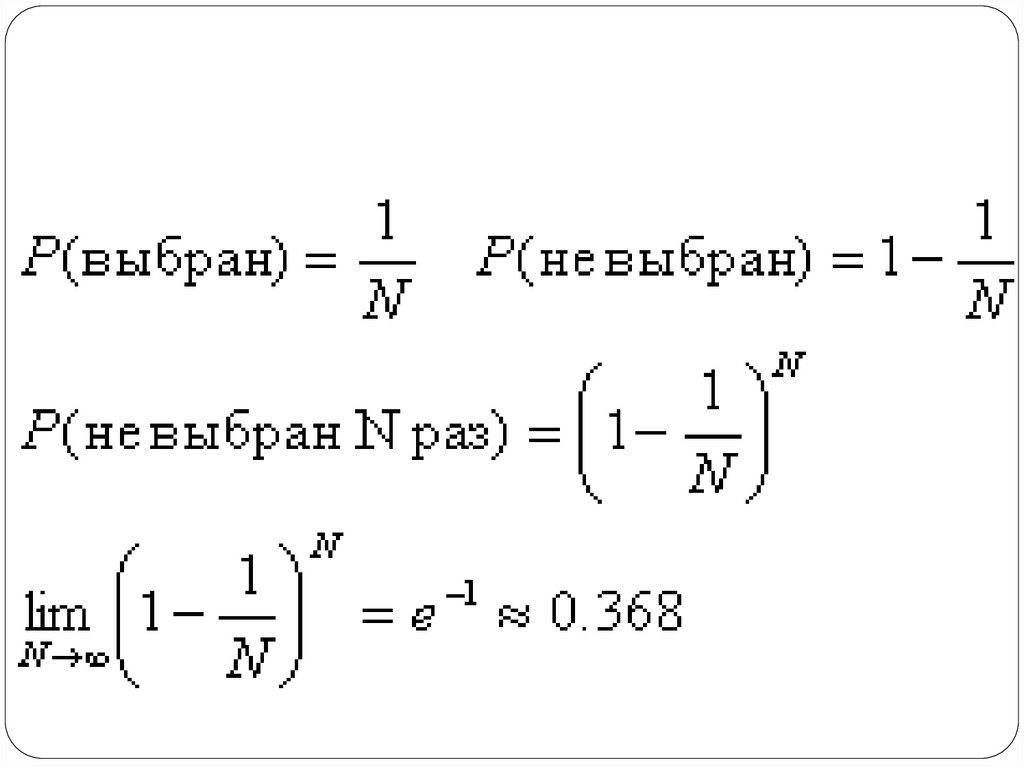


















 Информатика
Информатика