Введение. Методы отображения трёхмерного пространства на плоскости. Лекция 1

1.

ЭЛЕКТРОННЫЙ КУРС
ЛЕКЦИЙ ПО
НАЧЕРТАТЕЛЬНОЙ
ГЕОМЕТРИИ
АВТОР
ИОСИФ БАЦИКАДЗЕ

2.

I ЛЕКЦИЯ

3.

Введение.
Методы отображения трёхмерного пространства на
плоскости
1. Метод центрального проецирования;
2. Метод параллельного проецирования;
3. Метод ортогонального проецирования;
Методы обратимого отображения трёхмерного
пространства на плоскости:
1. Метод проекций с числовыми отметками;
2. Метод Монжа.

4.

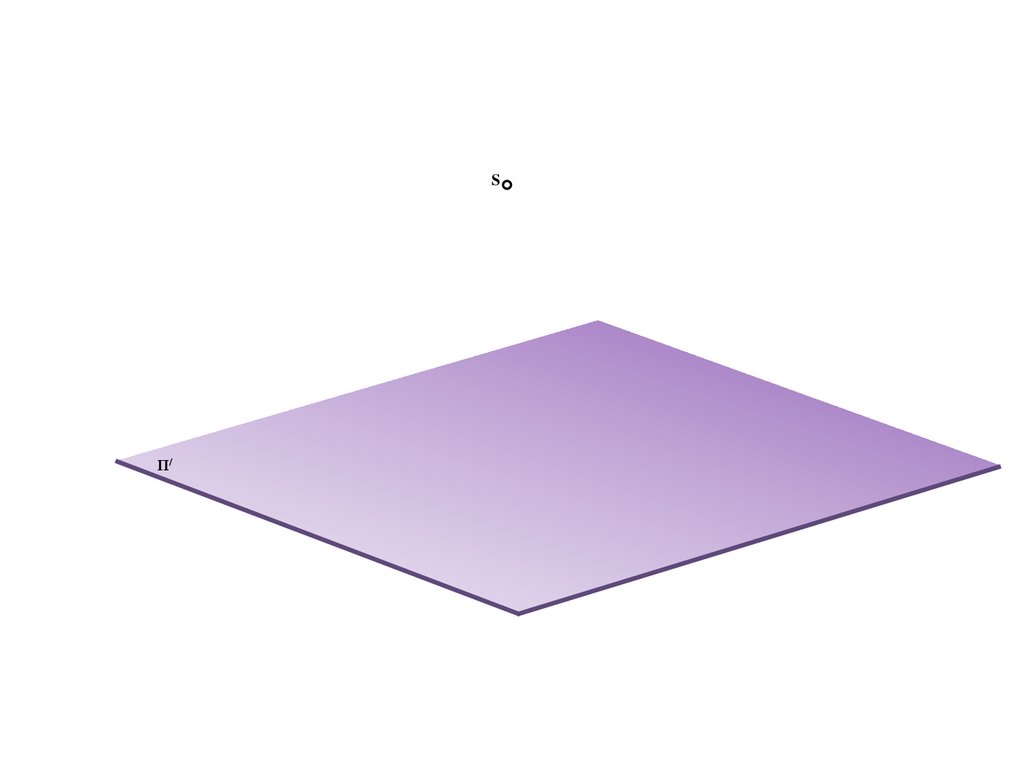
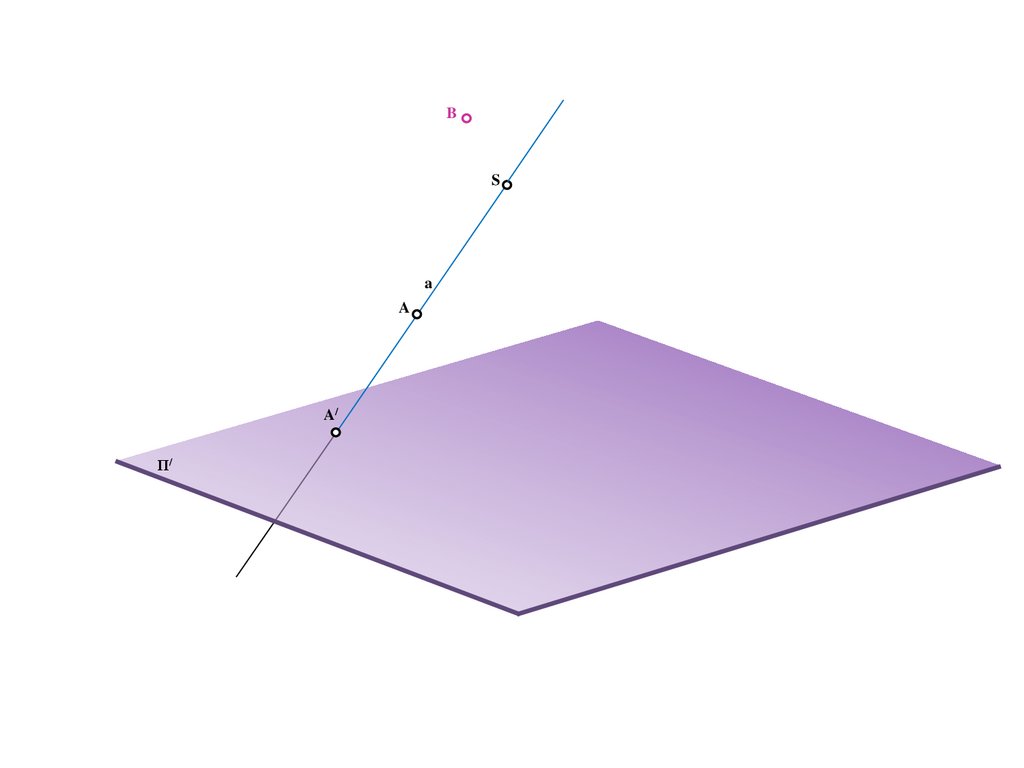
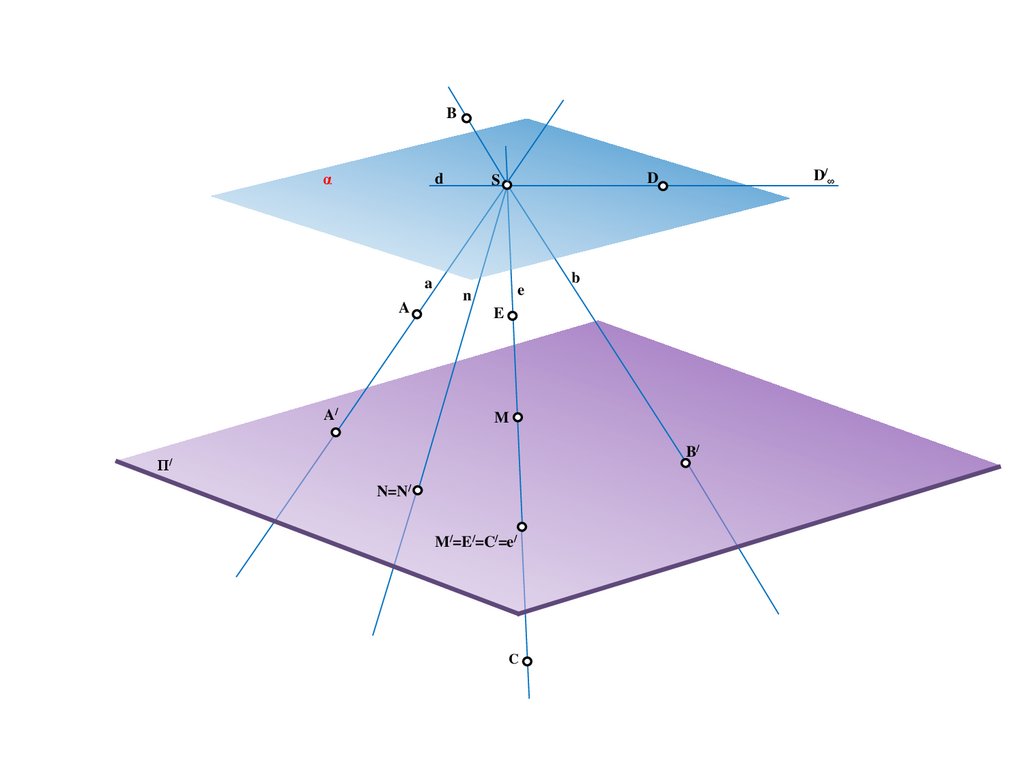
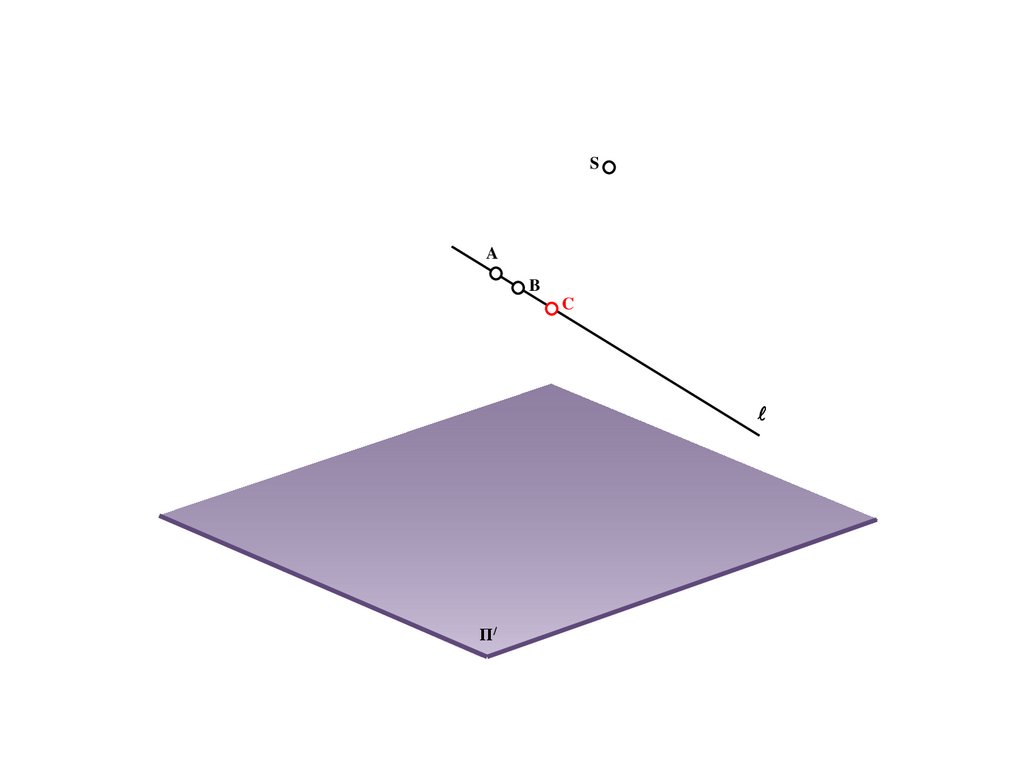
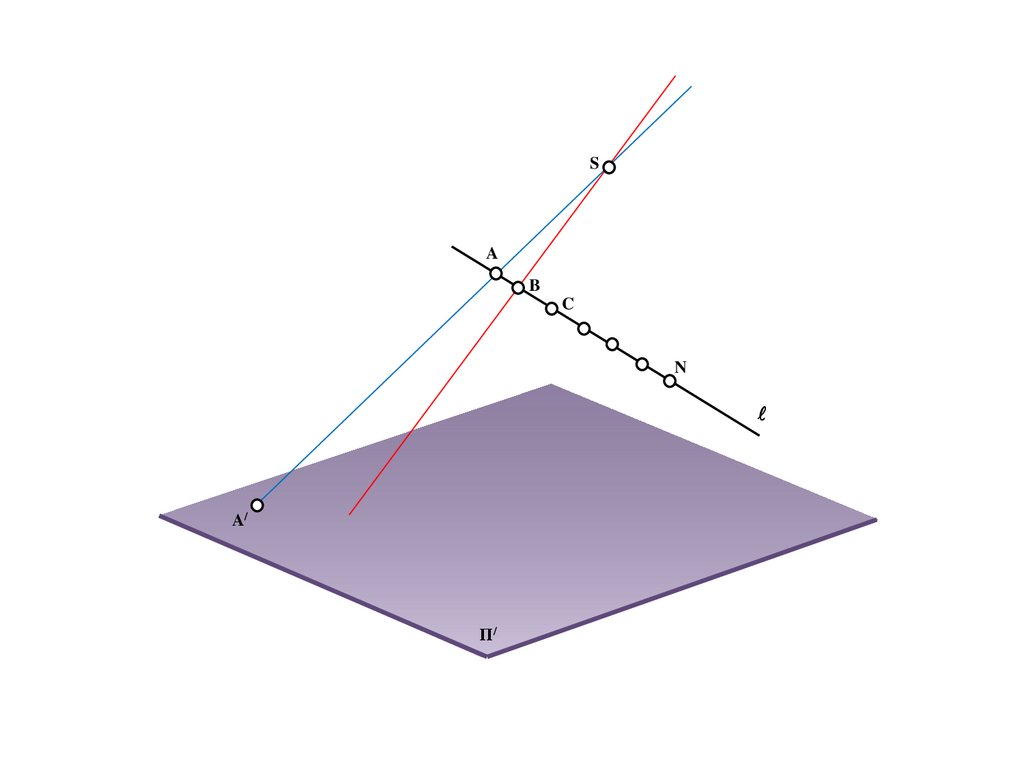
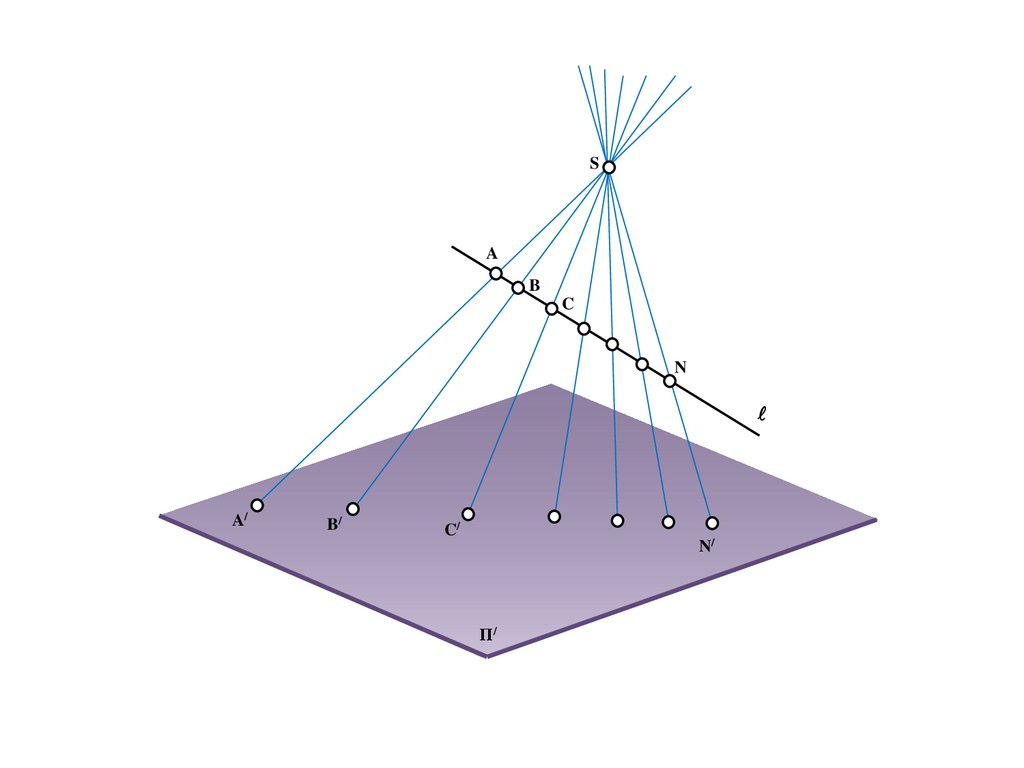
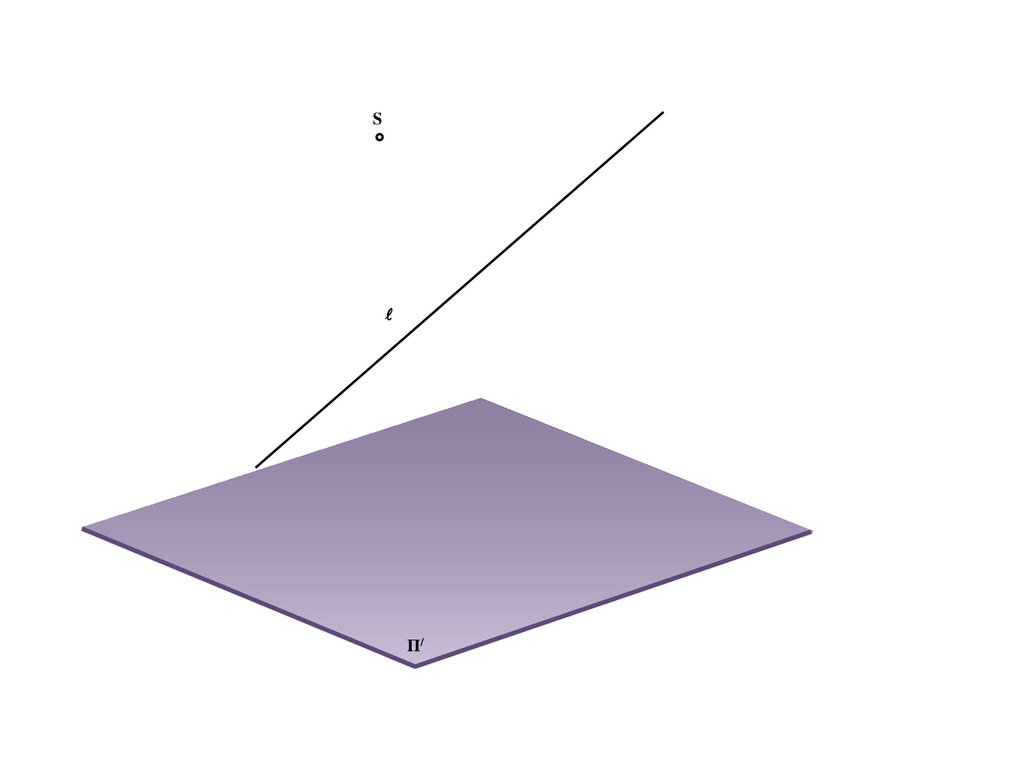
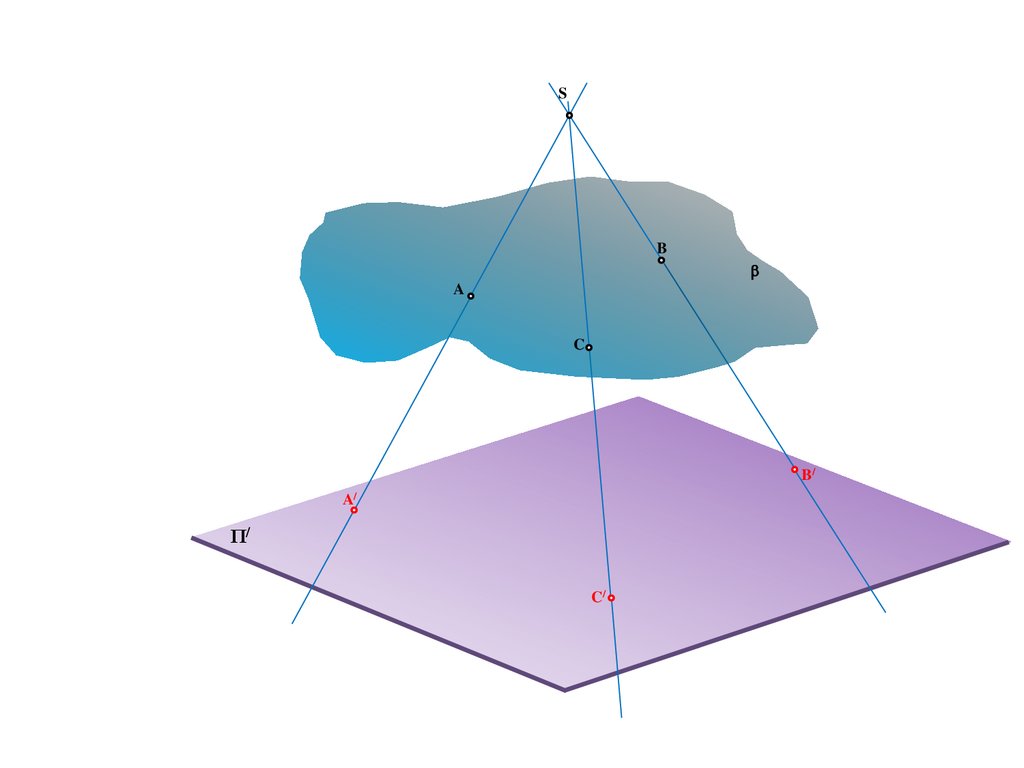
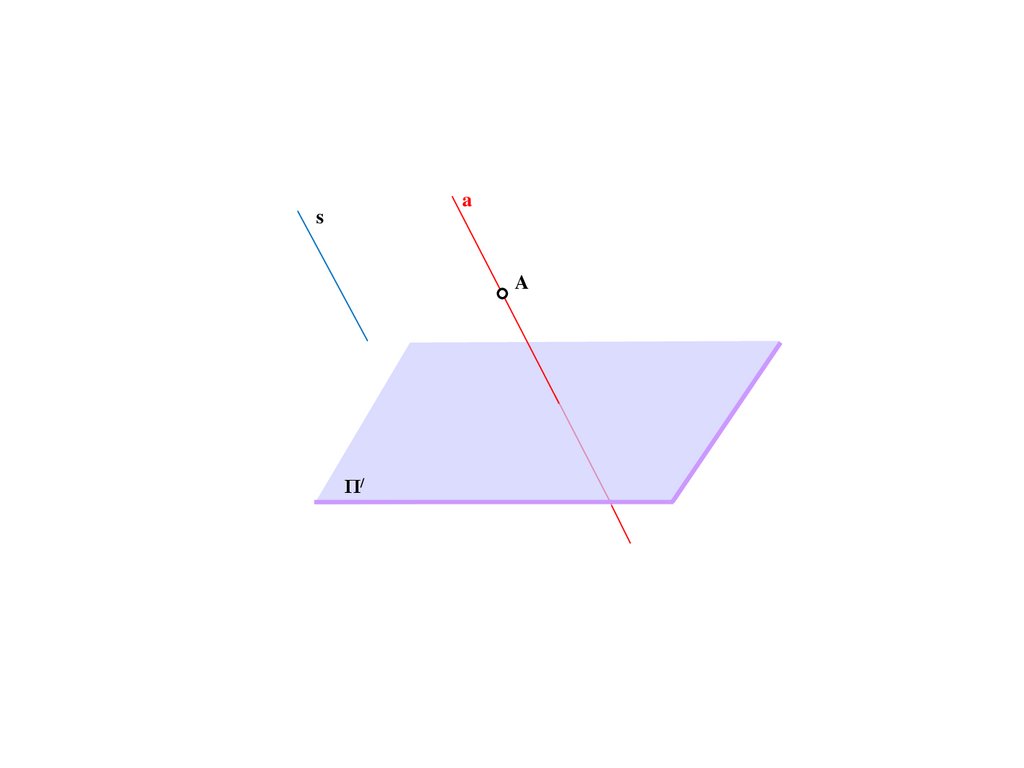
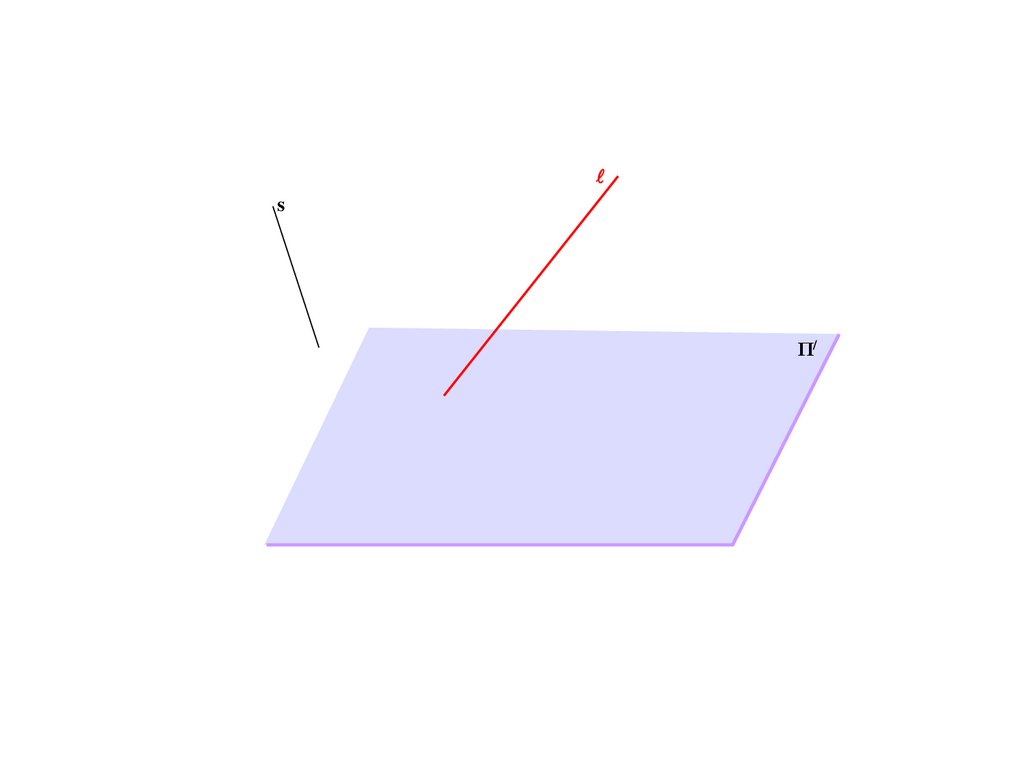
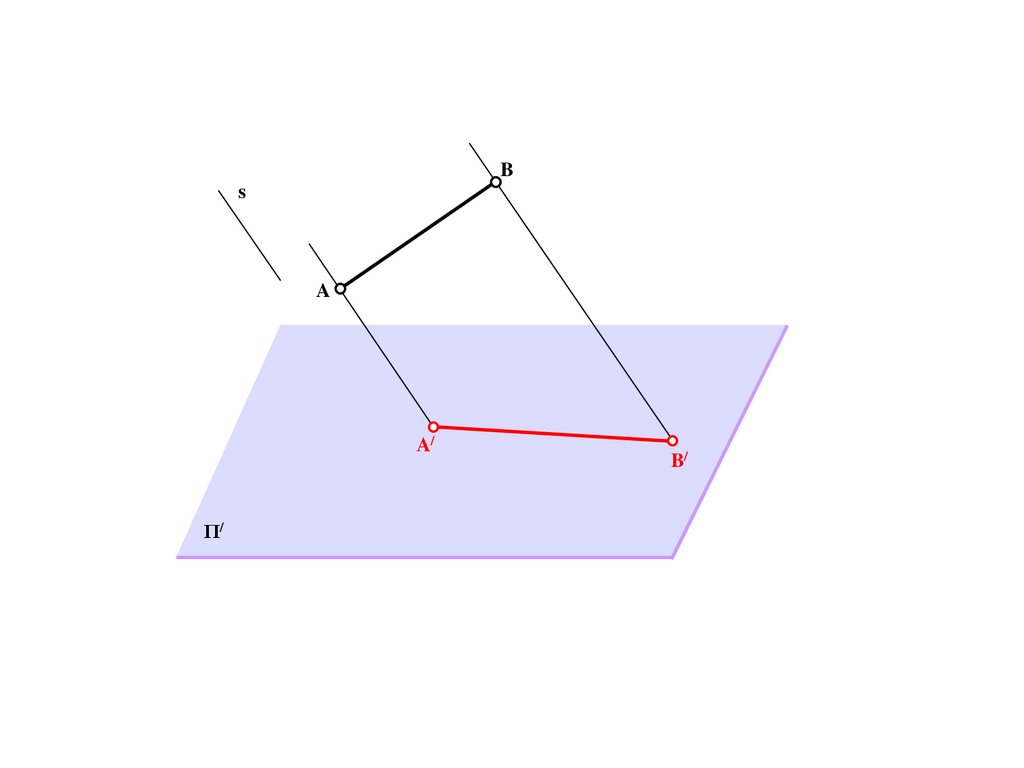
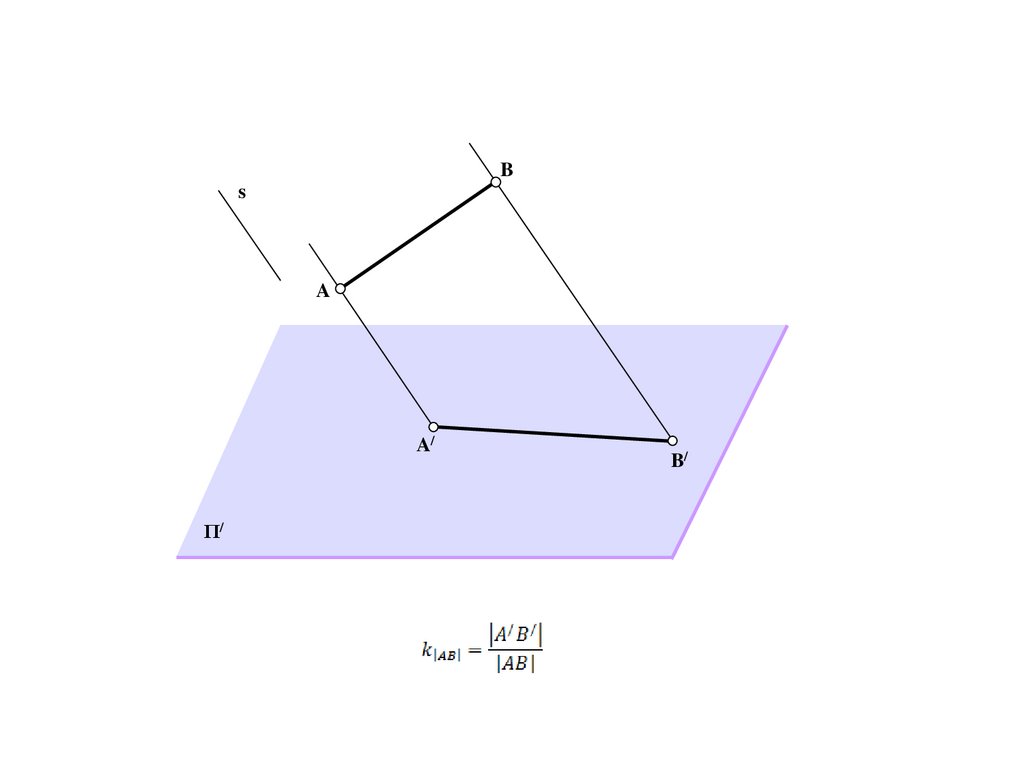
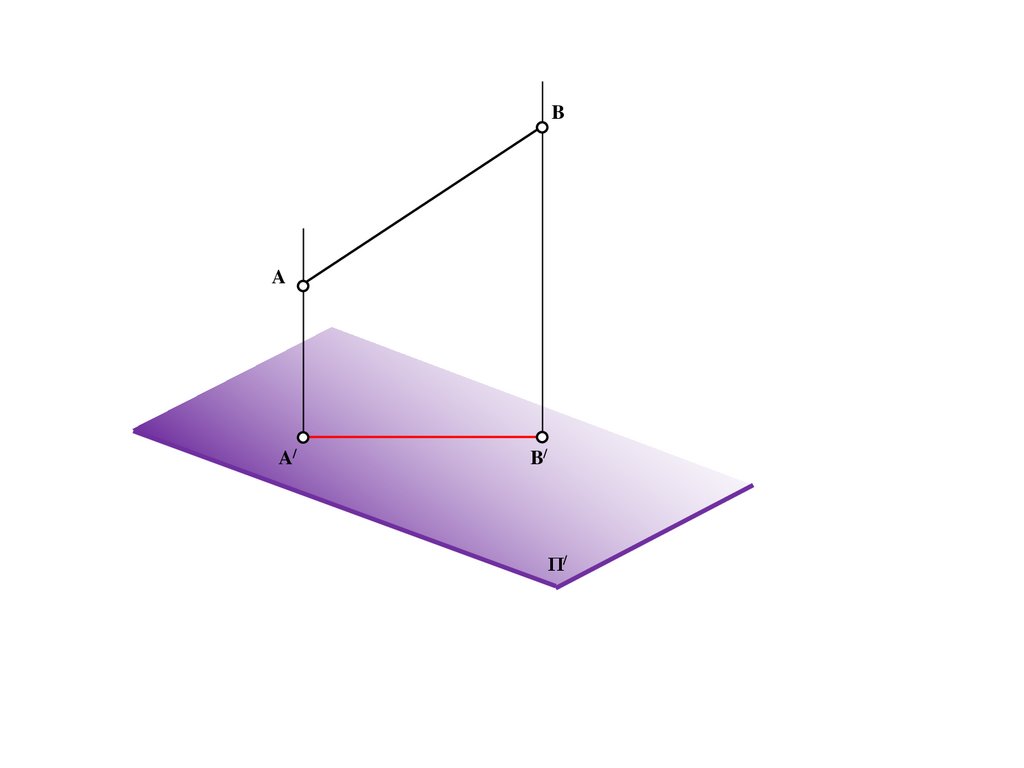
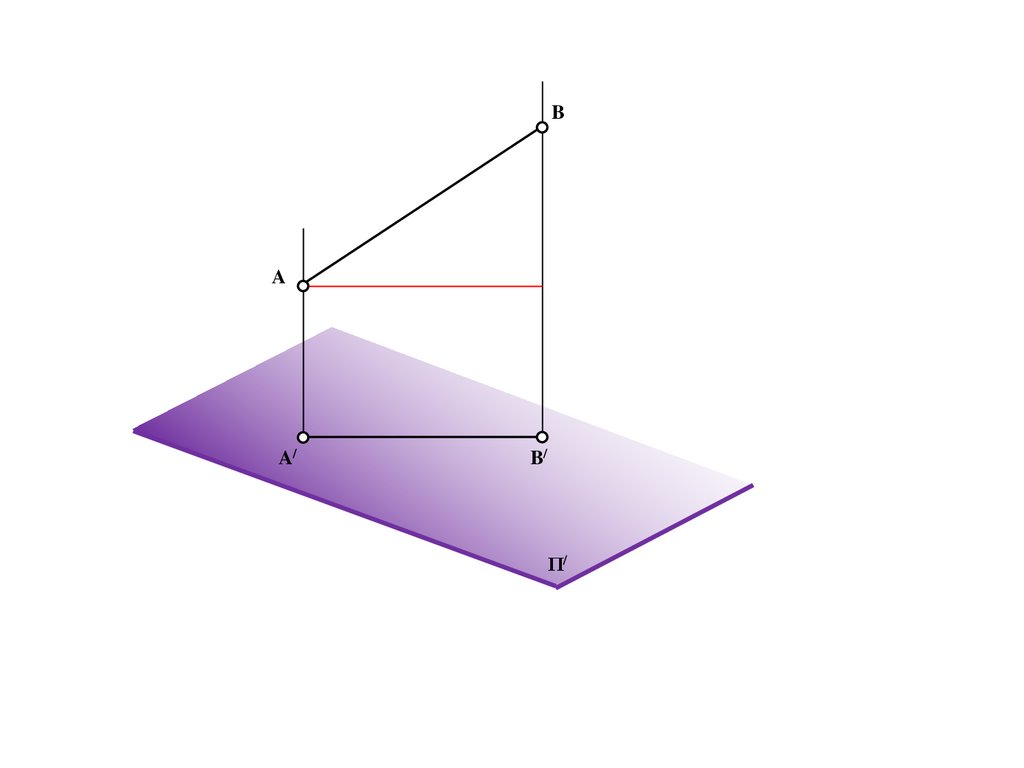
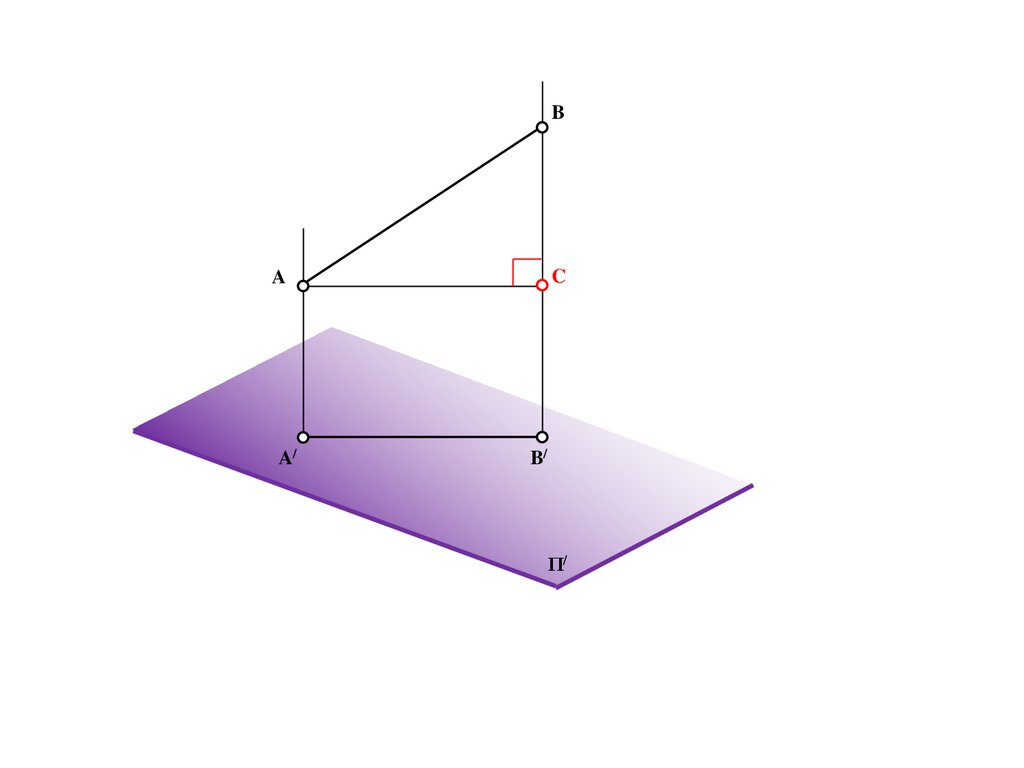
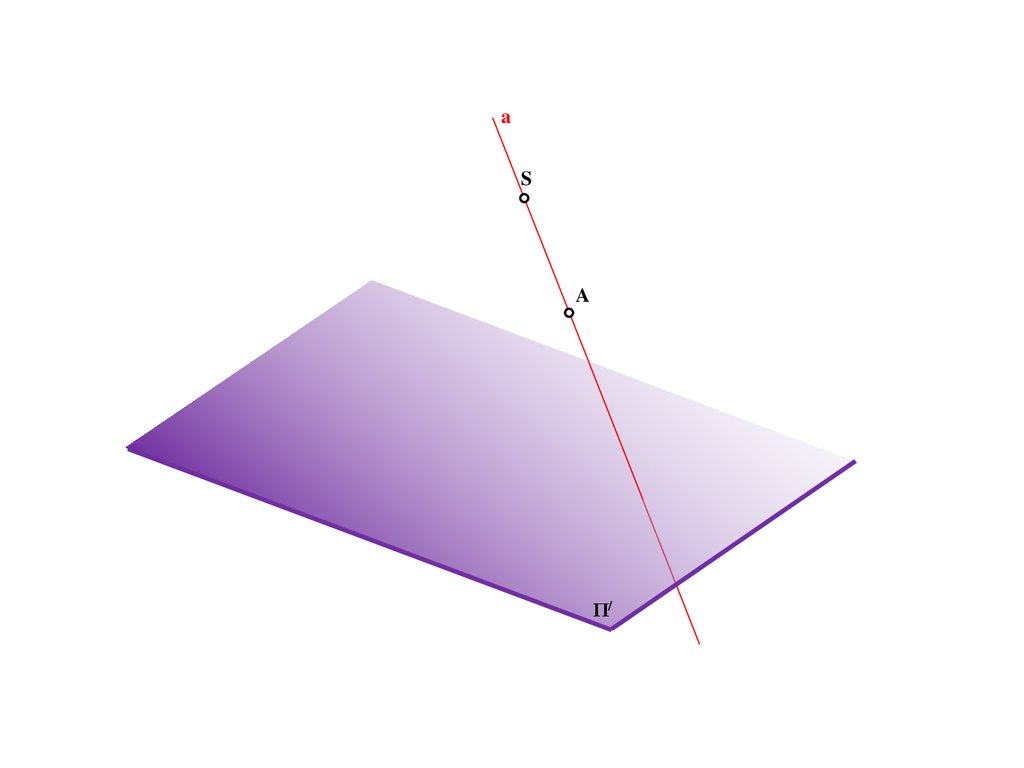
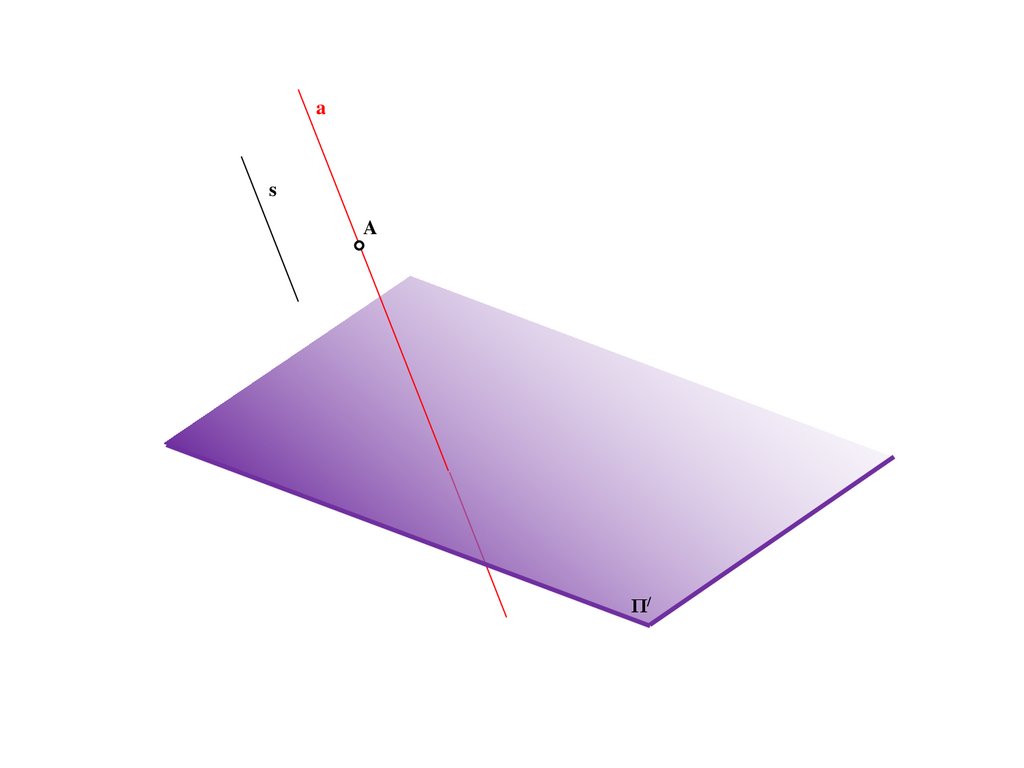
Метод центрального проецирования

5.

S
Π/

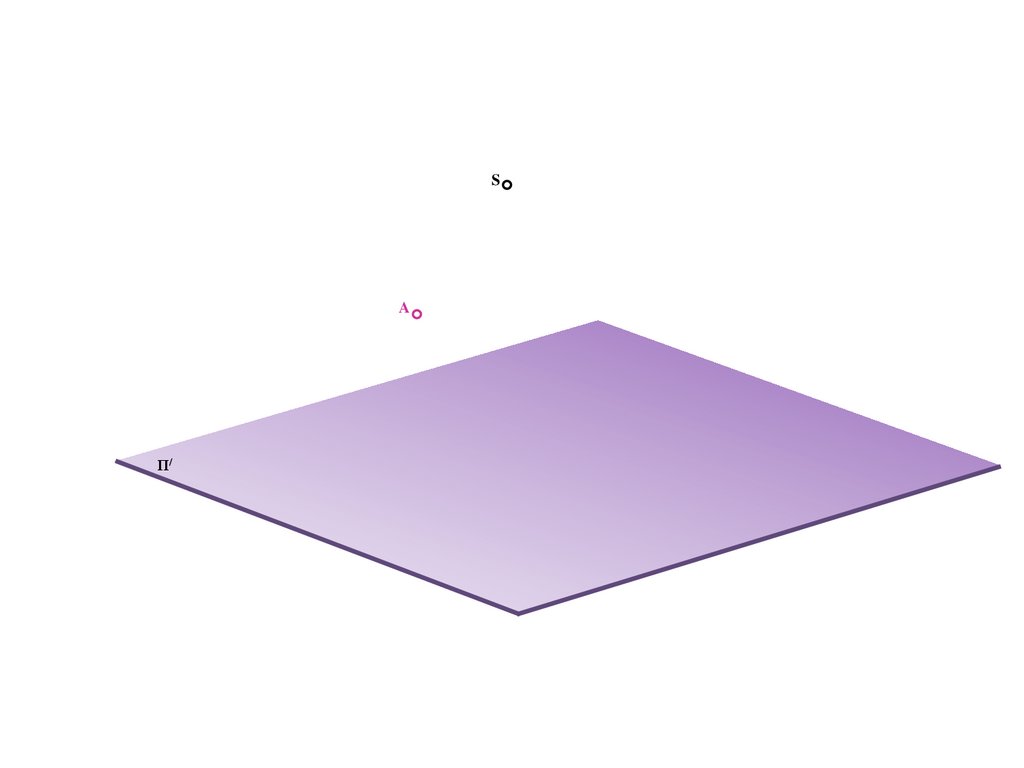
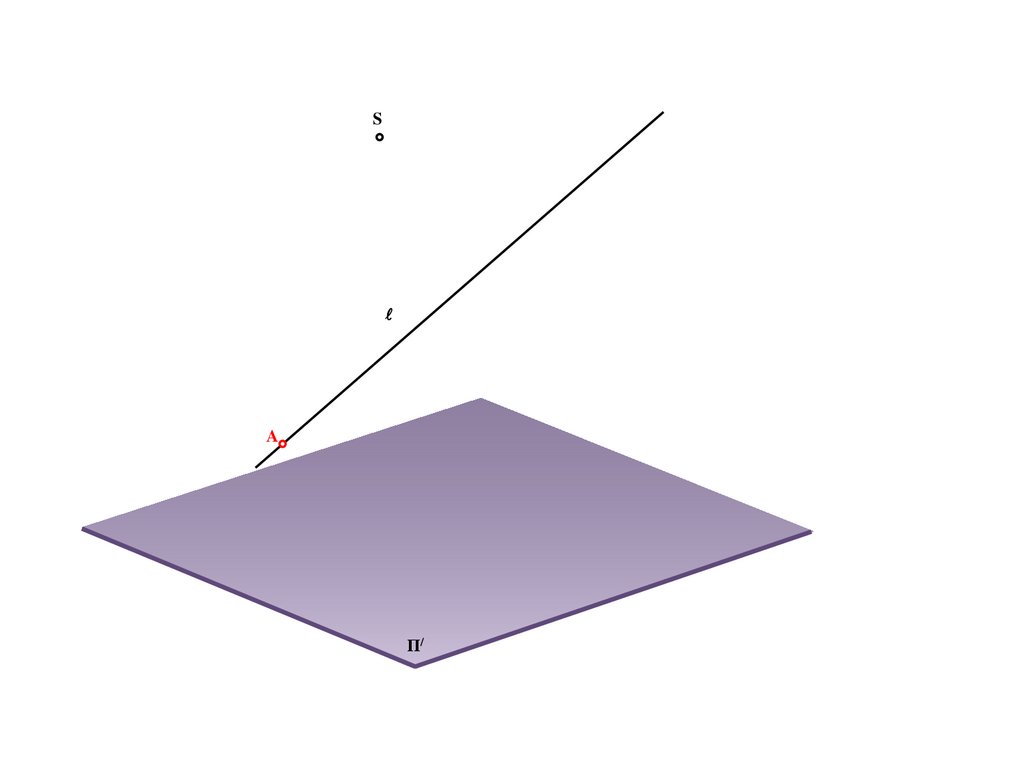
6.

S
A
Π/

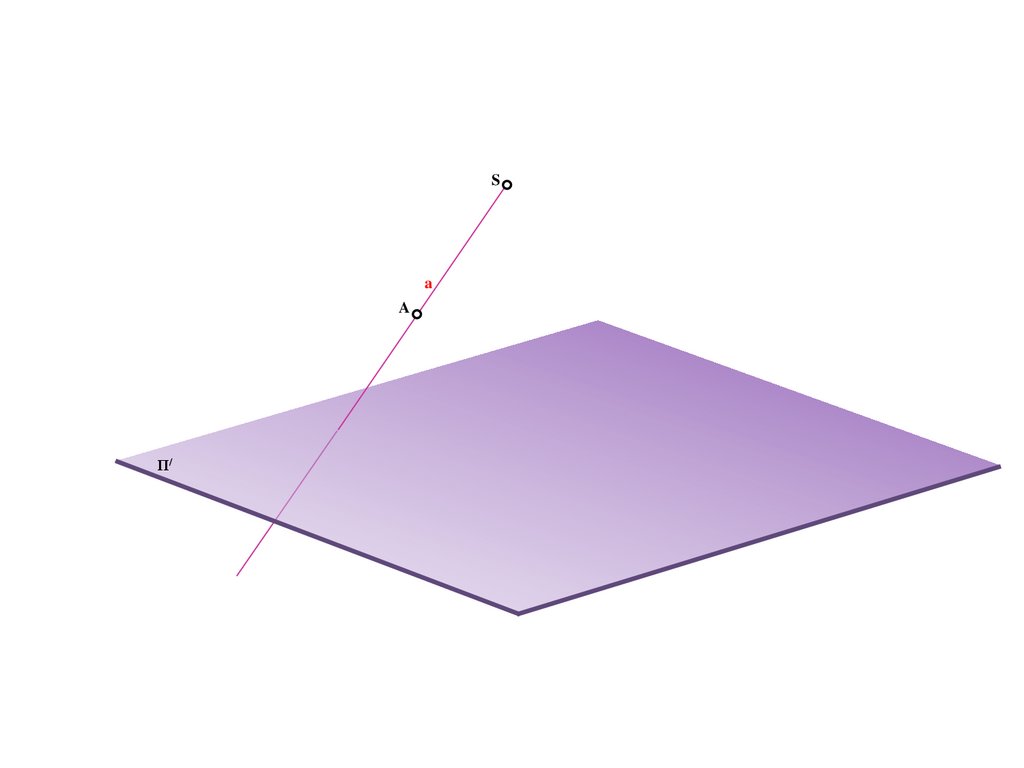
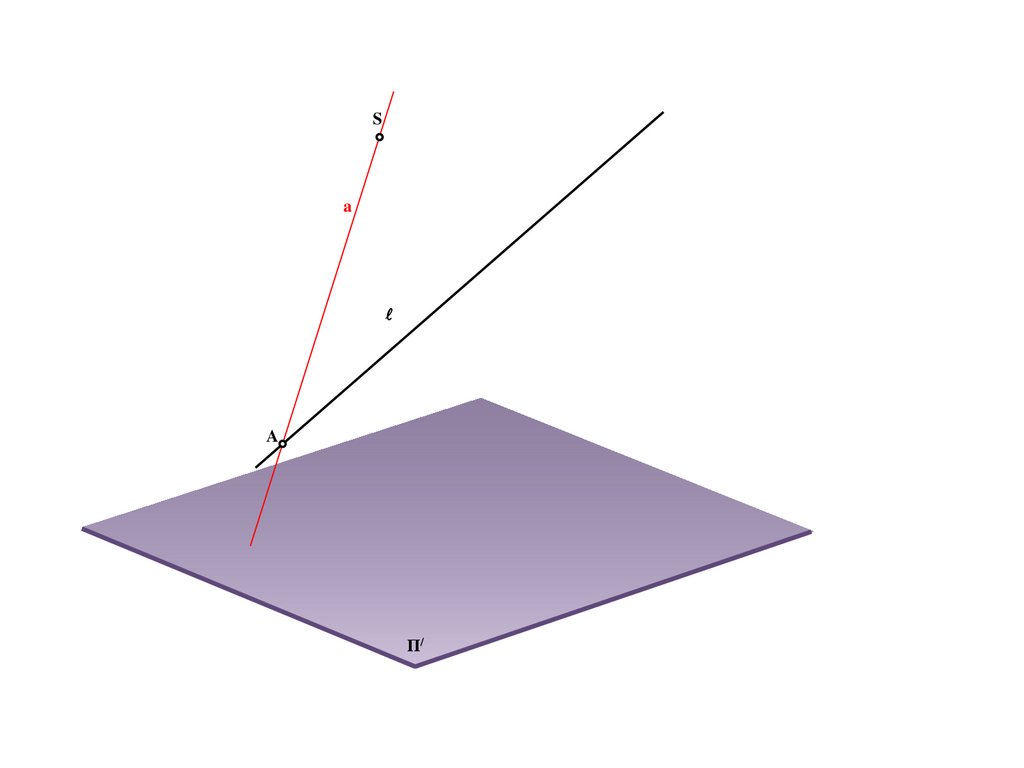
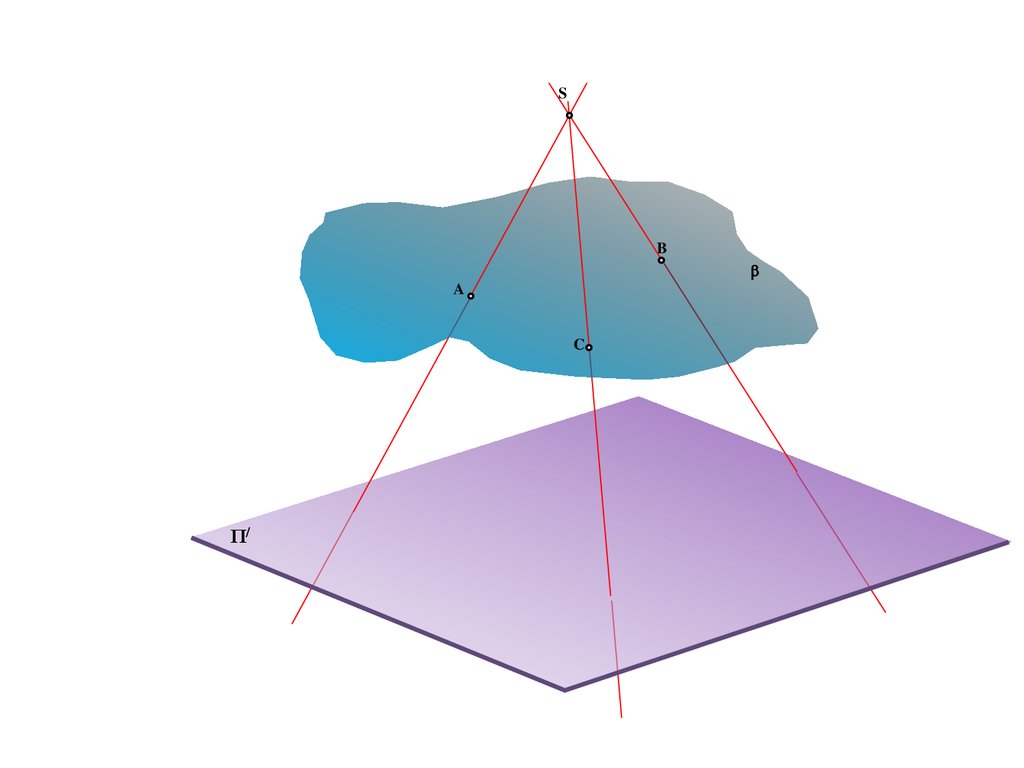
7.

S
a
A
Π/

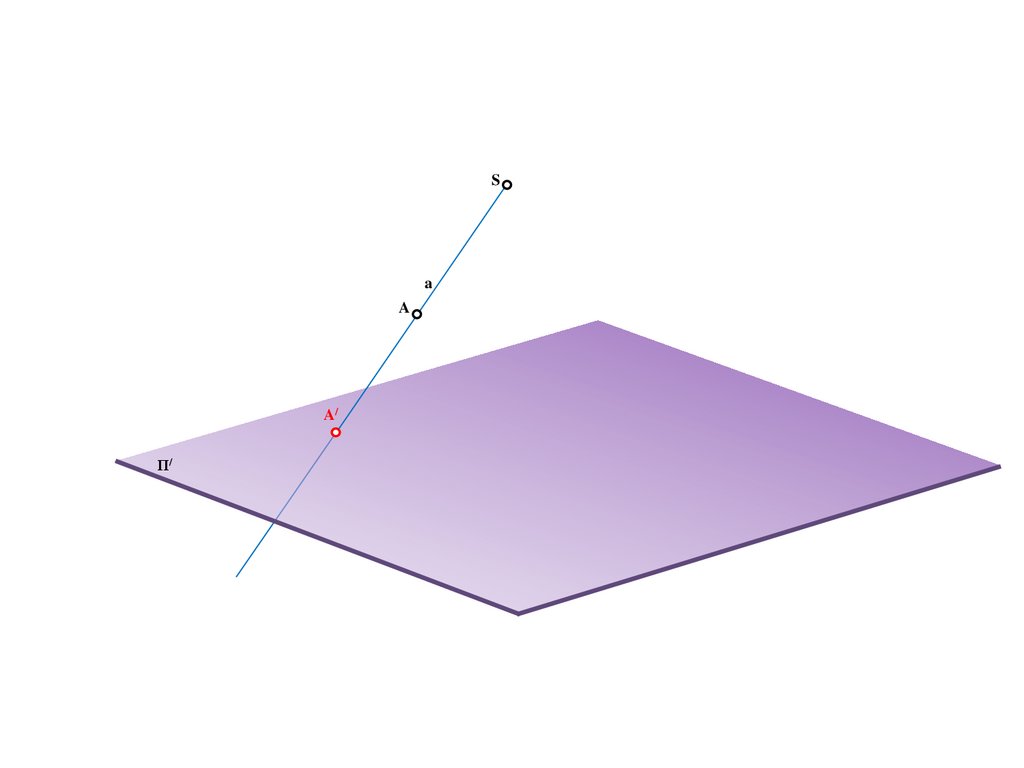
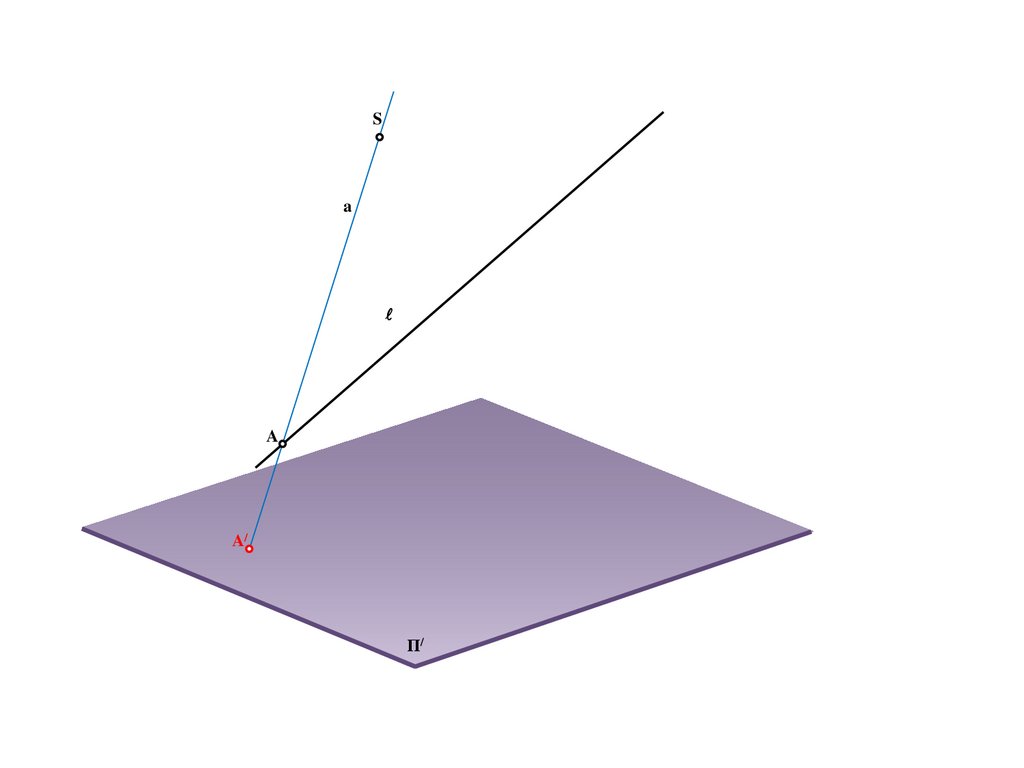
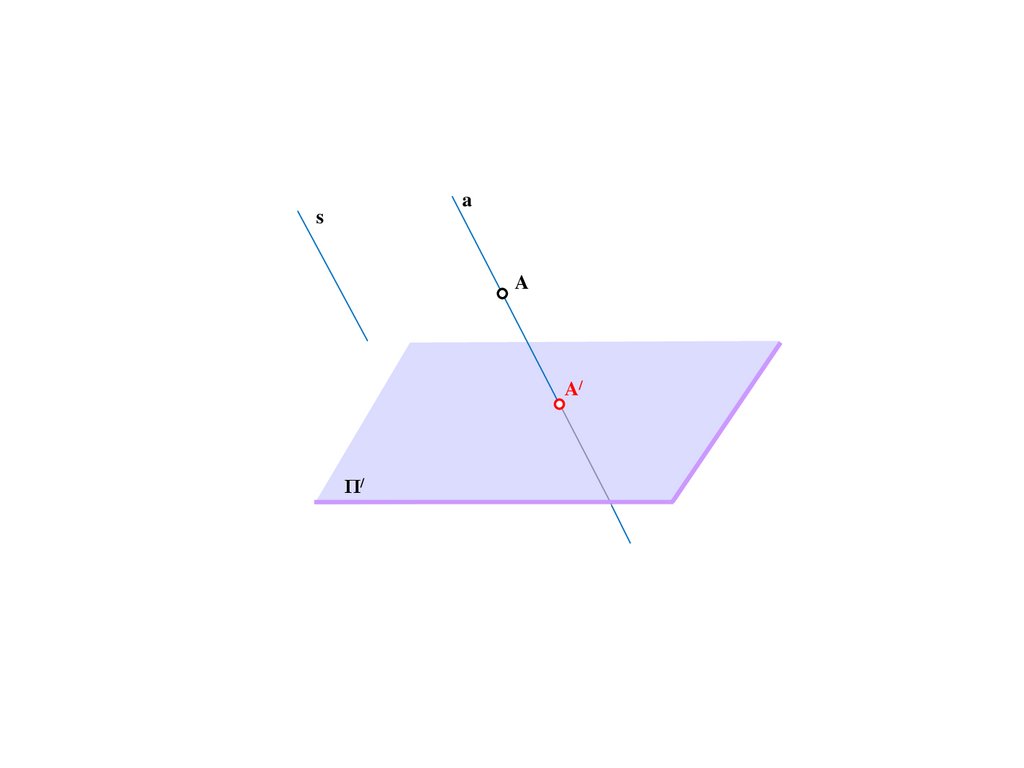
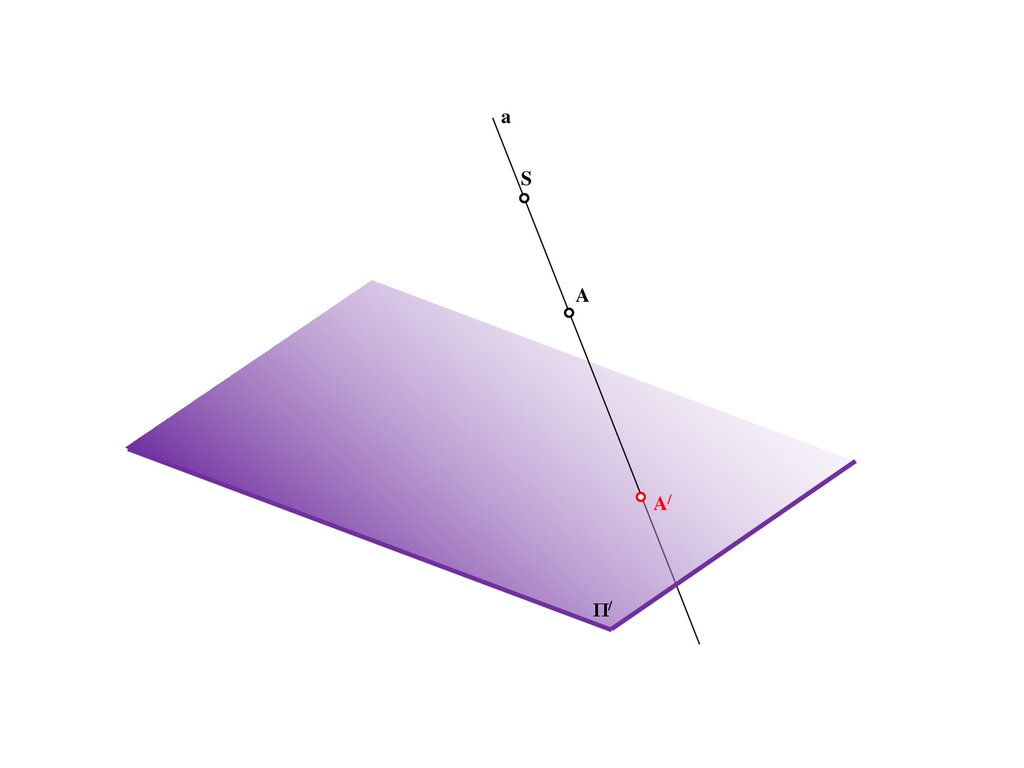
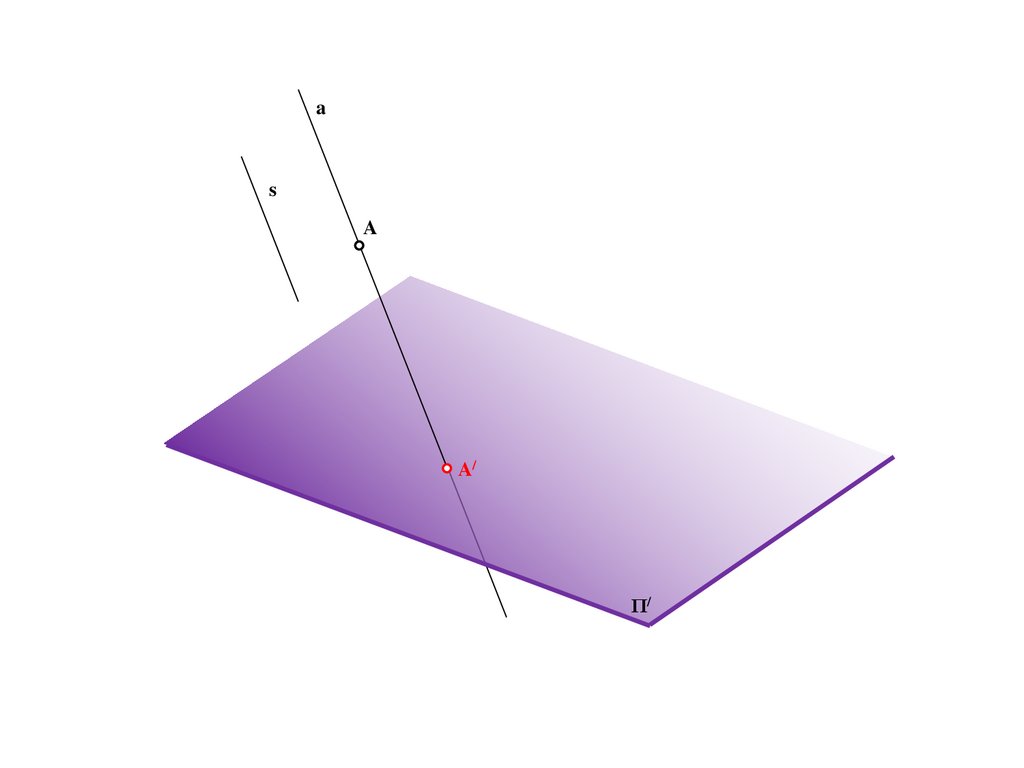
8.

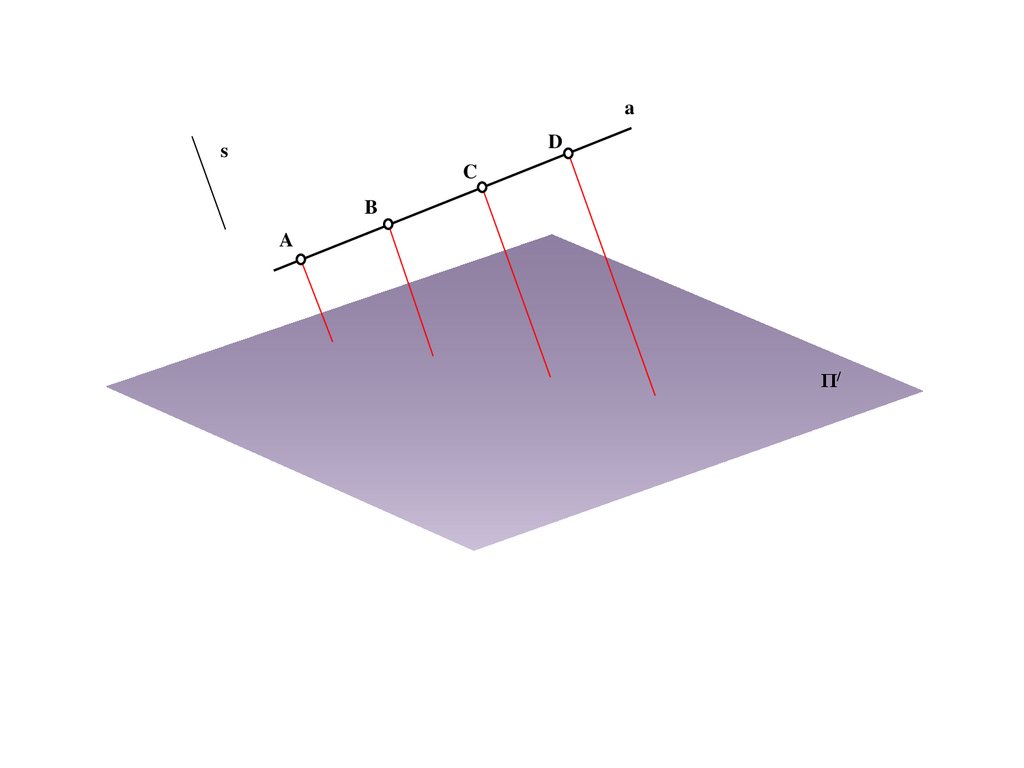
S
a
A
A/
Π/

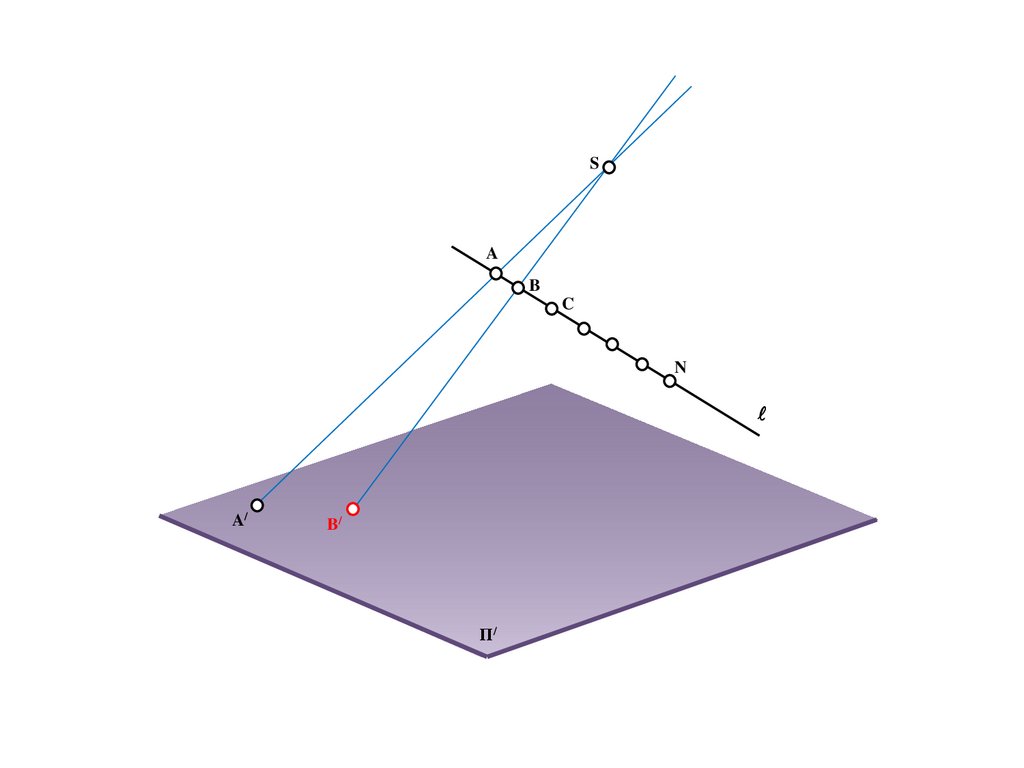
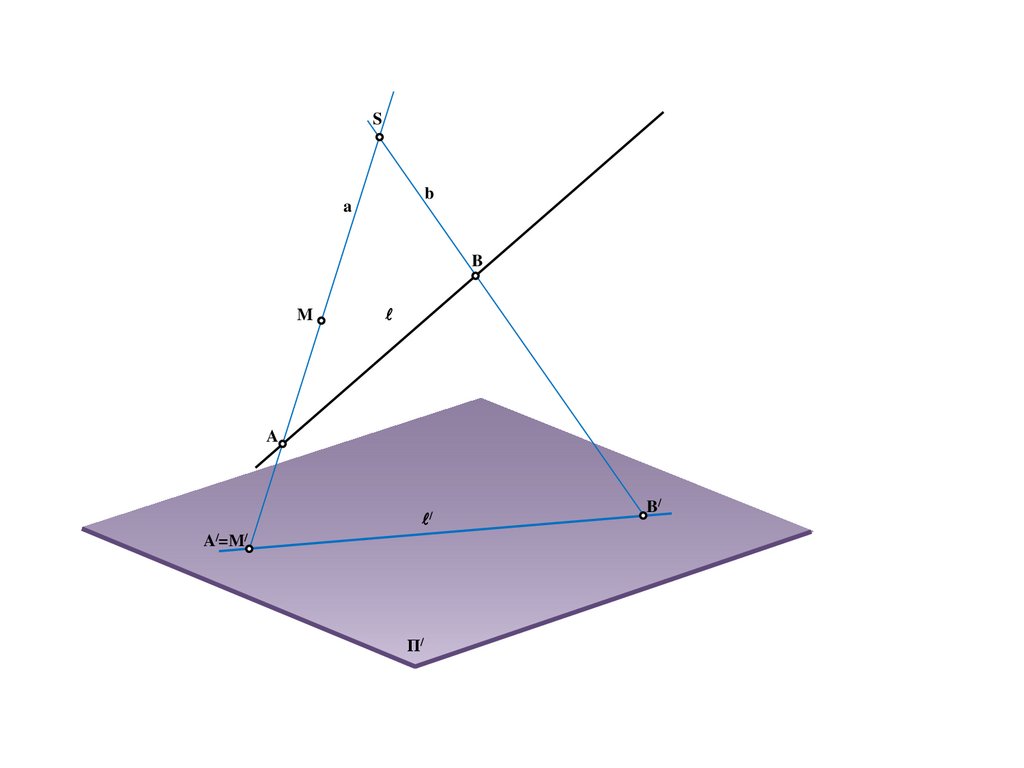
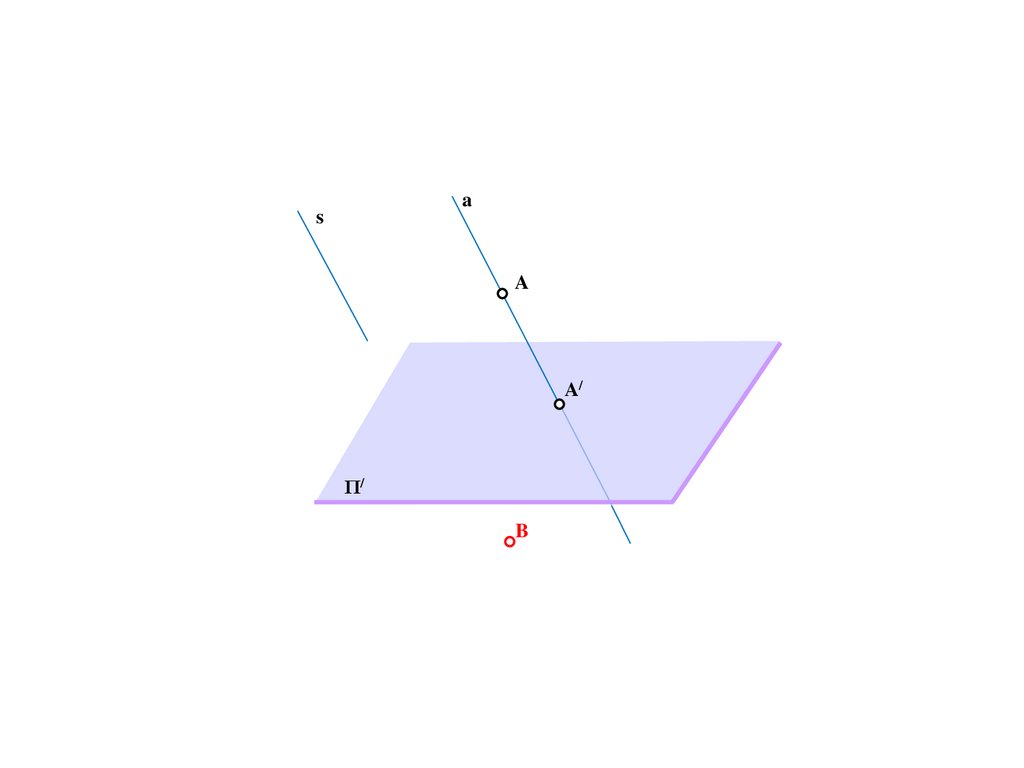
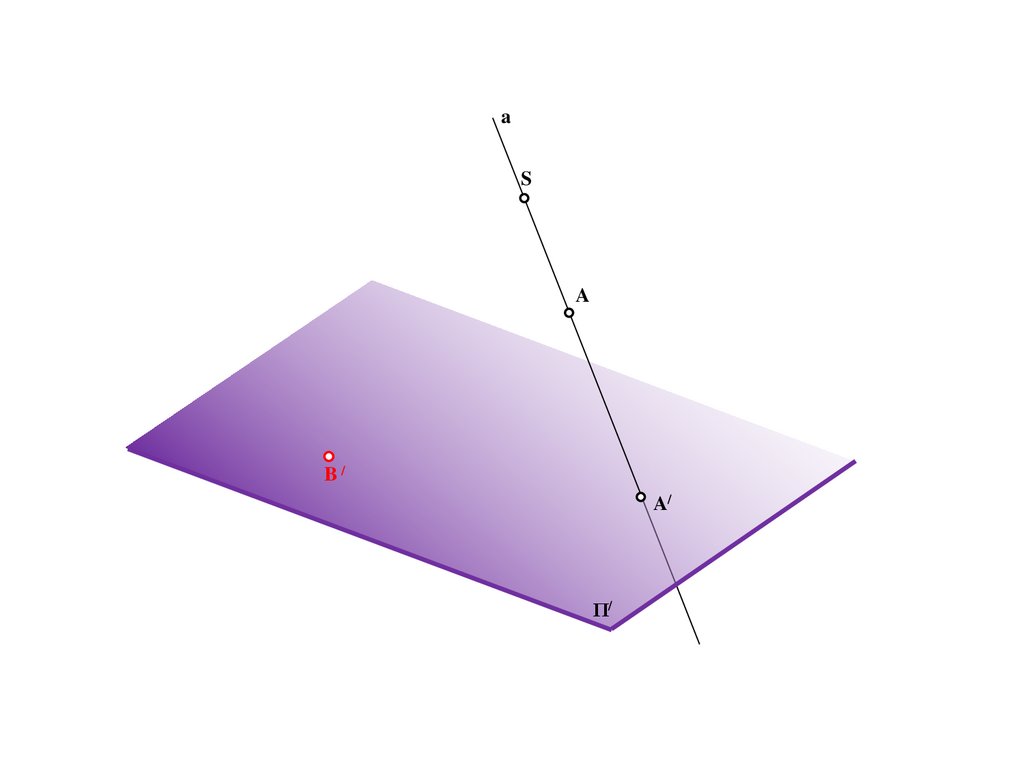
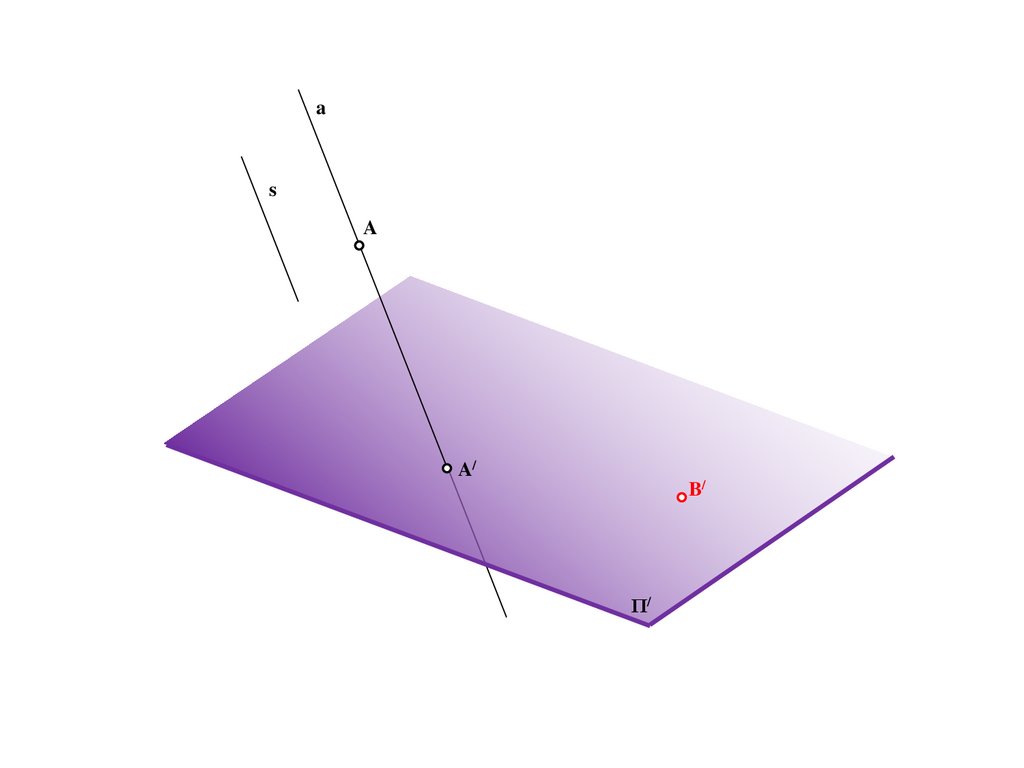
9.

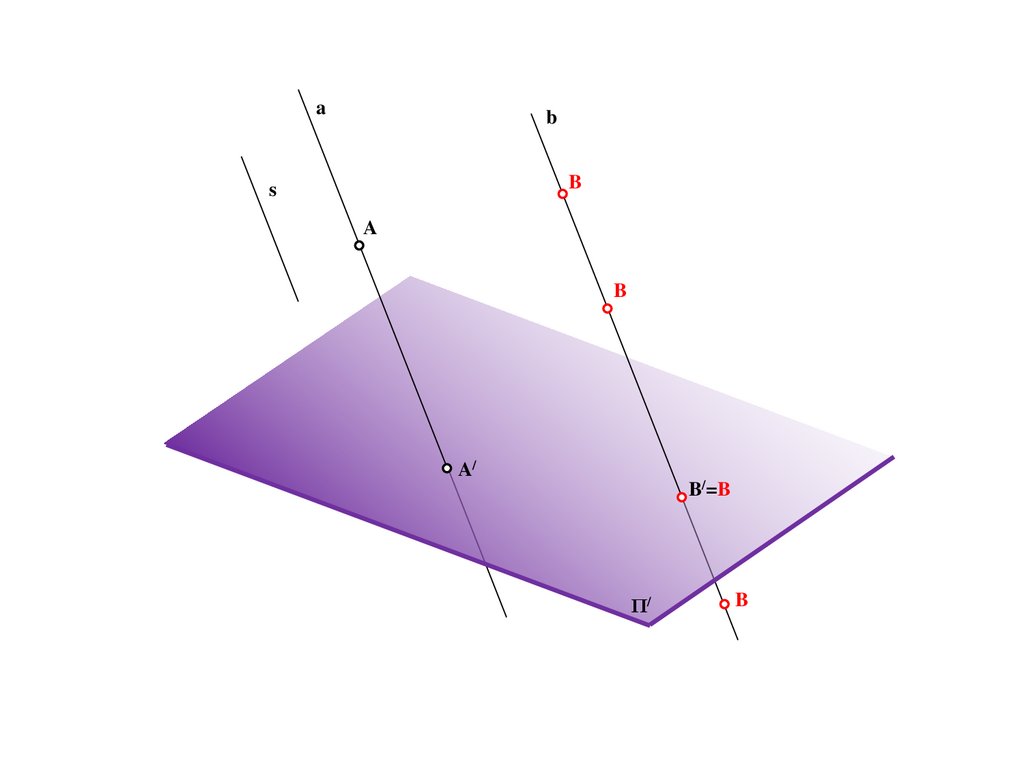
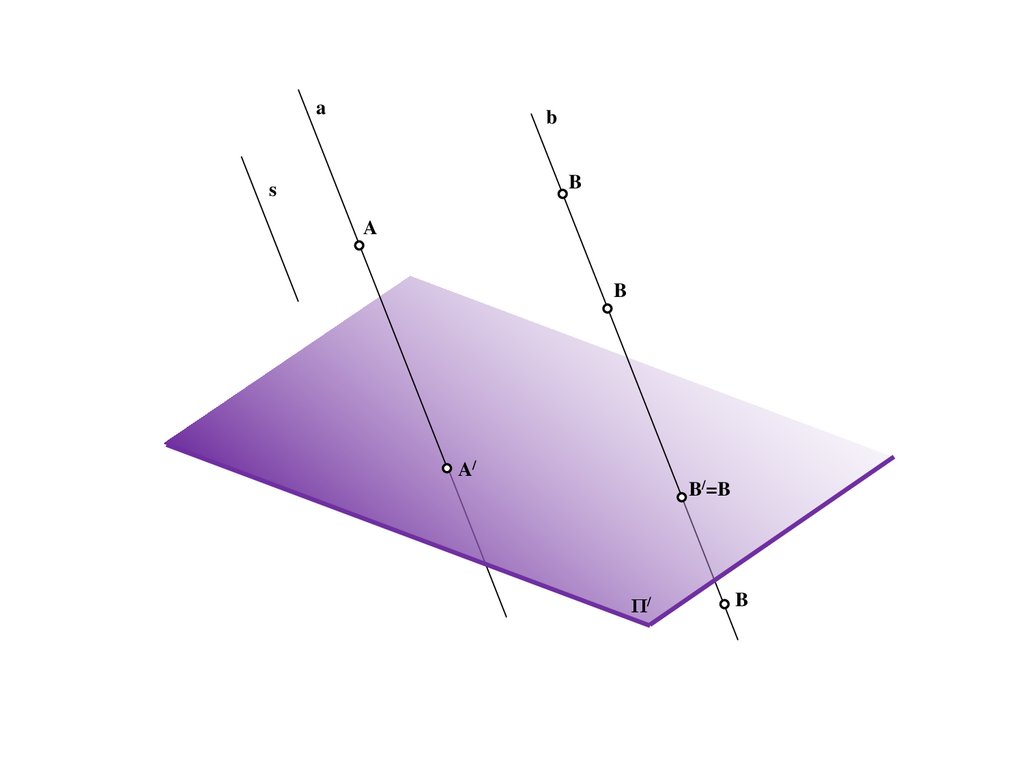
B
S
a
A
A/
Π/

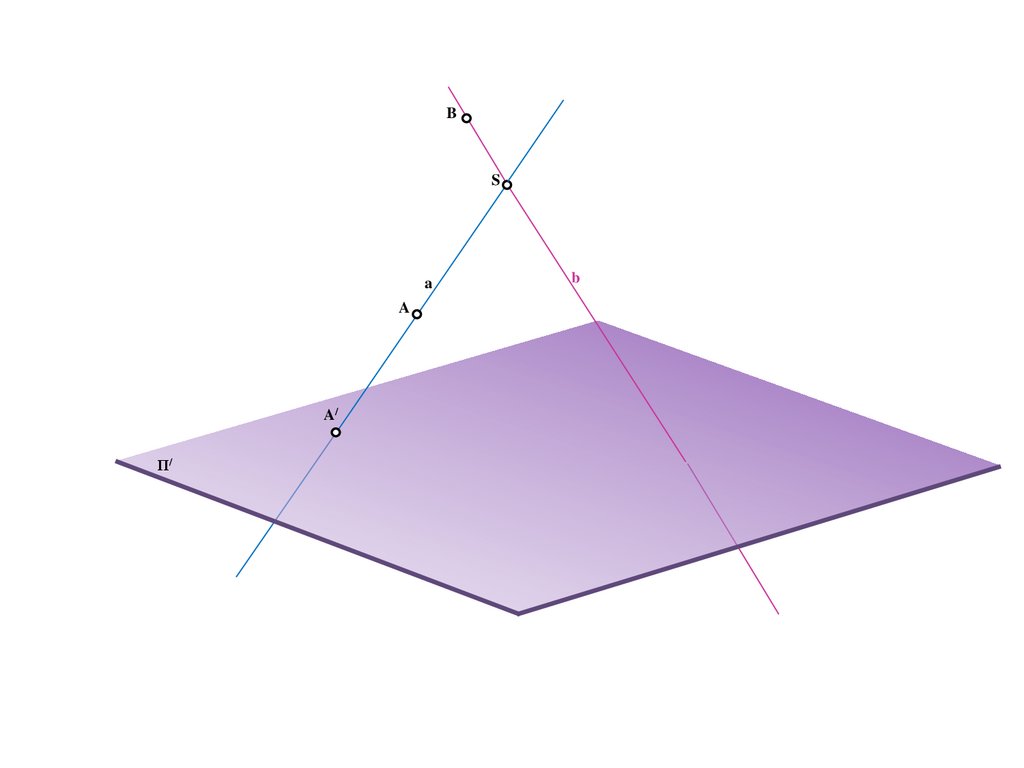
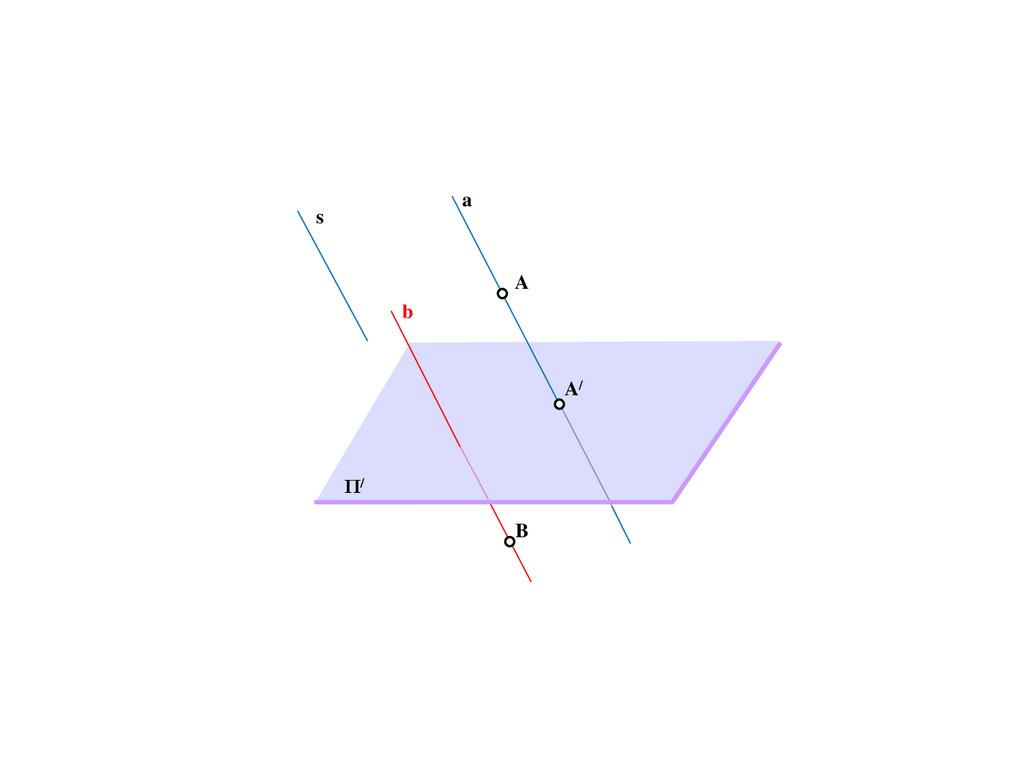
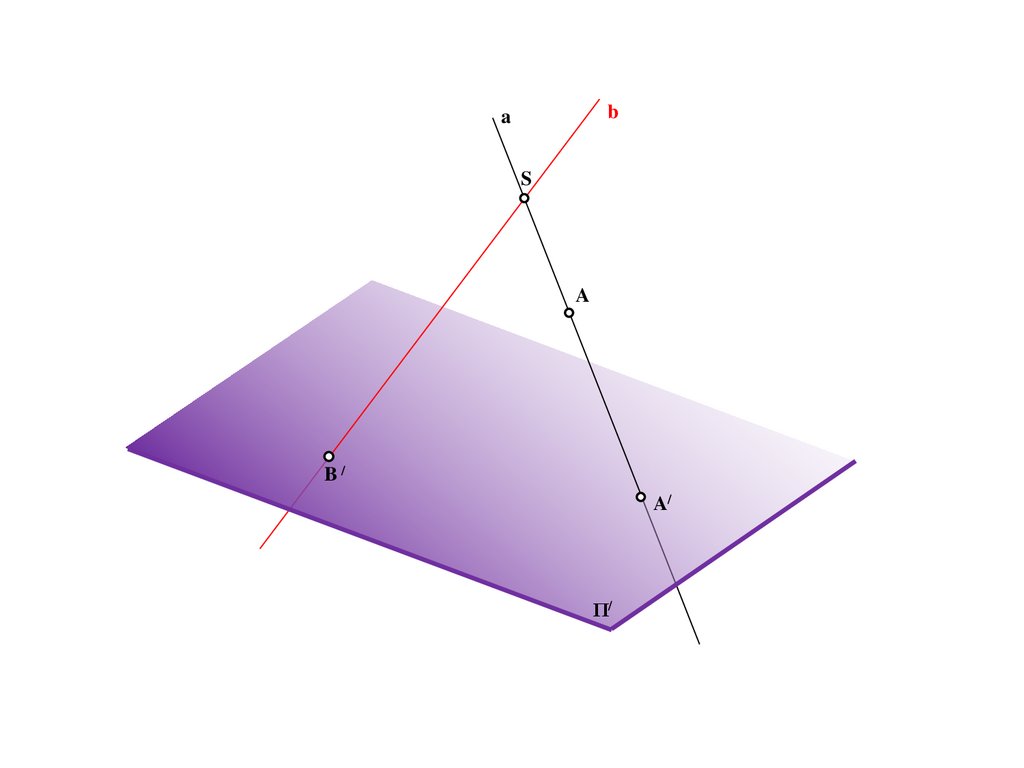
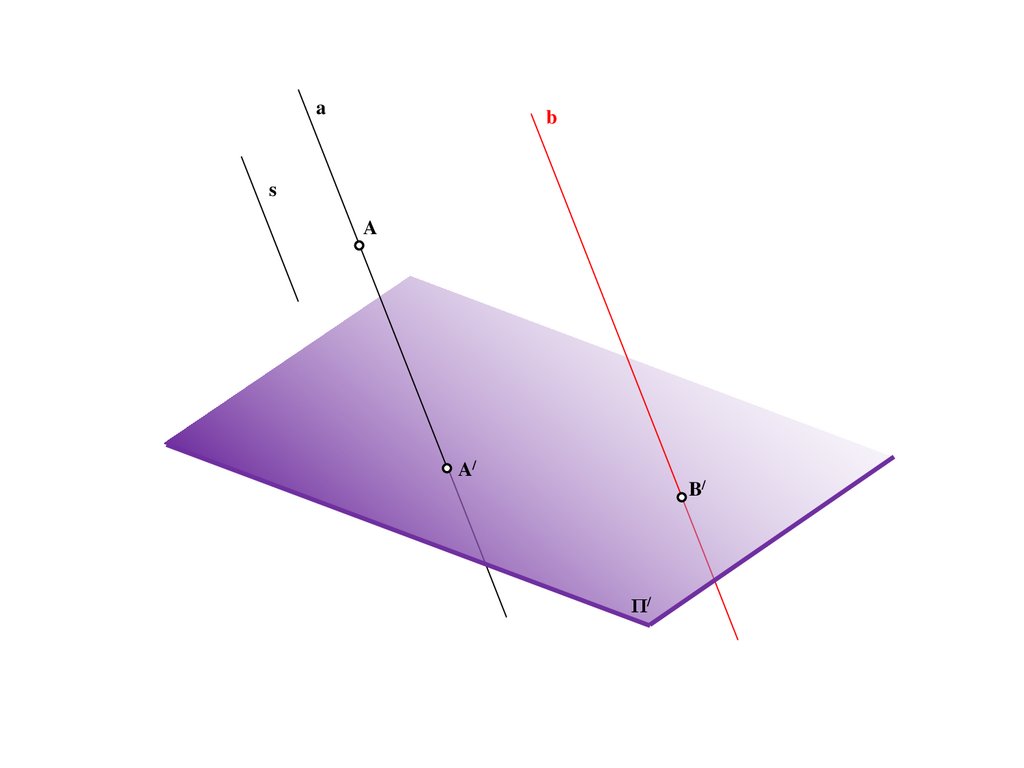
10.

B
S
a
A
A/
Π/
b

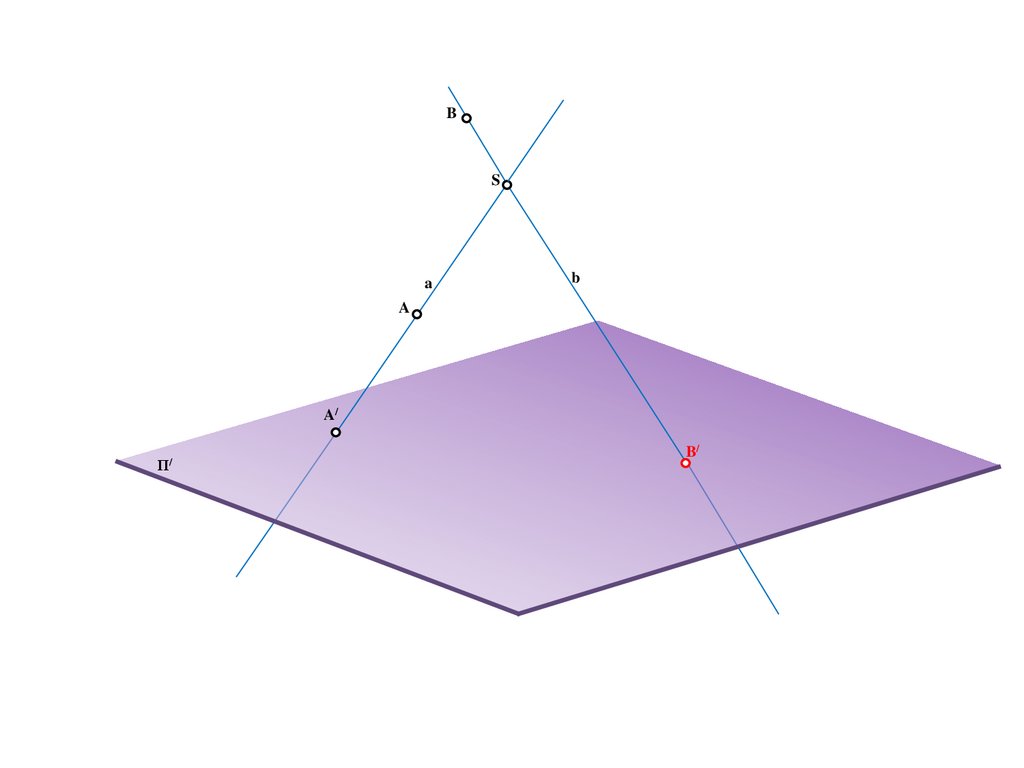
11.

B
S
a
b
A
A/
Π/
B/

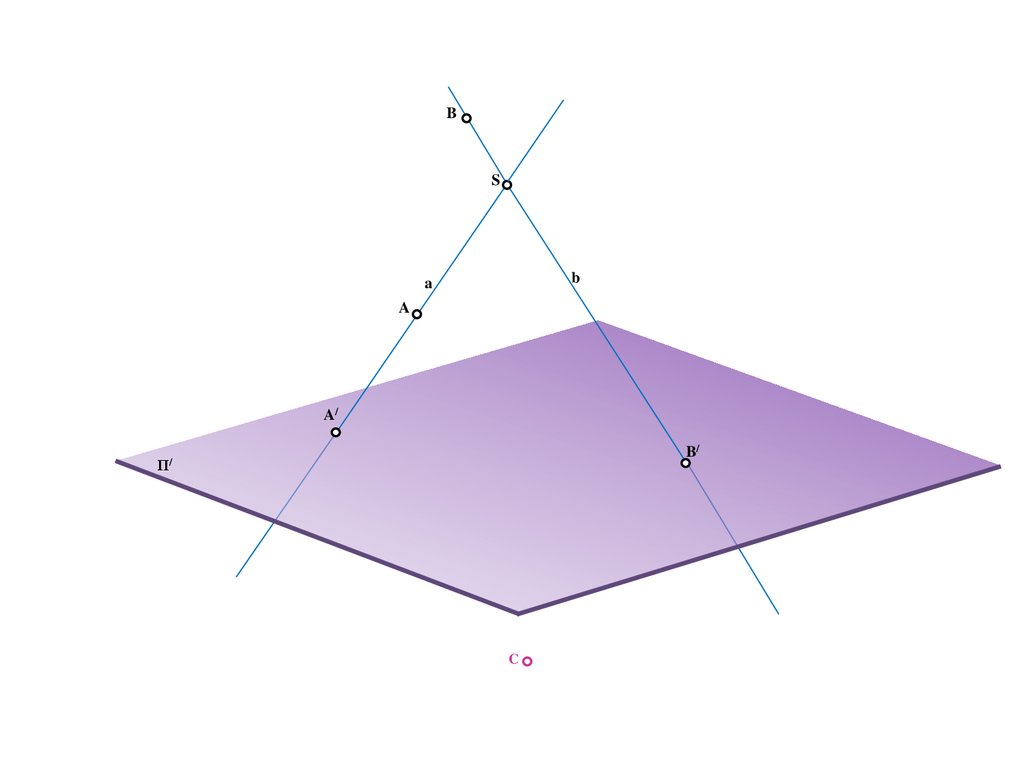
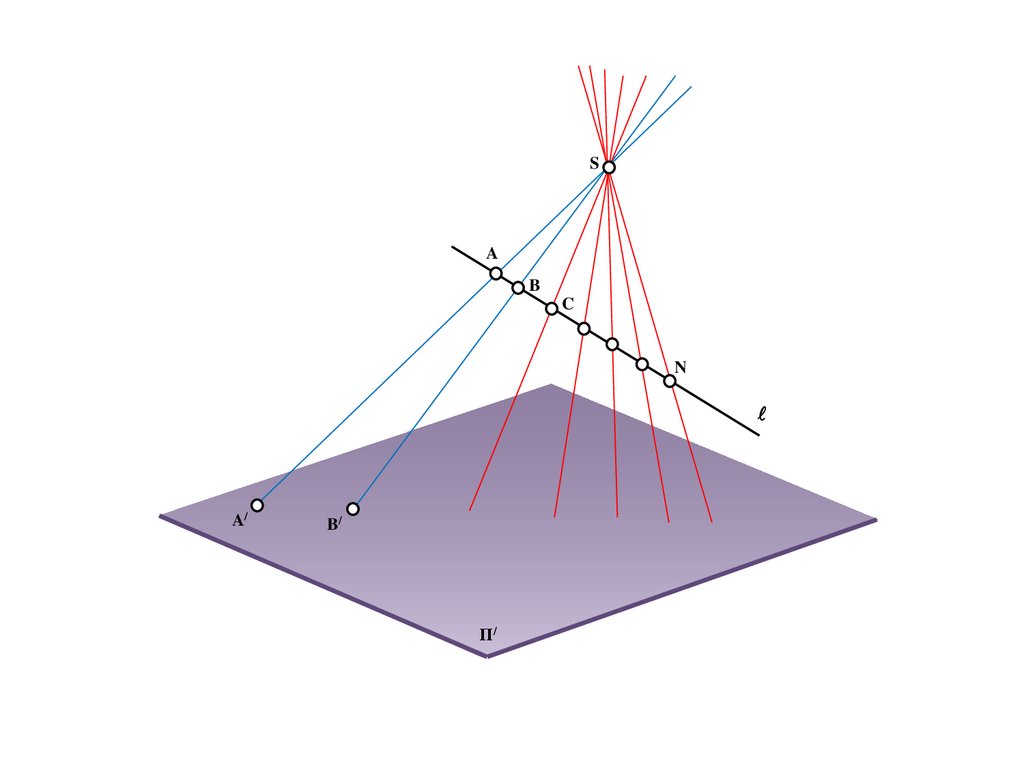
12.

B
S
b
a
A
A/
B/
Π/
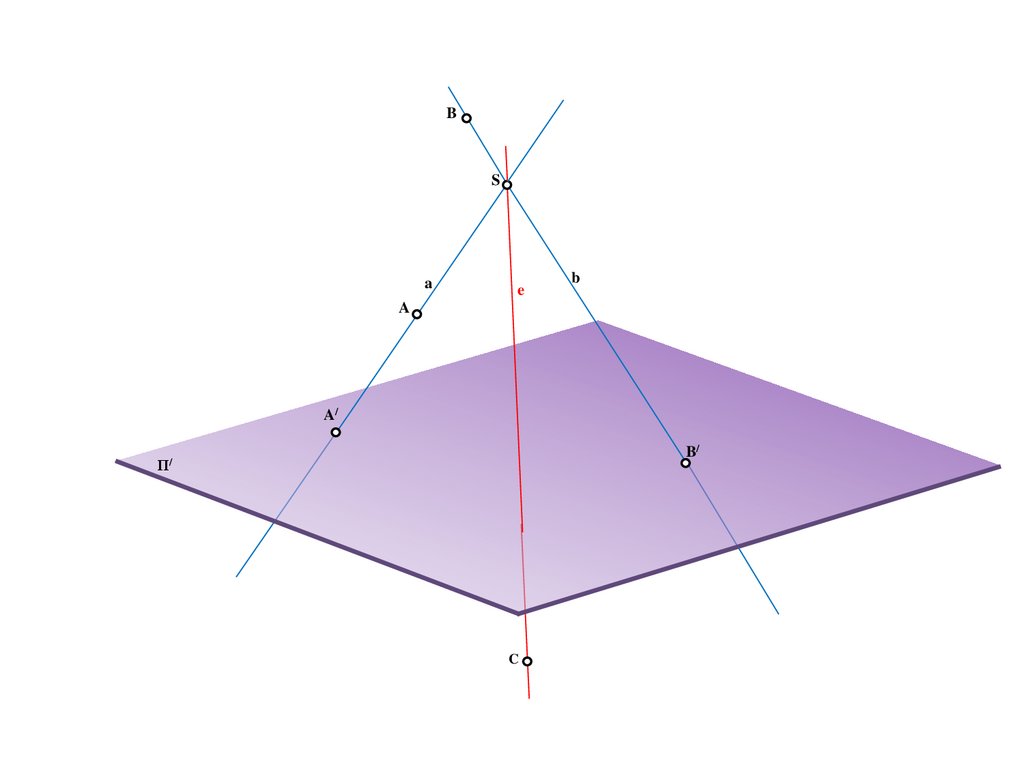
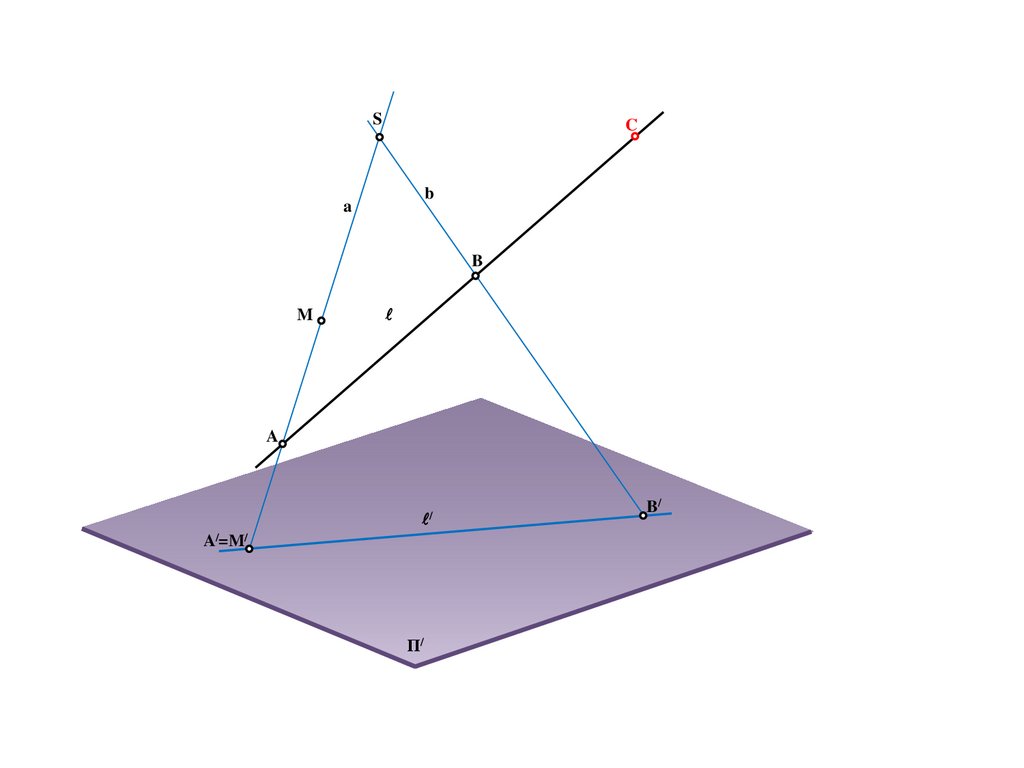
C

13.

B
S
a
e
b
A
A/
B/
Π/
C

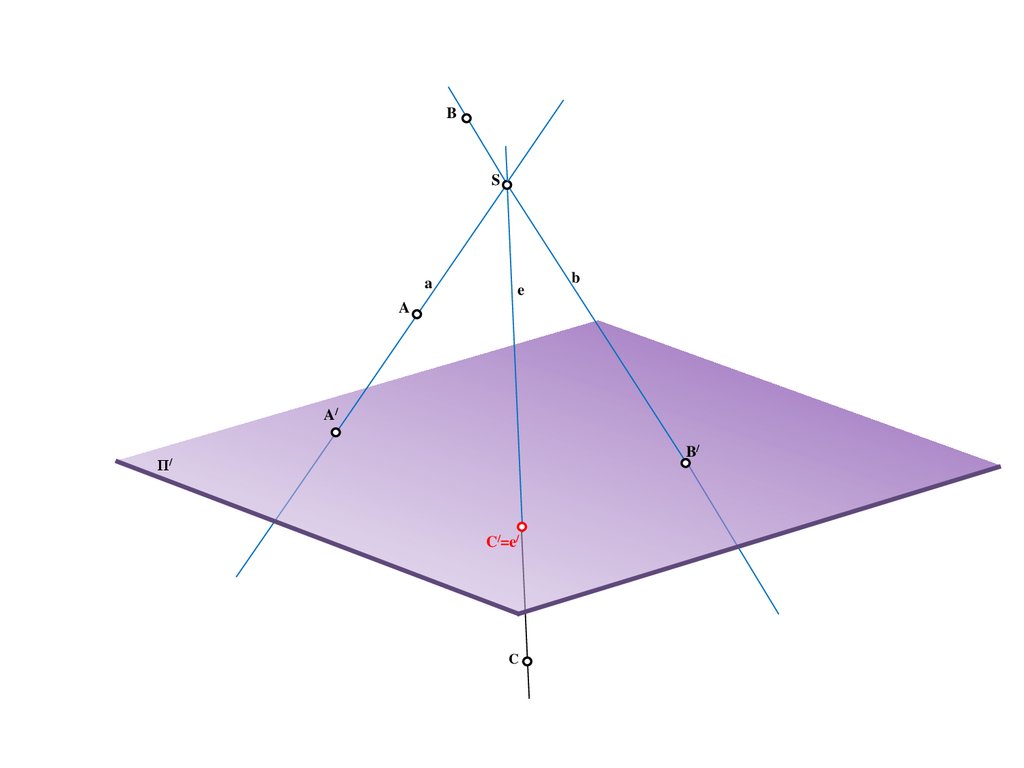
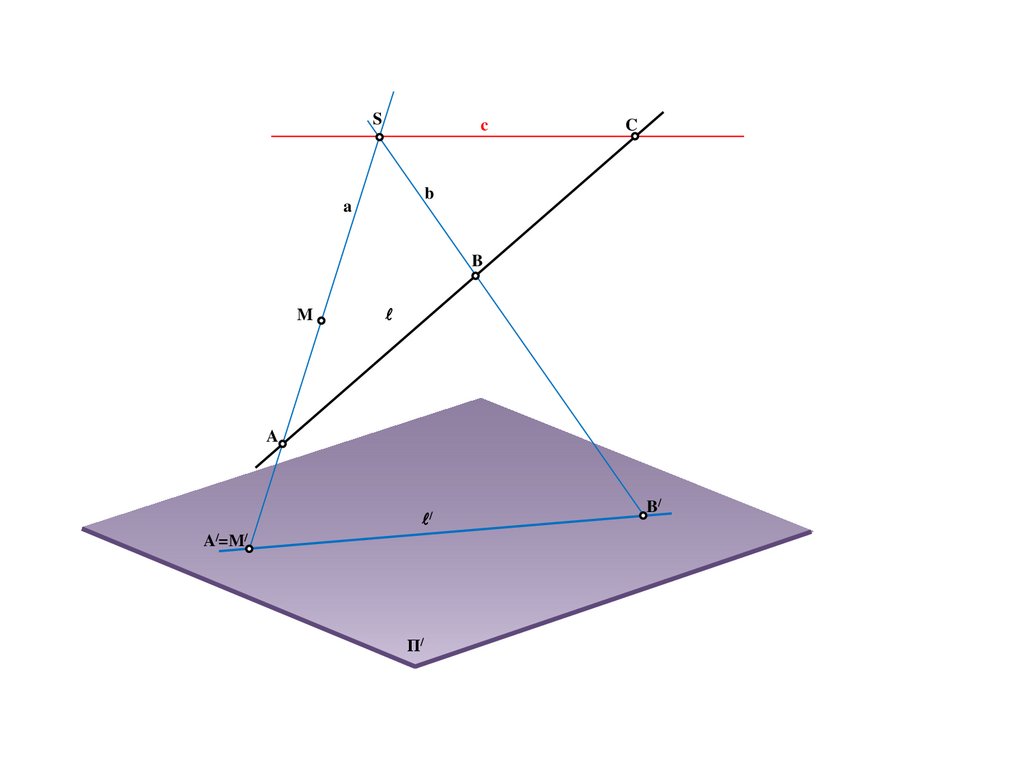
14.

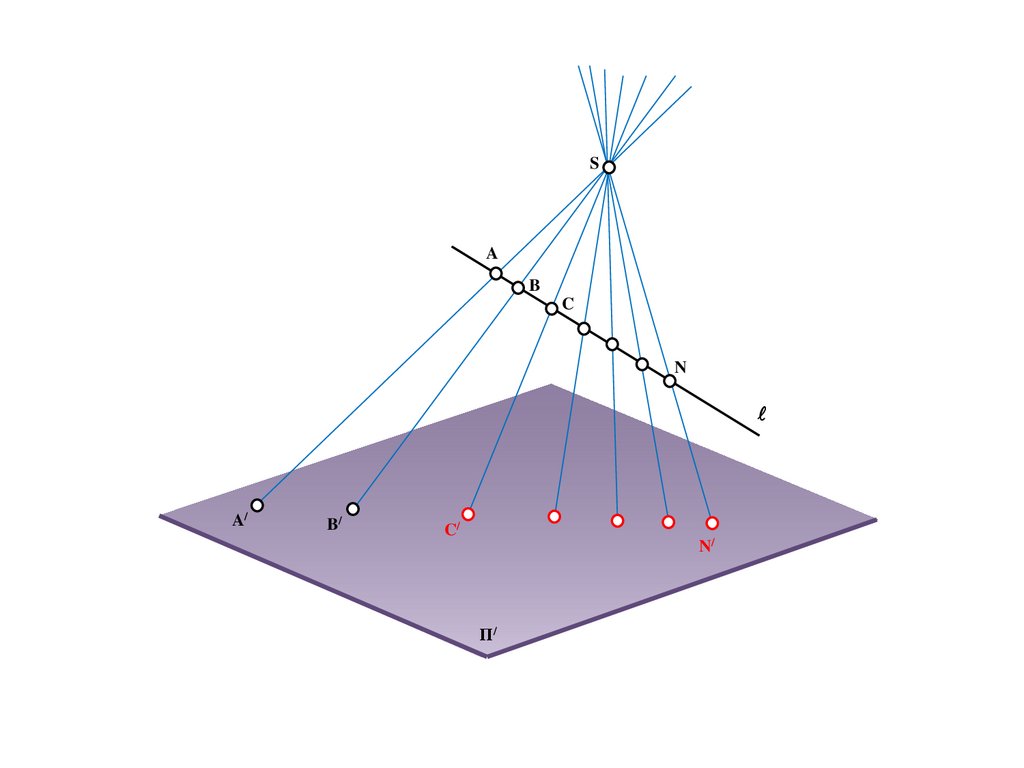
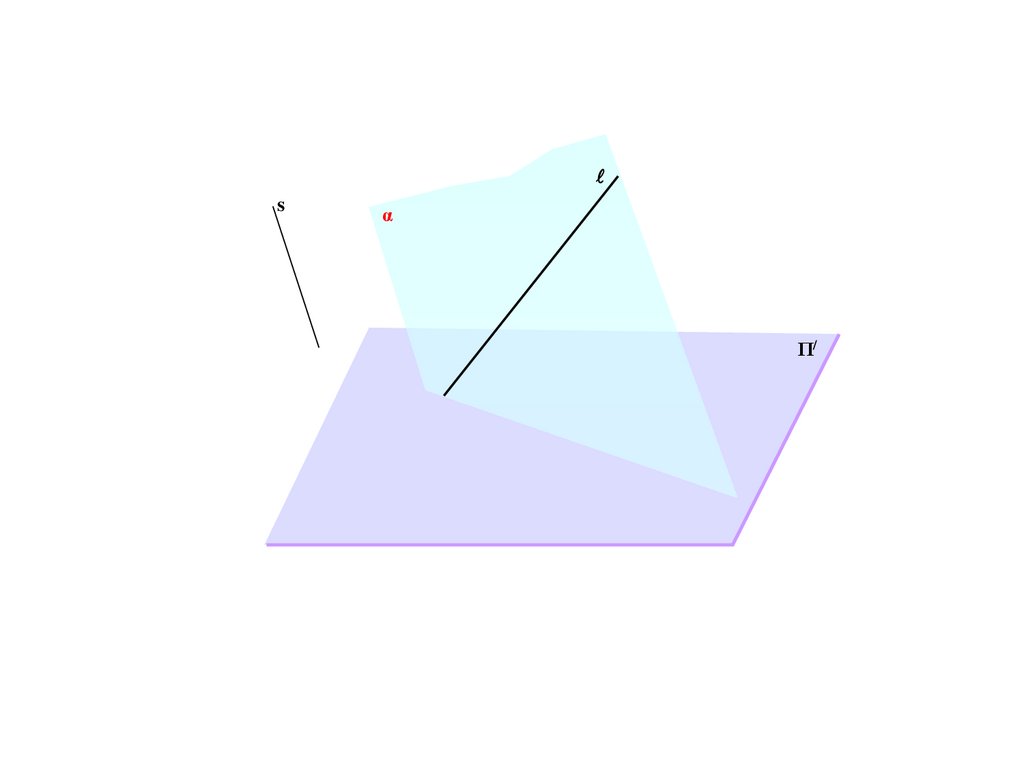
B
S
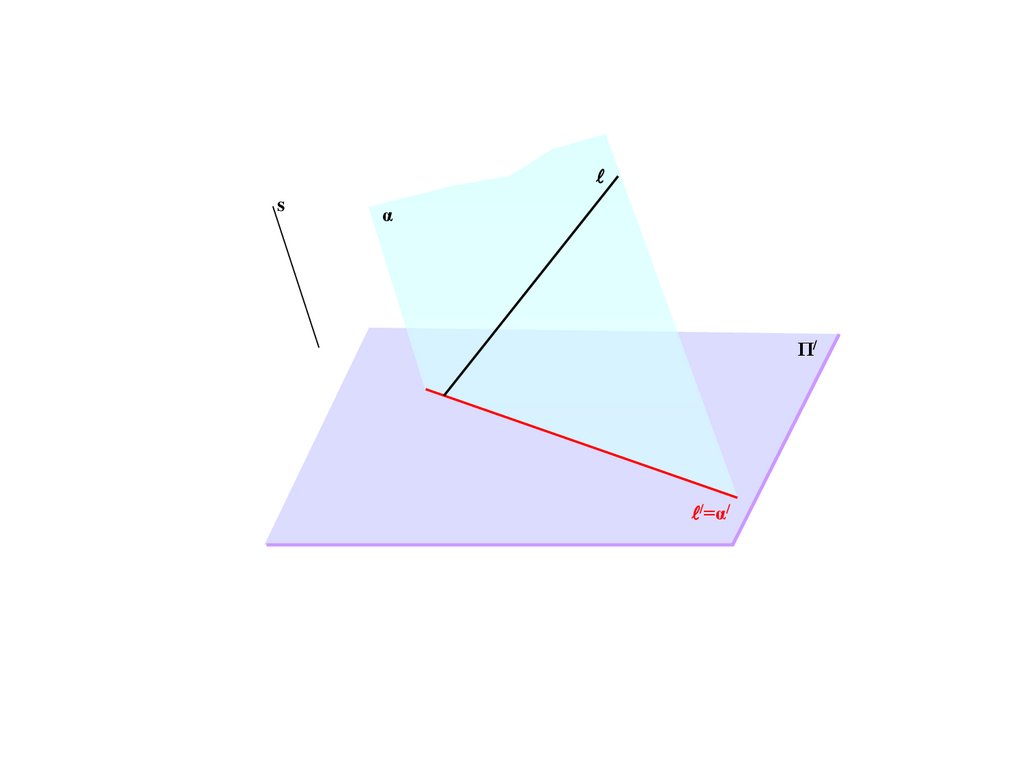
a
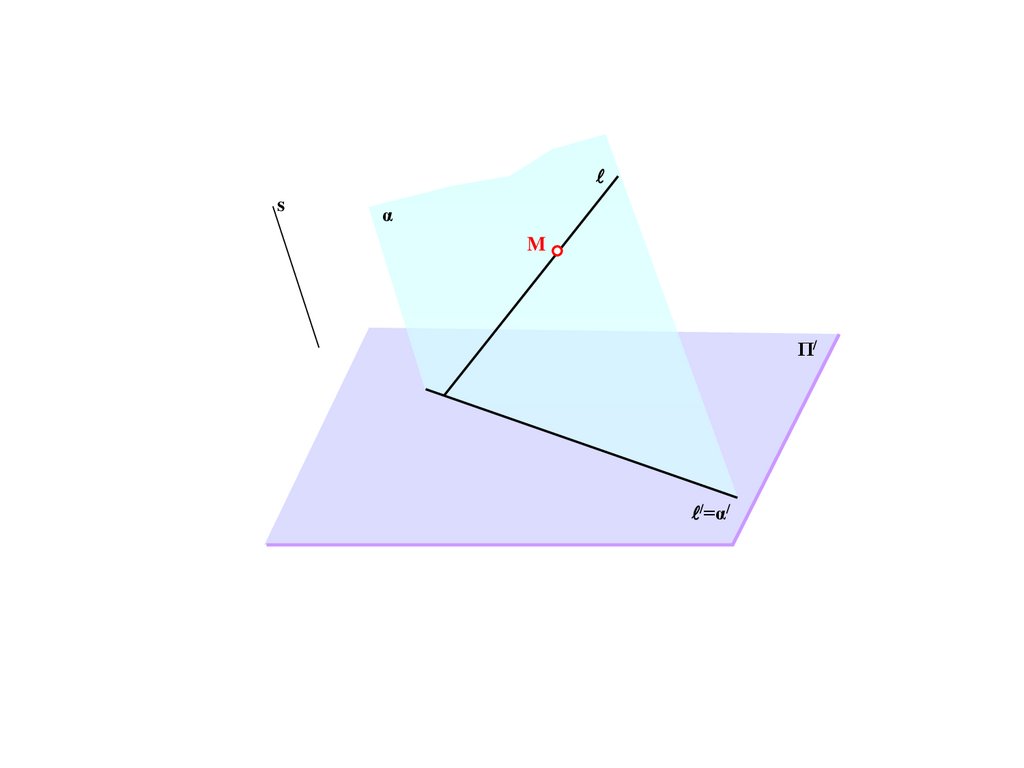
e
b
A
A/
B/
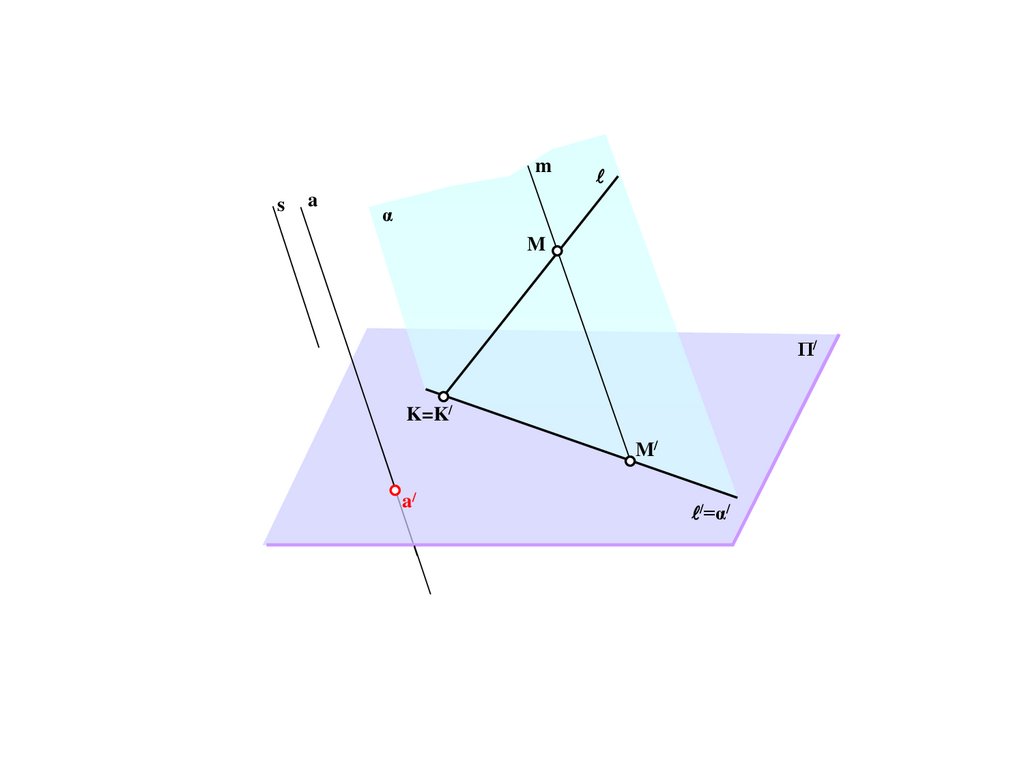
Π/
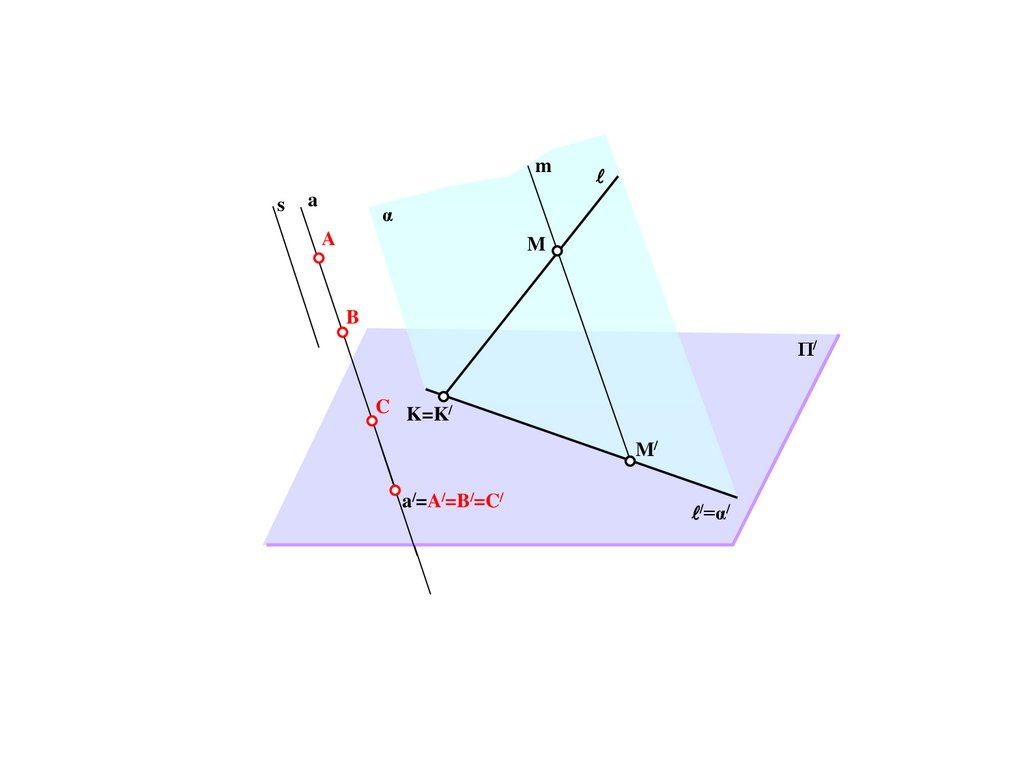
C/=e/
C

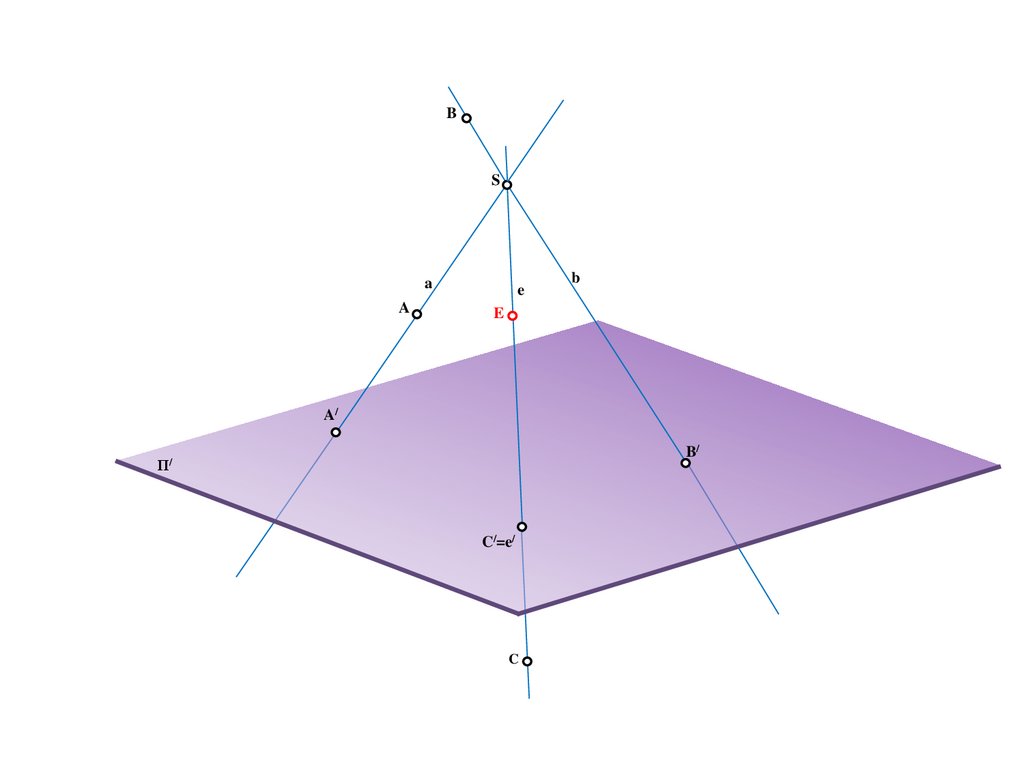
15.

B
S
a
A
e
b
E
A/
B/
Π/
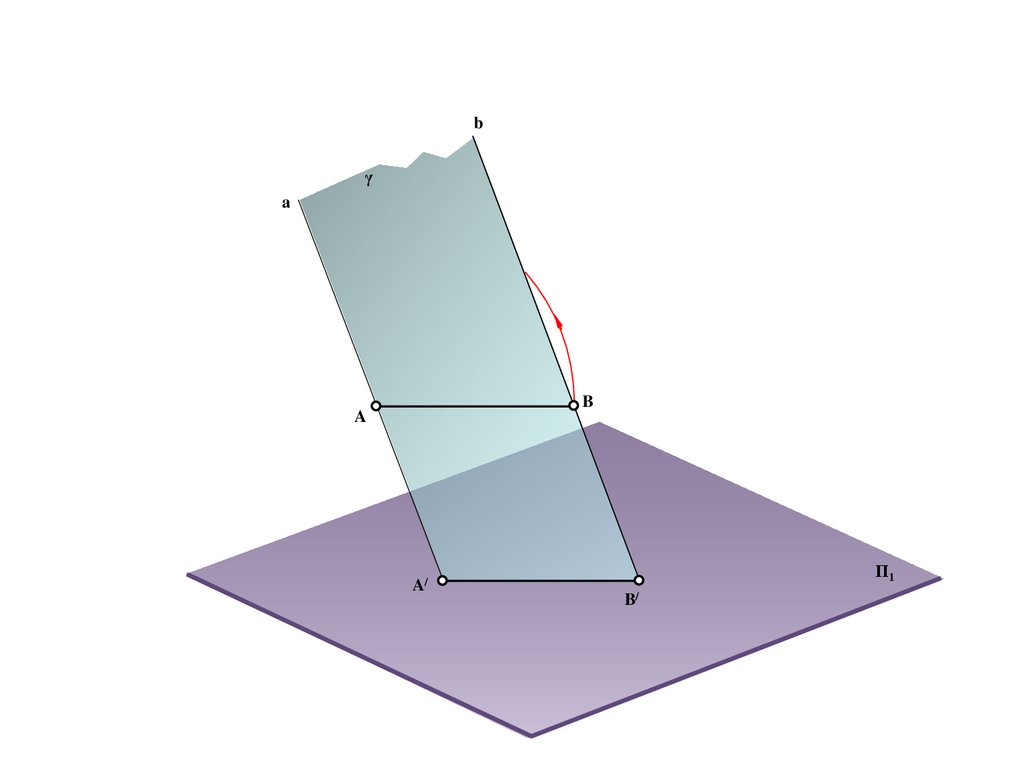
C/=e/
C

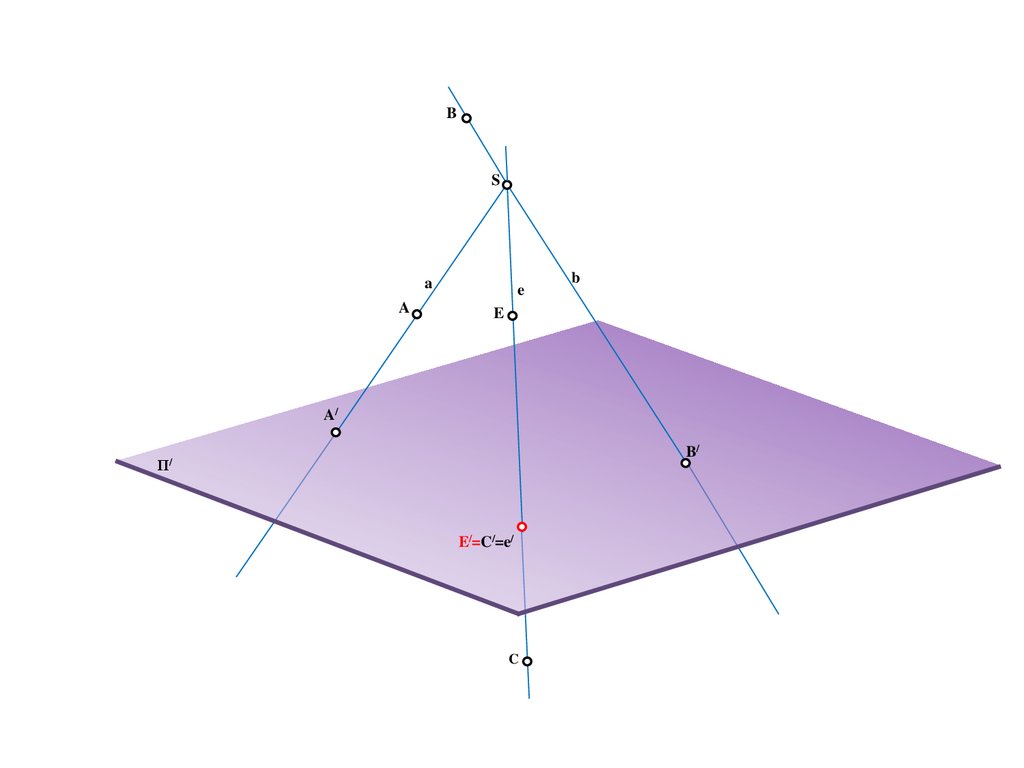
16.

B
S
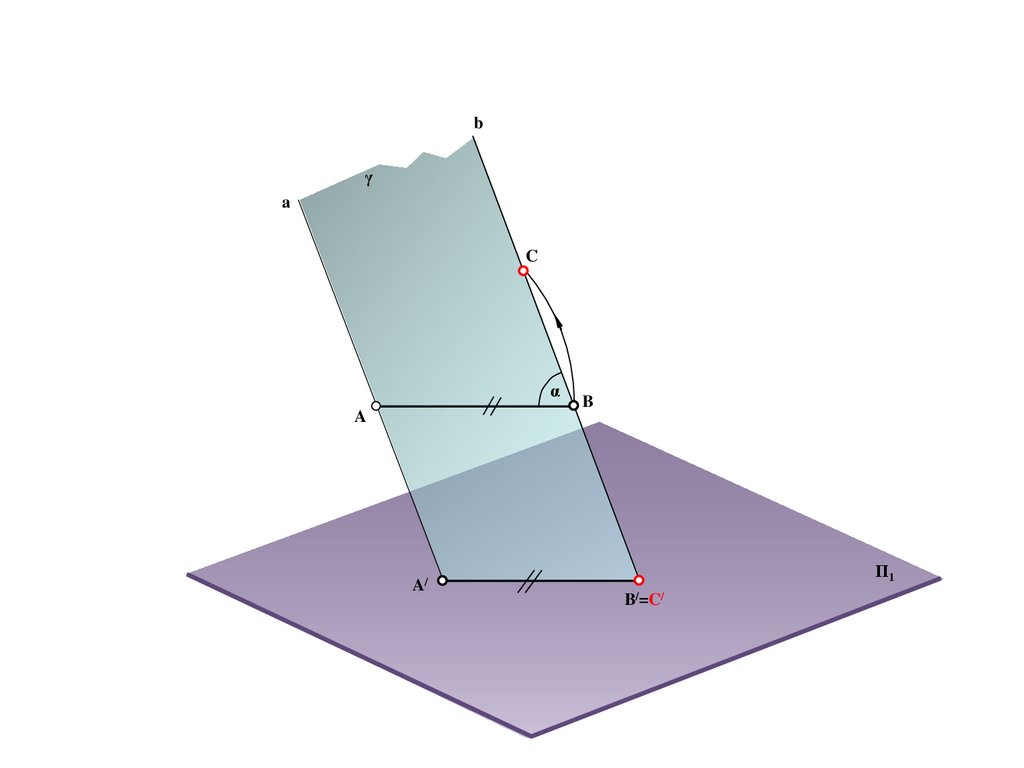
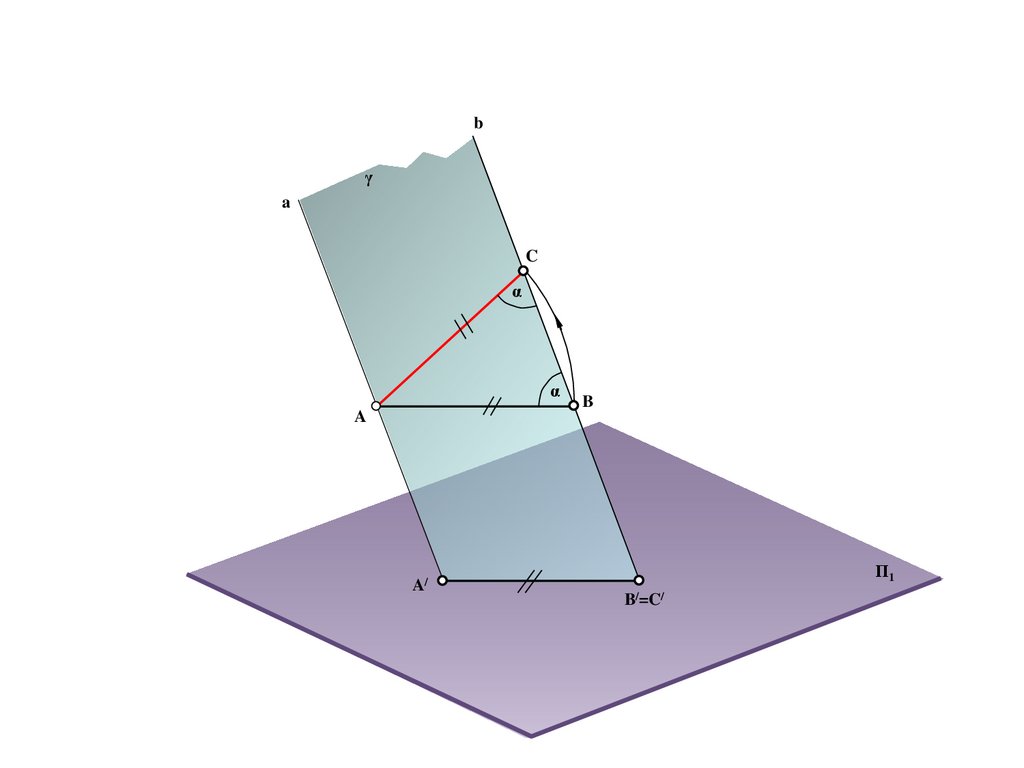
a
A
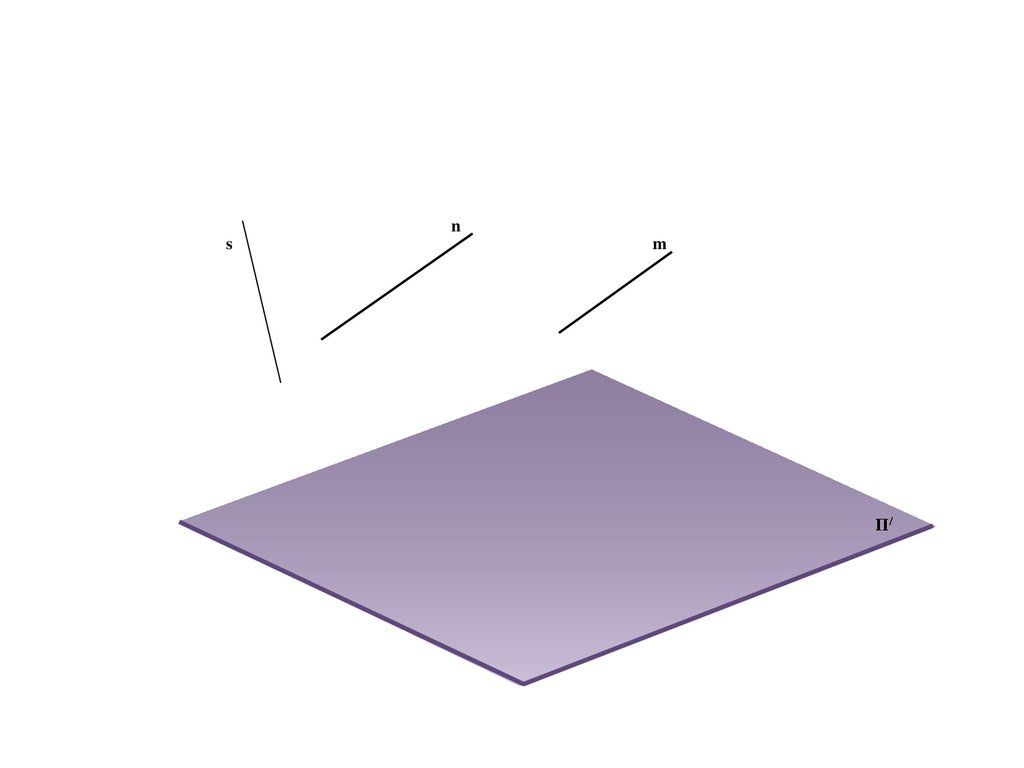
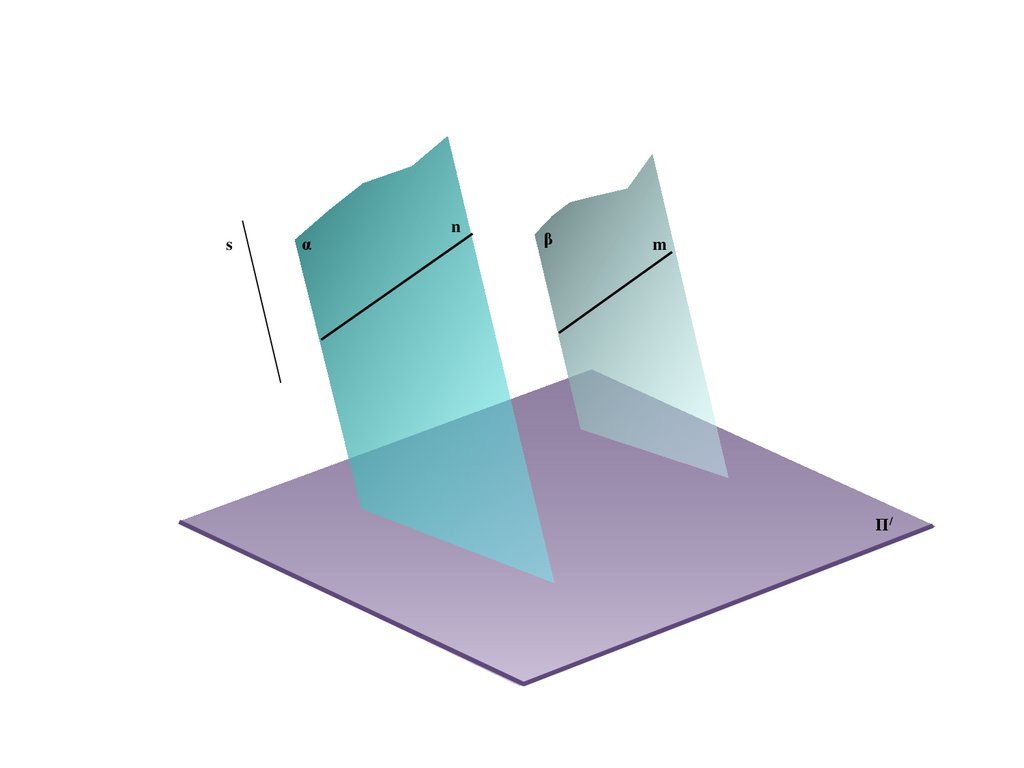
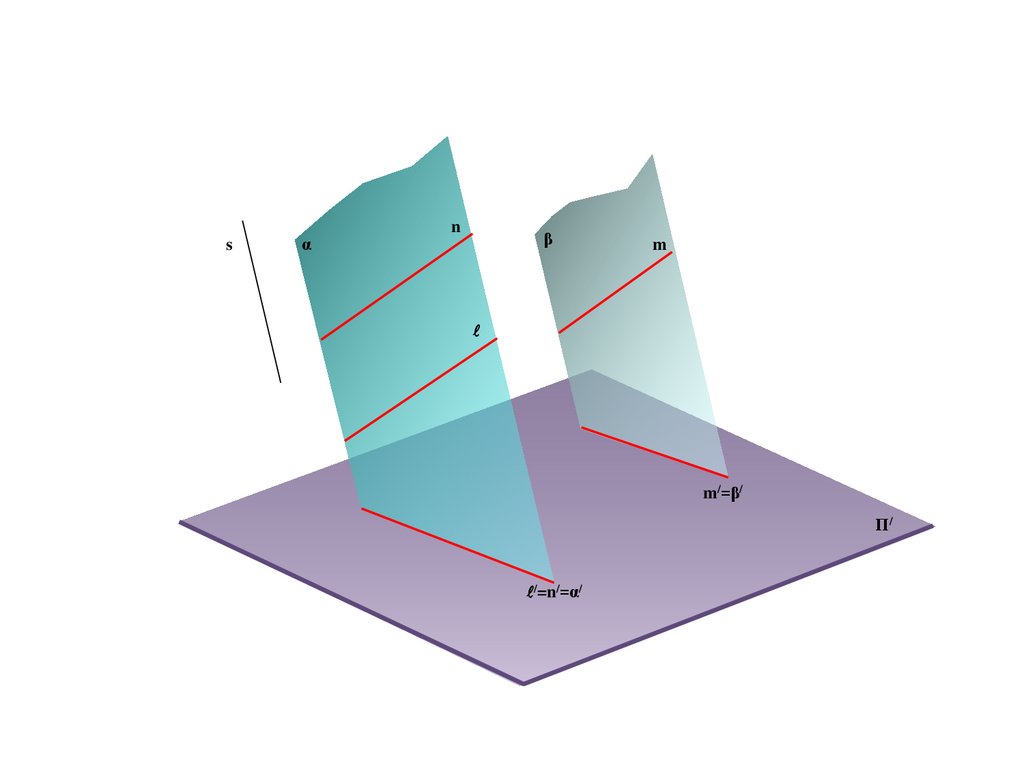
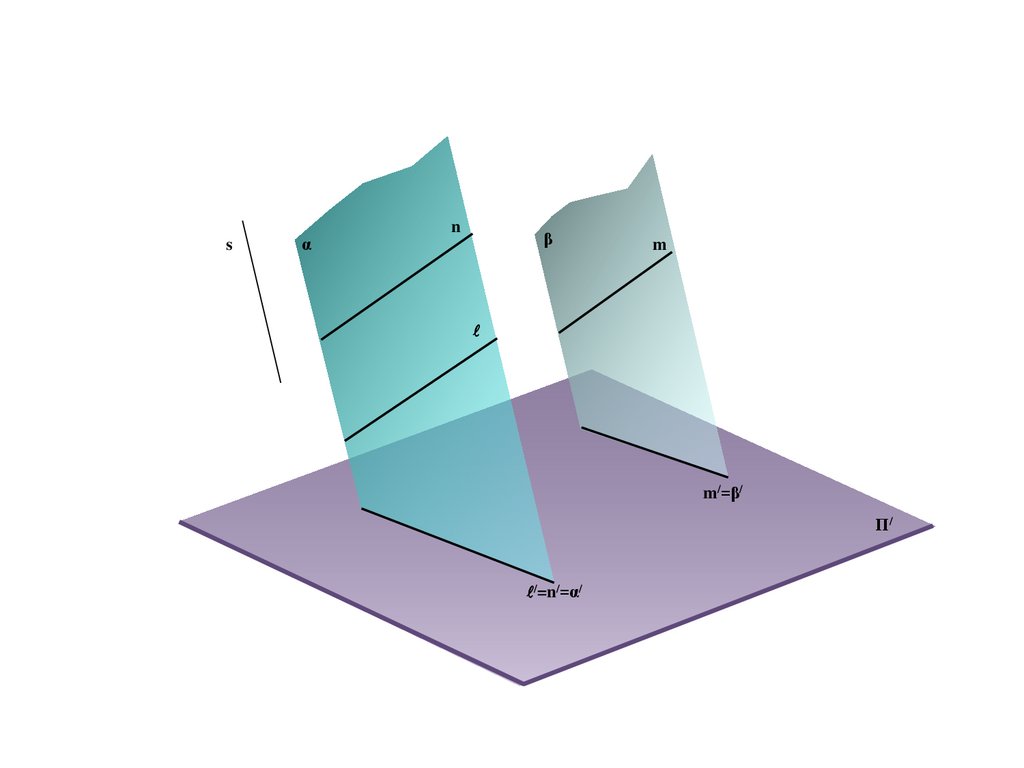
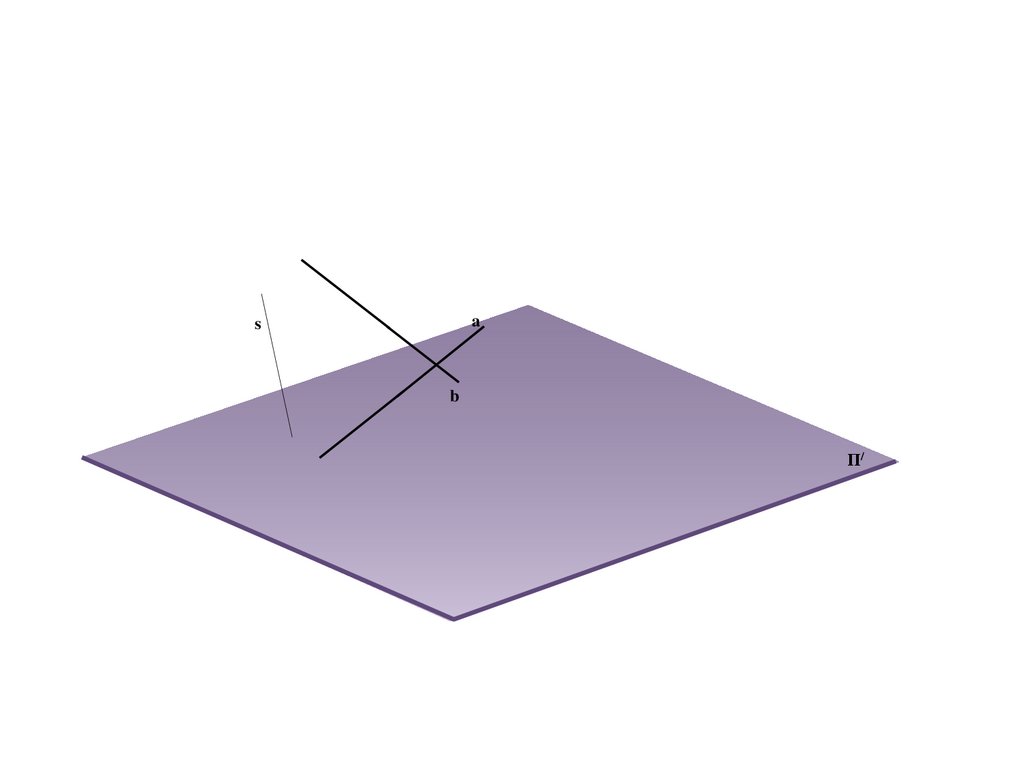
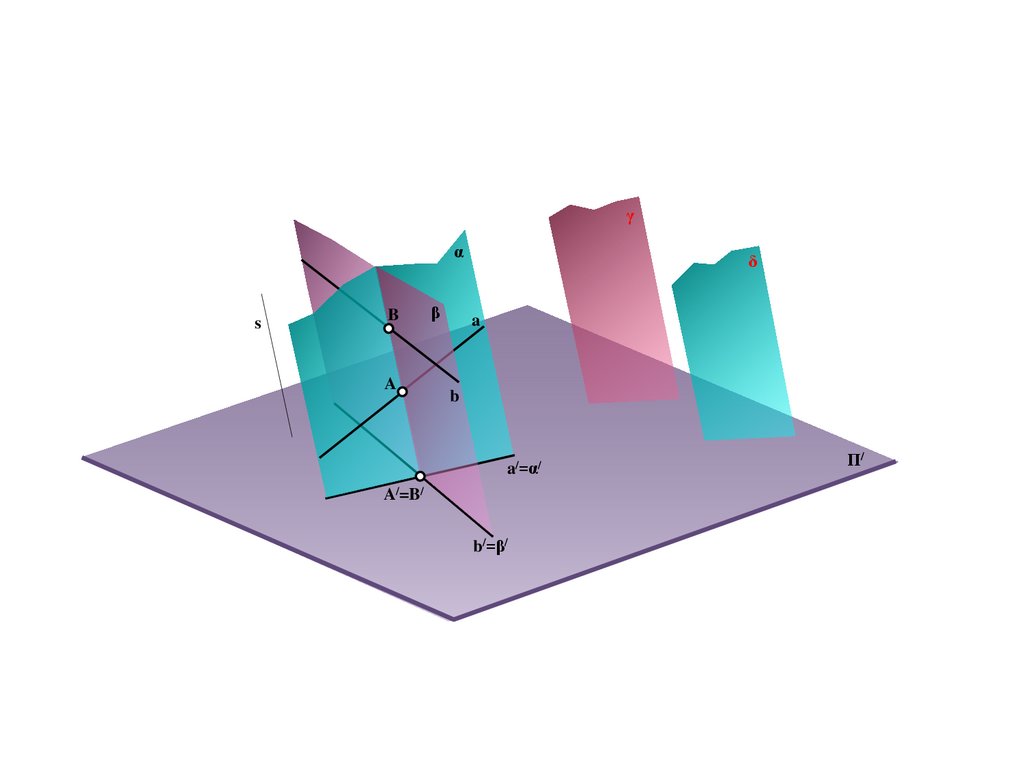
e
b
E
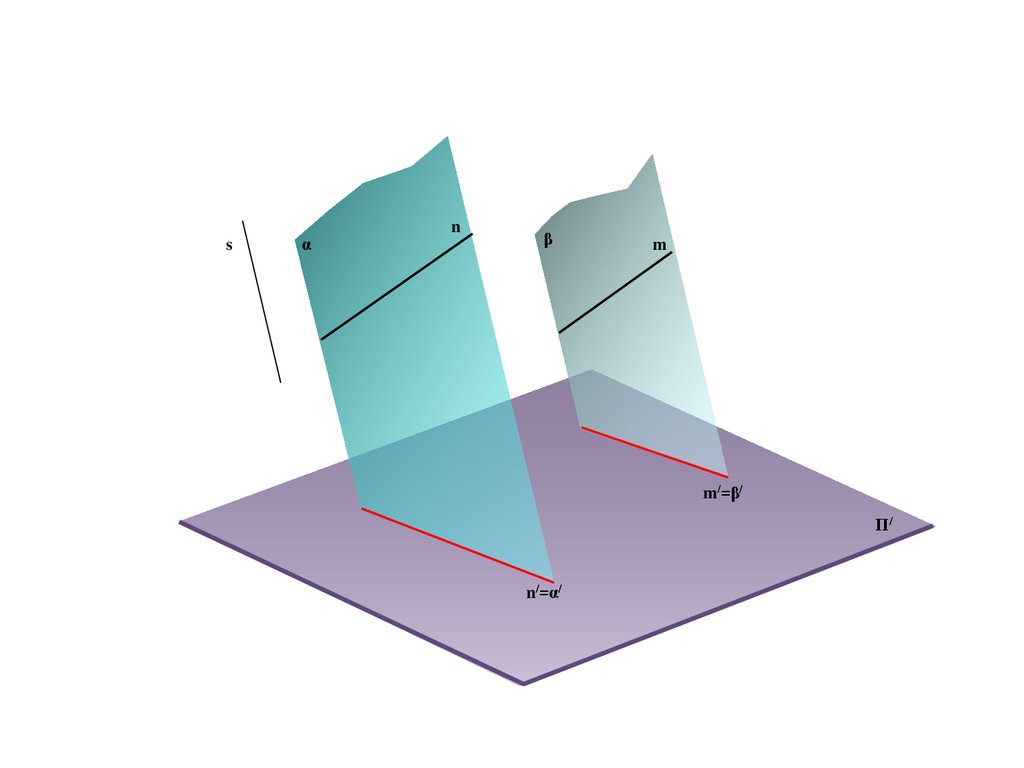
A/
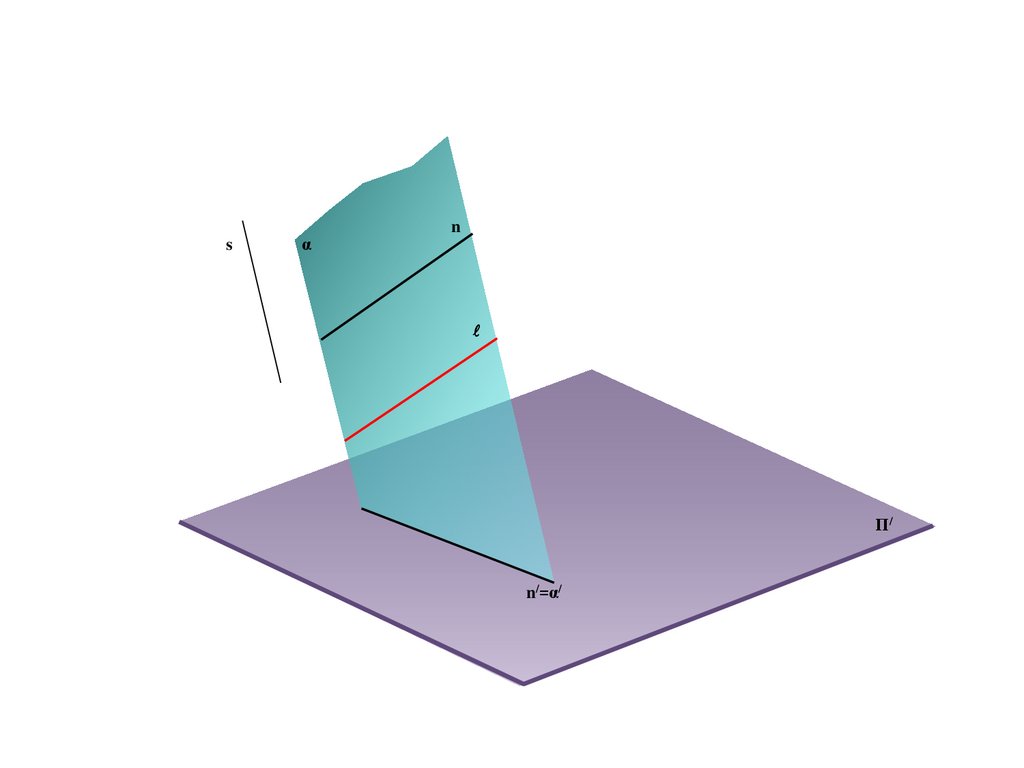
B/
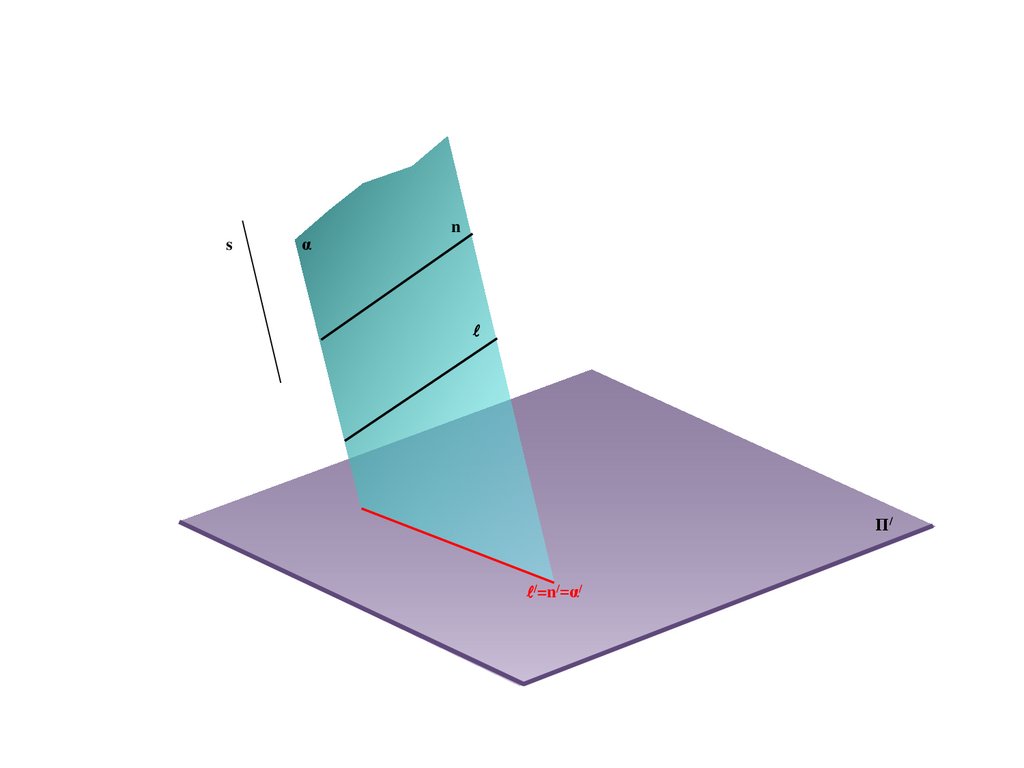
Π/
E/=C/=e/
C

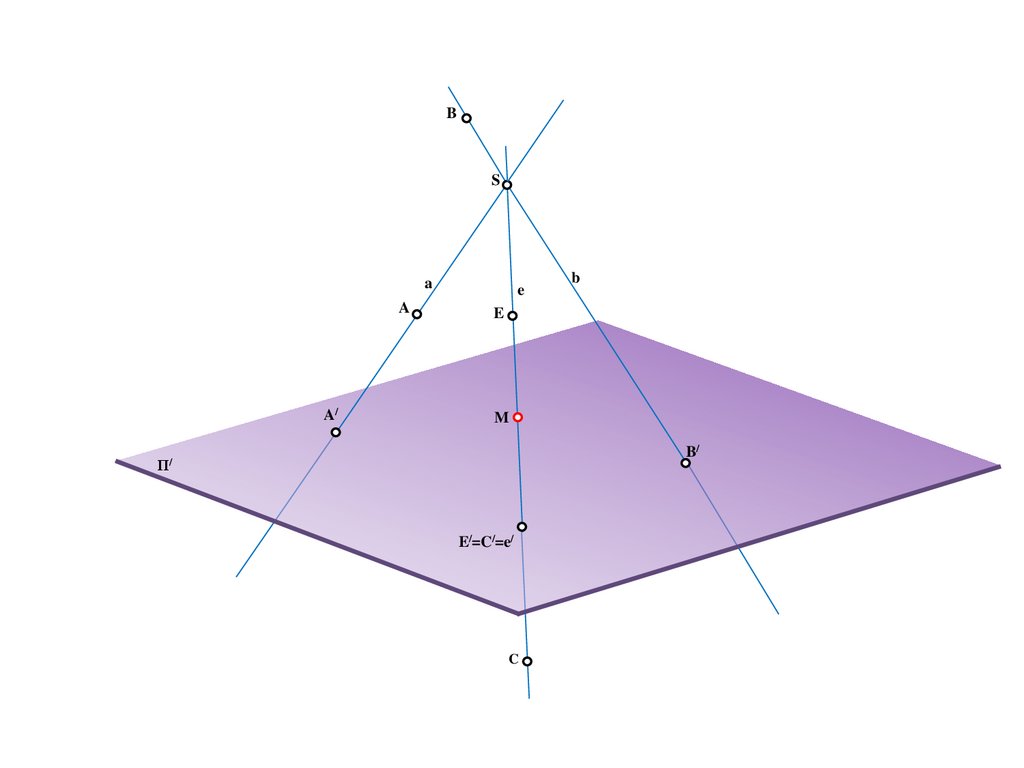
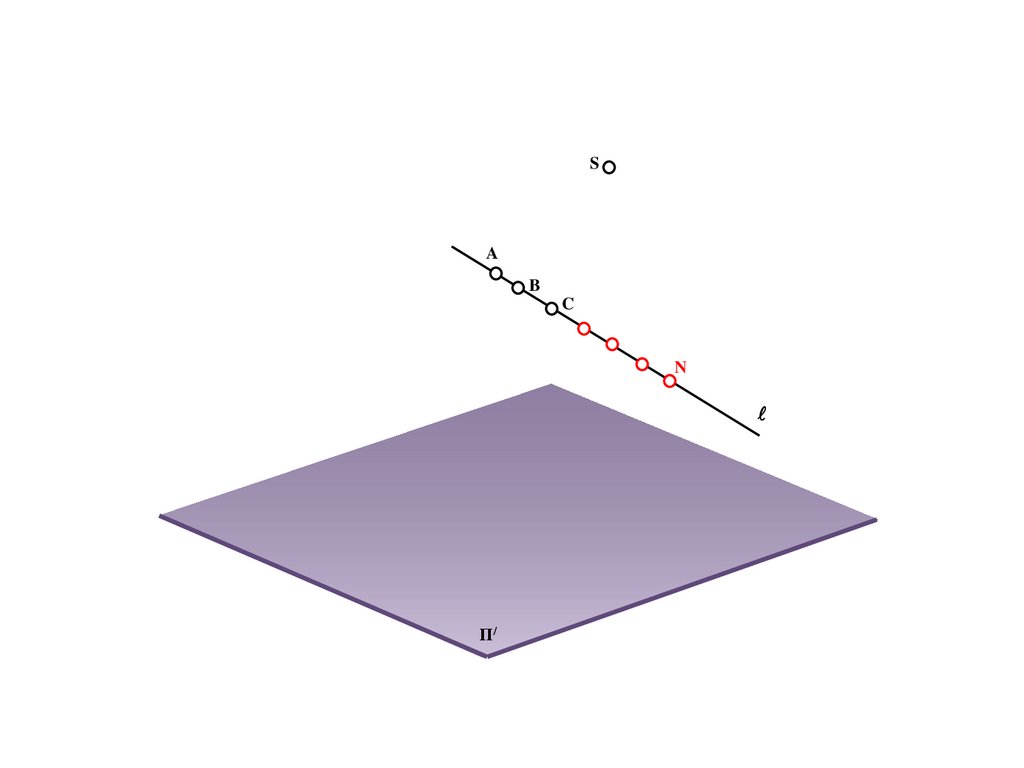
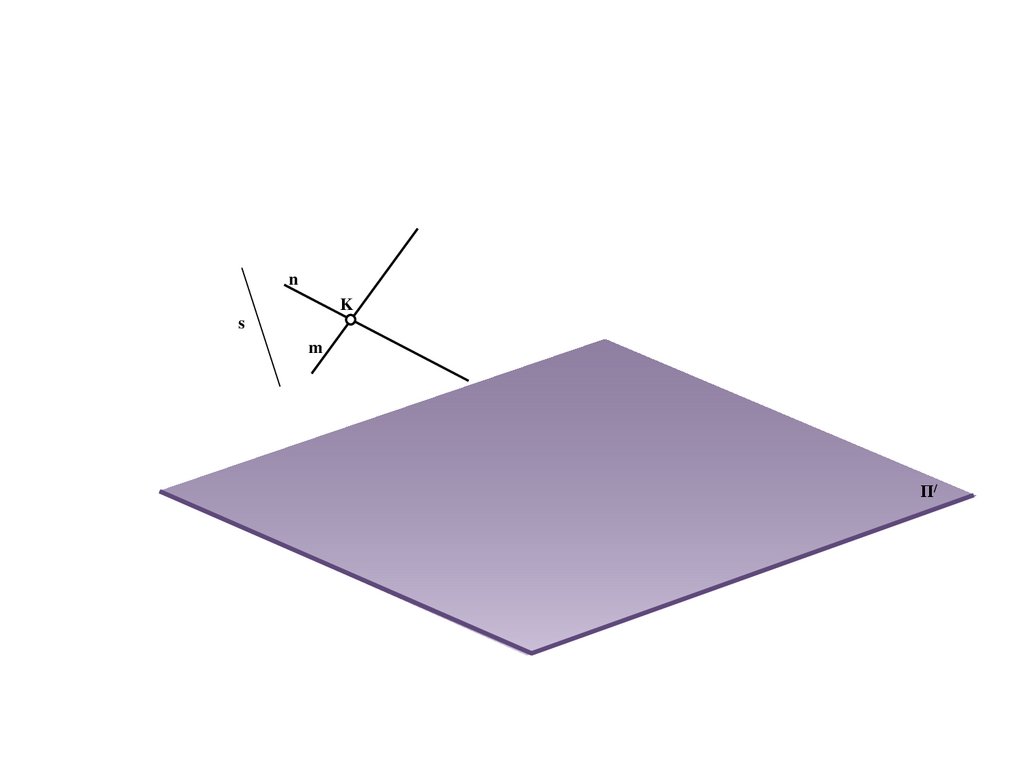
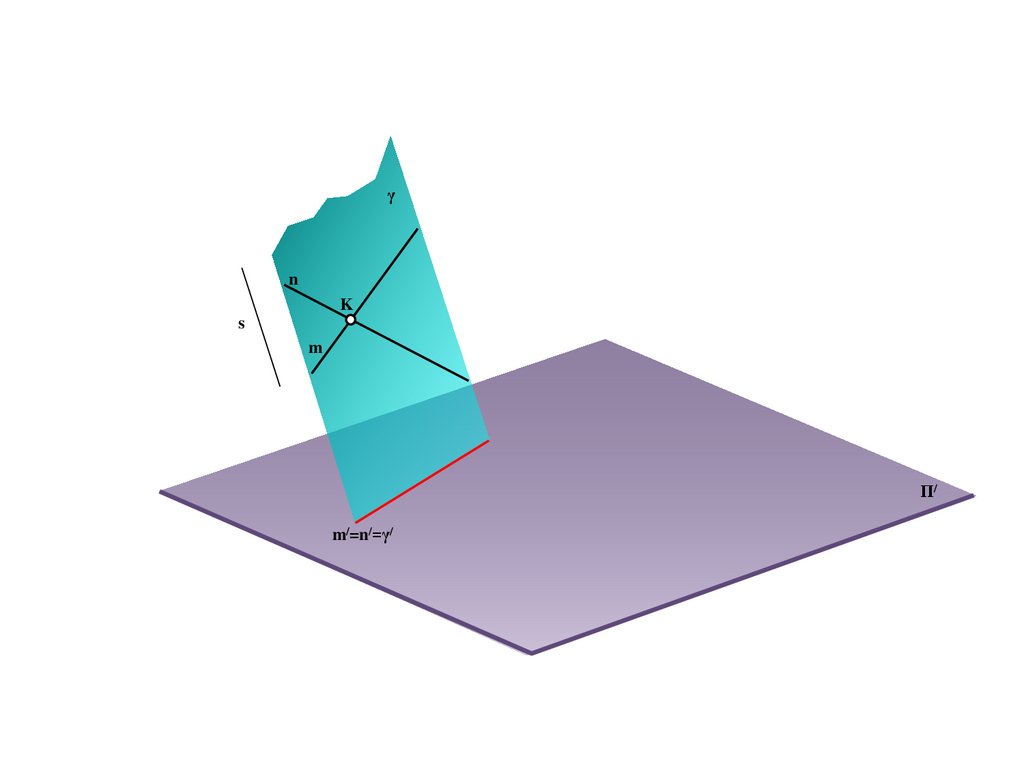
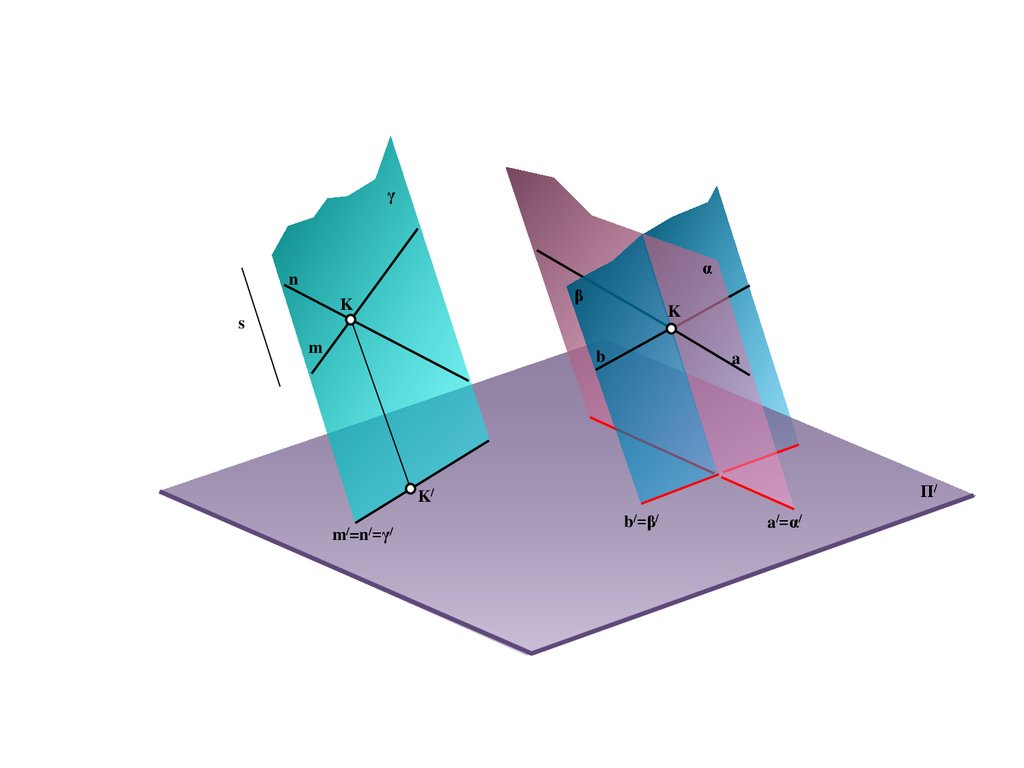
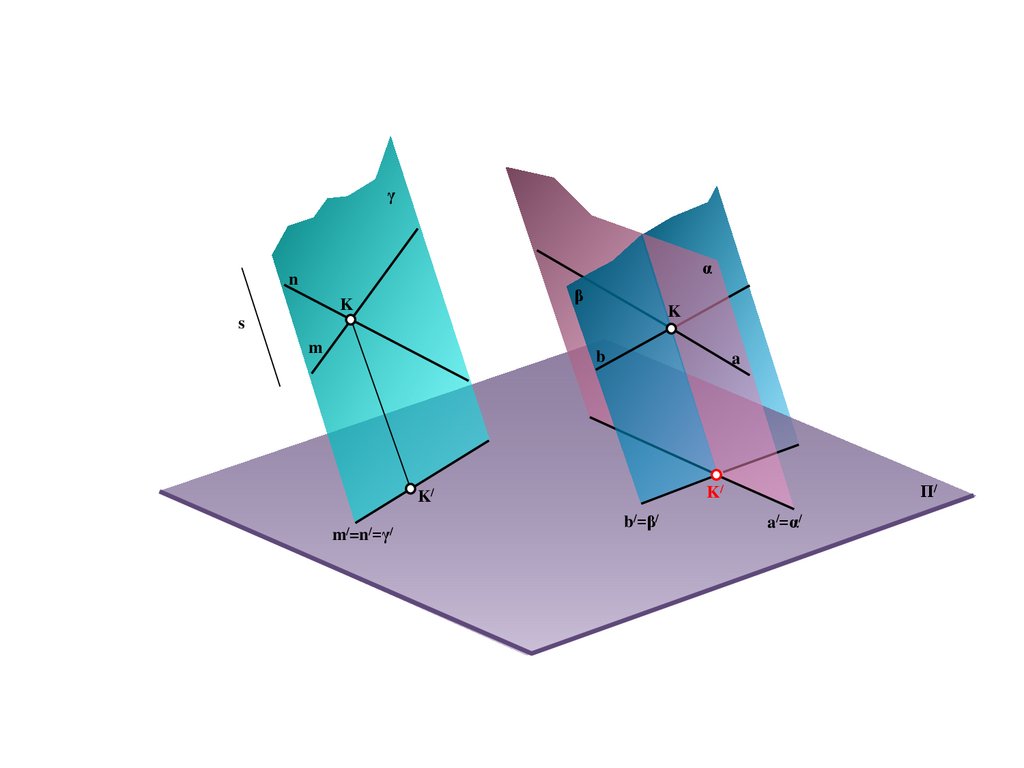
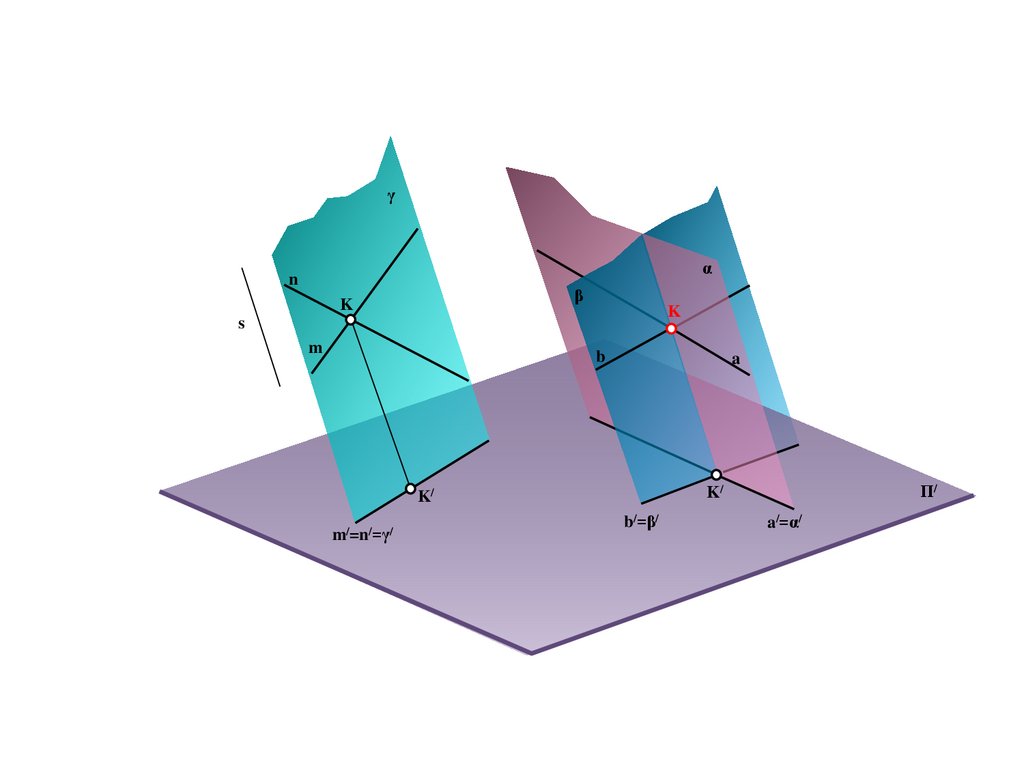
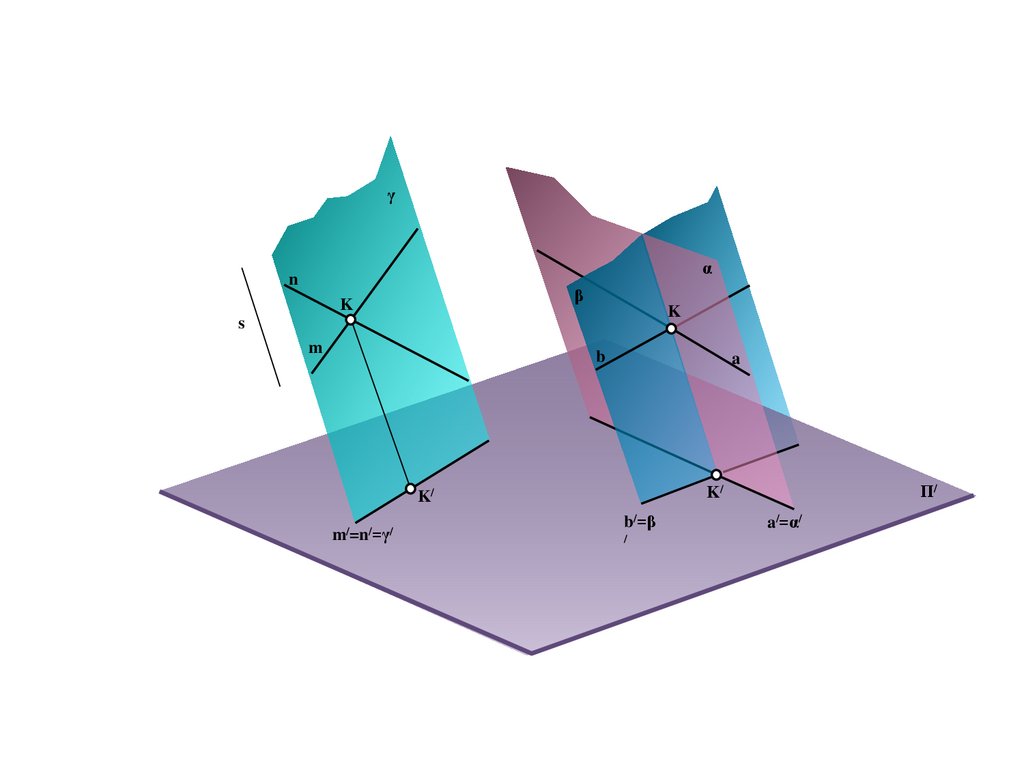
17.

B
S
a
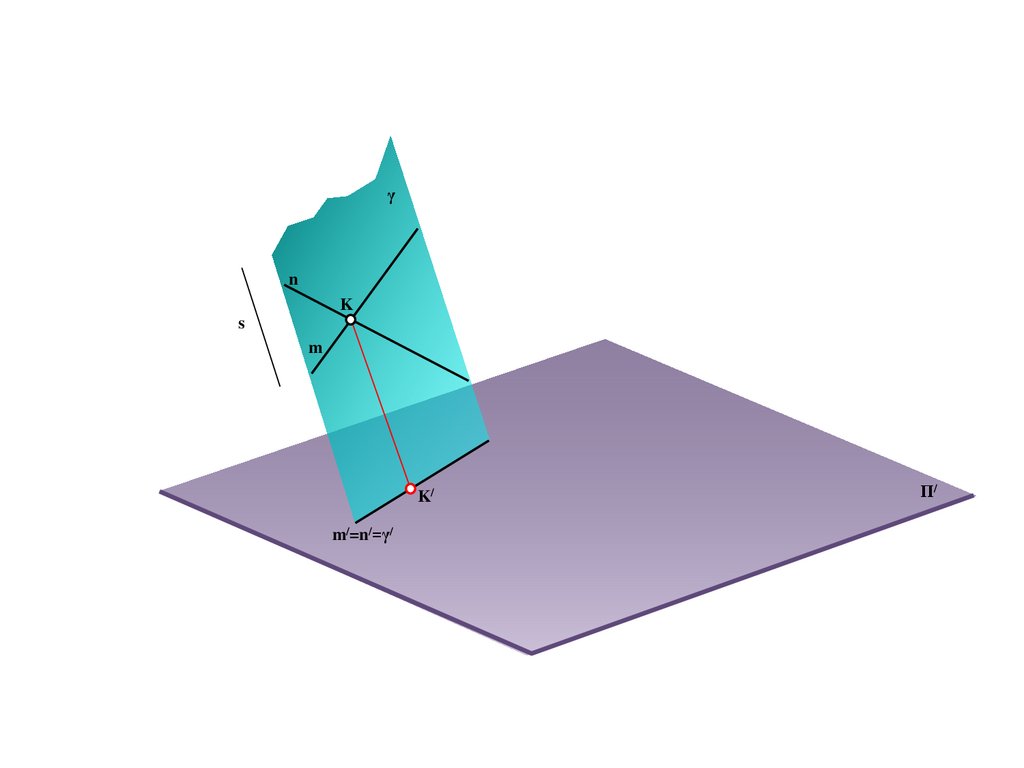
A
A/
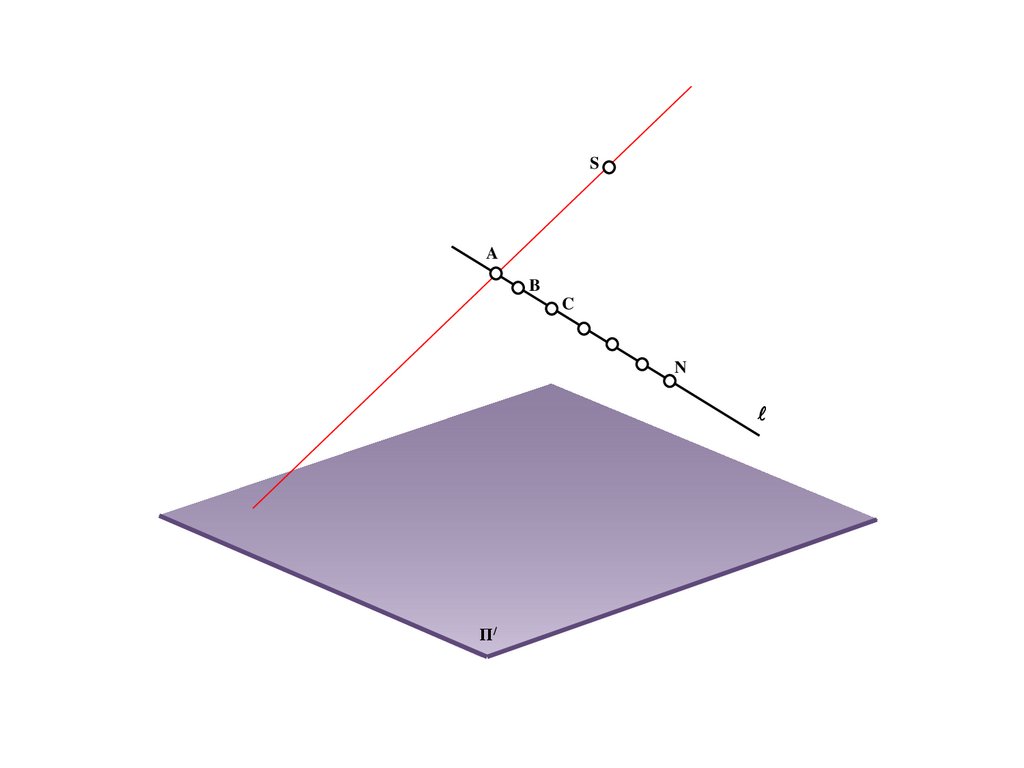
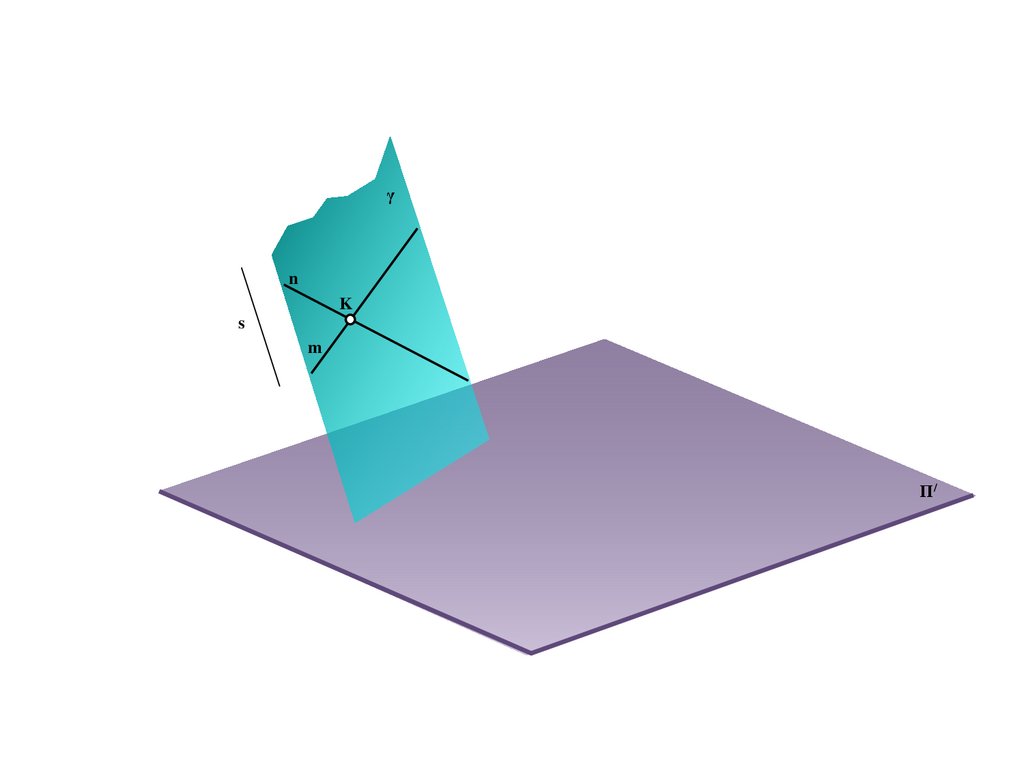
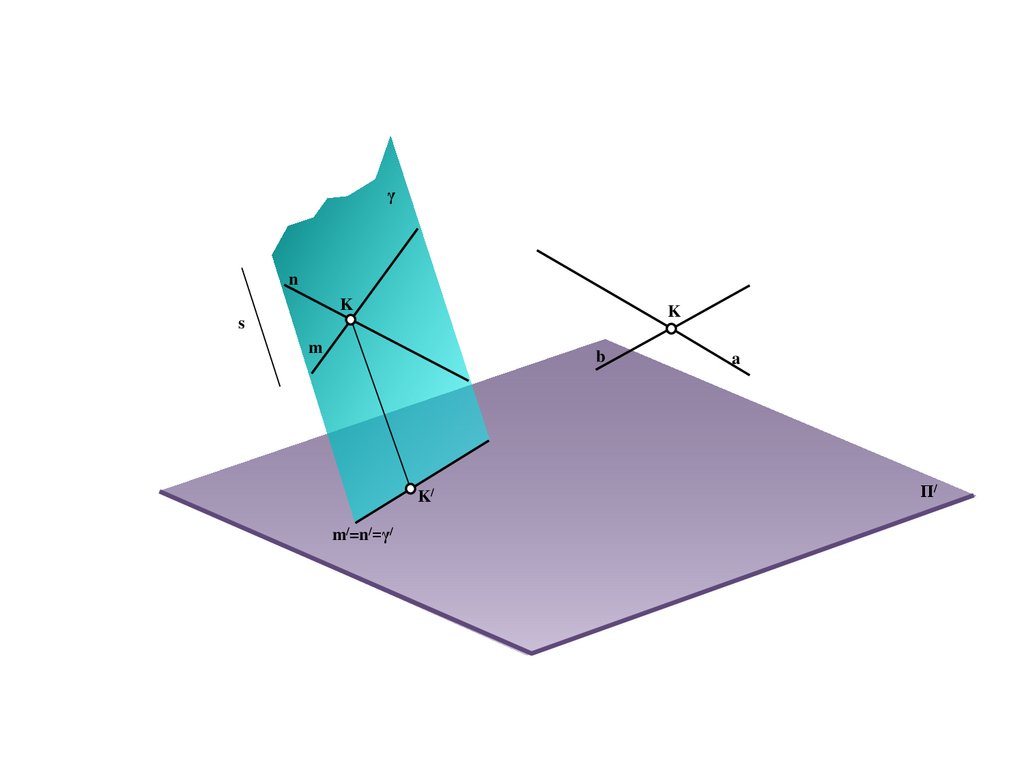
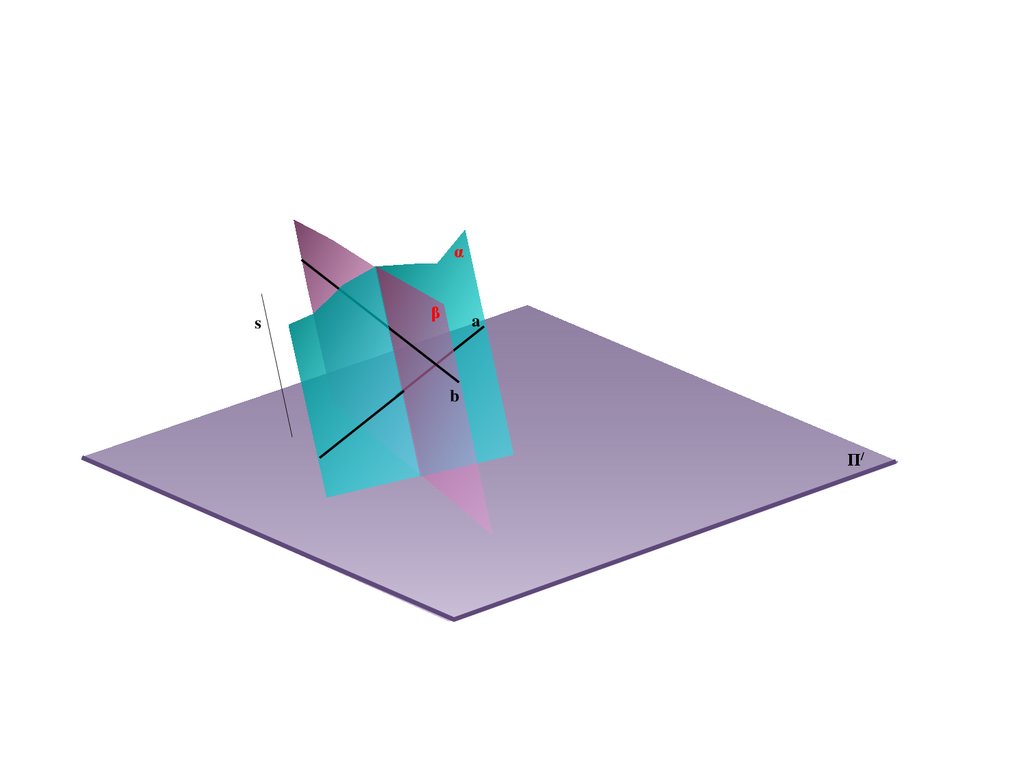
e
b
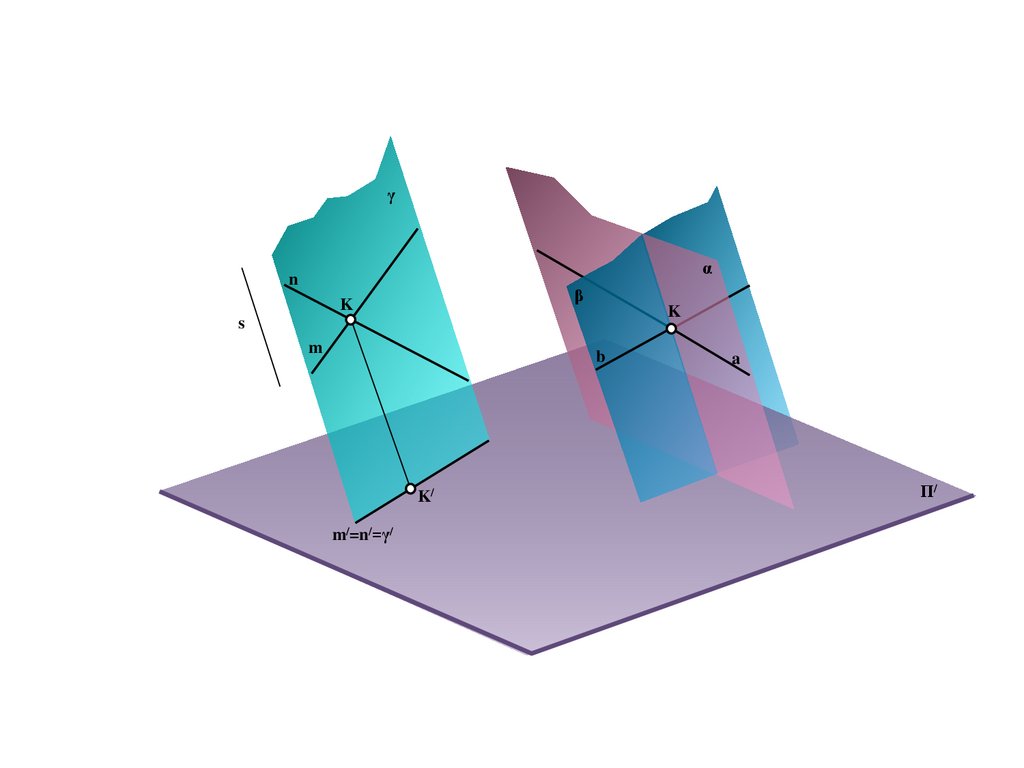
E
M
B/
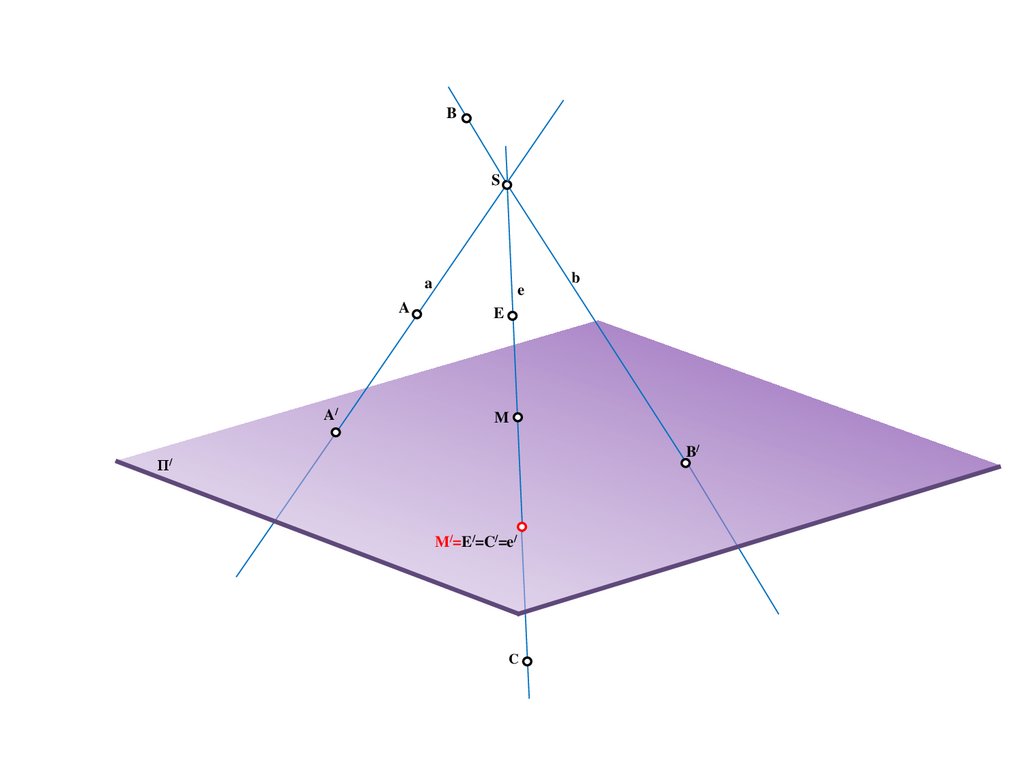
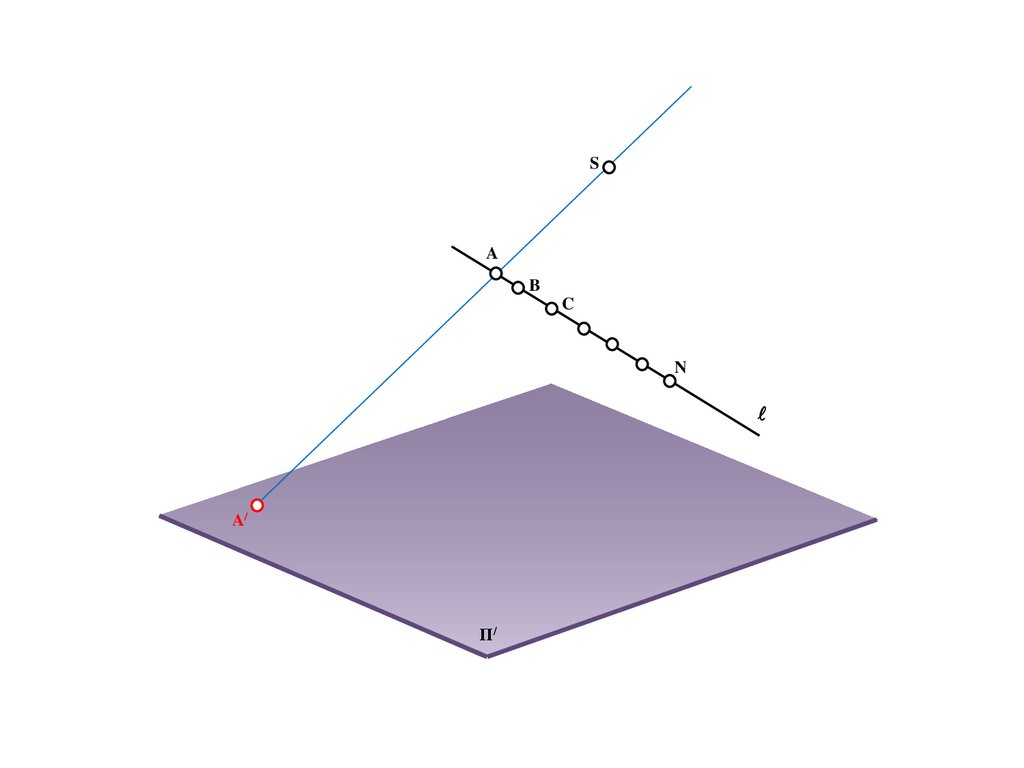
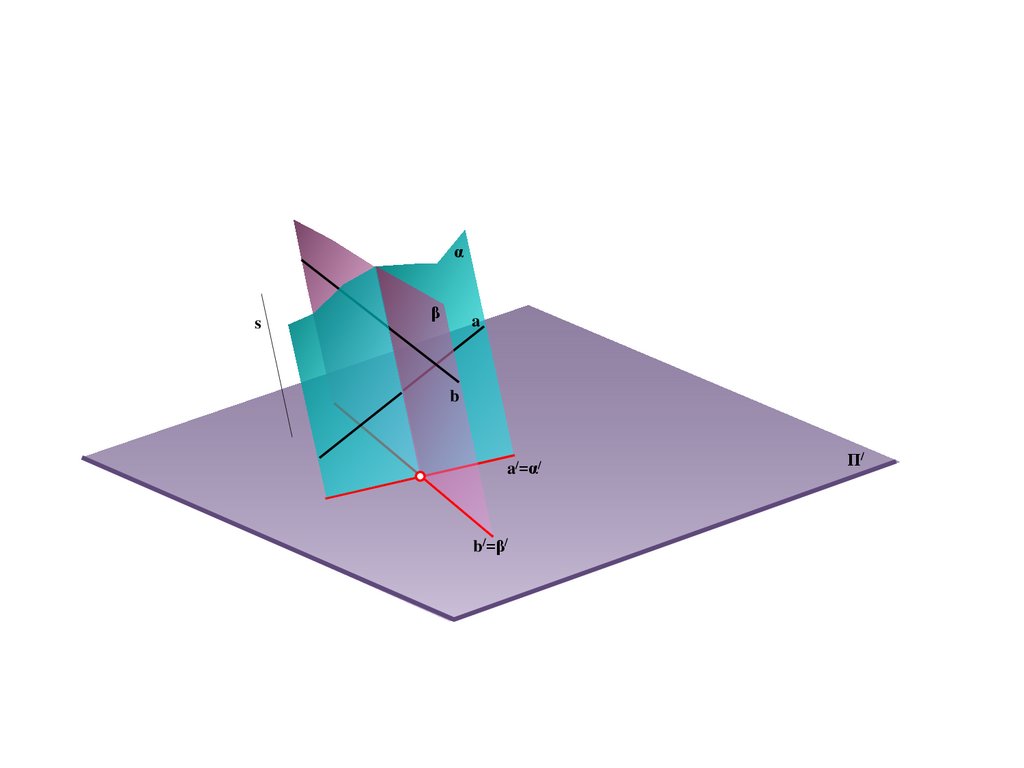
Π/
E/=C/=e/
C

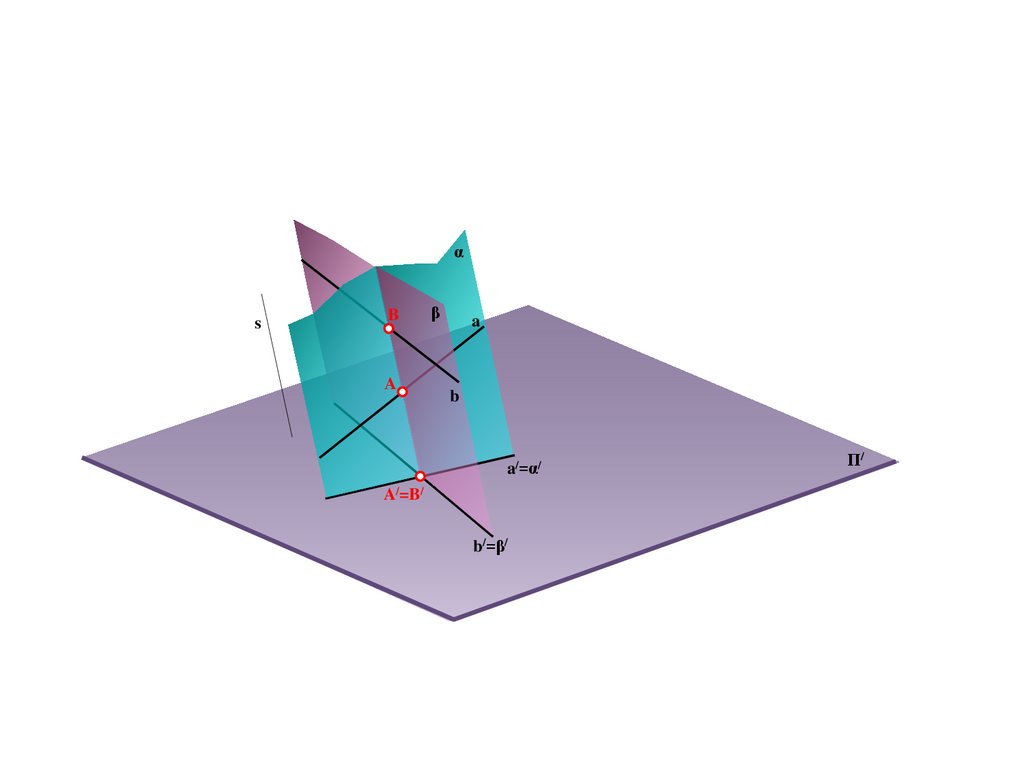
18.

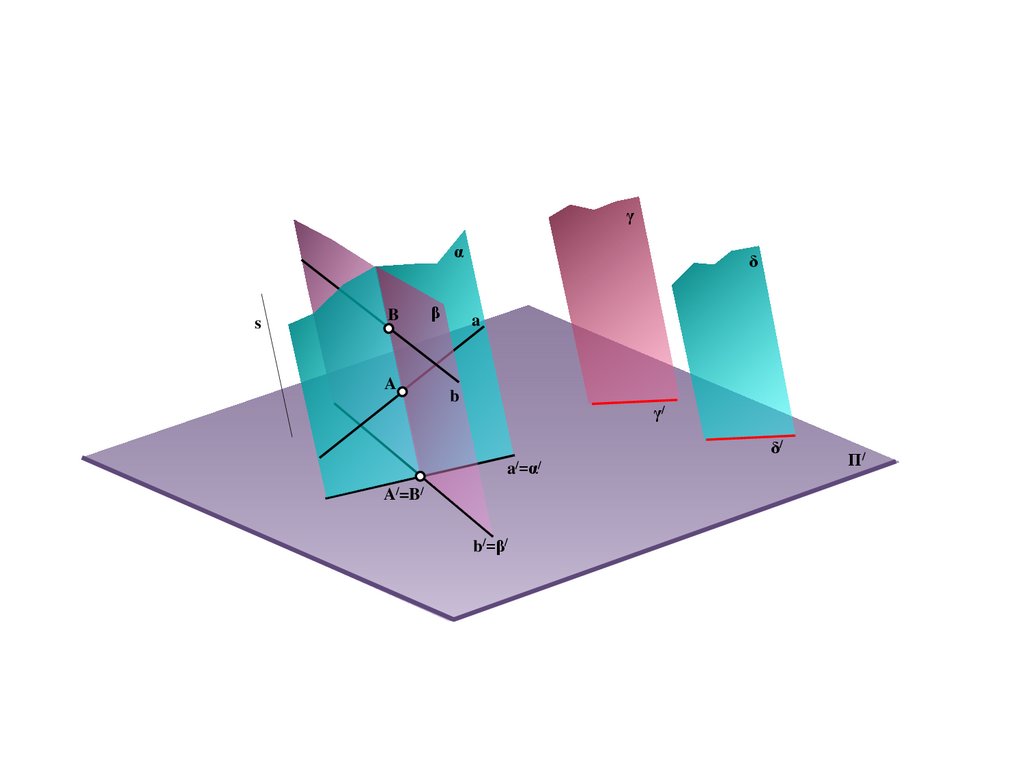
B
S
a
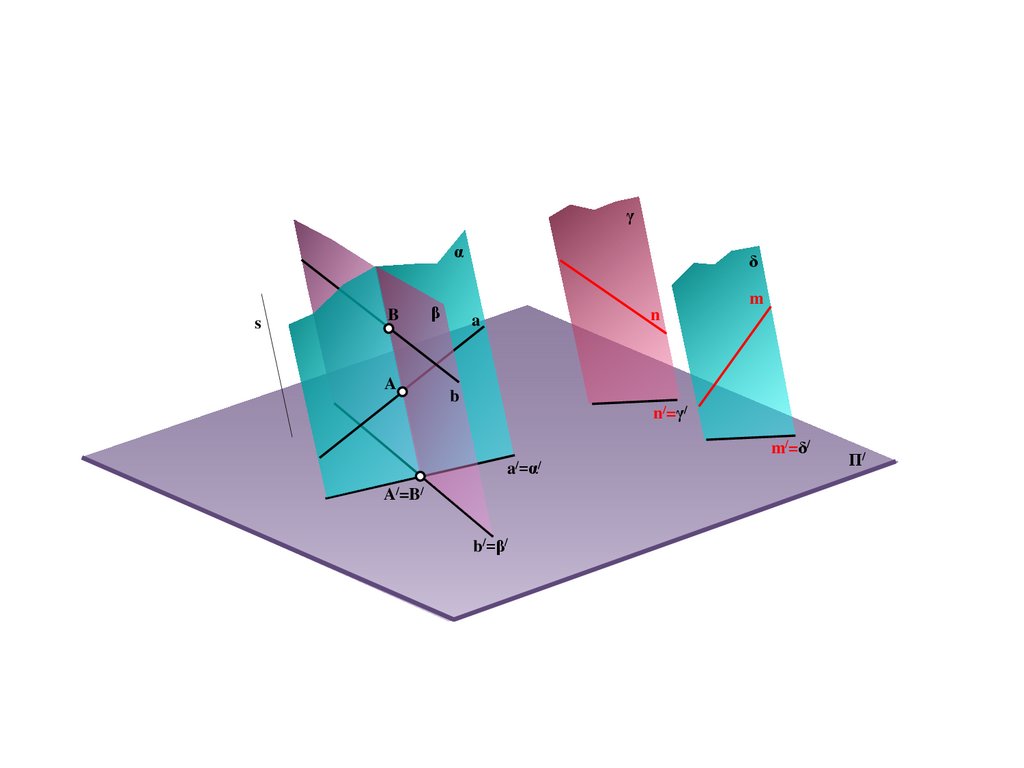
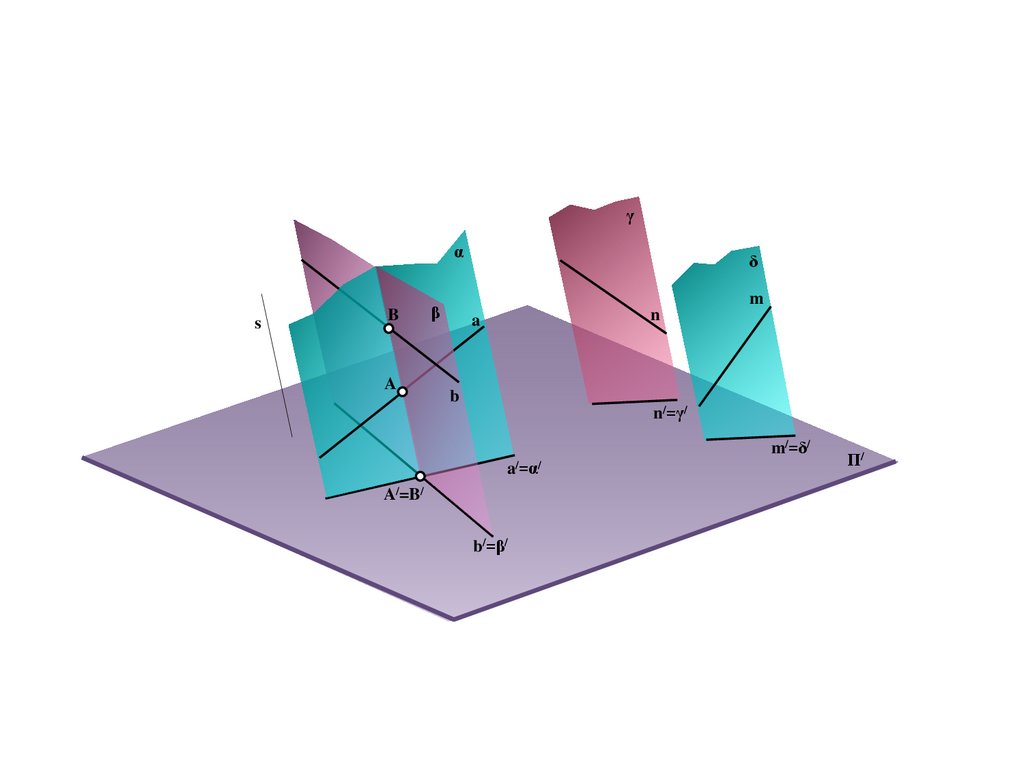
A
A/
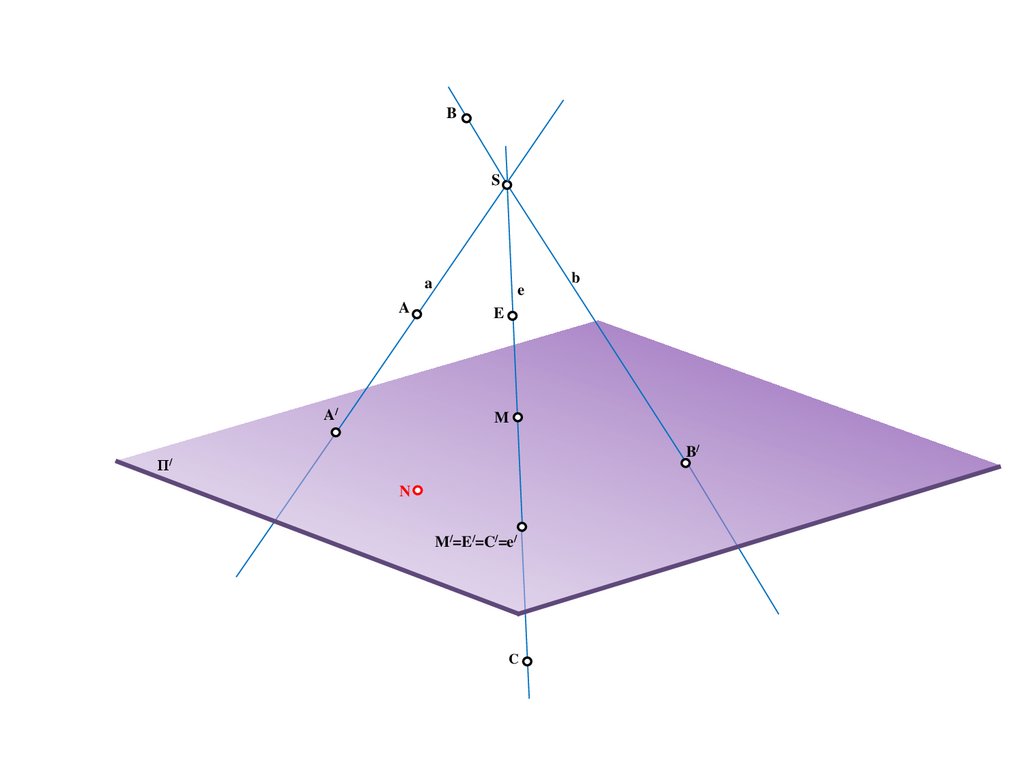
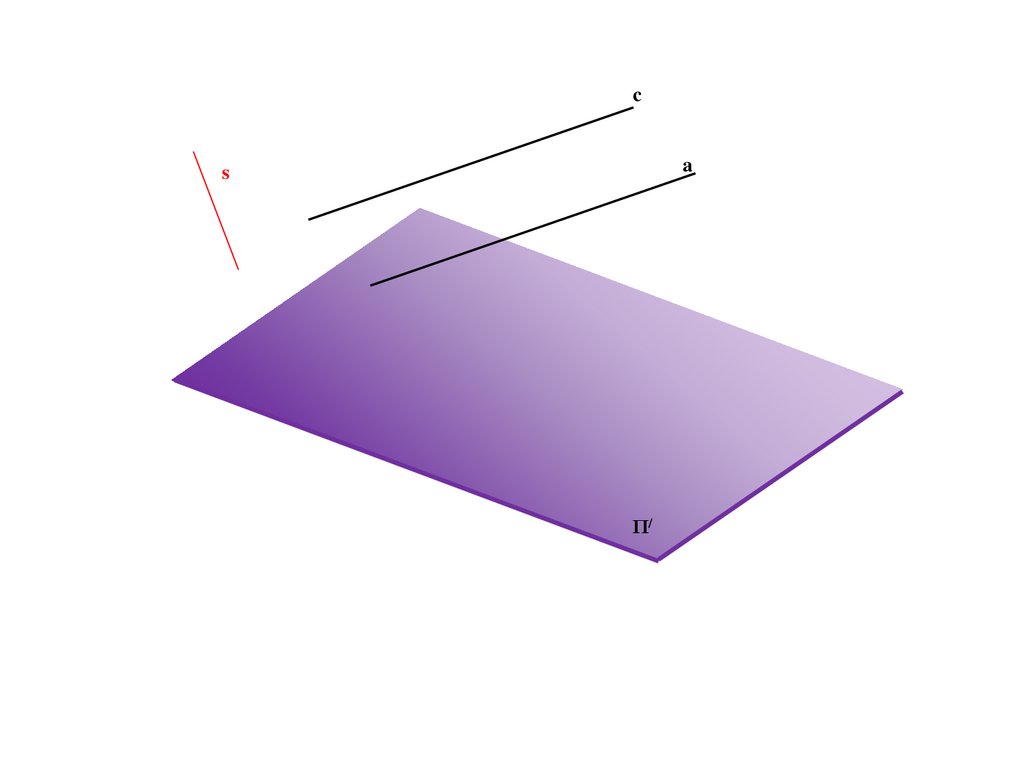
e
b
E
M
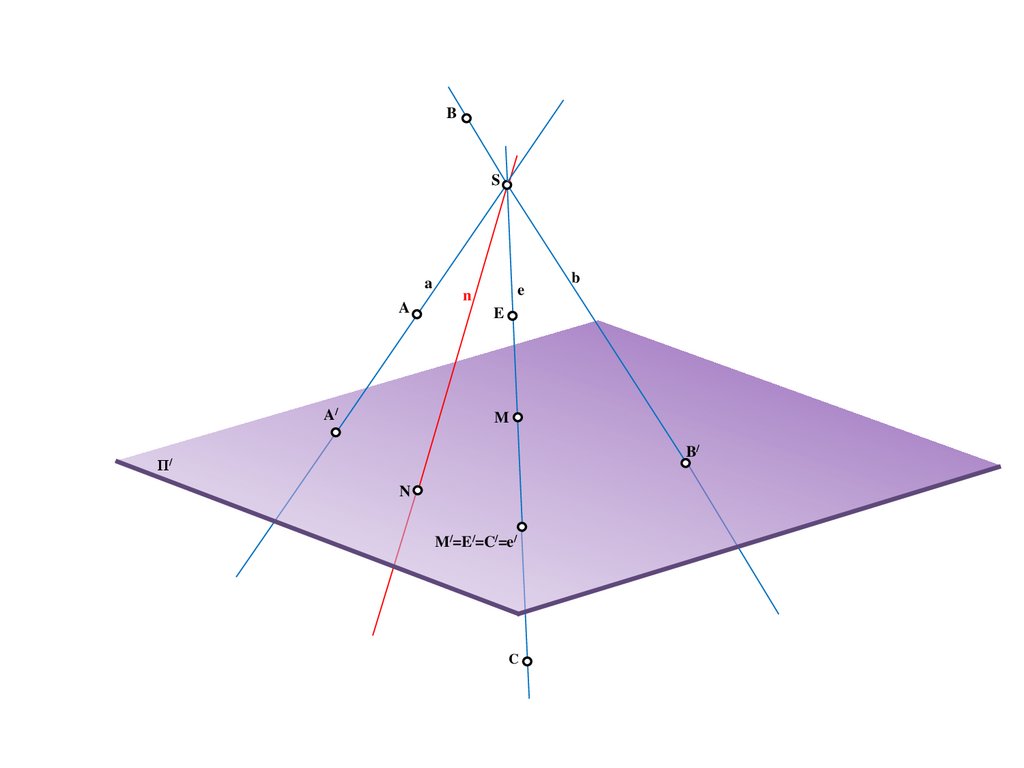
B/
Π/
M/=E/=C/=e/
C

19.

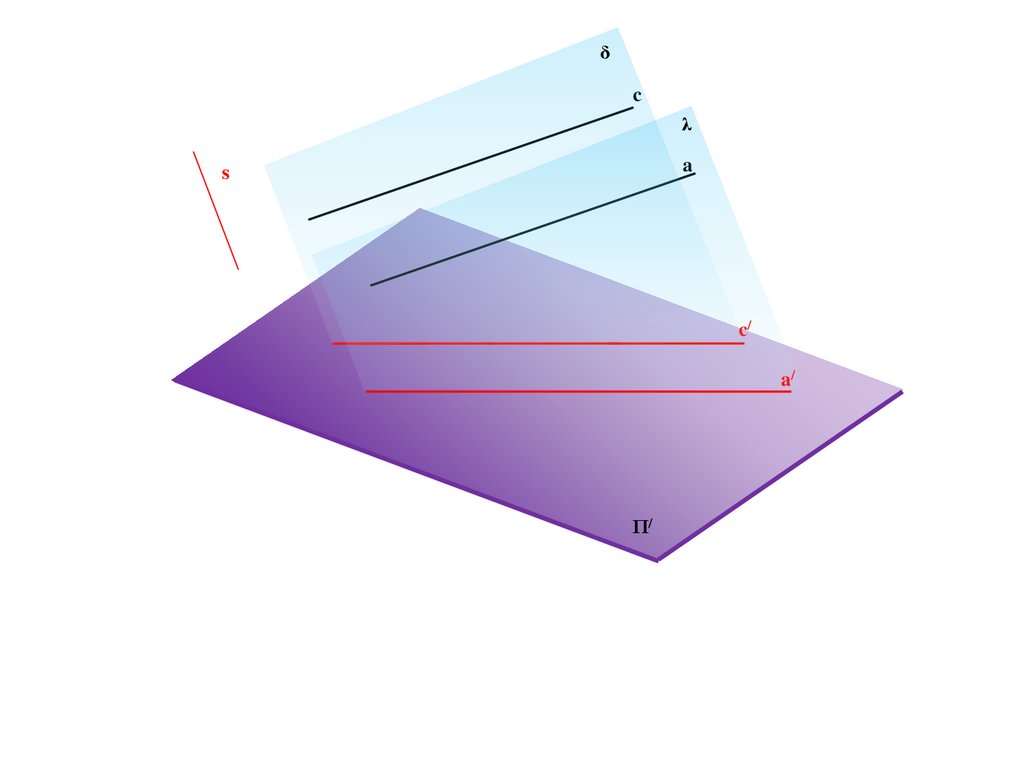
B
S
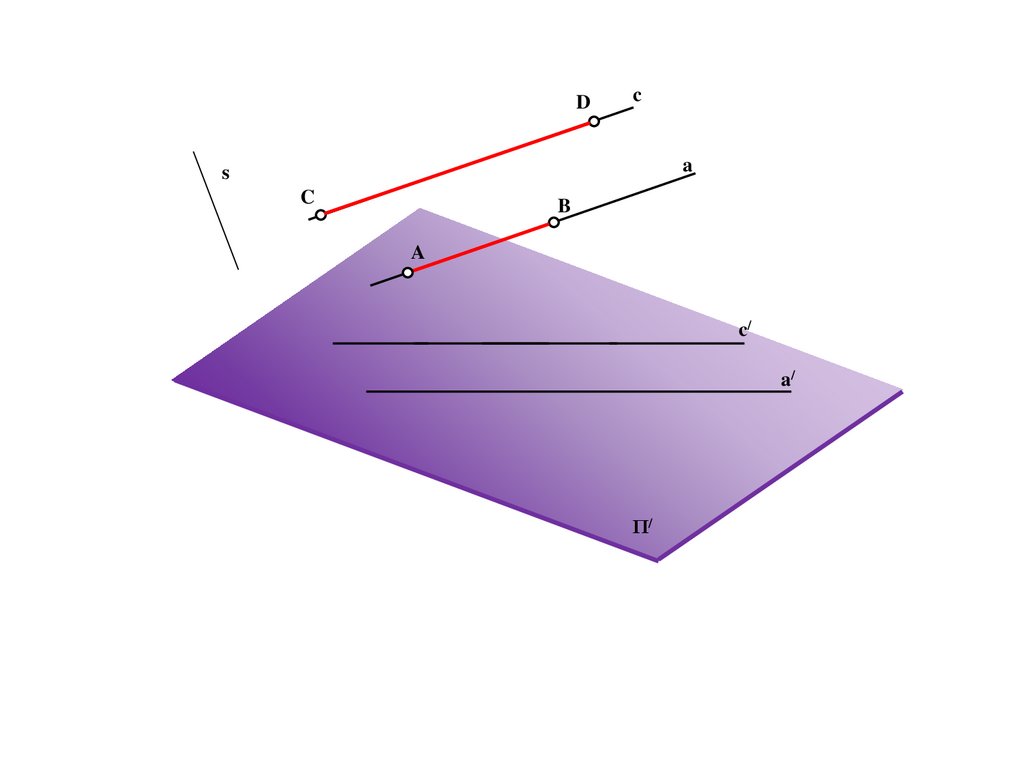
a
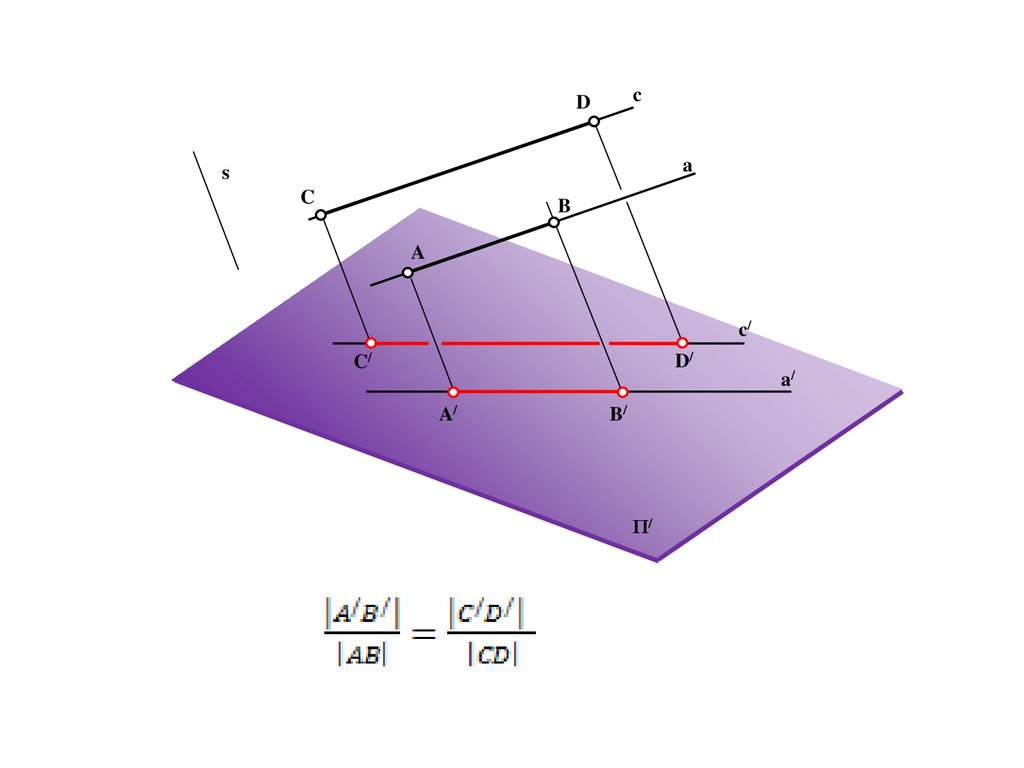
A
A/
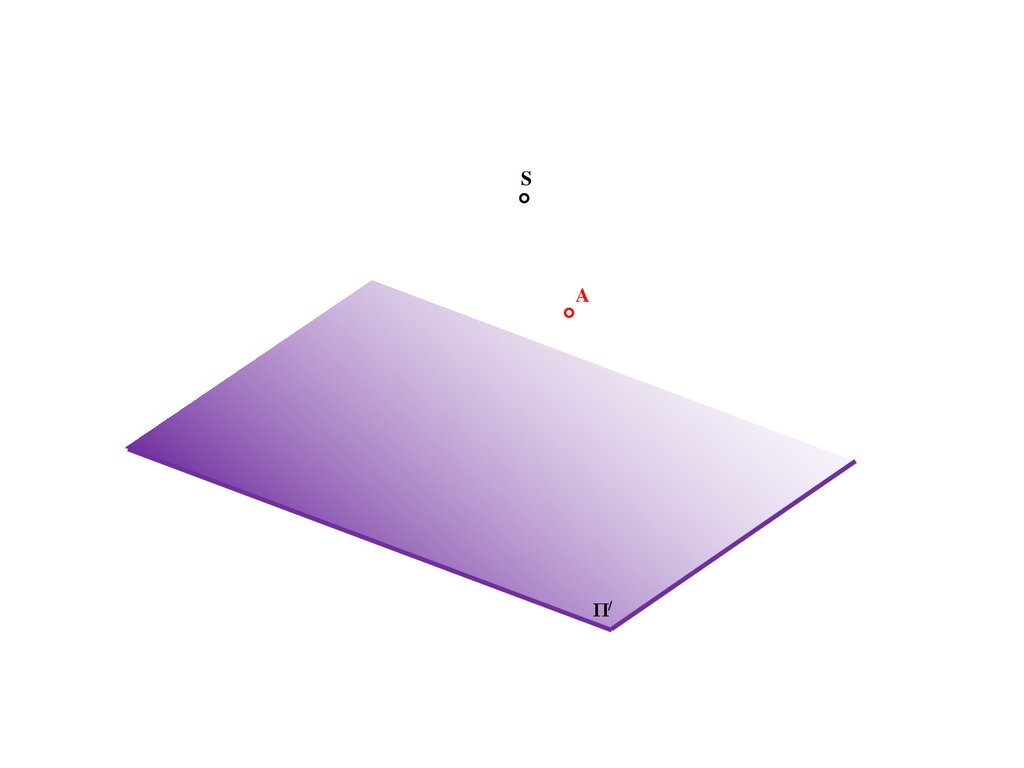
e
b
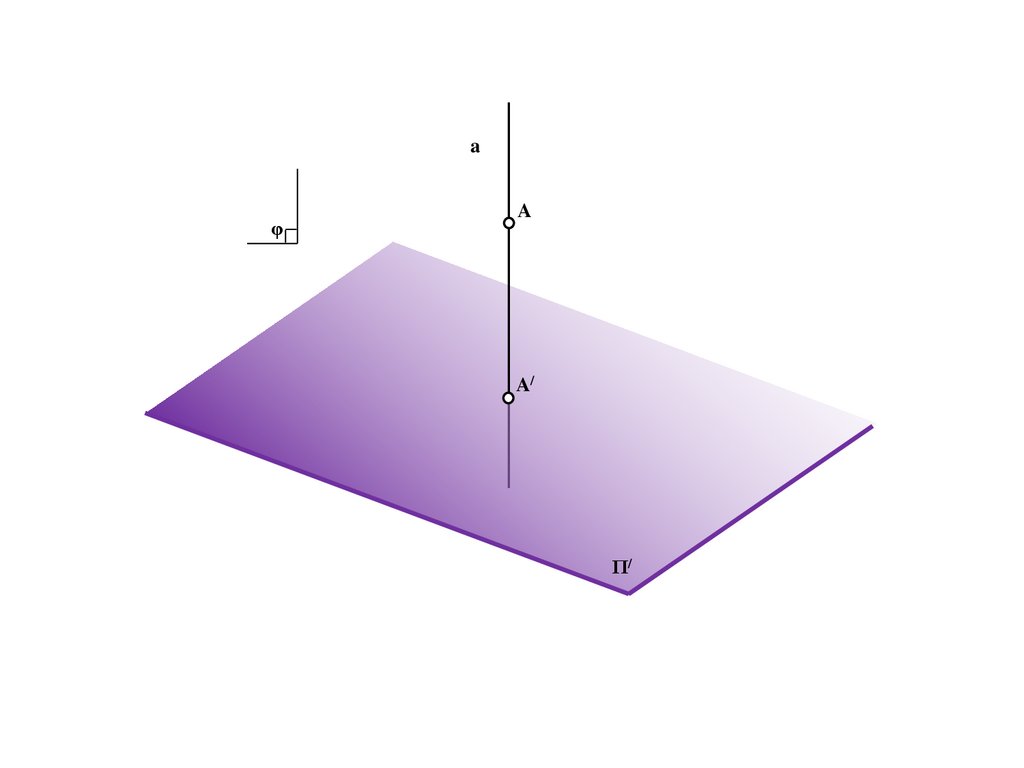
E
M
B/
Π/
N
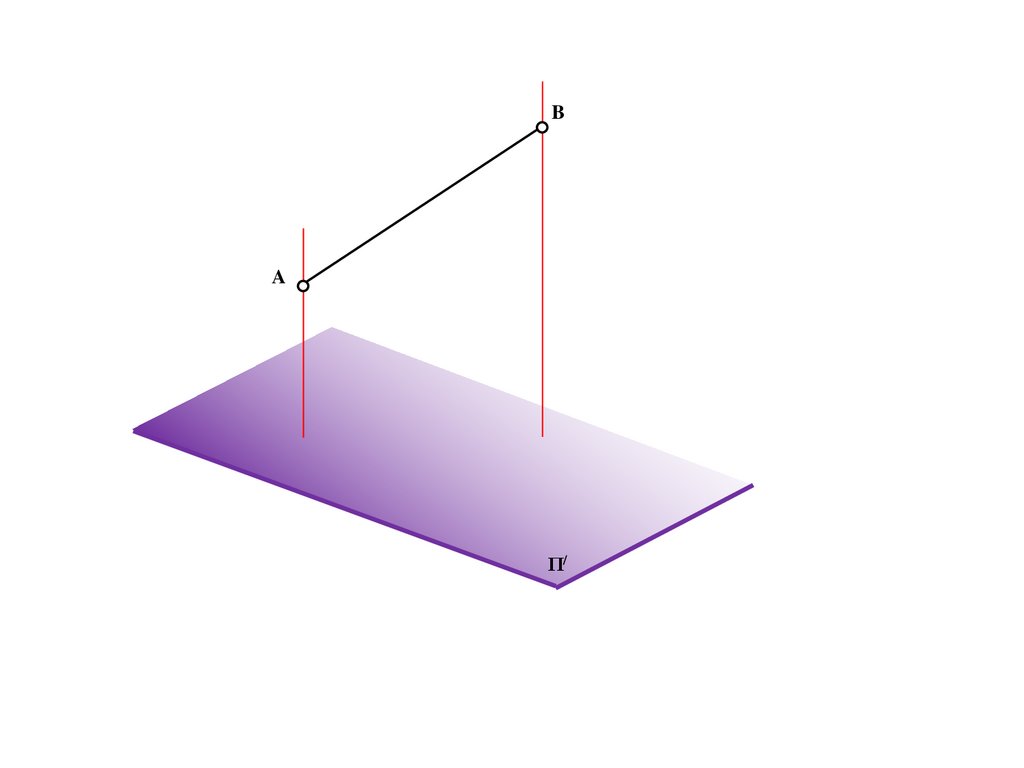
M/=E/=C/=e/
C

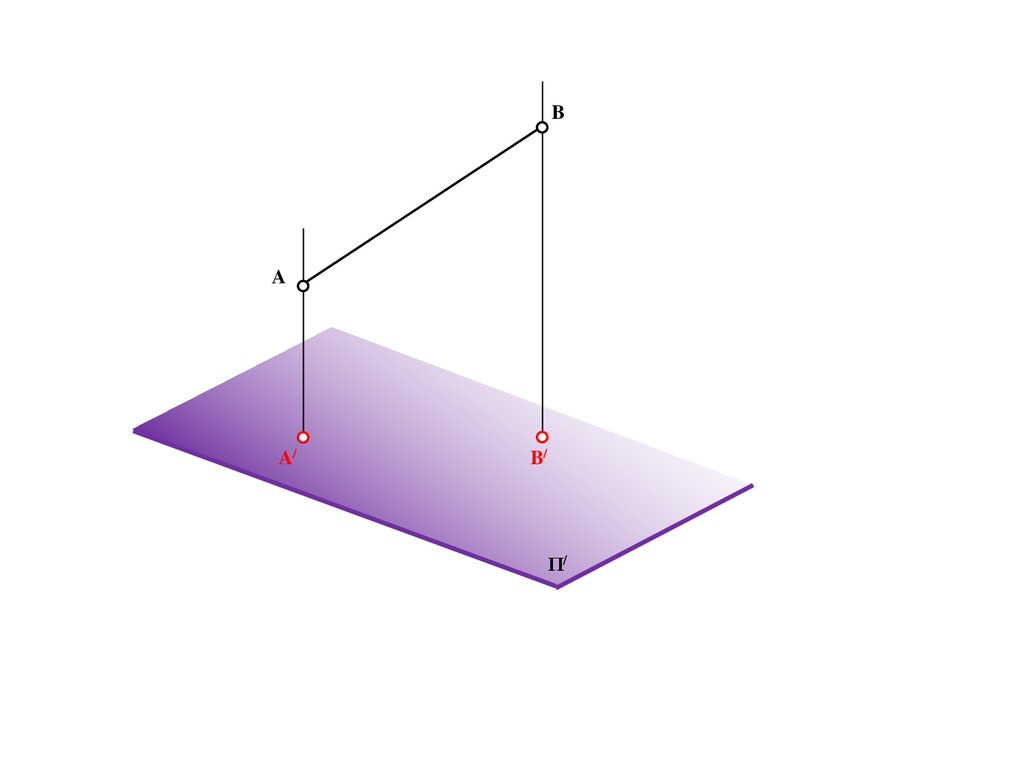
20.

B
S
a
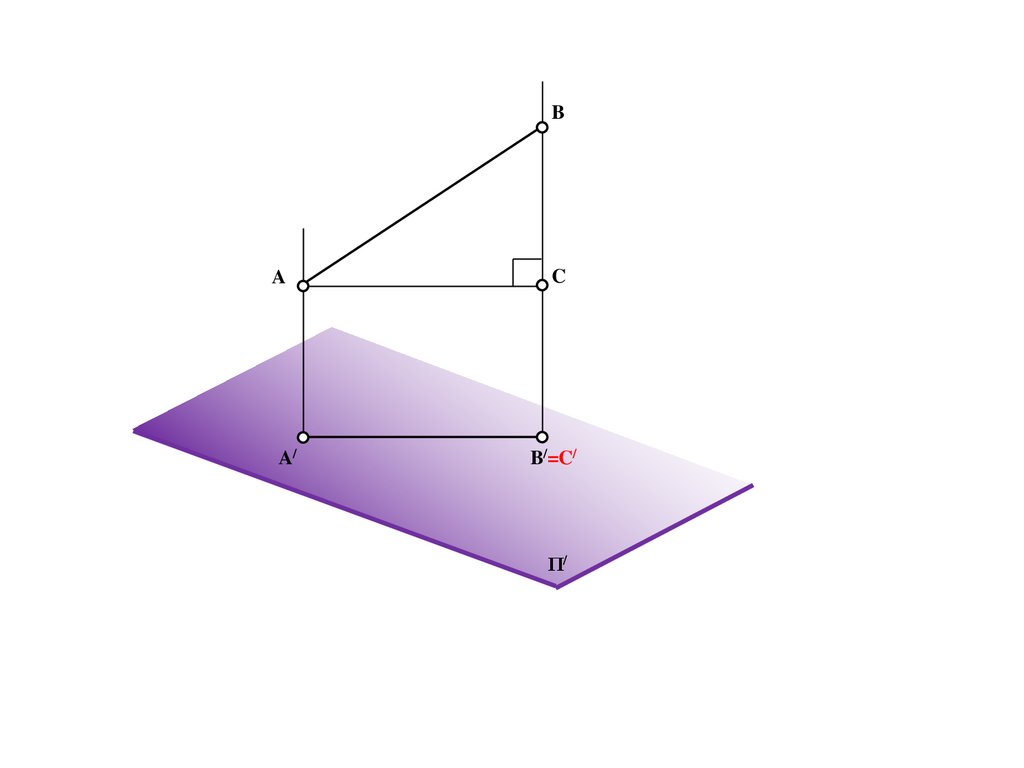
A
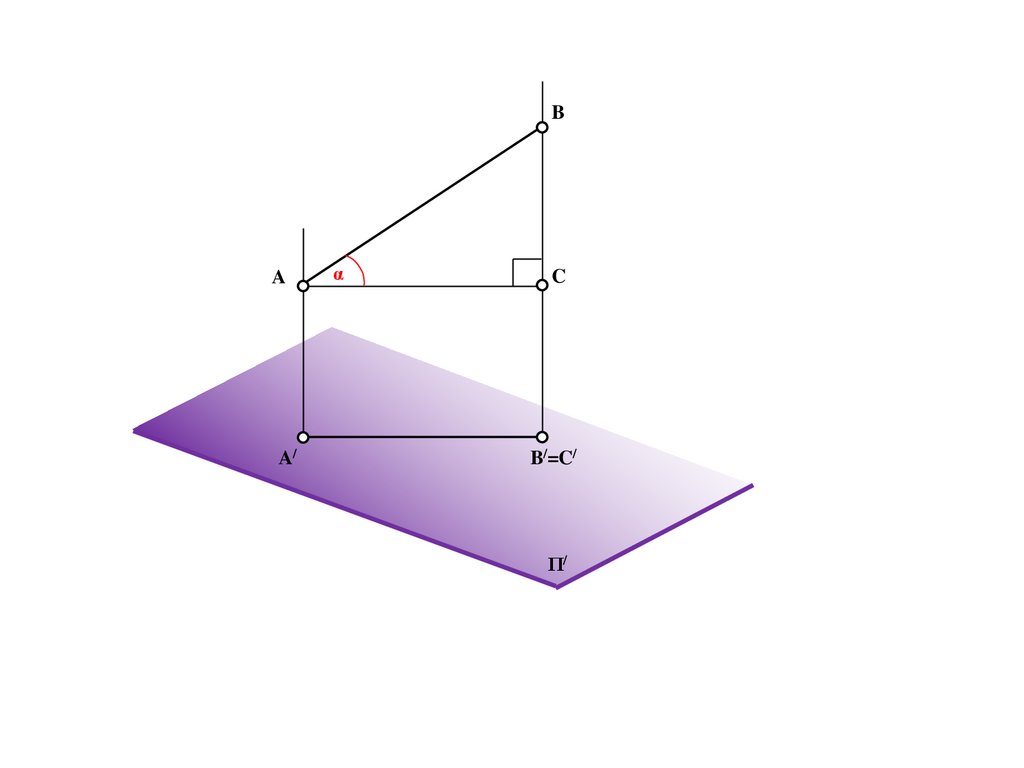
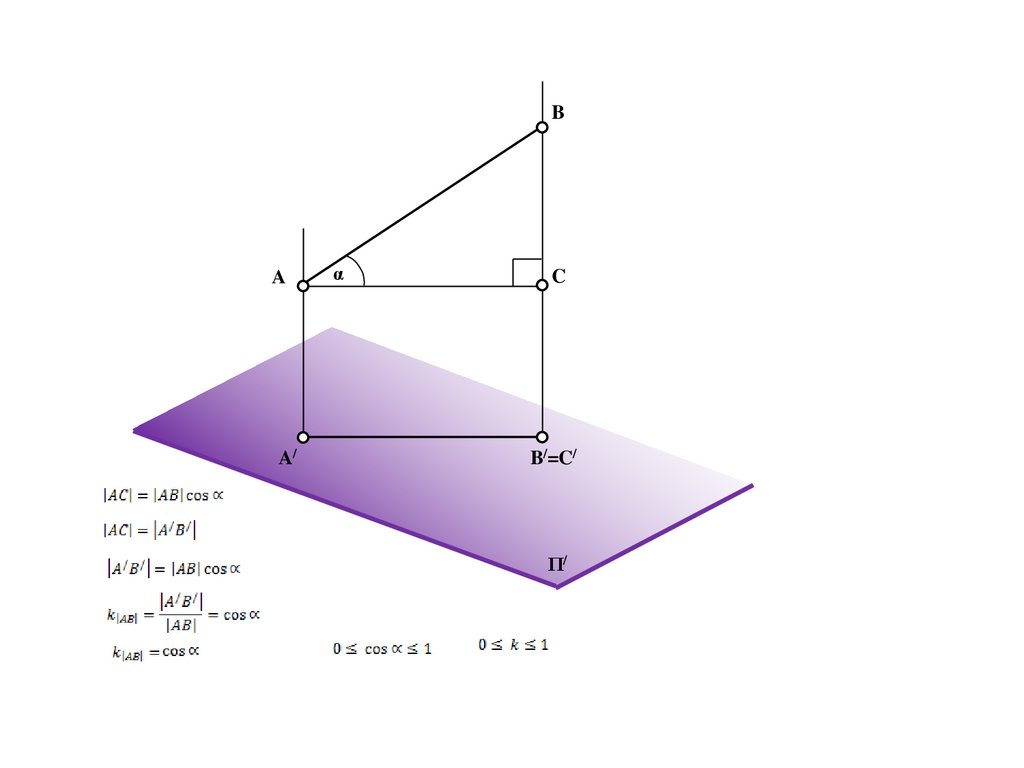
A/
e
n
b
E
M
B/
Π/
N
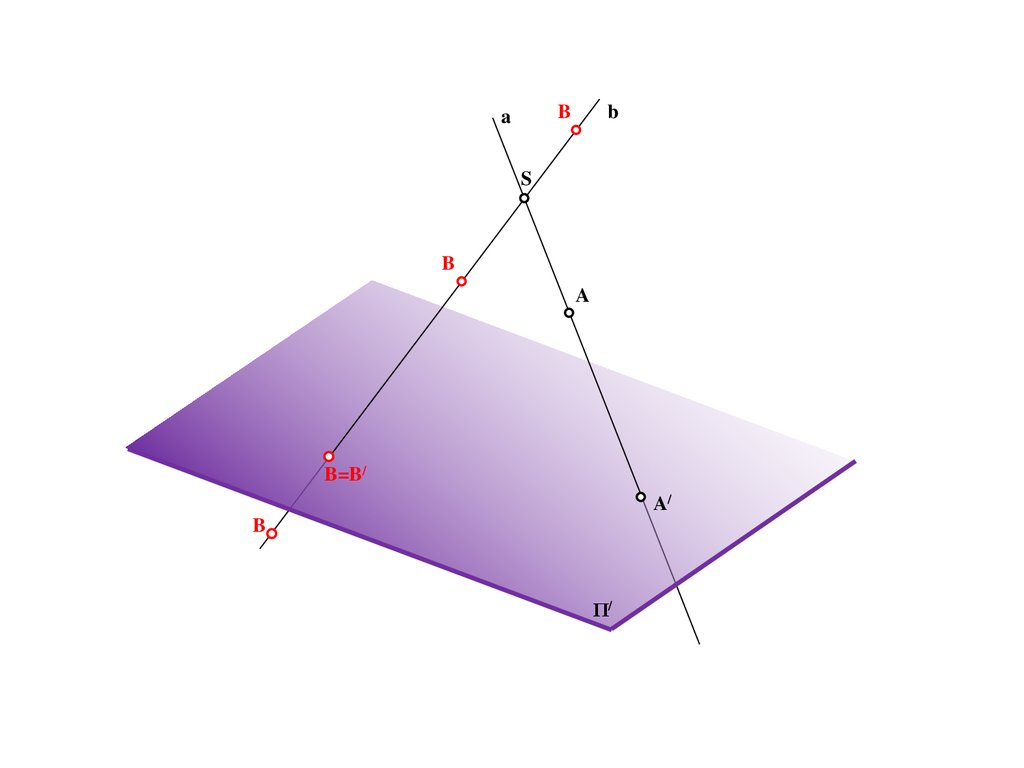
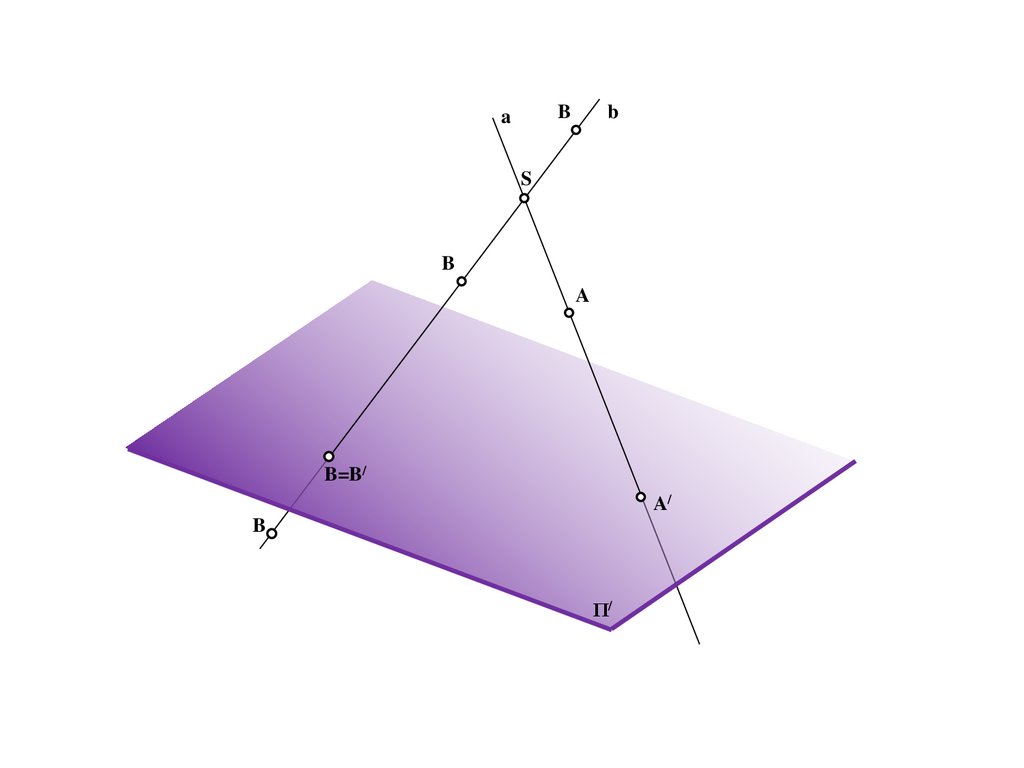
M/=E/=C/=e/
C

21.

B
S
a
A
A/
e
n
b
E
M
B/
Π/
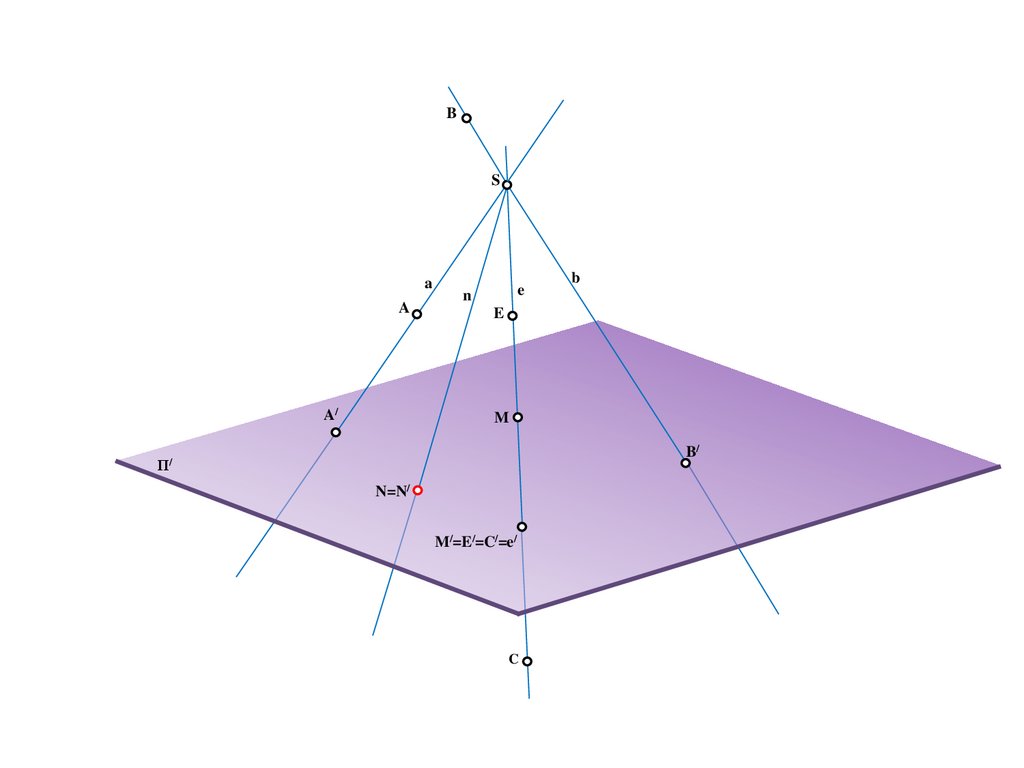
N=N/
M/=E/=C/=e/
C

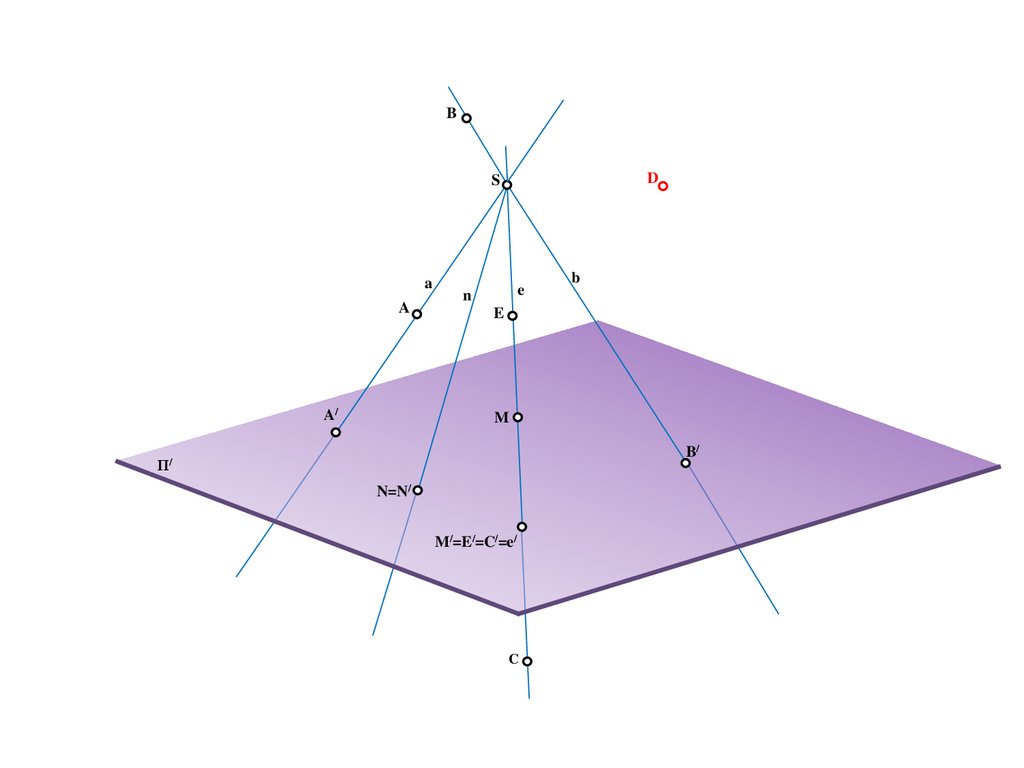
22.

B
D
S
a
A
A/
e
n
b
E
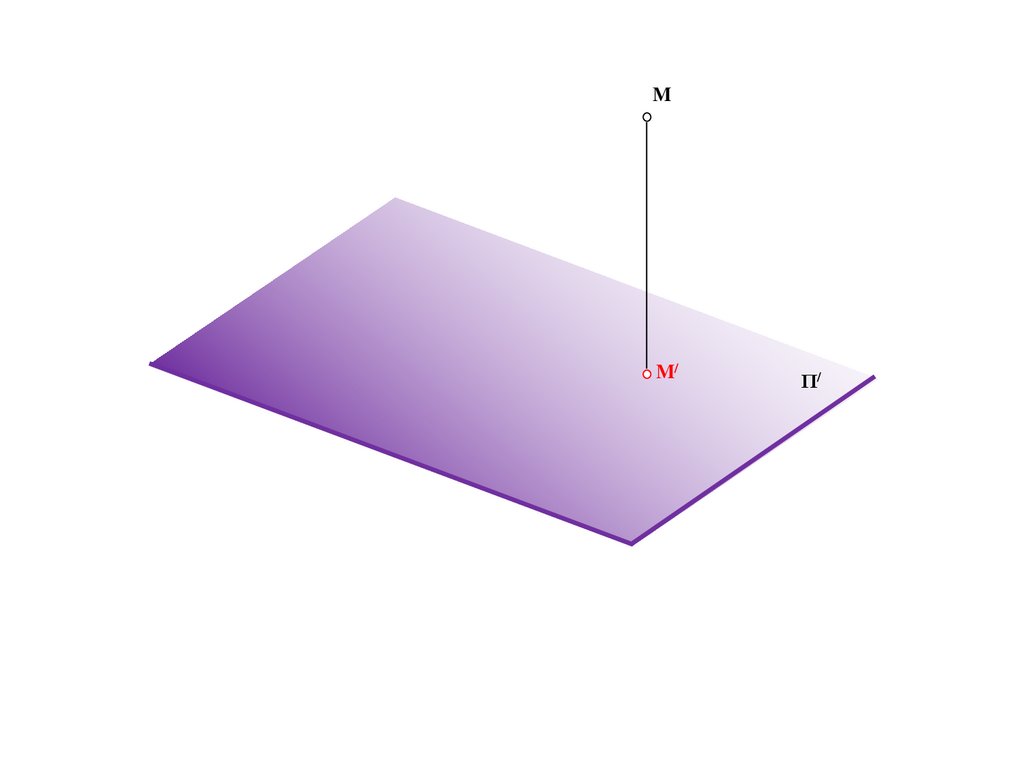
M
B/
Π/
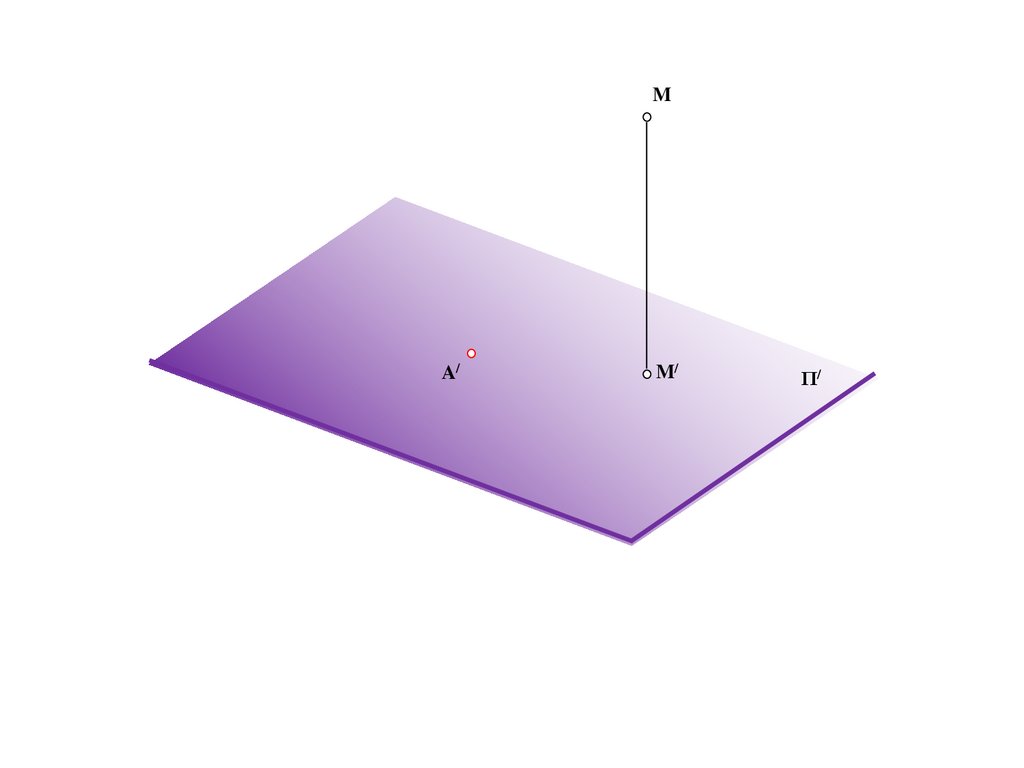
N=N/
M/=E/=C/=e/
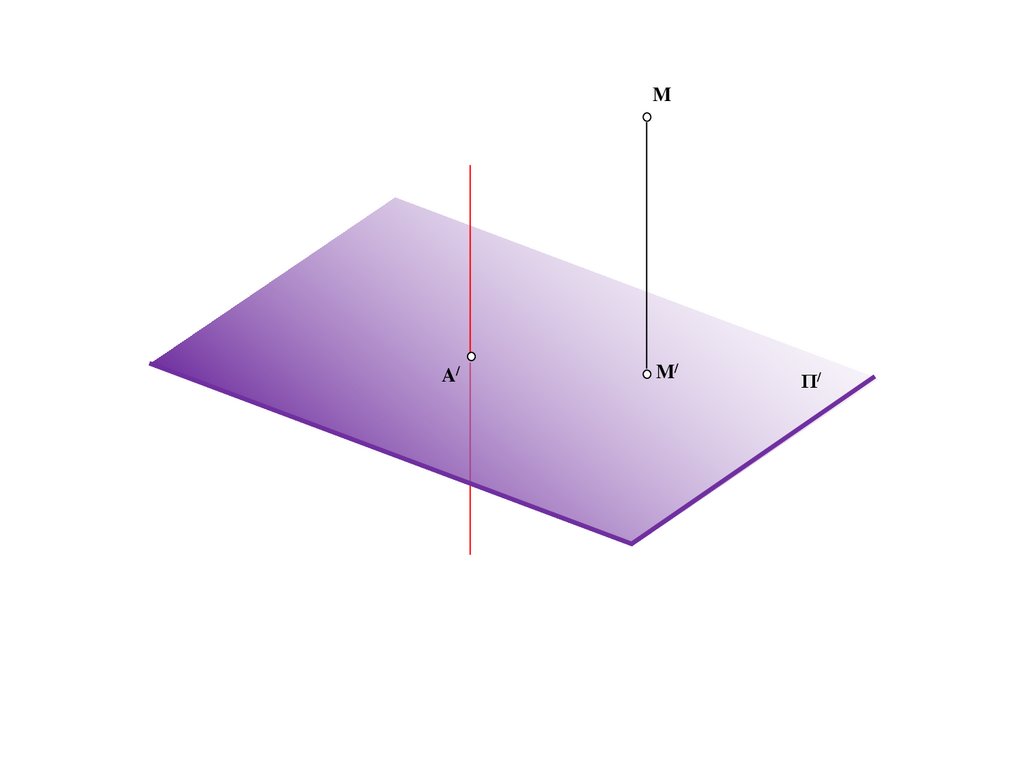
C

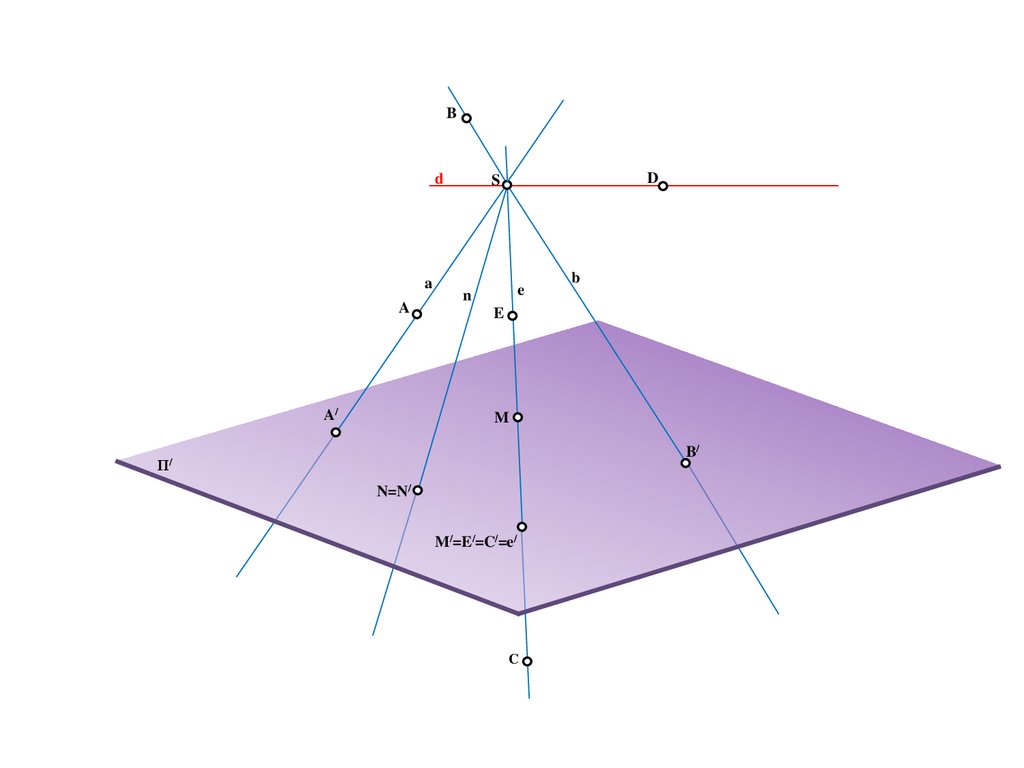
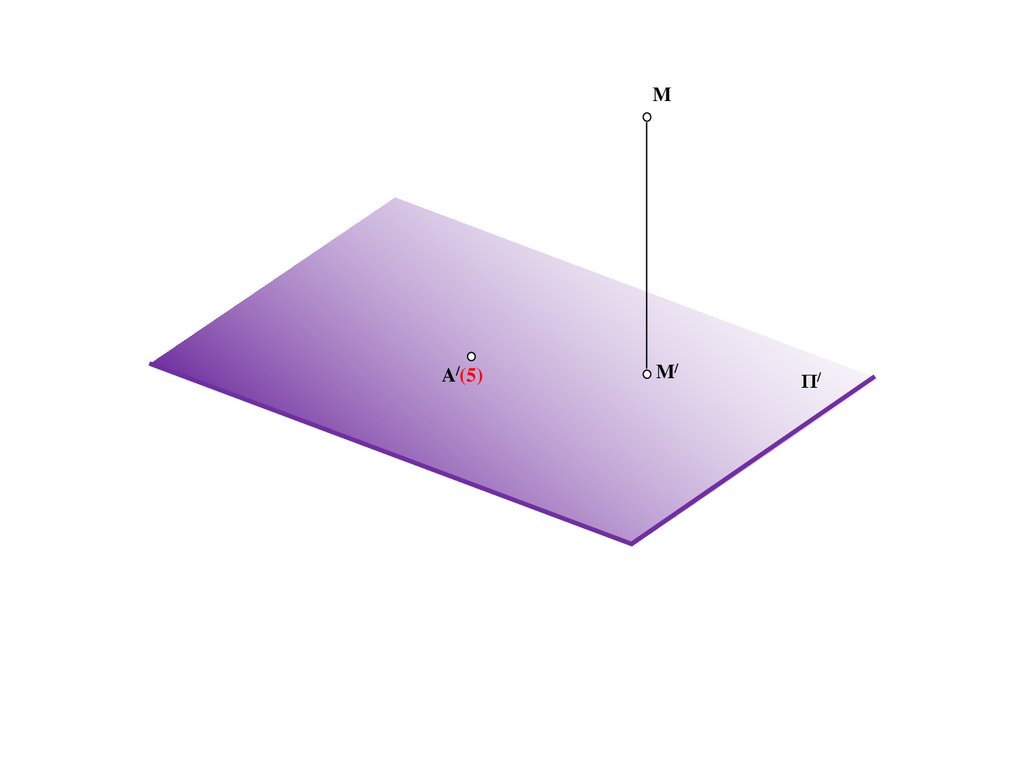
23.

B
d
a
A
A/
D
S
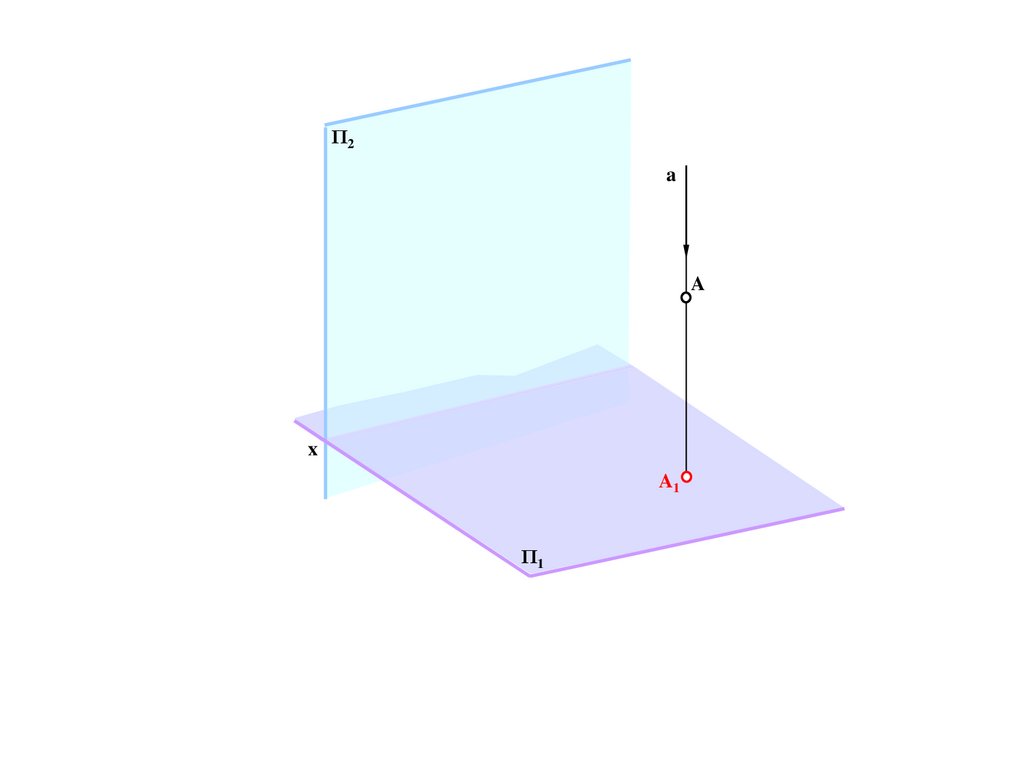
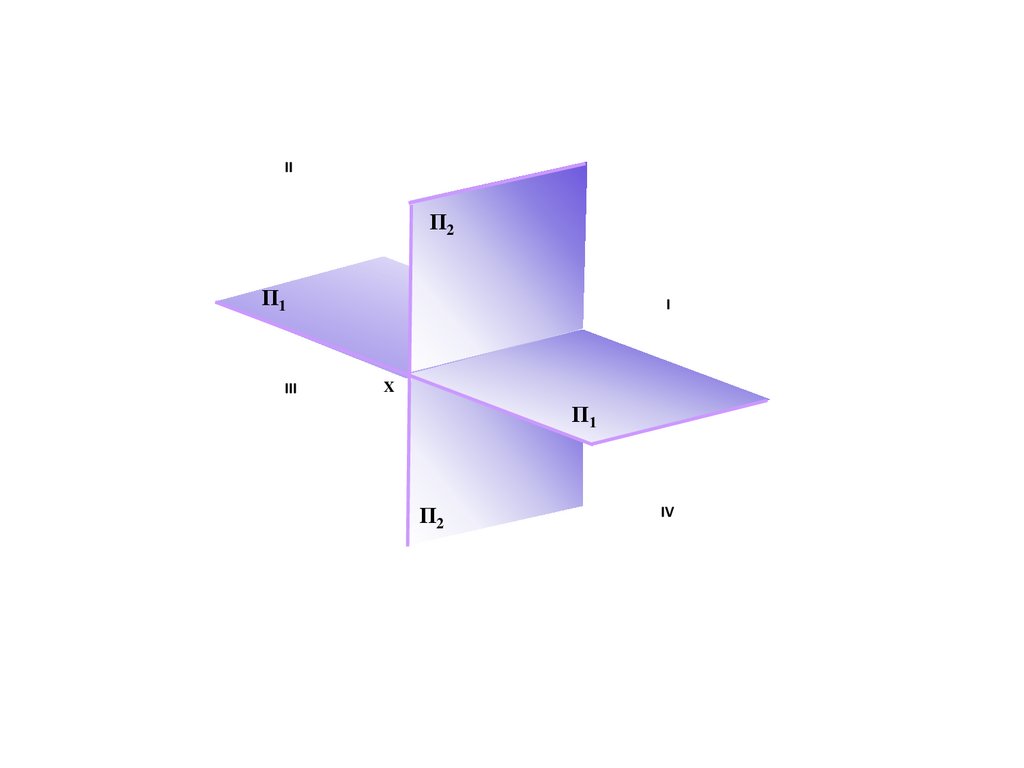
e
n
b
E
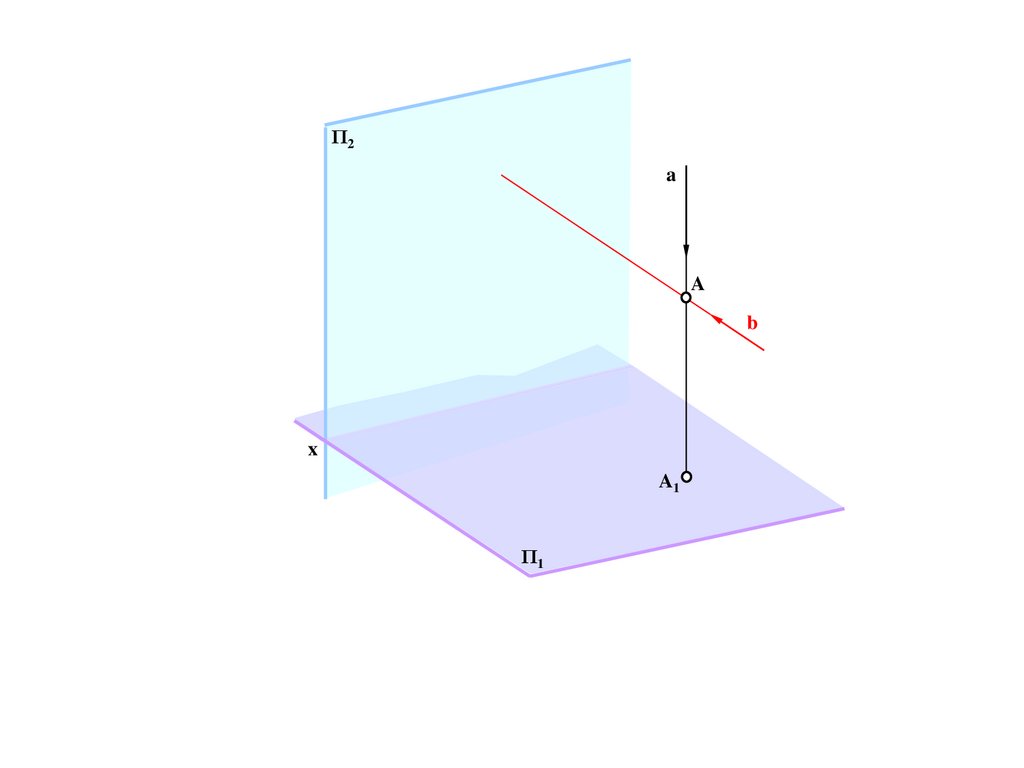
M
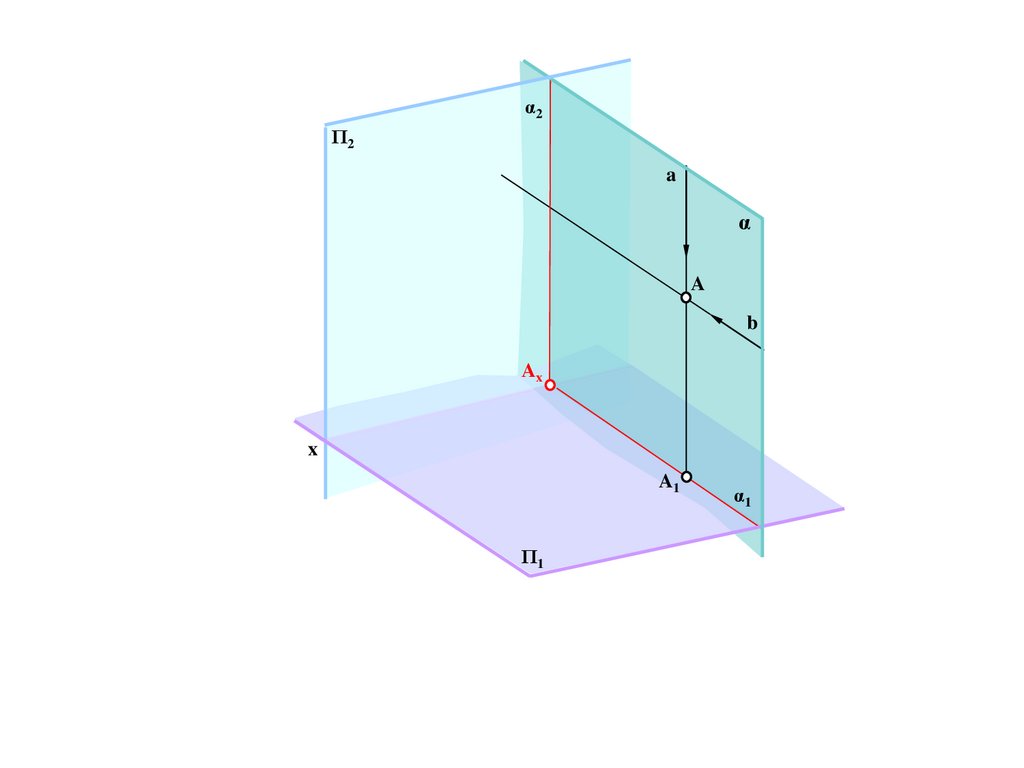
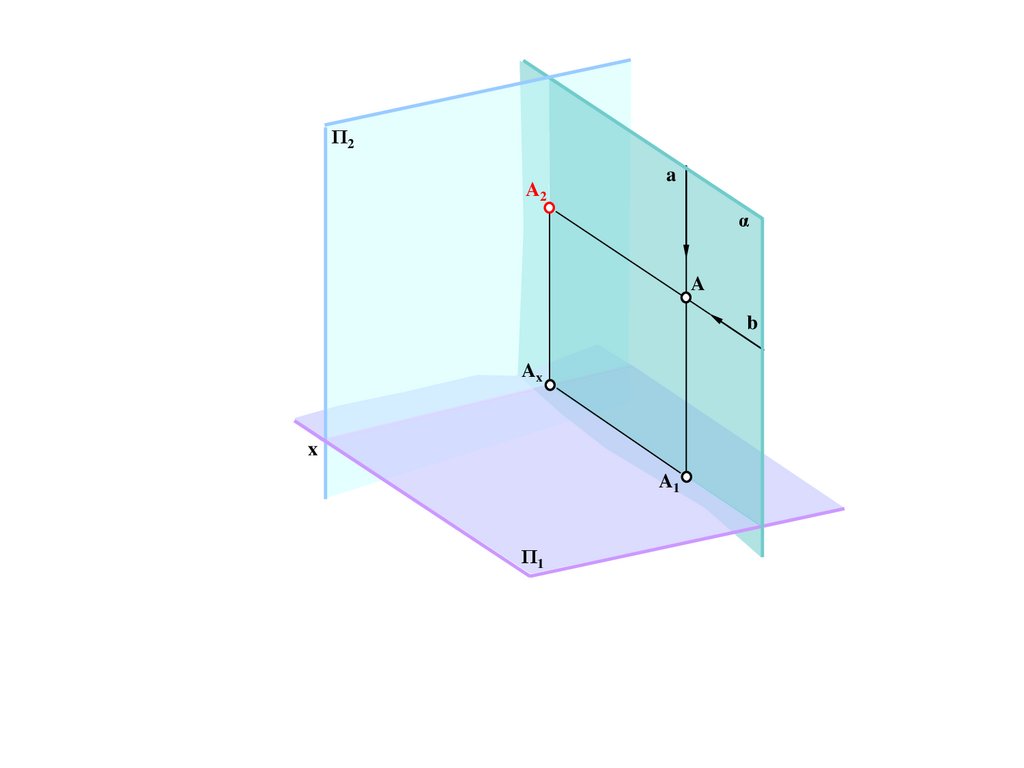
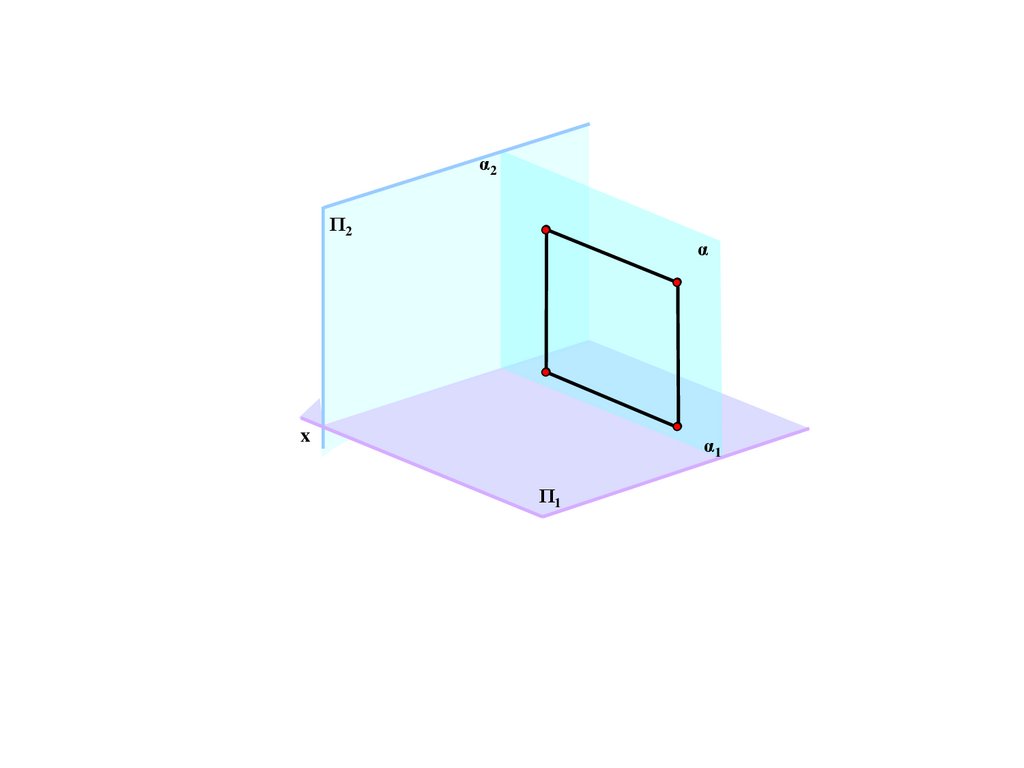
B/
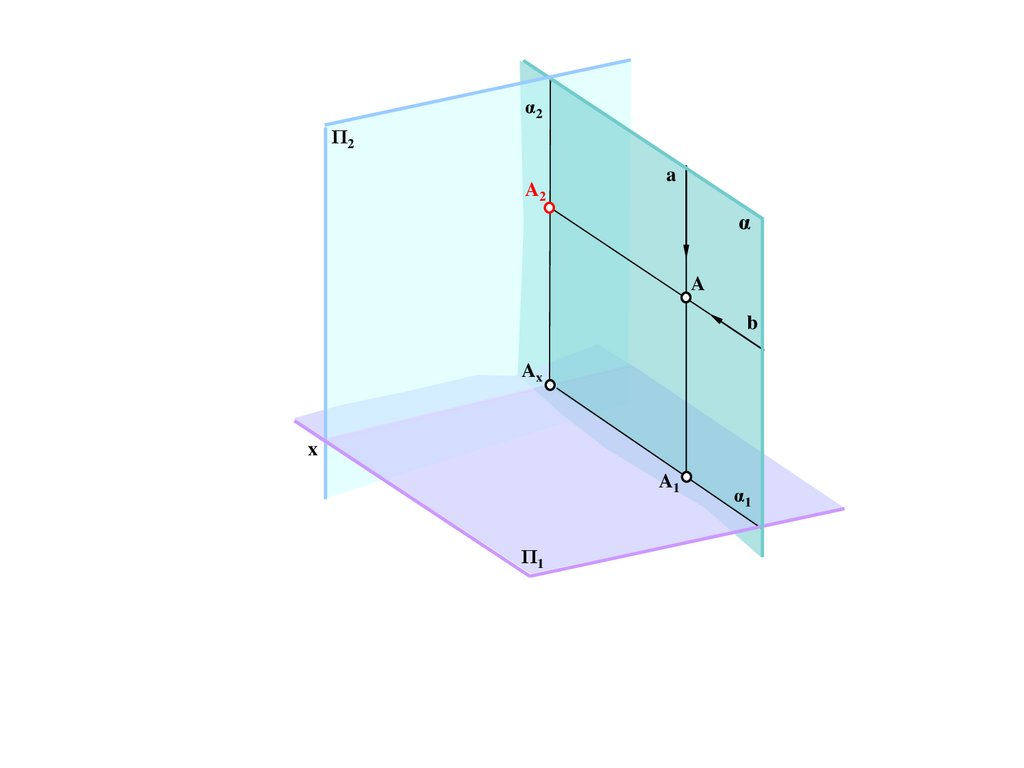
Π/
N=N/
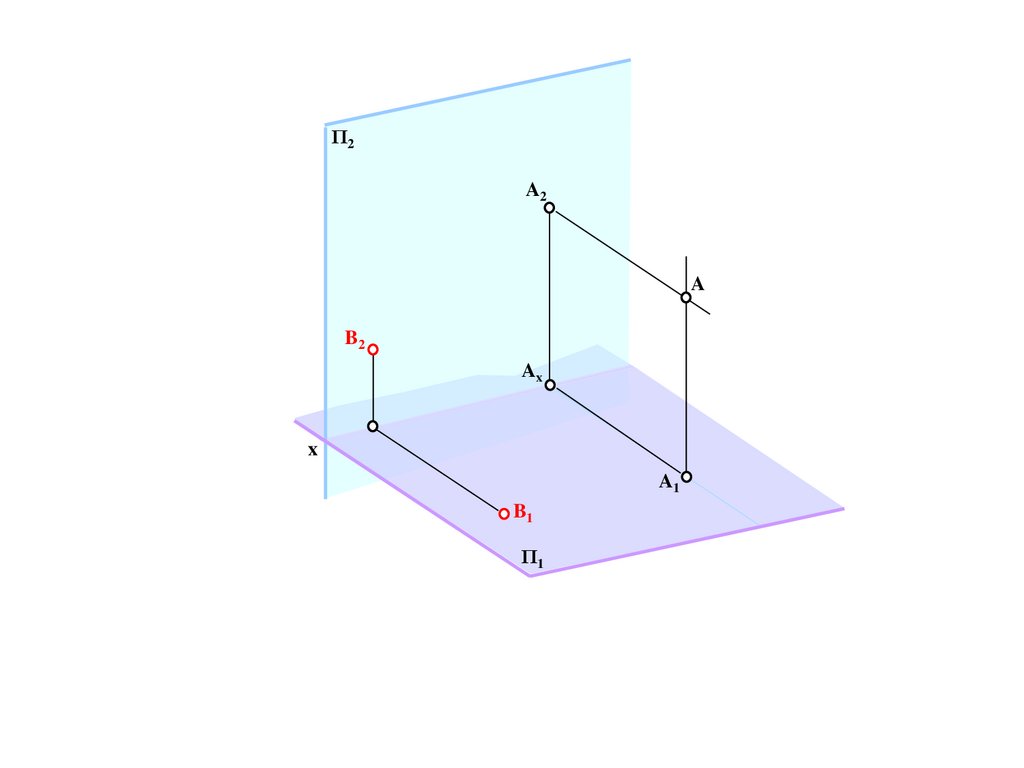
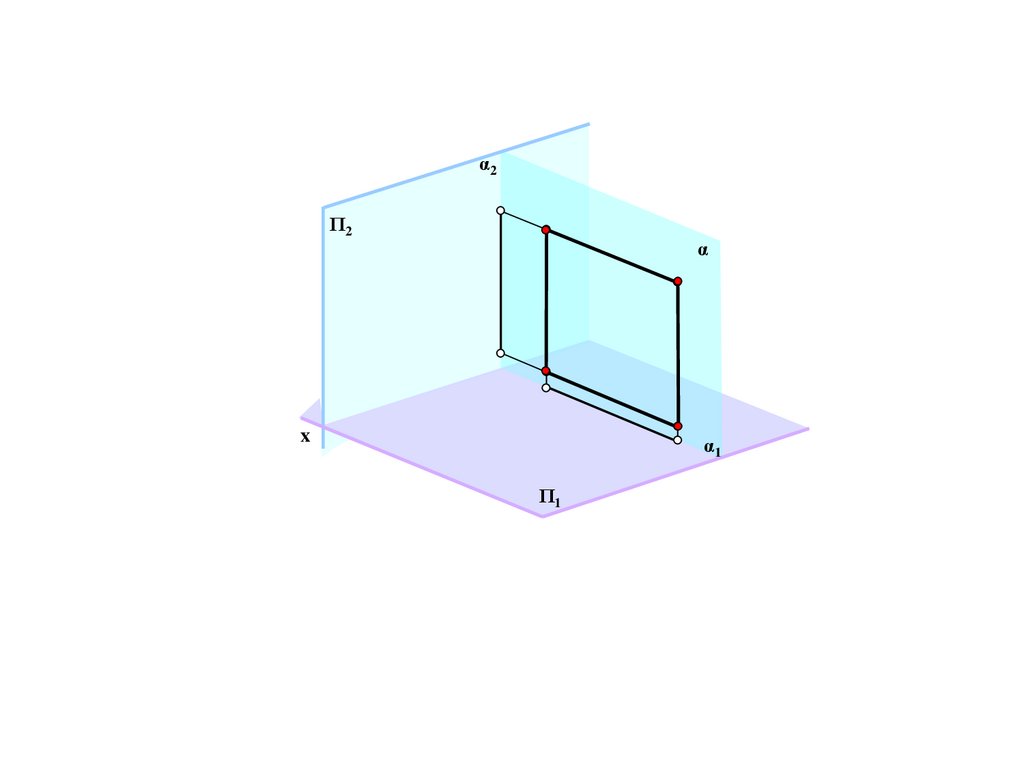
M/=E/=C/=e/
C

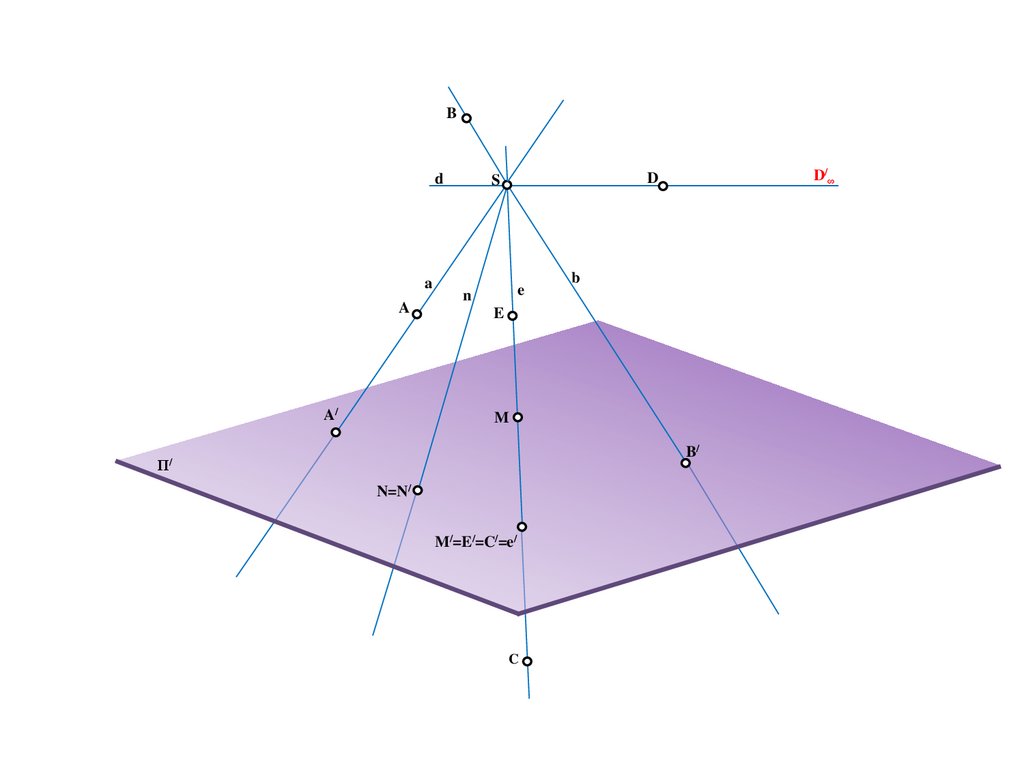
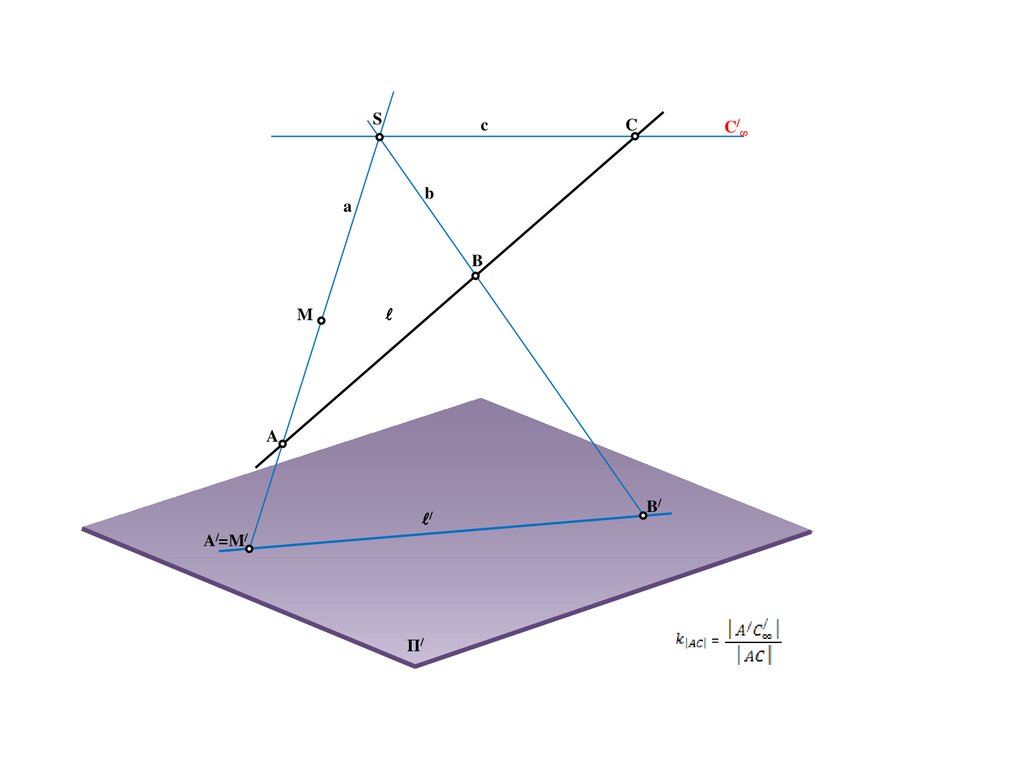
24.

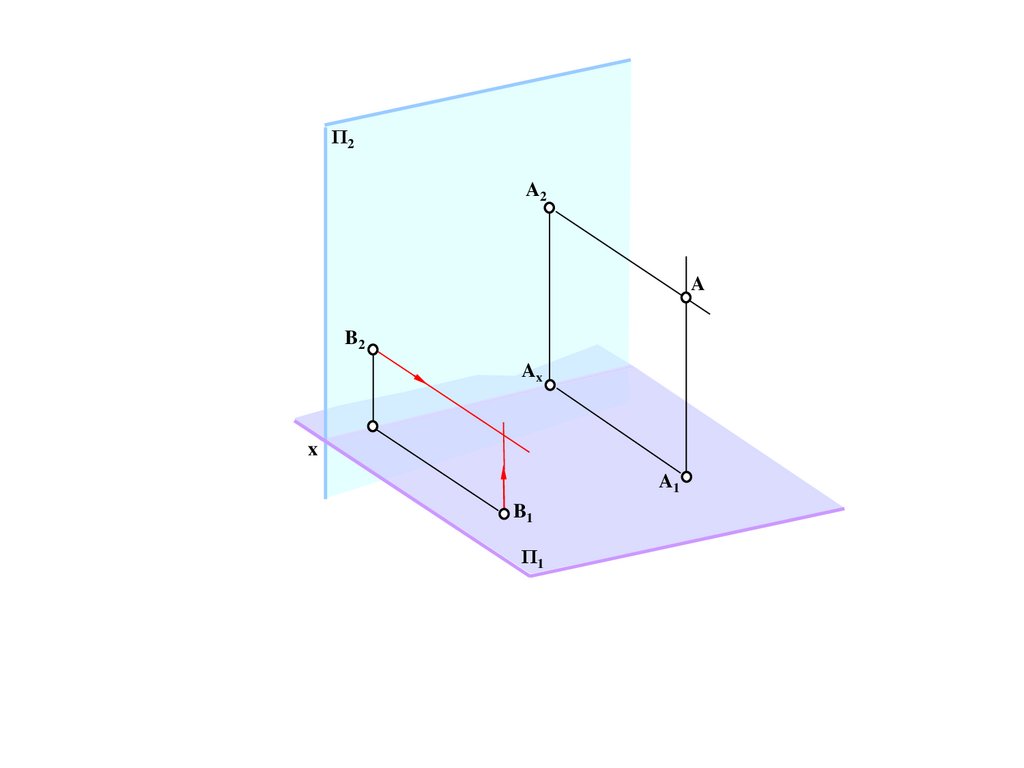
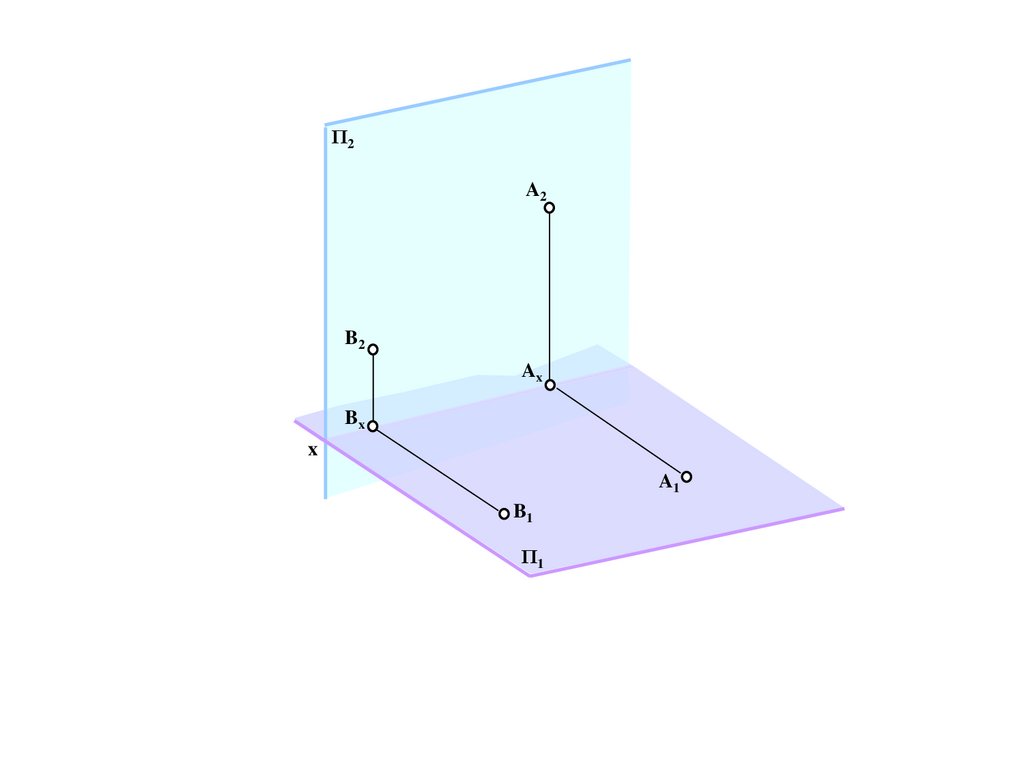
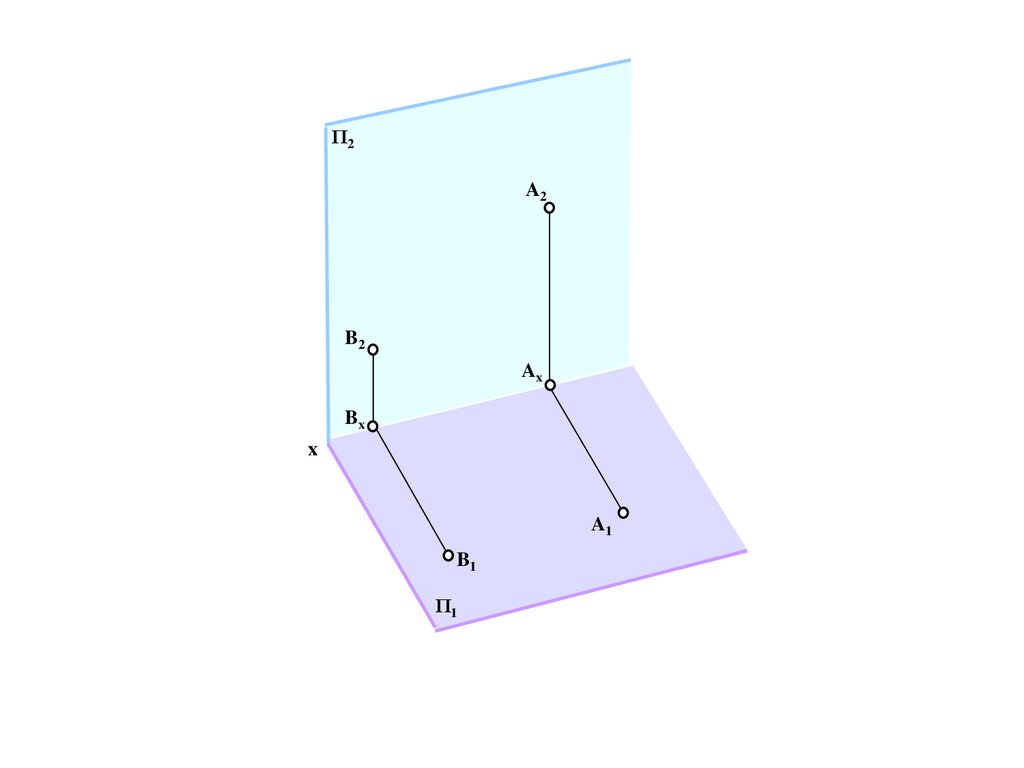
B
d
a
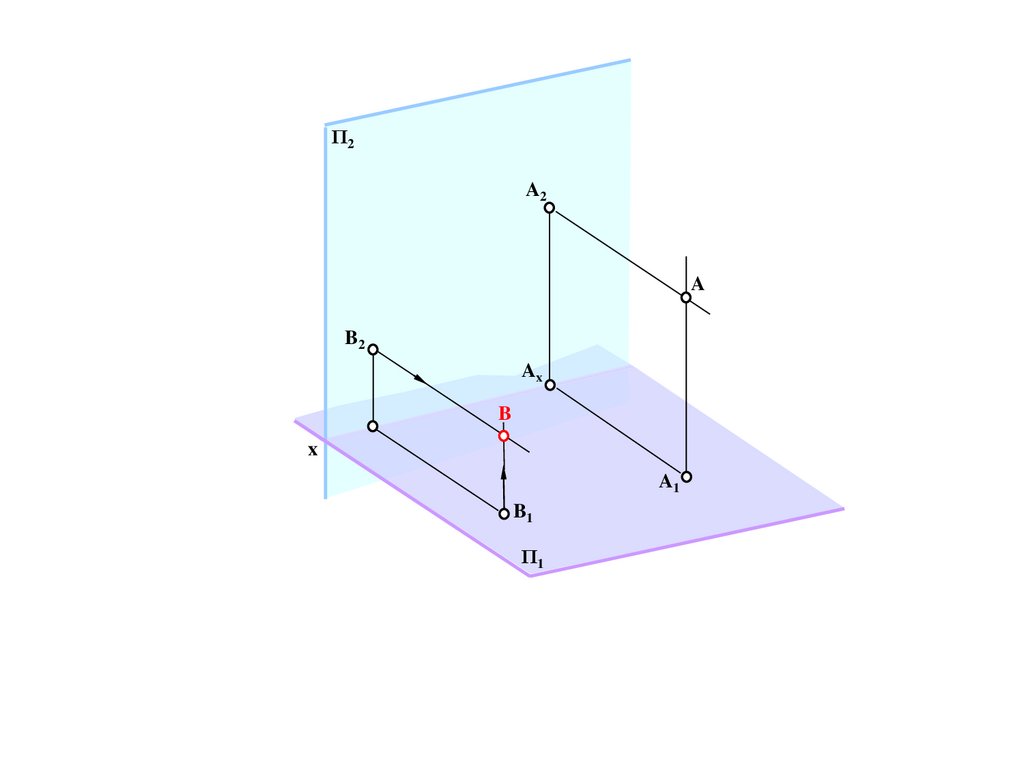
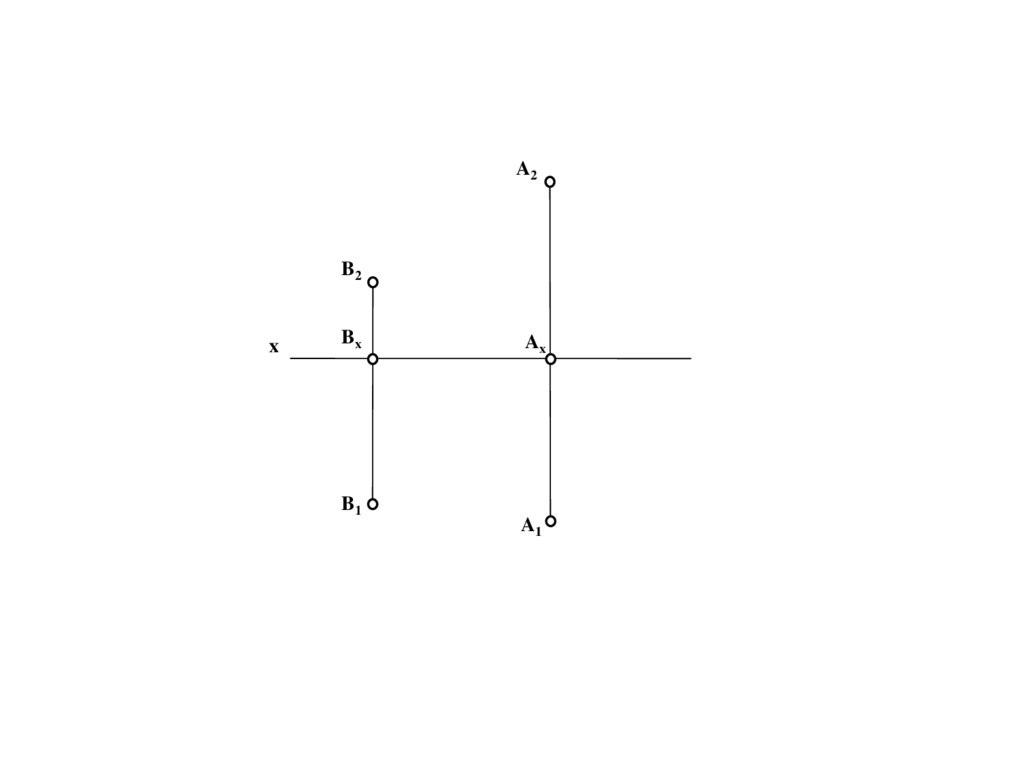
A
A/
D/∞
D
S
e
n
b
E
M
B/
Π/
N=N/
M/=E/=C/=e/
C

25.

B
α
d
a
A
A/
D/∞
D
S
e
n
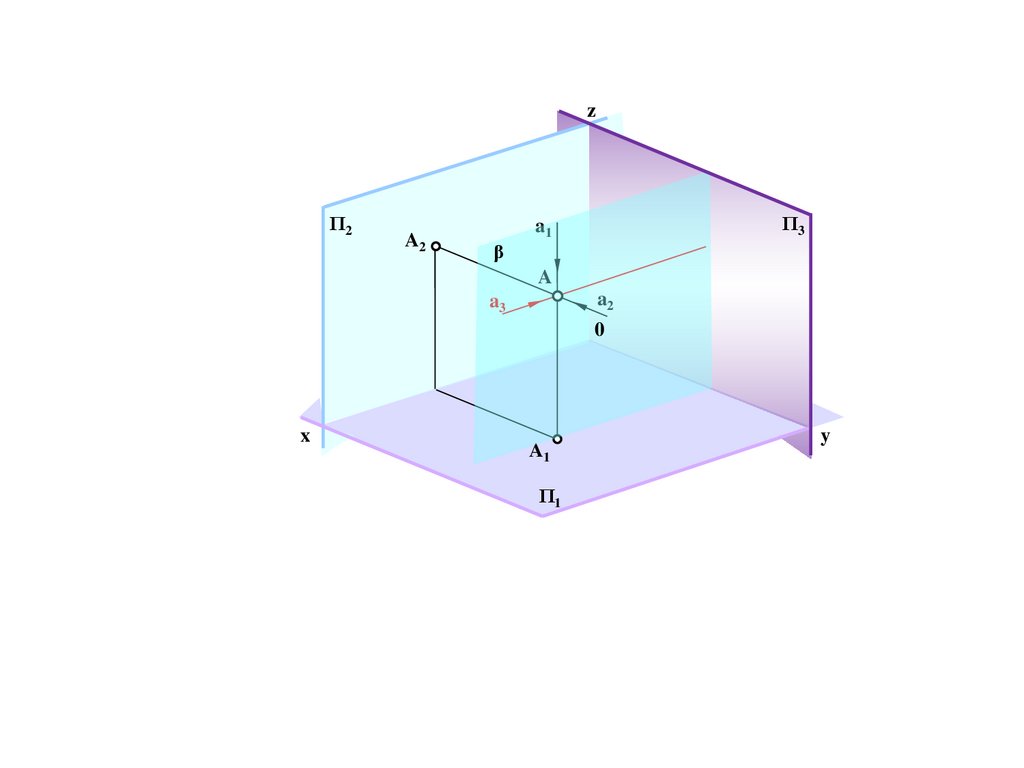
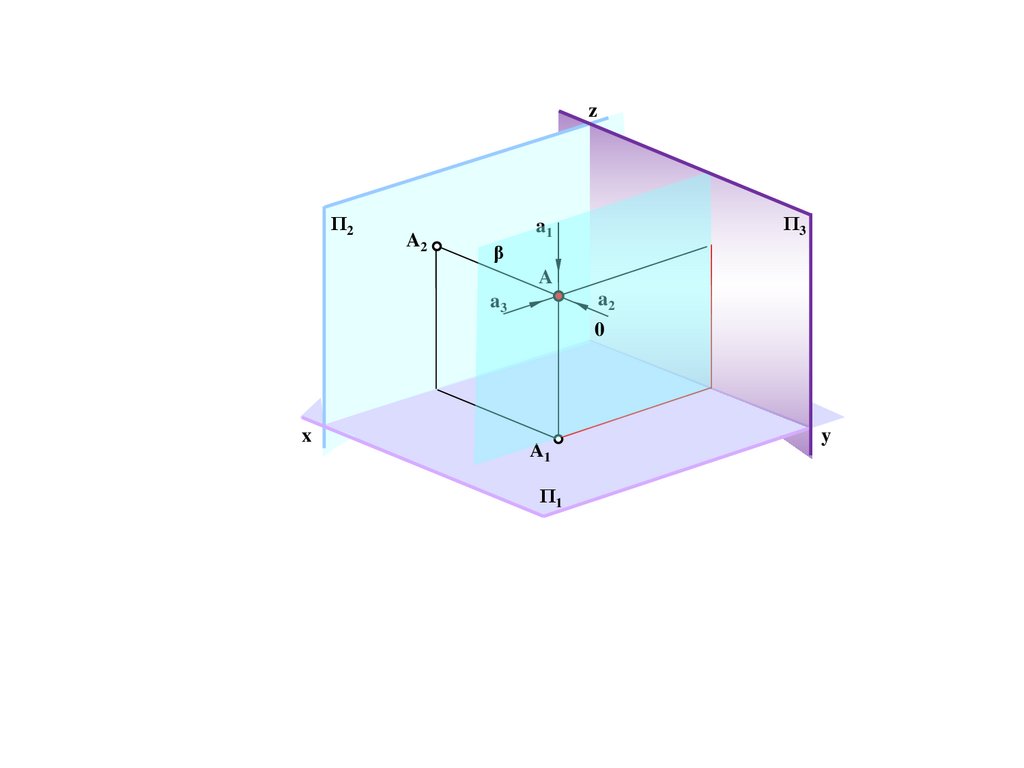
b
E
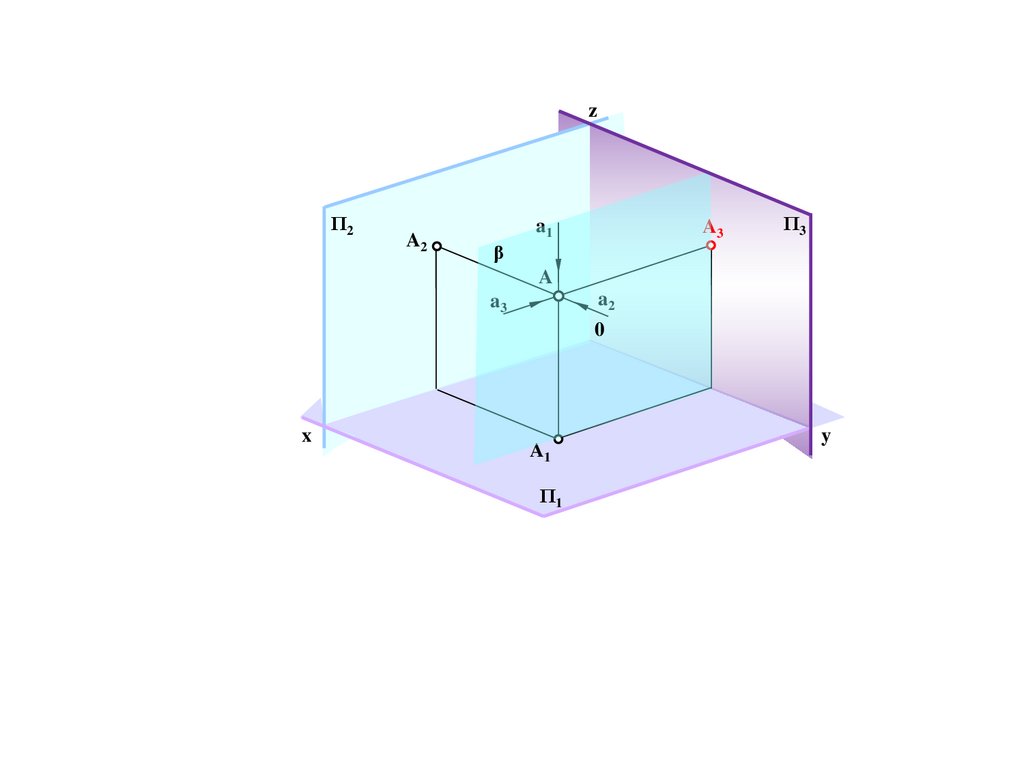
M
B/
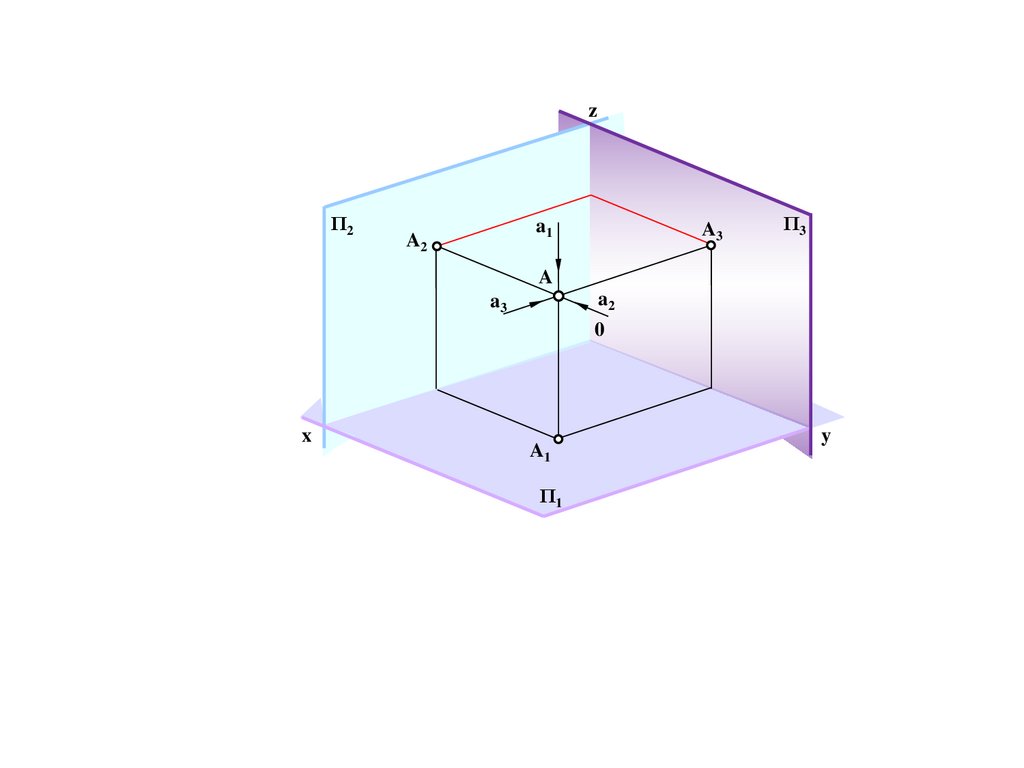
Π/
N=N/
M/=E/=C/=e/
C

26.

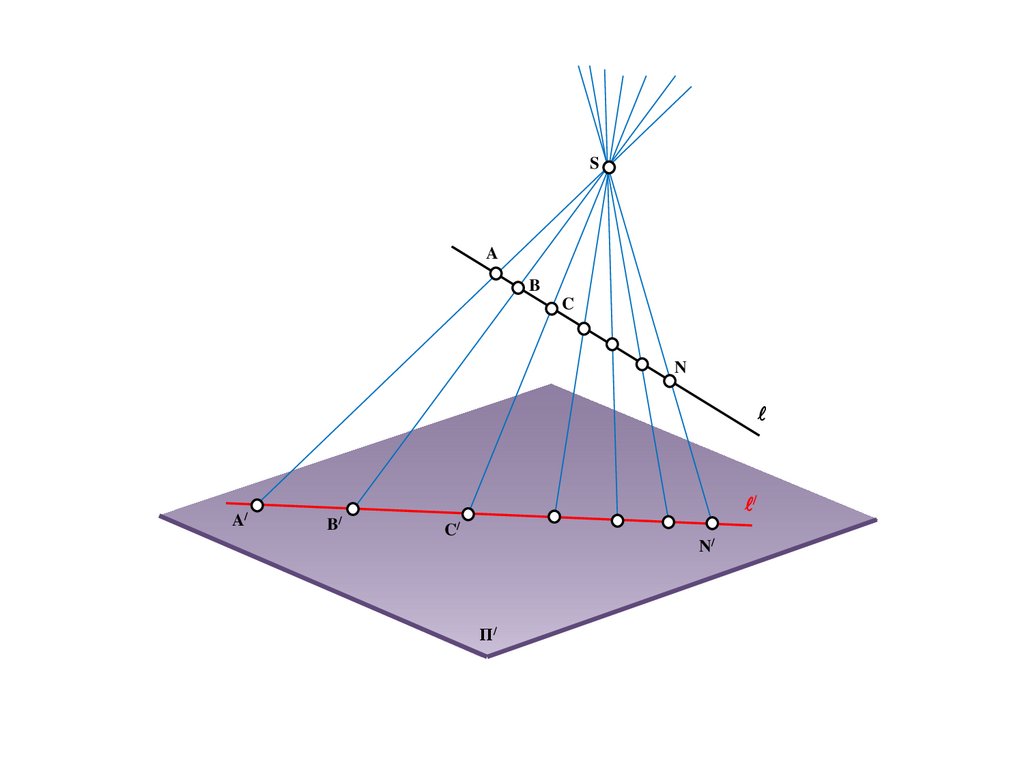
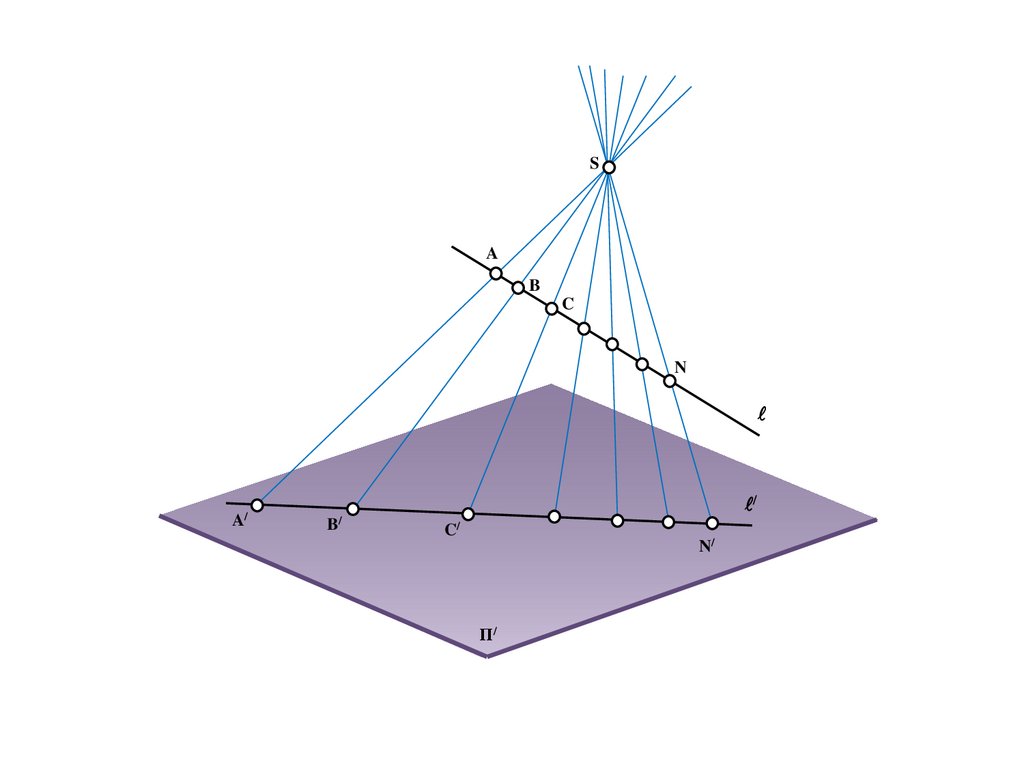
S
Π/

27.

S
A
Π/

28.

S
A
B
Π/

29.

S
A
B
C
Π/

30.

S
A
B
C
N
Π/

31.

S
A
B
C
N
Π/

32.

S
A
B
C
N
A/
Π/

33.

S
A
B
C
N
A/
Π/

34.

S
A
B
C
N
A/
B/
Π/

35.

S
A
B
C
N
A/
B/
Π/

36.

S
A
B
C
N
A/
B/
C/
N/
Π/

37.

S
A
B
C
N
A/
B/
C/
N/
Π/

38.

S
A
B
C
N
A/
/
B/
C/
N/
Π/

39.

S
A
B
C
N
A/
/
B/
C/
N/
Π/

40.

S
/
Π/

41.

S
Π/

42.

S
A
Π/

43.

S
a
A
Π/

44.

S
a
A
A/
Π/

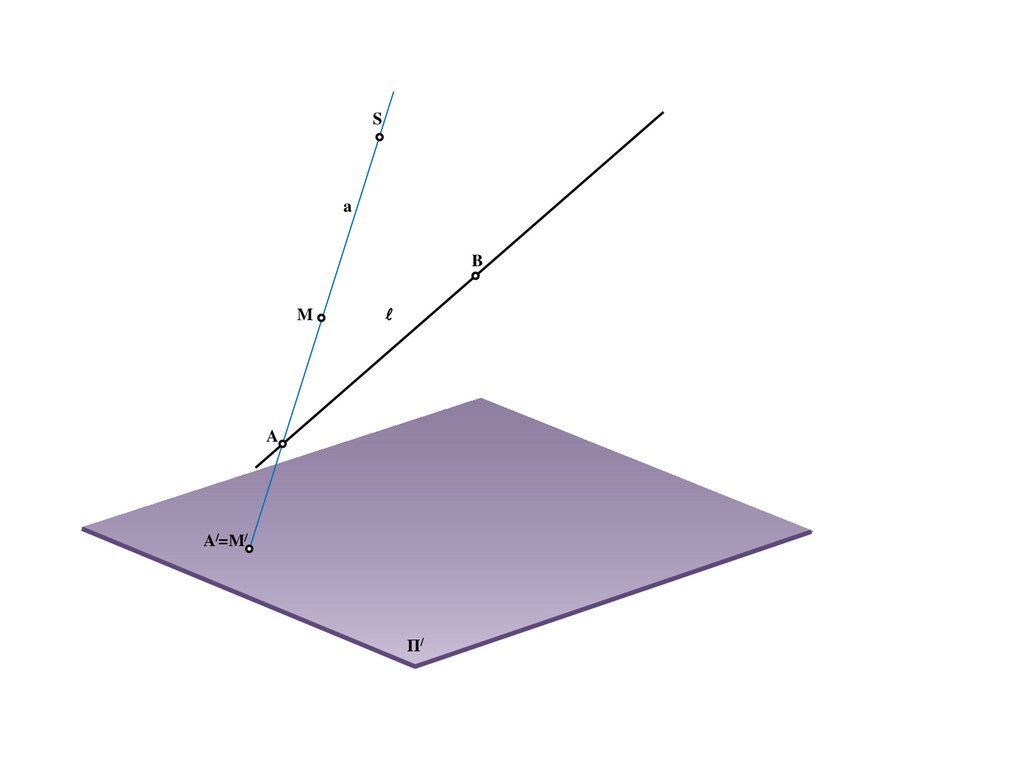
45.

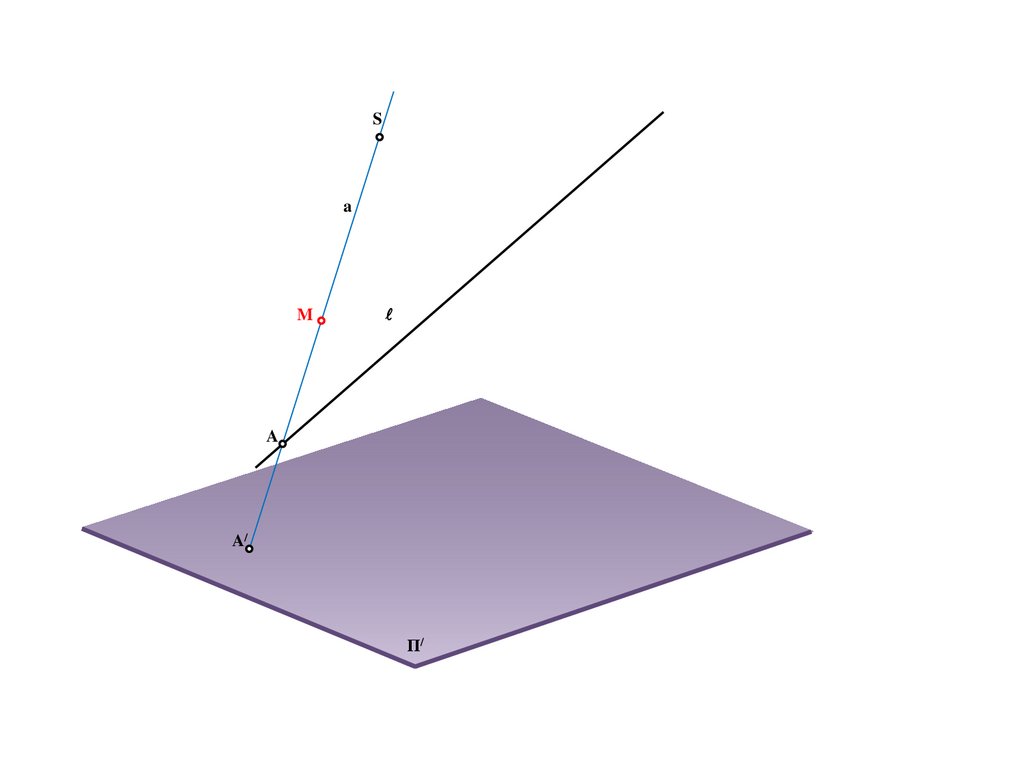
S
a
M
A
A/
Π/

46.

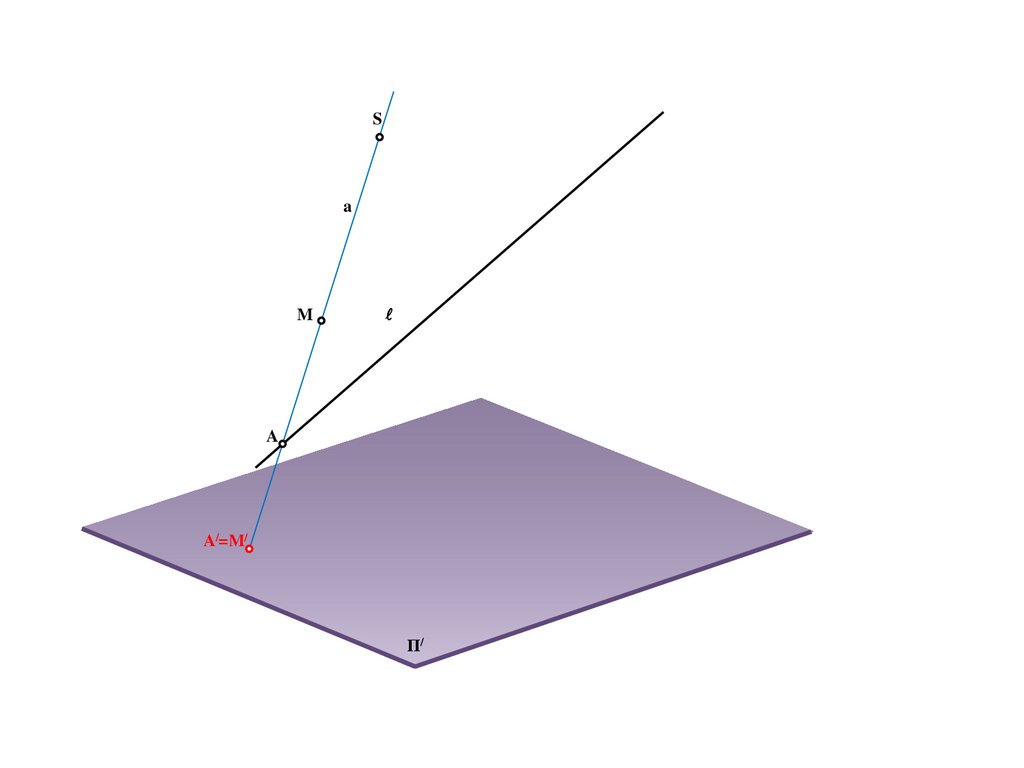
S
a
M
A
A/=M/
Π/

47.

S
a
M
A
A/=M/
Π/

48.

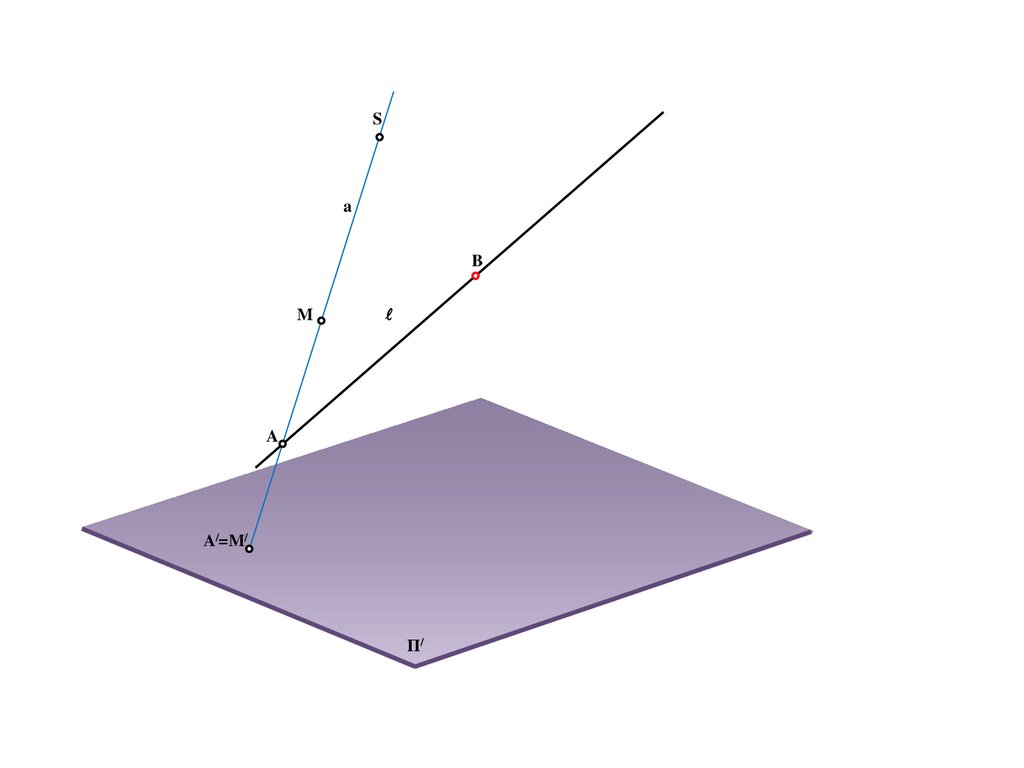
S
a
B
M
A
A/=M/
Π/

49.

S
a
B
M
A
A/=M/
Π/

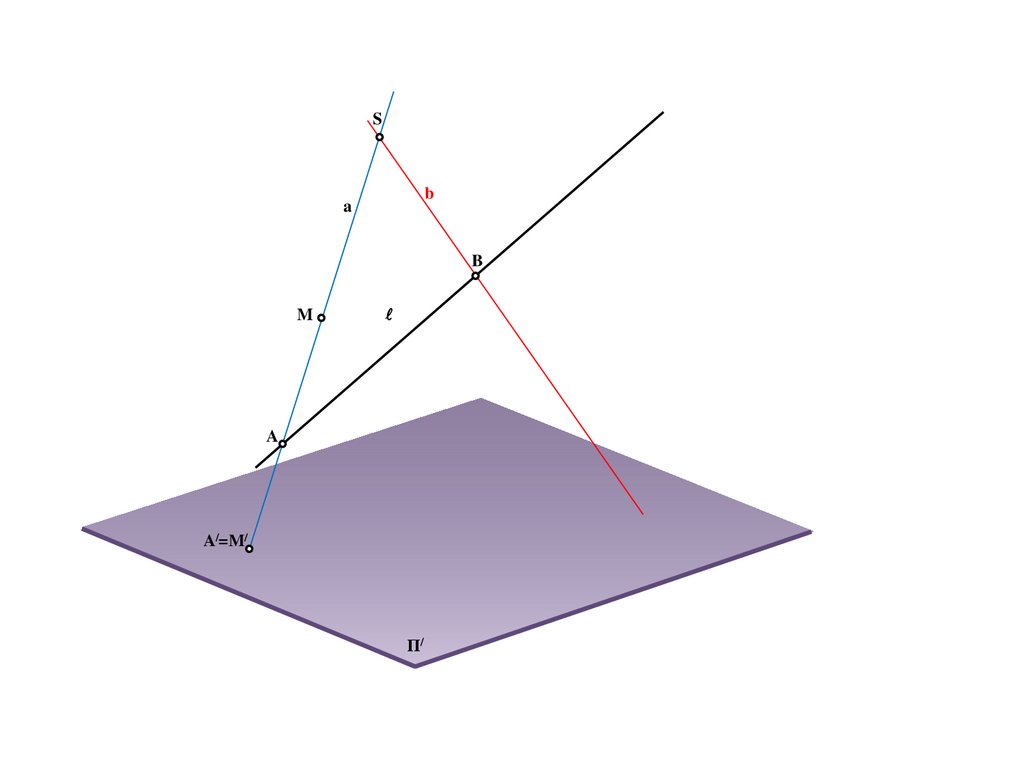
50.

S
b
a
B
M
A
A/=M/
Π/

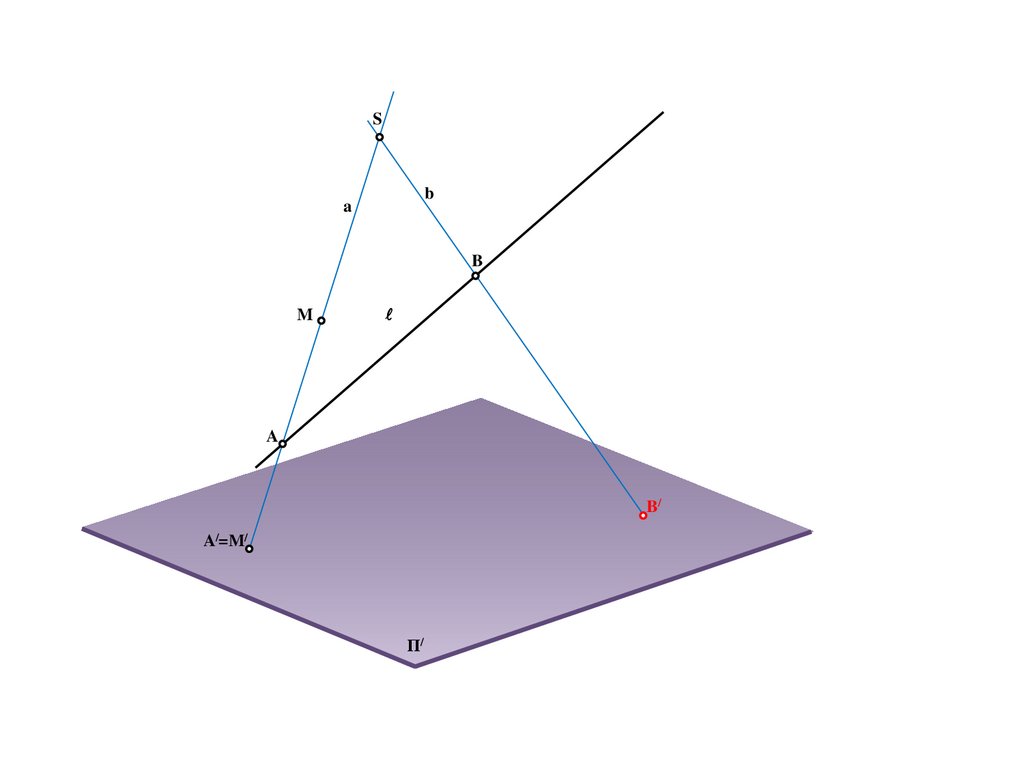
51.

S
b
a
B
M
A
B/
A/=M/
Π/

52.

S
b
a
B
M
A
/
A/=M/
Π/
B/

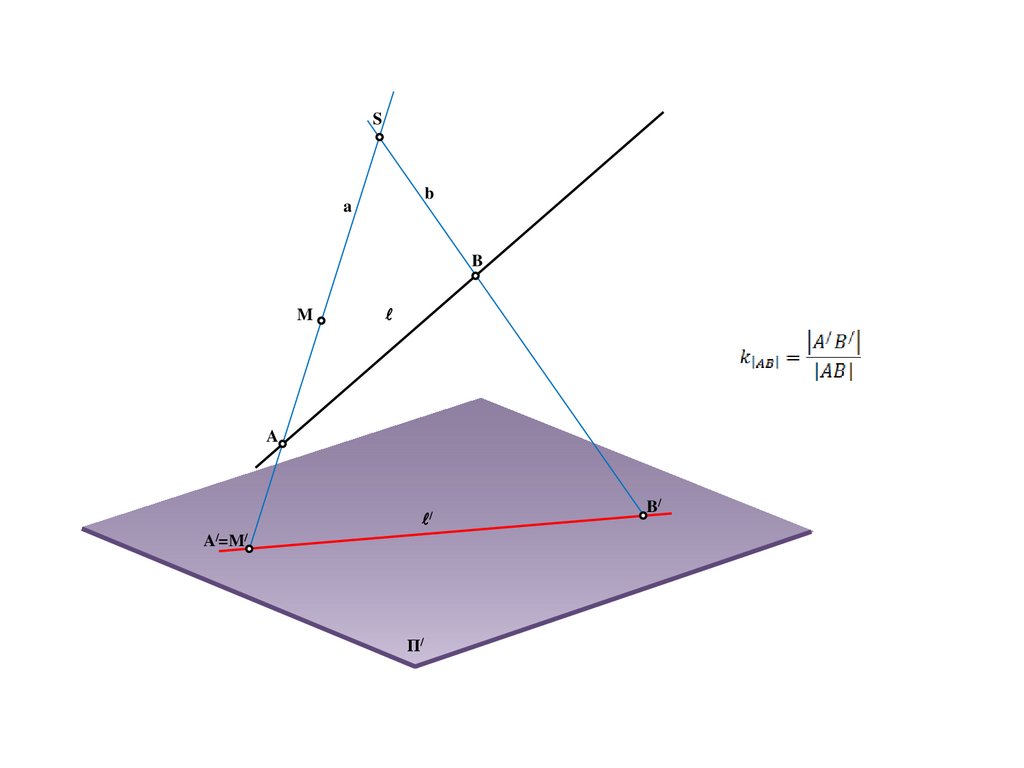
53.

S
b
a
B
M
A
/
A/=M/
Π/
B/

54.

S
C
b
a
B
M
A
/
A/=M/
Π/
B/

55.

S
c
C
b
a
B
M
A
/
A/=M/
Π/
B/

56.

S
c
C
C/∞
b
a
B
M
A
/
B/
A/=M/
Π/
=

57.

S
Π/

58.

S
Π/

59.

S
B
A
C
Π/

60.

S
B
A
C
Π/

61.

S
B
A
C
B/
A/
Π/
C/

62.

Метод паралельного проецирования

63.

s
Π/

64.

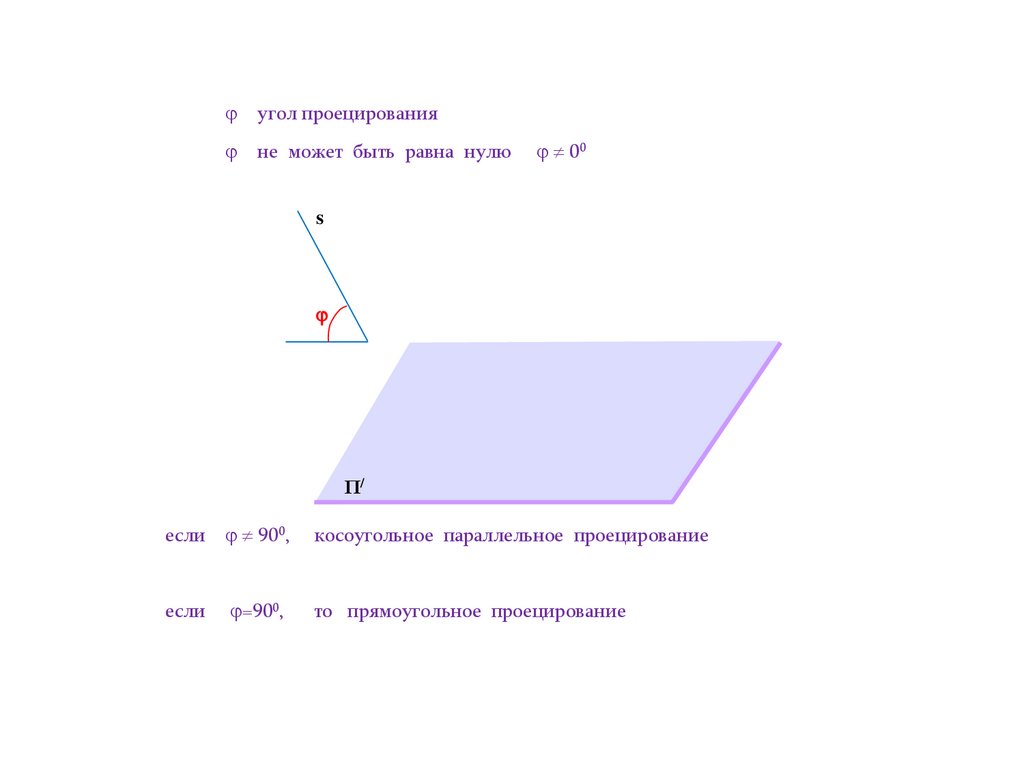
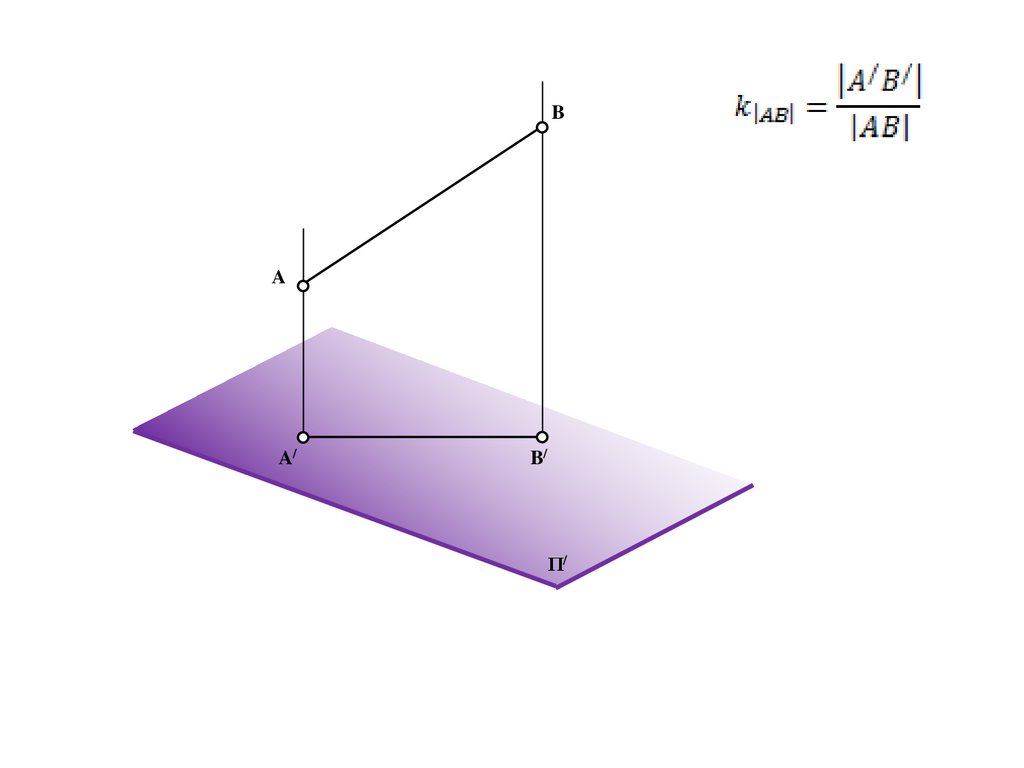
угол проецирования
не может быть равна нулю
00
s
Π/
если 900,
если
=900,
косоугольное параллельное проецирование
то прямоугольное проецирование

65.

s
A
Π/

66.

a
s
A
Π/

67.

a
s
A
A/
Π/

68.

a
s
A
A/
Π/
B

69.

a
s
A
b
A/
Π/
B

70.

a
s
A
b
A/
B/
Π/
B

71.

a
s
A
b
A/
B/
Π/
B
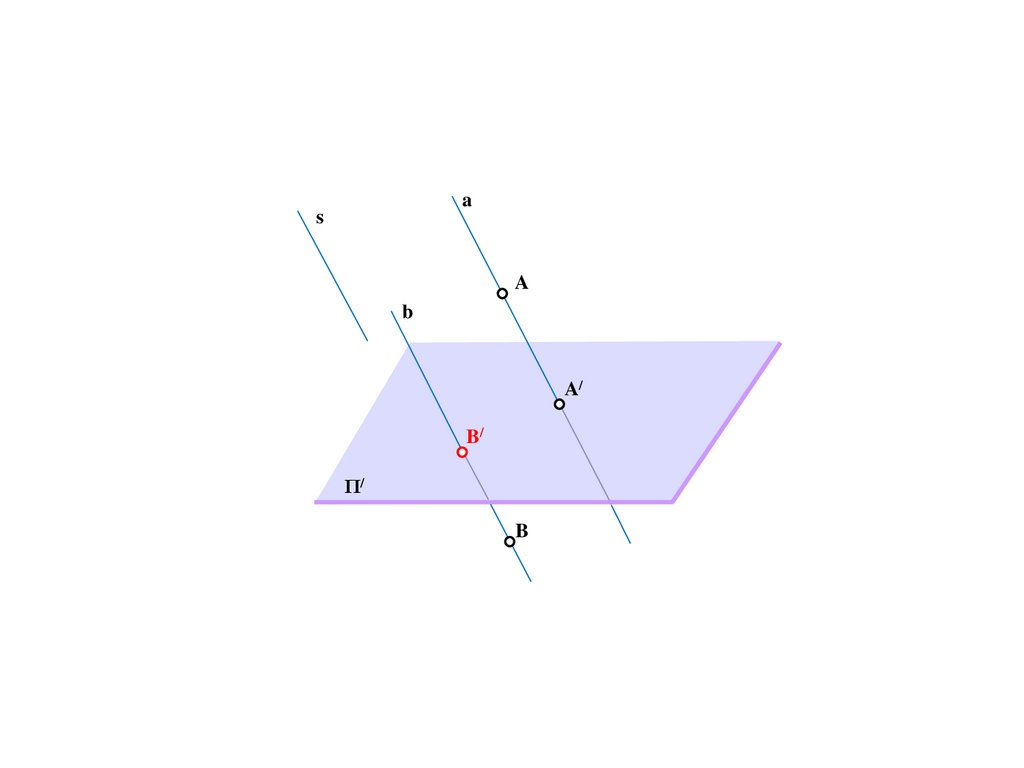
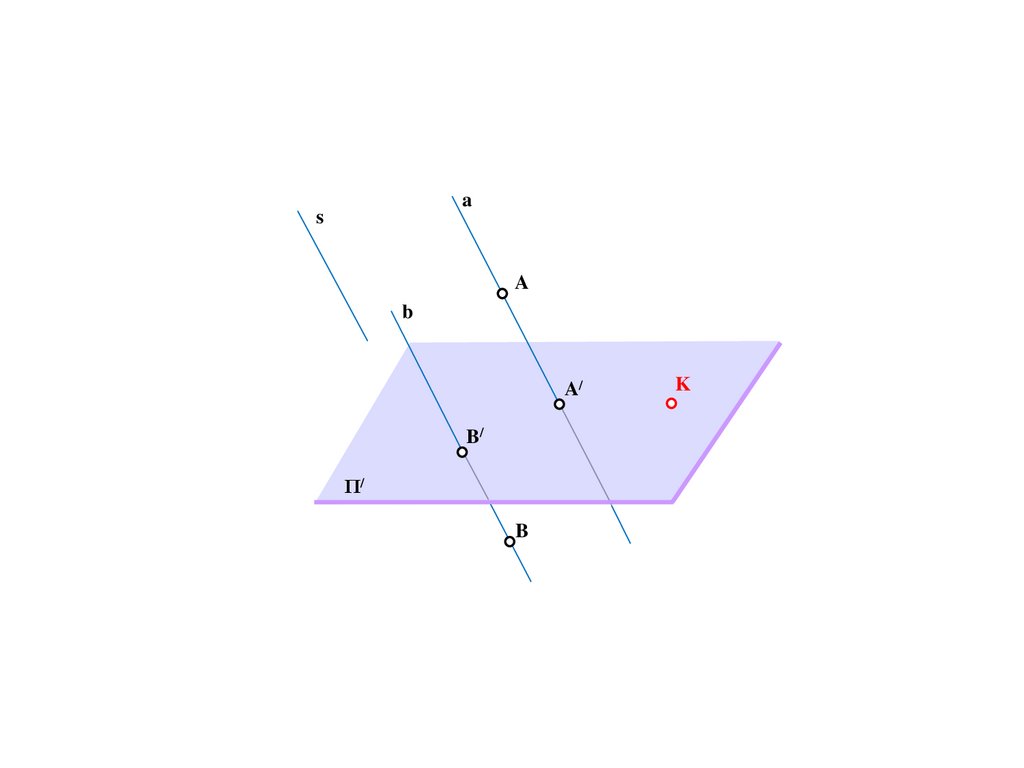
K

72.

a
s
k
A
b
A/
B/
Π/
B
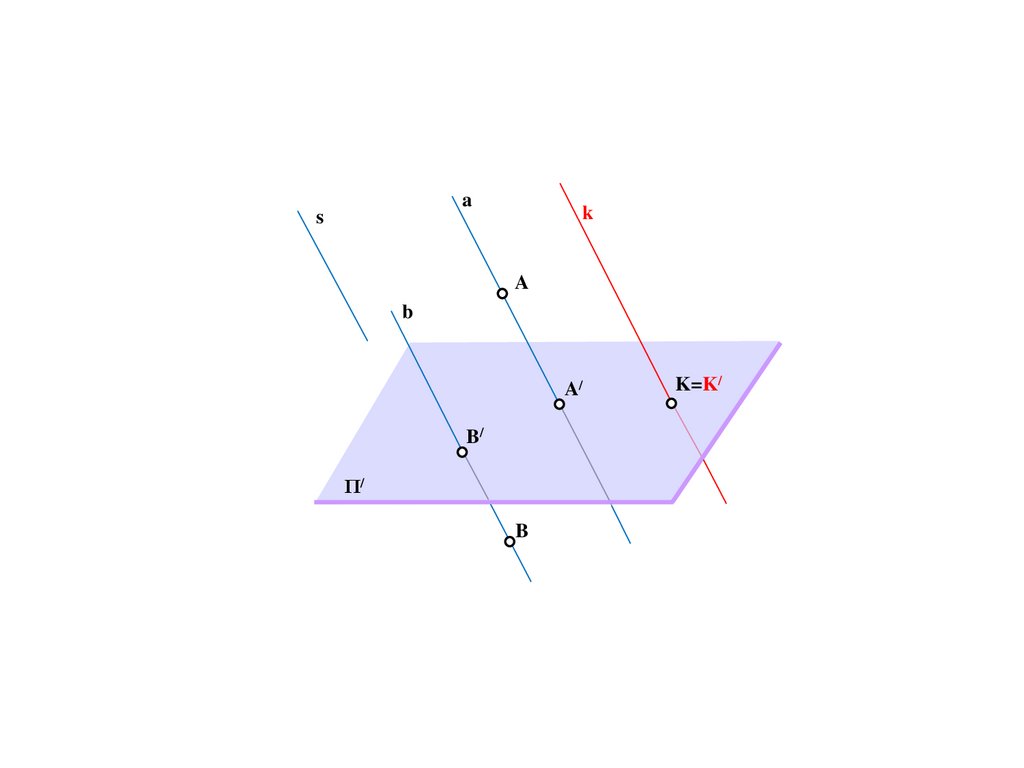
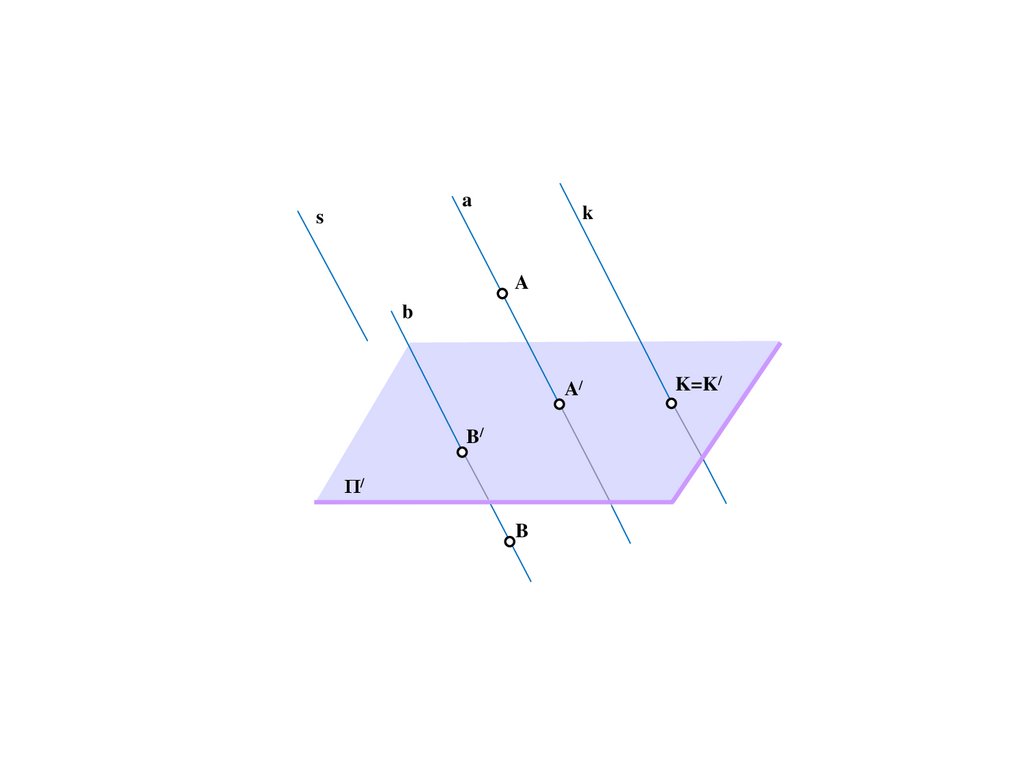
K=K/

73.

a
s
k
A
b
A/
B/
Π/
B
K=K/

74.

s
Π/

75.

s
α
Π/

76.

s
α
Π/
/=α/

77.

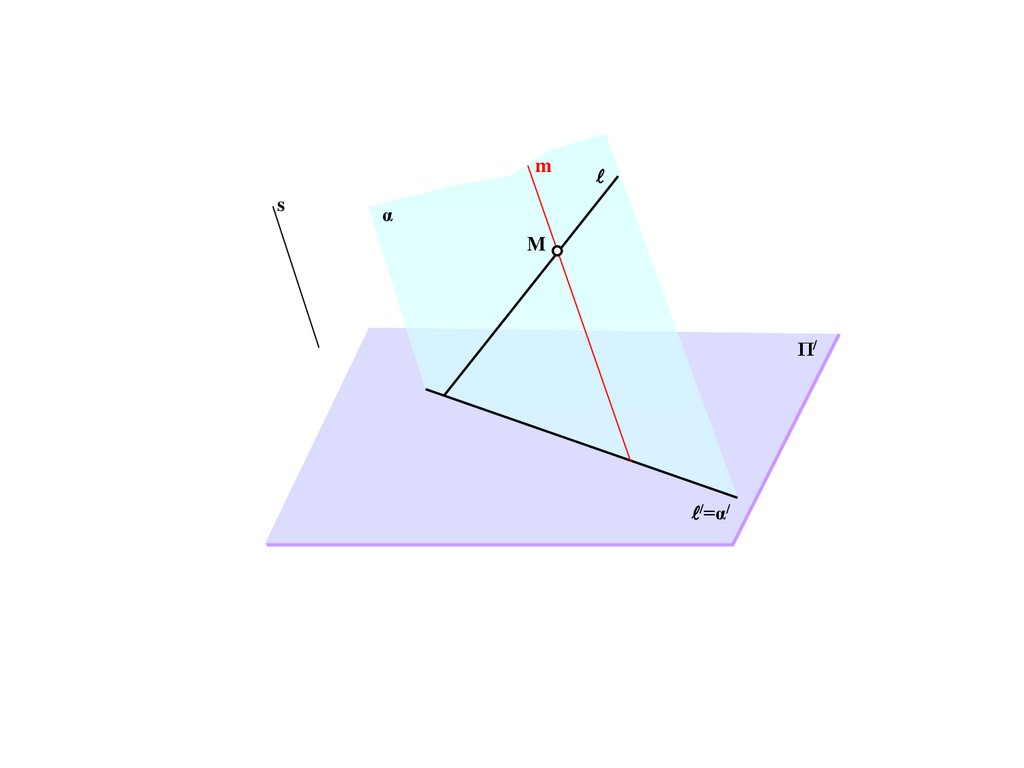
s
α
M
Π/
/=α/

78.

m
s
α
M
Π/
/=α/

79.

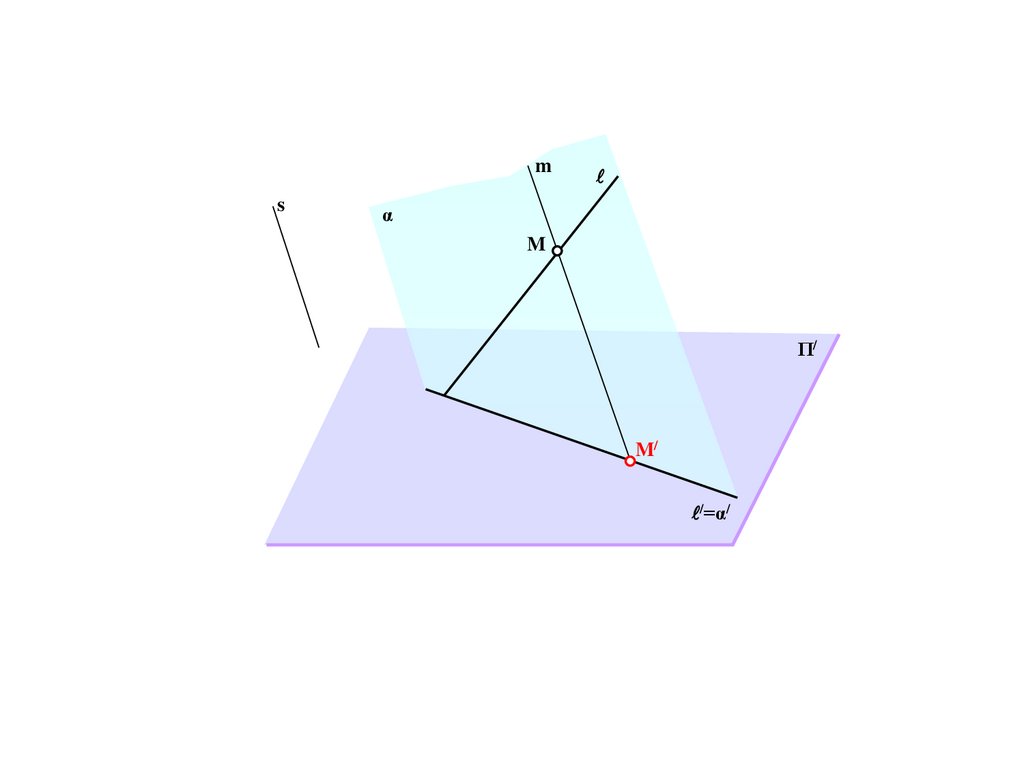
m
s
α
M
Π/
M/
/=α/

80.

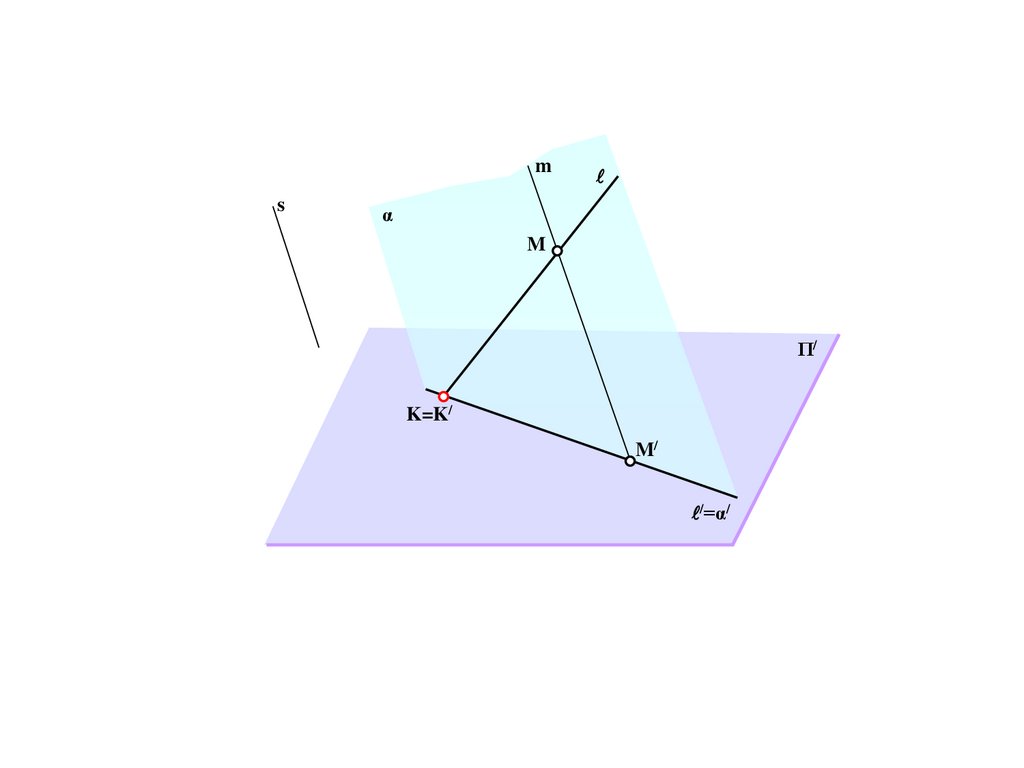
m
s
α
M
Π/
K=K/
M/
/=α/

81.

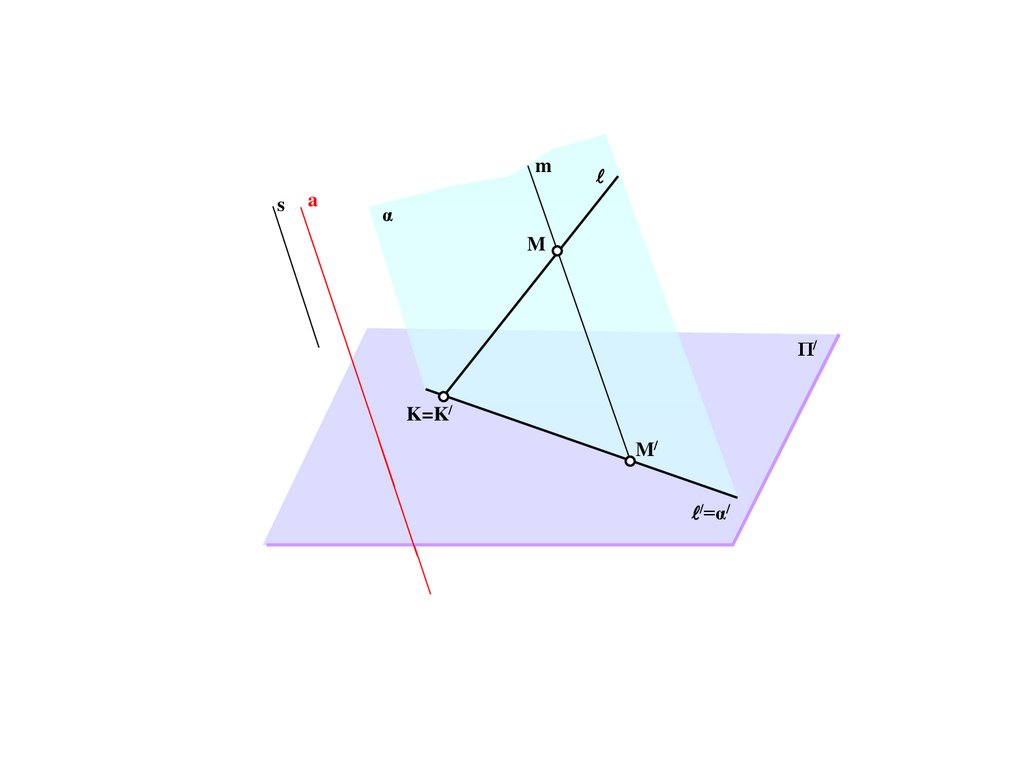
m
s
a
α
M
Π/
K=K/
M/
/=α/

82.

m
s
a
α
M
Π/
K=K/
M/
a/
/=α/

83.

m
s
a
α
A
M
B
Π/
C K=K/
M/
a/=A/=B/=C/
/=α/

84.

B
s
A
Π/

85.

B
s
A
Π/

86.

B
s
A
A/
Π/
B/

87.

B
s
A
A/
Π/
B/

88.

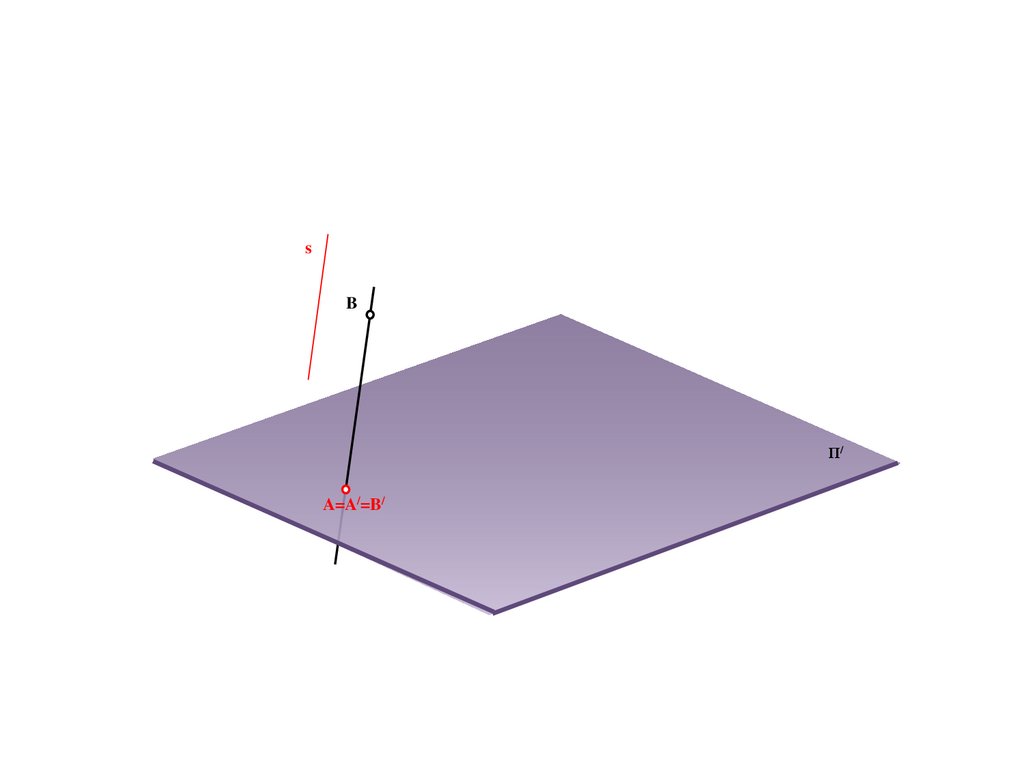
Π/

89.

B
Π/
A

90.

s
B
Π/
A=A/=B/

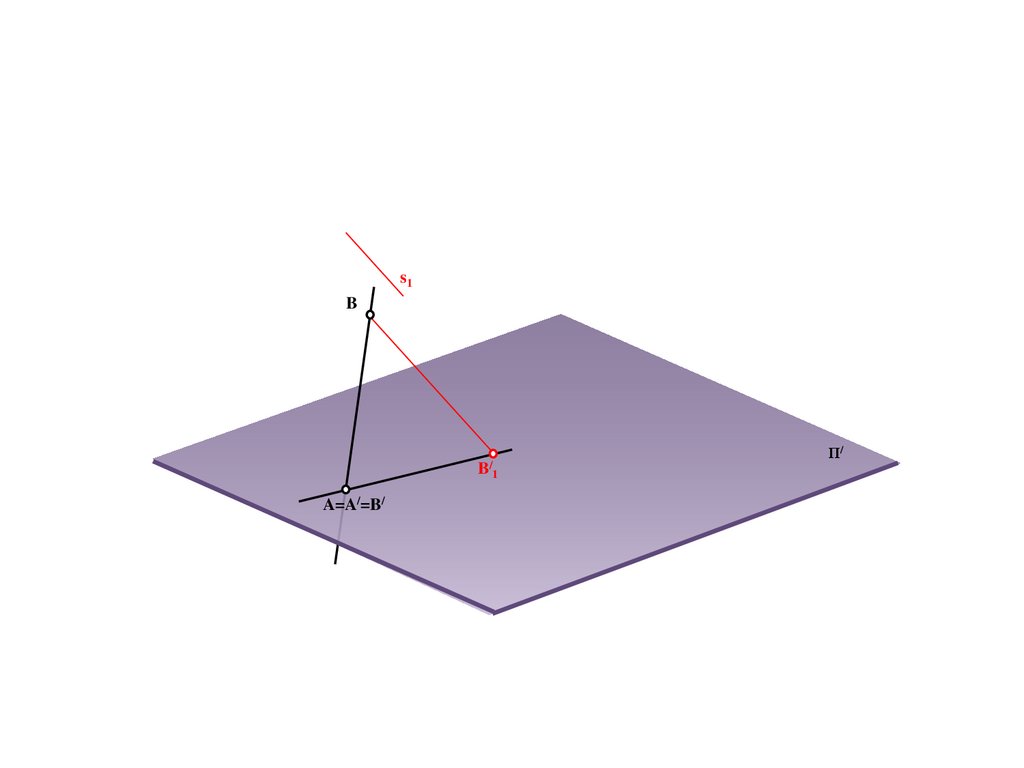
91.

s1
B
B/
A=A/=B/
Π/
1

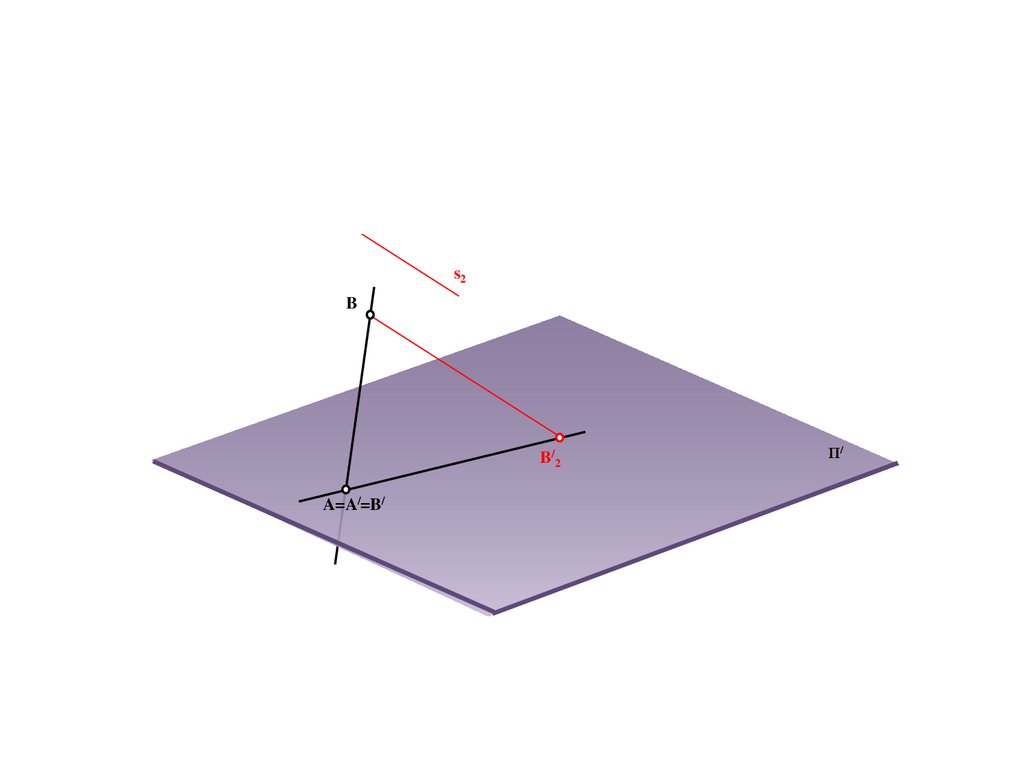
92.

s2
B
B/2
A=A/=B/
Π/

93.

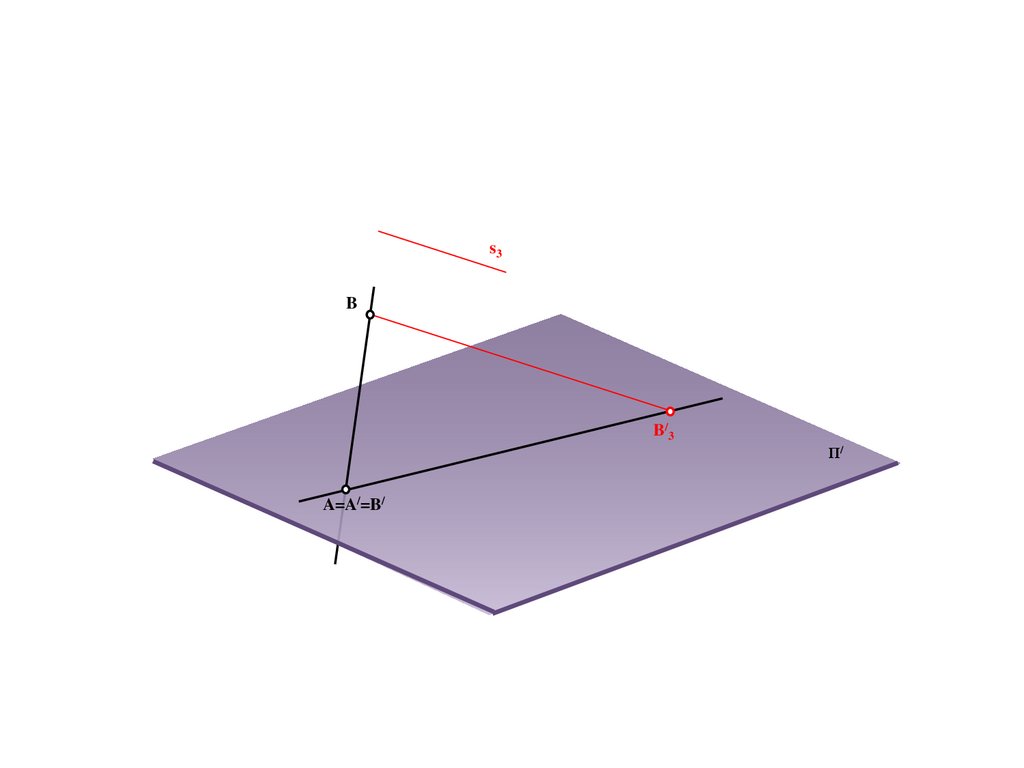
s3
B
B/3
Π/
A=A/=B/

94.

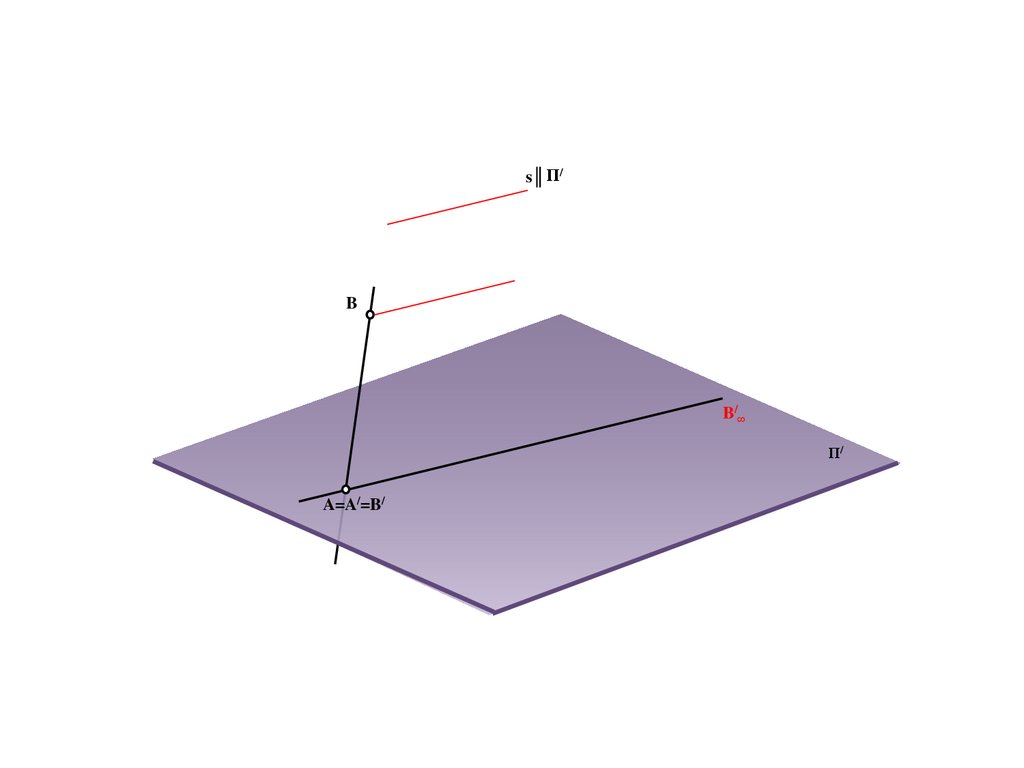
s║ Π/
B
B/ ∞
Π/
A=A/=B/

95.

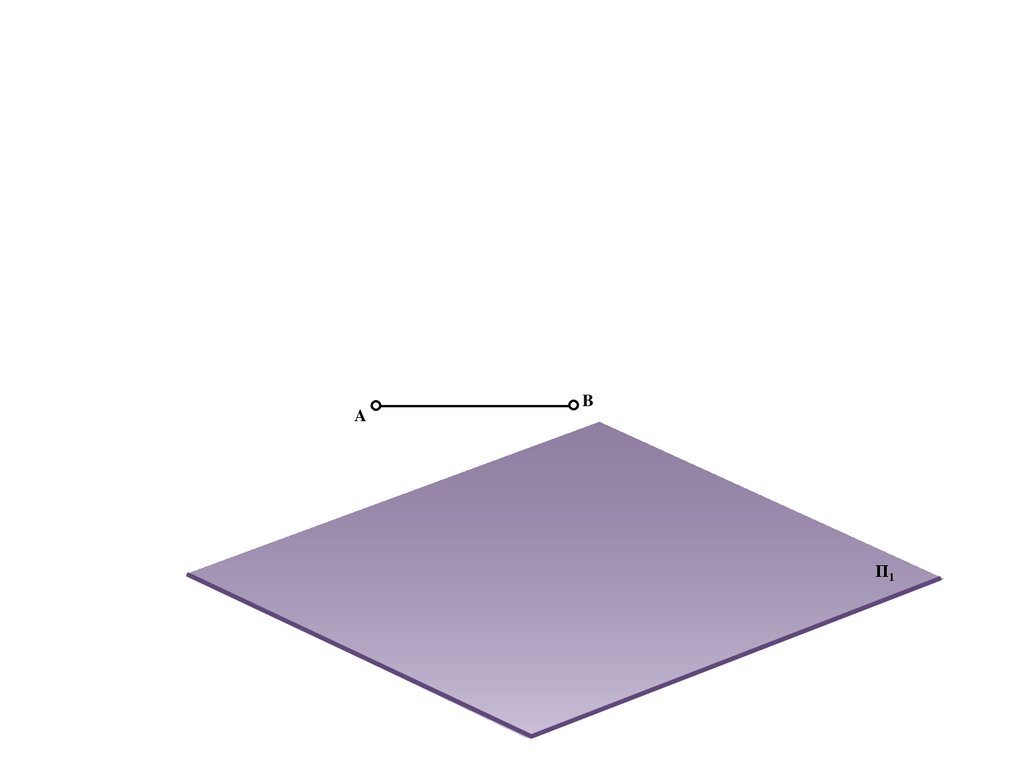
A
B
Π1

96.

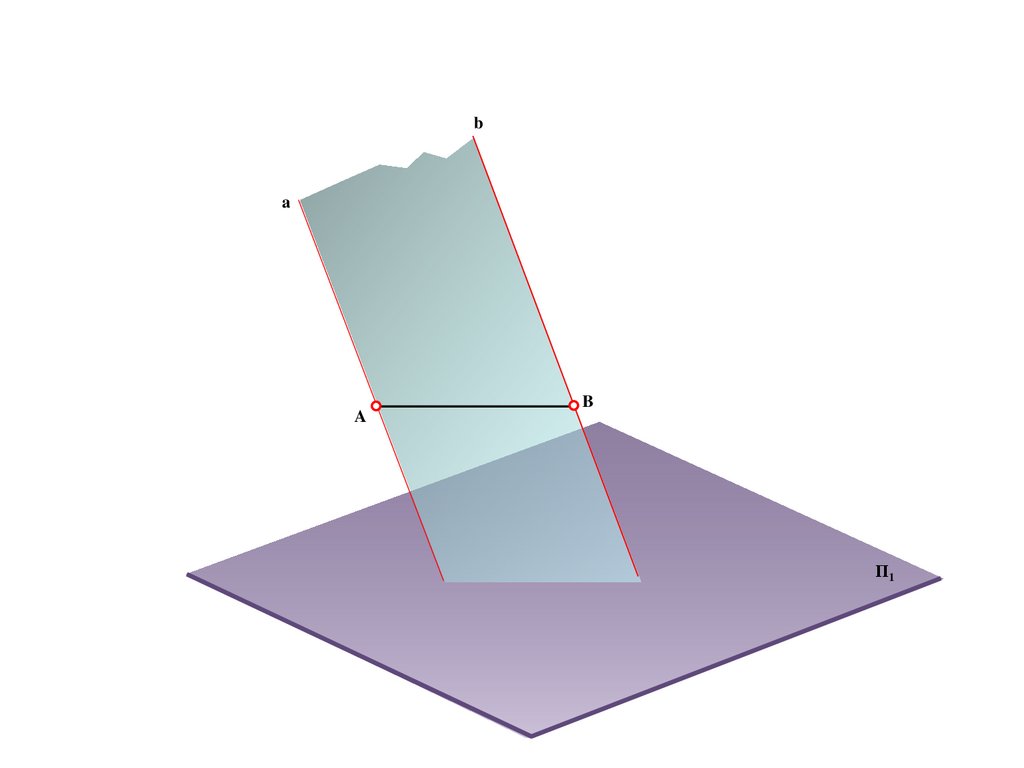
b
a
A
B
Π1

97.

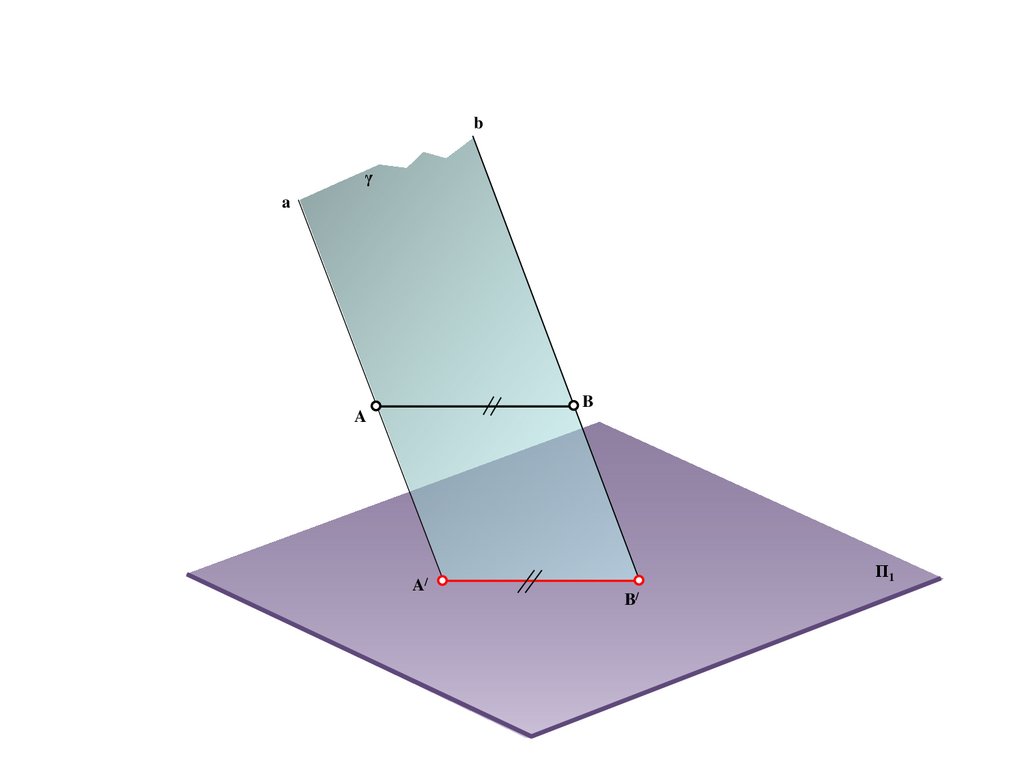
b
γ
a
B
A
A/
Π1
B/

98.

b
γ
a
B
A
A/
Π1
B/

99.

b
γ
a
C
α
A
A/
B
Π1
B/=C/

100.

b
γ
a
C
α
α
A
A/
B
Π1
B/=C/

101.

Взаимное расположение прямых
(параллельные, пересекающиеся и скрещивающиеся прямые);

102.

n
s
m
Π/

103.

s
α
n
β
m
Π/

104.

s
α
n
β
m
m/=β/
Π/
n/=α/

105.

s
α
n
Π/
n/=α/

106.

s
α
n
Π/
/=n/=α/

107.

s
α
n
β
m
m/=β/
Π/
/=n/=α/

108.

s
α
n
β
m
m/=β/
Π/
/=n/=α/

109.

n
K
s
m
Π/

110.

γ
n
K
s
m
Π/

111.

γ
n
K
s
m
Π/
m/=n/=γ/

112.

γ
n
K
s
m
K/
m/=n/=γ/
Π/

113.

γ
n
K
K
s
m
b
K/
m/=n/=γ/
a
Π/

114.

γ
α
n
β
K
K
s
m
b
K/
m/=n/=γ/
a
Π/

115.

γ
α
n
β
K
K
s
m
b
a
Π/
K/
m/=n/=γ/
b/=β/
a/=α/

116.

γ
α
n
β
K
K
s
m
b
a
m/=n/=γ/
Π/
K/
K/
b/=β/
a/=α/

117.

γ
α
n
β
K
K
s
m
b
a
m/=n/=γ/
Π/
K/
K/
b/=β/
a/=α/

118.

γ
α
n
β
K
K
s
m
b
a
m/=n/=γ/
Π/
K/
K/
b/=β
/
a/=α/

119.

a
s
b
Π/

120.

α
s
β
a
b
Π/

121.

α
s
β
a
b
a/=α/
b/=β/
Π/

122.

α
s
B
A
β
a
b
a/=α/
A/=B/
b/=β/
Π/

123.

γ
α
s
B
A
β
δ
a
b
a/=α/
A/=B/
b/=β/
Π/

124.

γ
α
s
B
A
β
δ
a
b
γ/
δ/
a/=α/
A/=B/
b/=β/
Π/

125.

γ
α
s
B
A
δ
m
β
n
a
b
n/=γ/
m/=δ/
a/=α/
A/=B/
b/=β/
Π/

126.

γ
α
s
B
A
δ
m
β
n
a
b
n/=γ/
m/=δ/
a/=α/
A/=B/
b/=β/
Π/

127.

a
Π/

128.

a
D
C
B
A
Π/

129.

a
D
s
C
B
A
Π/

130.

a
D
s
C
B
A
Π/

131.

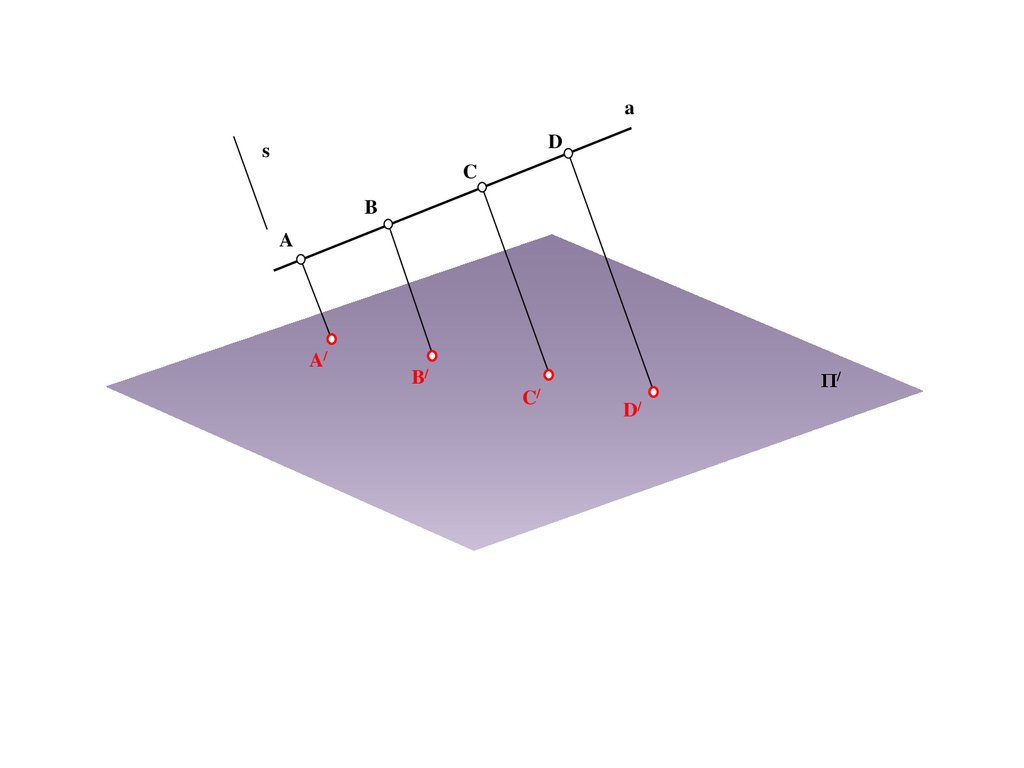
a
D
s
C
B
A
A/
B/
C/
Π/
D/

132.

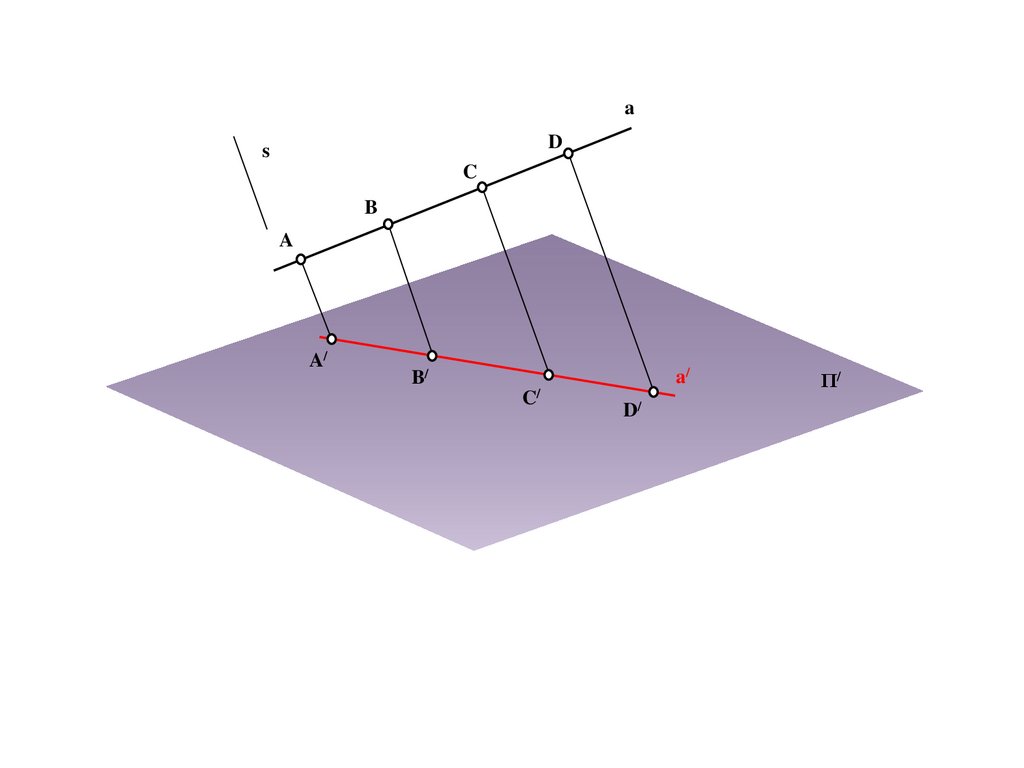
a
D
s
C
B
A
A/
a/
B/
C/
D/
Π/

133.

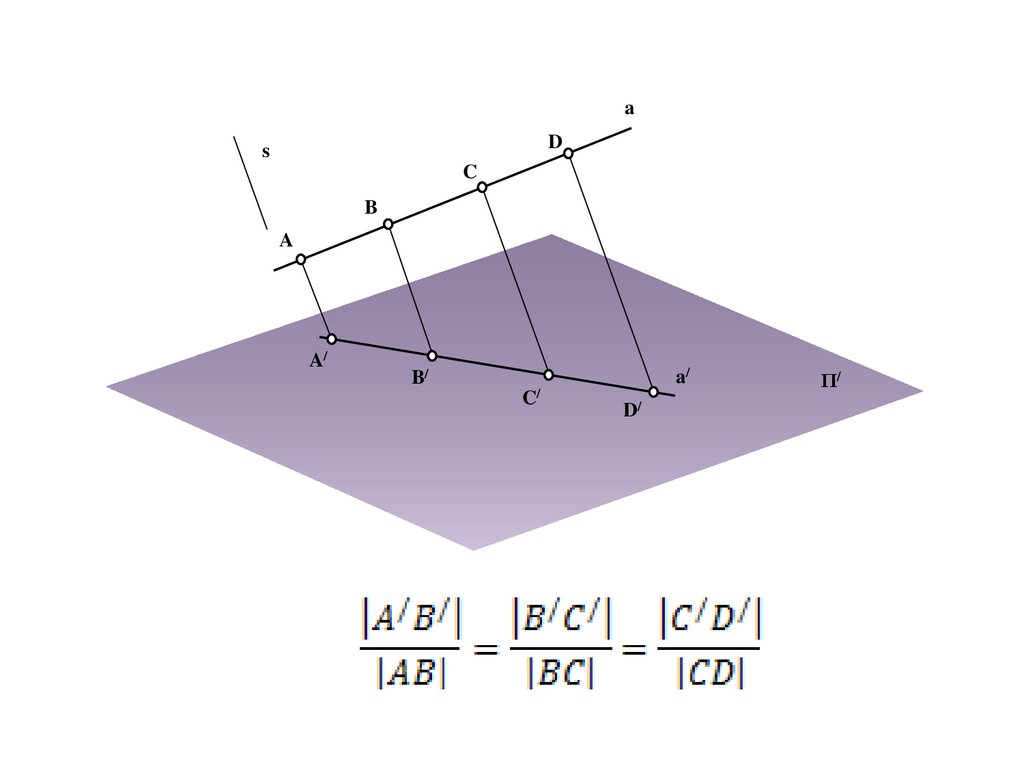
a
D
s
C
B
A
A/
a/
B/
C/
D/
Π/

134.

c
a
Π/

135.

c
a
s
Π/

136.

δ
c
λ
a
s
c/
a/
Π/

137.

D
c
a
s
C
B
A
c/
a/
Π/

138.

c
D
a
s
C
B
A
c/
D/
C/
A/
B/
Π/
a/

139.

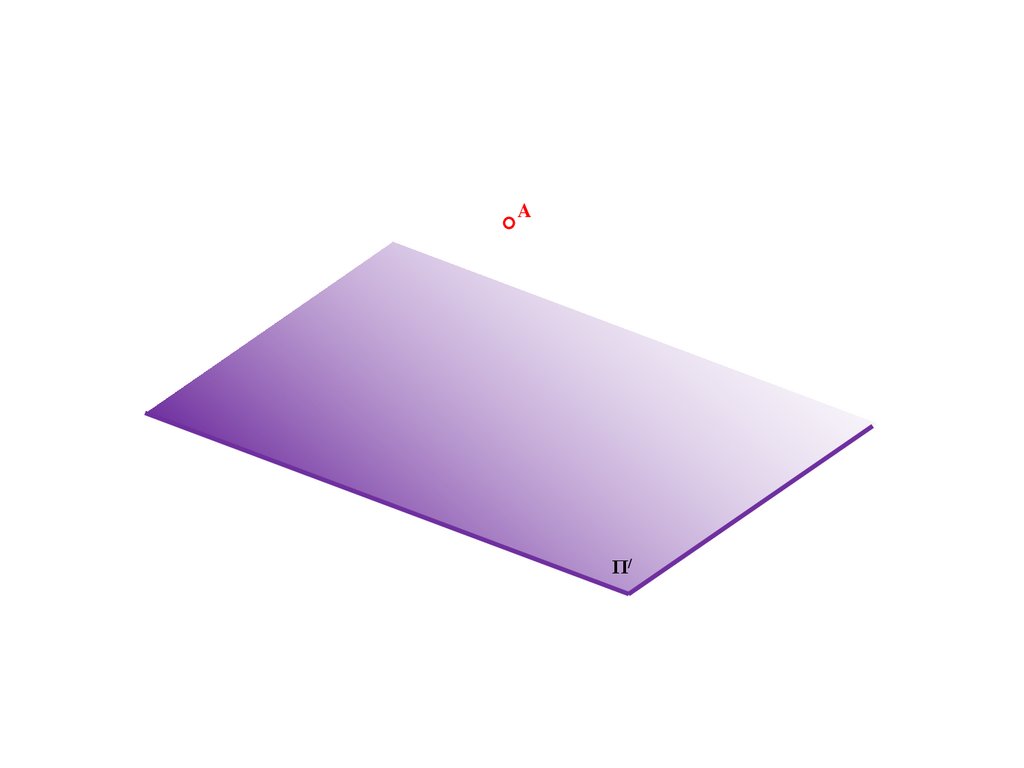
Метод ортогонального проецирования

140.

A
Π/

141.

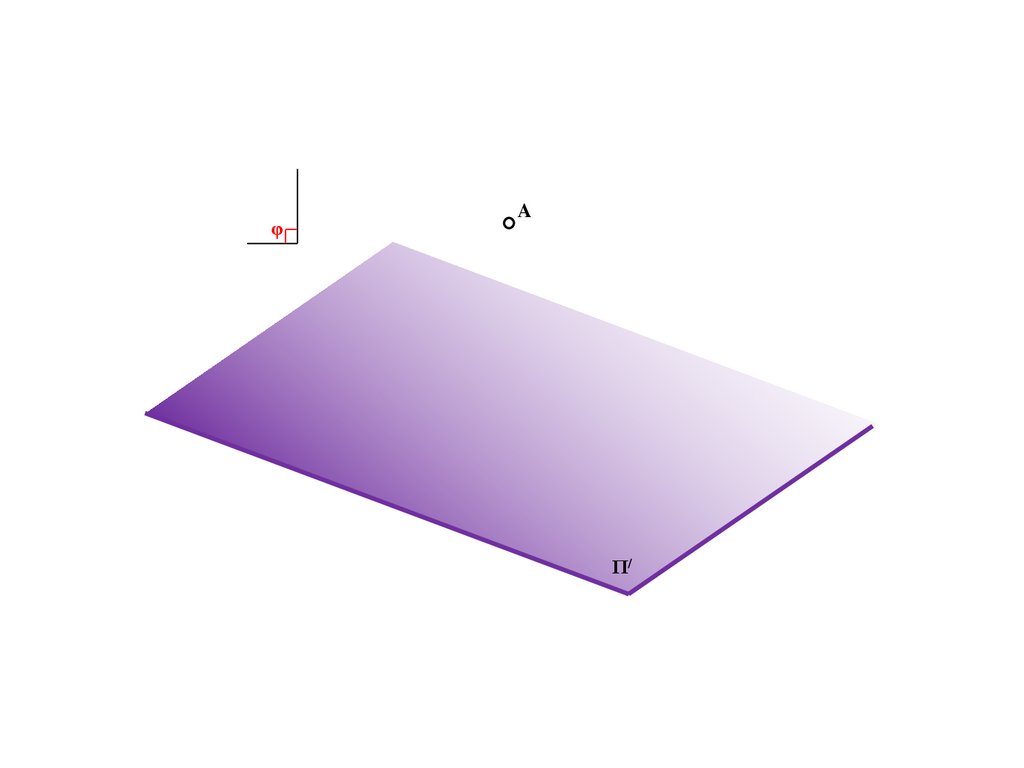
φ
A
Π/

142.

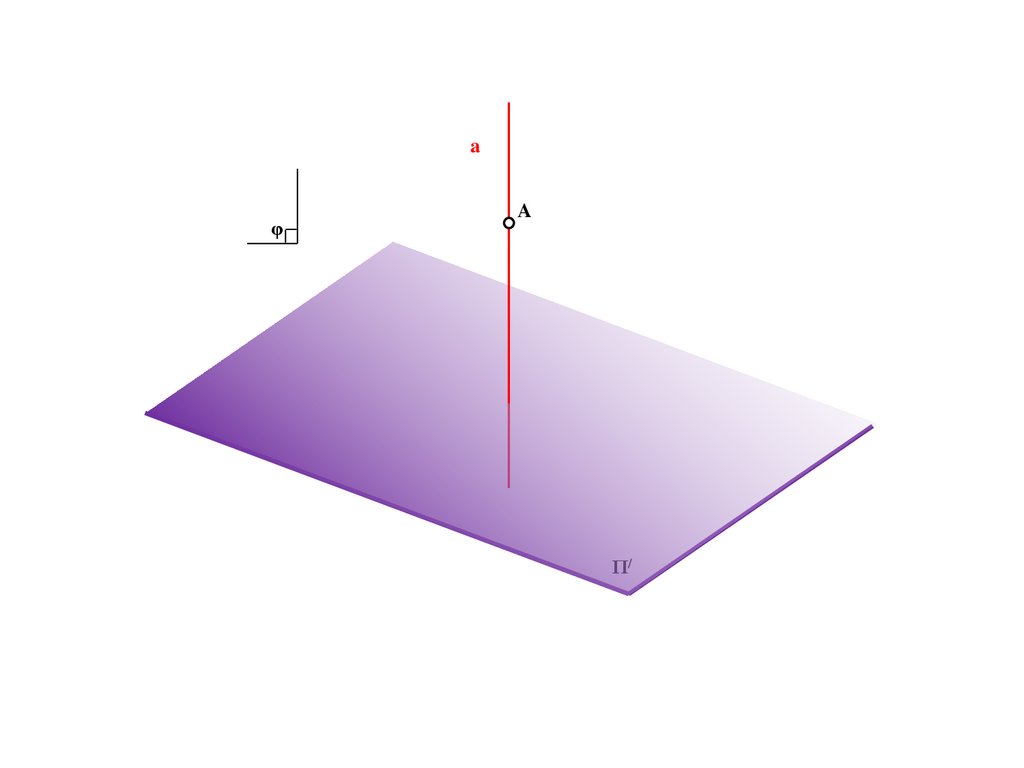
a
φ
A
Π/

143.

a
φ
A
A/
Π/

144.

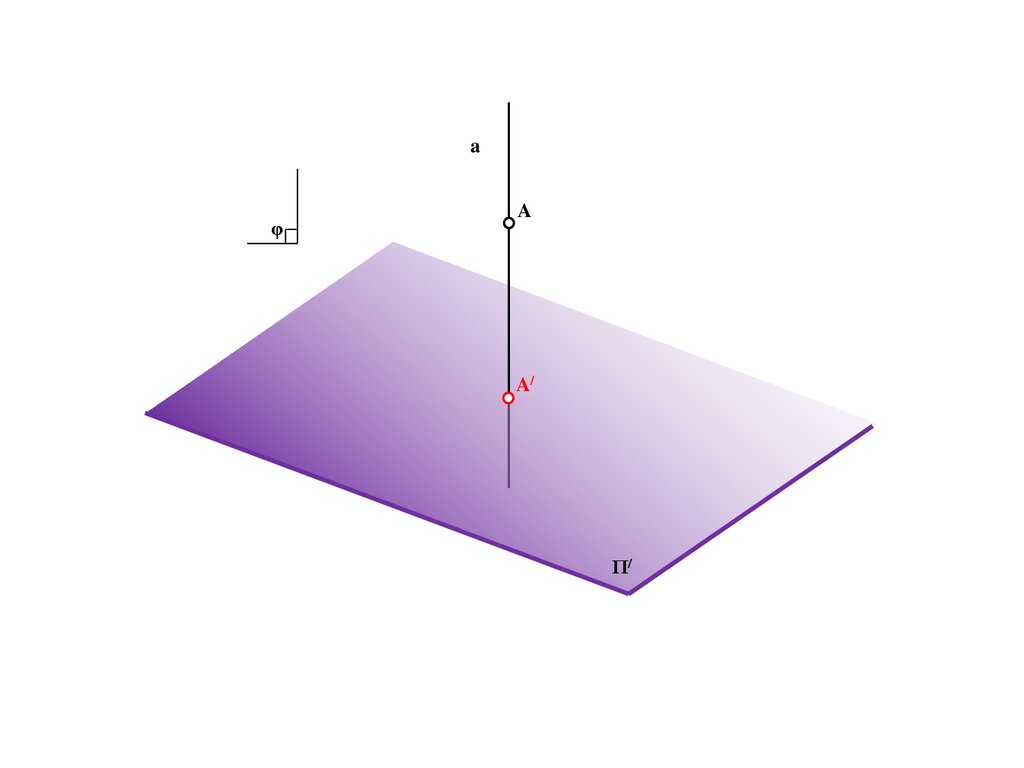
a
φ
A
A/
Π/

145.

B
A
Π/

146.

B
A
Π/

147.

B
A
A/
B/
Π/

148.

B
A
A/
B/
Π/

149.

B
A
A/
B/
Π/

150.

B
A
A/
B/
Π/

151.

B
C
A
A/
B/
Π/

152.

B
A
C
A/
B/=C/
Π/

153.

B
A
A/
α
C
B/=C/
Π/

154.

B
A
A/
α
C
B/=C/
Π/

155.

Пути получения обратимого отображения
трёхмерного пространства на плоскость

156.

S
Π/

157.

S
A
Π/

158.

a
S
A
Π/

159.

a
S
A
A/
Π/

160.

a
S
A
B/
A/
Π/

161.

b
a
S
A
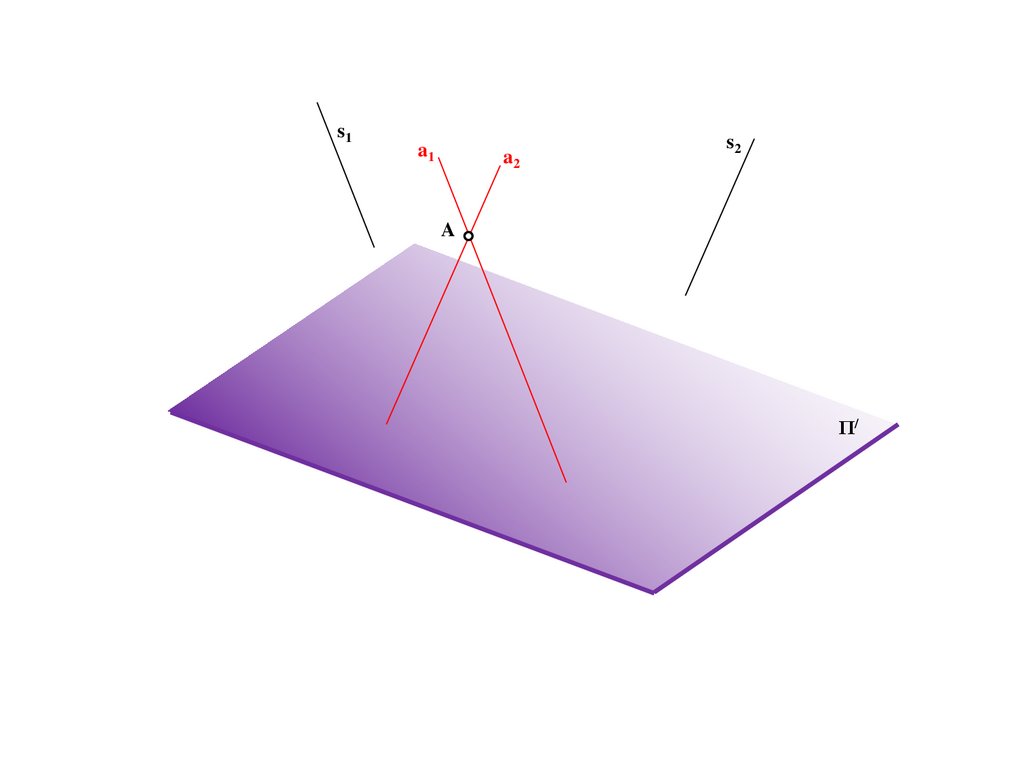
B/
A/
Π/

162.

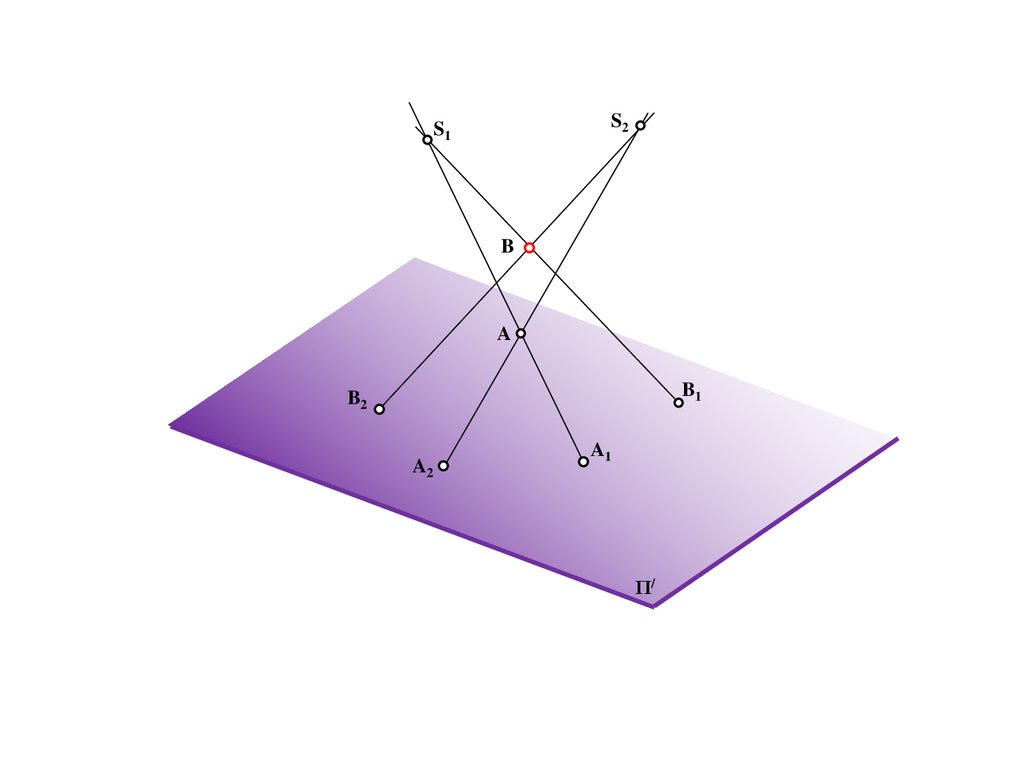
B
a
b
S
B
A
B=B/
A/
B
Π/

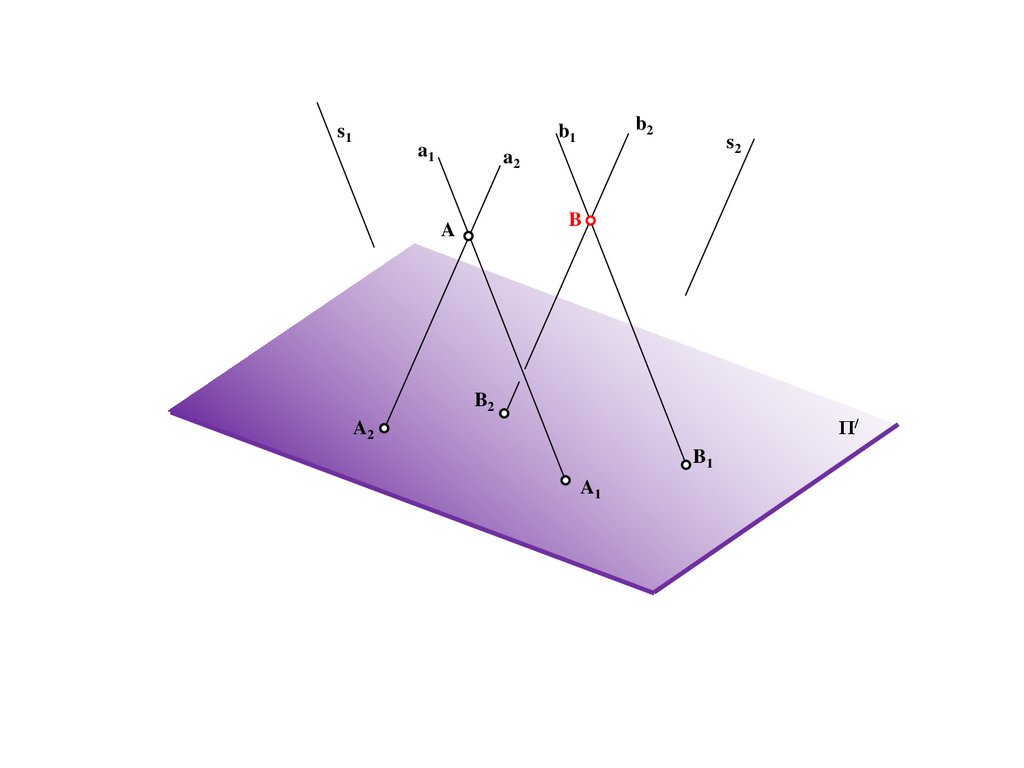
163.

B
a
b
S
B
A
B=B/
A/
B
Π/

164.

s
Π/

165.

s
A
Π/

166.

a
s
A
Π/

167.

a
s
A
A/
Π/

168.

a
s
A
A/
B/
Π/

169.

a
b
s
A
A/
B/
Π/

170.

a
b
B
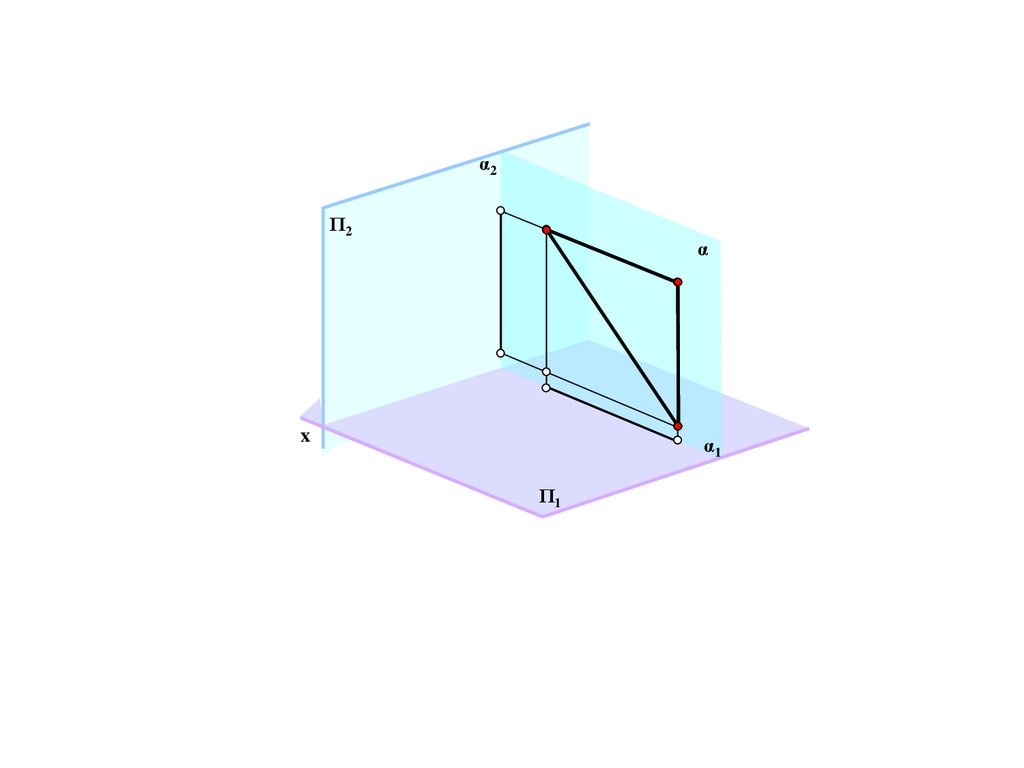
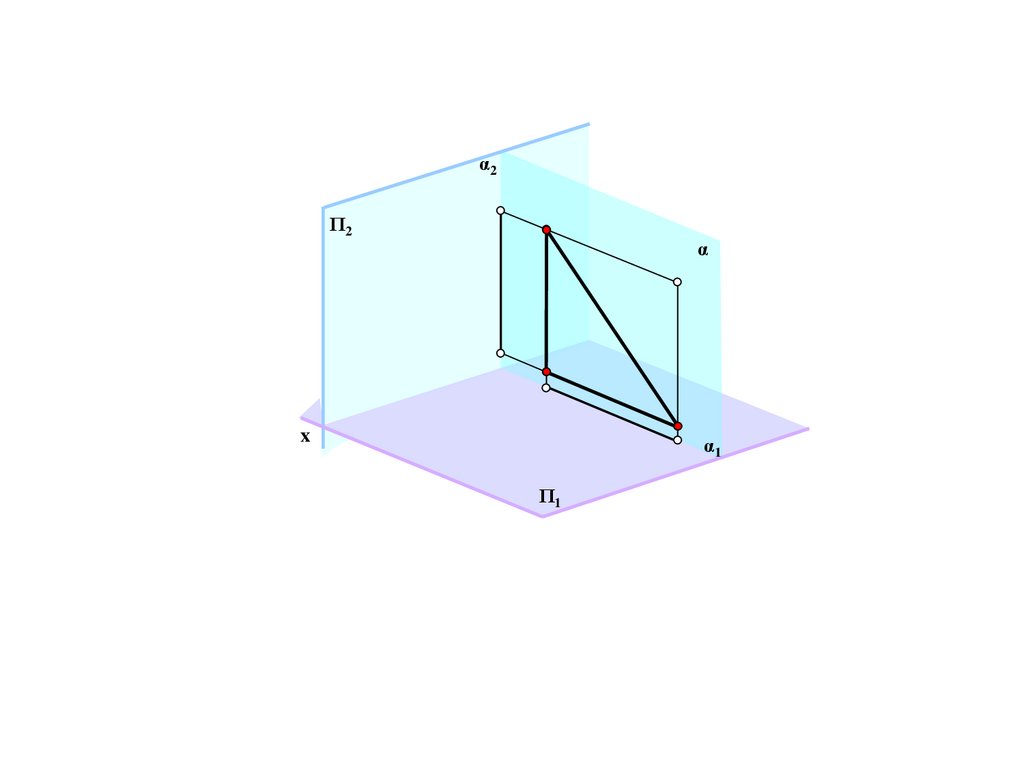
s
A
B
A/
B/=B
Π/
B

171.

a
b
B
s
A
B
A/
B/=B
Π/
B

172.

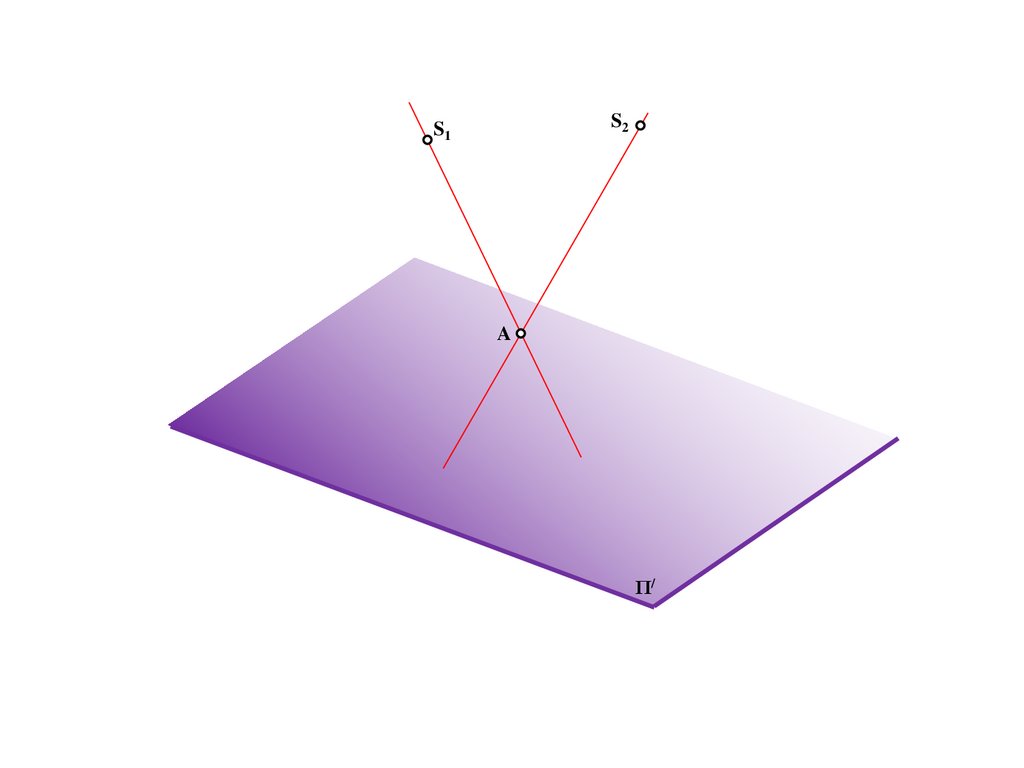
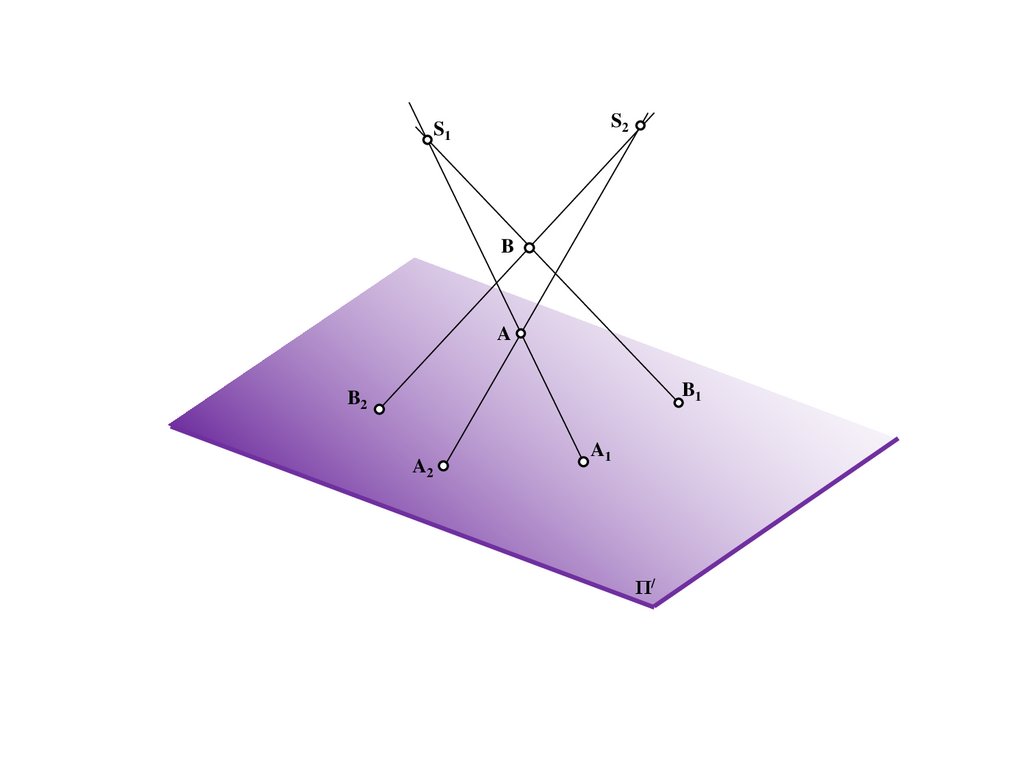
S1
S2
Π/

173.

S2
S1
A
Π/

174.

S2
S1
A
Π/

175.

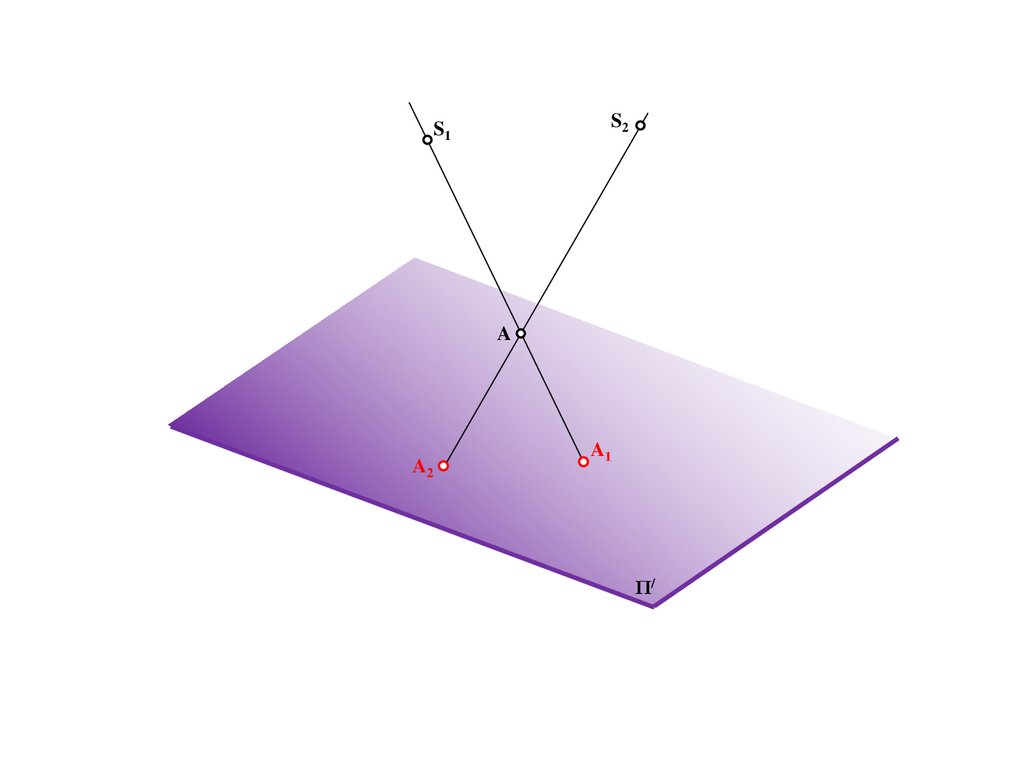
S2
S1
A
A2
A1
Π/

176.

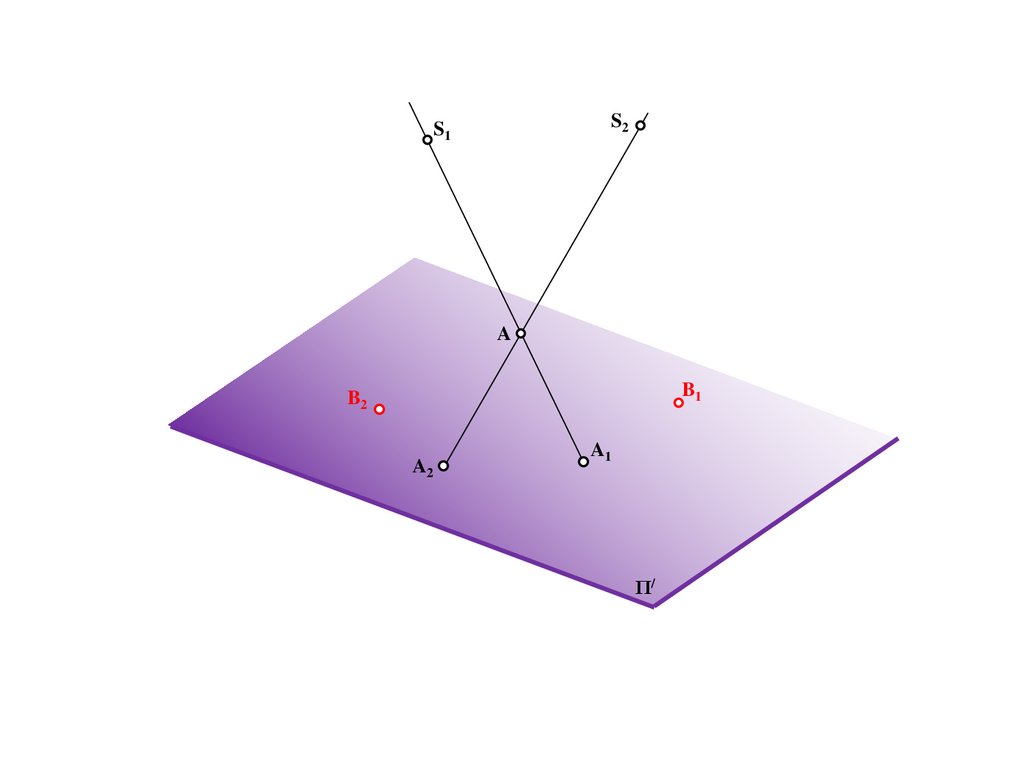
S2
S1
A
B1
B2
A2
A1
Π/

177.

S2
S1
A
B1
B2
A2
A1
Π/

178.

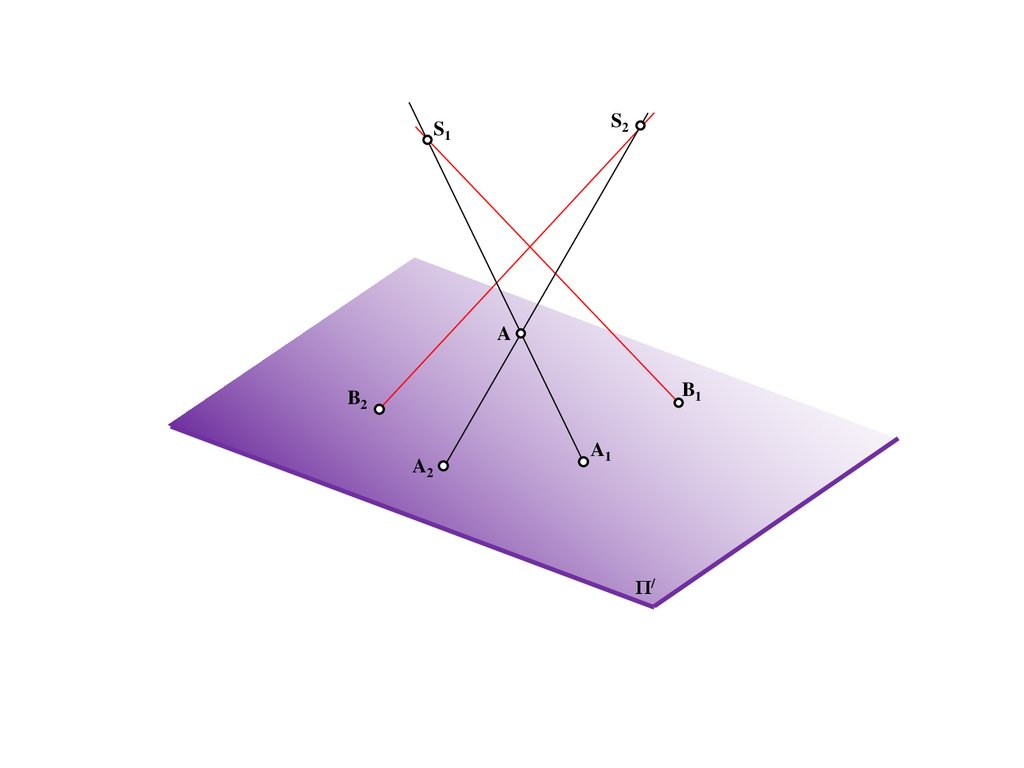
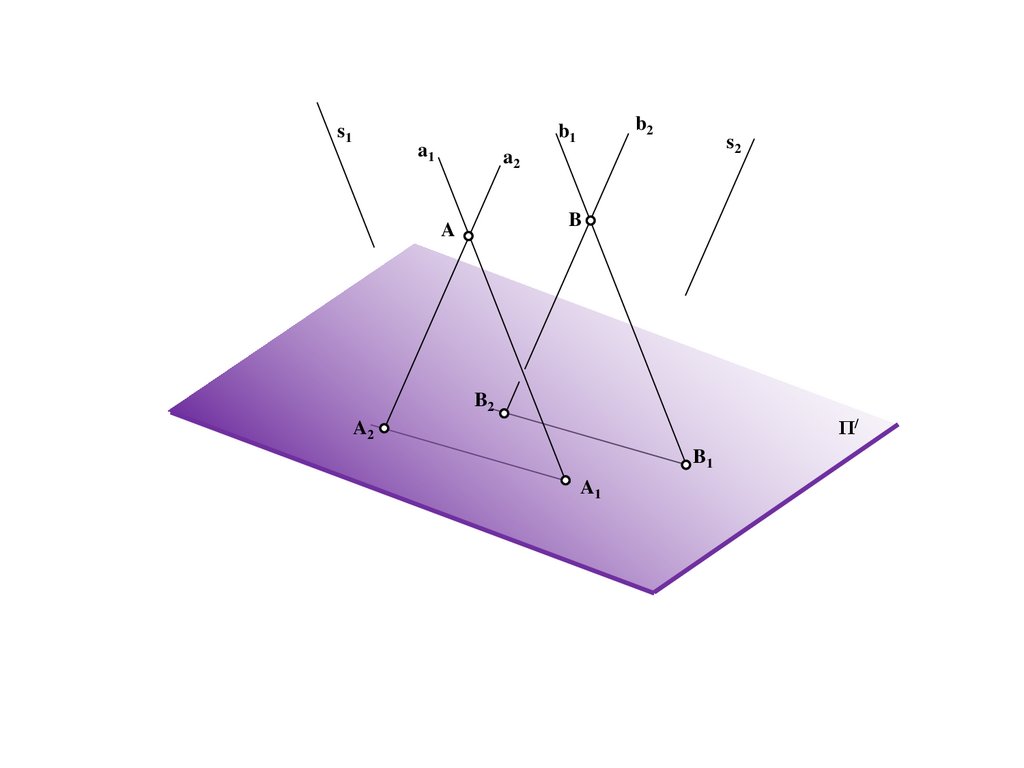
S2
S1
B
A
B1
B2
A2
A1
Π/

179.

S2
S1
B
A
B1
B2
A2
A1
Π/

180.

s1
s2
Π/

181.

s1
s2
A
Π/

182.

s1
a1
a2
s2
A
Π/

183.

s1
a1
s2
a2
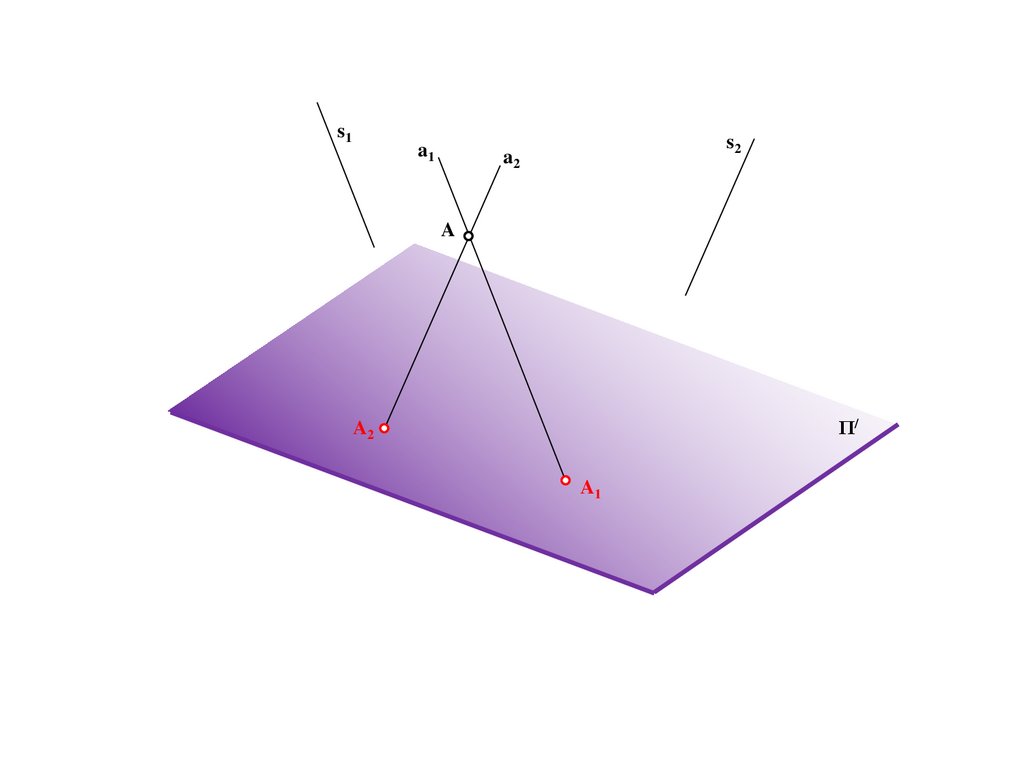
A
Π/
A2
A1

184.

s1
a1
s2
a2
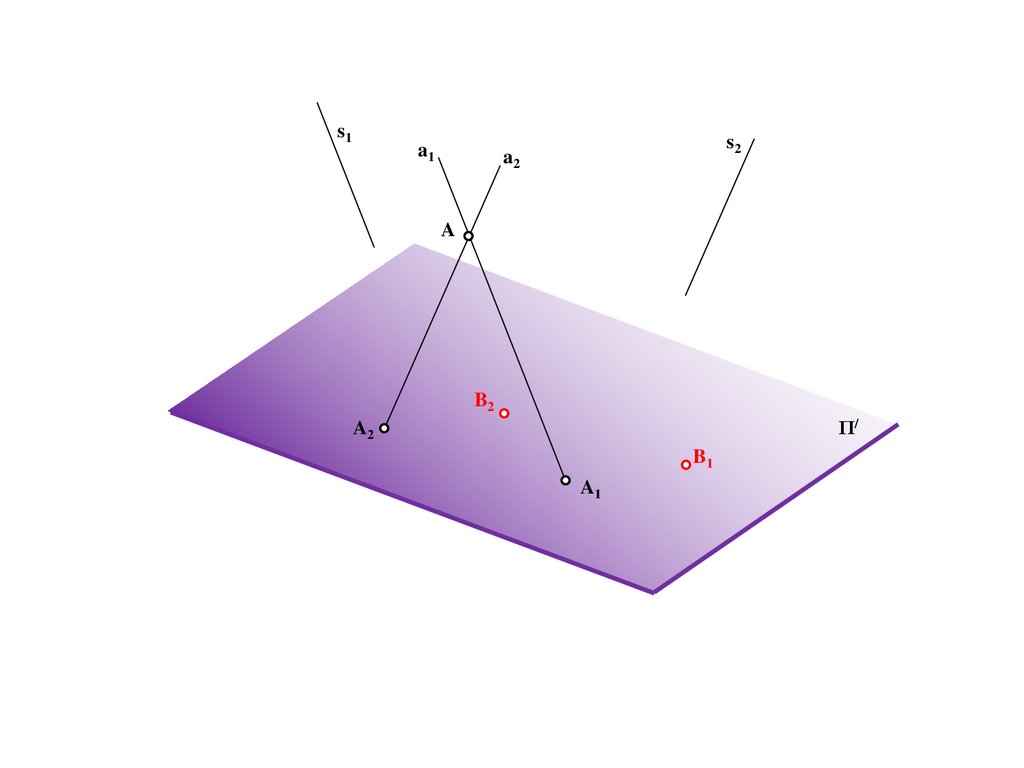
A
B2
Π/
A2
B1
A1

185.

s1
b2
b1
a1
s2
a2
A
B2
Π/
A2
B1
A1

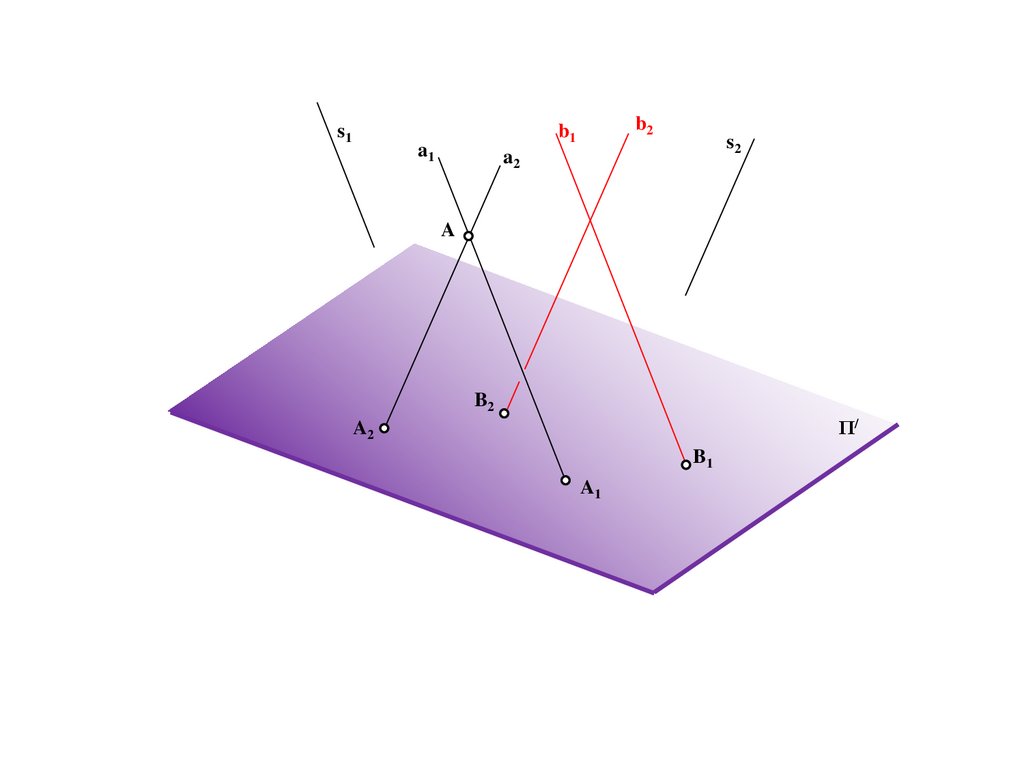
186.

s1
b2
b1
a1
s2
a2
B
A
B2
Π/
A2
B1
A1

187.

s1
b2
b1
a1
s2
a2
B
A
B2
Π/
A2
B1
A1

188.

Метод проекций с числовыми отметками

189.

M
Π/

190.

M
Π/

191.

M
M/
Π/

192.

M
A/
M/
Π/

193.

M
A/
M/
Π/

194.

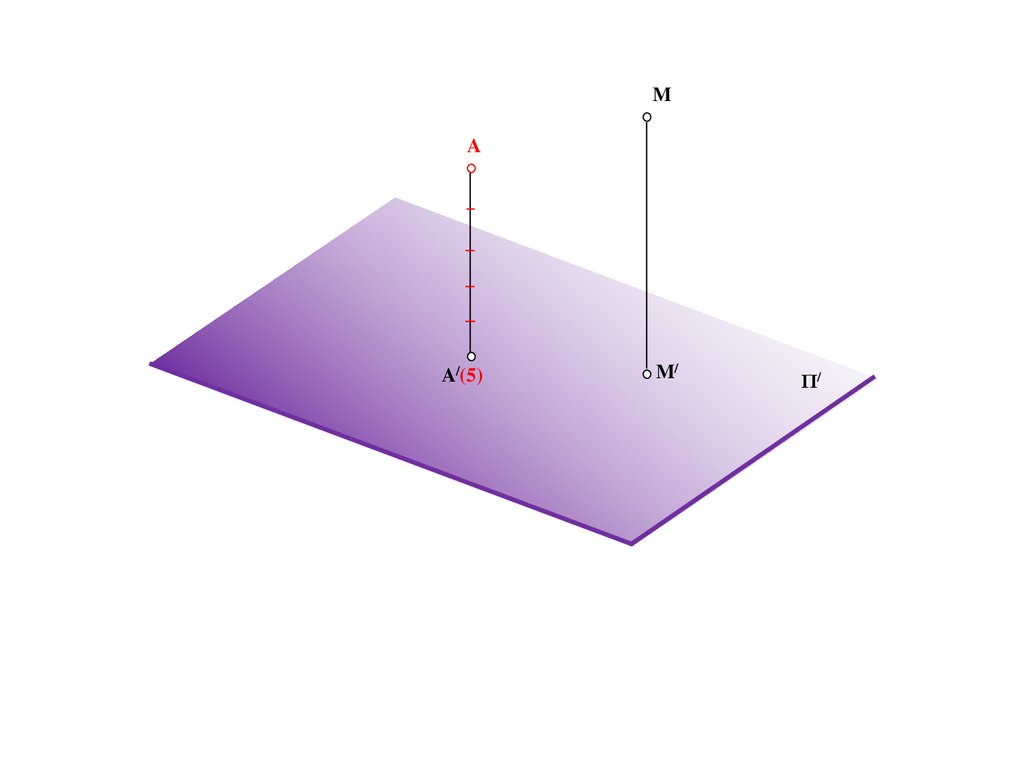
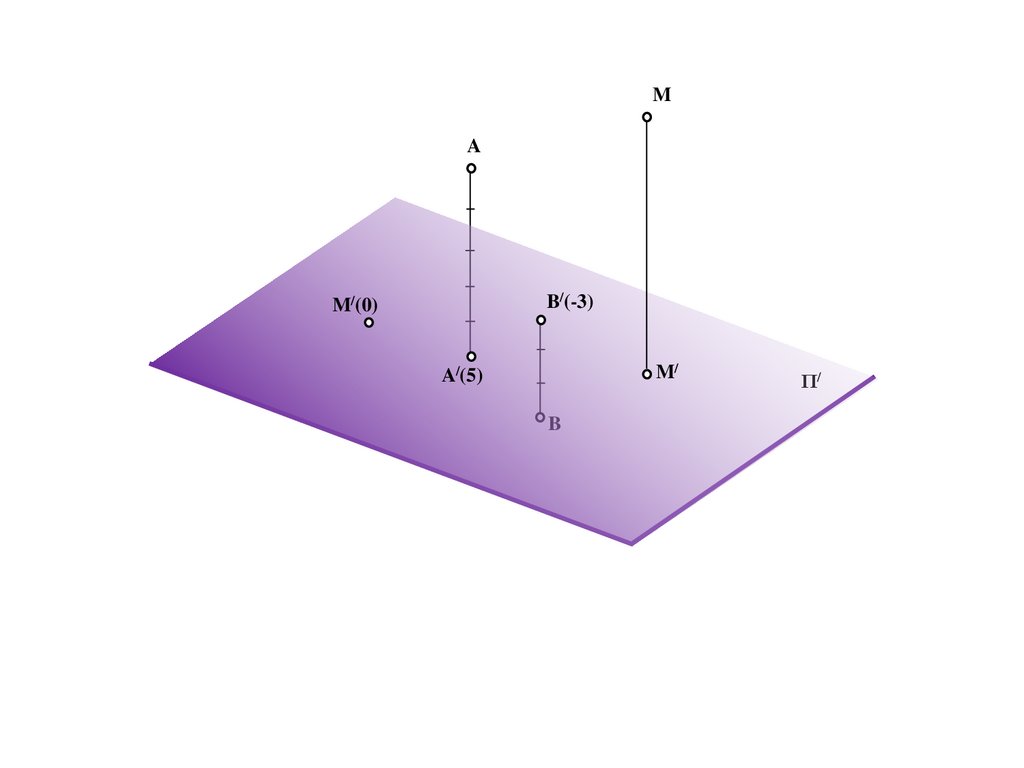
M
A/(5)
M/
Π/

195.

M
A
A/(5)
M/
Π/

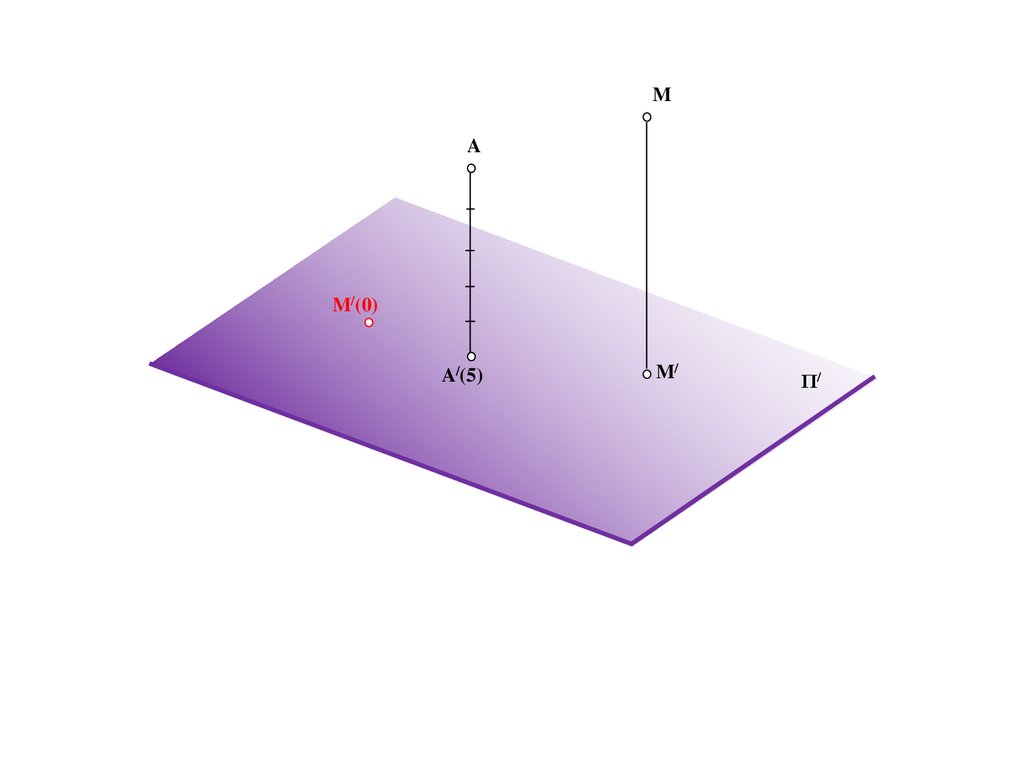
196.

M
A
M/(0)
A/(5)
M/
Π/

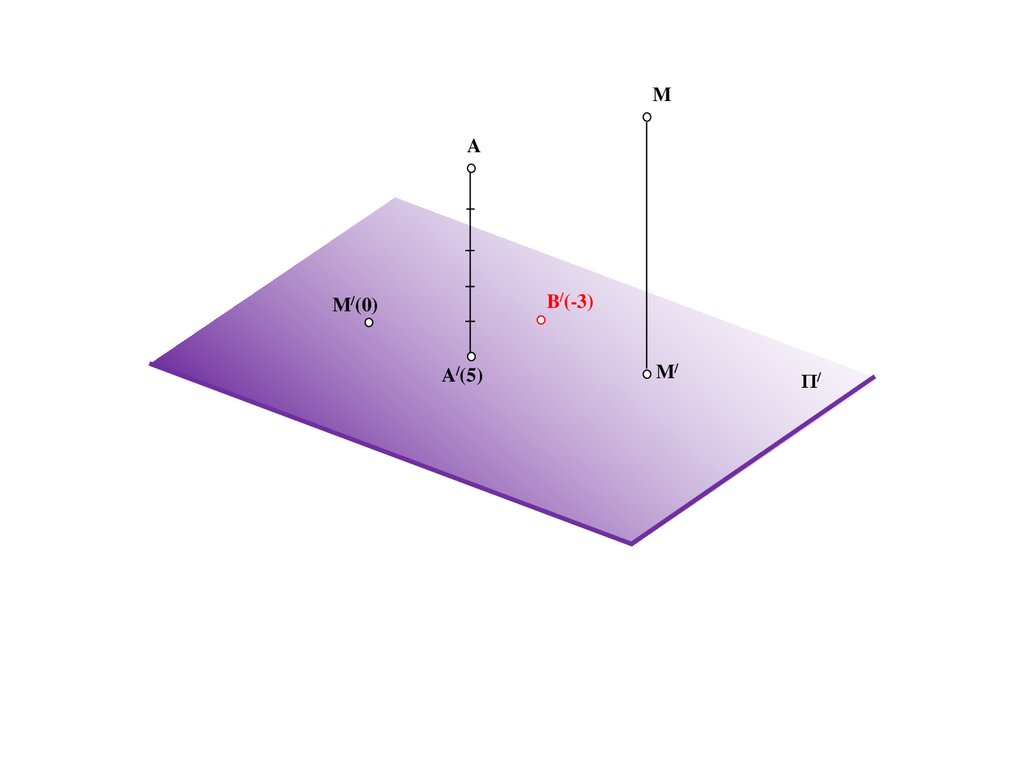
197.

M
A
B/(-3)
M/(0)
A/(5)
M/
Π/

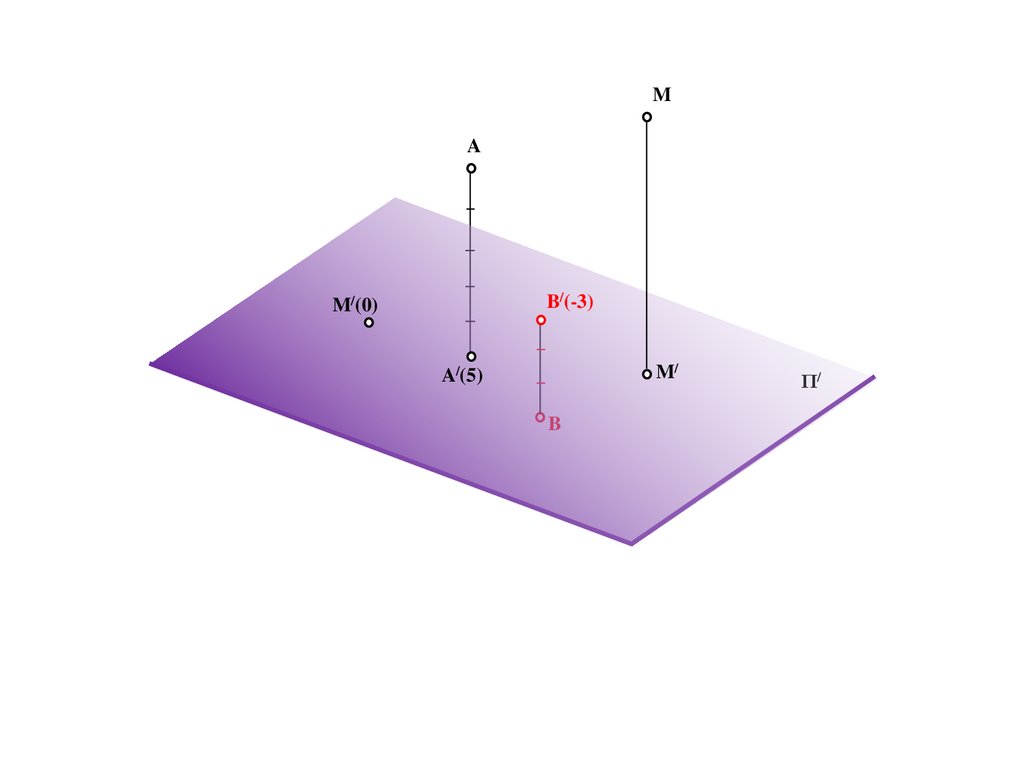
198.

M
A
B/(-3)
M/(0)
M/
A/(5)
B
Π/

199.

M
A
B/(-3)
M/(0)
M/
A/(5)
B
Π/

200.

Метод Монжа

201.

Ортогональное проецирование
на две взаимно
перпендикулярные плоскости

202.

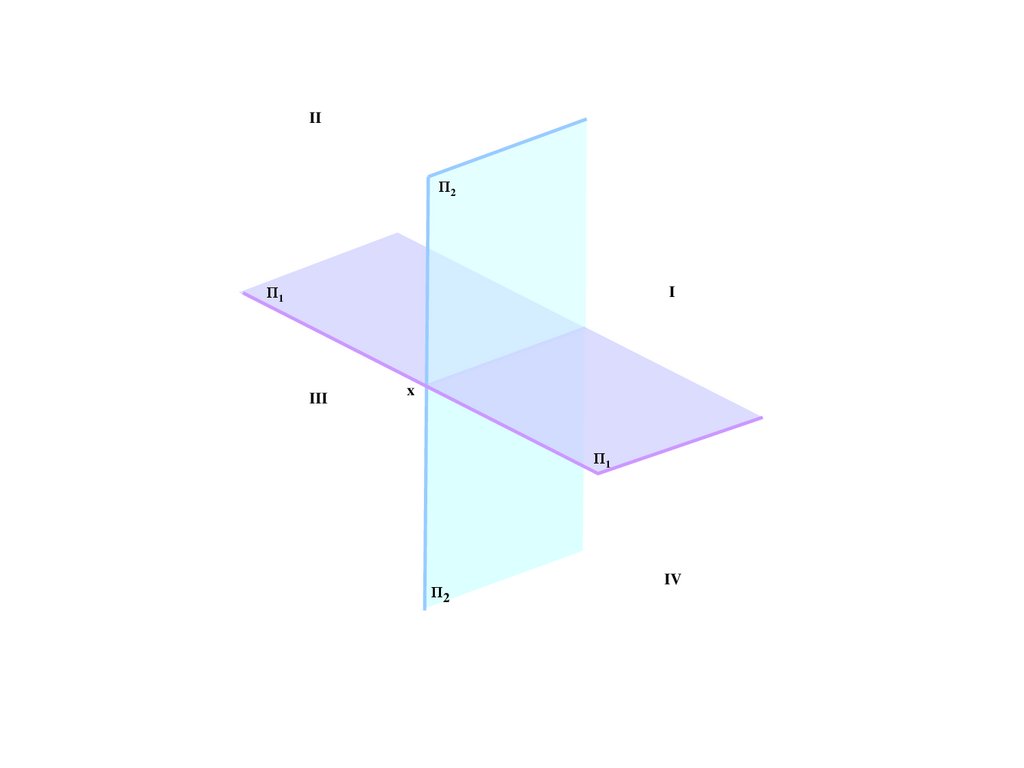
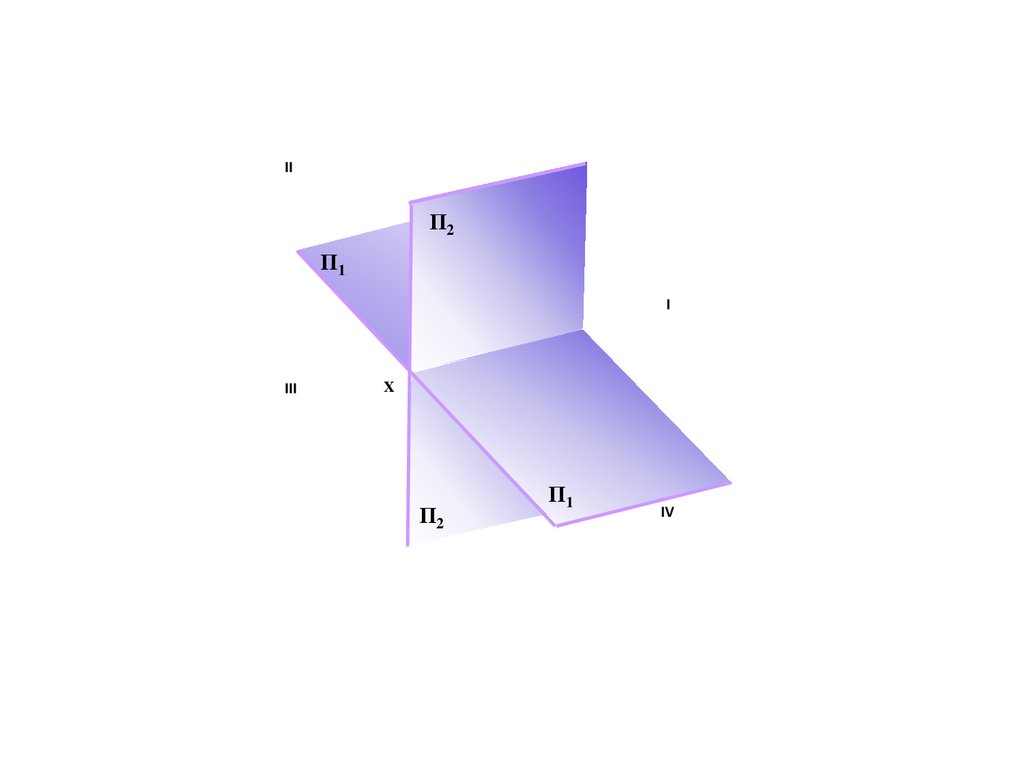
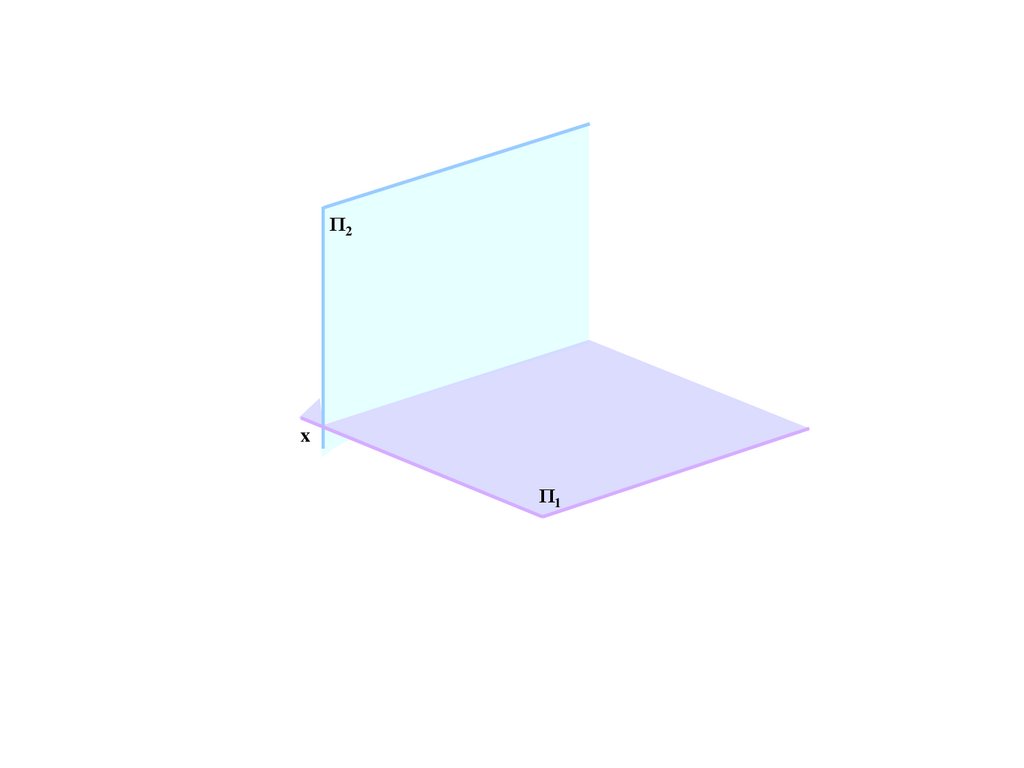
II
Π2
Π1
I
III
x
Π1
Π2
IV

203.

Π2
A
x
Π1

204.

Π2
a
A
x
Π1

205.

Π2
a
A
x
A1
Π1

206.

Π2
a
A
b
x
A1
Π1

207.

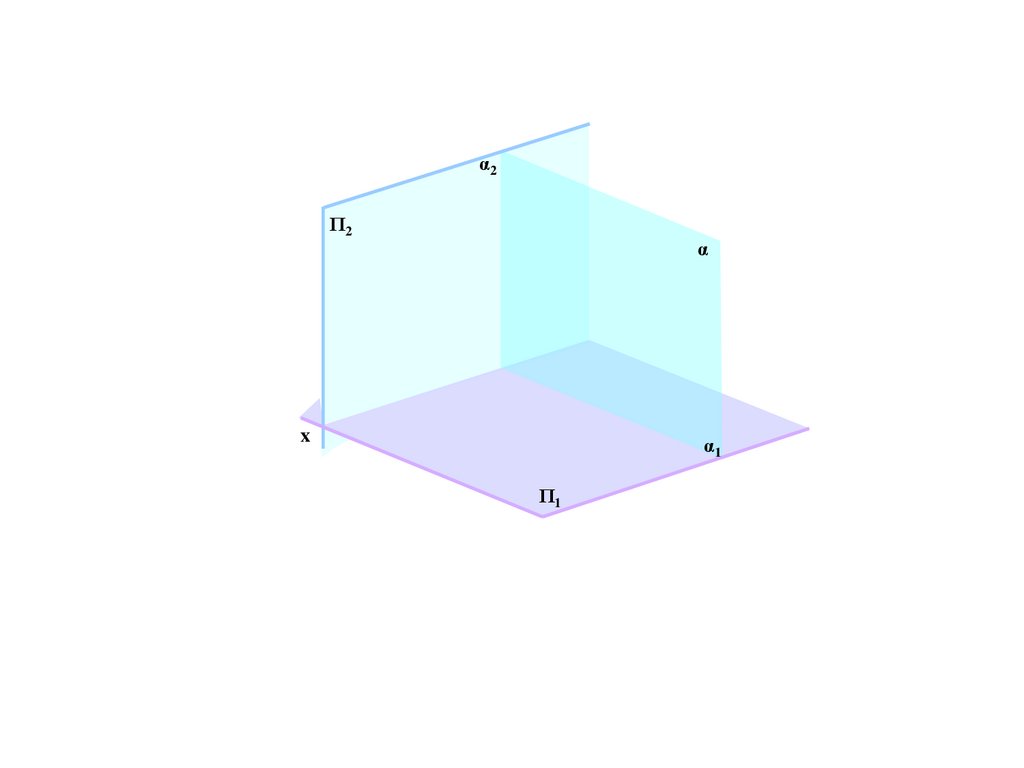
α2
Π2
a
α
A
b
Ax
x
A1
Π1
α1

208.

α2
Π2
A2
a
α
A
b
Ax
x
A1
Π1
α1

209.

Π2
A2
a
α
A
b
Ax
x
A1
Π1

210.

Π2
A2
A
B2
Ax
x
A1
B1
Π1

211.

Π2
A2
A
B2
Ax
x
A1
B1
Π1

212.

Π2
A2
A
B2
Ax
B
x
A1
B1
Π1

213.

Π2
A2
B2
Ax
Bx
x
A1
B1
Π1

214.

Π2
A2
B2
Ax
Bx
x
A1
B1
Π1

215.

A2
B2
x
Bx
Ax
B1
A1

216.

II
Π2
Π1
III
I
X
Π1
Π2
IV

217.

II
Π2
Π1
I
III
X
Π2
Π1
IV

218.

Π2 Π1
X
Π2 Π1

219.

X

220.

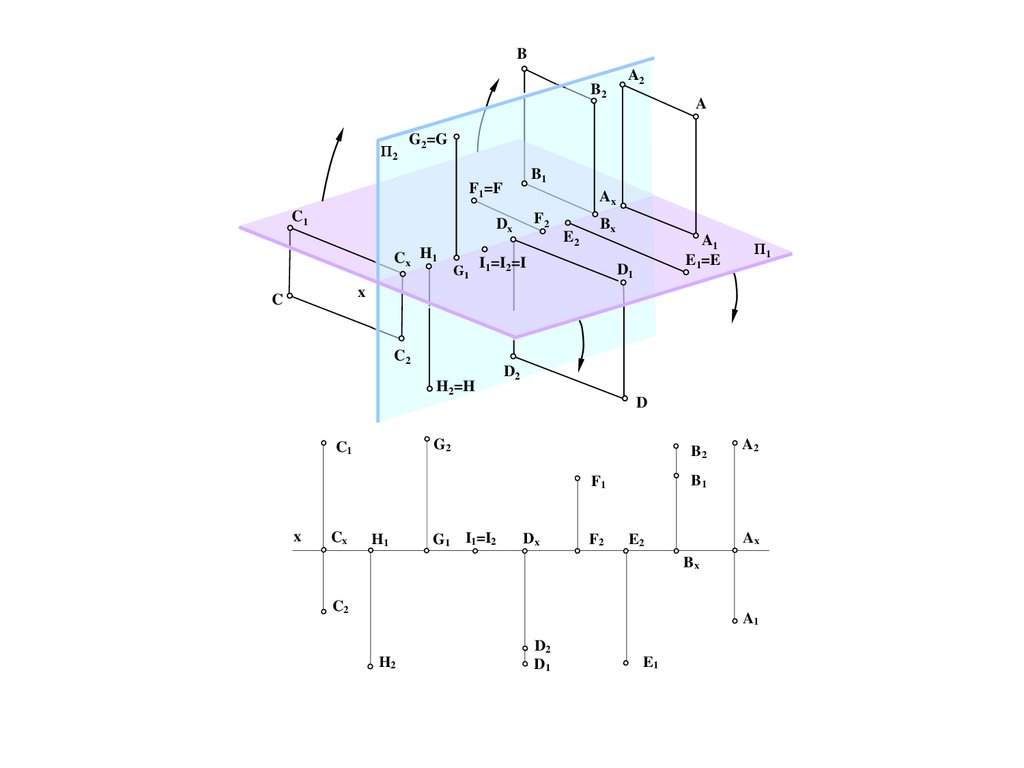
B
B
a)
B2
B2
Π2
C1
x
A
A
G2=G
B1
F1=F
Ax
B1
F1=F
A
Dx F2
Bx x
F2 E2
Bx
I1=I2=I
E2
Cx H1
I1=I2=I D
1
D1
x
Cx HG
1
D1
G1
C1
C
A2
G2=G
2
C
A2
A1
A
1
E1=E
E1=E
Π1
x
1
C2 C2
H2=H
H2=H
b)
D2D2
D
D
b)
G2
C1
B2
B1
F1
x
Cx
H1
G1 I1=I2
Dx
F2
A2
Ax
E2
Bx
C2
A1
D2
D1
H2
sur . 27
E1

221.

Ортогональное проецирование на три взаимно
перпендикулярные плоскости.
Координированный эпюр Монжа

222.

Π2
x
Π1

223.

α2
Π2
α
x
α1
Π1

224.

α2
Π2
α
x
α1
Π1

225.

α2
Π2
α
x
α1
Π1

226.

α2
Π2
α
x
α1
Π1

227.

α2
Π2
α
x
α1
Π1

228.

α2
Π2
α
x
α1
Π1

229.

α2
Π2
α
x
α1
Π1

230.

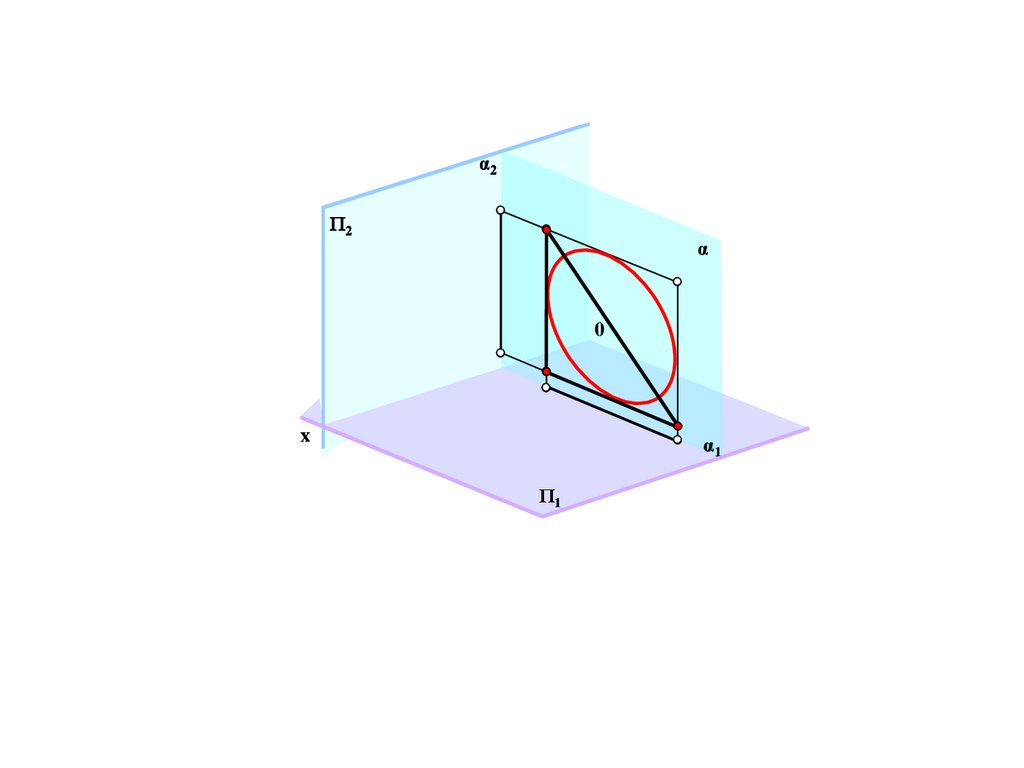
α2
Π2
α
0
x
α1
Π1

231.

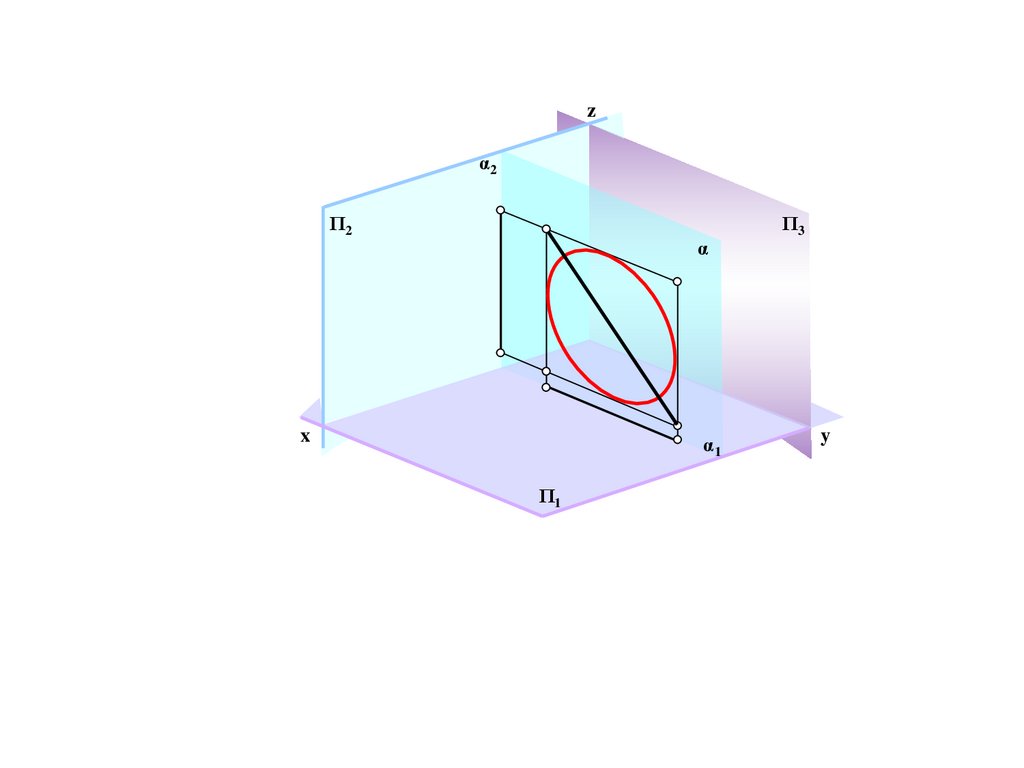
z
α2
Π2
α
x
α1
Π1
Π3
y

232.

z
Π2
α
Π3
0
x
y
Π1

233.

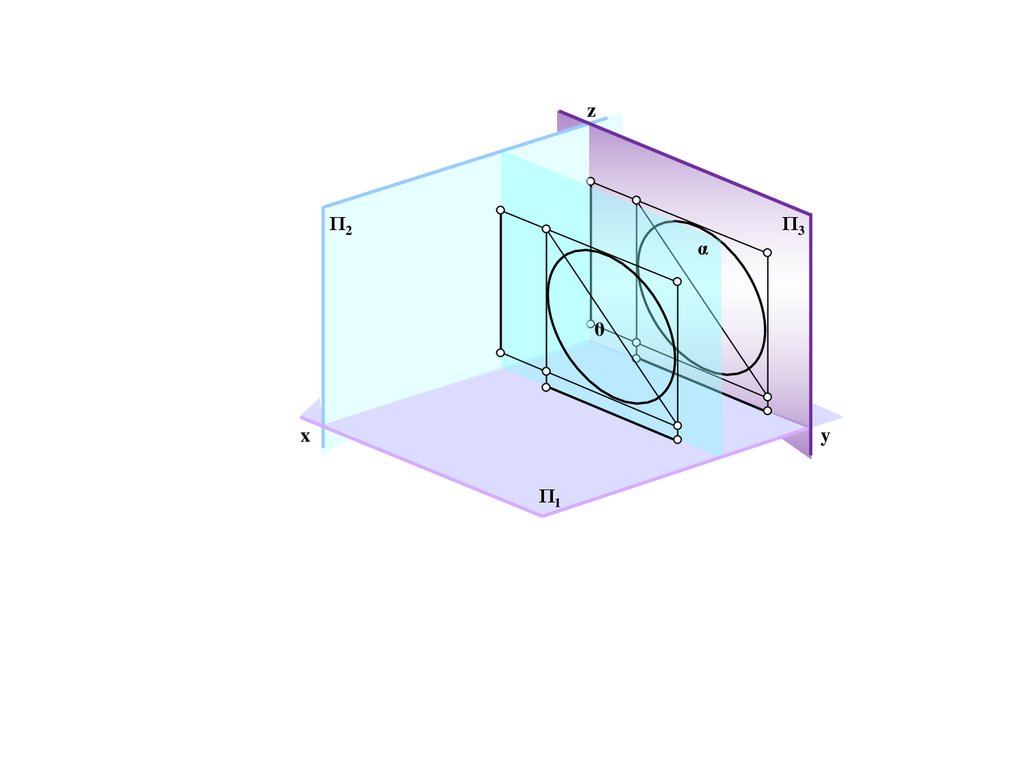
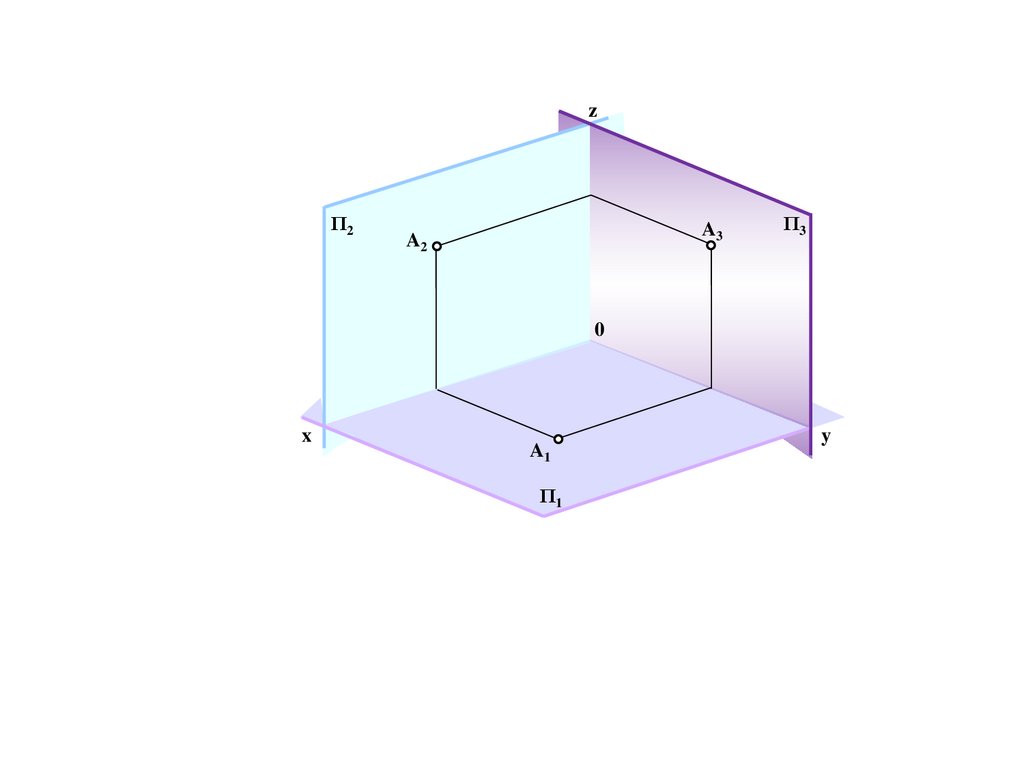
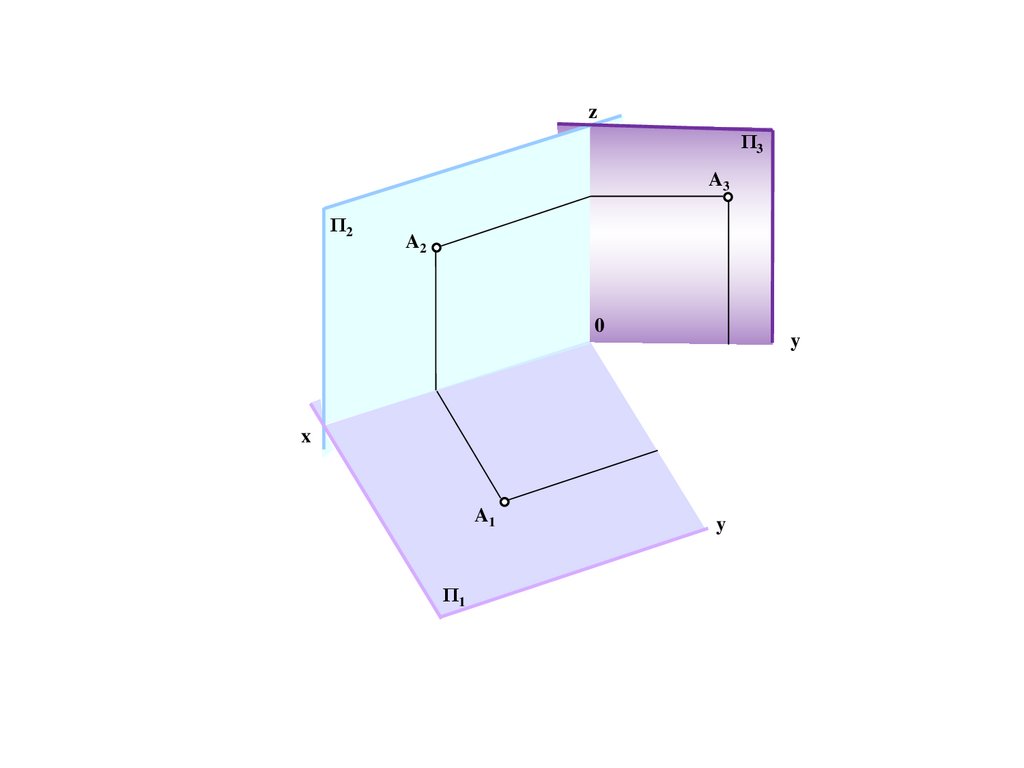
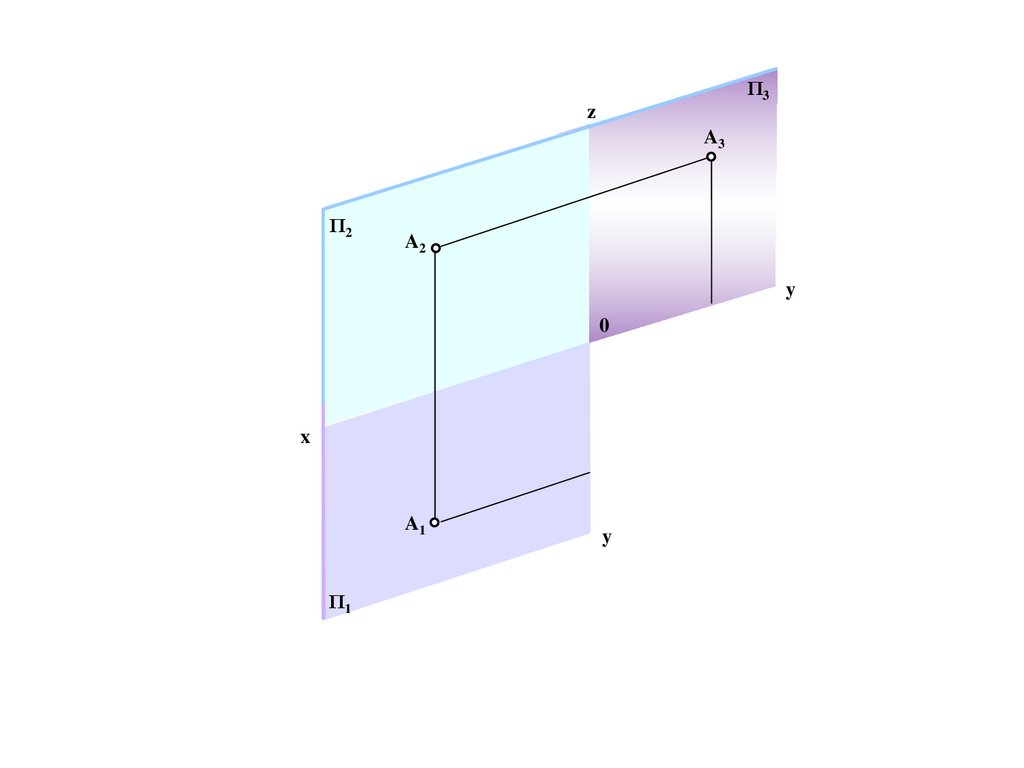
Проекция точки на три взаимно
перпендикулярные плоскости.
Координированный эпюр Монжа

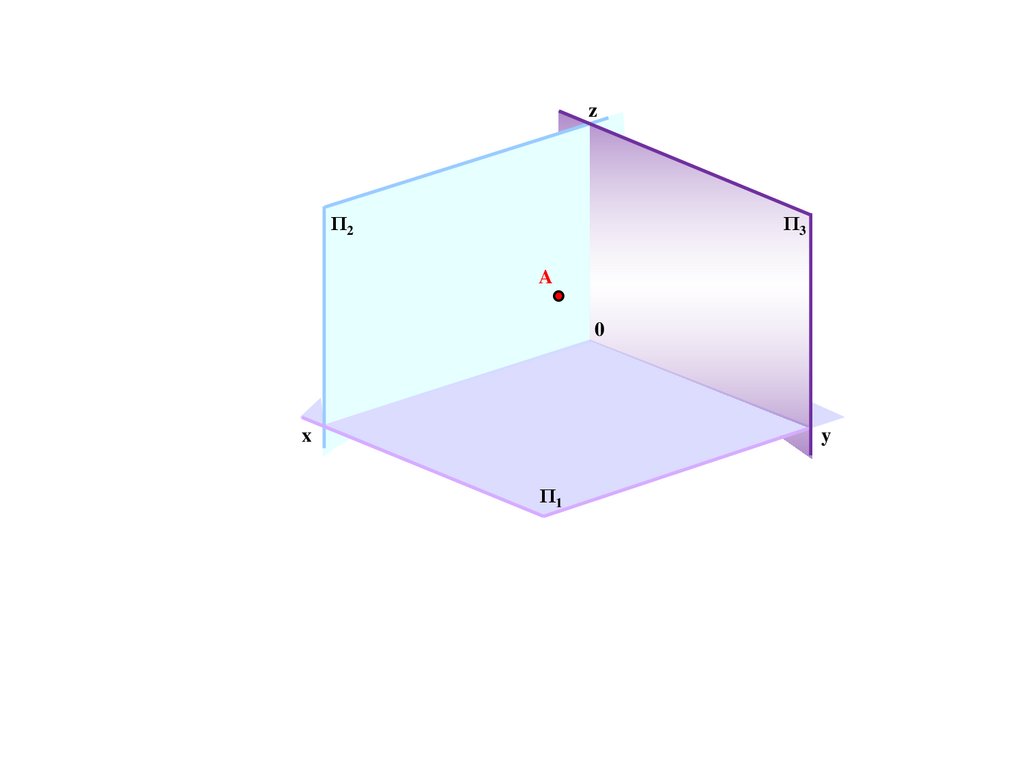
234.

z
Π3
Π2
A
0
x
y
Π1

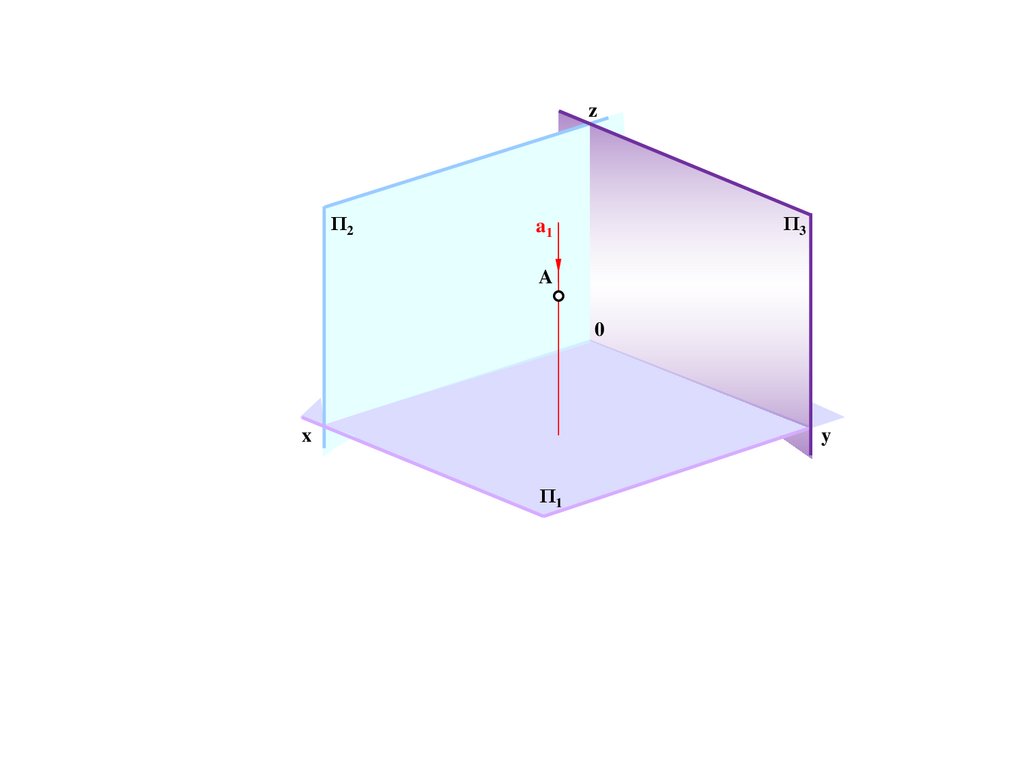
235.

z
Π2
Π3
a1
A
0
x
y
Π1

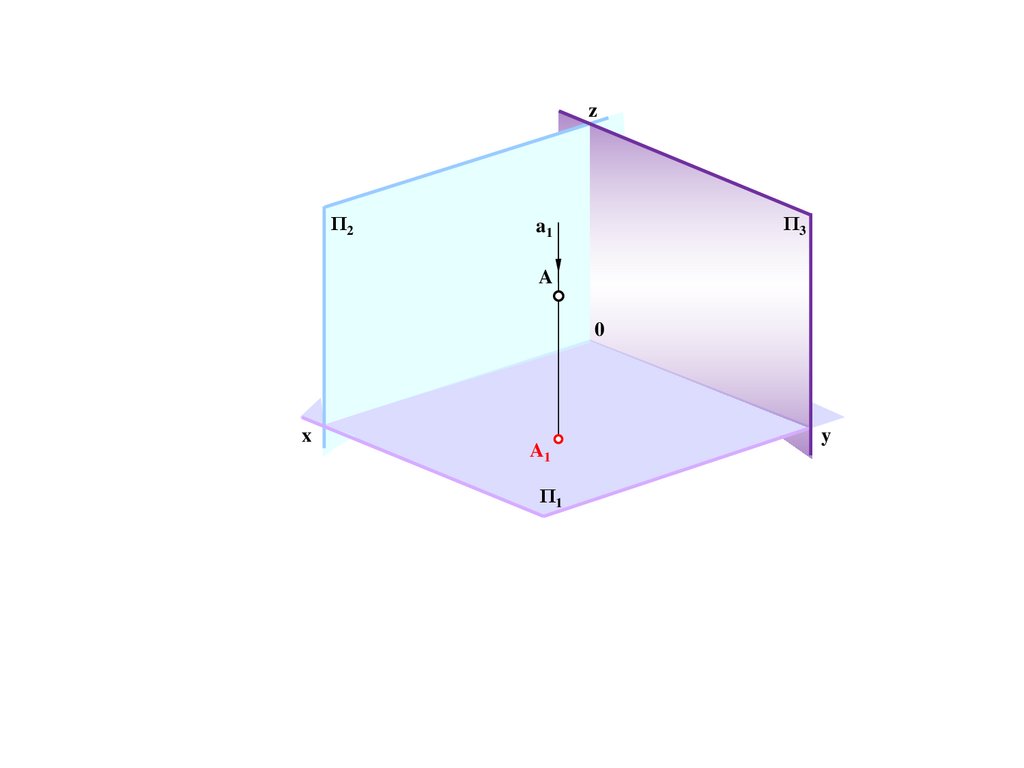
236.

z
Π2
Π3
a1
A
0
x
A1
Π1
y

237.

z
Π2
Π3
a1
A
a2
0
x
A1
Π1
y

238.

z
Π2
Π3
a1
α
A
a2
0
x
A1
Π1
y

239.

z
Π2
Π3
a1
α
A
a2
0
x
A1
Π1
y

240.

z
Π2
A2
Π3
a1
α
A
a2
0
x
A1
Π1
y

241.

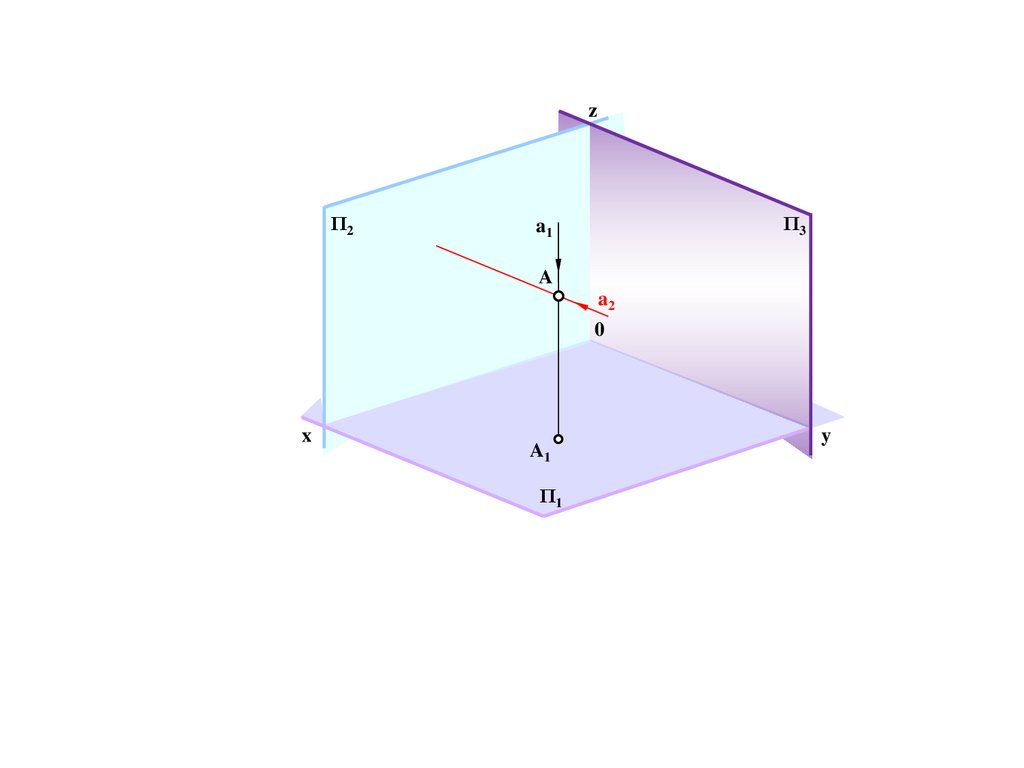
z
Π2
A2
Π3
a1
β
A
a2
a3
0
x
A1
Π1
y

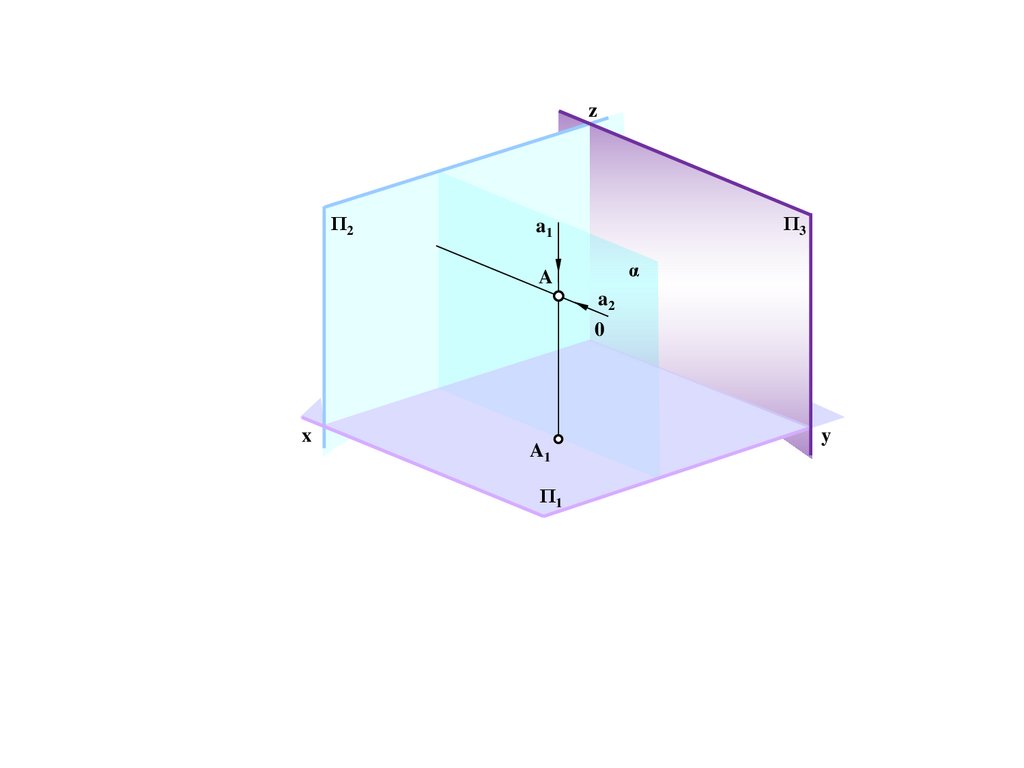
242.

z
Π2
A2
Π3
a1
β
A
a2
a3
0
x
A1
Π1
y

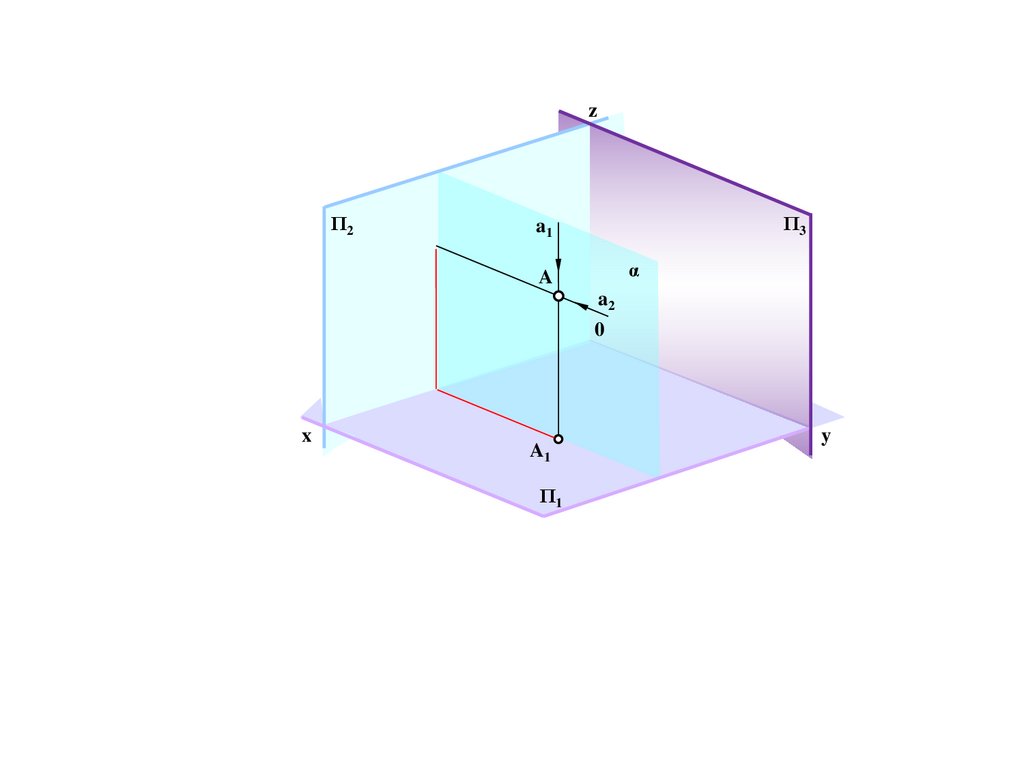
243.

z
Π2
A2
a1
A3
Π3
β
A
a2
a3
0
x
A1
Π1
y

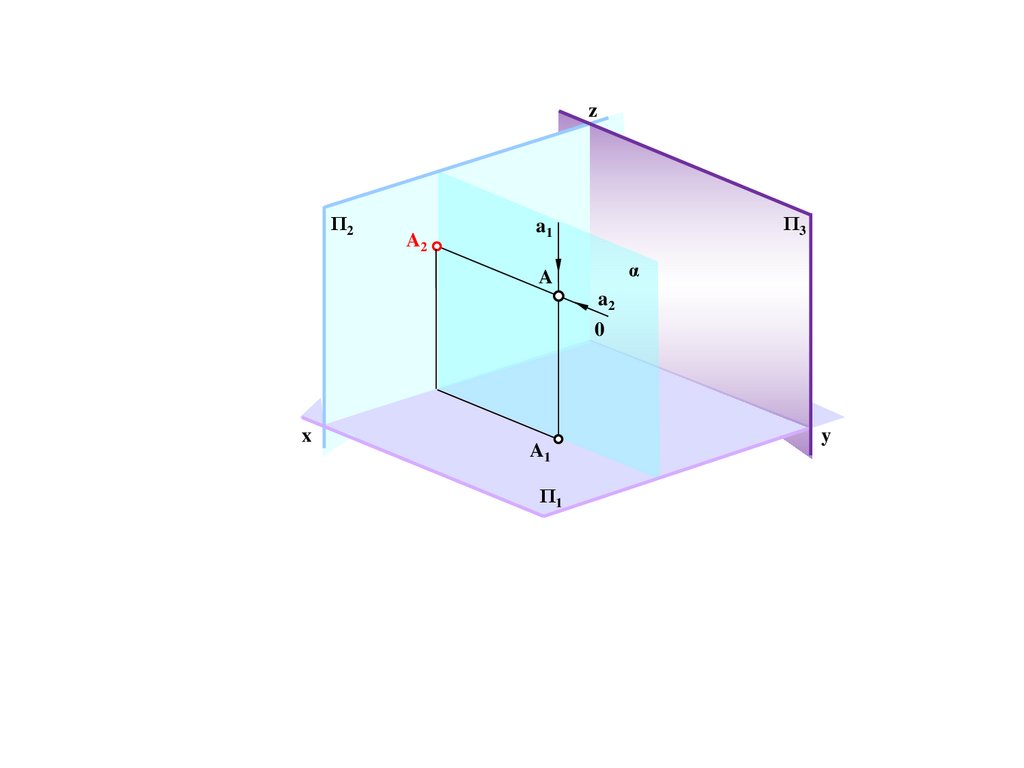
244.

z
Π2
a1
A2
A3
Π3
A
a2
a3
0
x
A1
Π1
y

245.

z
Π2
A3
A2
Π3
0
x
A1
Π1
y

246.

z
Π3
A3
Π2
A2
0
y
x
A1
Π1
y

247.

Π3
z
A3
Π2
A2
y
0
x
A1
Π1
y

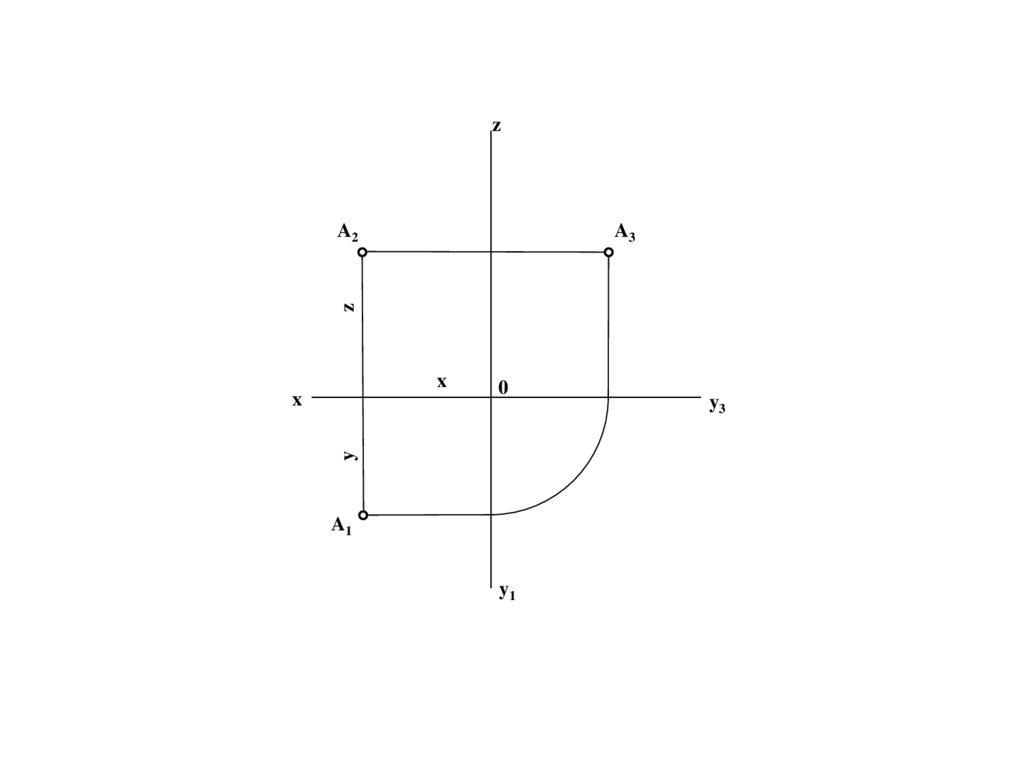
248.

z
A3
z
A2
x
0
y
x
A1
y1
y3

249.

КОНЕЦ

250.

251.

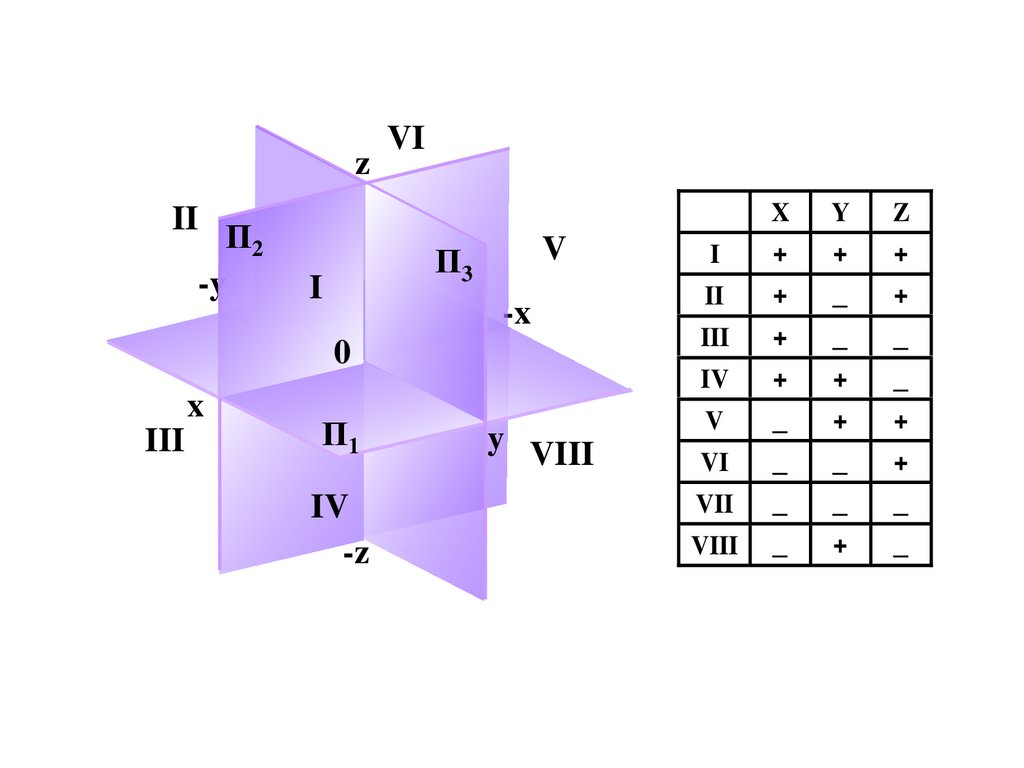
zz
VI
VI
II
Π2 2
-y-y
II
Π3
3
I
0
x
Π1
III
x
III
0
IV
1
-z
V
I
X
+
-x V
II
+
_
+
III
+
_
_
IV
+
+
_
-x
Y
+
Z
+
y VIII
V
_
+
+
VI
_
_
+
y VIII
VII
_
_
_
VIII
_
+
_
c xr . 1
-z
IV