Линейное программирование

1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

2.

Общей задачей линейного программирования
называется
задача,
в
которой
нужно
минимизировать или максимизировать F = с1х1 +
с2х2 + … сNxN, при условиях:
a11x1 + a12x2 + a1NxN <= b1
a21x1 + a22x2 + a2NxN <= b2
as1x1 + as2x2 + asNxN = bs
am1x1 + am2x2 + amNxN = bm
x1, x2, … xm >=0

3.

Вектор
x x1, x2 ,..., xn
координаты
которого
удовлетворяют
ограничениям,
называется допустимым решением задачи.
Множество допустимых решений задачи называют
областью допустимых решений.
Допустимое решение, на котором целевая функция достигает
своего максимума (минимума), называется оптимальным
решением или оптимальным планом задачи ЛП.

4. Составим математические модели некоторых задач линейного программирования

5.

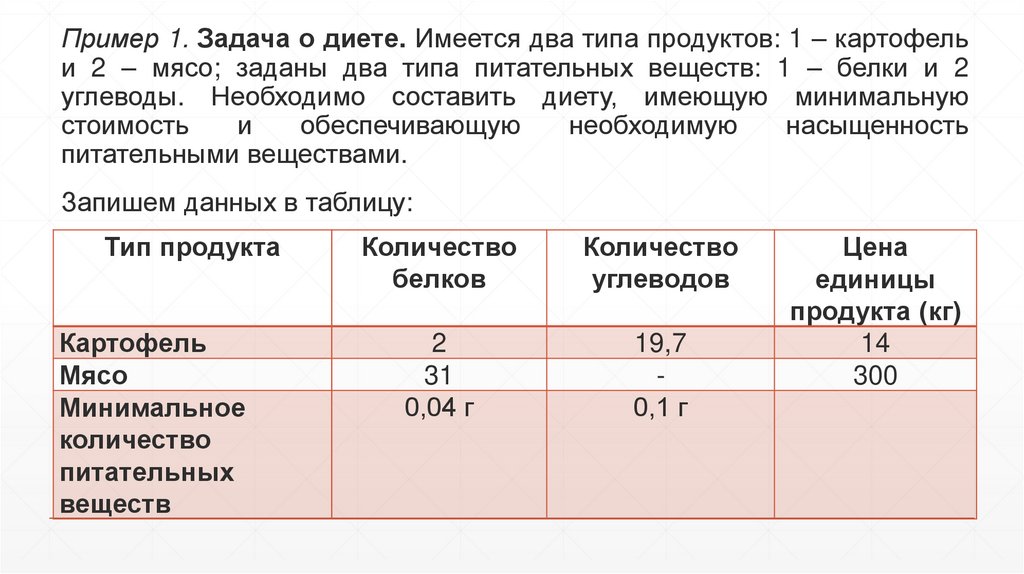
Пример 1. Задача о диете. Имеется два типа продуктов: 1 – картофель
и 2 – мясо; заданы два типа питательных веществ: 1 – белки и 2
углеводы. Необходимо составить диету, имеющую минимальную
стоимость
и
обеспечивающую
необходимую
насыщенность
питательными веществами.
Запишем данных в таблицу:
Тип продукта
Картофель
Мясо
Минимальное
количество
питательных
веществ
Количество
белков
Количество
углеводов
2
31
0,04 г
19,7
0,1 г
Цена
единицы
продукта (кг)
14
300

6.

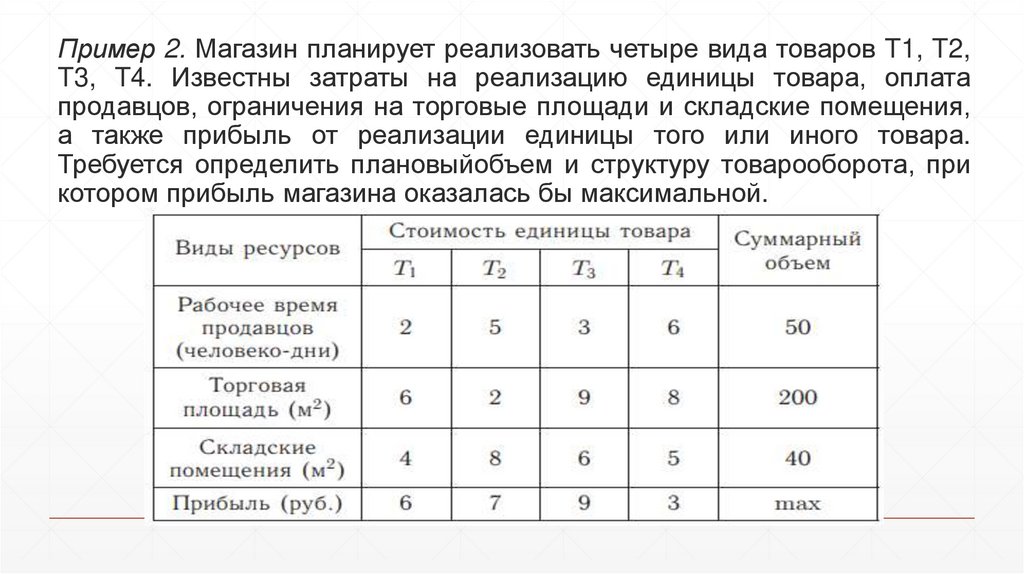
Пример 2. Магазин планирует реализовать четыре вида товаров T1, T2,
T3, T4. Известны затраты на реализацию единицы товара, оплата
продавцов, ограничения на торговые площади и складские помещения,
а также прибыль от реализации единицы того или иного товара.
Требуется определить плановыйобъем и структуру товарооборота, при
котором прибыль магазина оказалась бы максимальной.

7. Графический метод решения ЗЛП

Рассмотрим задачу линейного программирования с
двумя переменными

8. Алгоритм графического решения задачи линейного программирования состоит в выполнении следующих действий.

1. Построить ОДР.
2. Построить вектор нормали n = (c1, c2) целевой
функции (он указывает на направление возрастания
целевой функции).
3. Построить нижнюю и верхнюю опорные прямые p и
q, т. е. крайние линии уровня целевой функции,
имеющие общие точки с ОДР.
4. Определить координаты экстремальных точек (P
= p ∩ ОДР, Q = q ∩ ОДР) и вычислить значения
целевой функции в них.

9.

Примечания.
1. Если ОДР — пустое множество, то задача не имеет
решения ввиду несовместности системы ограничений.
2. Если ОДР не ограничена по направлению вектора n =
(c1, c2), то сама целевая функция не ограничена сверху
в этой области, и принимаем Lmax(X) = +∞. Если ОДР не
ограничена в направлении, противоположном n, то
принимаем Lmin(X) = -∞.

10.

11. Задача 1

Решим
графически
задачу
ЛП,
экономикоматематическая модель которой была составлена
заранее.

12. Задача 2

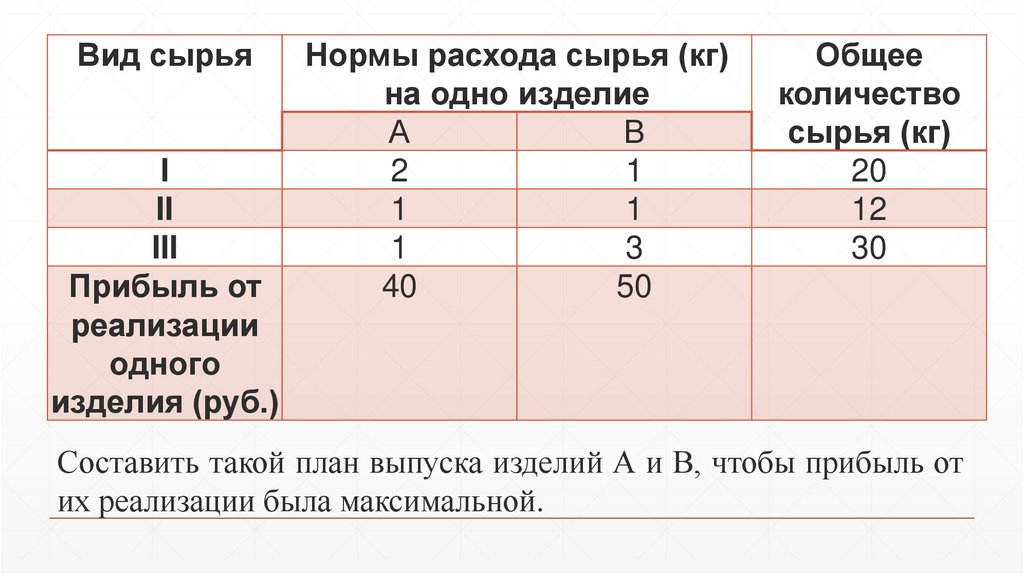
Для производства двух видов изделий А и В
предприятие использует три вида сырья. Нормы
расхода сырья каждого вида на изготовление
единицы продукции данного вида приведены в
таблице. В ней также указаны прибыль от
реализации одного изделия каждого вида, которое
может быть использовано предприятием.

13.

Вид сырья
I
II
III
Прибыль от
реализации
одного
изделия (руб.)
Нормы расхода сырья (кг)
на одно изделие
А
В
2
1
1
1
1
3
40
50
Общее
количество
сырья (кг)
20
12
30
Составить такой план выпуска изделий А и В, чтобы прибыль от
их реализации была максимальной.