Задача линейного программирования

1. Лекция 1 Задача линейного программирования

2. Постановка задачи линейного программирования

Z c1 x1 c2 x2 ... cn xn max (min).
a11 x1 a12 x2 ... a1n xn ( ; ; )b1 ;
целевая функция
a21 x1 a22 x2 ... a2 n xn ( ; ; )b2 ;
......
a x a x ... a x ( ; ; )b ;
m2 2
mn n
m
m1 1
система ограничений
x j 0 j 1, n.
Математическая модель задачи
линейного программирования
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

3. Постановка задачи линейного программирования

Задача линейного программирования может быть
записана в виде:
n
Z c j x j max (min)
n
j 1
a
j 1
ij
x j ( ; ; )bi ,
x j 0 j 1, n.
Здесь коэффициенты cj,
aij, bi заданные числа, а
величины
xj
неизвестные.
Каждое из ограничений
системы − одно из трех
возможных: ≤, =, ≥.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

4. Решение задачи линейного программирования

Любой набор чисел x1, x2,…, xn, удовлетворяющий системе
ограничений называется допустимым решением задачи
линейного программирования
Множество всех допустимых решений данной задачи
линейного программирования называется допустимой
областью.
Допустимое решение, на котором достигается требуемый
экстремум целевой функции - называется оптимальным
решением данной задачи линейного программирования.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

5. Формы записи задачи линейного программирования

1. Каноническая форма задачи линейного программирования
Z c1 x1 c2 x2 ... cn xn max (min).
a11 x1 a12 x2 ... a1n xn b1 ;
a21 x1 a22 x2 ... a2 n xn b2 ;
......
a x a x ... a x b ;
m2 2
mn n
m
m1 1
x j 0 j 1, n.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

6. Формы записи задачи линейного программирования

2. Векторно-матричная форма
Z c, x max (min)
Ax b
x 0
где
a12 ... a1n
ba
1 11
a22 ... a2 n
ba
строкаматрица коэффициентов левой части
2 21
B
столбец
коэффициентов
правой
части системы
ограничений
A x c
строкасистемы
коэффициентов
целевой
функции
,2...,
, ...,xncn
...x 1c,1 ,x2c...
неизвестных
ограничений
b
m
am1
am 2
... amn
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

7. Формы записи задачи линейного программирования

3. Стандартная (симметричная) форма задачи линейного
программирования
Z c1 x1 c2 x2 ... cn xn max (min).
n
a
j 1
ij
x j ( ; )bi ,
x j 0 j 1, n.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

8. Формы записи задачи линейного программирования

Описанные выше формы записи задачи
линейного программирования эквивалентны в том
плане, что каждая из них может быть приведена к
задаче другой формы с помощью несложных
преобразований.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

9. Графический метод решения задач линейного программирования

Задача линейного программирования с
неизвестными может быть решена графически
двумя
Пусть задача линейного программирования задана в виде:
Z c1 x1 c2 x2 max (min).
ai1 x1 ai 2 x2 ; ; bi ;
x1 0, x2 0.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

10. Алгоритм решения ЗЛП графическим методом

1. Построить область допустимых решений (ОДР) в
системе координат, заданную системой ограничений
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

11. Алгоритм решения ЗЛП графическим методом

2. Построить градиент целевой функции
f
f
c1;
c2 .
x2
x1
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

12. Алгоритм решения ЗЛП графическим методом

3. Построить линию уровня. Линия уровня строится
перпендикулярно вектору -градиенту целевой функции
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

13. Алгоритм решения ЗЛП графическим методом

4. Перемещаем линию уровня по направлению вектора градиента целевой функции, решением задачи на минимум
(максимум) является первая (последняя) точка касания линии
уровня с ОДР
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

14. Алгоритм решения ЗЛП графическим методом

4. Перемещаем линию уровня по направлению вектора градиента целевой функции, решением задачи на минимум
(максимум) является первая (последняя) точка касания линии
уровня с ОДР. Находим ее координаты и значение целевой
функции в этой точке.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

15. Алгоритм решения ЗЛП графическим методом

4. Перемещаем линию уровня по направлению вектора градиента целевой функции, решением задачи на минимум
(максимум) является первая (последняя) точка касания линии
уровня с ОДР. Находим ее координаты и значение целевой
функции в этой точке.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

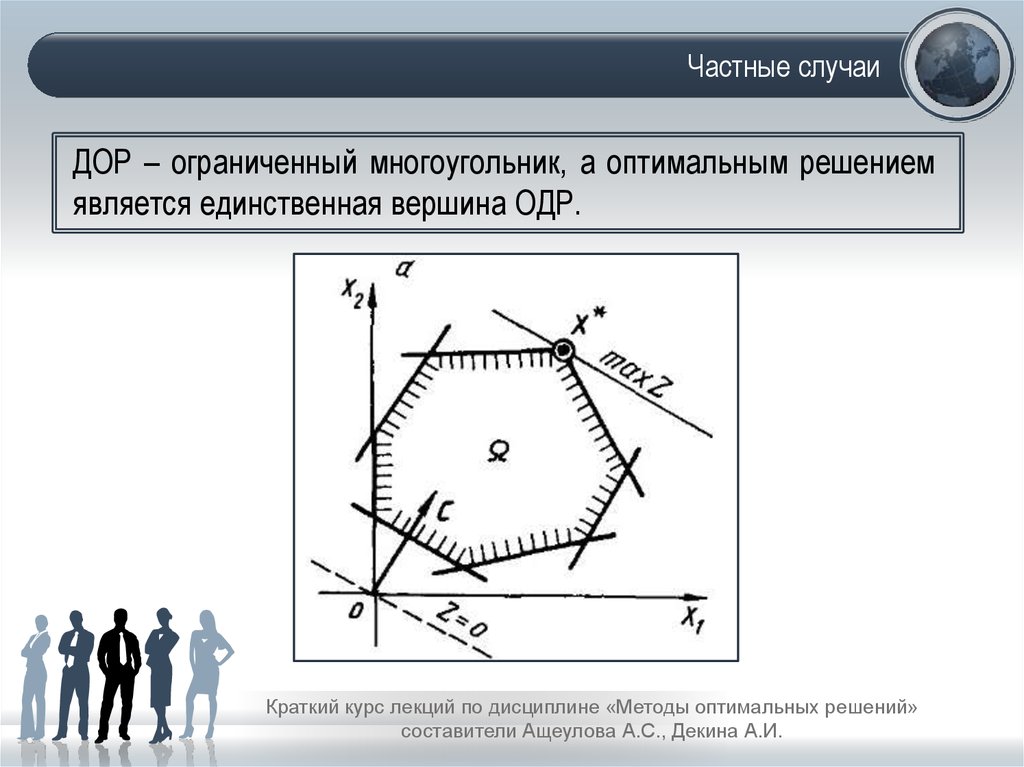
16. Частные случаи

ДОР – ограниченный многоугольник, а оптимальным решением
является единственная вершина ОДР.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

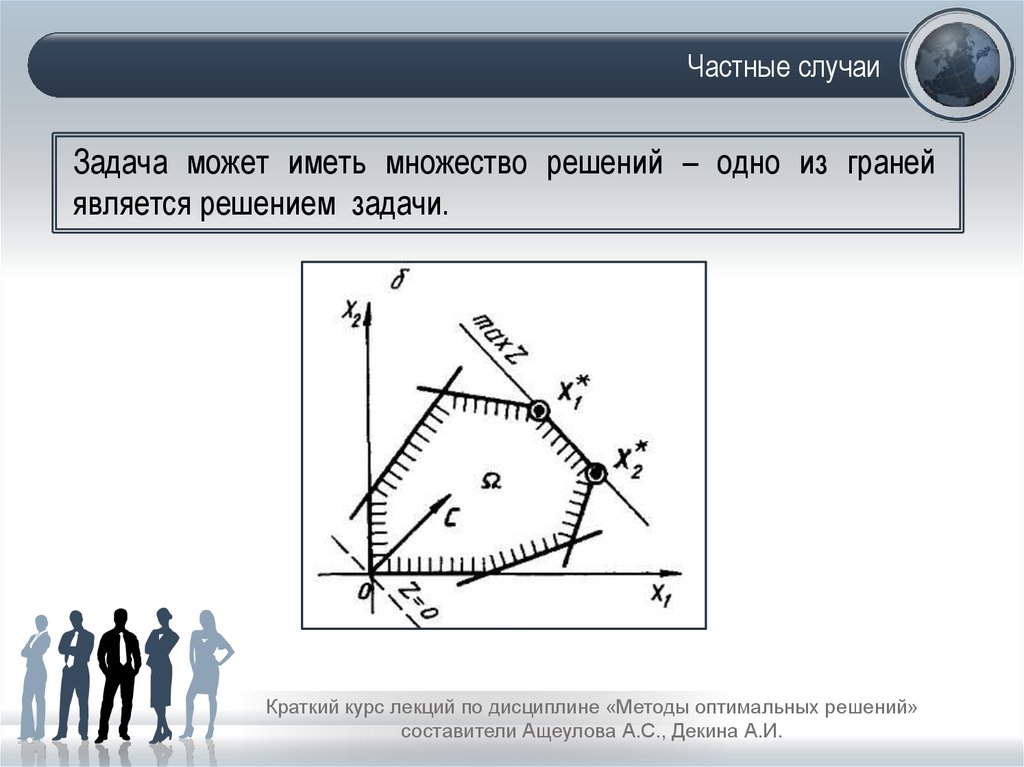
17. Частные случаи

Задача может иметь множество решений – одно из граней
является решением задачи.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

18. Частные случаи

ОДР не ограничена, задача не имеет решений.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

19. Частные случаи

ОДР не ограничена, задача единственное решение.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

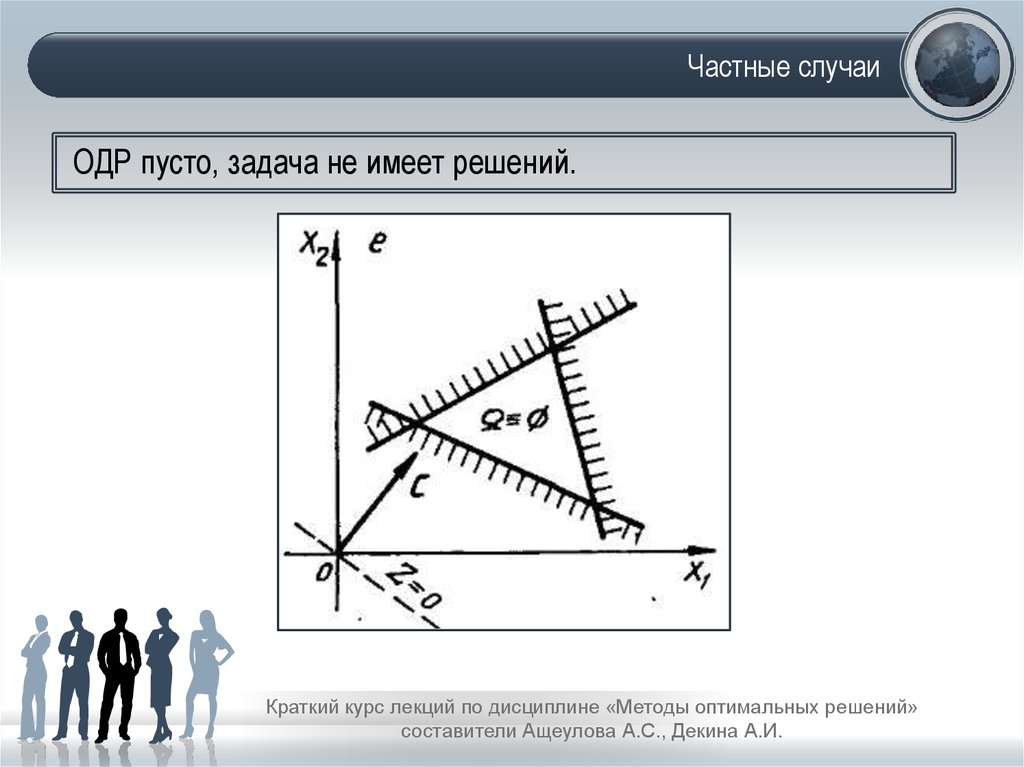
20. Частные случаи

ОДР пусто, задача не имеет решений.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.

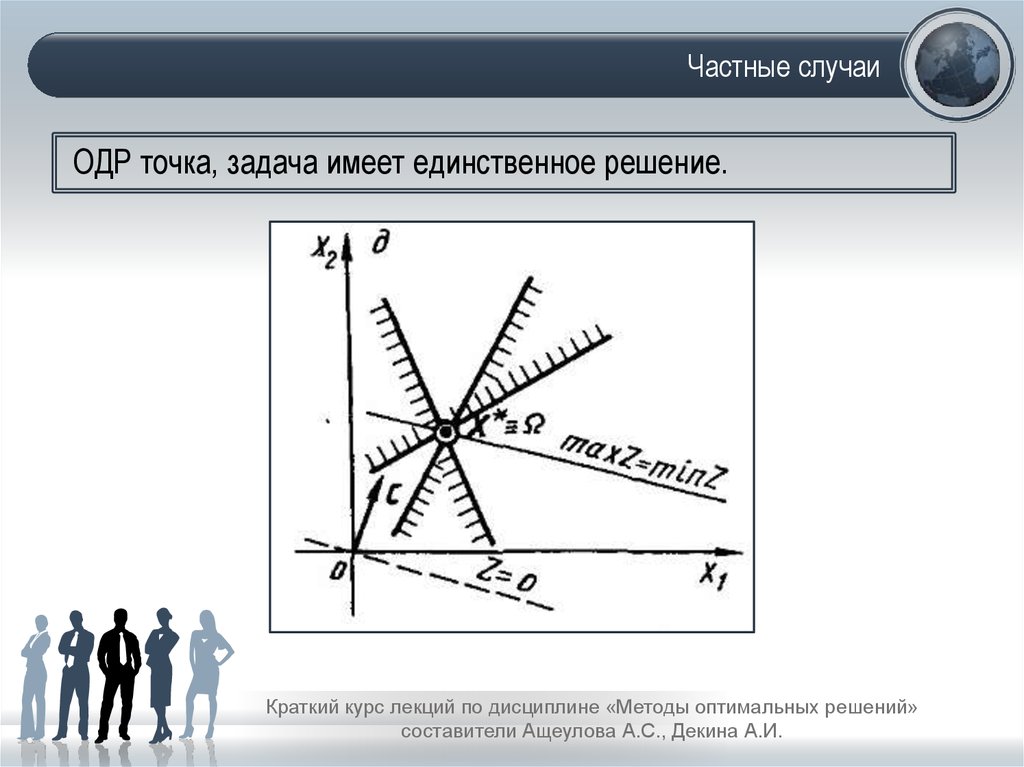
21. Частные случаи

ОДР точка, задача имеет единственное решение.
Краткий курс лекций по дисциплине «Методы оптимальных решений»
составители Ащеулова А.С., Декина А.И.