Взаимное расположение сферы и плоскости. Касательная плоскость сферы

1. Взаимное расположение сферы и плоскости. Касательная плоскость сферы.

Автор презентации:
Попов Дмитрий Сергеевич

2.

Повторите:
Сферой называется поверхность, состоящая из всех
точек пространства, расположенных на данном
расстоянии (R) от данной точки (центра - точки О).
dО
R
т. О – центр сферы
R – радиус сферы – отрезок,
соединяющий любую точку
сферы с центром.
d – диаметр сферы – отрезок,
соединяющий любые 2 точки
сферы и проходящий через центр.

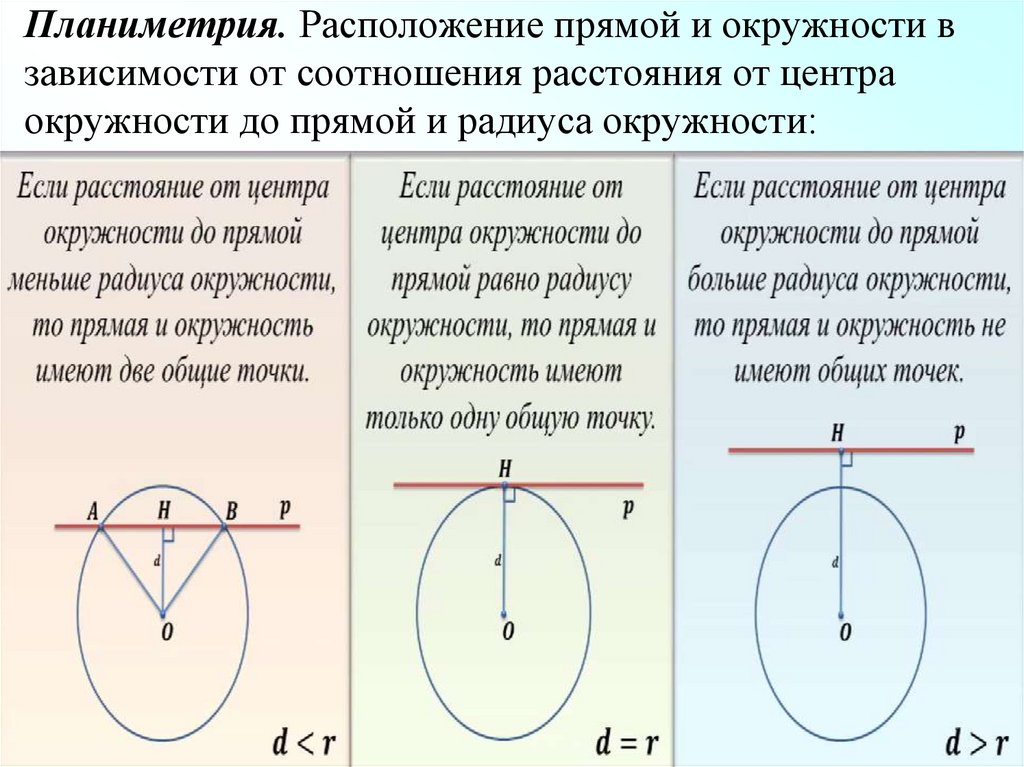
3. Планиметрия. Расположение прямой и окружности в зависимости от соотношения расстояния от центра окружности до прямой и радиуса

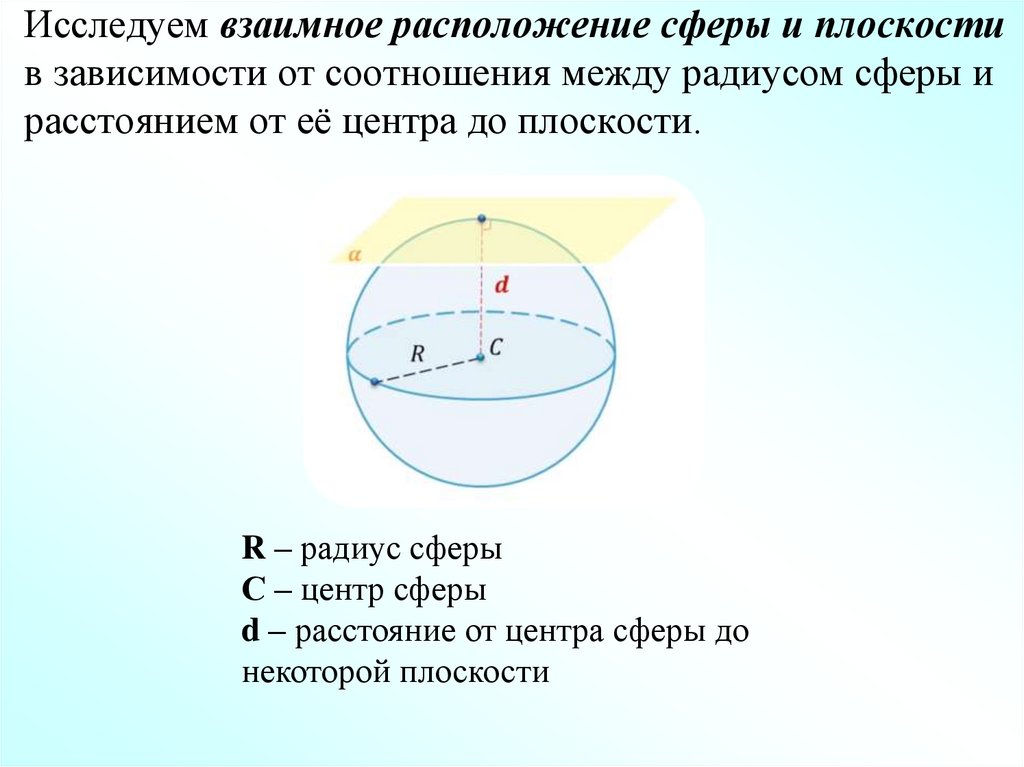
окружности:

4. Исследуем взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от её центра

до плоскости.
R – радиус сферы
С – центр сферы
d – расстояние от центра сферы до
некоторой плоскости

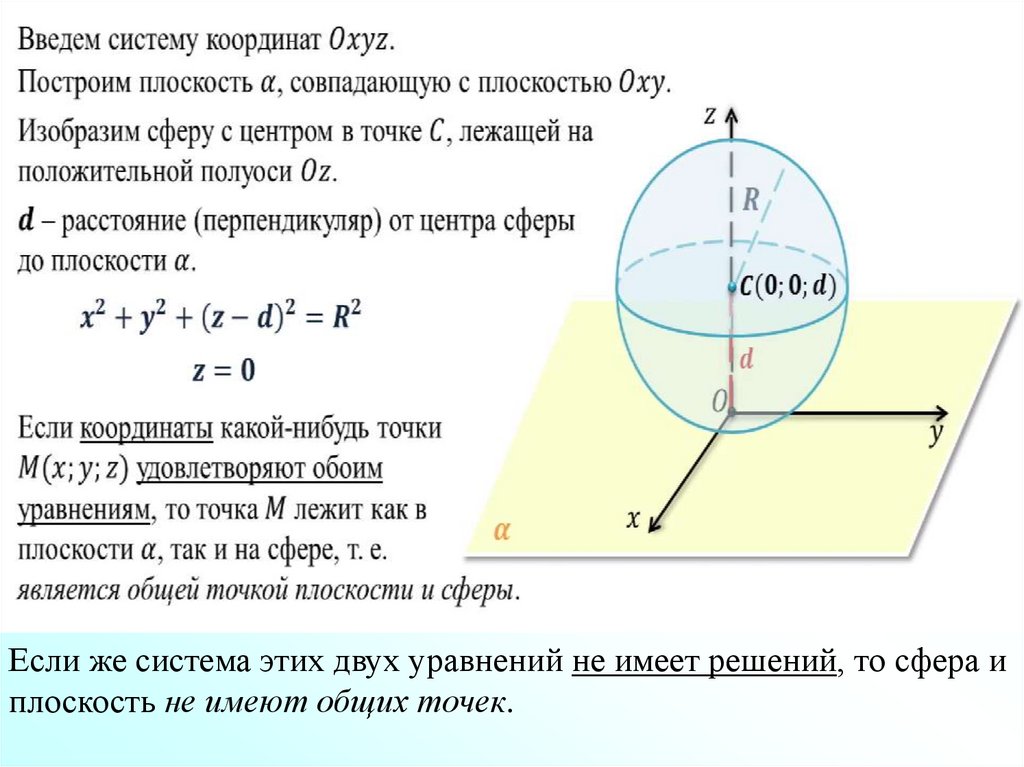
5.

Если же система этих двух уравнений не имеет решений, то сфера и
плоскость не имеют общих точек.

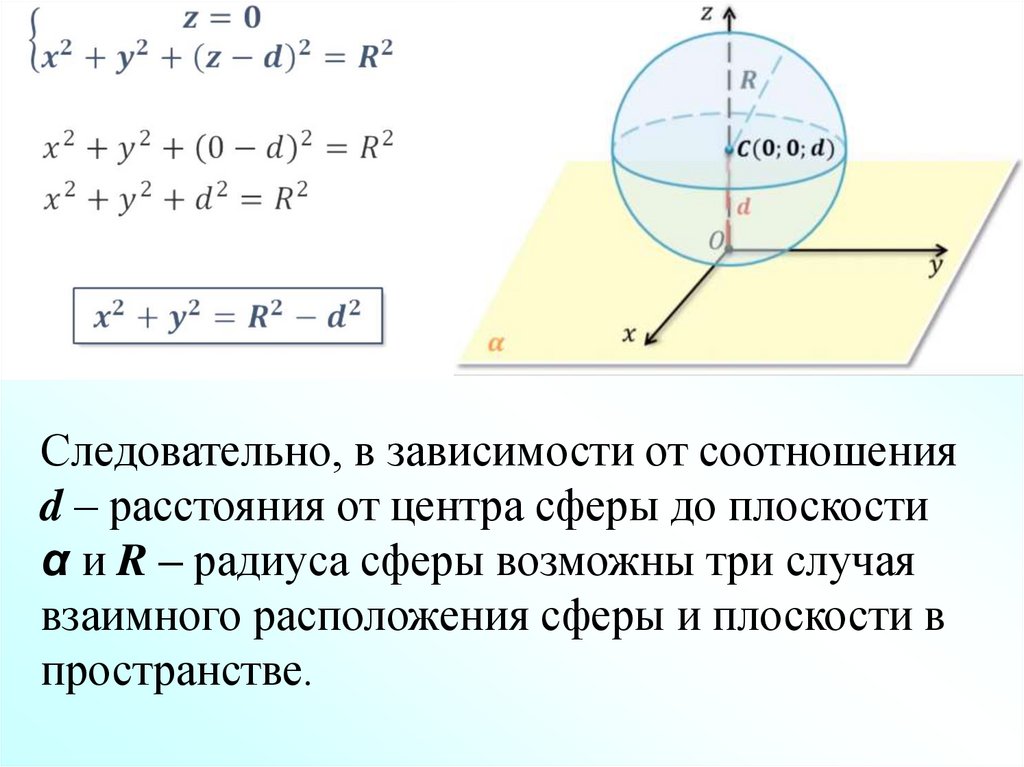
6.

Следовательно, в зависимости от соотношения
d – расстояния от центра сферы до плоскости
α и R – радиуса сферы возможны три случая
взаимного расположения сферы и плоскости в
пространстве.

7.

Координаты любой точки М (x; у; 0) этой окружности удовлетворяют как
уравнению плоскости α, так и уравнению сферы, т.е. все точки этой
окружности являются общими точками плоскости и сферы.
В данном случае сфера и плоскость пересекаются по окружности.
Если расстояние от центра сферы до плоскости меньше
радиуса сферы, то сечение сферы плоскостью есть
окружность.

8.

Сечение шара плоскостью есть круг.
Плоскость, проходящая через диаметр
шара, называется диаметральной.
Круг, полученный в результате сечения,
называется большим кругом шара.
r < R

9.

Следовательно, только координаты точки О (0; 0; 0)
удовлетворяют обоим уравнениям, значит,
О – единственная общая точка сферы и плоскости.
Если расстояние от центра сферы до
плоскости равно радиусу сферы, то сфера и
плоскость имеют только одну общую точку.

10.

Если расстояние от центра сферы до
плоскости больше радиуса сферы, то сфера и
плоскость не имеют общих точек.

11.

Касательной плоскостью называется
плоскость, имеющая со сферой только
одну общую точку, данную общую точку
называют точкой касания.
– касательная плоскость к сфере
А – точка касания

12.

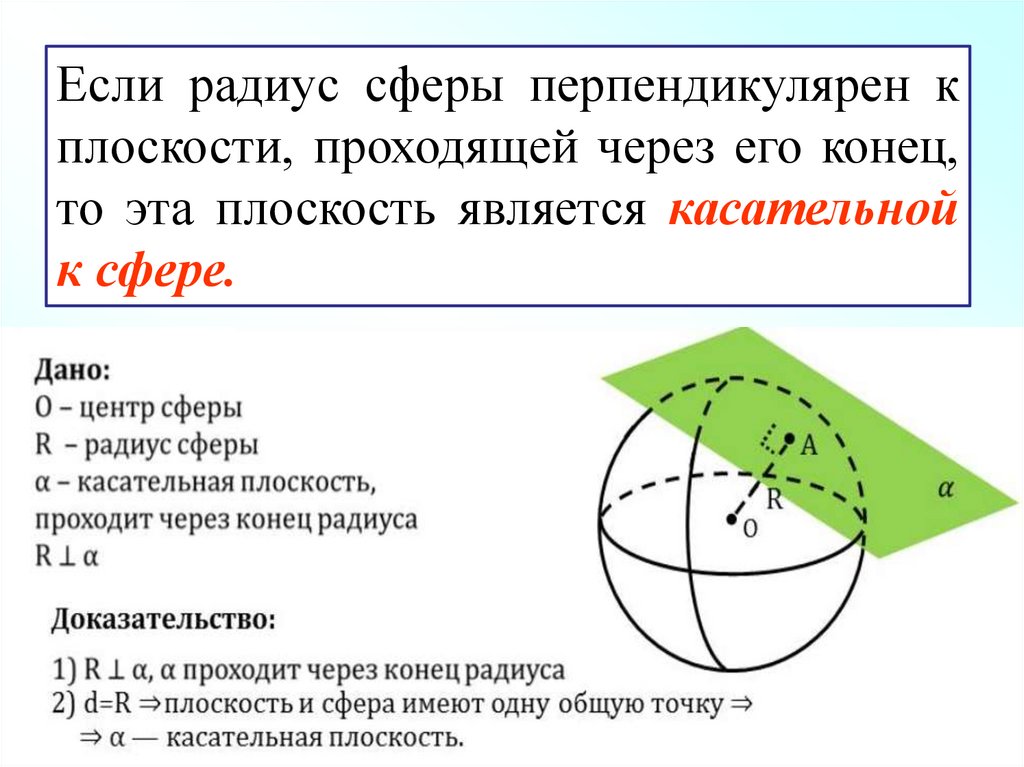
Если радиус сферы перпендикулярен к
плоскости, проходящей через его конец,
то эта плоскость является касательной
к сфере.

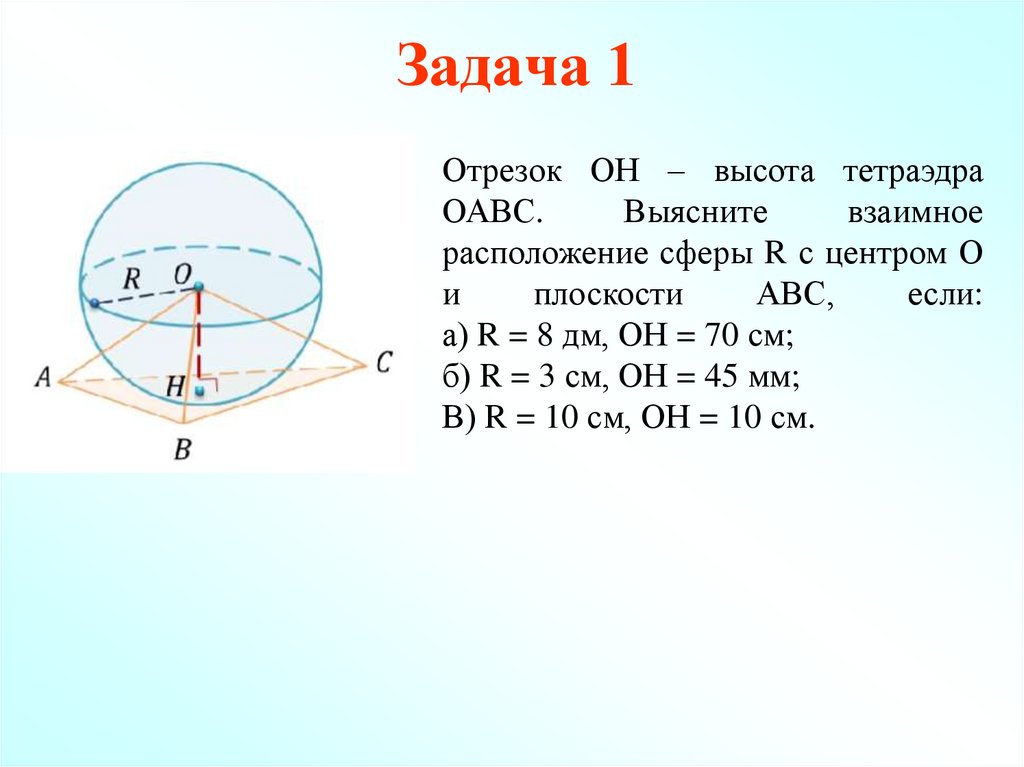
13. Задача 1

Отрезок ОН – высота тетраэдра
ОАВС.
Выясните
взаимное
расположение сферы R с центром О
и
плоскости
АВС,
если:
а) R = 8 дм, ОН = 70 см;
б) R = 3 см, ОН = 45 мм;
В) R = 10 см, ОН = 10 см.

14. Задача 2

Шар пересечён плоскостью. Площадь
сечения равна 576π см2. Расстояние
от центра шара до плоскости сечения
равно 7 см. Найдите радиус шара.

15. Задача 3

Зевс создал планету, радиус которой 25 км, и пересёк её
плоскостью, которая прошла на расстоянии 24 км от
центра. Найдите площадь сечения.
Задача 4
Гермес решил не отставать от Зевса, создал свою планету
и тоже пересёк её плоскостью, которая прошла на
расстоянии 2 км от центра. Площадь сечения получилась
равной 16π. Определите радиус этой планеты.
Задача 5
Афродита решила сделать хитрее и создала свою планету
радиусом 112 км и построила касательную плоскость к ней.
Она взяла точку на плоскости, удалённую от точки касания
на 15. Найдите расстояние от этой точки до ближайшей к
ней точке сферы.