Lecture3b

1. Lecture 3 b Geometric Constructions

MAE 201 Computer Aided Design
Dr. Eng. Konstantinos Kostas
Fall 2025

2. Outline

• Introduction
• The triangle
• The quadrilateral
• Polygons
• Circles
• Tangency
• Loci
Computer Aided Design - Fall 2025
2

3. Circles

Apart from its practical applications, the
circle has an aesthetic value which makes it
unique among plane figures. The ancients called
it ‘the perfect curve’ and its symmetry and
simplicity has led artists and craftspeople to
use the circle as a basis for design for many
thousands of years.
A circle is the locus of points having a fixed
distance from another stationary point (i.e.,
the center).
• Concentric circles are circles that have the
Computer Aided Design - Fall 2025
3
same center.

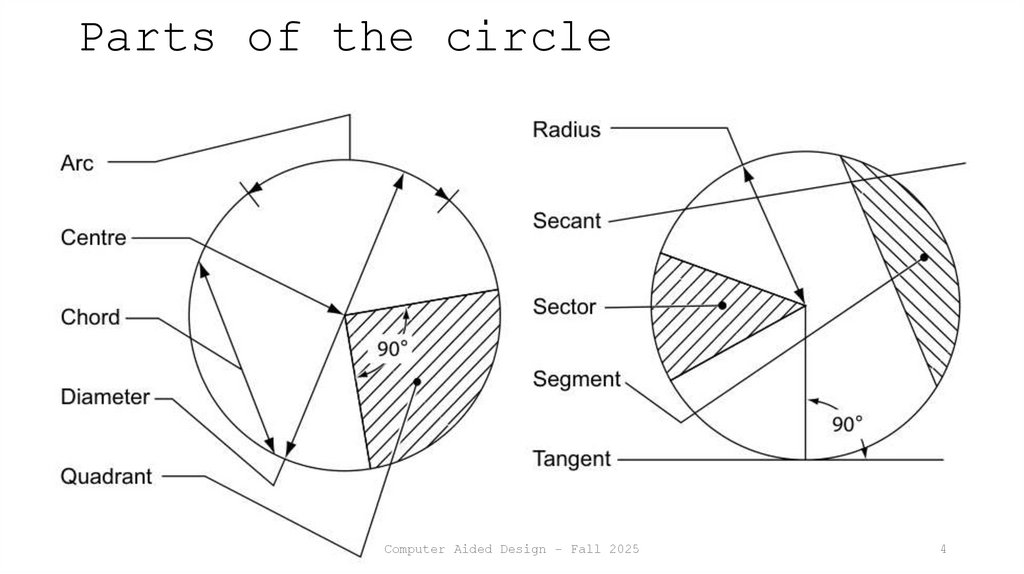
4. Parts of the circle

Computer Aided Design - Fall 2025
4

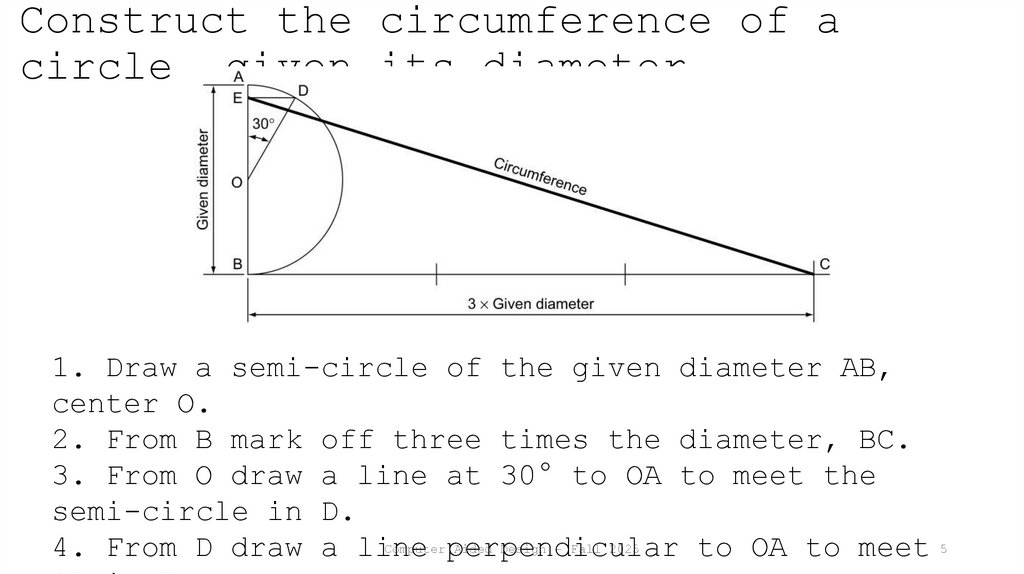
5. Construct the circumference of a circle, given its diameter

1. Draw a semi-circle of the given diameter AB,
center O.
2. From B mark off three times the diameter, BC.
3. From O draw a line at 30° to OA to meet the
semi-circle in D.
Computer perpendicular
Aided Design - Fall 2025
4. From D draw a line
to OA to meet 5

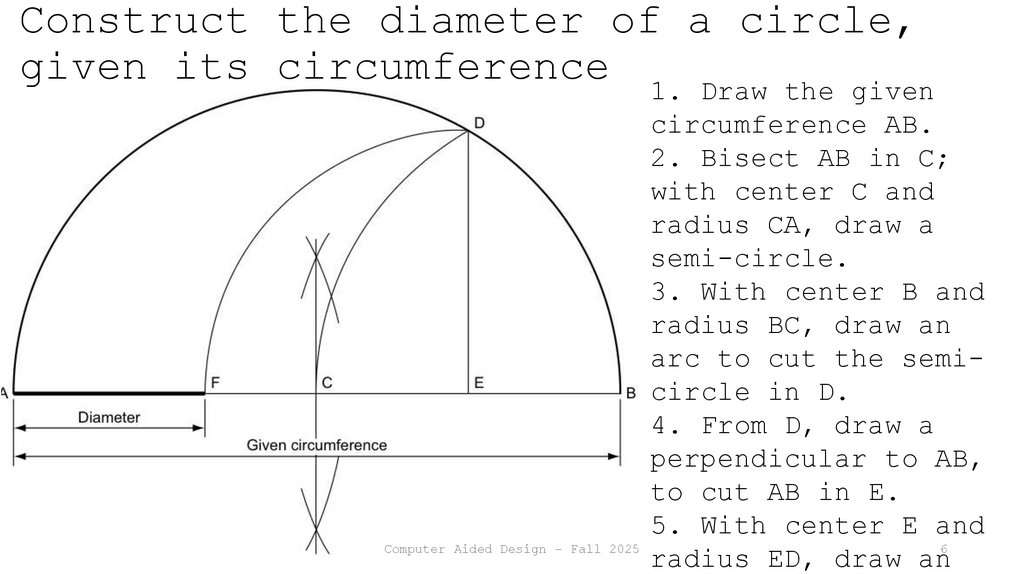
6. Construct the diameter of a circle, given its circumference

1. Draw the given
circumference AB.
2. Bisect AB in C;
with center C and
radius CA, draw a
semi-circle.
3. With center B and
radius BC, draw an
arc to cut the semicircle in D.
4. From D, draw a
perpendicular to AB,
to cut AB in E.
5. With center E and
Computer Aided Design - Fall 2025
radius ED, draw an6

7. Find the center of any circle

1. Draw any two
chords.
2. Construct
perpendicular
bisectors to these
chords
3. The intersection
of the bisectors is
the required center
O
Computer Aided Design - Fall 2025
7

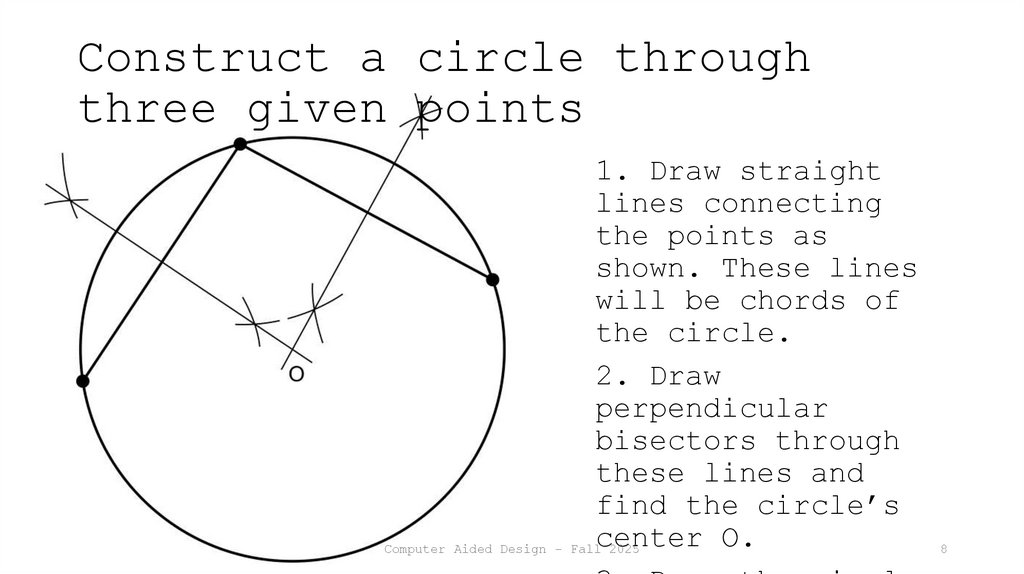
8. Construct a circle through three given points

1. Draw straight
lines connecting
the points as
shown. These lines
will be chords of
the circle.
2. Draw
perpendicular
bisectors through
these lines and
find the circle’s
center O.
Computer Aided Design - Fall 2025
8

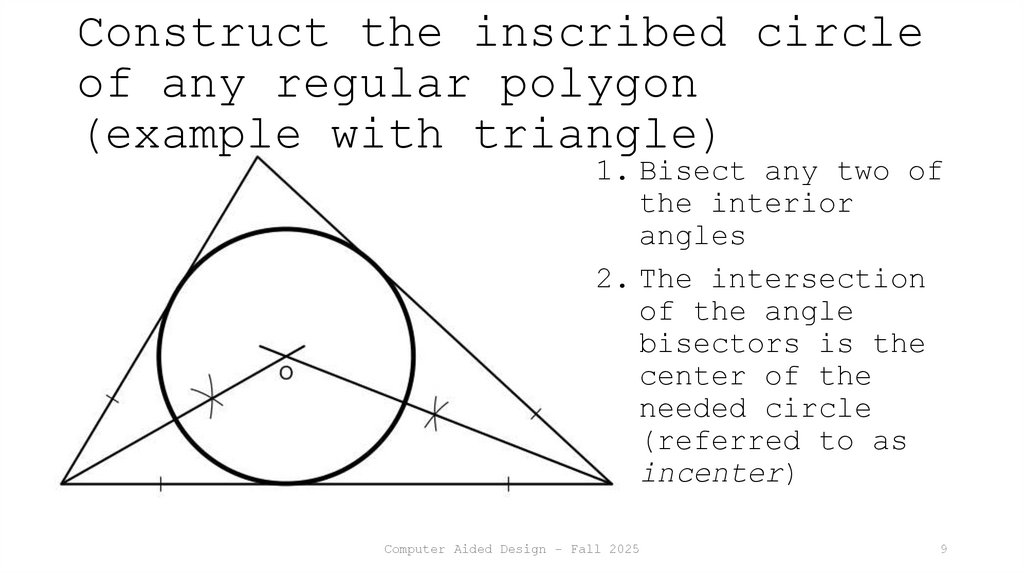
9. Construct the inscribed circle of any regular polygon (example with triangle)

1. Bisect any two of
the interior
angles
2. The intersection
of the angle
bisectors is the
center of the
needed circle
(referred to as
incenter)
Computer Aided Design - Fall 2025
9

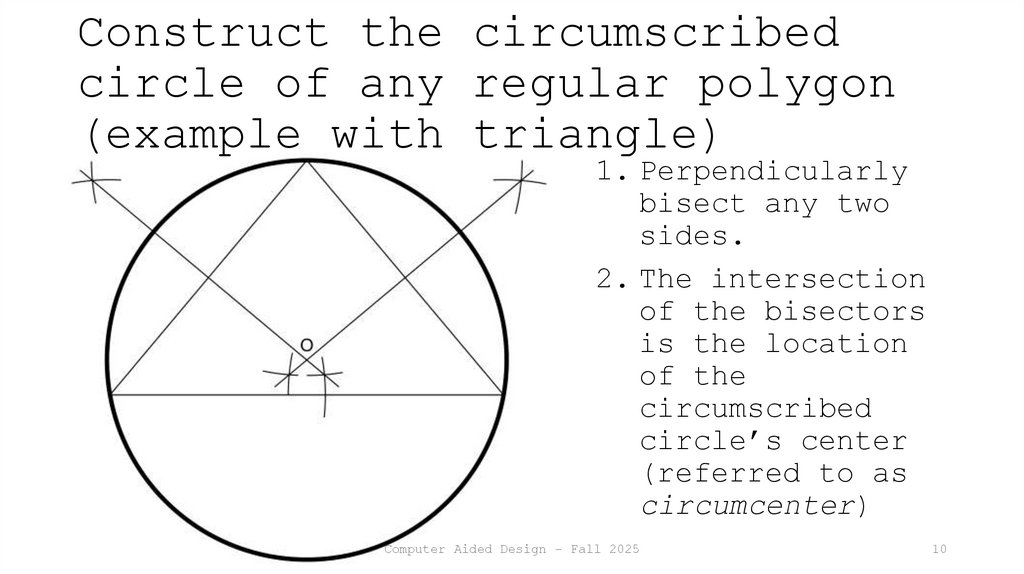
10. Construct the circumscribed circle of any regular polygon (example with triangle)

1. Perpendicularly
bisect any two
sides.
2. The intersection
of the bisectors
is the location
of the
circumscribed
circle’s center
(referred to as
circumcenter)
Computer Aided Design - Fall 2025
10

11. Construct a circle that passes through a given point A and is tangent to a given line at point B

1. Join AB.
2. From B, erect a
perpendicular (BC)
to the given line.
3. From A, construct
angle BÂO equal to
angle CB̂A, and
intersect the
constructed
perpendicular,
i.e., BC.
4. The new
intersection
Computer Aided Design - Fall 2025point, O, is the
11

12. Construct a circle that passes through two given points, A and B, and is tangent to a given line

1. Join AB and extend the
line to intersect the
given line at C.
2. Extend the line further
so that BC = CD.
3. Construct a semi-circle
with AD as its diameter.
4. Erect a perpendicular
from C to cut the semicircle in E.
5. Make CF = CE.
6. From F erect a
perpendicular.
7. Perpendicularly bisect
AB to meet the
Computer Aided Design - Fall 2025
12
perpendicular from F at O.

13. Construct a circle that touches two given lines and passes through a given point P

Note that we assume two intersecting line and that there are
two circles satisfying the requirements.
1. Bisect the angle formed by the two lines.
2. From any point on the bisector draw a circle, say with
center B, touching the two lines
3. Draw PA and cut the
circle at C and D.
4. Draw PO1 and PO2,
parallel to CB and DB,
respectively.
O1 and O2 are the centers
of the required circles.
Computer Aided Design - Fall 2025
13

14. Construct a circle of a given radius, R, tangent to both another circle and a given line

1. Draw a line parallel
to the given line; the
distance between the two
lines should be equal to
the radius R of the
circle we want to
construct.
2. With the compass
point at the center of
the given circle and
radius set at R + r,
where r is the radius of
the given circle, draw
an arc to cut the
Computer Aided Design - Fall 2025
14
parallel line at O.

15. Construct a circle that touches another circle and two tangents of that circle

1. Bisect the angle formed by the
two tangents lines, cutting the
given circle at E and D
2. From B (or C), i.e., the point
of contact
of the given circle and one of its
tangents, construct a perpendicular
to
cut the bisector at O1. This is the
center of the
given circle.
3. Join BD and Draw EF parallel to
DB.
Computer Aided Design - Fall 2025
4. Draw FO2 parallel to BO1.
Here we
assume that
the two
tangents
15
intersect

16. Construct three circles touching each other, given the position of their centers

1. Draw the triangle
connecting the 3
centers.
2. Find the center of
the triangle, e.g., by
bisecting two of the
interior angles.
3. From this center,
create a perpendicular
to one of the triangle
sides.
4. The two circles
Computer Aided Design - Fall 2025
16
that have their

17. Construct any number of equal, touching circles within another circle; example with 5

1. Divide the circle into the same
number of sectors as needed circles.
2. Bisect all sectors and use one of
the bisectors to cut the circle at a
point, say D in our example.
3. From D erect a perpendicular to
the bisector to meet the neighboring
sector edge OB at E.
4. Bisect DÊO to meet OD at F.
5. F is the center of the first
circle. The remaining circles have
the same radius and centers on the
Computer
Aided Design - Fall 2025of the sector bisectors
17
intersections

18. Tangency

Tangents can be drawn to any curve, but we
mainly focus here on tangents to circles.
A tangent to a circle is a straight infinite
line that touches the circle at only one point.
Tangents to circles have wide applications in
engineering drawings since the outlines of most
engineering details are made up of straight
lines and arcs. Wherever a straight line meets
an arc, a tangent meets a circle.
Computer Aided Design - Fall 2025
18

19. Thales’ Theorem

The angle in a semicircle is a right
angle
This fact is made use of in many tangent
Computer Aided Design - Fall 2025
19

20. Draw a tangent to a circle from any point on the circumference

1. Draw the radius of the
circle.
At any point on the
circumference of a
circle, the tangent and
the radius are
perpendicular to each
other.
2. Thus, the tangent is
found by constructing an
angle of 90° from the
Computer Aided point
Design - Fall where
2025
the radius 20

21. Construct a tangent from an arbitrary point P to a given circle

1. Join the
Computer Aided Design - Fall 2025
center of the
given circle
with the given
point, drawing
line OP.
2. Bisect OP and
create the
corresponding
semi-circle from
OP
3. The semi- 21

22. Construct a tangent to two equal circles

Common
Exterior
Tangent
1. Join the centers of the two
circles.
Exterior: 2. From each center,
construct lines at 90° to the
joining line. The intersection of
these perpendiculars with the
circles gives the points of
tangency.
Interior: 2. Bisect the joining
line and using either side bisect
it to create point B.
Computer Aided Design - Fall 2025
3. From B generate a semi-circle
Construct
a tangent
to two
equal
circles
Common
Interior
Tangent
22

23. Construct a tangent to two unequal circles

1. Join the centers of the two circles.
Exterior:
Interior:
2.
2. Bisect
Bisect the
the joining
joining line
line and
and create
create point
point
A.
A.
3.
3. From
From AA generate
generate aa semi-circle.
semi-circle.
4.
4. Using
Using the
the biggest
biggest circle’s
circle’s center
center create
create
aa concentric
concentric circle
circle with
with radius
radius R-r
R+r and
and
find
find point
point B.
B. The
OB will
extension
cut the
of biggest
OB will cut
the
circle
biggest
at C.circle at C.
5.
5. Draw
Draw OO11DD parallel
parallel to
to OC;
OC; CD
CD is
is
the
the
Common
required
required tangent
tangent
Exterior
Construct
a tangent
to two
unequal
circles
Tangent
Common
Interior
Tangent
Computer Aided Design - Fall 2025
23

24. Smooth blending of lines and curves

The inclusion of curves within the outline of a
component may be for several reasons: to
eliminate sharp edges, thereby making it safer
to handle; to eliminate a stress centers,
thereby making it stronger; to avoid extra
machining, thereby making it cheaper; and last,
but by no means least, to improve its
appearance.
A series of constructions blending straight
lines and/or circles with arcs will be presented
in sequel. However, smooth blending can be
accomplished with Computer
entities
other than arcs in
Aided Design - Fall 2025
24

25.

Any Questions?
Computer Aided Design - Fall 2025
25