Похожие презентации:
Нагрузки на элерон и расчет его на прочность
1. Нагрузки на элерон и расчет его на прочность
Санкт-Петербургский государственный университет гражданской авиацииКафедра № 24 - «Авиационной техники»
Нагрузки на элерон и
расчет его на прочность
Санкт-Петербург
2009
2.
Основной внешней нагрузкой, действующейна элерон и принимаемой при расчетах
элерона, является аэродинамическая
нагрузка.
Остальными нагрузками можно пренебречь
из-за их малой величины.
3.
Аэродинамическая нагрузка элерона неявляется величиной постоянной.
Она зависит
• от режима (скорости) полета и
• от величины угла отклонения элерона.
4.
Нормы прочности предусматриваютнеобходимость обеспечить прочность
элерона в двух вариантах его работы:
a)элерон, работающий как часть крыла;
b)элерон при резком его отклонении на
большой скорости.
Второй вариант (при резком его отклонении на
большой скорости) обычно является самым
тяжелым вариантом в работе элерона.
5.
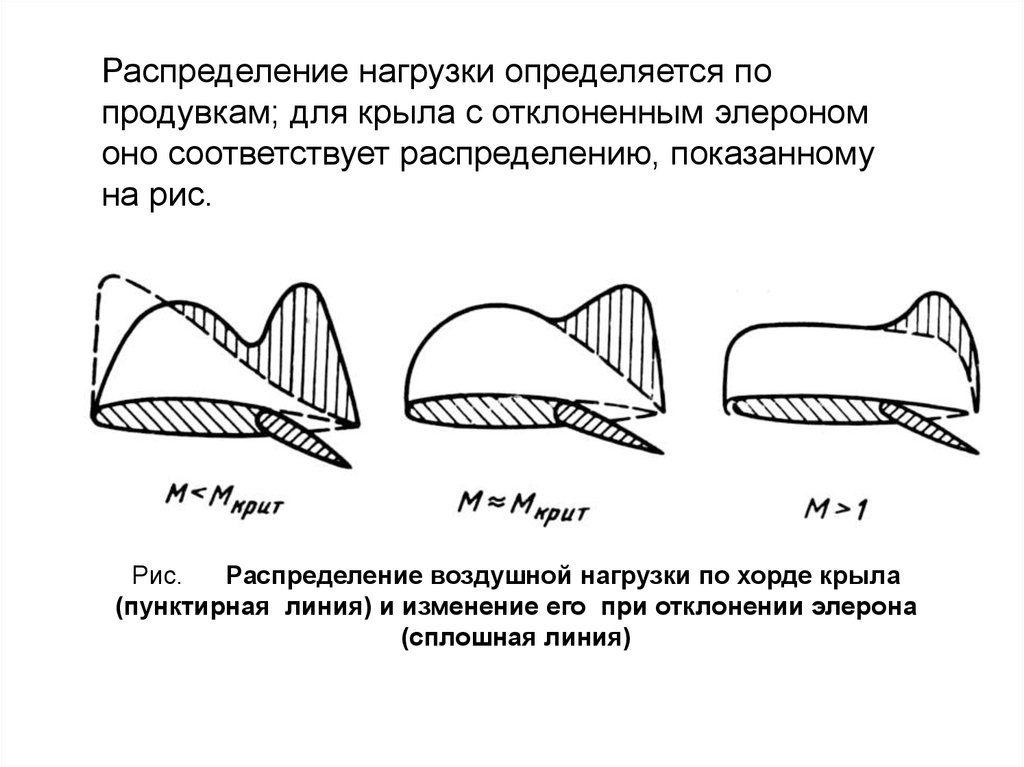
Распределение нагрузки определяется попродувкам; для крыла с отклоненным элероном
оно соответствует распределению, показанному
на рис.
Рис.
Распределение воздушной нагрузки по хорде крыла
(пунктирная линия) и изменение его при отклонении элерона
(сплошная линия)
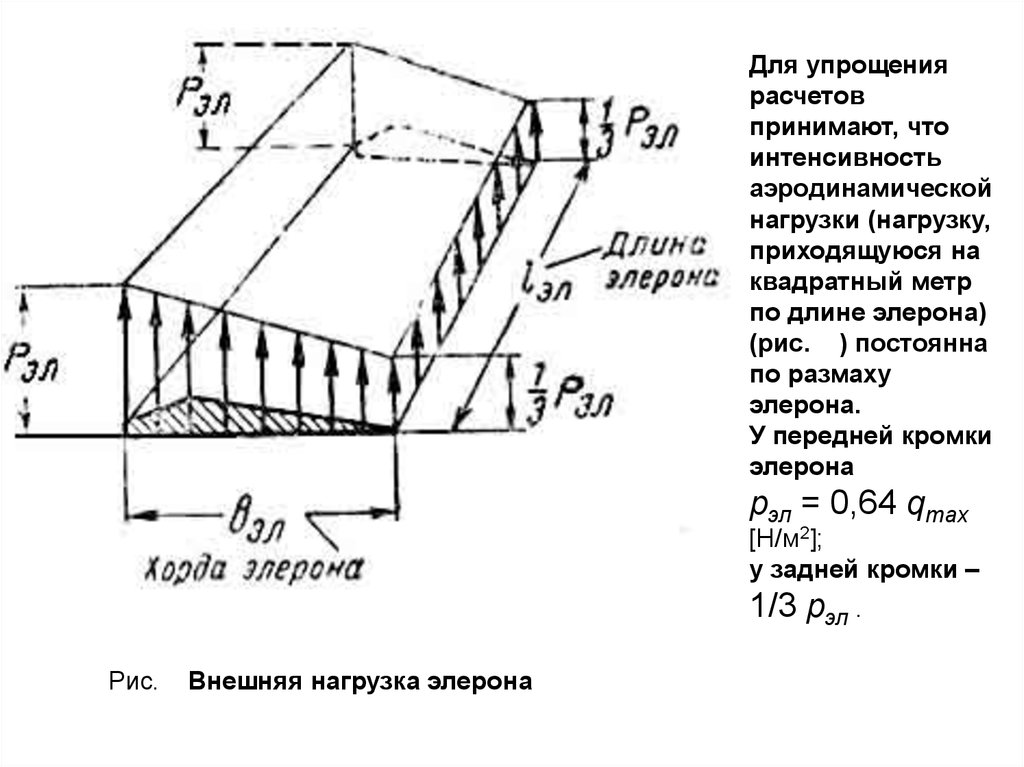
6.
Для упрощениярасчетов
принимают, что
интенсивность
аэродинамической
нагрузки (нагрузку,
приходящуюся на
квадратный метр
по длине элерона)
(рис. ) постоянна
по размаху
элерона.
У передней кромки
элерона
рэл = 0,64 qmax
[Н/м2];
у задней кромки –
1/3 рэл .
Рис.
Внешняя нагрузка элерона
7.
Направление аэродинамической нагрузкипринимается по нормали к плоскости элерона.
Величина погонной нагрузки по размаху элерона на
основании приятого допущения (упрощения)
определяется так:
qэл = bэл∙(рэл+ рэл /3) /2 [Н/м]
8.
Работа элеронаДопустим, что на
элерон действует
распределенная
аэродинамическая
нагрузка qэл,
направленная
снизу вверх (рис.
).
Рис.
Уравновешивание внешней
нагрузки элерона
Распределенная аэродинамическая нагрузка qэл стремится
перемещать элерон вверх. Этому поступательному
перемещению препятствуют кронштейны-опоры своими
реакциями R1, R2, R3, R4.
9.
Во избежаниеаэродинамической
перекомпенсации
ось вращения
всегда
располагается
заведомо спереди
линии центров
давления элерона.
Рис.
Уравновешивание внешней
нагрузки элерона
Так как элерон подвешен на нескольких опорах к крылу, то
крыло в этих опорах будет создавать силы реакции: R1, R2,
R3, R4. Сумма этих сил уравновешивает нагрузку элерона.
Следовательно,
10.
R1 + R2 + R3 + R4 = ∑qэл,где
∑qэл = qэл ср ∙ lэл
qэл ср – средняя погонная нагрузка
элерона;
lэл
– размах элерона.
11.
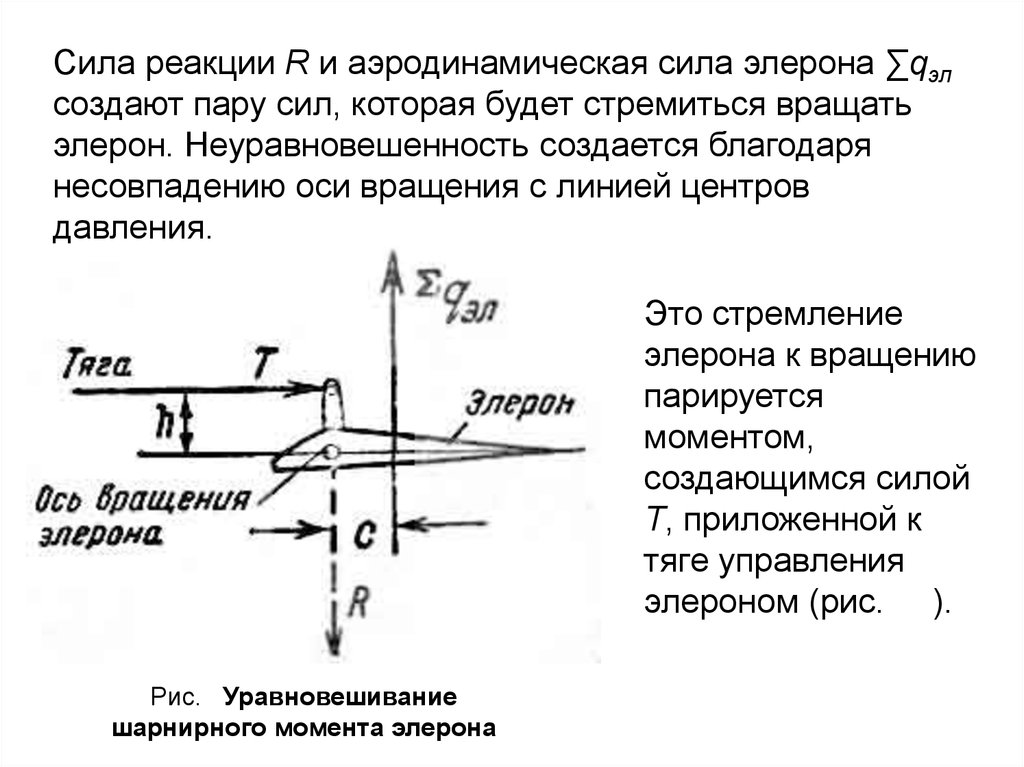
Сила реакции R и аэродинамическая сила элерона ∑qэлсоздают пару сил, которая будет стремиться вращать
элерон. Неуравновешенность создается благодаря
несовпадению оси вращения с линией центров
давления.
Это стремление
элерона к вращению
парируется
моментом,
создающимся силой
Т, приложенной к
тяге управления
элероном (рис. ).
Рис. Уравновешивание
шарнирного момента элерона
12.
Рис. Распределение суммарной реакции опор R иуправляющей силы Т
Равновесие элерона достигается равенством
соответствующих моментов:
с∙∑qэл = Т∙h
С точки зрения строительной механики элерон представляет собой
многоопорную балку переменной жесткости, нагруженную
распределенной аэродинамической силой qэл, действующей в
плоскости, перпендикулярной хордам, и силой от управления Т,
действующей по оси тяги проводки управления (рис. ).
13.
В таких неразрезных или многоопорных балках более рациональнораспределяются изгибающие моменты по сравнению с разрезными.
При увеличении числа опор уменьшаются величины перерезывающих
сил и изгибающих моментов, что ведет к снижению массы элерона,
уменьшаются его прогибы, что выгодно в аэродинамическом
отношении, повышается живучесть.
Но одновременно увеличивается возможность заклинивания элеронов
при деформации крыла, усложняется технологический процесс
навески элерона и обеспечение требований взаимозаменяемости.
Рис.
Схема, объясняющая
возможность заклинивания
элеронов при деформации
крыла
14.
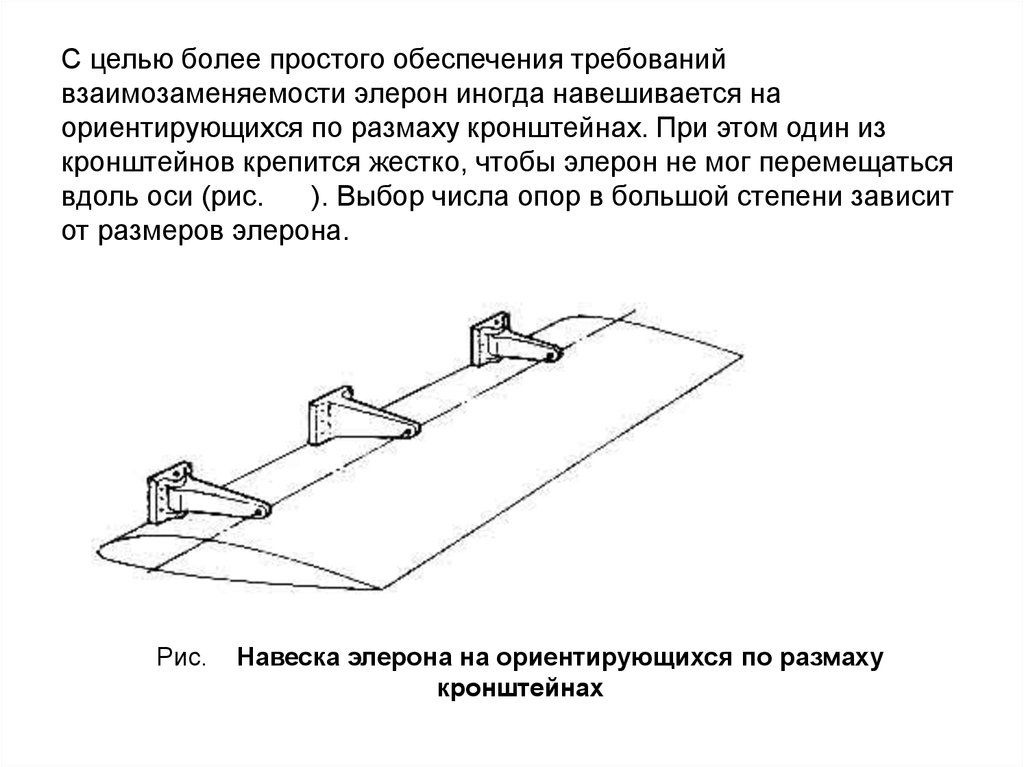
С целью более простого обеспечения требованийвзаимозаменяемости элерон иногда навешивается на
ориентирующихся по размаху кронштейнах. При этом один из
кронштейнов крепится жестко, чтобы элерон не мог перемещаться
вдоль оси (рис.
). Выбор числа опор в большой степени зависит
от размеров элерона.
Рис.
Навеска элерона на ориентирующихся по размаху
кронштейнах
15.
Для расчета элерона необходимо строить эпюры погонныхнагрузок по размаху элерона, изгибающих моментов Ми и
поперечных сил Q.
Однако определение опорных реакций в таких многопролетных или
неразрезных балках на основании использования только уравнений
равновесия невозможно, так как число уравнений равновесия только
два (уравнение сил и уравнение моментов), а опорных реакций
больше двух – «много».
Такие балки называют статически неопределимыми. Они не могут
быть рассчитаны с помощью одних лишь уравнений статики. Для их
расчета составляются дополнительные уравнения, выражающие
условия совместной работы балки с ее опорными закреплениями.
Число дополнительных уравнений соответствует степени статической
неопределимости балки.
16.
Если число опор будет больше двух, то дляопределения реакций в этих опорах можно
воспользоваться теоремой о трех
моментах или уравнением Клапейрона
(Clapeyron).
Рис. Клапейрон
(Clapeyron)
Бенуа Поль
Эмиль
(1799 - 1864),
французский
физик и инженер.
В 1820 – 1830
работал в России
Суть метода раскрытия статической
неопределимости реакций опор
многоопорной балки состоит в следующем.
Многоопорную балку представляют в виде
системы двухопорных (статически
определимых) балок, мысленно разрезая в
местах постановки опор и в этих разрезах
прикладывая неизвестные опорные
моменты.
17.
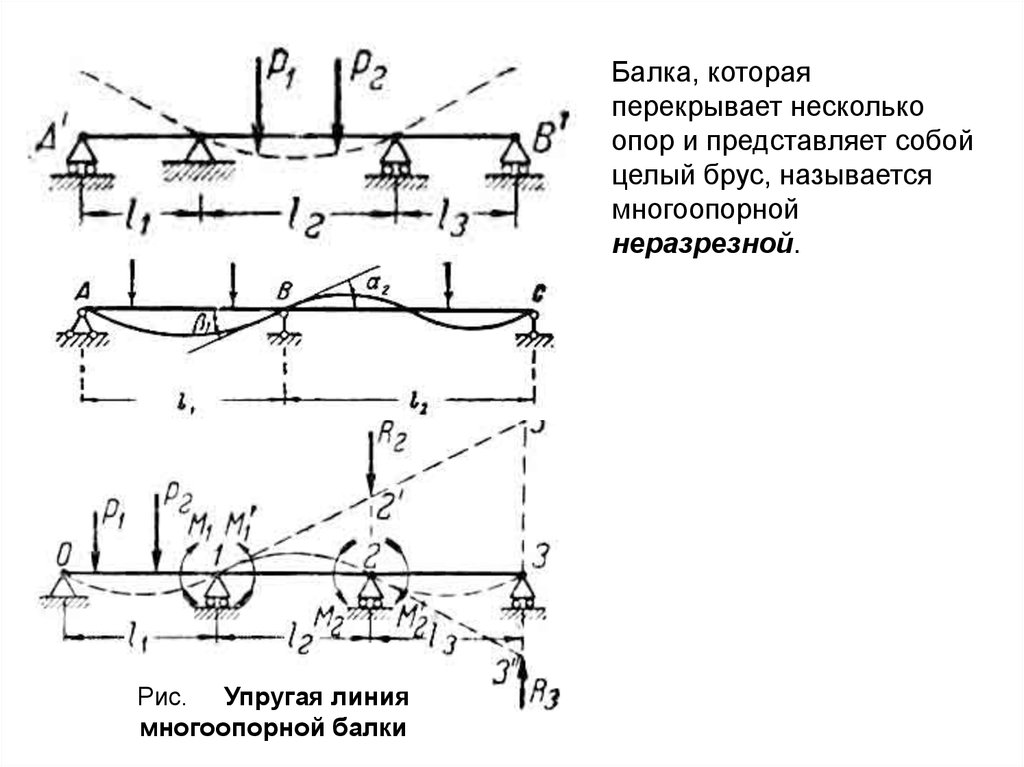
Балка, котораяперекрывает несколько
опор и представляет собой
целый брус, называется
многоопорной
неразрезной.
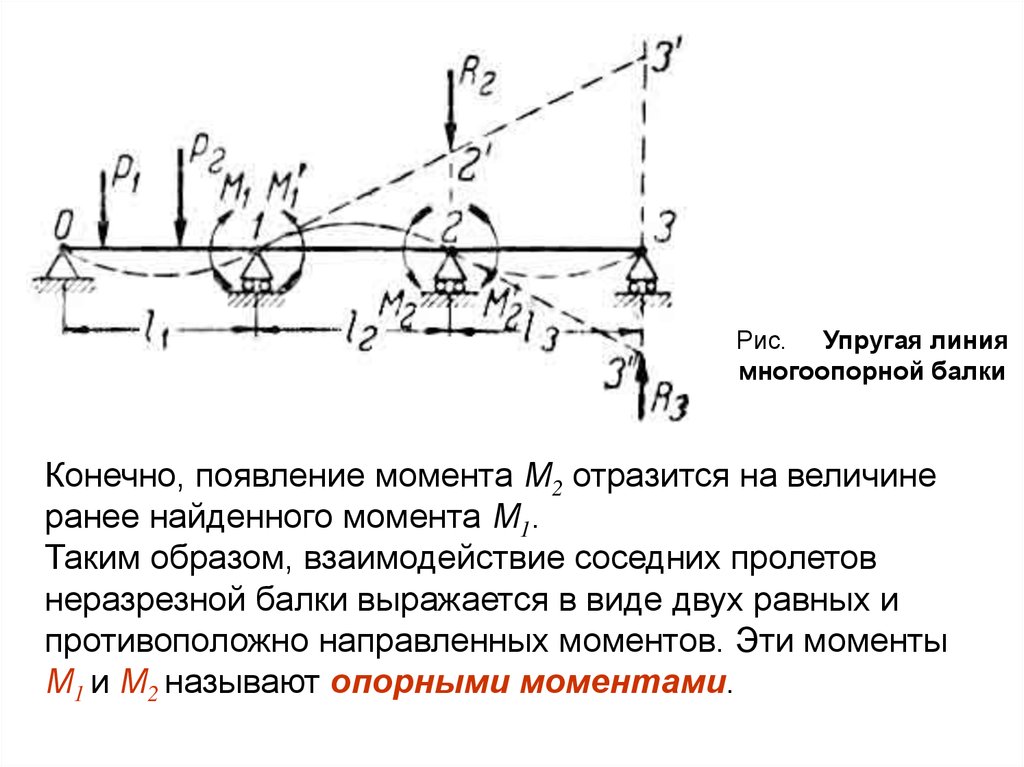
Рис. Упругая линия
многоопорной балки
18.
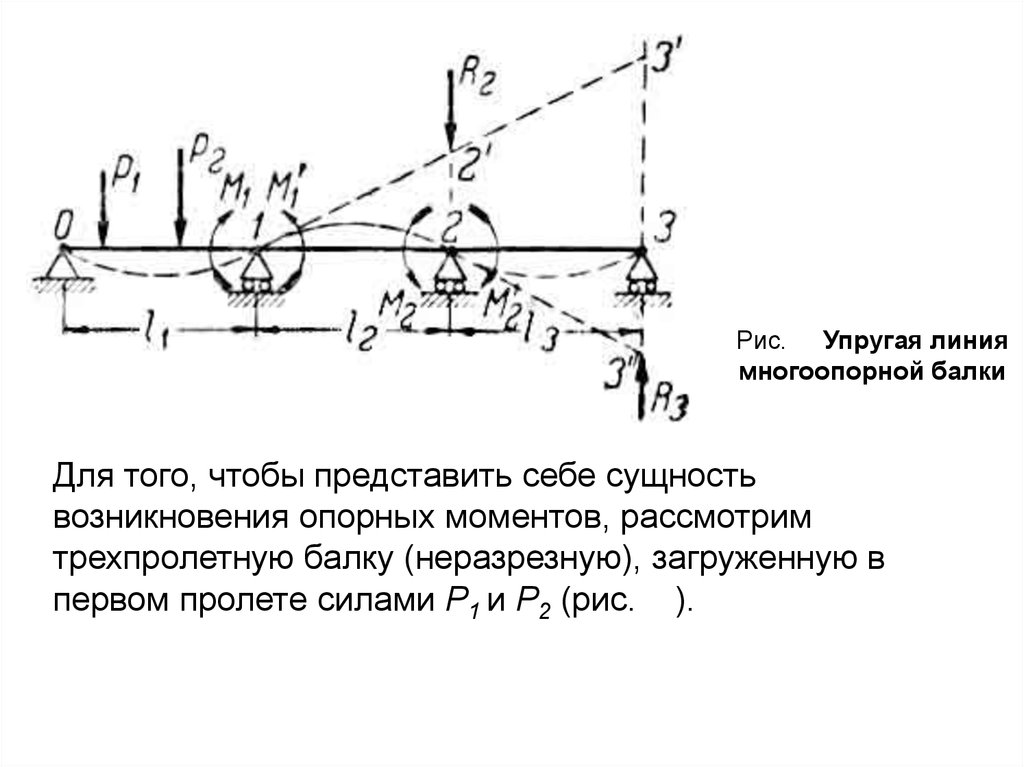
Рис. Упругая линиямногоопорной балки
Для того, чтобы представить себе сущность
возникновения опорных моментов, рассмотрим
трехпролетную балку (неразрезную), загруженную в
первом пролете силами Р1 и Р2 (рис. ).
19.
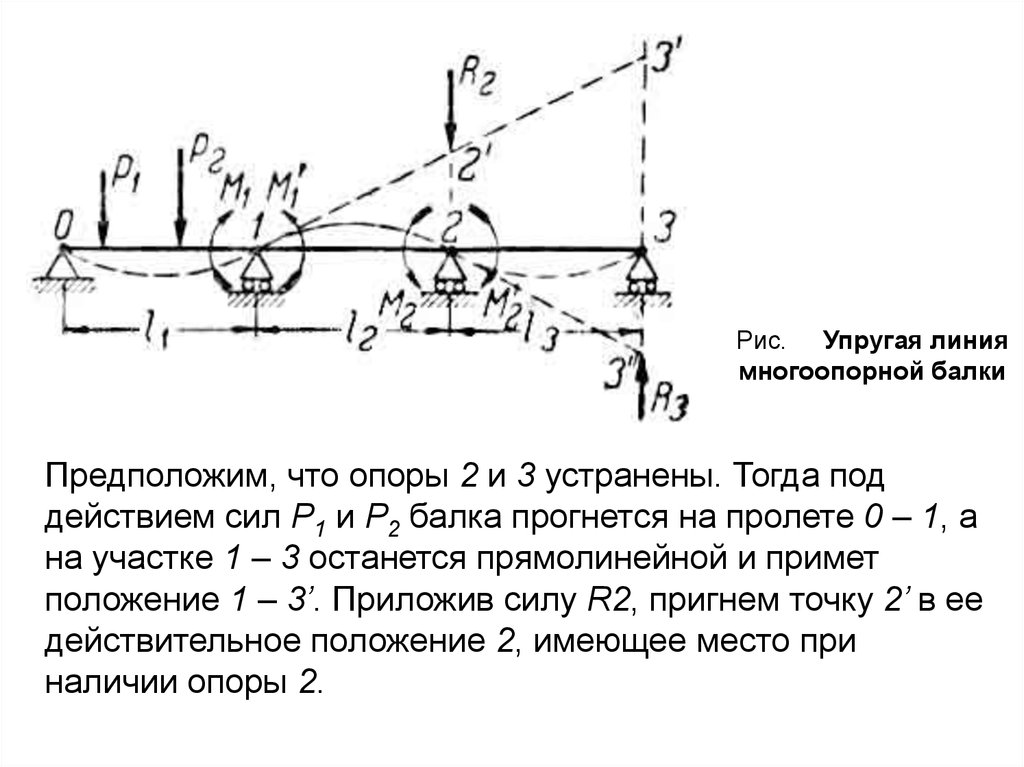
Рис. Упругая линиямногоопорной балки
Предположим, что опоры 2 и 3 устранены. Тогда под
действием сил Р1 и Р2 балка прогнется на пролете 0 – 1, а
на участке 1 – 3 останется прямолинейной и примет
положение 1 – 3’. Приложив силу R2, пригнем точку 2’ в ее
действительное положение 2, имеющее место при
наличии опоры 2.
20.
Рис. Упругая линиямногоопорной балки
При этом в сечении балки под опорой 1 (как в балке,
заделанной одним концом) возникает момент М1 = R2∙l2,
выражающий действие второго пролета на первый.
Обратно: действие первого пролета на второй по закону
действия и противодействия должно быть таким же по
величине, но обратным по направлению, то есть
выразиться моментом М’1 = - М1.
21.
Рис. Упругая линиямногоопорной балки
Прогибая балку в опоре 2, мы заметим, что ее участок 2’ –
3’ останется прямолинейным и примет положение 2 – 3’ ’.
Приложив силу R3 , прижмем точку 3’ ’ в ее
действительное положение 3. Тогда в сечении 2,
возникнет момент М2= R3 ∙l3., представляющий действие
третьего пролета на второй. Действие второго пролета на
третий, подобно предыдущему, выразится моментом М’2.
22.
Рис. Упругая линиямногоопорной балки
Конечно, появление момента М2 отразится на величине
ранее найденного момента М1.
Таким образом, взаимодействие соседних пролетов
неразрезной балки выражается в виде двух равных и
противоположно направленных моментов. Эти моменты
М1 и М2 называют опорными моментами.
23.
Для расчета неразрезной многоопорной балки мысленноразрезают ее в сечениях на опорах на ряд
однопролетных балок. На каждую из полученных таким
образом балок действует как непосредственная нагрузка,
так и усилия, передаваемые с соседних участков –
опорные моменты.
Заметим, что опорные моменты представляют собой
изгибающие моменты в сечениях неразрезной балки над
опорами.
Эти опорные моменты МА и МВ мы принимаем за лишние,
неизвестные величины, причем основной статически
определимой системой является ряд простых
однопролетных балок.
24.
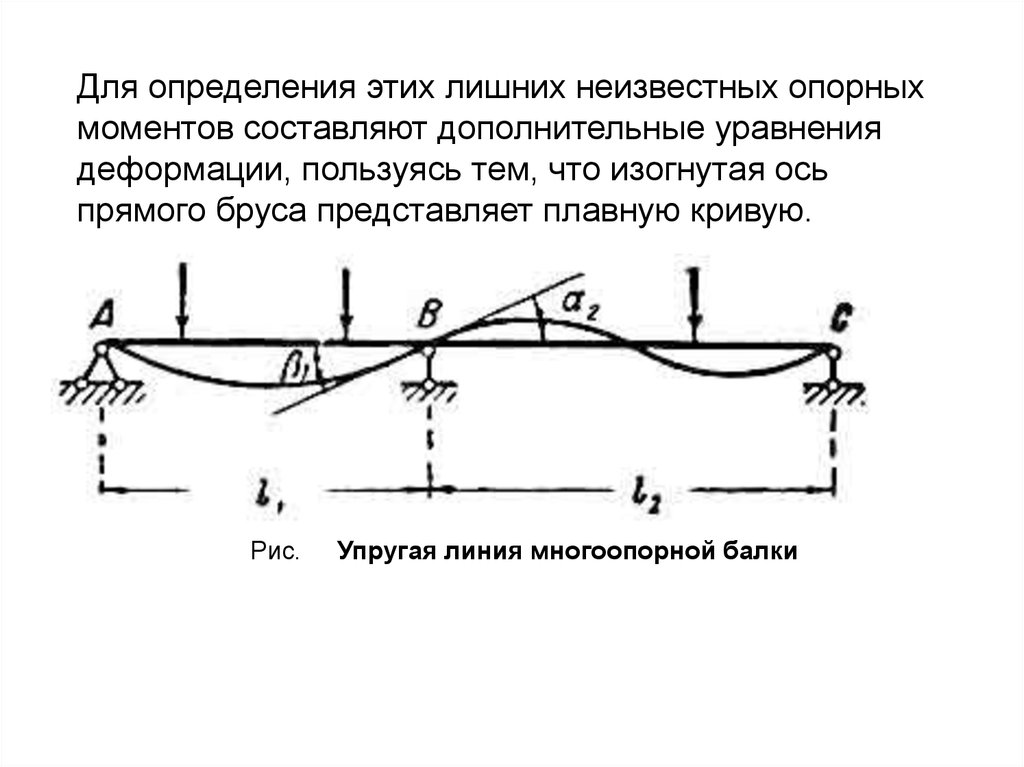
Для определения этих лишних неизвестных опорныхмоментов составляют дополнительные уравнения
деформации, пользуясь тем, что изогнутая ось
прямого бруса представляет плавную кривую.
Рис.
Упругая линия многоопорной балки
25.
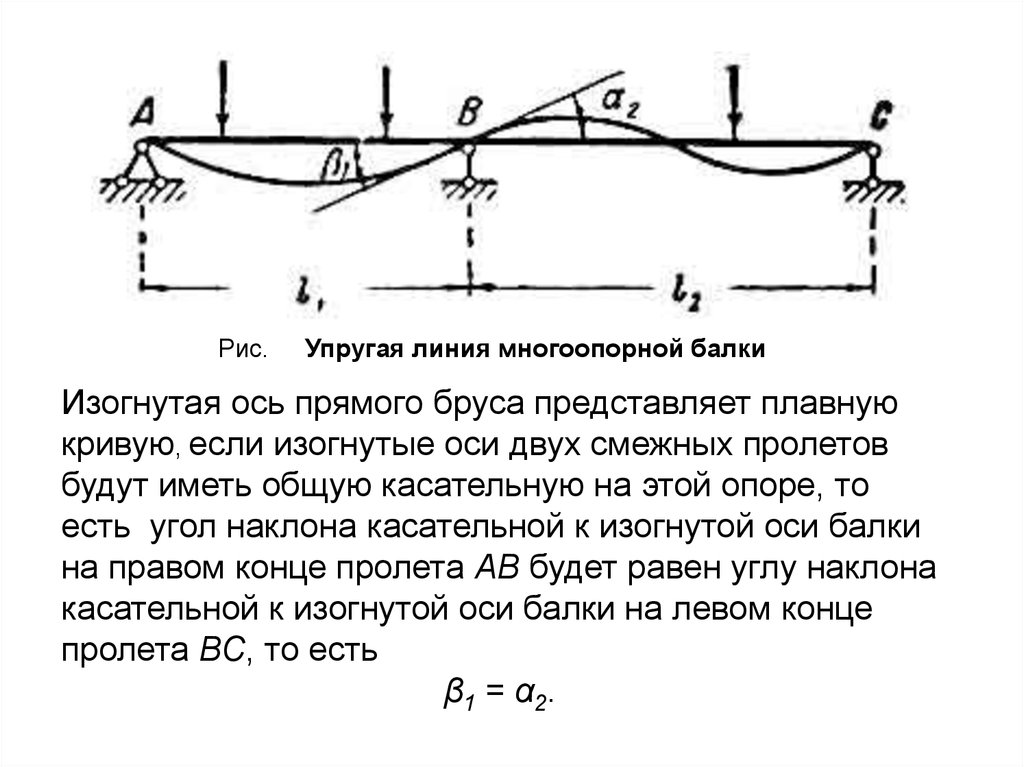
Рис.Упругая линия многоопорной балки
Изогнутая ось прямого бруса представляет плавную
кривую, если изогнутые оси двух смежных пролетов
будут иметь общую касательную на этой опоре, то
есть угол наклона касательной к изогнутой оси балки
на правом конце пролета АВ будет равен углу наклона
касательной к изогнутой оси балки на левом конце
пролета ВС, то есть
β1 = α2.
26.
Определение угла наклона касательной кизогнутой оси балки на конце пролета
достаточно
просто
определить
как
следствие
частного
решения
дифференциального уравнения упругой
линии
балки
на
основе
способа,
предложенного профессором О. Мором (О.
Mohr).
Рис.
Христиан Отто Мор
(нем. Christian Otto Mohr; 8 октября
1835, Вессельбурен — 2 октября
1918, Дрезден) — немецкий инженер
и учёный в области теоретической
механики и сопротивления
материалов
27.
Эпюру изгибающих моментов дляпоследующего удобно считать эпюрой
некоторой фиктивной нагрузки. Иногда
эту нагрузку называют моментной
нагрузкой. Ордината ее изображает
изгибающий момент в данной точке и имеет
размерность
|сила|·|длина|.
Фиктивная нагрузка на некотором участке
АВ есть площадь эпюры изгибающих
моментов на этом участке, то есть
∫Мdx,
имеет размерность
|сила|·|длина|2.
Рис. К определению угла φ
между касательными,
проведенными в двух
произвольных точках
Угол φ равен фиктивной нагрузке
на участке АВ, деленной на
жесткость.
28.
Афn = Ф∙d / l – фиктивная реакцияна опоре А;
Вфn = Ф∙c / l – фиктивная реакция
на опоре В.
Ф – площадь эпюры изгибающих
Рис. К определению фиктивных
реакций двухопорной балки
моментов от заданных нагрузок
(фиктивная нагрузка);
c, d – расстояния от центра
тяжести грузовой площадки Ф
соответственно для левой и правой
опор.
В случае балки на двух опорах углы наклона касательной
на опорах:
α = Афn /EJ и β = Вфn /EJ.
Афn = Ф∙d / l – фиктивная реакция на опоре А;
Вфn = Ф∙c / l – фиктивная реакция на опоре В.
29.
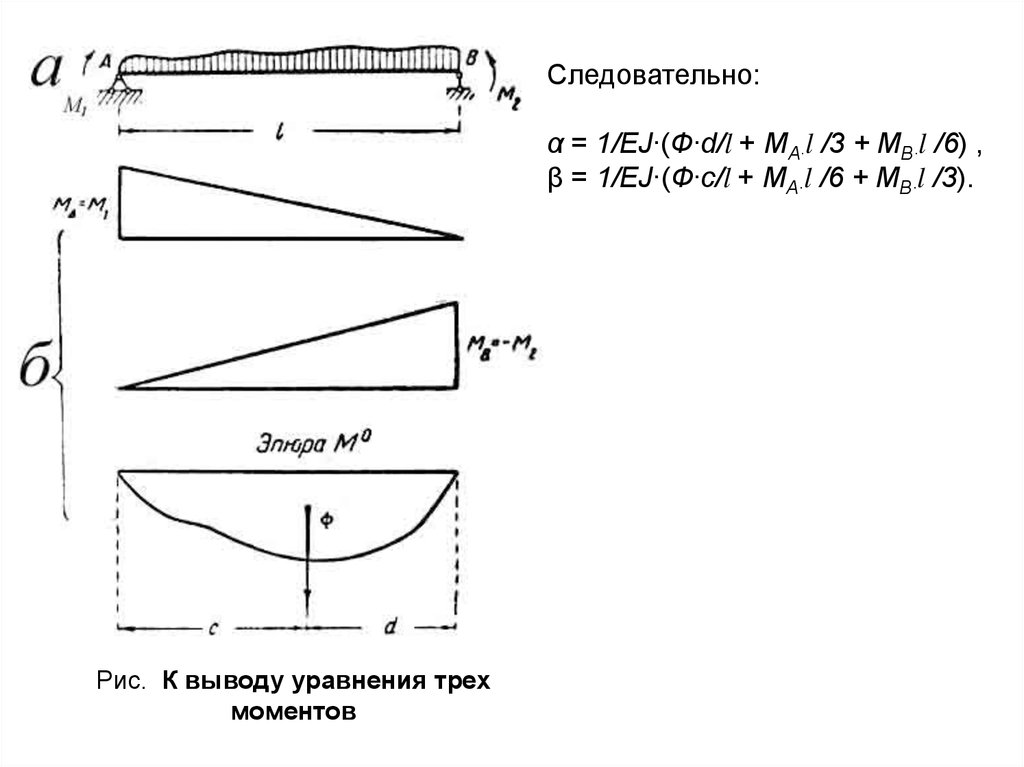
Следовательно:α = 1/EJ∙(Ф∙d/l + МА∙l /3 + МВ∙l /6) ,
β = 1/EJ∙(Ф∙с/l + МА∙l /6 + МВ∙l /3).
Рис. К выводу уравнения трех
моментов
30.
Для трехопорной балки уравнение трех моментовимеет вид
М1∙l1 + 2 М2(l1 + l2) + М3∙l2 = - 6Rф2,
Rф2 – суммарная фиктивная реакция на второй
опоре от фиктивной нагрузки, действующей на
левом и правом пролетах.
Rф2 = Ф2∙d/l + Ф1∙с/l.
31.
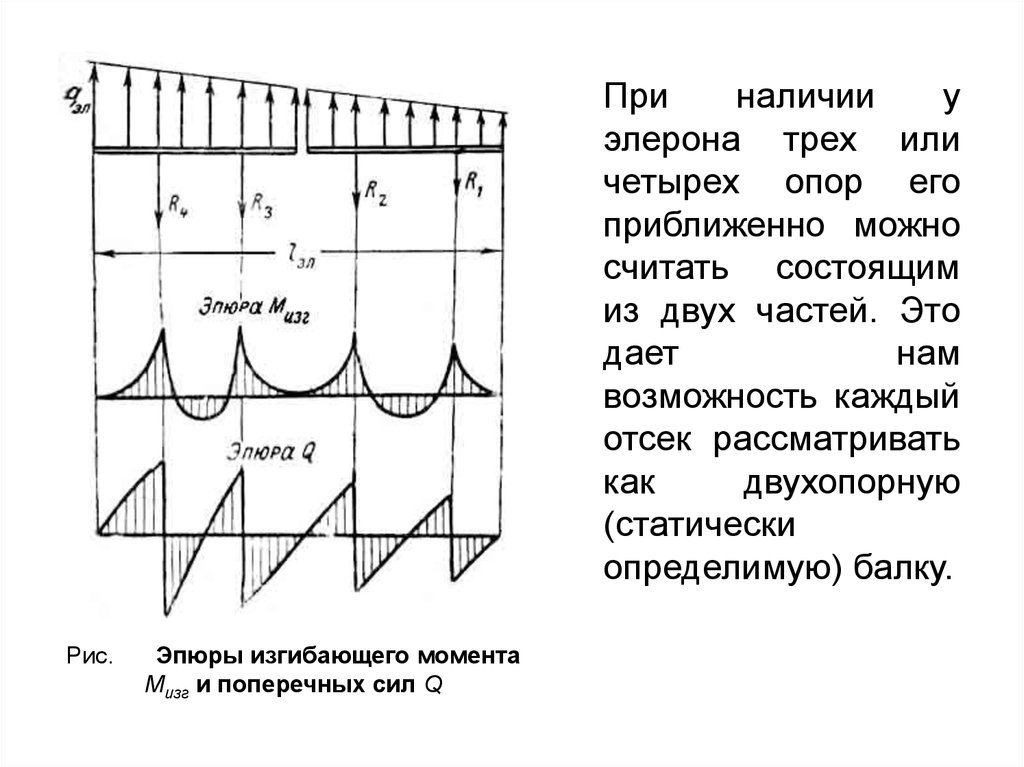
Приналичии
у
элерона трех или
четырех опор его
приближенно можно
считать состоящим
из двух частей. Это
дает
нам
возможность каждый
отсек рассматривать
как
двухопорную
(статически
определимую) балку.
Рис.
Эпюры изгибающего момента
Мизг и поперечных сил Q
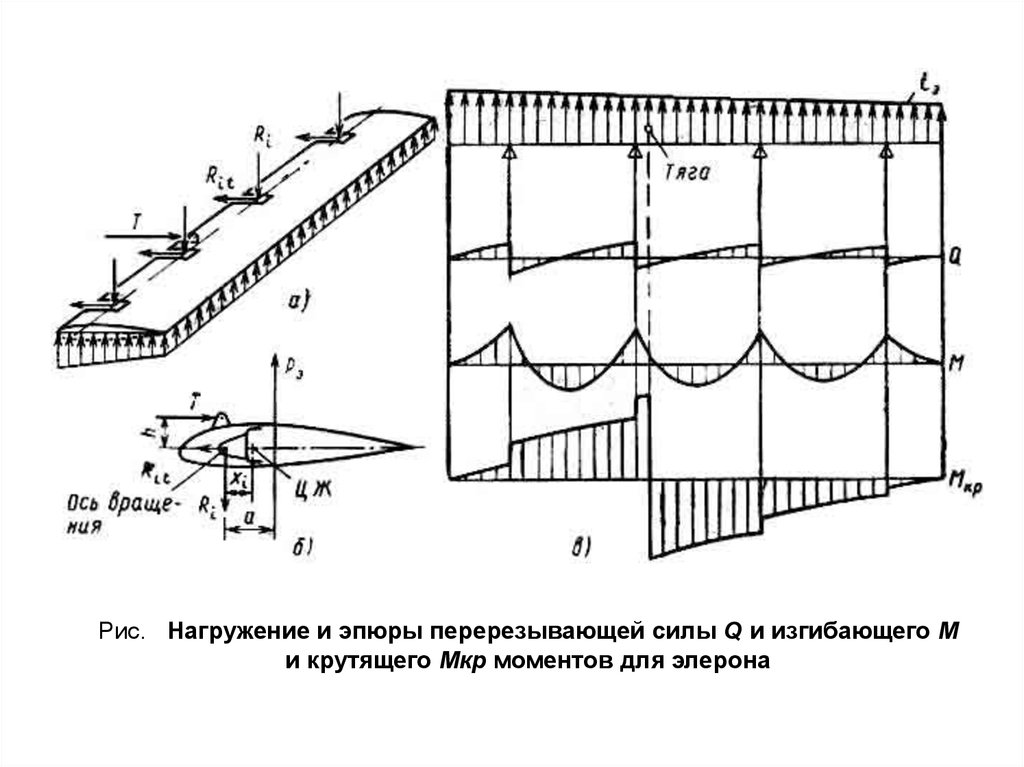
32.
Рис. Нагружение и эпюры перерезывающей силы Q и изгибающего Ми крутящего Мкр моментов для элерона
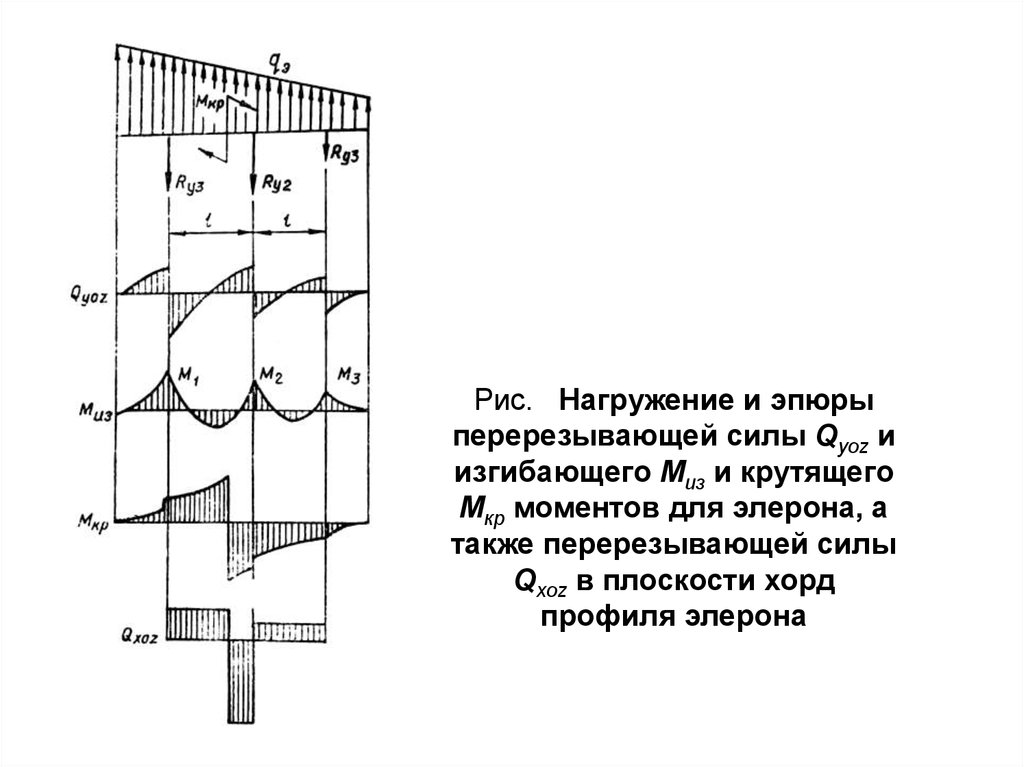
33.
Рис. Нагружение и эпюрыперерезывающей силы Qyoz и
изгибающего Миз и крутящего
Мкр моментов для элерона, а
также перерезывающей силы
Qxoz в плоскости хорд
профиля элерона
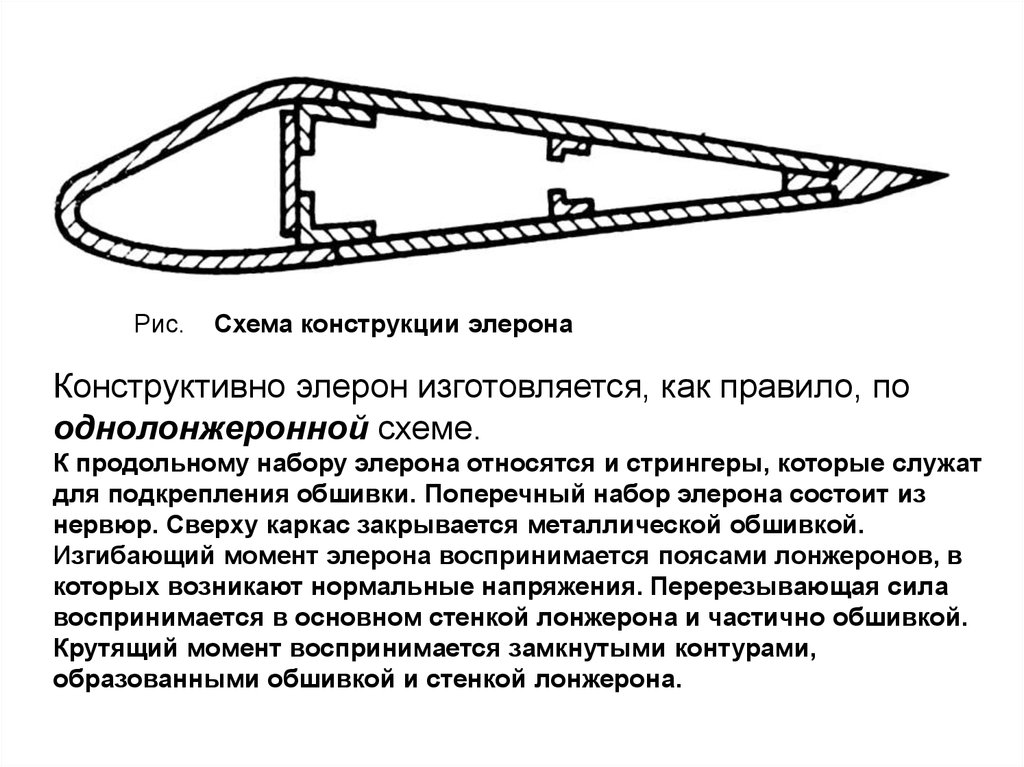
34.
Рис.Схема конструкции элерона
Конструктивно элерон изготовляется, как правило, по
однолонжеронной схеме.
К продольному набору элерона относятся и стрингеры, которые служат
для подкрепления обшивки. Поперечный набор элерона состоит из
нервюр. Сверху каркас закрывается металлической обшивкой.
Изгибающий момент элерона воспринимается поясами лонжеронов, в
которых возникают нормальные напряжения. Перерезывающая сила
воспринимается в основном стенкой лонжерона и частично обшивкой.
Крутящий момент воспринимается замкнутыми контурами,
образованными обшивкой и стенкой лонжерона.
35.
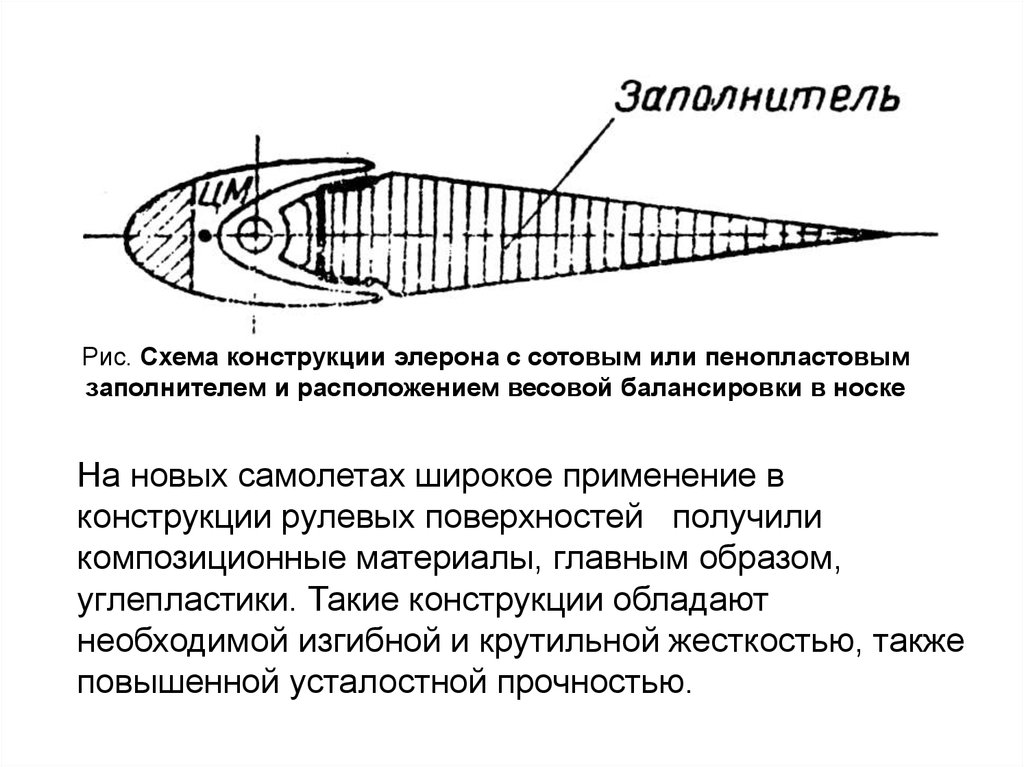
Рис. Схема конструкции элерона с сотовым или пенопластовымзаполнителем и расположением весовой балансировки в носке
На новых самолетах широкое применение в
конструкции рулевых поверхностей получили
композиционные материалы, главным образом,
углепластики. Такие конструкции обладают
необходимой изгибной и крутильной жесткостью, также
повышенной усталостной прочностью.
36.
Рис. Конструктивная схема элерона – компенсация выреза вноске элерона
37.
Рис. Крепление элеронаПодвеска элеронов осуществляется специальными сварными,
литыми или клепаными узлами. Получающийся вырез жесткой
обшивки носка при швеллерном лонжероне компенсируется
косыми нервюрами, поверх которых кладут жесткую обшивку.
38.
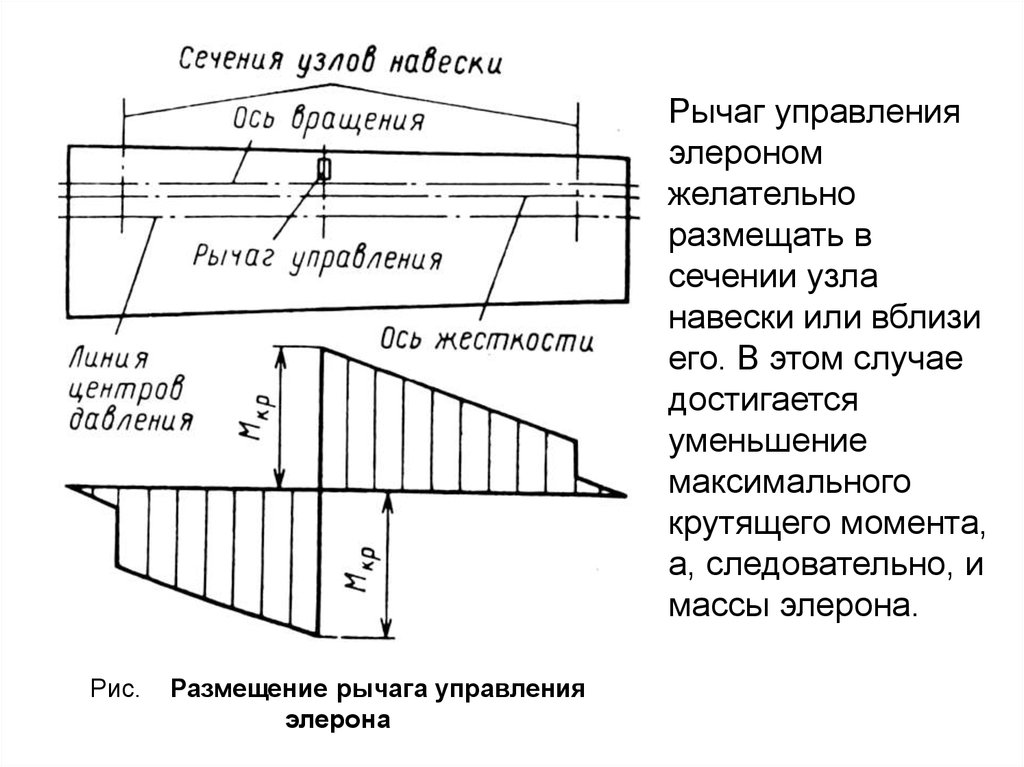
Рычаг управленияэлероном
желательно
размещать в
сечении узла
навески или вблизи
его. В этом случае
достигается
уменьшение
максимального
крутящего момента,
а, следовательно, и
массы элерона.
Рис.
Размещение рычага управления
элерона
39.
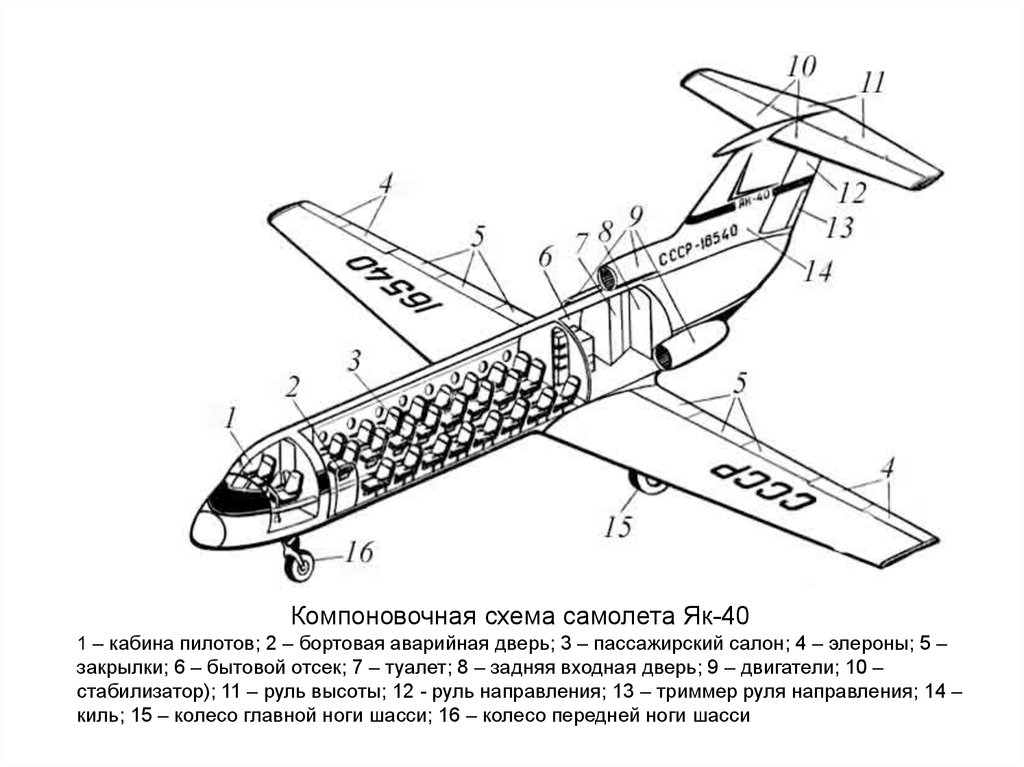
Компоновочная схема самолета Як-401 – кабина пилотов; 2 – бортовая аварийная дверь; 3 – пассажирский салон; 4 – элероны; 5 –
закрылки; 6 – бытовой отсек; 7 – туалет; 8 – задняя входная дверь; 9 – двигатели; 10 –
стабилизатор); 11 – руль высоты; 12 - руль направления; 13 – триммер руля направления; 14 –
киль; 15 – колесо главной ноги шасси; 16 – колесо передней ноги шасси
40.
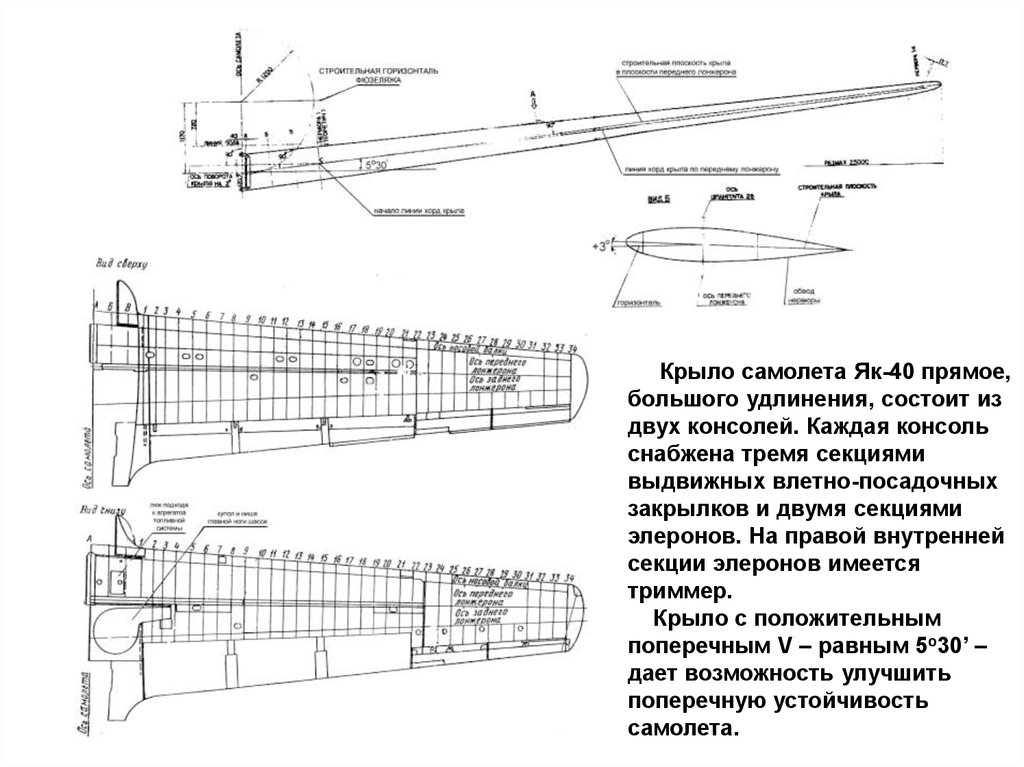
КрылоКрыло самолета Як-40 прямое,
большого удлинения, состоит из
двух консолей. Каждая консоль
снабжена тремя секциями
выдвижных влетно-посадочных
закрылков и двумя секциями
элеронов. На правой внутренней
секции элеронов имеется
триммер.
Крыло с положительным
поперечным V – равным 5о30’ –
дает возможность улучшить
поперечную устойчивость
самолета.
41.
На каждой консоли крыла междунервюрами № 22…28 и 28…34
расположены соответственно корневая
и концевая секции элеронов, имеющие
весовую балансировку и
аэродинамическую компенсацию. Для
обеспечения весовой балансировки к
носкам секций приклепаны выносные
балансиры 10. Кроме того, носок
концевой секции за средним узлом
подвески выполнен в виде
балансировочного груза 2. В средней
части каждой секции снизу к
лонжерону прикреплен рычаг 13 для
тяги управления.
Для ограничения углов отклонения
элеронов служат неподвижные упоры,
установленные в хвостовой части
нервюры № 22, и подвижный упор,
установленный в носке корневой
секции элерона. Неподвижные упоры
выполнены в виде двух кронштейнов с
регулировочными болтами.
Правый элерон самолета Як-40:
1 – концевой элерон; 2, 10 – грузы; 3 – торцовый узел подвески; 4 -, 11 – серьга среднего узла; 5 –
шплинт; 6 -, 15 – торцовые кронштейны; 7 – серьги; 8 – подшипник; 9 – штырь; 12 – втулка; 1 3 –
рычаг крепления тяги управления; 14 – ось; 16 – крышка люка механизма триммера; 17 –
триммер; 18 =- корневой элерон; 19 – стыковочный болт; 20 – вильчатый кронштейн; 21 –
крепежные болты; 12 – нож; 23 – подвижный упор; 24 – регулируемый упор; 25 кронштейн
42.
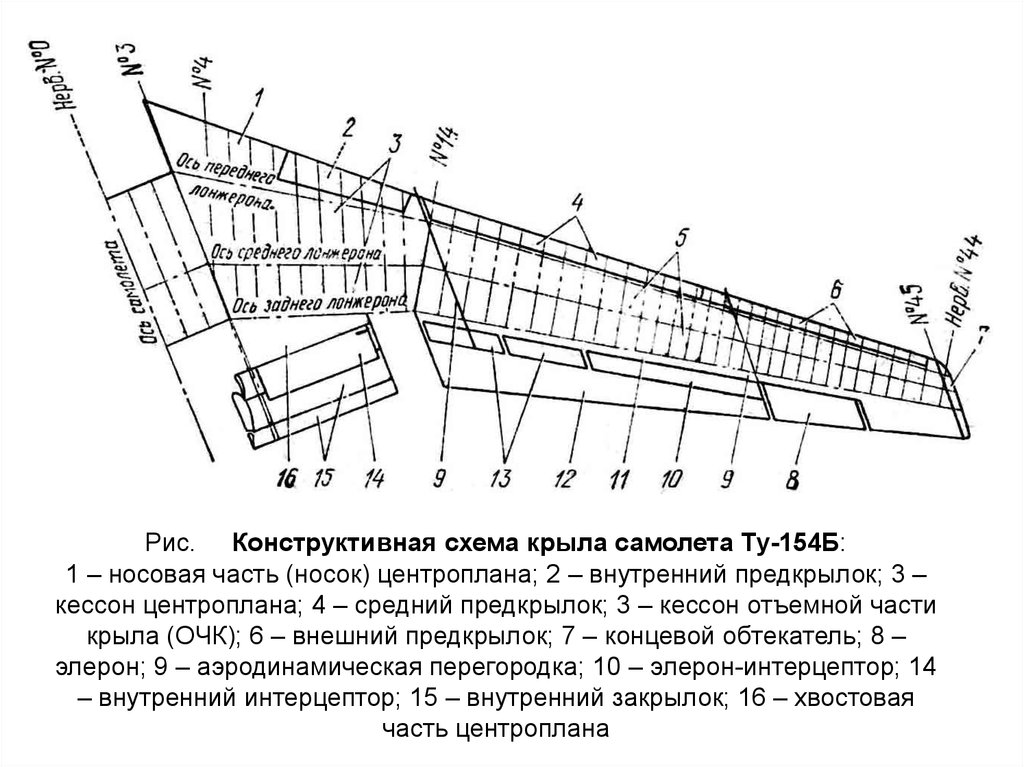
Рис. Конструктивная схема крыла самолета Ту-154Б:1 – носовая часть (носок) центроплана; 2 – внутренний предкрылок; 3 –
кессон центроплана; 4 – средний предкрылок; 3 – кессон отъемной части
крыла (ОЧК); 6 – внешний предкрылок; 7 – концевой обтекатель; 8 –
элерон; 9 – аэродинамическая перегородка; 10 – элерон-интерцептор; 14
– внутренний интерцептор; 15 – внутренний закрылок; 16 – хвостовая
часть центроплана
43.
Санкт-Петербургский государственный университет гражданской авиацииКафедра № 24 - «Авиационной техники»
Использованная литература:
1. Конструкция и прочность летательных аппаратов гражданской авиации:
Учебник для вузов гражданской авиации/ М. С. Воскобойник, П. Ф.
Максютинский, К. Д. Миртов и др.; Под общ. Ред. К. Д. Миртова, Ж. С.
Черненко. – М.: Машиностроение, 1991. – 448 с.: ил.
2. Черненко Ж. С. Сабитов Н. Г., Гаража В. В. и др. Конструкция и
прочность воздушных судов: Учебное пособие / Ж. С. Черненко, Н. Г.
Сабитов, В. В. Гаража, И. П. Челюканов, И. Г. Павлов. – Киев : КИИГА,
1985. – 88 с.
3. Гребеньков О. А. Конструкция самолетов: Учеб. пособие для авиационных
вузов. – М.: Машиностроение, 1984. – 240 с., ил.
4. Кузнецов А. Н. Основы конструкции и технической эксплуатации
воздушных судов: Учеб. для сред. Спец. Учеб. заведений. М.: Транспорт,
1990. – 294 с.
5. Кан С. Н. Прочность самолета: Учеб. пособие для авиационных
техникумов. – М: Оборонгиз, 1946. - 292 с.
Якущенко В.Ф. Конструкция и прочность воздушных судов:
Учебное пособие / СПбГУГА. С.-Петербург, 2009.







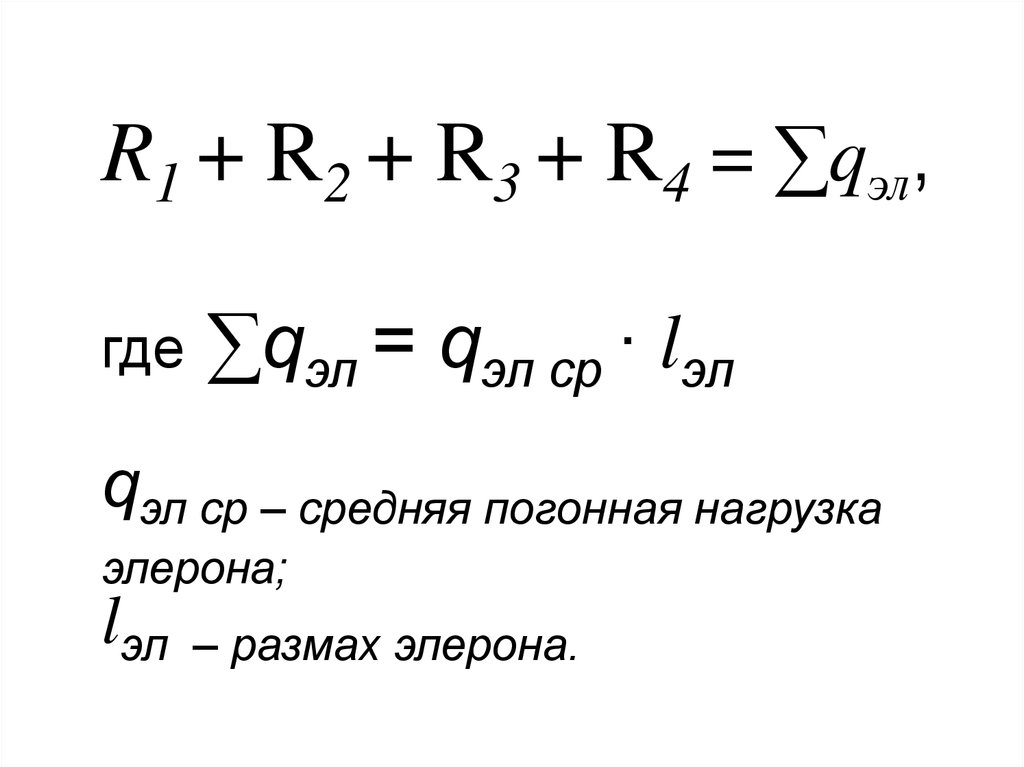















 Промышленность
Промышленность








