Расчет крыла на прочность

1.

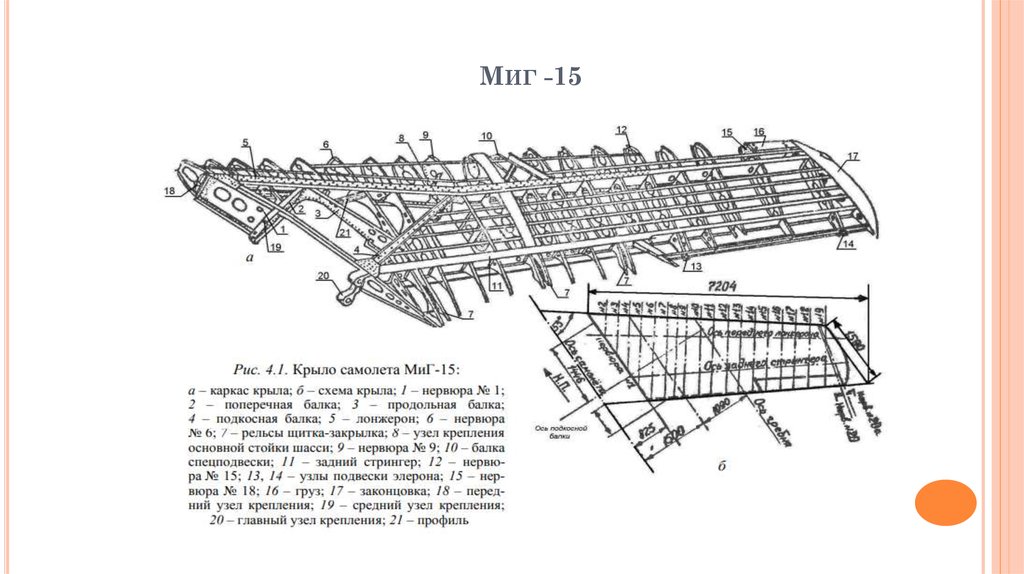
2. Миг -15

МИГ -15

3. Су-15

СУ-15

4. МЕТОДИКА РЕШЕНИЯ ЗАДАЧИ

1.
2.
3.
4.
5.
Выбор прототипа самолета и определение его характеристик
Выбор расчетного случая, определяющего характер нагрузок
Определение нагрузок на крыло
Определение положения центра давления по сечениям крыла
Построение эпюр перерезывающих сил и моментов

5.

Основные исходные данные
1.
Взлетный вес самолета G0, вес крыла Gкр и максимальная эксплуатационная
перегрузка nЭymax. Определяются прототипом и классом самолета.
Максимальные эксплуатационные перегрузки
Тип самолета
Легкий учебный или спортивный самолет
Легкий скоростной пассажирский самолет
Средний магистральный пассажирский самолет
Тяжелый транспортный или пассажирский самолет
nЭymax
8-9
4-6
3-4
2-3

6.

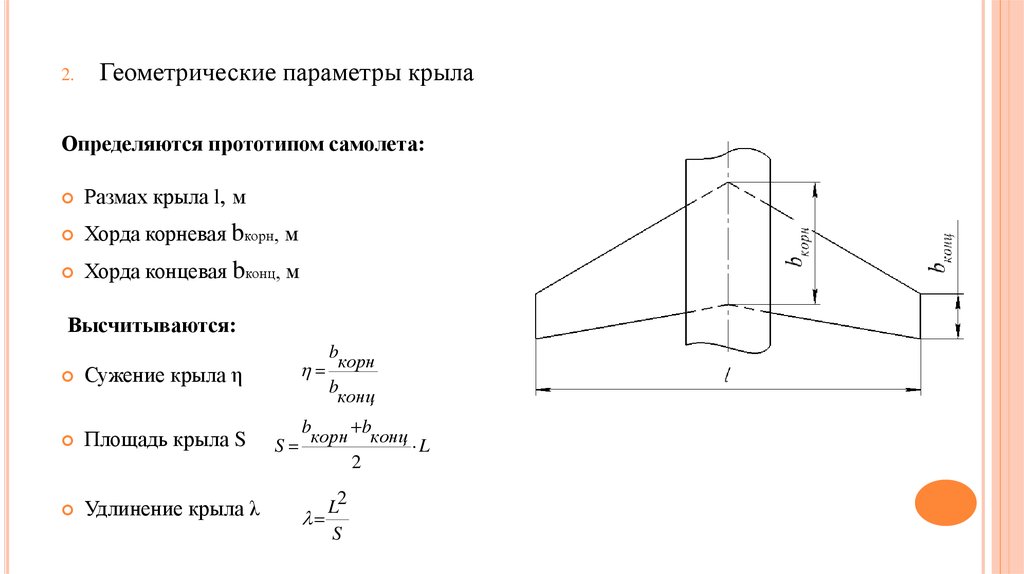
2.
Геометрические параметры крыла
Определяются прототипом самолета:
Размах крыла l, м
Хорда корневая bкорн, м
Хорда концевая bконц, м
Высчитываются:
Сужение крыла η
Площадь крыла S
Удлинение крыла λ
b
корн
b
конц
b
b
корн
конц L
S
2
L2
S

7. Расчетный случай, определяющий совокупность и характер нагрузок на самолет

РАСЧЕТНЫЙ СЛУЧАЙ, ОПРЕДЕЛЯЮЩИЙ СОВОКУПНОСТЬ И ХАРАКТЕР
НАГРУЗОК НА САМОЛЕТ
Расчетный случай определяет следующие параметры расчета:
коэффициент безопасности f;
перегрузку ny;
коэффициент подъемной силы cy;
скоростной поток q.
Максимальную эксплуатационную перегрузку определяют:
э
n y max 3,8 при m ≤ 8000 кг
э
n y max 2,5 при m ≤ 27500 кг
Для промежуточных значений полетной массы перегрузка равна:
250
э
n y max 1
m
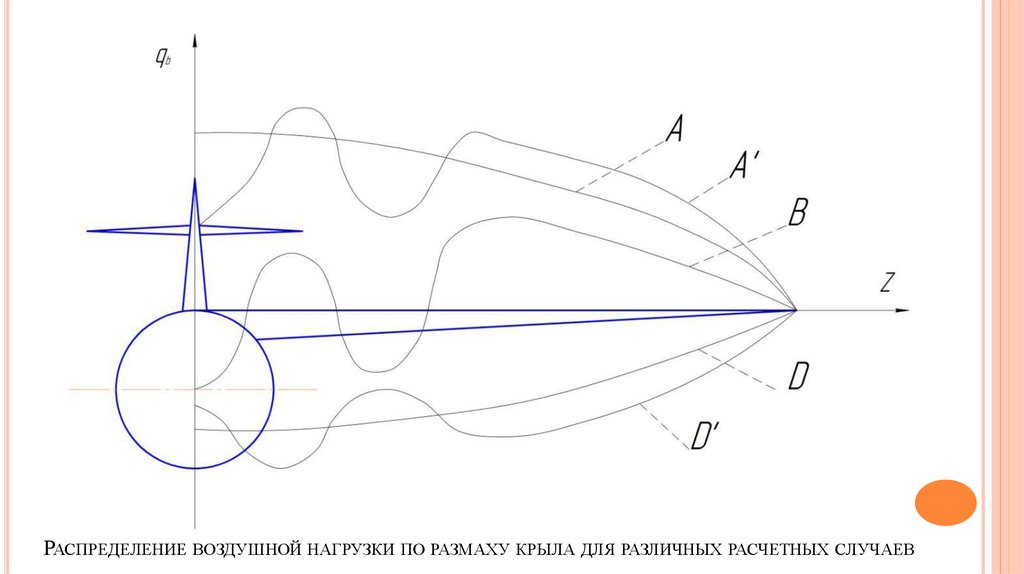
Основные полетные расчетные случаи делятся на:
А, А', В, С, D, D'
Как правило выбирается случай A или A’.

8.

Расчетный
случай
ny
q
cy
f
A
Криволинейный полет. Горка, выход из
пикирования. Действие вертикального порыва
ветра.
n yэ max
-
cyma
1.5
A’
Криволинейный полет. Выход из пикирования.
Полет в болтанку. Полет на большой скорости.
n yэ max
qmax
-
1.5
B
Криволинейный полет на малых углах атаки с
отклоненными элеронами
Вертикальное пикирование с отклоненными
элеронами.
0.5nyэ max qmax
-
1.5
0
2.0
C
Описание
D
Криволинейный полет на углах атаки,
соответствующих cymin. Резкий переход на
планирование, полет в неспокойном воздухе.
Характерен обратным нагружением
D’
Криволинейный полет при небольших
отрицательных углах атаки. налогичен случаю D,
но при больших скоростях полета
0
0.5n
qmax
э
y max
-
0.5n yэ max qmax
x
cymin 1.5
-
1.5

9. Определение нагрузок на крыло

В общем случае на крыло воздействуют следующие нагрузки:
Аэродинамические нагрузки, распределенные по поверхности крыла.
Объемные массовые силы от конструкции крыла и топлива, размещенного в крыле, а также
сосредоточенные силы от масс агрегатов, расположенных на крыле (двигатель, топливные
баки, шасси).
Тепловой нагрев от скоростного напора.
В расчете будем учитывать только первые два вида нагрузки аэродинамическую и массовую.

10. Определение аэродинамических и массовых нагрузок на крыло

ОПРЕДЕЛЕНИЕ АЭРОДИНАМИЧЕСКИХ И МАССОВЫХ НАГРУЗОК НА
,
КРЫЛО
Sq или Y fn G
Величина подъемной силы крыла определяется по формуле: Y cкр
y
э
кр
c
где y – коэффициент подъемной силы крыла;
S – площадь крыла;
V 2 – скоростной напор;
q
2
G – вес самолета.
Массовые силы определяются по формуле:
P fn G
кр
э кр
где Gкр – вес конструкции крыла.
Нагрузки от агрегатов, расположенных в крыле определяются аналогично: Pагрi fnэGагрi
где Gагрi – вес i-го агрегата.

11. Распределение нагрузок по длине крыла

РАСПРЕДЕЛЕНИЕ НАГРУЗОК ПО ДЛИНЕ КРЫЛА
Распределение аэродинамических нагрузок
Распределение погонной аэродинамической нагрузки вдоль крыла производится по закону
распределения подъемной силы по длине крыла:
fn G
cos
, где Г сумм - величина суммарной циркуляции;
q э Г сум
y
L
cos
a – угол атаки крыла;
– угол между вектором равнодействующей аэродинамических сил и вектором подъемной
силы крыла – tg cxкк c yкк
Для упрощения рекомендуется использовать специальные упрощенные таблицы
распределения относительной циркуляции плоского крыла. При этом разрешается
использовать ближайший столбец по значению , а интерполировать только по 2Lц L

12.

Относительная циркуляция крыла Г сумм учитывает неравномерность распределения
аэродинамической нагрузки (изменение коэффициента подъемной силы) по размаху крыла.
У прямого крыла величина циркуляции зависит от сужения крыла η.
Относительная циркуляция крыла определяется экспериментально или приближенно по
графикам, приведенным в нормах прочности для крыльев различной формы в плане.
В качестве примера представлен подобный график зависимости f 2 z ;
пр
где z – текущая координата по полуразмаху крыла L/2;
bкорн
bкорн
- сужение крыла.
Зависимость относительной циркуляции пр от
сужения крыла η
L

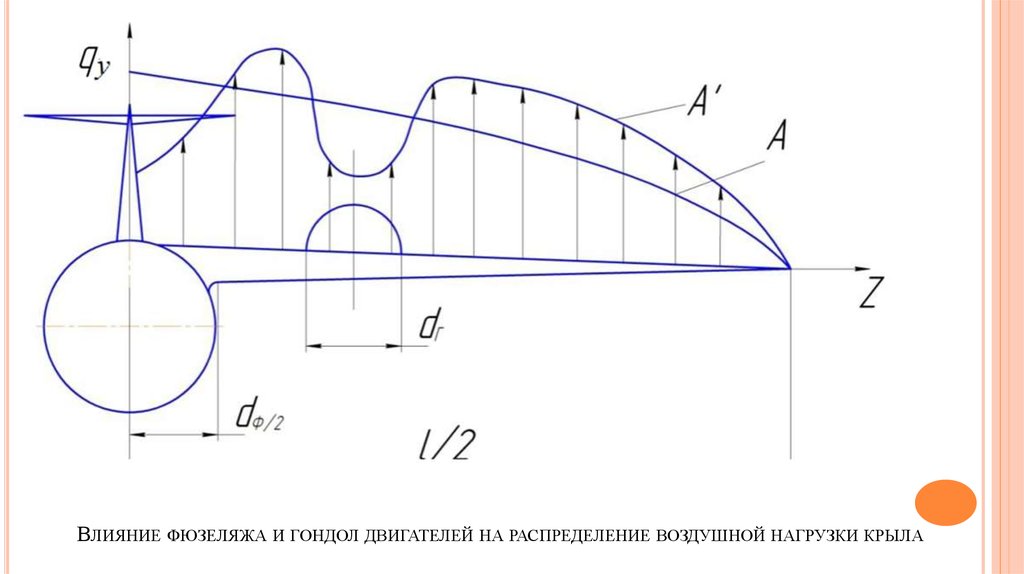
13. Распределение воздушной нагрузки по размаху крыла для различных расчетных случаев

РАСПРЕДЕЛЕНИЕ ВОЗДУШНОЙ НАГРУЗКИ ПО РАЗМАХУ КРЫЛА ДЛЯ РАЗЛИЧНЫХ РАСЧЕТНЫХ СЛУЧАЕВ

14.

Распределение массовых нагрузок
Вес конструкции крыла Gкр задан в задании (без агрегатов). Распределение его по размаху
производится либо на основании существующих взвешиваний или расчетов., а при отсутствии
таковых допускается использование распределения массы по длине крыла пропорционально
хордам
P b fn G b
кр
э кр
*
q
кр
S
S
где Gкр – вес крыла;
b – величина хорды в данном сечении;
S – площадь крыла.
Для стреловидного крыла дополнительно учитываем стреловидность
fn G b
э кр cos
q
cos
кр
S
cos
где χ – угол стреловидности по линии 1/4 хорд.

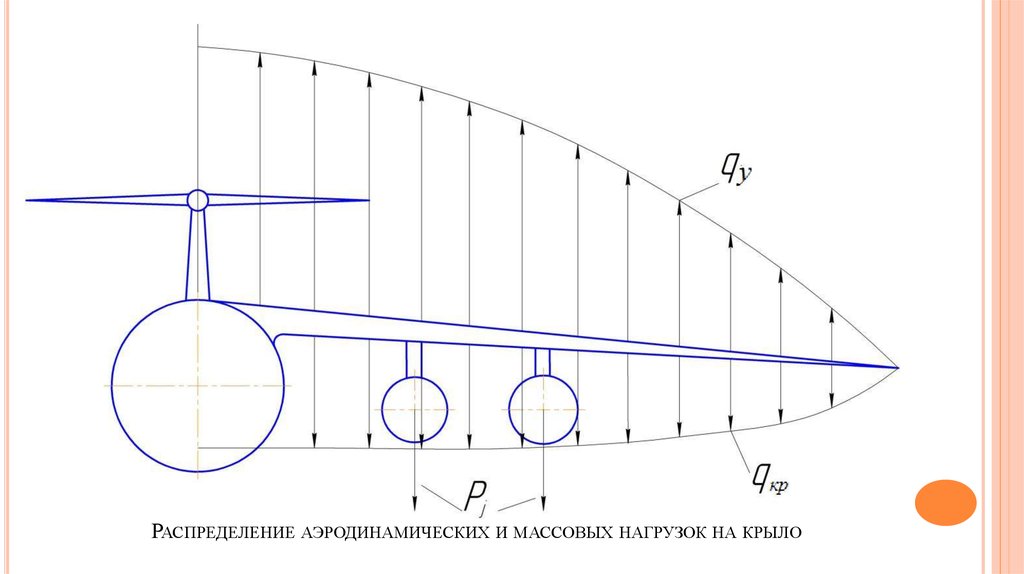
15. Распределение аэродинамических и массовых нагрузок на крыло

РАСПРЕДЕЛЕНИЕ АЭРОДИНАМИЧЕСКИХ И МАССОВЫХ НАГРУЗОК НА КРЫЛО

16. Влияние фюзеляжа и гондол двигателей на распределение воздушной нагрузки крыла

ВЛИЯНИЕ ФЮЗЕЛЯЖА И ГОНДОЛ ДВИГАТЕЛЕЙ НА РАСПРЕДЕЛЕНИЕ ВОЗДУШНОЙ НАГРУЗКИ КРЫЛА

17. Определение положения центра давления по сечениям крыла

ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ ЦЕНТРА ДАВЛЕНИЯ ПО СЕЧЕНИЯМ КРЫЛА
Точка приложения воздушной нагрузки в сечении крыла называется центром давления
c
Х
y cm0
Д
XД
, где Хд – расстояние от носка профиля до центра
кр
b z c
m cy
c
y
– абсолютное значение производной для профиля, берется из
c
m
cm 0
профильной характеристики;
– коэффициент момента
Эти параметры могут задаваться в задании в качестве
характеристик крыла (вернее профиля крыла) или определяются
кр
c
прототипом, а
при c y 0 либо определяется заданием, либо
y
вычисляется по формуле
кр
c
y
n G Sq
э
давления;

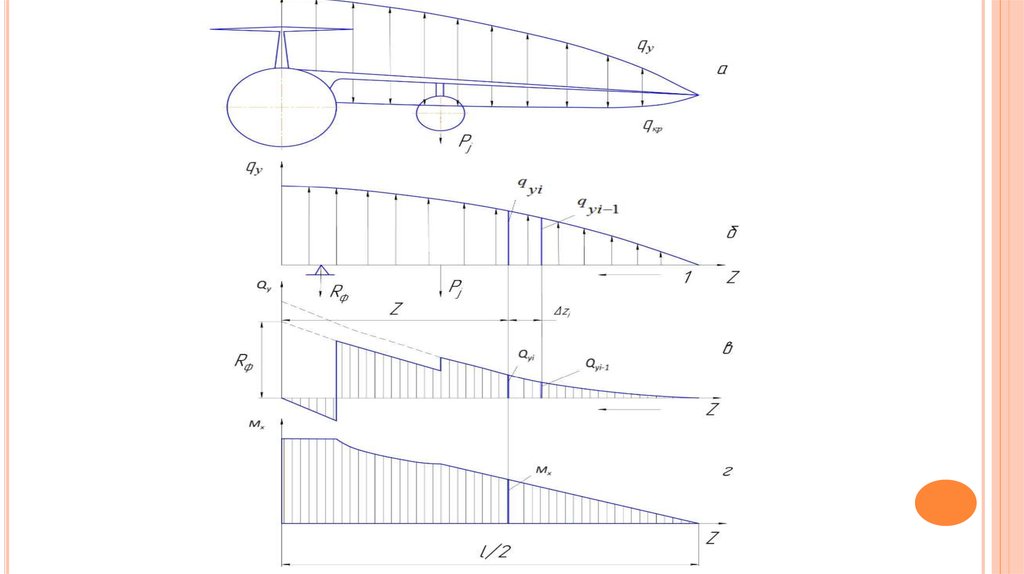
18. Построение эпюр перерезывающих сил и моментов крыла

ПОСТРОЕНИЕ ЭПЮР ПЕРЕРЕЗЫВАЮЩИХ СИЛ И МОМЕНТОВ КРЫЛА
Для расчета крыла в отдельных его сечениях необходимо знать величину перерезывающей
силы Qy изгибающего момента Mx и крутящего момента Mz
С этой целью следует построить эпюры Qy Mx Mz для крыла, как для двухопорной балки,
нагруженной распределенными и сосредоточенными силами. Опорами крыла являются узлы
его крепления к фюзеляжу.
Допустимо в качестве расчетной схемы принять консоль крыла здесь в виде балки,
защемленной в плоскости симметрии самолета.
Для определения распределения перерезывающих сил Qy и изгибающих моментов Mx
необходимо вычислить значение интегралов
Z
Q q( z )dz P
y
агр
L/2
Z
M Q ( z )dz
x
y
L/2
и
Дополнительно необходимо учитывать массовые силы от агрегатов находящихся на крыле.
Величина усилия в направлении перпендикулярном хорде вычисляется так
cos
P fn G
, где q – угол между вектором равнодействующей аэродинамических сил и
i
э агрi cos
вектором подъемной силы крыла – tg cxкк c yкк

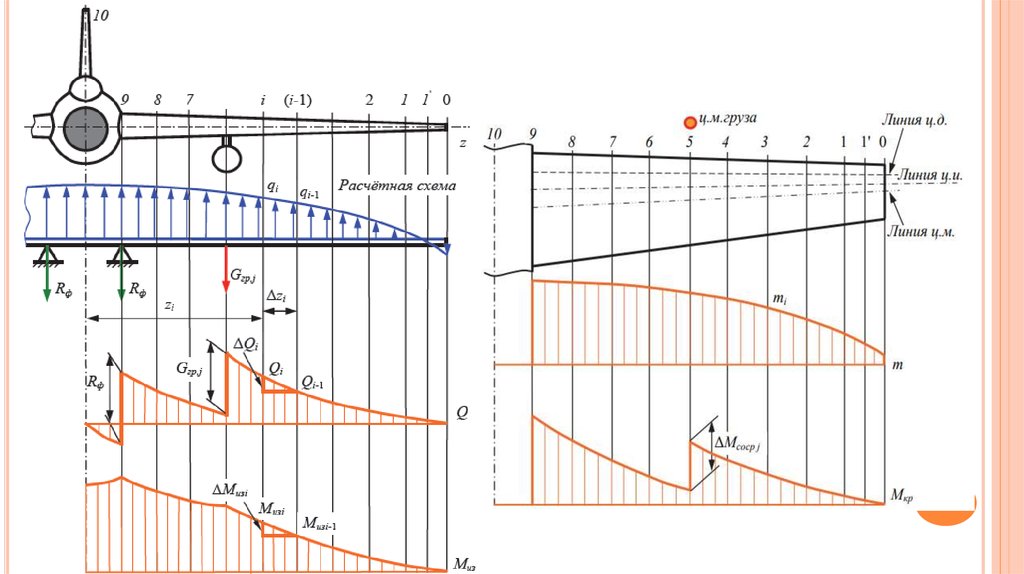
19.

Каждый агрегат дает в своем сечении скачок эпюры перерезывающих сил Qy на величину Рi Также
каждый агрегат вносит поправку в эпюру изгибающих моментов Mx. Величина поправки
P (Z Z
) ,
xаагр i i
агрi
где Zi – координата сечения;
Zагрi – координата агрегата.
Эпюра крутящих моментов Mz строится относительно оси жесткости крыла. Если ось жесткости не
определена, то эпюра крутящих моментов строится относительно произвольной оси параллельной
оси Z.
m q a q ,c
Предварительно строится эпюра погонных изгибающих моментов mz
z
y
кр
где a – расстояние от оси центров давления до оси Z;
c – расстояние от оси центров тяжести до оси Z.
В целях сокращения вычислений можно приближенно принимать центр тяжести в следующих
пределах:
- для прямого крыла хТ = (0,42 ... 0,45) b;
- для стреловидного крыла хТ = (0,38 ... 0,42) b;
- для треугольного крыла хТ = (0,40 ... 0,44) b.
Для построения эпюры крутящих моментов необходимо
Z
вычислить интеграл
M
M m ( z )dz
z
z
L/2