2 урок Случайные события, вероятности и частоты.pp

1.

2.

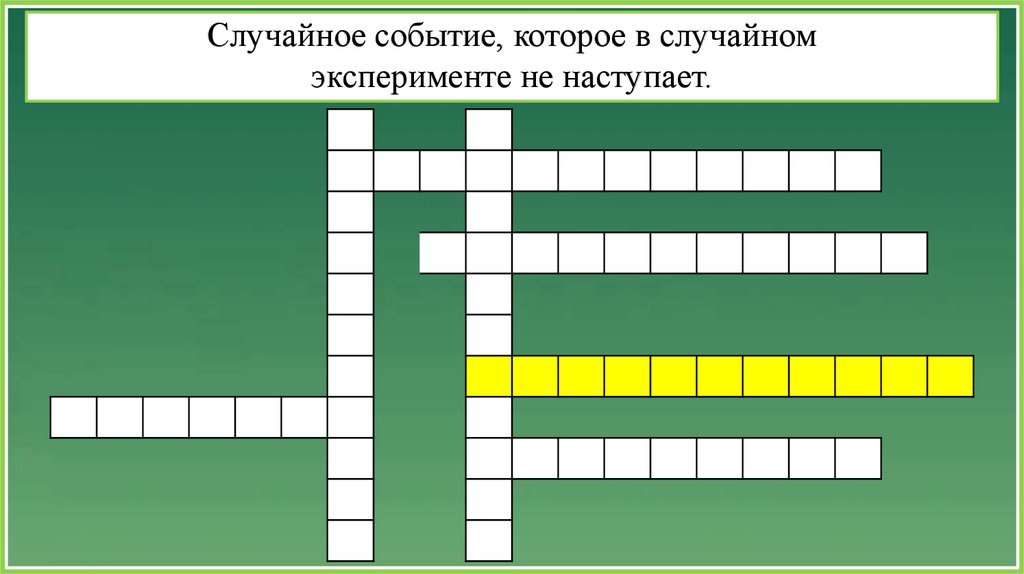
Случайное событие, которое в случайном
эксперименте не наступает.

3.

Случайное событие, которое в случайном
эксперименте не наступает.
Н
Е
В
О
З
М О
Ж Н
О
Е

4.

Случайное событие, которое в случайном
эксперименте обязательно наступает.
Н
Е
В
О
З
М О
Ж Н
О
Е

5.

Случайное событие, которое в случайном
эксперименте обязательно наступает.
Д
О
С
Т
О
В
Е
Р
Н
Е
В
О
З
М О
Н
О
Е
Ж Н
О
Е

6.

Событие, которое в случайном эксперименте
может произойти, а может не произойти.
Д
О
С
Т
О
В
Е
Р
Н
Е
В
О
З
М О
Н
О
Е
Ж Н
О
Е

7.

Событие, которое в случайном эксперименте
может произойти, а может не произойти.
Д
О
С
Т
О
В
Е
Н
Е
В
О
З
С
Л
У
Ч
А
Р
О
Е
М О
Ж Н
О
Й
О
Н
Н
Е
Е

8.

Численная мера объективной
возможности наступления события.
Д
О
С
Т
О
В
Е
Н
Е
В
О
З
С
Л
У
Ч
А
Р
О
Е
М О
Ж Н
О
Й
О
Н
Н
Е
Е

9.

Численная мера объективной
возможности наступления события.
В
Е
Р
Д
О
С
Т
О
В
Е
Е
В
О
З
Л
У
Ч
А
Р
Н
О
Е
М О
Ж Н
О
Й
О
Я
Т
Н
О
С
Т
Ь
Н
Е
Е

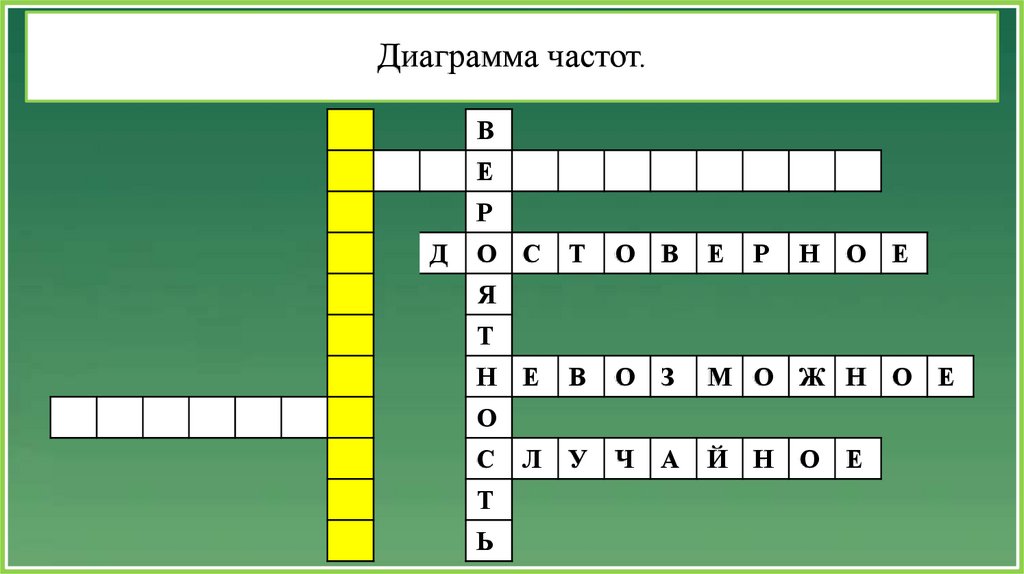
10.

Диаграмма частот.
В
Е
Р
Д
О
С
Т
О
В
Е
Е
В
О
З
Л
У
Ч
А
Р
Н
О
Е
М О
Ж Н
О
Й
О
Я
Т
Н
О
С
Т
Ь
Н
Е
Е

11.

Диаграмма частот.
Г
В
И
Е
С
Р
Т
Д
О
О
Я
Г
Т
Р
Н
А
О
М
С
М
Т
А
Ь
С
Т
О
В
Е
Е
В
О
З
Л
У
Ч
А
Р
О
Е
М О
Ж Н
О
Й
О
Н
Н
Е
Е

12.

Непостоянство величины, обусловленное
действием случайных причин.
Г
В
И
Е
С
Р
Т
Д
О
О
Я
Г
Т
Р
Н
А
О
М
С
М
Т
А
Ь
С
Т
О
В
Е
Е
В
О
З
Л
У
Ч
А
Р
О
Е
М О
Ж Н
О
Й
О
Н
Н
Е
Е

13.

Непостоянство величины, обусловленное
действием случайных причин.
Г
И
В
З
М Е
С
Т
Н
Ч
И
В
О
С
Т
Ь
С
Т
О
В
Е
Р
Н
О
Е
Е
В
О
З
М О
Ж Н
О
Л
У
Ч
А
Й
О
Р
Д
О
О
Я
Г
Т
Р
Н
А
О
М
С
М
Т
А
Ь
Н
Е
Е

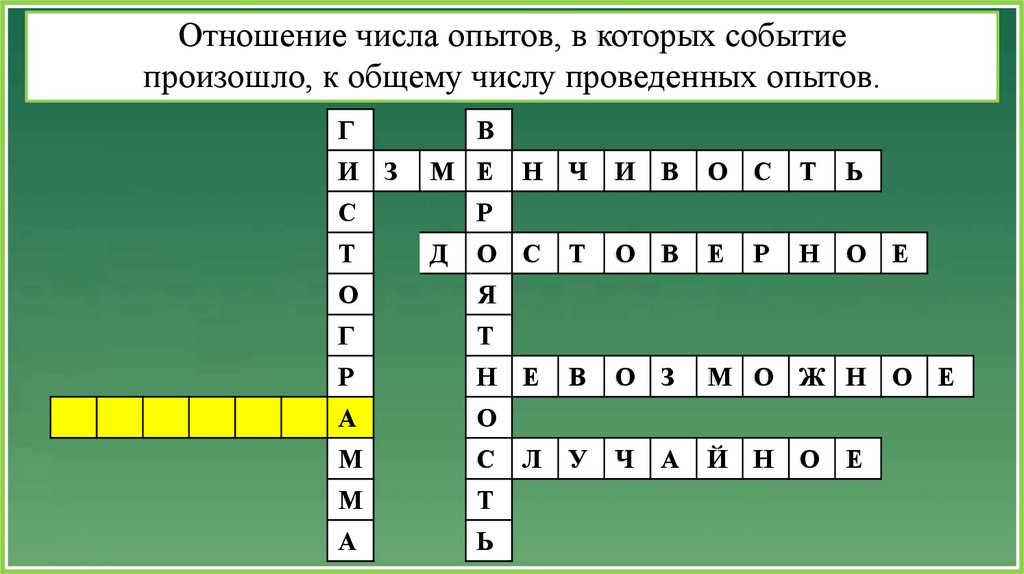
14.

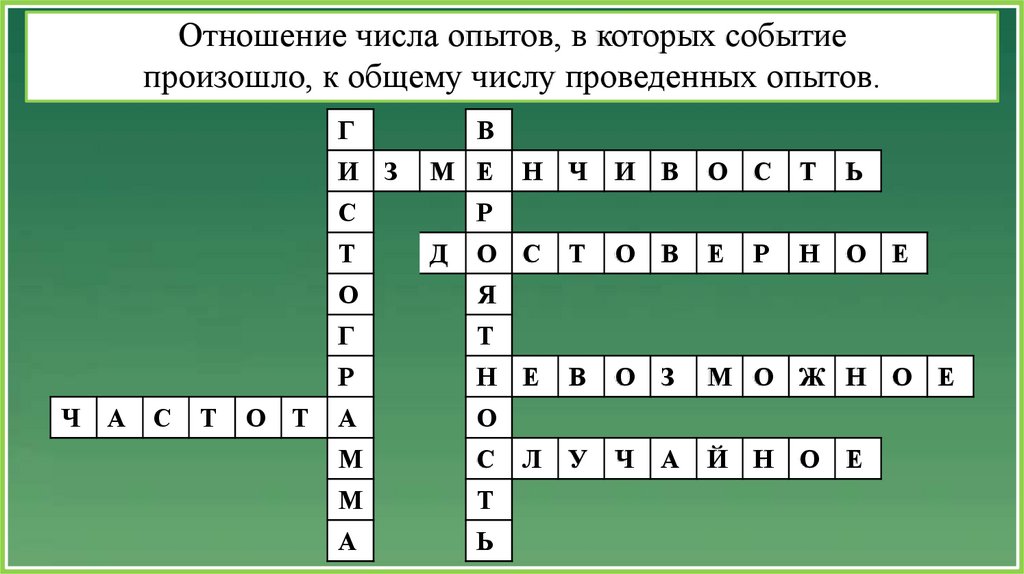
Отношение числа опытов, в которых событие
произошло, к общему числу проведенных опытов.
Г
И
В
З
М Е
С
Т
Н
Ч
И
В
О
С
Т
Ь
С
Т
О
В
Е
Р
Н
О
Е
Е
В
О
З
М О
Ж Н
О
Л
У
Ч
А
Й
О
Р
Д
О
О
Я
Г
Т
Р
Н
А
О
М
С
М
Т
А
Ь
Н
Е
Е

15.

Отношение числа опытов, в которых событие
произошло, к общему числу проведенных опытов.
Г
И
В
З
М Е
С
Т
Ч
А
С
Т
О
Т
Н
Ч
И
В
О
С
Т
Ь
С
Т
О
В
Е
Р
Н
О
Е
Е
В
О
З
М О
Ж Н
О
Л
У
Ч
А
Й
О
Р
Д
О
О
Я
Г
Т
Р
Н
А
О
М
С
М
Т
А
Ь
Н
Е
Е

16.

17.

Массовое производство.
это неустойчивость
величины, связанная с
действием случайных
факторов или причин,
часть из которых может
быть неизвестна.
В магазинах на упаковках
товаров всегда указана
их номинальная масса. Но по
факту не значит, что масса
или объём будут совпадать
с указанным номиналом.
Причины проблемы:
транспортировка,
некачественная настройка
оборудования, разное сырьё…

18.

Рост человека.
это неустойчивость
величины, связанная с
действием случайных
факторов или причин,
часть из которых может
быть неизвестна.
Самый простой и
распространённый пример.
Невозможно без
измерения определить рост
незнакомого нам человека,
поэтому данная величина для
исследователя будет
являться случайной. Факторов,
влияющих на рост
человека, большое количество.

19.

№1. Вставьте пропущенное слово.
Случайная ………. ‒ это неустойчивость величины, связанная
с действием случайных факторов или причин, часть из
которых может быть неизвестна.
1) изменяемость
2) изменчивость

20.

№2. Вставьте пропущенное слово.
………. масса ‒ это идеальное значение, к которому должно
стремиться каждое производство.
1) номинальная
2) нормальная
3) правильная

21.

№3. При покупке мотка пряжи на этикетке указывается
её длина: 210 м ± 4 м. Укажи, какой длины может
быть пряжа в мотке.
1) 212
2) 216
3) 206
4) 214

22.

№4. Разрешенная скорость на участке автомобильной дороги
110 км/ч. Камеры контроля движения транспорта
фиксируют нарушения в случае превышения скорости
на 20 км/ч. В каком случае будет выписан штраф?
1) 121 км/ч
2) 89 км/ч
3) 131 км/ч
4) 101 км/ч
110

23.

№5. Погрешность напольных электронных весов — 0,5 кг.
Когда Матвей встаёт на весы, они показывают 60,3 кг.
Каким может быть вес Матвея?
1) 59,6 кг
2) 60,4 кг
3) 60 кг
4) 61 кг

24.

№6. Длина ленты, указанная на упаковке, составляет
50м ± 6%. Какой может быть длина ленты?
1) 44 м
2) 48 м
3) 56 м
4) 53 м

25.

№7. Номинальная масса батончика 200 г. Ребята купили 10
таких батончиков. Массы купленных батончиков оказались
следующими: 199,7; 200,5; 200,1; 200,0; 200,3; 198,1; 199,7;
199,8; 201,1; 201,6. Найти наибольший вес батончика.

26.

№8. Номинальная масса батончика 200 г. Ребята купили 10
таких батончиков. Массы купленных батончиков оказались
следующими: 199,7; 200,5; 200,1; 200,0; 200,3; 198,1; 199,7;
199,8; 201,1; 201,6. Найти наибольшее отклонение (по модулю)
от номинального веса батончика.

27.

№9. Номинальная масса батончика 200 г. Ребята купили 10
таких батончиков. Массы купленных батончиков оказались
следующими: 199,7; 200,5; 200,1; 200,0; 200,3; 198,1; 199,7;
199,8; 201,1; 201,6. Найти средний вес батончика.

28.

№10. Номинальная масса батончика 200 г. Ребята купили 10
таких батончиков. Массы купленных батончиков оказались
следующими: 199,7; 200,5; 200,1; 200,0; 200,3; 198,1; 199,7;
199,8; 201,1; 201,6. У скольких батончиков вес превышает
номинальный?

29.

№11. Номинальная масса батончика 200 г. Ребята купили 10
таких батончиков. Массы купленных батончиков оказались
следующими: 199,7; 200,5; 200,1; 200,0; 200,3; 198,1; 199,7;
199,8; 201,1; 201,6. Какой процент составляют батончики, у
которых вес ниже номинального?

30.

31.

Случайное событие ‒ это
событие, которое в
случайном эксперименте
может произойти, а
может не произойти.
это числовая
мера правдоподобия
этого события.
это случайное
событие, которое в
случайном эксперименте
не наступает.
это случайное
событие, которое в
случайном эксперименте
обязательно наступает.

32.

Частота случайного
события ‒ отношение
числа опытов, в которых
событие произошло,
к общему числу
проведённых опытов.
Пусть провели один и тот
же эксперимент 100 раз,
и событие А произошло
в 36 случаях.
Частота случайного
события А равна
отношению количества раз,
когда событие А
произошло, к общему числу
проведенных опытов.
36 : 100 = 0,36

33.

Элементарное событие ‒
это событие, которое
нельзя разделить на более
простые.
Равновозможные
элементарные события ‒
это события случайного
эксперимента, которые
имеют одинаковые шансы
на осуществление.
Бросок игрального кубика.
Элементарные события
(выпадение 1, 2, 3, 4, 5, 6
очков) являются
равновозможными, так как
шансы этих шести
элементарных событий
одинаковы.

34.

Элементарные
благоприятствующие
событию А события ‒
это события, благодаря
которым исполняется
событие А.
Бросок игрального кубика.
Событию «на кубике
выпадет чётное число
очков» благоприятствуют
три элементарных события:
«на кубике два очка», «на
кубике четыре очка», «на
кубике шесть очков».

35.

сумма вероятностей
элементарных событий,
благоприятствующих
этому событию.
Пусть событию А
благоприятствуют события
а, b и с, тогда
P(А) = P(а) + P(b) + P(c).
Бросок игрального кубика.
Событию А = «на кубике
выпадет чётное число
очков» благоприятствуют
три элементарных события:
«на кубике два очка», «на
кубике четыре очка», «на
кубике шесть очков».
Р(А)
1 1 1 3 1
6 6 6 6 2

36.

Формула для расчёта
классической вероятности
события А ‒ это
отношение числа m
элементарных событий,
благоприятствующих
событию А, к числу n всех
элементарных событий.
P(A) = m : n
На тарелке лежат
одинаковые на вид
пирожки: 4 с мясом, 10 с
капустой и 6 с вишней.
Катя наугад берёт один
пирожок. Найти
вероятность того, что
пирожок окажется с
вишней.
Р
6
6
3
0,3
4 10 6 20 10

37.

№1. Витя и Маша играют в настольную игру, в которой для
дальнейшего хода нужно бросать кубик. Сопоставь события.
А) невозможное
1) выпадет меньше 9 очков
Б) случайное
2) выпадет 9 очков
В) достоверное
3) выпадет больше 3 очков, но меньше 5
А
Б
В

38.

№2. Один и тот же опыт проводится 100 раз. Событие В
в этом опыте произошло 43 раза.
Какой будет частота случайного события В?
1) 0,57
2) 0,43
3) 0,5

39.

№3. В коробке лежат яблоки красного, жёлтого и зелёного
цвета. Красных яблок ‒ 13 штук, жёлтых ‒ 7 штук,
зелёных ‒ 5 штук. Какова частота события «наугад
взятое яблоко красного цвета»?
1) 0,28
2) 0,20
3) 0,52

40.

№4. Случайный опыт заключается в том, что стрелок стреляет
по мишени до тех пор, пока не попадёт. Опыт провели десять
раз. Найдите частоту события «стрелок попал в мишень с
третьего раза».
Номер
опыта
1
2
3
4
5
6
7
8
9
10
С какого
выстрела
попал
5
4
1
3
2
7
3
4
5
3

41.

№5. Назовите номер интервала с наибольшей частотой.
0,25
0,2
0,15
0,1
0,05
0
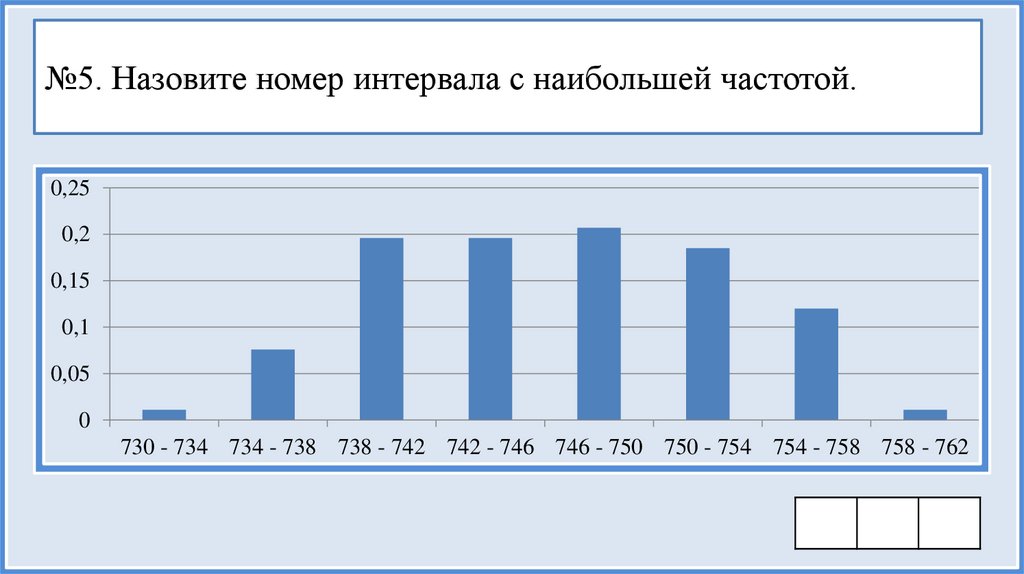
730 - 734 734 - 738 738 - 742 742 - 746 746 - 750 750 - 754 754 - 758 758 - 762

42.

№6. Книгу, в которой 184 страницы, открывают случайным
образом. Какова вероятность события «книгу открыли
на 194 странице»?
1) 0,5
2) 1
3) 0

43.

№7. Какова вероятность события «масса человека не
превышает одну тонну»?
1) 0,5
2) 1
3) 0

44.

№8. У бабушки 15 чашек: 3 желтых, остальные ‒ зелёные.
Бабушка наливает чай в случайно выбранную чашку. Найдите
вероятность того, что эта чашка будет зелёная.
1) 0,2
2) 0,75
3) 0,8

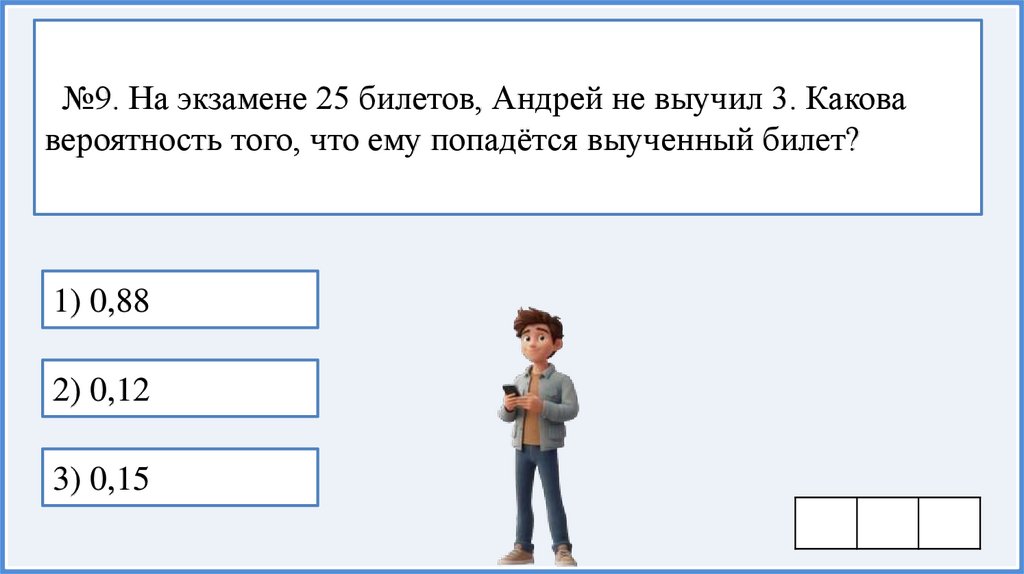
45.

№9. На экзамене 25 билетов, Андрей не выучил 3. Какова
вероятность того, что ему попадётся выученный билет?
1) 0,88
2) 0,12
3) 0,15

46.

№10. На тарелке 5 яблок, два из которых ‒ красные. Юра не
глядя берёт одно яблоко. Какова вероятность того, что это
яблоко окажется красным?
1) 0,6
2) 0,2
3) 0,4

47.

№11. В фирме такси в данный момент свободно 20 машин: 8
белых, 7 зелёных и 5 жёлтых. По вызову выехала одна из
машин, случайно оказавшаяся ближе всего к заказчику.
Найдите вероятность того, что к нему приедет жёлтое такси.
1) 0,4
2) 0,25
3) 0,35