Кривые II порядка

1.

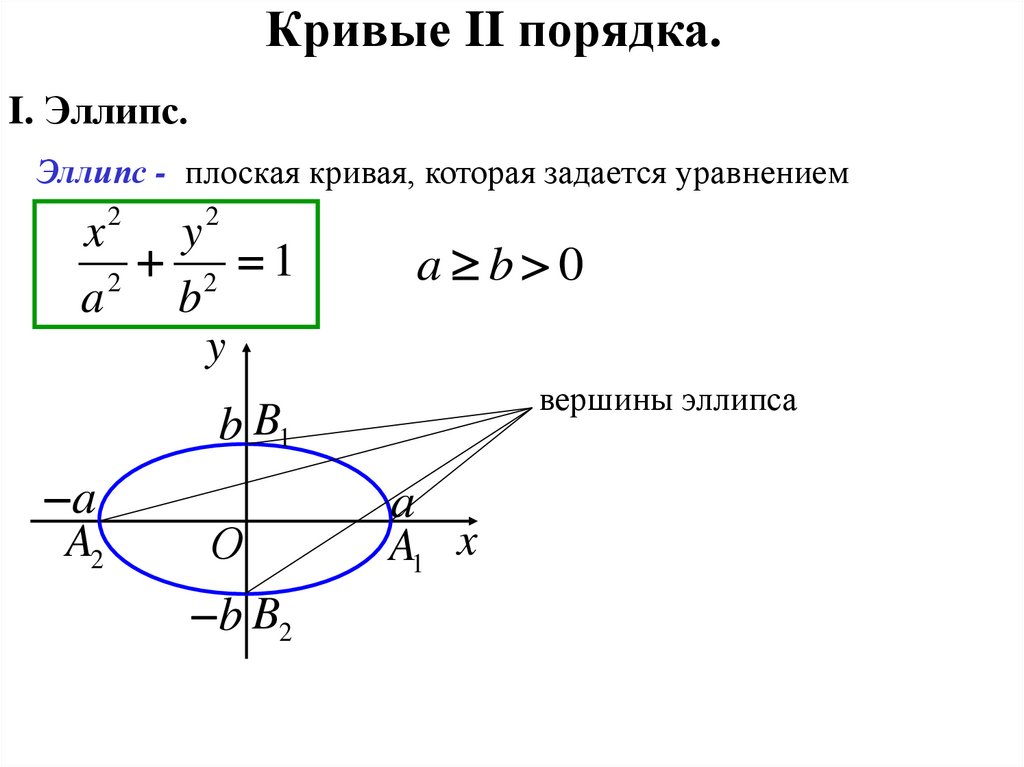
Кривые II порядка.
I. Эллипс.
Эллипс - плоская кривая, которая задается уравнением
2
2
x
y
2 1
2
a
b
y
a b 0
вершины эллипса
b B1
a
A2
О
b B2
a
A1 x

2.

y
x2 y2
2 1
2
a
b
b B1
a
A2
a
A1 x
О
b B2
Отрезок A2 A1 и число 2а - большая ось
Отрезок B B и число 2b - малая ось
1
2
a и b - большая и малая полуоси
c a 2 b2
c
e
- эксцентриситет,
a
e 1
a b 0

3.

K
y
2
M
F 2 О
F 1
L
x
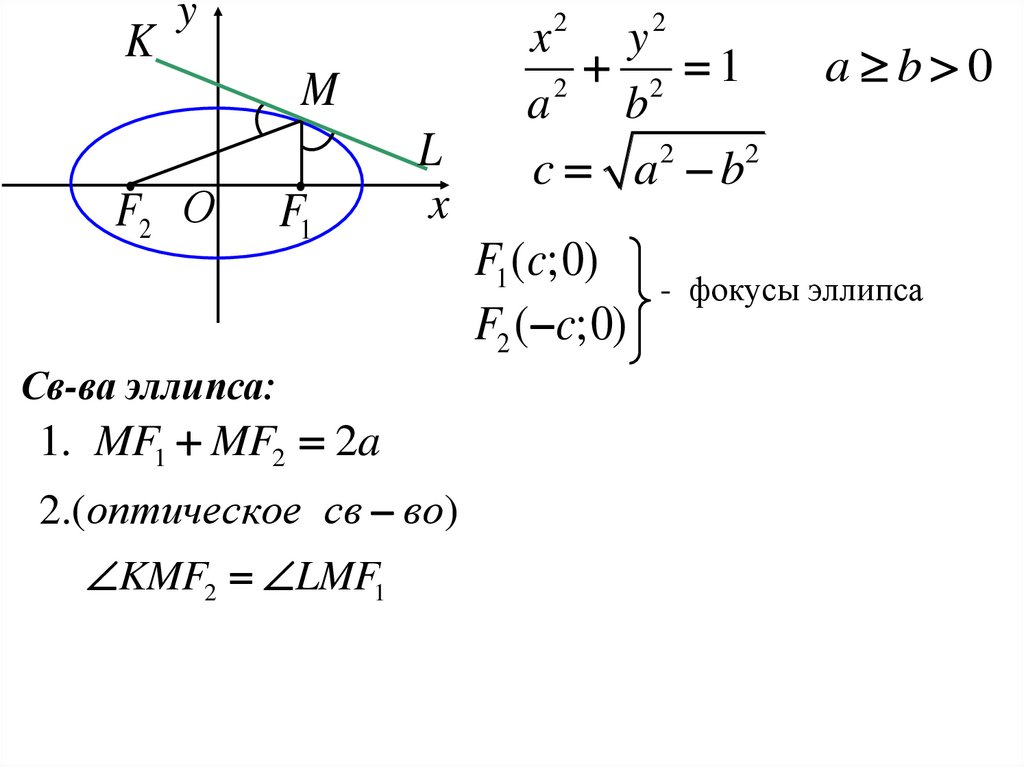
Св-ва эллипса:
1. MF1 MF2 2a
2.(оптическое св во)
KMF2 LMF1
2
x
y
2 1
2
a
b
2
2
c a b
a b 0
F1 (c;0)
- фокусы эллипса
F2 ( c;0)

4.

y
2
x
y
2 1
2
a
b
b B1
a
A2
О
a
A1 x
c a b
2
b B2
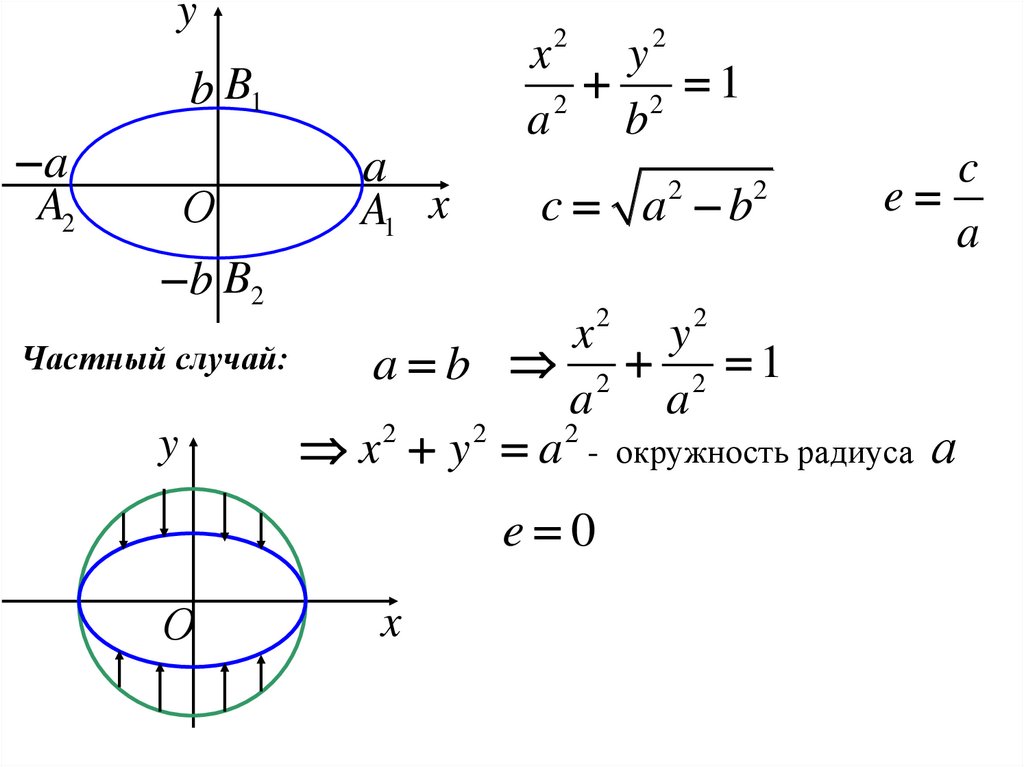
Частный случай:
y
2
2
2
c
e
a
x
y
a b 2 2 1
a
a
2
2
2
x y a - окружность радиуса а
e 0
О
2
x

5.

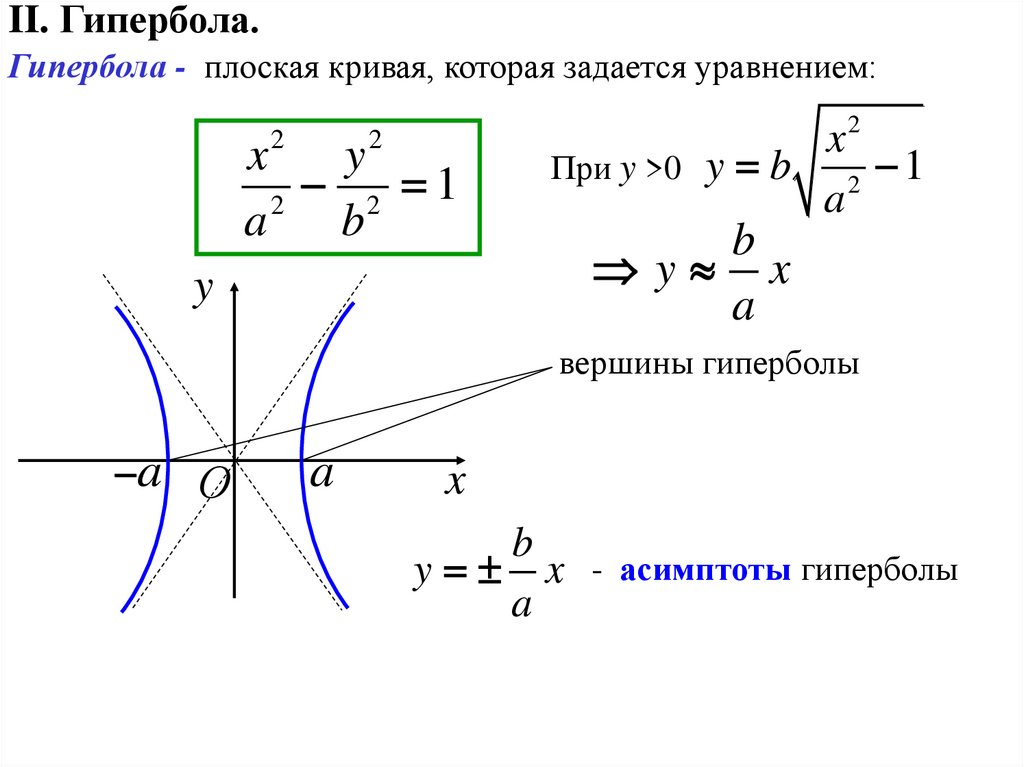
II. Гипербола.
Гипербола - плоская кривая, которая задается уравнением:
2
2
x
y
2 1
2
a
b
y
x2
1
При y >0 y b
2
a
b
y x
a
вершины гиперболы
a О
a
x
b
y x - асимптоты гиперболы
a

6.

2
y
b B1
A2
F2 a О
a F 1
A1
2
x
y
2 1
2
a
b
b - асимптоты
y x
a
x
b B2
Отрезок A2 A1 и число 2а - действительная ось
Отрезок B2 B1 и число 2b - мнимая ось
a и b - действительная и мнимая полуоси
c a 2 b2
c
- эксцентриситет,
e
a
e 1

7.

2
K
y
x
y
2
2
2 1 c a b
2
a
b
M
F 2 a О
L
2
a F
1
x
F1 (c;0)
F2 ( c;0)
Св-ва гиперболы:
1. MF1 MF2 2a
2.(оптическое св во)
LMF2 LMF1
- фокусы гиперболы

8.

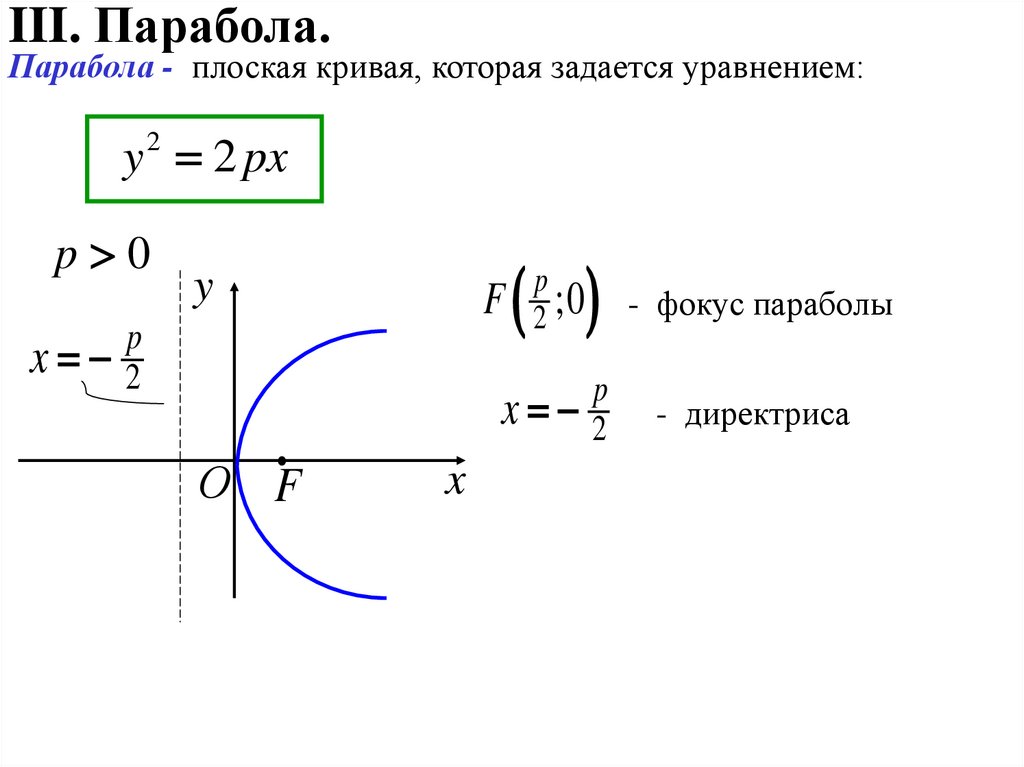
III. Парабола.
Парабола - плоская кривая, которая задается уравнением:
y 2 px
2
p 0
y
F
p
x 2
О F
- фокус параболы
p
2 ;0
p
x 2
x
- директриса

9.

K
y
G
L
p
x 2
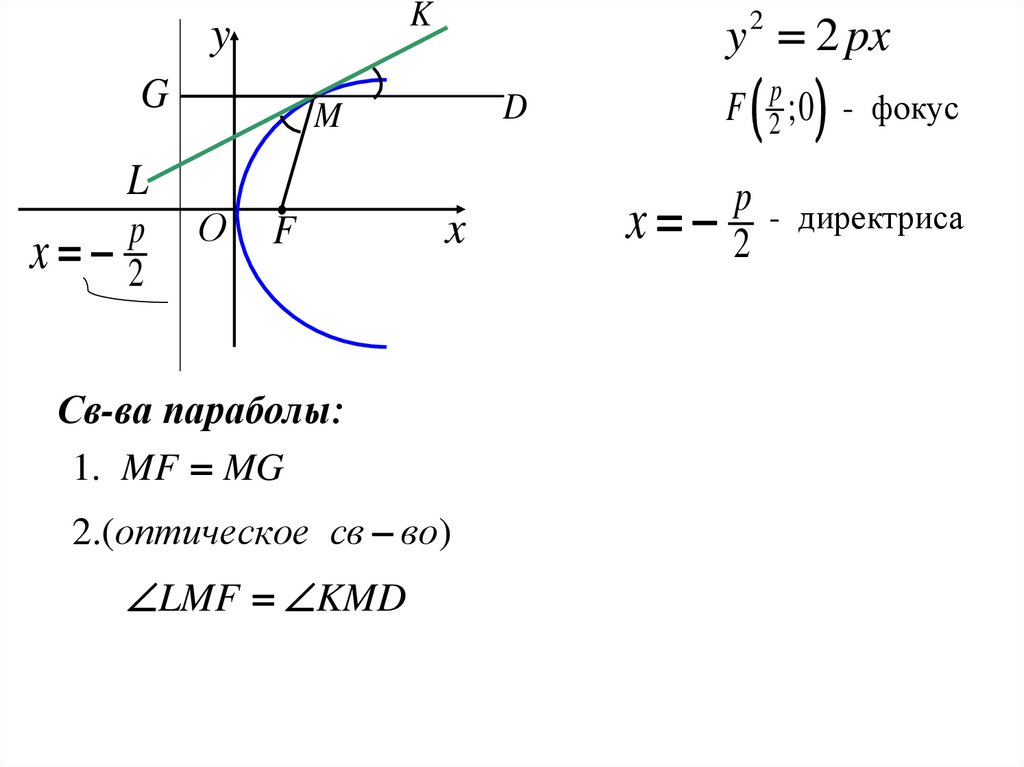
y 2 px
2
D
M
О F
x
Св-ва параболы:
1. MF MG
2.(оптическое св во)
LMF KMD
F
p
2 ;0 - фокус
p - директриса
x 2

10.

Сдвиг и поворот кривых
Если
l : F ( x, y ) 0, c 0
F ( x c, y ) 0
F ( x c, y ) 0
F ( x, y c ) 0
F ( x, y c ) 0
F ( y, x) 0
- сдвиг вдоль оси Ox вправо
- сдвиг вдоль оси Ox влево
- сдвиг вдоль оси Oy вверх
- сдвиг вдоль оси Oy вниз
- поворот на
90

11.

Примеры.
Определить вид кривых, найти координаты их точек пересечения
и сделать чертеж.
1. x 2 4 y 2 25, x 2 y 2 5 2
2
x
y
2
2
1) x 4 y 25 - эллипс:
25 1
25 4
y
2,5
О
2) x y 5 - гипербола:
2
5
5
x
2
2
2
x
y
1
5
5

12.

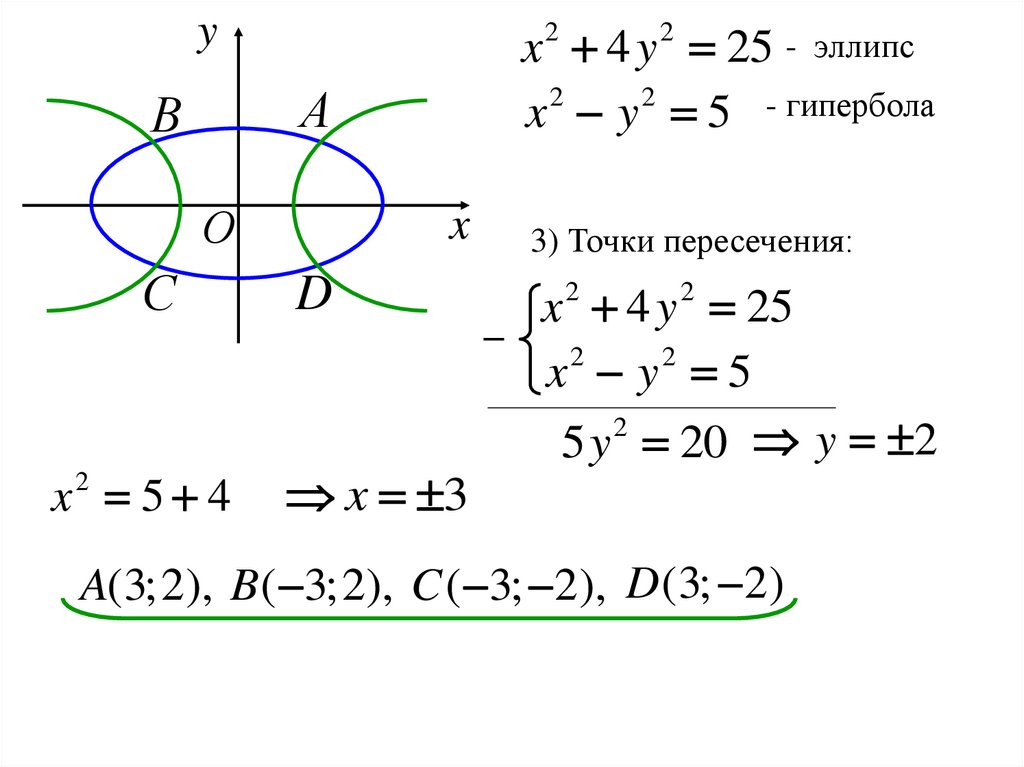
y
x 4 y 25 - эллипс
2
2
x y 5 - гипербола
2
А
В
О
С
x2 5 4
x
D
x 3
2
3) Точки пересечения:
x 4 y 25
x2 y2 5
2
5 y 20 y 2
2
2
A(3;2), B( 3;2), C ( 3; 2), D (3; 2)

13.

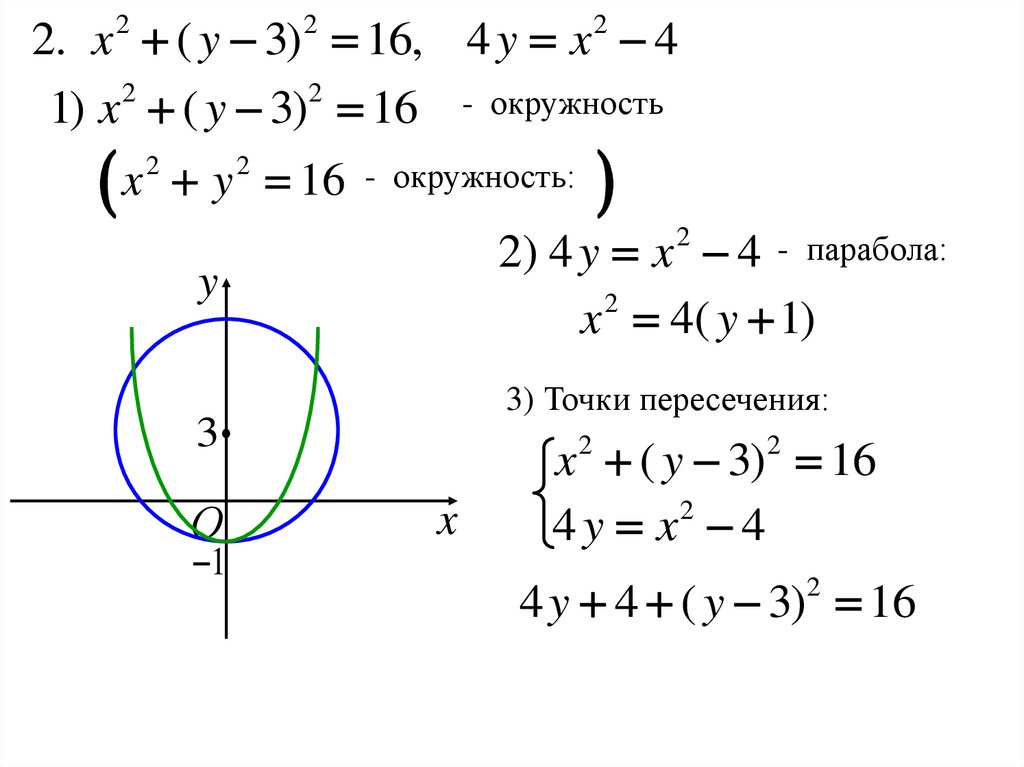
2. x 2 ( y 3)2 16, 4 y x 2 4
1) x 2 ( y 3)2 16 - окружность
x y 16 - окружность:
2
2
2) 4 y x 4 - парабола:
x 2 4( y 1)
2
y
3) Точки пересечения:
3
О
1
x ( y 3) 16
4 y x2 4
2
x
2
4 y 4 ( y 3) 16
2

14.

y
В
3
О
1 С
3) Точки пересечения:
А
x
x 2 ( y 3)2 16
2
4y x 4
x 4y 4
4 y 4 ( y 3) 16
2
y 2 y 13 16
2
y 2y 3 0
3 x 4
y1,2
1 x 0
A(4;3), B( 4;3), C (0; 1)
2

15.

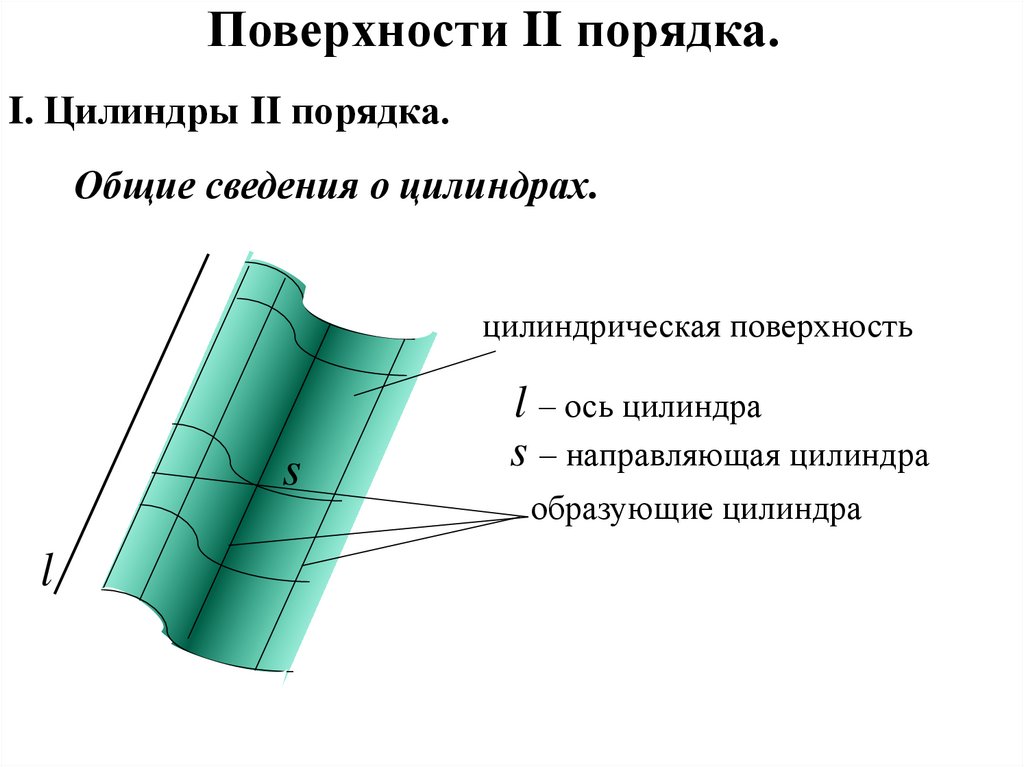
Поверхности II порядка.
I. Цилиндры II порядка.
Общие сведения о цилиндрах.
цилиндрическая поверхность
s
l
l – ось цилиндра
s – направляющая цилиндра
образующие цилиндра

16.

Уравнение цилиндра с образующими, параллельными оси
z
F ( x, y ) 0
Oz:
- кривая в пл-ти Oxy
s – направляющая цилиндра
F ( x, y ) 0
s
x
F ( x, z ) 0
F ( y, z ) 0
y
M ( x; y; z )
– в пространстве
цилиндрическая поверхность с
образующими, параллельными оси
Oz
–цилиндрическая поверхность с
образующими, параллельными оси Oу
– цилиндрическая поверхность с
образующими, параллельными оси Ox

17.

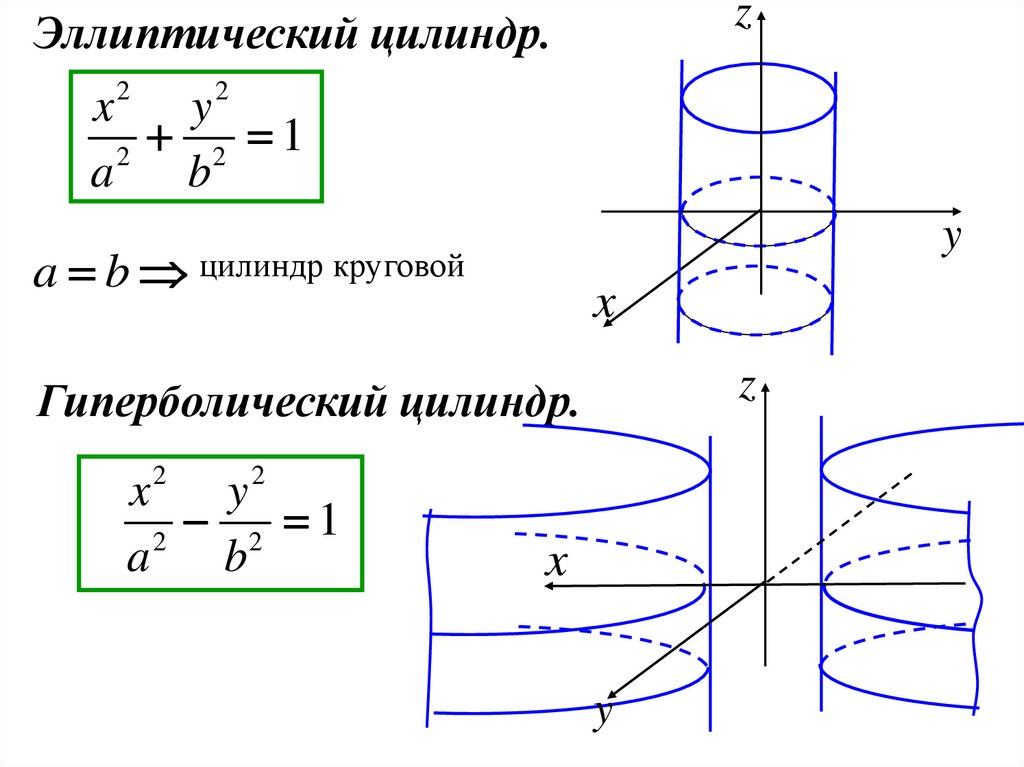
z
Эллиптический цилиндр.
2
2
x
y
2 1
2
a
b
y
a b цилиндр круговой
x
z
Гиперболический цилиндр.
x2 y2
2 1
2
a
b
x
y

18.

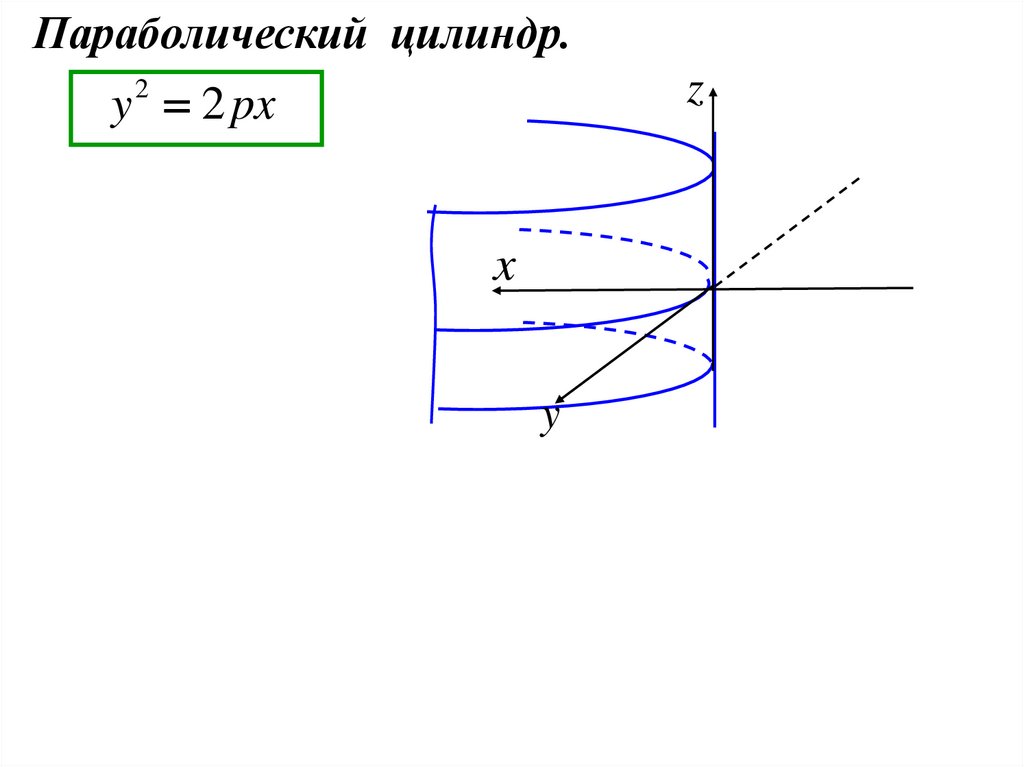
Параболический цилиндр.
z
y 2 px
2
x
y

19.

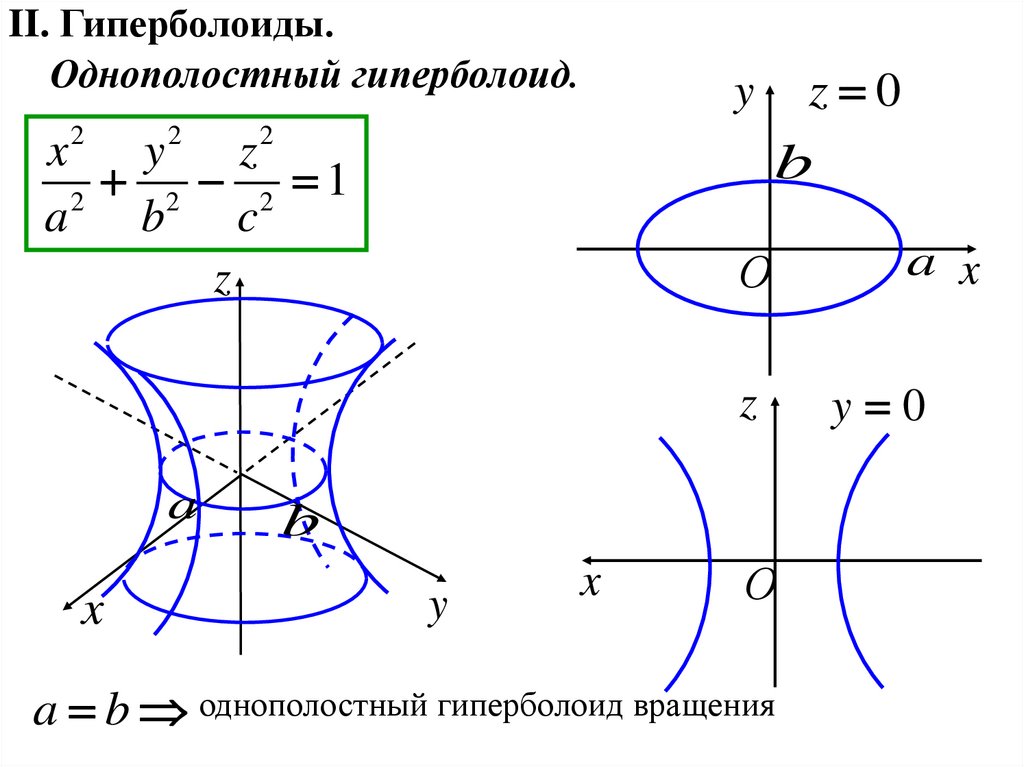
II. Гиперболоиды.
Однополостный гиперболоид.
2
2
2
x
y
z
2 2 1
2
a
b
c
z
z 0
y
b
О
z
a
x
b
y
x
О
a b однополостный гиперболоид вращения
a x
y 0

20.

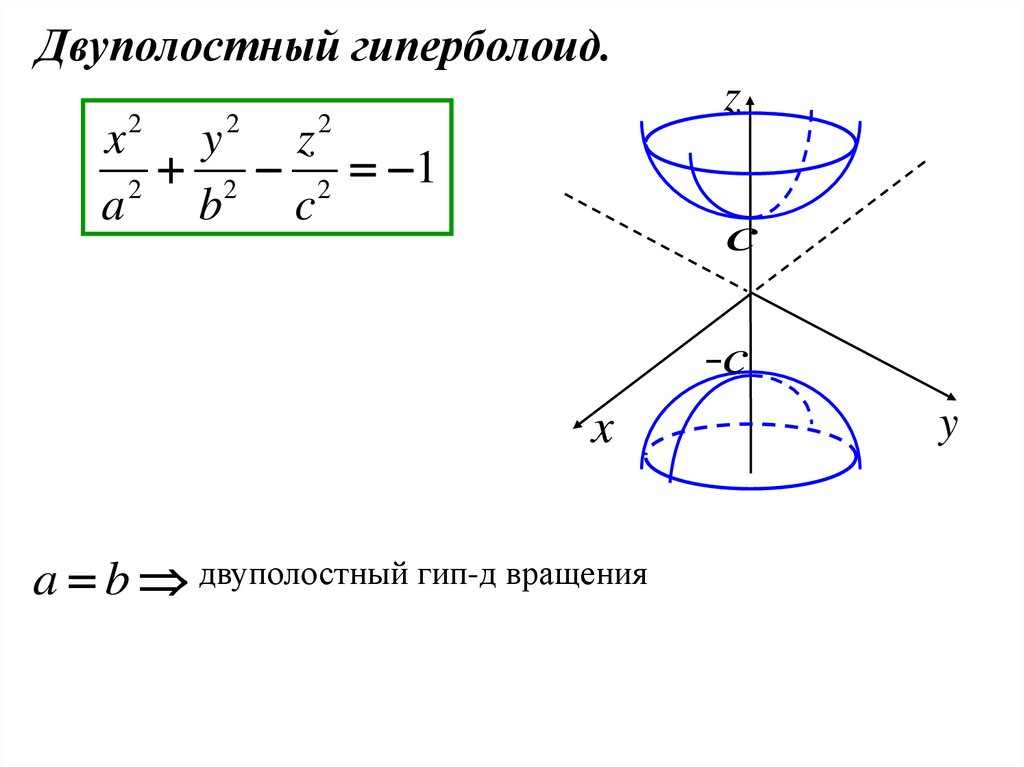
Двуполостный гиперболоид.
2
2
z
2
x
y
z
2 2 1
2
a
b
c
c
-c
x
a b двуполостный гип-д вращения
y

21.

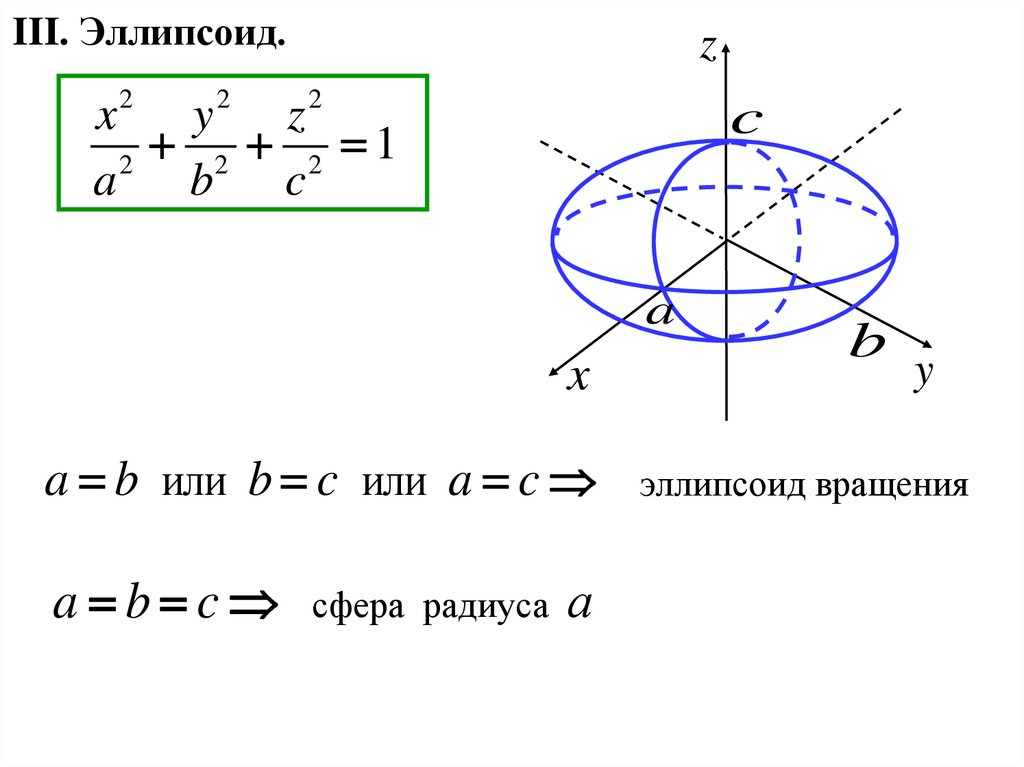
III. Эллипсоид.
z
x2 y2 z2
2 2 1
2
a
b
c
c
a
x
a b или b c или a c
a b c сфера радиуса а
b
y
эллипсоид вращения

22.

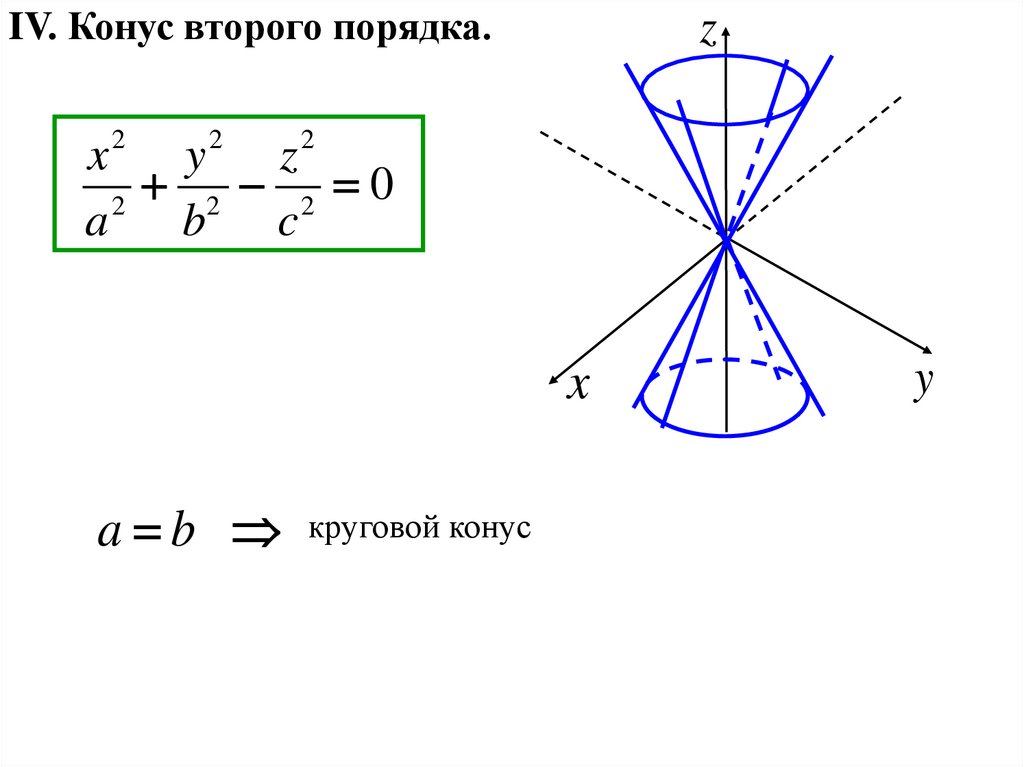
IV. Конус второго порядка.
2
2
z
2
x
y
z
2 2 0
2
a
b
c
x
a b круговой конус
y

23.

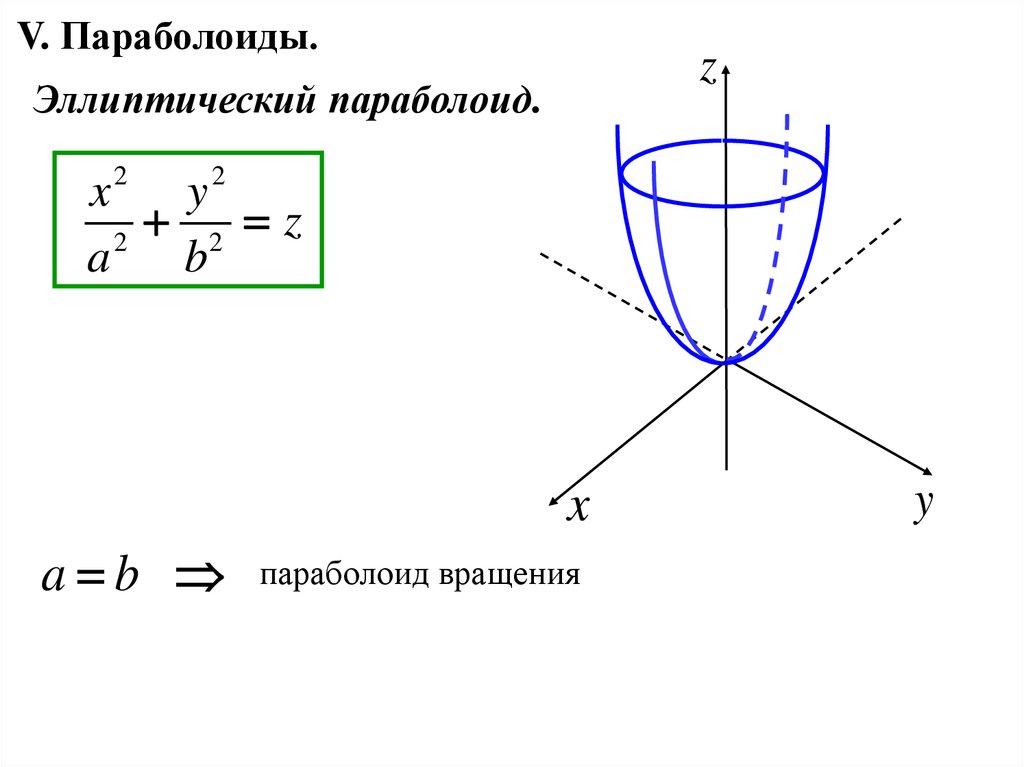
V. Параболоиды.
z
Эллиптический параболоид.
2
2
x
y
2 z
2
a
b
x
a b параболоид вращения
y

24.

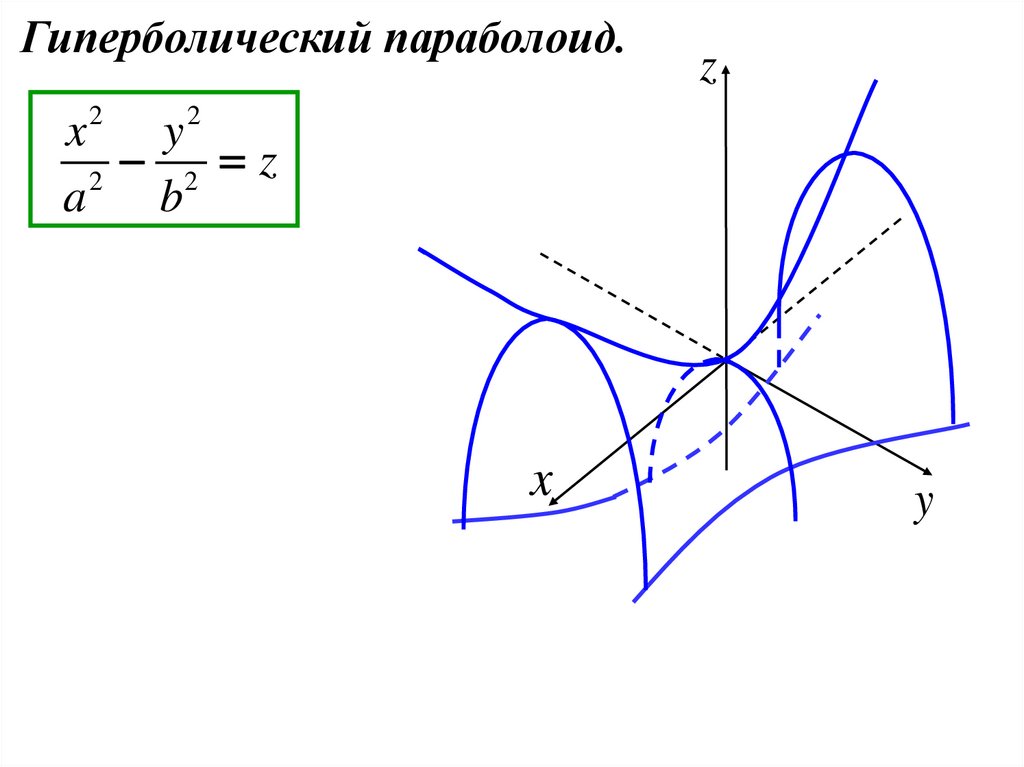
Гиперболический параболоид.
z
x2 y2
2 z
2
a
b
x
y

25.

Примеры.
Тело задано системой неравенств. Написать уравнение пов-тей,
ограничивающих тело и опр-ть их вид. Опр-ть, по каким линиям
и в каких пл-тях пересекаются пов-ти. Сделать схематический
чертеж тела.
x y z 25
1. 2
2
x y 9
2
2
2
Решение:
1) x y z 25 - сфера радиуса 5
2
2
2
x y 9
2
2
- круговой цилиндр вдоль Oz

26.

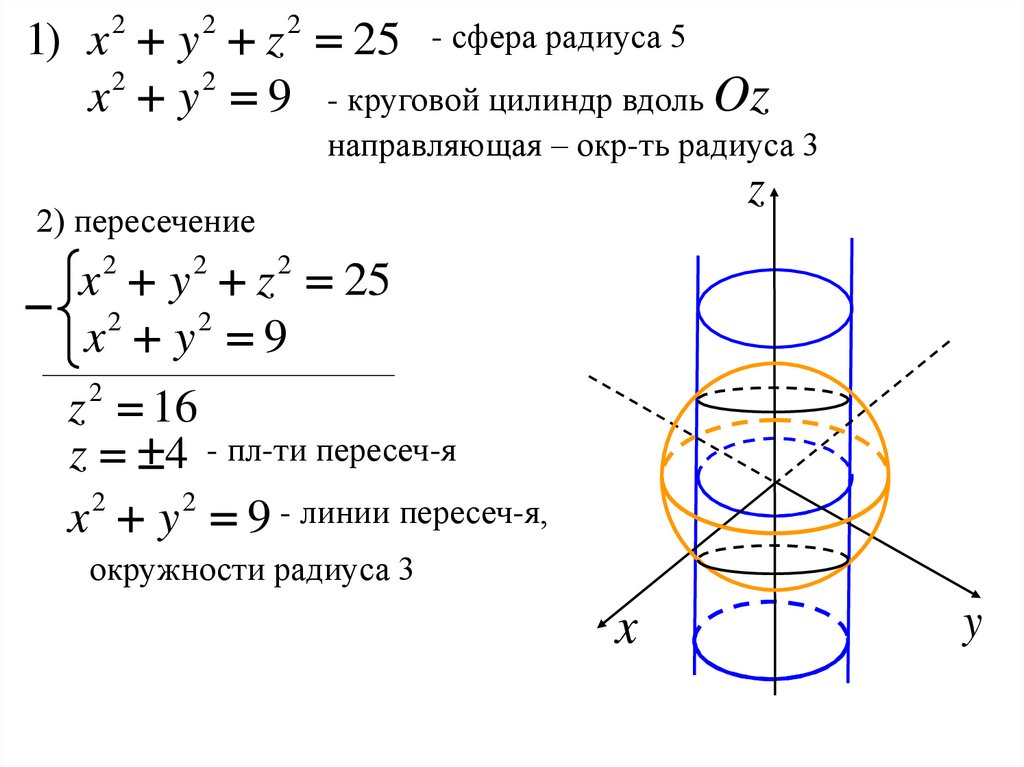
1) x 2 y 2 z 2 25 - сфера радиуса 5
x 2 y 2 9 - круговой цилиндр вдоль Oz
направляющая – окр-ть радиуса 3
z
2) пересечение
x 2 y 2 z 2 25
2 2
x y 9
2
z 16
z 4 - пл-ти пересеч-я
2
2
x y 9 - линии пересеч-я,
окружности радиуса 3
x
y

27.

z
z 4 - пл-ти пересеч-я
x 2 y 2 9 - линии пересеч-я,
окружности радиуса 3
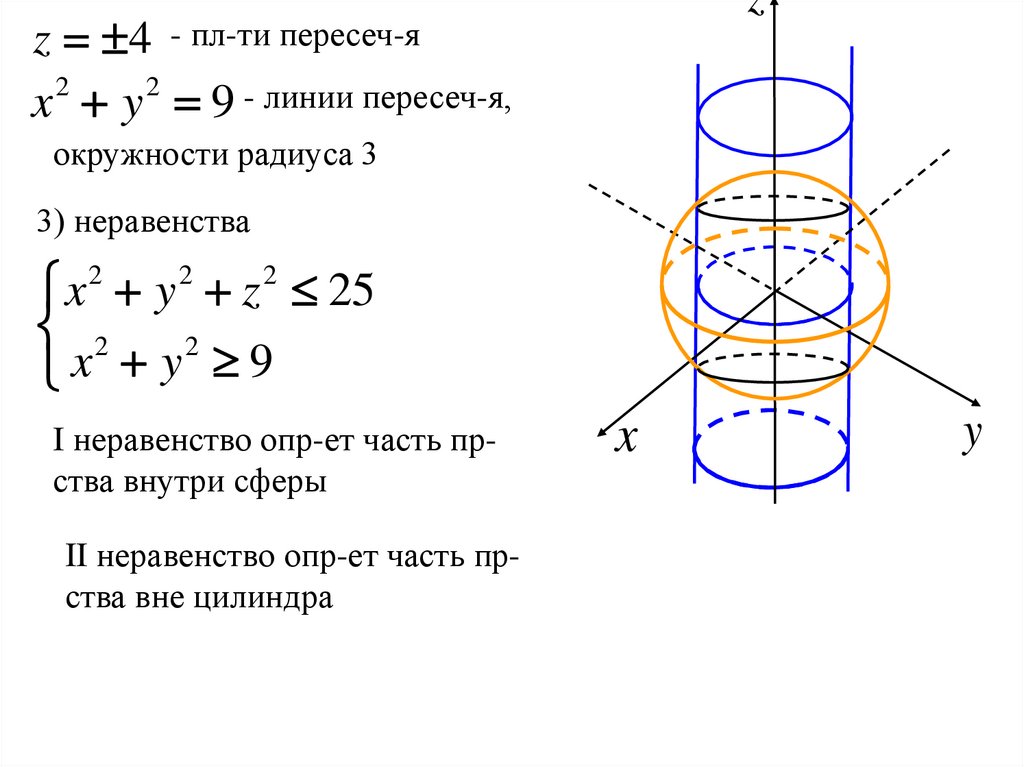
3) неравенства
x 2 y 2 z 2 25
2
2
x y 9
I неравенство опр-ет часть прства внутри сферы
II неравенство опр-ет часть прства вне цилиндра
x
y

28.

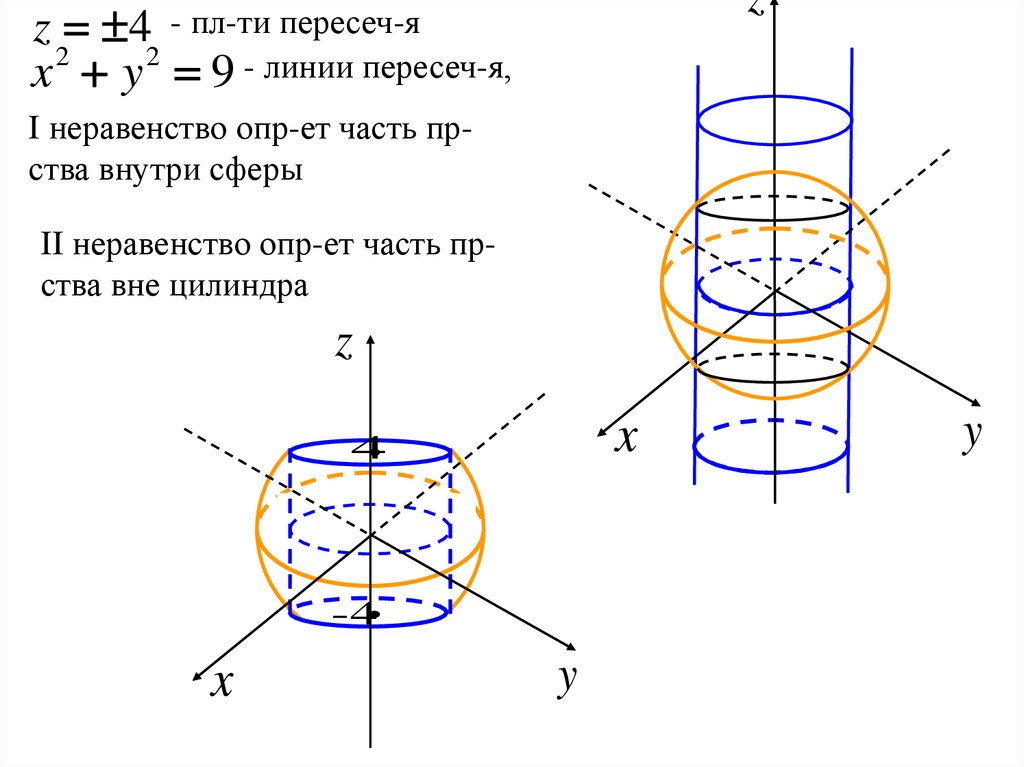
z
z 4 - пл-ти пересеч-я
2
2
x y 9 - линии пересеч-я,
I неравенство опр-ет часть прства внутри сферы
II неравенство опр-ет часть прства вне цилиндра
z
4
x
-4
x
y
y

29.

x 2 y 2 4( z 1)
2. 2
2
2
x y z 9
Решение:
1) x y 4( z 1) - параболоид вращ-я, вершина (0;0;1)
x 2 y 2 z 2 9 - двуполостный гиперболоид
2
2
вращения

30.

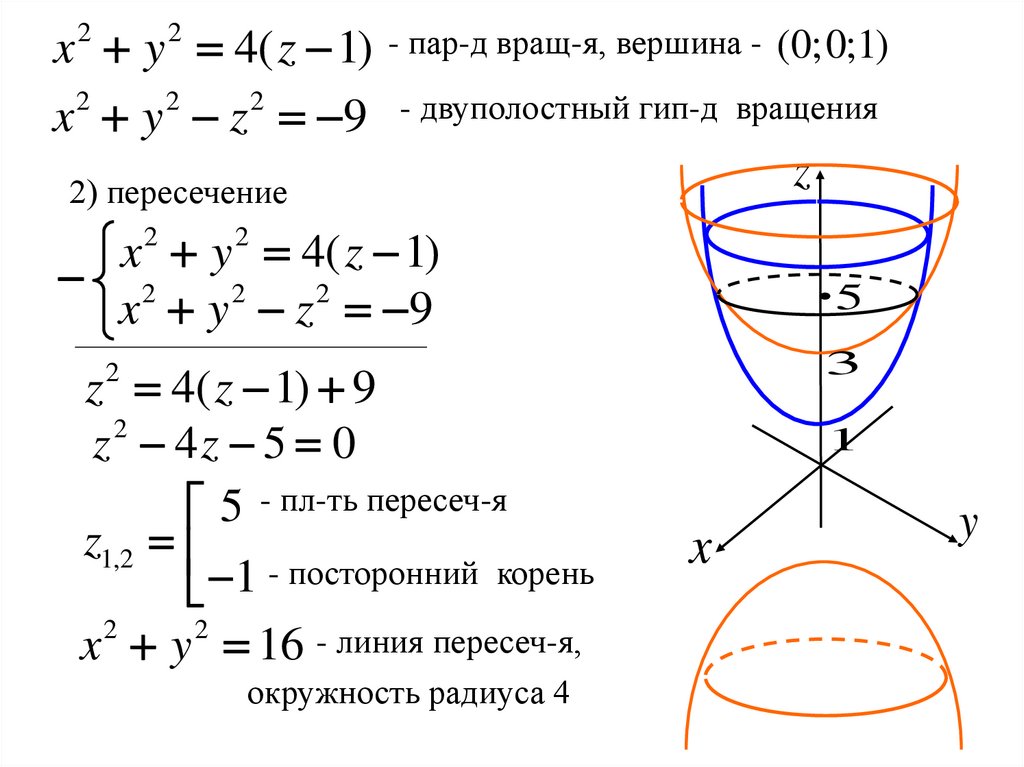
x y 4( z 1) - пар-д вращ-я, вершина - (0;0;1)
2
2
2
x y z 9 - двуполостный гип-д вращения
2
2
z
2) пересечение
x y 4( z 1)
2 2 2
x y z 9
2
2
z 4( z 1) 9
2
z 4z 5 0
5 - пл-ть пересеч-я
z1,2
1 - посторонний корень
x 2 y 2 16 - линия пересеч-я,
5
3
2
окружность радиуса 4
1
x
y

31.

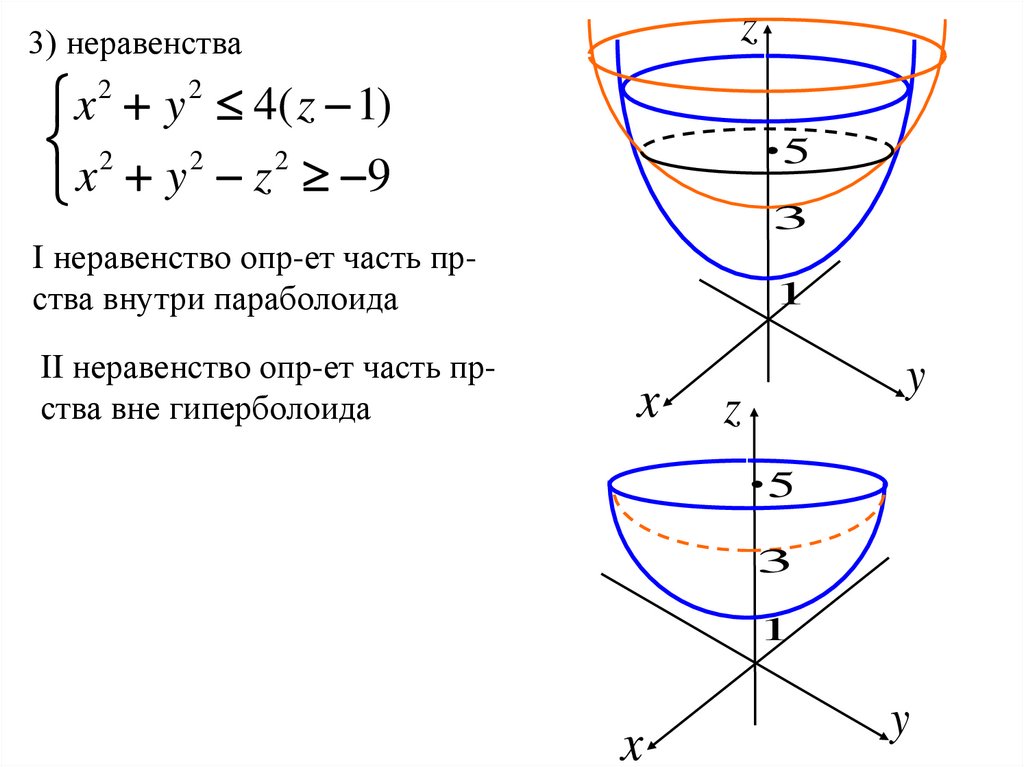
z
3) неравенства
x 2 y 2 4( z 1)
2
2
2
x y z 9
5
3
I неравенство опр-ет часть прства внутри параболоида
II неравенство опр-ет часть прства вне гиперболоида
1
x
y
z
5
3
1
x
y