Дәріс 2. Алгоритмнің күрделілігі Алгоритмдердің күрделілігін бағалау

1. Дәріс 2. Алгоритмнің күрделілігі

Алгоритмдердің күрделілігін
бағалау

2. Тармақталған алгоритм

Тармақталған алгоритм – бұл бағдарлама орындау кезінде белгілі бір шарттарға
байланысты әр түрлі жолдармен жүретін алгоритм түрі. Басқаша айтқанда, ол
шартқа (немесе бірнеше шартқа) негізделген таңдаулар жасайды, яғни бір қадамды
орындау немесе басқа бір қадамды орындау арқылы нәтижеге жетеді.
Мысалы, тармақталған алгоритмнің құрылымы мынадай болуы мүмкін:
1.Шарт қойылады.
2.Егер шарт орындалса, бір әрекет орындалады.
3.Егер шарт орындалмаса, басқа әрекет орындалады.
Тармақталған алгоритмнің мысалы:
Егер температура > 30° болса онда сыртта су ішу керек әйтпесе, үйде болу керек
Бұл жағдайда, температура 30°-дан жоғары болса, сыртта су ішу керек, ал
температура 30°-тан төмен болса, үйде болу керек.
Бұл алгоритмдерде шарттар көбінесе "егер" және "онда" түрінде құрылып, бірнеше
мүмкін таңдауларды ұсынады.

3.

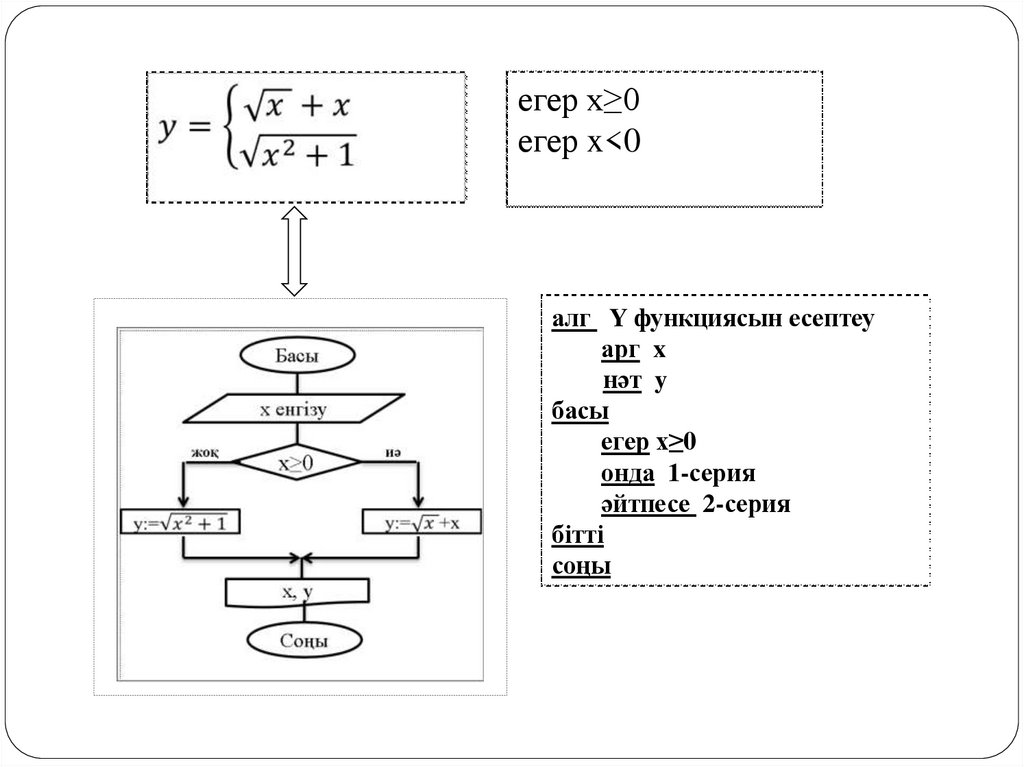
егер x≥0
егер x<0
алг Y функциясын есептеу
арг x
нәт y
басы
егер x≥0
онда 1-серия
әйтпесе 2-серия
бітті
соңы

4.

Тармақталу операторы көрсетілген шартқа тәуелді құрамына кіретін
операторлардың орындалуын немесе орындалмауын қамтамасыз етеді.
Тармақталған алгоритмдерді бағдарланған кезде мынадай қызметші
сөздер қолданылады: if - егер , then – онда , else - әйтпесе.
Оператор программадағы іс-әрекеттердің орындалу реттілігін
өзгертетін мүмкіндіктің ең кең тараған тәсілі болып табылады. Толық
оператордың жазылу түрі:
{Егер шарт онда 1 оператор әйтпесе 2 оператор орындалады.}
IF <шартты өрнек> THEN <1 оператор> ELSE <2 оператор>;
Егер шарттың мәні «ақиқат» болса, THEN сөзінен кейінгі оператор,
ал мән «жалған» болса, ELSE сөзінен кейінгі оператор орындалады.
Қысқа оператордың жазылу түрі:
IF <шартты өрнек> THEN <1 оператор> ;

5. Мысал 1: Егер сан оң болса, оны шығару, керісінше теріс болса – теріс санды шығару.

#include <iostream>
2.
using namespace std;
3.
int main() {
4.
int num; cout << "Санды енгізіңіз: ";
5.
cin >> num;
6.
if (num > 0) {
7.
cout << "Сан оң: " << num << endl;
8.
} else {
9.
cout << "Сан теріс: " << num << endl;
10. }
11. return 0;
12. }
1.

6.

Мысал 2: Егер сан жұп болса, жұп сан екенін шығару, тақ болса – тақ сан екенін
шығару.
1. #include <iostream>
2. using namespace std;
3. int main() {
4. int num;
5. cout << "Санды енгізіңіз: ";
6. cin >> num;
7. if (num % 2 == 0) {
8. cout << "Сан жұп!" << endl;
9. } else {
10. cout << "Сан тақ!" << endl;
11. }
12. return 0;
13. }

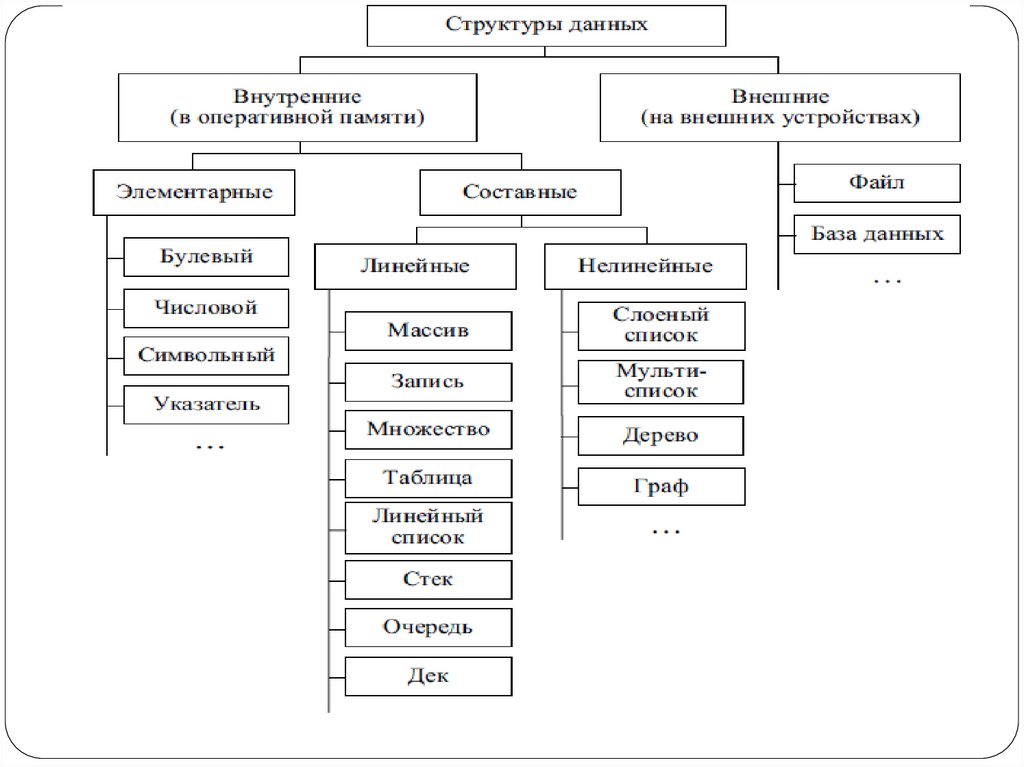
7. Негізгі ұғымдар

Жалпы жағдайда деректер құрылымы көптеген деректер элементтерін
және олардың арасындағы байланыстарды білдіреді.
Деректердің физикалық құрылымы-деректерді компьютер жадында
физикалық түрде ұсыну тәсілі.
Абстрактілі немесе логикалық құрылым деп еректер құрылымын оның
жадтағы көрінісін ескермей қарастыруын атады.
Әр түрдегі ақпарат нақты анықтайды:
• көрсетілген типтегі деректерді сақтау құрылымы, яғни жадты бөлу,
ондағы деректерді ұсыну және деректерге қол жеткізу әдісі;
• сипатталған типтегі белгілі бір объект болуы мүмкін рұқсат етілген
мәндер жиынтығы;
• сипатталған типтегі объектіге қолданылатын рұқсат етілген
операциялар жиынтығы.

8.

9. Күрделілігі алгоритмнің

Алгоритмдердің күрделілігі – алгоритмнің орындалу уақыты мен
ресурстарын оның кіріс деректерінің көлеміне тәуелділігі арқылы бағалау.
Бағдарламалаудағы алгоритмдердің күрделілігін бағалау үшін Big-O
(«үлкен О») деп аталатын арнайы белгі жасалды . Big-O алгоритмнің
орындалу уақыты оған берілген деректерге қаншалықты тәуелді екенін
бағалауға мүмкіндік береді .
• Big-O нотациясы – алгоритмдердің уақыттық немесе кеңістік күрделілігін
көрсетудің стандартты тәсілі.
• Big-O бізге деректердің көлемі өскен сайын алгоритмнің қалай жұмыс істейтінін
сипаттайды.
• Мақсат – алгоритмдерді салыстырып, ең тиімдісін таңдау.
Графика: Big-O белгісін түсіндіретін диаграмма.

10. Күрделі алгоритімнің бағалау теориясы

•Big-O нотациясы алгоритмнің күрделілігін сипаттайтын
математикалық белгілеу.
•Кейбір негізгі Big-O белгілері:
• O(1) — Тұрақты күрделілік: Алгоритмнің орындалуы
деректер көлеміне тәуелсіз.
• O(N) — Сызықтық күрделілік: Алгоритмнің орындалу уақыты
деректер көлеміне пропорционалды артады.
• O(log N) — Логарифмдік күрделілік: Алгоритм деректер
көлемінің логарифмдік қатынасы бойынша орындалады.
• O(N²) — Квадраттық күрделілік: Алгоритмнің орындау
уақыты деректер көлемінің квадратына пропорционалды
артады.
Графика: Әртүрлі Big-O күрделіліктерін түсіндіретін диаграммалар.

11.

O(1) - Тұрақты күрделілік
Мазмұн:
•O(1) белгісі тұрақты күрделілікті білдіреді, яғни алгоритмнің орындау
уақыты деректердің көлеміне тәуелсіз.
•Мысал:
• LinkedList-ке элемент қосу (егер ол тізімнің басына қосылса).
• Мұнда деректер саны қанша болса да, алгоритмнің уақыттық
күрделілігі өзгермейді.
•Бұл ең тиімді күрделілік түрі.
Графика: LinkedList диаграммасы мен элементті қосу процесінің сызбасы.
O(N) - Сызықтық күрделілік
Мазмұн:
•O(N) белгісі алгоритмнің уақыттық күрделілігінің деректер көлеміне
пропорционалды екенін білдіреді.
•Мысал:
• Массивтен барлық элементтерді шығару.
• Мысалы, бізде 100 сан бар, оларды экранға шығарғанда 100 қадам
орындалады. Егер 10 000 сан болса, 10 000 қадам орындалады.
•Әрбір жаңа элемент алгоритмнің уақытын ұзартады.
Графика: Массивтен элементтерді шығару процесінің диаграммасы.

12.

O(log N) - Логарифмдік күрделілік
Мазмұн:
•O(log N) белгісі алгоритмнің деректердің көлемі өскен сайын тексерулер
санының логарифмдік түрде өсуін білдіреді.
•Мысал:
• Екілік іздеу алгоритмі.
• Бұл алгоритм деректерді әр қадам сайын екіге бөліп, жартысын алып
тастайды. Деректер саны артқан сайын, тексерулер саны тек сәл ғана
көбейеді.
•Екілік іздеудің ең жақсы қасиеті – оның логарифмдік күрделілігі.
O(N²) - Квадраттық күрделілік
Мазмұн:
•O(N²) белгісі алгоритмнің уақыттық күрделілігі деректердің көлемінің
квадратына пропорционалды екенін білдіреді.
•Мысал:
• Сұрыптау алгоритмдері: Таңдау арқылы сұрыптау немесе көпіршік
сұрыптау.
• Бұл алгоритмдерде әр элементті салыстыру үшін көптеген қадамдар
қажет болады.
•Бұл күрделілік деректер саны көбейген сайын өте баяу жұмыс істейді.
Графика: Таңдау сұрыптау немесе көпіршік сұрыптау алгоритмдерінің
қадамдары.

13.

Тиімді алгоритмді таңдау
Мазмұн:
•Бағдарламалау кезінде тиімді алгоритмді таңдау өте маңызды.
•Бір мәселені шешудің бірнеше түрлі алгоритмдері болуы мүмкін. Бірақ
олардың тиімділігі әртүрлі.
•Big-O нотациясы арқылы біз алгоритмдердің уақытын және ресурстарын
салыстыра аламыз.
•Мысалы:
• Егер сізге 100 элементті сұрыптау қажет болса, көпіршік сұрыптау
алгоритмі өте баяу болады. Ал Merge Sort немесе Quick Sort әлдеқайда
тиімді.
Графика: Әртүрлі алгоритмдердің уақыт графигін салыстыратын диаграмма.

14.

Практикалық мысалдар
Мазмұн:
•Сызықтық іздеу (O(N)) және Екілік іздеу (O(log N)) арасындағы
айырмашылық.
• Сызықтық іздеу барлық элементтерді бір-бірден тексереді, ал екілік
іздеу деректерді екіге бөліп, тек жартысын тексереді.
• Мысал: 1000 элементтік массивте сызықтық іздеу 1000 тексеру
жасауы мүмкін, ал екілік іздеу бар-жоғы 10 тексерумен табады.
•Интернет арқылы деректер жіберу vs Amazon Snowmobile.
• 10 мегабайттық файлды интернет арқылы жіберу жылдам, бірақ 800
терабайттық деректерді тасымалдау үшін Amazon Snowmobile
тиімдірек болады.
Графика: Екі алгоритмді салыстыратын диаграмма.

15. Бірінші — сызықтық іздеу мен екілік іздеуді салыстыру, ал екіншісі — интернет арқылы деректер жіберу мен Amazon Snowmobile

арасындағы салыстыруды қарастырамыз.1. Сызықтық іздеу (O(N)) және екілік іздеу (O(log
N)):Сызықтық іздеу (Linear Search)Сызықтық іздеуде біз массивтің әрбір элементін тексереміз. Оны C++ тілінде былай
жазуға болады:
#include <iostream>
#include <vector> //Бұл кітапхана C++ тілінде динамикалық массивтермен жұмыс жасауға мүмкіндік береді.
using namespace std;
int linearSearch(const vector<int>& arr, int target) { // Бұл параметр массивтің (вектордың) адресін қабылдайды. const кілт
сөзі массивтің мәнін өзгертуге болмайтынын білдіреді.
for (int i = 0; i < arr.size(); i++) {
if (arr[i] == target) {
return i; // Target табылса, индекс қайтарылады
}
}
return -1; // Егер target табылмаса
}
int main() {
vector<int> arr(1000); // 1000 элементтік массив
for (int i = 0; i < 1000; i++) {
arr[i] = i + 1; // Массивті 1-ден 1000-ға дейінгі сандармен толтырамыз }
int target = 500; // 500 санын іздейміз
int result = linearSearch(arr, target);
if (result != -1) {
cout << "Элемент " << target << " индексте " << result << endl;
} else {
cout << "Элемент табылмады!" << endl;
}
return 0;
}

16.

Екілік іздеу (Binary Search)
Екілік
іздеу
тек
сұрыпталған
массивтерде жұмыс істейді, себебі ол деректерді
жартылай бөліп, тексерулер жүргізеді. Оны C++
тілінде былай жазуға болады:
АЛГ тілінде
1.
1.
2.
3.
4.
5.
6.
7.
8.
9.
Бастау ->
Ізделген санды анықтау (target) ->
Цикл басталуы (i = 0) ->
arr[i] == target?
Иә -> Индекс қайтару -> Нәтиже: "Элемент табылды, индекс
i"
Жоқ -> Келесі элемент (i++).
Цикл аяқталды ма?
Массивті толтыру (arr) ->
Иә -> Нәтиже: "Элемент табылмады!"
Аяқтау.

17. Қорытынды

•Алгоритмдердің
тиімділігі
мен
бағдарламалауда үлкен рөл атқарады.
күрделілігі
•Big-O нотациясын дұрыс түсіну және қолдану арқылы
біз ең тиімді алгоритмді таңдай аламыз.
•Алгоритмдер мен олардың күрделілігін зерттеу
бағдарламалаудағы маңызды дағдылардың бірі болып
табылады.

18.

1. Жалпы сұрақтар:
1.Алгоритм дегеніміз не және ол қандай мақсатта қолданылады?
2.Алгоритмдердің уақыттық күрделілігін анықтаудың негізгі әдістері қандай?
3.Алгоритмнің кеңістік күрделілігі дегеніміз не? Оны қалай бағалауға болады?
4.Алгоритмдердің күрделілігін бағалауда Big-O нотациясының маңызы қандай?
5.Алгоритмдердің уақыттық күрделілігі мен кеңістік күрделілігін салыстырудың қандай маңызы бар?
2. Big-O нотациясы мен оның түрлері туралы сұрақтар:
1.O(1) және O(n) уақыттық күрделілігі арасындағы айырмашылықты түсіндіріңіз.
2.O(n^2) күрделілігі бар алгоритмдерді қандай жағдайда қолдану тиімді деп санайсыз?
3.Алгоритмнің O(log n) күрделілігі не үшін тиімді және оны қандай алгоритмдер қолданады?
4.Big-O, Big-Omega, және Big-Theta нотацияларының айырмашылығы неде?
5.Неліктен O(n log n) күрделілігі O(n^2)-ден тиімді болып табылады?
3. Алгоритмдер мен олардың мысалдары туралы сұрақтар:
1.Сызықтық іздеу алгоритмі (linear search) қандай күрделілікке ие және оның артықшылықтары мен кемшіліктері қандай?
2.Бинарлық іздеу алгоритмі қалай жұмыс істейді және оның тиімділігі неге байланысты?
3.Қатты сұрыптау (Bubble Sort) және Тез сұрыптау (Quick Sort) алгоритмдерінің күрделілігін салыстырыңыз.
4.Неліктен сұрыптау алгоритмдерінің уақыттық күрделілігін білу маңызды, әсіресе деректердің көп көлемінде жұмыс
істегенде?
4. Алгоритмдердің тиімділігін талдау мен оңтайландыру туралы сұрақтар:
1.Алгоритмдердің тиімділігін қалай салыстыруға болады? Бұл салыстырудың маңызы қандай?
2.Алгоритмдерді оңтайландыру үшін қандай әдістер қолдануға болады?
3.Динамикалық бағдарламалау әдісі алгоритмдердің тиімділігін қалай жақсартады?
4.Көпшілік алгоритмдерде орындалатын қай қадамдар оңтайландыруға ең қолайлы болып табылады?
5.Алгоритмдердің күрделілігін жақсартудың шектеулері қандай болуы мүмкін?
5. Қолдану мен өмірдегі мысалдар:
1.Алгоритмдер күрделілігін талдау қай салаларда маңызды болып табылады?
2.Алгоритмдердің күрделілігі бизнес процестерін немесе ғылыми зерттеулерді қалай жақсарта алады?
3.Қай жерде сызықтық іздеу алгоритмі тиімді, ал қай жерде бинарлық іздеу әлдеқайда пайдалы болады?
6. Қорытынды сұрақтар:
1.Неліктен барлық алгоритмдер бірдей тиімді болмайды? Қалай дұрыс таңдау жасауға болады?
2.Алгоритмдердің күрделілігін төмендету әрқашан мүмкін бе? Қандай жағдайларда бұл мүмкін болмайды?
3.Күрделілігі жоғары алгоритмдерді шектеулі ресурстармен қалай пайдалану керек?

19. Сандық алгоритмдер

Қосу операциясы
Мысал: 53+35
Алгоритмнің күрделілігі: O(n).
Көбейту операциясы
Мысал: 11*13
Тізбектей қосу үшін n сандар, қажет болады
(n-1) қадамдар:
Әдіс Әл-Хорезми
Алгоритмнің күрделілігі: Ω(n2).