Негізгі позициялық есептер. 4-дәріс

1.

4-дәріс
Негізгі позициялық есептер
Қарымсақов Уалихан Төленұлы

2.

Проекция
Проекция
Projection
Нүкте
Точка
Point
Түзу
Прямая
Straight Line
Жазықтық
Плоскость
Plane
Қиылысу
Пересечение
Intersect
Өзара орналасуы
Взаимное
расположение
Mutual Positions
Бәсекелес
нүктелер
Конкурирующие
точки
Competing points

3.

Негізгі позициялық есептер деп
нүктелердің, түзулердің және
жазықтықтардың өзара орналасуын
анықтауға арналған есептерді айтамыз.

4.

Негізгі позициялық есептер:
екі нүктенің өзара орналасуы;
нүкте мен түзудің өзара орналасуы;
екі түзудің өзара орналасуы;
түзу мен жазықтықтың өзара орналасуы;
нүкте мен жазықтықтың өзара орналасуы;
екі жазықтықтың өзара орналасуы.

5.

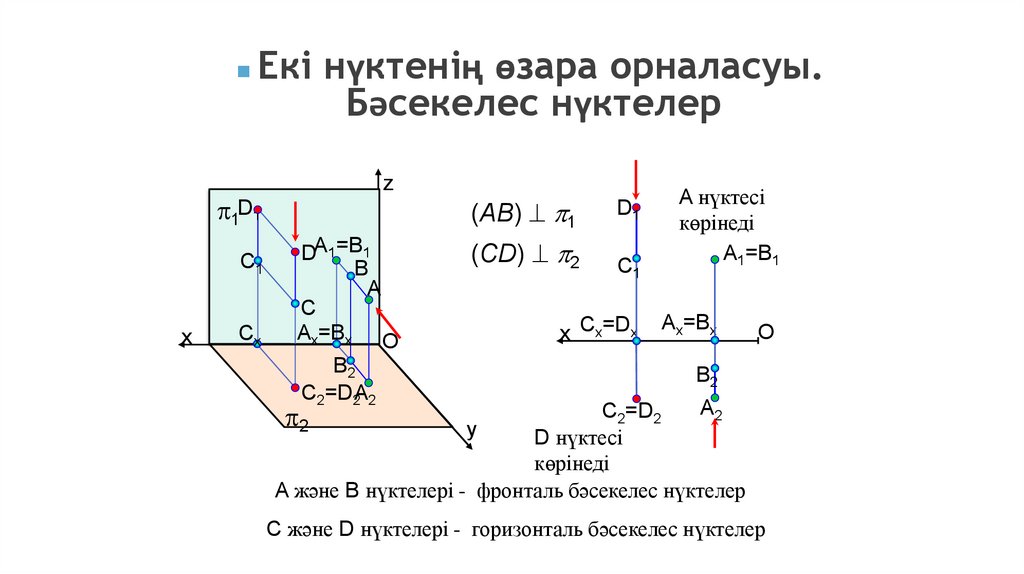
Екі нүктенің өзара орналасуы.
Бәсекелес нүктелер
z
p1D1
C1
x
Сx
DA1=B1
B
A
С
Ax=Bx O
B2
С2=D2A2
(АВ) p1
D1
(CD) p2
C1
x Cx=Dx
A нүктесі
көрінеді
A1=B1
Ax=Bx
O
B2
A2
С2=D2
y
D нүктесі
көрінеді
A және В нүктелері - фронталь бәсекелес нүктелер
p2
С және D нүктелері - горизонталь бәсекелес нүктелер

6.

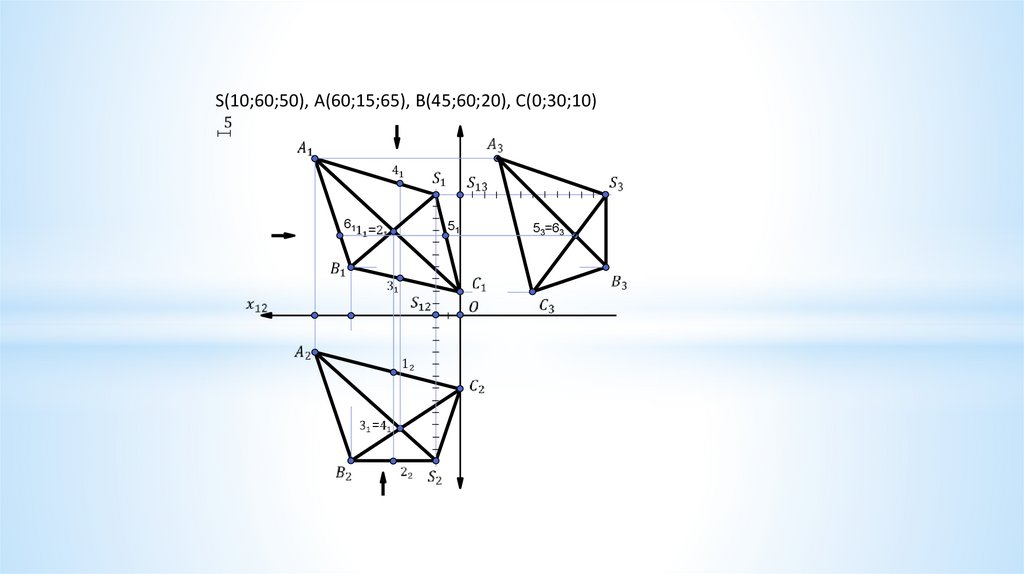
S(10;60;50), A(60;15;65), B(45;60;20), C(0;30;10)
61
51
53=63

7.

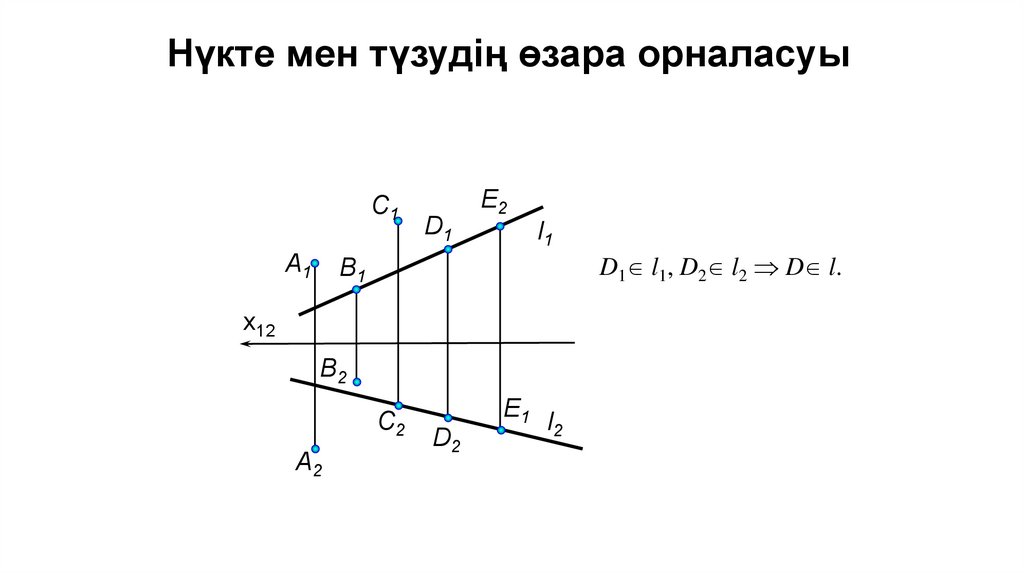
Нүкте мен түзудің өзара орналасуы
С1
А1
D1
E2
l1
В1
х12
В2
C2
А2
E1
D2
l2
D1 l1, D2 l2 D l.

8.

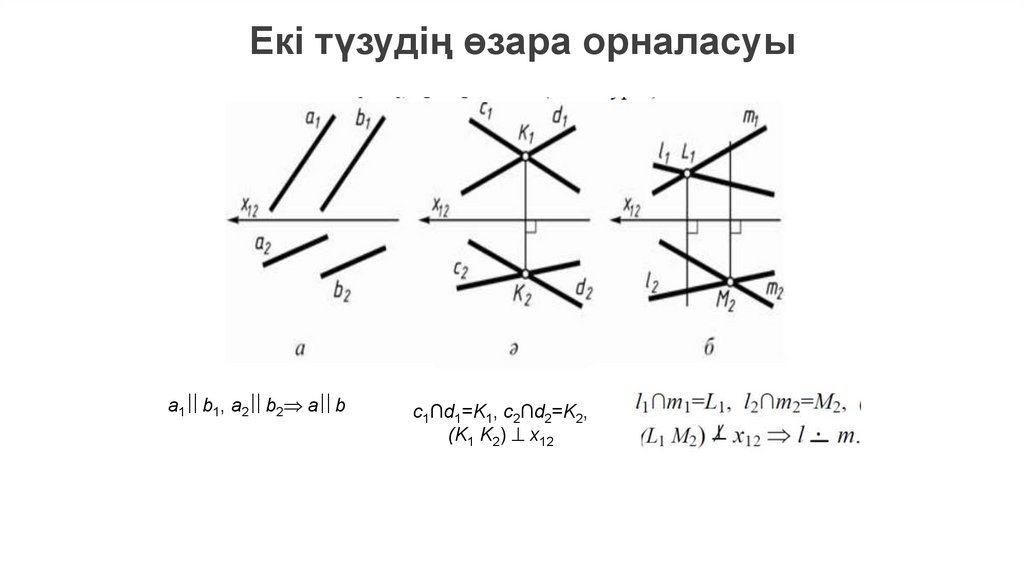
Екі түзудің өзара орналасуы
a1 b1, a2 b2 a b
с1∩d1=K1, с2∩d2=K2,
(K1 K2) x12

9.

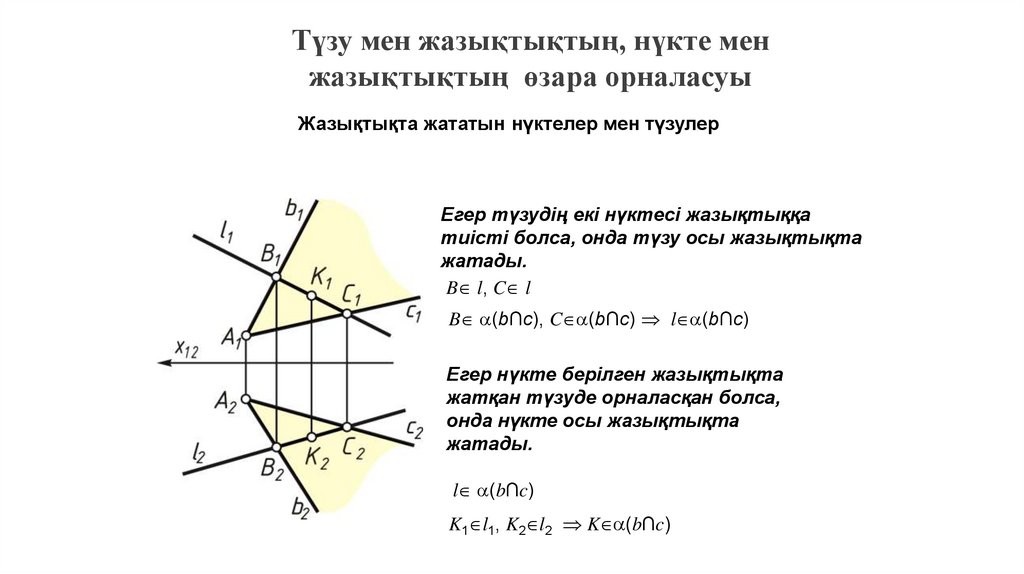
Түзу мен жазықтықтың, нүкте мен
жазықтықтың өзара орналасуы
Жазықтықта жататын нүктелер мен түзулер
Егер түзудің екі нүктесі жазықтыққа
тиісті болса, онда түзу осы жазықтықта
жатады.
B l, C l
B (b∩c), C (b∩c) l (b∩c)
Егер нүкте берілген жазықтықта
жатқан түзуде орналасқан болса,
онда нүкте осы жазықтықта
жатады.
l (b∩c)
K1 l1, K2 l2 K (b∩c)

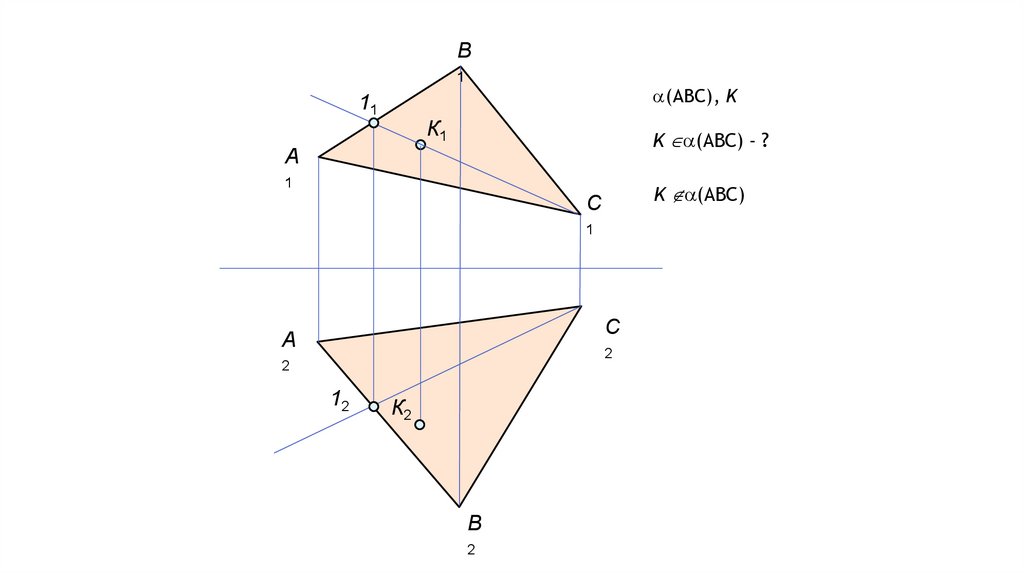
10.

B
1
11
(ABC), K
К1
K (ABC) - ?
A
1
K (ABC)
C
1
C
A
2
2
12
К2
B
2

11.

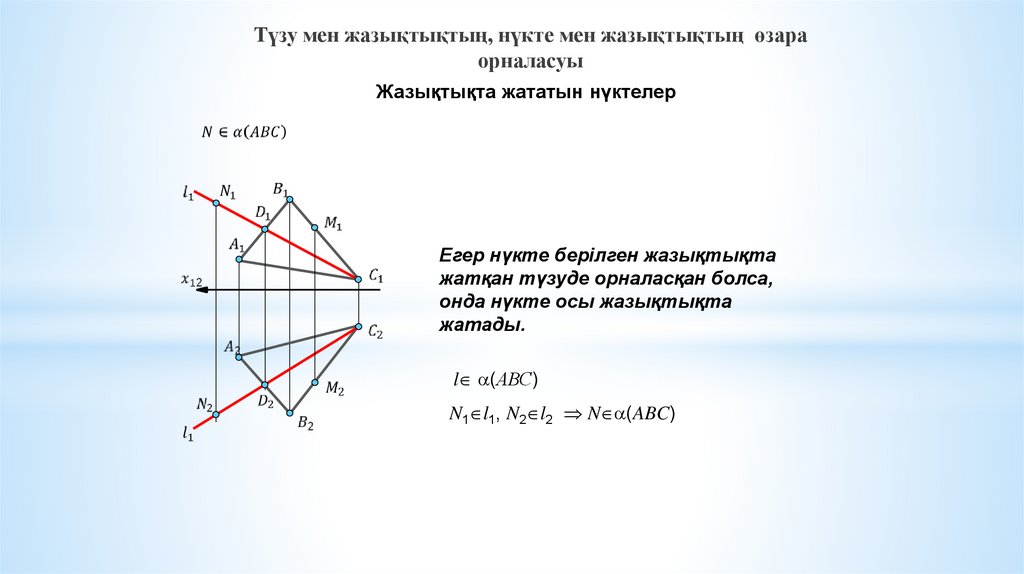
Түзу мен жазықтықтың, нүкте мен жазықтықтың өзара
орналасуы
Жазықтықта жататын нүктелер
Егер нүкте берілген жазықтықта
жатқан түзуде орналасқан болса,
онда нүкте осы жазықтықта
жатады.
l (АВС)
N1 l1, N2 l2 N (ABC)

12.

Түзу мен жазықтықтың өзара орналасуы
Түзу мен жазықтық үш түрлі орналасуы мүмкін:
1. Түзу жазықтыққа тиісті болуы мүмкін;
2. Түзу жазықтыққа параллель болуы мүмкін;
3. Түзу жазықтықпен қиылысуы мүмкін.

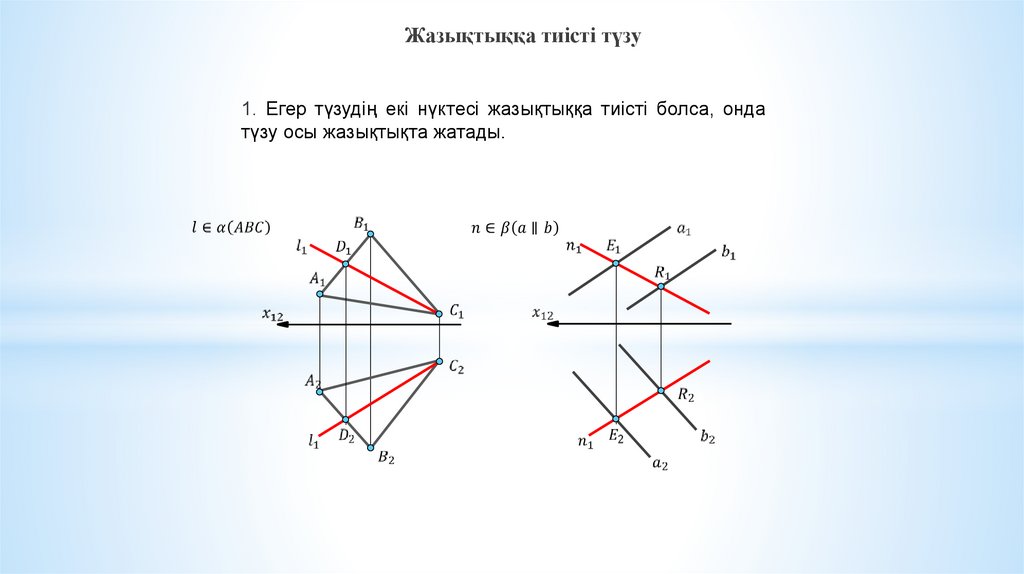
13.

Жазықтыққа тиісті түзу
1. Егер түзудің екі нүктесі жазықтыққа тиісті болса, онда
түзу осы жазықтықта жатады.

14.

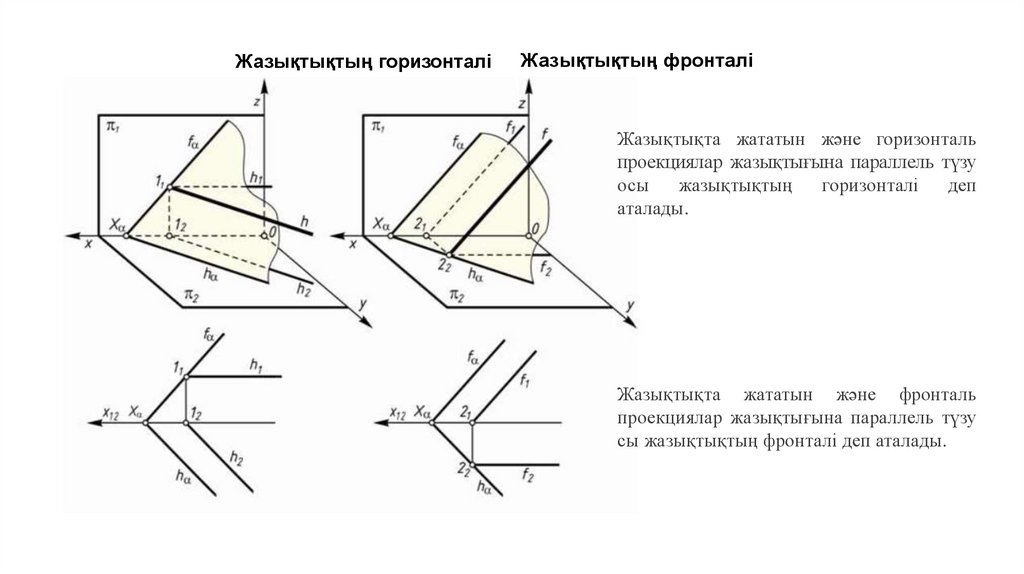
Жазықтықтың горизонталі
Жазықтықтың фронталі
Жазықтықта жататын және горизонталь
проекциялар жазықтығына параллель түзу
осы
жазықтықтың
горизонталі
деп
аталады.
Жазықтықта жататын және фронталь
проекциялар жазықтығына параллель түзу
сы жазықтықтың фронталі деп аталады.

15.

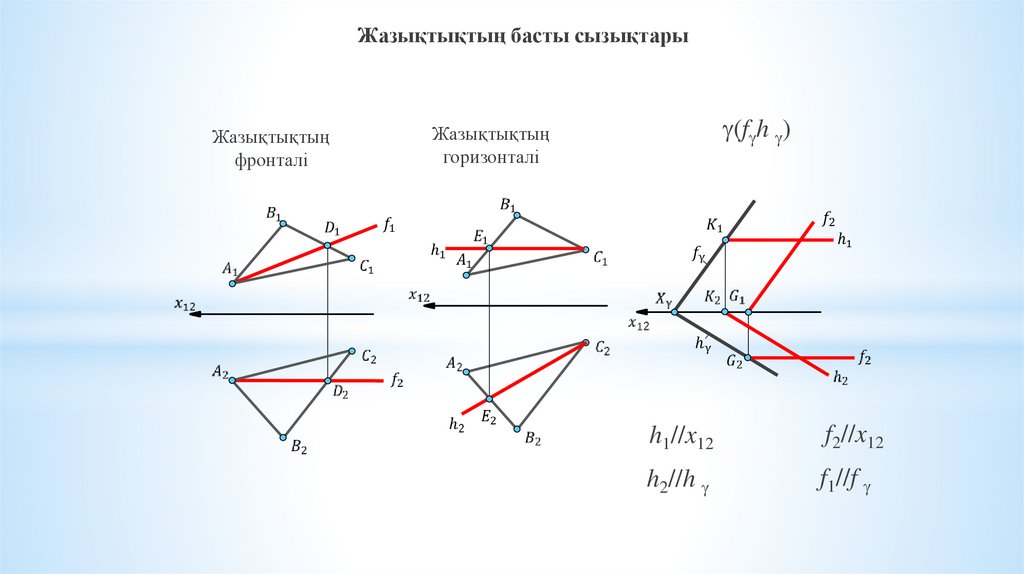
Жазықтықтың басты сызықтары
Жазықтықтың
фронталі
(f h )
Жазықтықтың
горизонталі
h1//x12
f2//x12
h2//h
f1//f

16.

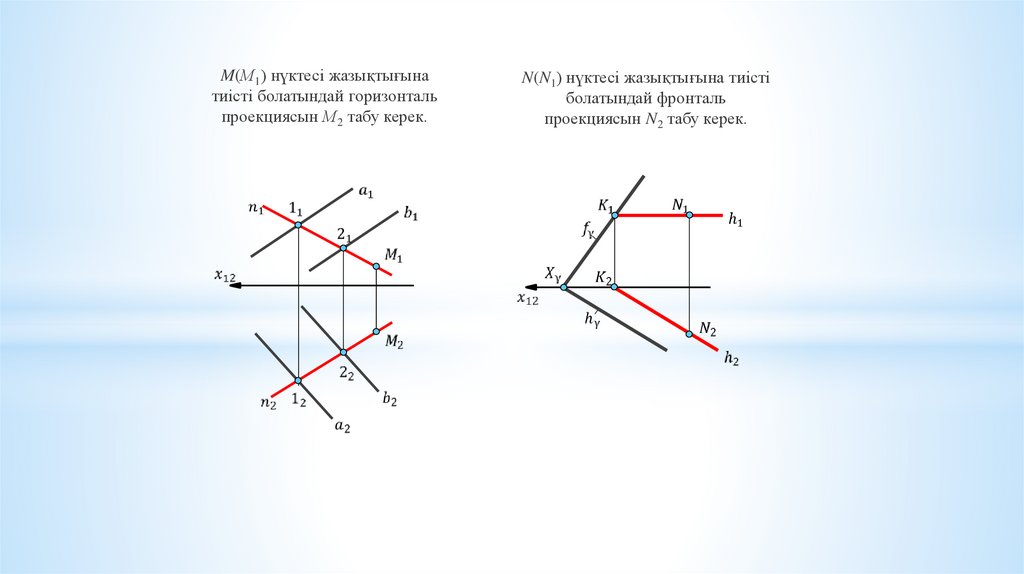
M(М1) нүктесі жазықтығына
тиісті болатындай горизонталь
проекциясын М2 табу керек.
N(N1) нүктесі жазықтығына тиісті
болатындай фронталь
проекциясын N2 табу керек.

17.

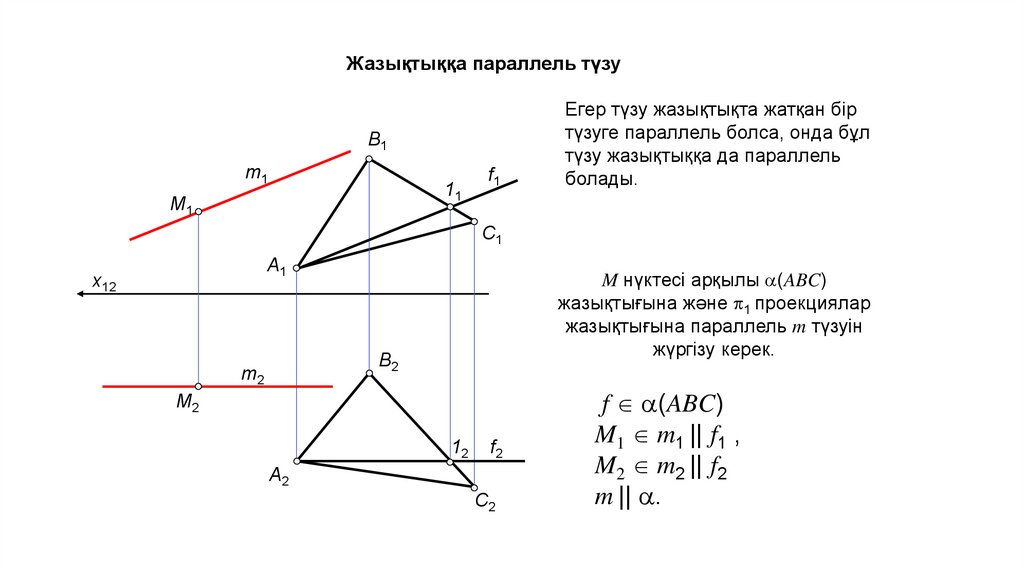
Жазықтыққа параллель түзу
B1
m1
11
M1
f1
Егер түзу жазықтықта жатқан бір
түзуге параллель болса, онда бұл
түзу жазықтыққа да параллель
болады.
C1
А1
x12
M нүктесі арқылы (ABC)
жазықтығына және p1 проекциялар
жазықтығына параллель m түзуін
жүргізу керек.
B2
m2
M2
12
f2
А2
С2
f (ABC)
M1 m1 || f1 ,
M2 m2 || f2
m || .

18.

Түзу мен жазықтықтың қиылысу нүктесін салу
Түзу мен жазықтықтың қиылысуының үш түрлі
жағдайын қарастырайық:
1. Проекциялаушы түзудің жалпы жағдай жазықтығымен
қиылысуы;
2. Жалпы жағдайдағы түзудің проекциялаушы
жазықтықпен қиылысуы;
3. Жалпы жағдайдағы түзудің жалпы жағдайдағы
жазықтықпен қиылысуы.

19.

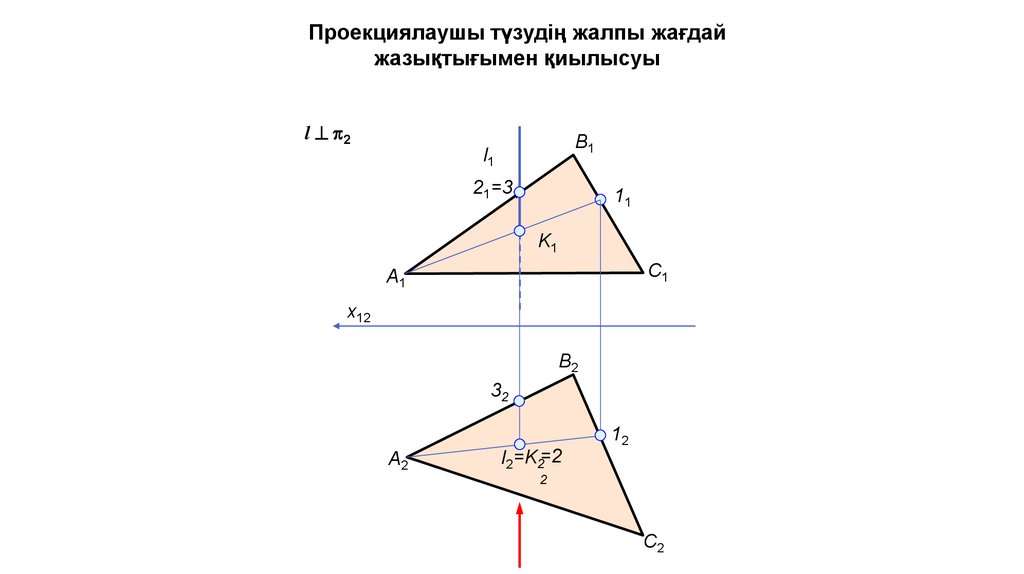
Проекциялаушы түзудің жалпы жағдай
жазықтығымен қиылысуы
l p2
B1
l1
21=31
11
K1
C1
А1
x12
B2
32
А2
12
l2=K2=2
2
С2

20.

Проекциялаушы түзудің жалпы жағдай
жазықтығымен қиылысуы

21.

Жалпы жағдайдағы түзудің
проекциялаушы жазықтықпен
қиылысуы

22.

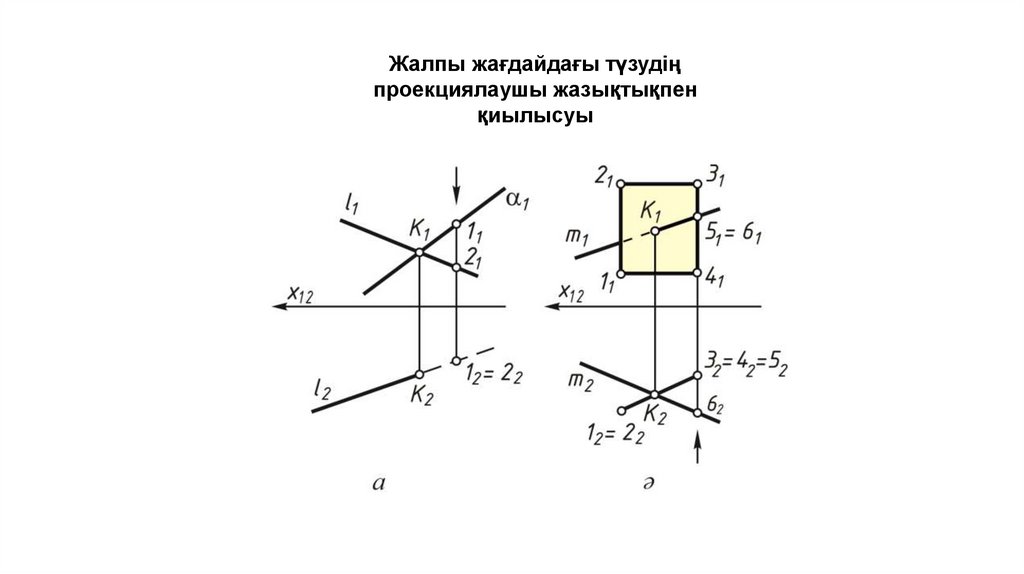
. Жалпы жағдайдағы түзудің жалпы
жағдайдағы жазықтықпен қиылысуы.
m
C
21
l1
3
1
1
K
A1
1
1
x1
1
41=
51
B
1
1
2
A
K2 2
2
2
l2 2
l2= 2=m
С2
52
12
12=3
2
42
B2
Көрінетіндікті анықтау.
1. Берілген l түзуі арқылы горизонтальпроекциялаушы жазықтығын жүргіземіз.
2. Көмекші жазықтығының жазықтығымен
қиылысу сызығы m түзуін жүргіземіз: m=( ∩ ).
m және l түзулері горизонталь-проекциялаушы
жазықтығында жатады, яғни горизонталь
бәсекелес болып табылады, сондықтан: l2= 2=m2.
m2∩(A2B2)=12.
m2∩(A2C2)=22.
12 11 (A1B1).
22 21 (A1C1).
(11 21)=m1.
3. a) m1 =l1 l ;
ә) m1 | | l1 l | | ;
б) m1 ∩ l1 l ∩ .
1 (AB), 3 l
1 және 3 нүктелері – горизонталь-бәсекелес.
3 нүктесі биік орналасқан, сондықтан горизонталь проекцияда l
түзуінің K2 мен 22 нүктелерінің арасы көрінбейді.
4 l, 5 (BС)
4 және 5 нүктелері – фронталь-бәсекелес.
5 нүктесі жақын орналасқан, сондықтан фронталь проекцияда l
түзуінің K1 мен 41 нүктелерінің арасы көрінбейді.
(m1 ∩ l1 ) =K1.
K1 K2 l2.
K=(l∩ ).

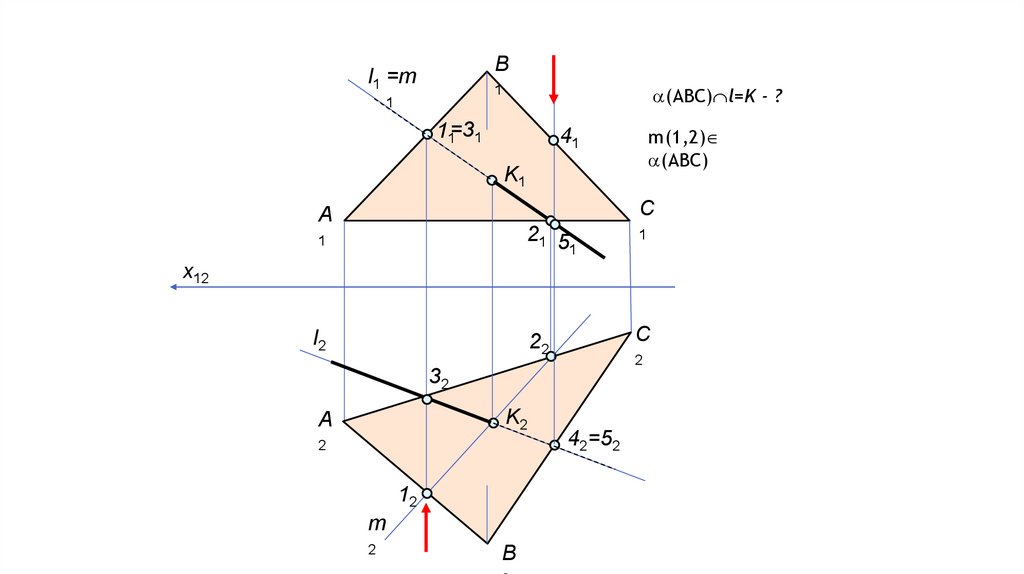
23.

B
l1 =m
(ABC) l=K - ?
1
1
11=31
m(1,2)
(ABC)
41
K1
C
A
1
21 5
l2
22
1
1
x12
C
2
32
K2
A
2
12
m
2
B
42=52

24.

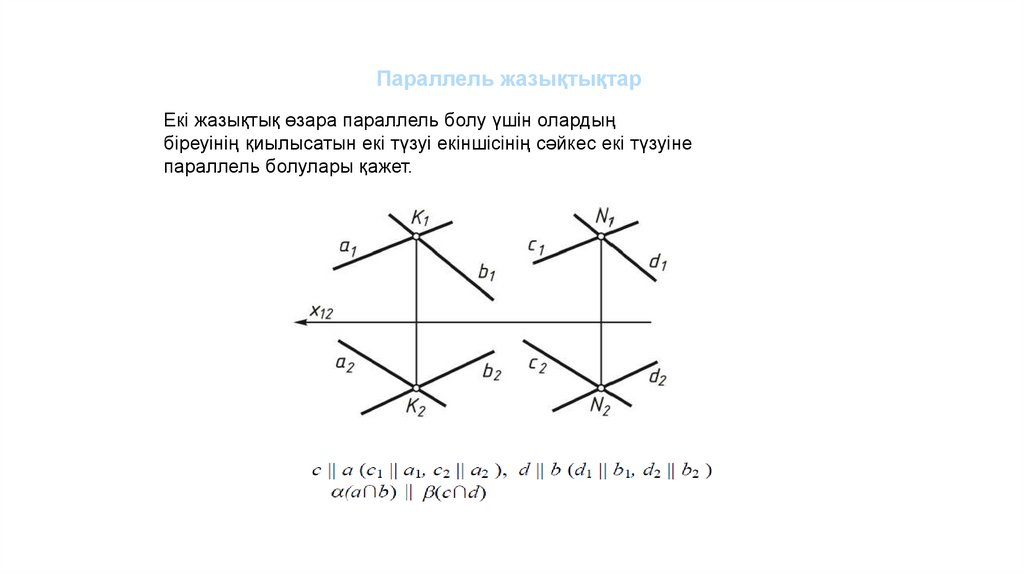
Параллель жазықтықтар
Екі жазықтық өзара параллель болу үшін олардың
біреуінің қиылысатын екі түзуі екіншісінің сәйкес екі түзуіне
параллель болулары қажет.

25.

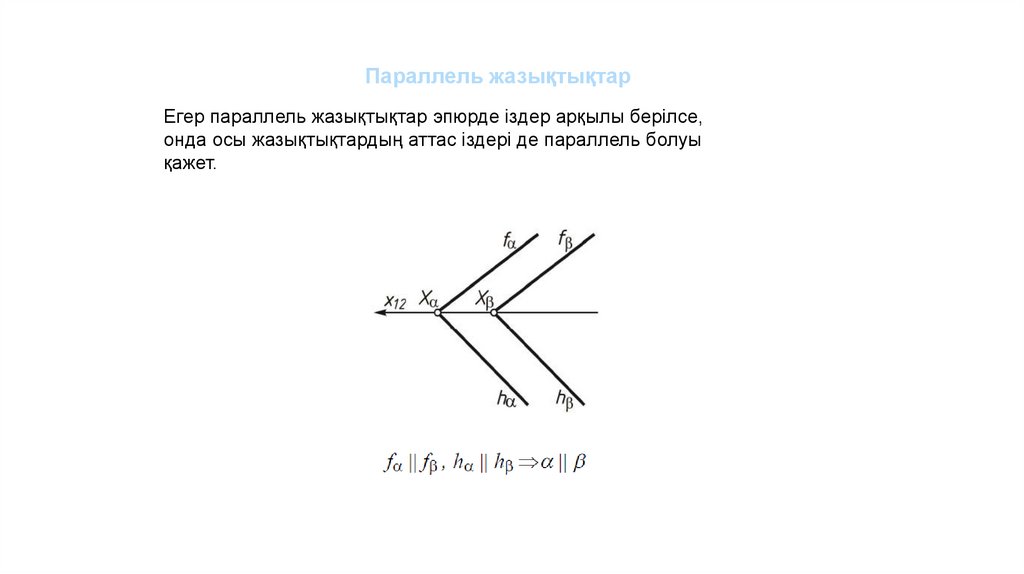
Параллель жазықтықтар
Егер параллель жазықтықтар эпюрде іздер арқылы берілсе,
онда осы жазықтықтардың аттас іздері де параллель болуы
қажет.

26.

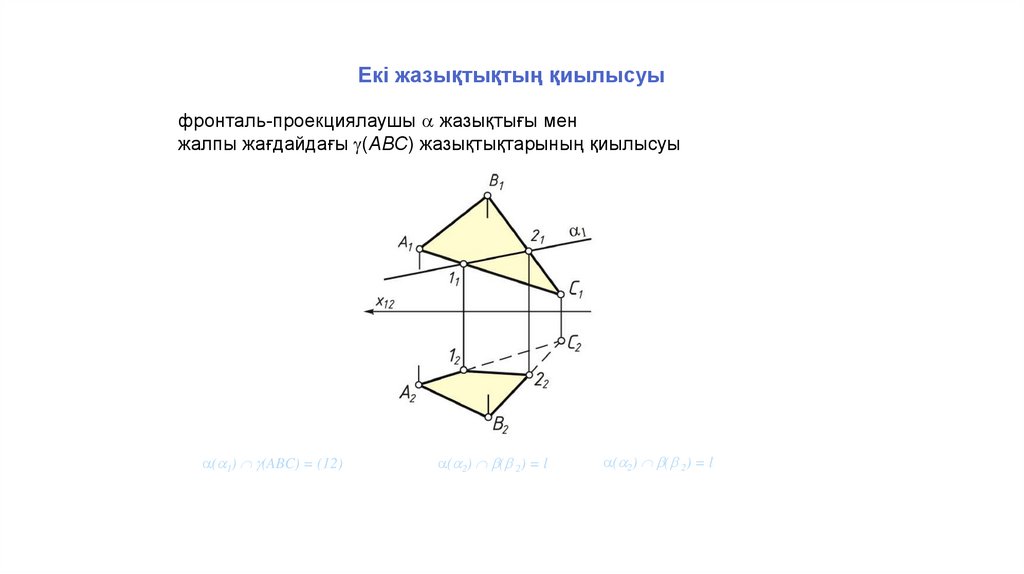
Екі жазықтықтың қиылысуы
фронталь-проекциялаушы жазықтығы мен
жалпы жағдайдағы (АВС) жазықтықтарының қиылысуы
( 1) (ABC) = (12)
( 2) ( 2) = l
( 2) ( 2) = l

27.

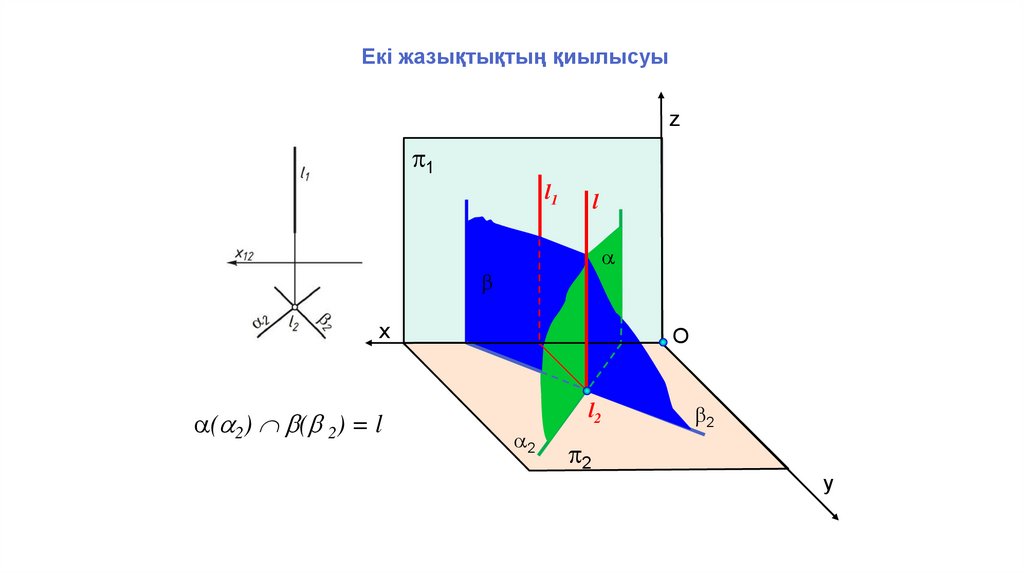
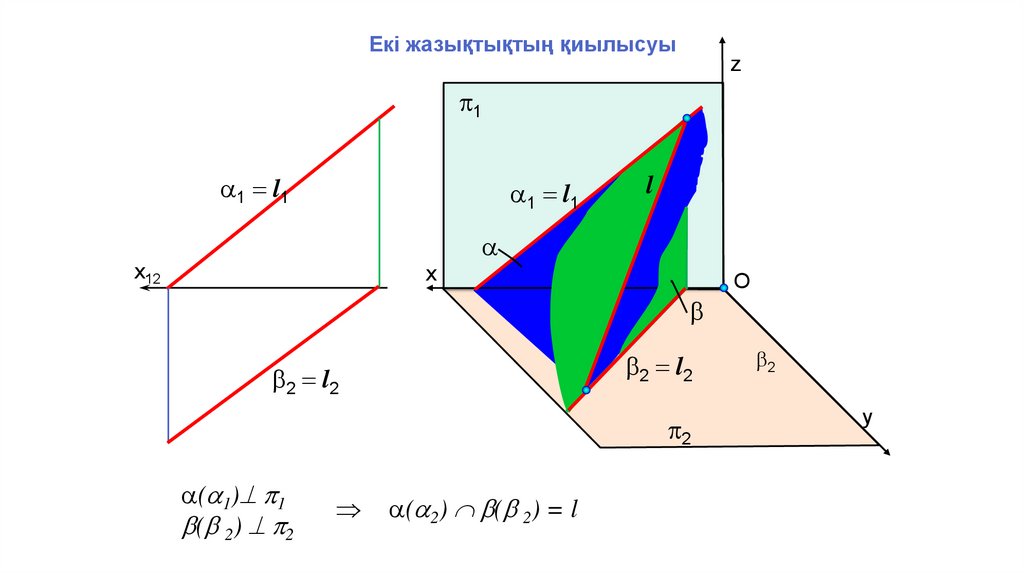
Екі жазықтықтың қиылысуы
z
p1
l1
l
x
( 2) ( 2) = l
O
l2
2
2
p2
y

28.

Екі жазықтықтың қиылысуы
z
p1
1 = l1
1 = l1
l
x12
x
O
2 = l 2
2 = l 2
p2
( 1) p1
( 2) p2
( 2) ( 2) = l
2
y

29.

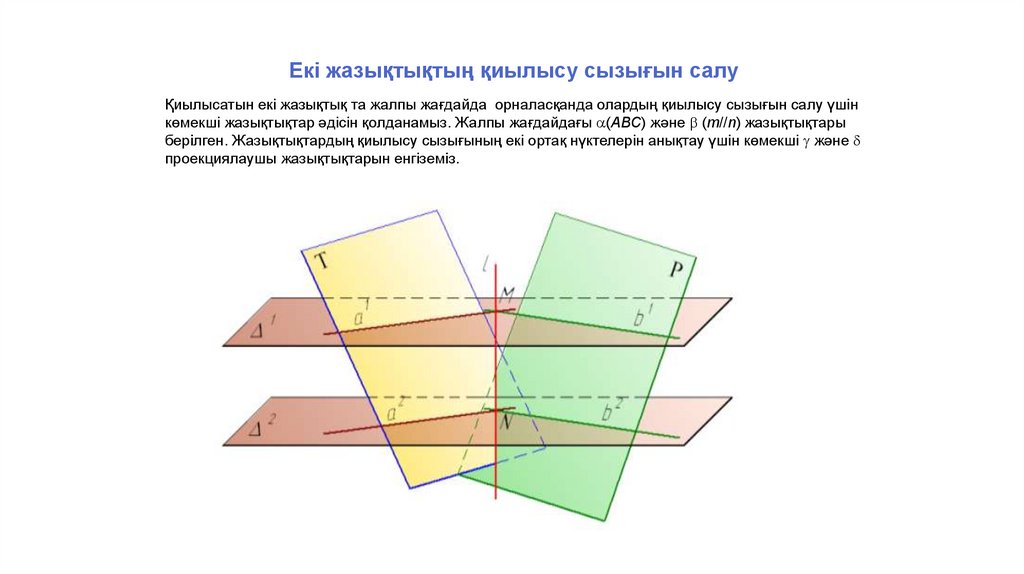
Екі жазықтықтың қиылысу сызығын салу
Қиылысатын екі жазықтық та жалпы жағдайда орналасқанда олардың қиылысу сызығын салу үшін
көмекші жазықтықтар әдісін қолданамыз. Жалпы жағдайдағы (АВС) және (m//n) жазықтықтары
берілген. Жазықтықтардың қиылысу сызығының екі ортақ нүктелерін анықтау үшін көмекші және
проекциялаушы жазықтықтарын енгіземіз.

30.

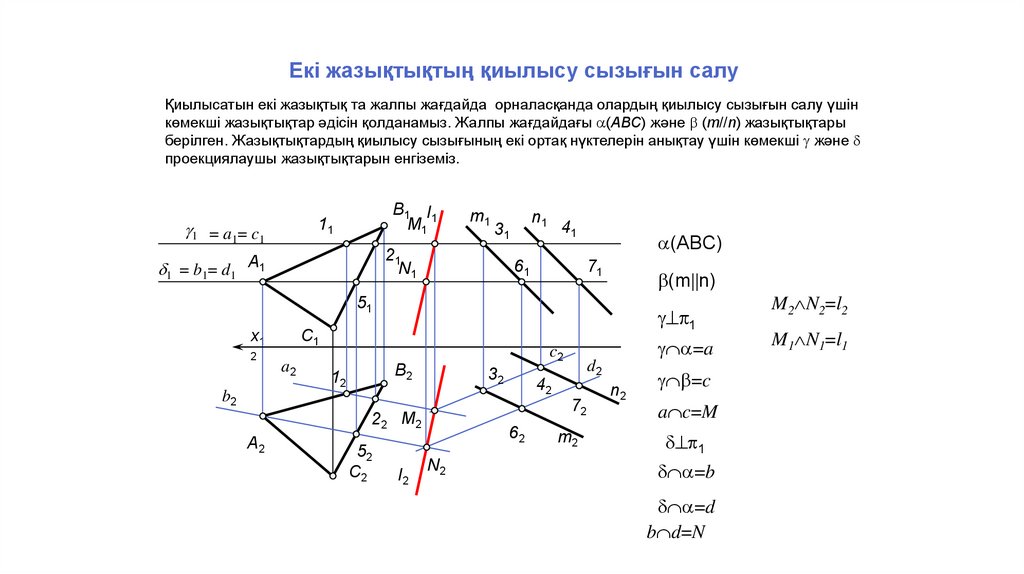
Екі жазықтықтың қиылысу сызығын салу
Қиылысатын екі жазықтық та жалпы жағдайда орналасқанда олардың қиылысу сызығын салу үшін
көмекші жазықтықтар әдісін қолданамыз. Жалпы жағдайдағы (АВС) және (m//n) жазықтықтары
берілген. Жазықтықтардың қиылысу сызығының екі ортақ нүктелерін анықтау үшін көмекші және
проекциялаушы жазықтықтарын енгіземіз.
В1 l 1
M1
11
1 = a1= c1
m1
21
N1
1 = b1= d1 A1
n1
31
41
61
(ABC)
71
(m n)
51
С1
x1
2
p1
a2
В2
12
32
72
22 M2
52
С2
l2
d2
42
b2
A2
=a
c2
62
N2
m2
n2
=c
a c=M
p1
=b
=d
b d=N
M2 N2=l2
M1 N1=l1

31.

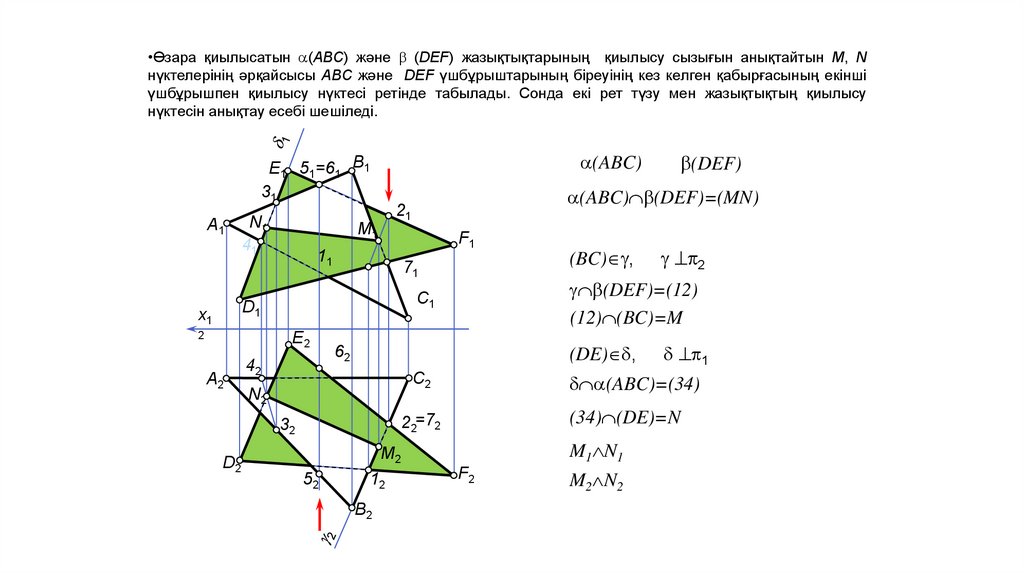
•Өзара қиылысатын (АВС) және (DEF) жазықтықтарының қиылысу сызығын анықтайтын M, N
нүктелерінің әрқайсысы АВС және DEF үшбұрыштарының біреуінің кез келген қабырғасының екінші
үшбұрышпен қиылысу нүктесі ретінде табылады. Сонда екі рет түзу мен жазықтықтың қиылысу
нүктесін анықтау есебі шешіледі.
(ABC)
E1 51=61 B1
31
A1
N1
41
F1
11
2
42
62
(DE) ,
N2
32
D2
12
B2
p1
C2
(ABC)=(34)
22=72
(34) (DE)=N
M1 N1
M2
52
p2
(DEF)=(12)
(12) (BC)=M
C1
E2
A2
(BC) ,
71
D1
x1
(ABC) (DEF)=(MN)
21
M1
(DEF)
F2
M2 N2

32.

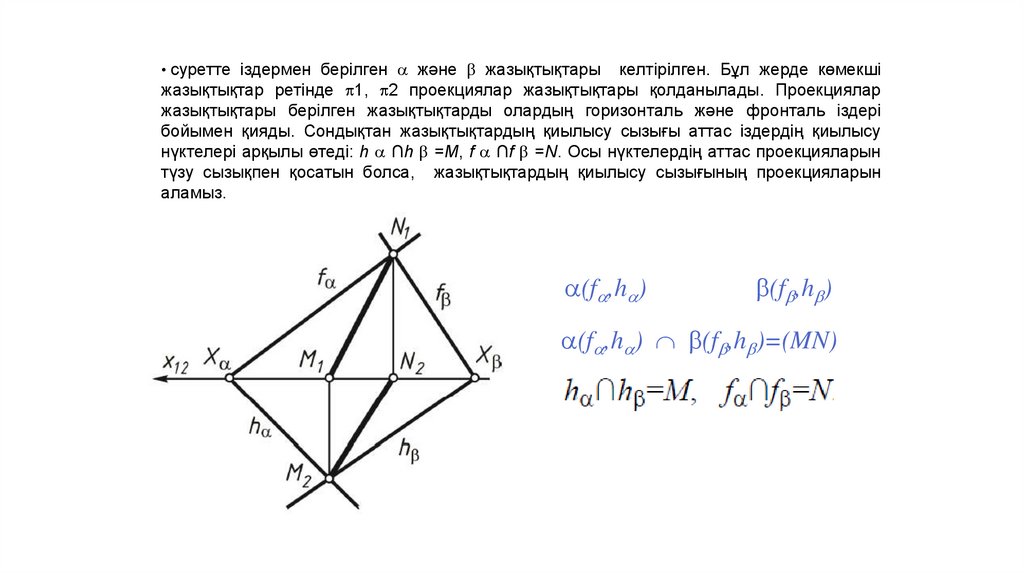
• суретте іздермен берілген және жазықтықтары
келтірілген. Бұл жерде көмекші
жазықтықтар ретінде p1, p2 проекциялар жазықтықтары қолданылады. Проекциялар
жазықтықтары берілген жазықтықтарды олардың горизонталь және фронталь іздері
бойымен қияды. Сондықтан жазықтықтардың қиылысу сызығы аттас іздердің қиылысу
нүктелері арқылы өтеді: h ∩h =M, f ∩f =N. Осы нүктелердің аттас проекцияларын
түзу сызықпен қосатын болса, жазықтықтардың қиылысу сызығының проекцияларын
аламыз.
(f ,h )
(f ,h )
(f ,h ) (f ,h )=(MN)

33.

,
Бақылау сұрақтары:
1. Сызбада екі жазықтықтың параллельдігін қалай анықтауға
болады?
2. Түзудің жалпы жағдайдағы жазықтықпен қиылысу нүктесін
тұрғызудың қадамдарын атаңыз.