Смежные и вертикальные углы

1. СМЕЖНЫЕ И ВЕРТИКАЛЬНЫЕ УГЛЫ

2. Определение смежных углов

Давайте построим развёрнутый угол АОС и
проведём в нём луч ОВ. В результате у нас
получилось два угла ∠АОВ – острый угол и
∠ВОС– тупой угол.
Стороны АО и ОС – продолжают друг
друга, ВО– общая сторона. Углы АОВ и ВОС
– это смежные углы.
На основании этого сформулируем
определение смежных углов.
Два угла, у которых одна сторона общая, а
две другие являются продолжениями друг
друга, называются смежными.

3. Свойство смежных углов

Обратите, внимание, что смежные углы АОВ и
ВОС лежат на развёрнутом угле АОС. Отсюда
можно сделать вывод: сумма смежных углов
равна 180о.
Свойство смежных углов: сумма смежных
углов равна 180о.
Давайте докажем это свойство.
Доказательство. Пусть углы ∠АОВ и ∠ВОС –
смежные, луч ОВ – проходит между
сторонами развёрнутого угла ∠АОС. Поэтому,
сумма углов ∠АОВ и ∠ВОС равна ∠АОС, а этот
угол развёрнутый, он равен 180о. Свойство
доказано.

4. Свойство смежных углов

Укажем
ещё
одно
свойство
смежных
углов.
Если два угла равны, то
и смежные с ними углы
равны.
Если 1 = 3, а 3 и
4 – смежные, 1 и 2
– смежные, то 2 = 4

5. Свойства смежных углов

Сейчас
давайте
вспомним
определение прямого угла: угол,
равный 900, называется прямым
углом.
Опираясь на свойство суммы
смежных углов, можно сделать
вывод: угол, смежный с прямым
углом, есть прямой угол.
Если 1 и 2 – смежные, а 1 = 90 ,
то 2 = 90

6. Определение вертикальных углов

Теперь построим две пересекающиеся прямые, АС и BD.
Посмотрите, при пересечении прямых у нас получилось четыре
угла: ∠АОВ, ∠АОD, ∠CОD, ∠BОC. Из них попарно являются
смежными углы: ∠АОВ и ∠АОD, ∠АОD и ∠CОD, ∠CОD и ∠BОC, ∠АОВ
и ∠BОC.
Углы, которые не являются смежными:
∠АОВ и ∠CОD; ∠АОD и ∠BОC. Пары этих углов
называются вертикальными углами.
Два угла называются вертикальными,
если стороны одного угла являются
продолжениями сторон другого.

7. Свойство вертикальных углов

Свойство вертикальных
углов: вертикальные углы равны.
Убедимся в справедливости этого
свойства, докажем его.
Доказательство. Посмотрим на чертёж:
пары углов 1 и 2, 2 и 3, 3 и 4, 4 и 1–
смежные углы. Угол 2 одновременно
является смежным с углом 1 и с углом 3.
По свойству смежных углов
∠1+ ∠2= 1800 и ∠3+ ∠2= 1800. Получаем,
что ∠1+ ∠2= ∠3+ ∠2, значит, ∠1= ∠3. Углы
∠1 и ∠3 – вертикальные. Мы доказали
справедливость этого свойства.

8. Задача 1

Используя чертёж, найдите угол ∠ВОК.
Решение. Воспользуемся свойством
смежных углов: сумма смежных углов равна
1800. По условию задачи ∠АОК= 110, то
∠ВОК+ ∠АОК= 1800
∠ВОК+ 110= 1800
∠ВОК= 1800– 110= 1690.
Ответ: ∠ВОК= 1690

9. Задача 2

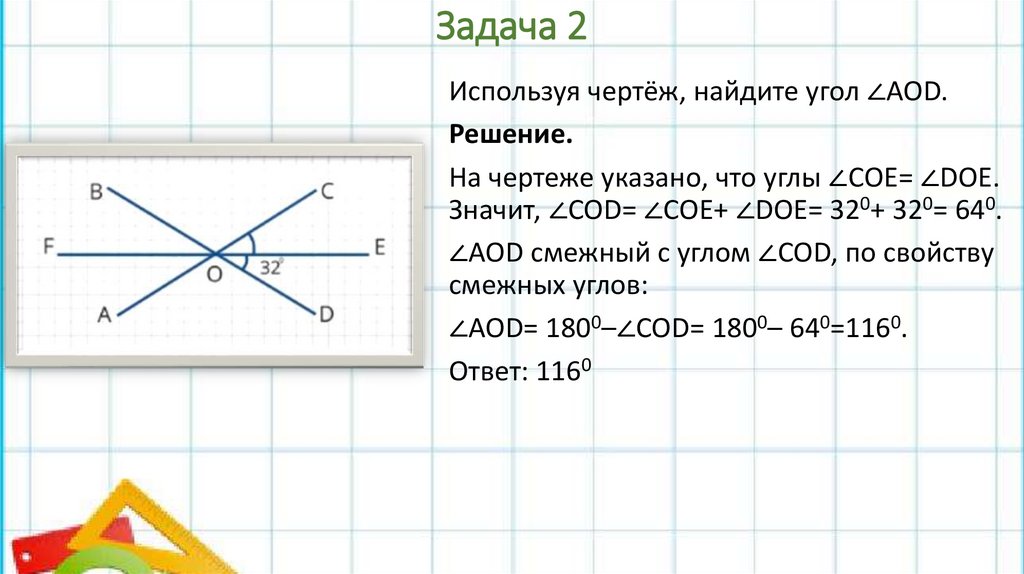
Используя чертёж, найдите угол ∠AOD.
Решение.
На чертеже указано, что углы ∠СОЕ= ∠DOE.
Значит, ∠COD= ∠СОЕ+ ∠DOE= 320+ 320= 640.
∠AOD смежный с углом ∠COD, по свойству
смежных углов:
∠AOD= 1800–∠COD= 1800– 640=1160.
Ответ: 1160

10. Задача 3

Используя чертёж, найдите градусную меру
угла ∠BMD, если ∠AMD= 1250, ∠BMC= 1150.
Решение. По чертежу можно увидеть, что
∠BМD является частью ∠AMD и ∠BMC.
Рассмотрим ∠DMC и ∠AMD. Эти углы –
смежные, т.е. их сумма равна 1800. Значит,
зная градусную меру ∠AMD, мы сможем
найти градусную меру ∠DMC= 1800–∠AMD=
1800-–1250= 550. Теперь рассмотрим ∠BMC=
∠BMD+ ∠DMC. Мы знаем градусные меры
∠BMC и ∠DMC, значит, мы сможем найти
градусную меру ∠BMD.
∠BMD= ∠BMC–∠DMC= 1150– 550= 600.
Ответ: 600

11.

12. Подведем итог урока:

Попробуйте ответить на вопросы:
1. Какие углы называются смежными?
2. Перечислите свойства смежных углов.
3. Какие углы называются вертикальными?
4. Перечислите свойства вертикальных углов.
5. Могут ли оба смежных угла быть острыми?
6. Могут ли оба смежных угла быть тупыми?
7. Могут ли оба смежных угла быть прямыми?
Примечание. Если какой – то вопрос вызвал у вас затруднение, то
просмотрите материал урока еще раз.