Основы логики для самоподготовки

1. Основы логики

2.

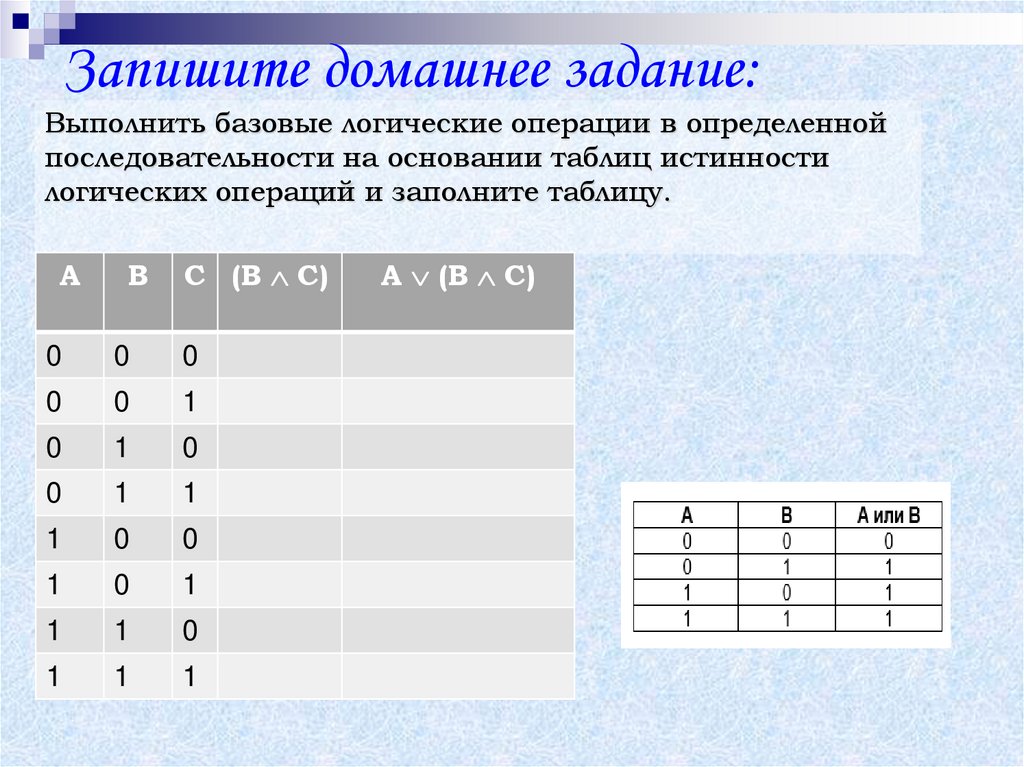
Запишите домашнее задание:
Выполнить базовые логические операции в определенной
последовательности на основании таблиц истинности
логических операций и заполните таблицу.
A
B
C (В С)
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
А (В С)

3. Записать только определения, остальное прочитать.

4. Логика. Основные понятия логики.

Внутри машины все числа (а так же информация другого
рода: буквы, знаки и др.) представлена в виде двоичных кодов.
При
выполнении
программы
арифметическо-логическое
устройство (АЛУ) производит различные операции над
двоичными числами, выдавая результаты также в виде
двоичных чисел. Поэтому АЛУ можно рассматривать как
сложный функциональный преобразователь, на вход которого
поступают исходные двоичные числа, а на выходе выдаётся
новое двоичное число, являющееся той или иной функцией от
входных чисел.
Запишите определение:
Опр: Раздел математики, занимающийся
логических функций, называется алгеброй логики.
исследованием

5.

Мы рассмотрим лишь некоторые элементарные вопросы
алгебры логики, нужные для уяснения смысла логических команд
и работы логических схем, из которых строятся вычислительные
и управляющие устройства ЭВМ.
Запишите определение логики:
Опр: Логика – (logos (др. гр.) – слово, мысль, понятие, закон,
рассуждение) – наука о законах и формах мышления.
Теперь рассмотрим основные понятия логики. Первым
таким понятием будет понятие высказывания.
Запишите:
Каждая мысль выражается словами в предложении, которые
представляют собой различные суждения
Например:
«3 – простое число»,
«Сегодня – выходной день»,
«Решите задачу».

6.

Как математика оперирует числами, письменность буквами
– логика оперирует высказываниями.
Запишите определение высказывания:
Опр: Высказывание – повествовательное предложение,
относительно которого можно судить истинно(1) оно или
ложно(0).
Давайте посмотрим какие из вышеуказанных суждений
будут высказываниями и определим истинно это высказывание
или ложно.
Запишите примеры:
«3 – простое число» (высказывание, 1)
Сегодня – выходной день (высказывание по определению)
Если сегодня выходной – значит 1. Если нет – 0.
Нельзя сказать истинное это высказывание или ложное.
Решите задачу (не является высказыванием по определению)

7.

Исходя из определения высказывания можно сказать какие
предложения не будут являться высказываниями. Запишите:
Высказываниями не являются:
1. предложения, содержащие переменные,
так как нам не известно, какое значение принимает переменная
и, соответственно, неизвестно будет истинным это предложение
или ложным.
2. восклицательные и вопросительные предложения,
это не повествовательные предложения.
3. определения.
мы не можем судить о том истинно такое предложение или
ложно, ведь определение – это мы что-то так назвали и
расшифровали, что это такое. Кто-то может сказать, что это не
так и придумать своё определение.

8.

Рассмотрим примеры:
1. 50 · 4 (не является высказыванием – нельзя сказать 1 или 0)
2. 50 = 42 + 8 (высказывание, 1)
3. Я сижу за компьютером (высказывание, 1)
4. В атаку! (не является высказыванием - восклицательное)
5. 5х – 6 = 9 (не является высказыванием – есть переменная)
6. 9 > 12 (высказывание, 0)
7. х < 43 (не является высказыванием – есть переменная)
8. Здравствуйте (не является высказыванием – нельзя сказать 1
или 0)
9. Две прямые в пространстве называются параллельными, если
они лежат на одной плоскости и не пересекаются (не является
высказыванием, так как определение)

9.

Рассмотрим следующие основные
простые и сложные высказывания.
Запишите определение:
понятия
логики:
Опр: Простое высказывание – это высказывание, в котором
никакая его часть не является высказыванием (обозначение p, q, h,
r, s, t…). Если это условие не выполняется, то высказывание
называется сложным.
Рассмотрим примеры простых и сложных высказываний:
1. На улице хорошая погода (простое)
2. Когда я пойду домой, по дороге куплю хлеб (сложное, состоит из
двух простых: «я пойду домой» и «я по дороге куплю хлеб»)
Вернуться к содержанию

10. Основные логические операции. Таблицы истинности.

Рассмотрим следующие примеры сложных высказываний
и связь между простыми высказываниями:
1. Если 12 делится на 6, то делится и на 3 (простые высказывания:
«12 делится на 6» и «12 делится на 3»; связь «если, то»).
2. На улице льёт дождь или светит солнце (простые высказывания:
«на улице льёт дождь» и «на улице светит солнце»; связь «или»)
3. Дома отключили свет и воду (простые высказывания: «дома
отключили свет» и «дома отключили воду»; связь «и»)
4. Два числа равны тогда и только тогда, когда их разность не равна
нулю (простые высказывания: «два числа равны» и «разность двух
чисел не равна нулю»; связь «тогда и только тогда, когда» и «не»)

11.

Пометьте, что
«не», «и», «или», «если, то», «тогда и только тогда, когда» логические связки.
Над простыми высказываниями
элементарные логические операции.
Запишите:
можно
производить
Сложные высказывания получают из простых (истинных или
ложных) при помощи элементарных логических операций.
Сложные высказывания так же будут истинными или ложными.
Перед тем, как рассмотреть эти логические операции
(ввести их определения) рассмотрим такое понятие, как
таблица истинности.

12.

Таблица истинности
В этой таблице расписываются значения:
простых высказываний (с помощью которых составлено данное
сложное высказывание);
промежуточных сложных высказываний (тех, которые ещё не
являются данным окончательным высказыванием);
данного сложного высказывания.
Значения простых высказываний расписываются следующим
образом (можно не записывать):
1. Если сложное высказывание А состоит из
одного простого высказывания р, то (по
определению
высказывания)
значения
высказывания – это 0 и 1.
р …
А
0 …
знач
ения
А
1 …

13.

2. Если сложное высказывание А состоит
из двух простых р и q, то (по
определению высказывания) значения
высказывания p – это 0 и 1 и значения
высказывания q – это тоже 0 и 1. Но ведь
при p принимающем значения 0, q может
принимать значения и 0 и 1. Аналогично
при значении р, равном 0 – q может
быть и 0 и 1.
р q
…
А
…
знач
ения
А
…
…
…
Заполнить значения p и q поможет следующая схема:
p имеет значения 0 и 1 (по определению).
при значении 0 высказывания p высказывание q
может принимать значения 0 и 1.
и при значении 1 высказывания p высказывание q
может принимать значения 0 и 1.
Осталось только записать комбинации значений в
таблицу, двигаясь по линиям: 0 – 0, 0 – 1, 1 – 0, 1 – 1.

14.

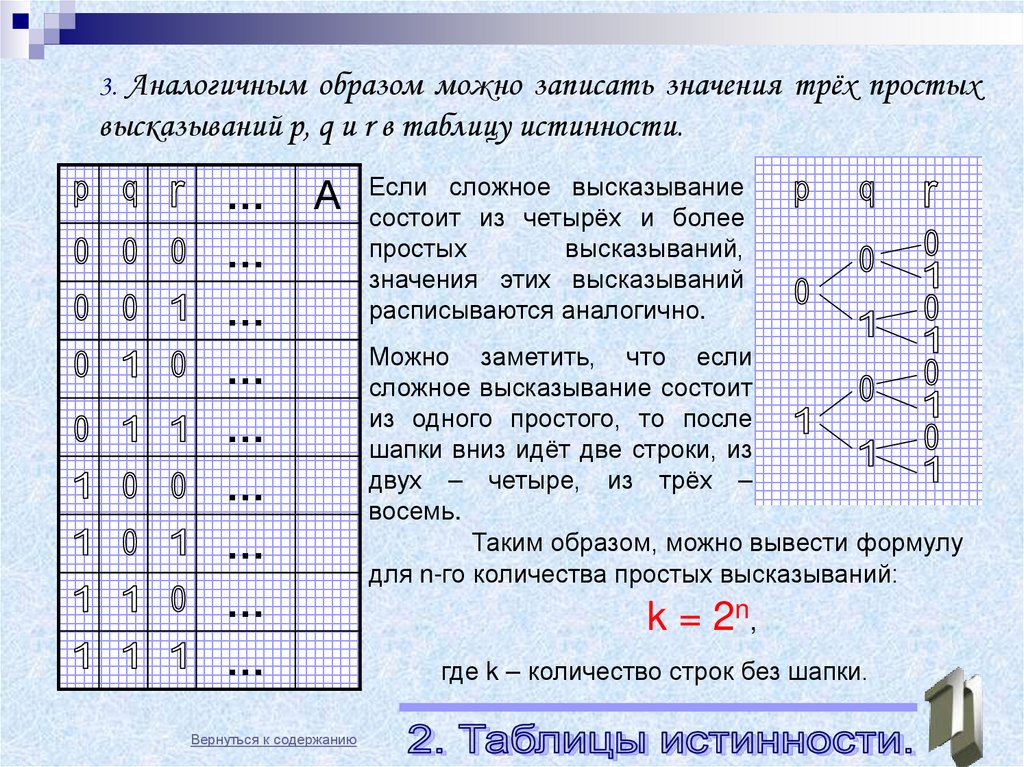
3. Аналогичным образом можно записать значения трёх простых
высказываний p, q и r в таблицу истинности.
…
…
…
…
…
…
…
…
…
сложное высказывание
А Если
состоит из четырёх и более
Вернуться к содержанию
простых
высказываний,
значения этих высказываний
расписываются аналогично.
Можно заметить, что если
сложное высказывание состоит
из одного простого, то после
шапки вниз идёт две строки, из
двух – четыре, из трёх –
восемь.
Таким образом, можно вывести формулу
для n-го количества простых высказываний:
k = 2n,
где k – количество строк без шапки.

15. Записать:

Логические операции, таблицы
истинности к ним записать и знать,
порядок выполнения логических
операций.

16.

Итак, понятие таблицы истинности уже есть. Перейдём к
определению
основных
логических
операций
над
высказываниями.
Зарисуйте таблицы истинности:
Запишите:
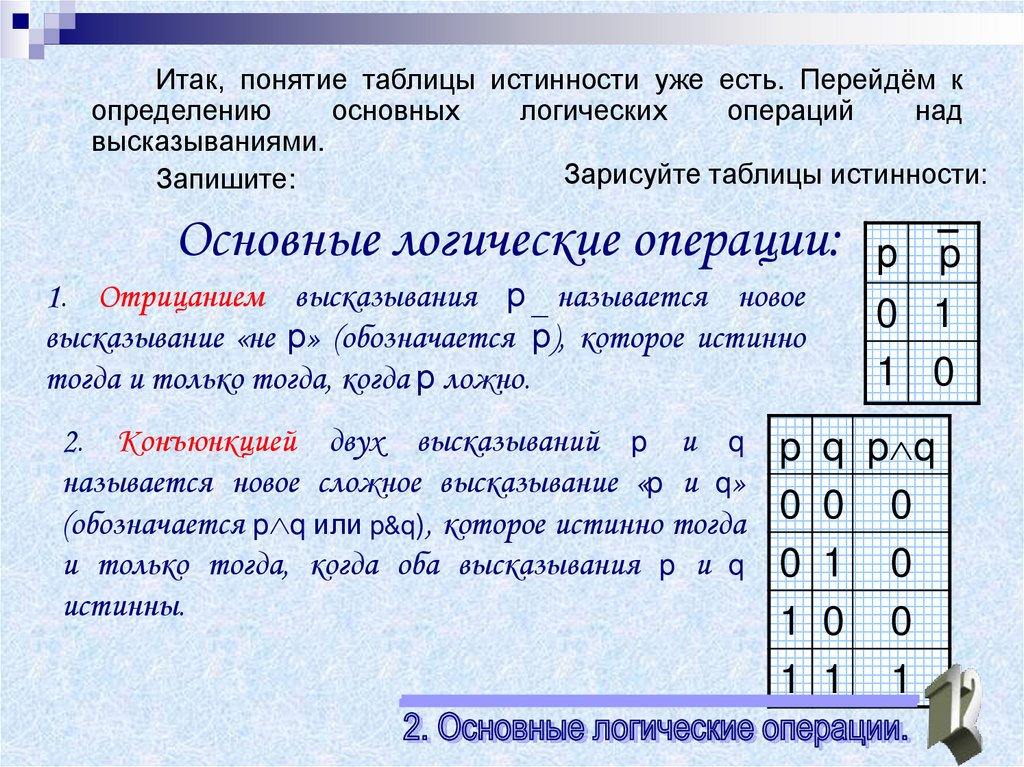
Основные логические операции: р p
1. Отрицанием высказывания р называется новое
высказывание «не р» (обозначается р), которое истинно
тогда и только тогда, когда р ложно.
2. Конъюнкцией двух высказываний p и q
называется новое сложное высказывание «p и q»
(обозначается p q или p&q), которое истинно тогда
и только тогда, когда оба высказывания p и q
истинны.
0 1
1 0
p q p q
0 0 0
0 1 0
1 0 0
1 1 1

17.

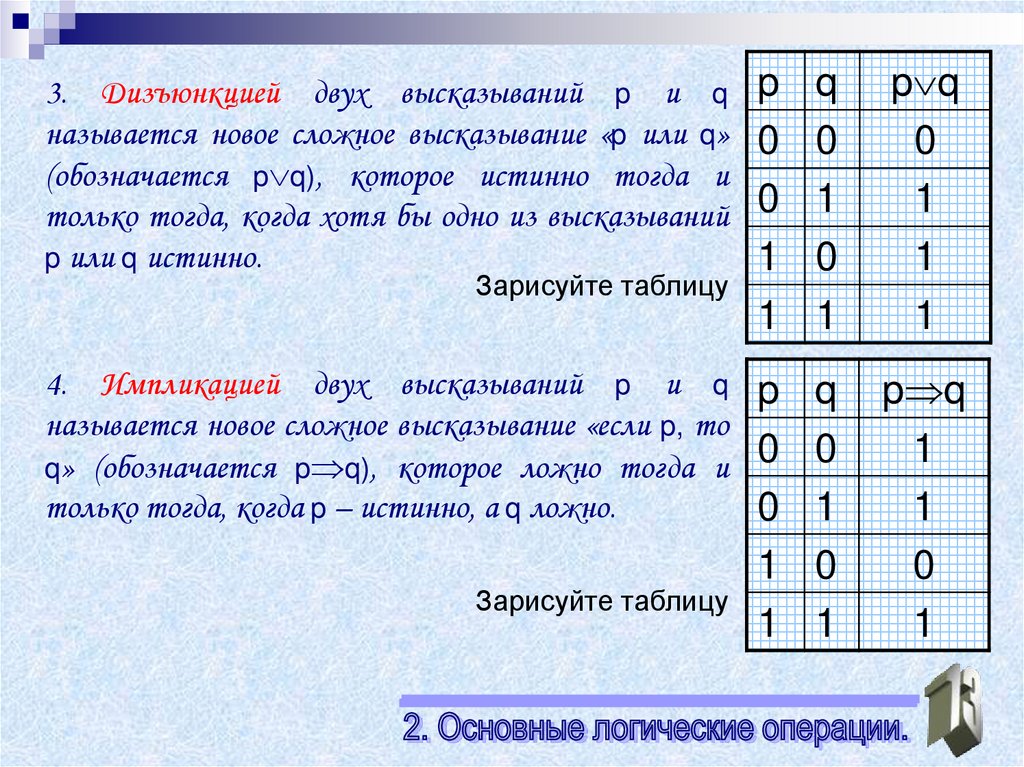
3. Дизъюнкцией двух высказываний p и q
называется новое сложное высказывание «p или q»
(обозначается p q), которое истинно тогда и
только тогда, когда хотя бы одно из высказываний
p или q истинно.
Зарисуйте таблицу
p
0
0
1
1
q
0
1
0
1
p q
0
1
1
1
q
0
1
1 0
1 1
p q
1
1
0
1
4. Импликацией двух высказываний p и q p
называется новое сложное высказывание «если p, то
0
q» (обозначается p q), которое ложно тогда и
только тогда, когда p – истинно, а q ложно.
0
Зарисуйте таблицу

18.

5. Эквивалентностью двух высказываний p и q p
называется новое сложное высказывание «p тогда и
только тогда, когда q» (обозначается p q), 0
которое истинно тогда и только тогда, когда и p, и 0
q либо истинны, либо ложны одновременно.
Зарисуйте таблицу
q
0
1
1 0
1 1
p q
1
0
0
1
Для того, чтобы составлять таблицы истинности для различных
сложных высказываний, необходимо определить порядок основных
логических операций (как, к примеру, при подсчёте значения какоголибо выражения, сначала умножаем, потом складываем).
Вернуться к содержанию

19.

Запишите:
Порядок логических операций в сложных высказываниях
1. Если в сложном высказывании содержатся скобки, то действия
сначала выполняются в скобках.
2. Если в сложном высказывании нет скобок, то действия выполняются
в следующем порядке: (отрицание), (конъюнкция), (дизъюнкция),
(импликация), (эквивалентность).

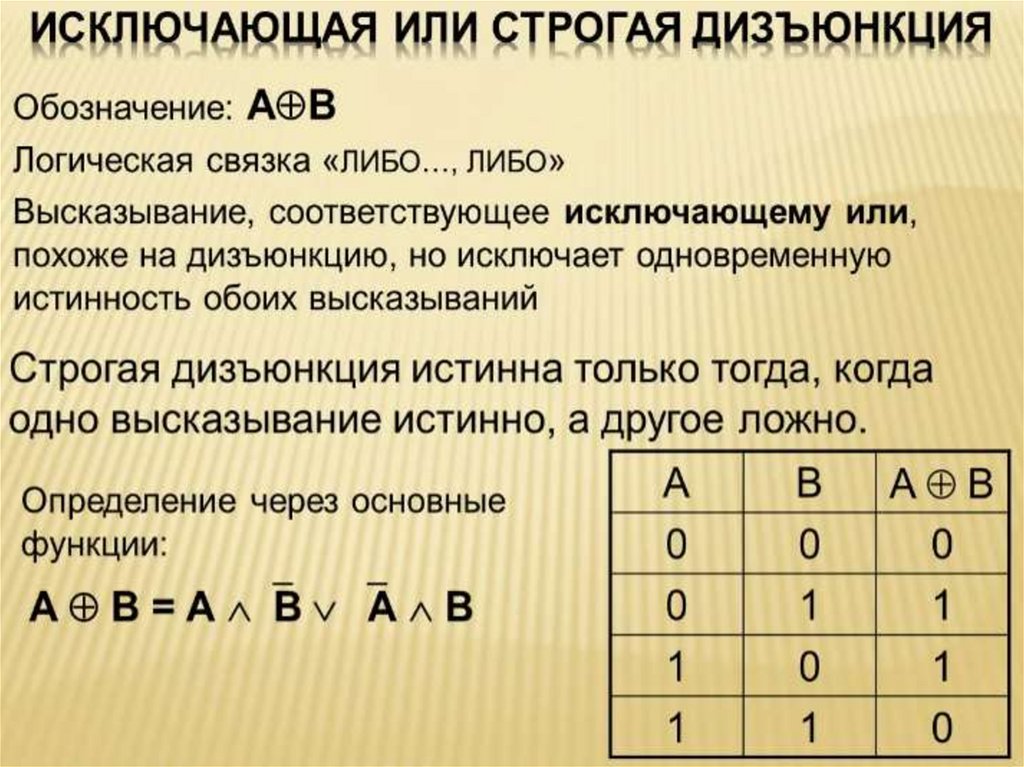
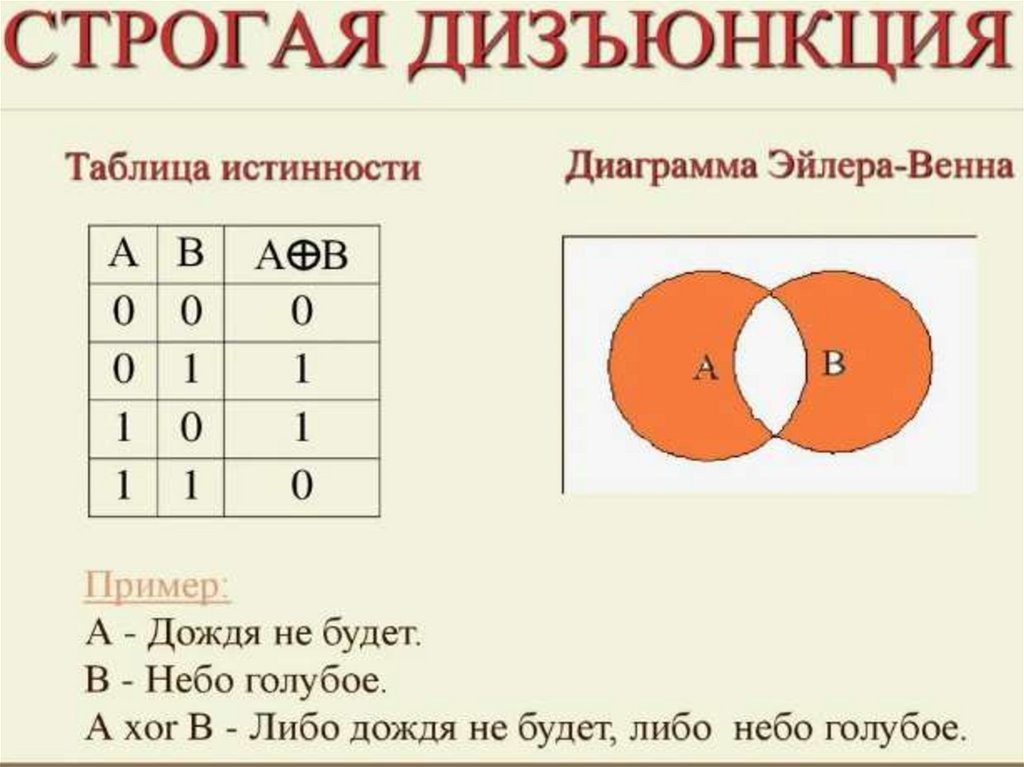
20. Еще одна логическая операция

21.

22.

23. *Сводная таблица (записываем)

24.

Теперь рассмотрим, как составляются таблицы истинности для
сложных высказываний. Рассмотрим пример:
пример: составить таблицы истинности для
следующих высказываний: p p p p
Запишите:
p p p p p p p p p p p p p
Так как в этом сложном высказывании участвует только одно простое (р), то после
шапки вниз пойдёт ещё две строчки. Заполним значения высказывания р: по
определению это 0 и 1. Теперь рассмотрим нашу формулу: скобок в ней нет, значит
действия выполняем по порядку: , , , , .
Вернуться к содержанию

25.

Заполнение таблицы на предыдущем слайде
пошагово (можно не записывать)
Следующий шаг должен бы быть отрицание дизъюнкции, НО
невозможно определить значения отрицания дизъюнкции, если
неизвестны значения самой дизъюнкции!
По определению дизъюнкция ложна, когда левая и правая части
(составляющие эту дизъюнкцию) ложны. В нашем случае везде истина.
Теперь отрицание дизъюнкции. Подумайте, почему получены именно
такие значения…
Следующее действие – конъюнкция. Слева от неё – отрицание
дизъюнкции, справа – отрицание р. Поэтому рассматриваем значения
второго и четвёртого столбика
Следующее и последнее действие – импликация. В шапке запишется
вся формула. Левая часть – первый столбик, правая – пятый.
Импликация ложна, когда левая часть истинна, а правая – ложна (или
из истины следует ложь). В нашем случае: 0 – 0 – истина (1), 1 – 0 –
ложь (0).
Таким образом таблица истинности для данного высказывания
построена.