Axiomy25-26

1.

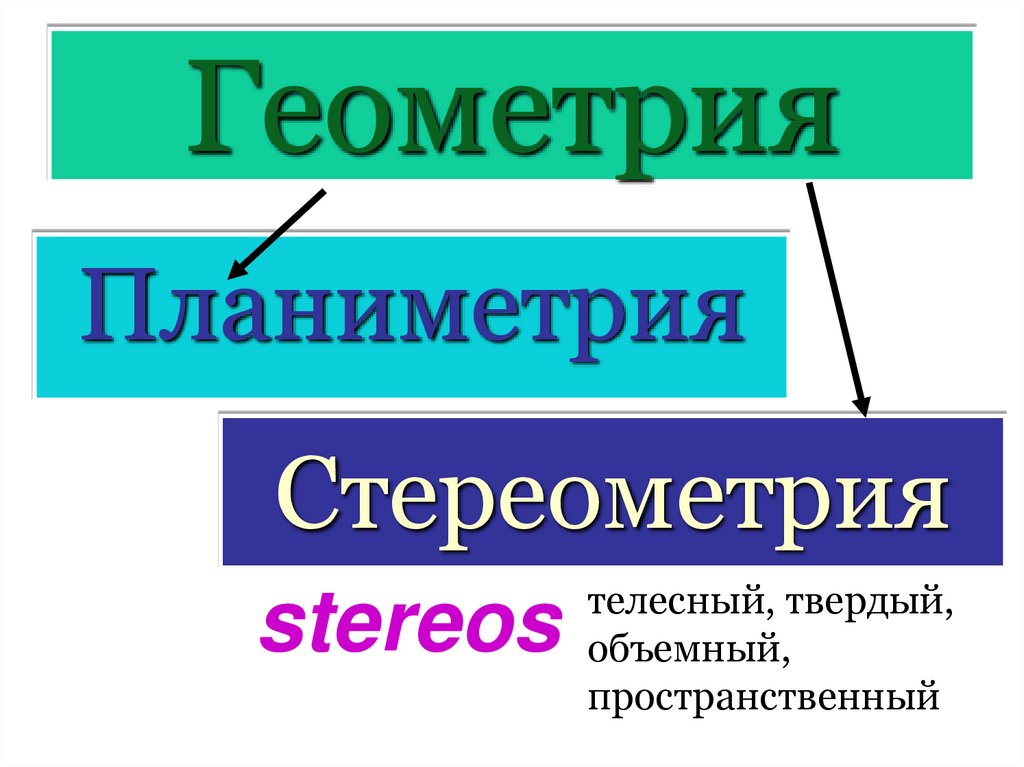
2. Геометрия

Планиметрия
Стереометрия
stereos
телесный, твердый,
объемный,
пространственный

3.

- Что такое геометрия?
Геометрия – наука о свойствах геометрических фигур
«Геометрия» - (греч.) – «землемерие»
- Что такое планиметрия?
Планиметрия – раздел геометрии, в котором
изучаются свойства фигур на плоскости.
- Основные понятия планиметрии?
Основные понятия планиметрии:
А
точка
а
прямая

4.

Планиметрия
Стереометрия
Изучает свойства
геометрических фигур
на плоскости
Изучает свойства фигур
в пространстве
В переводе с греческого
слово «геометрия»
означает «землемерие»
«гео» – по-гречески
земля, «метрео» –
мерить
Слово «стереометрия»
происходит от греческих
слов «стереос» объемный,
пространственный,
«метрео» – мерить

5.

Планиметрия
Основные фигуры:
точка, прямая
Стереометрия
Основные фигуры: точка,
прямая, плоскость
Другие фигуры: отрезок, Наряду с этими фигурами
мы будем рассматривать
луч, треугольник,
геометрические тела и их
квадрат, ромб,
поверхности.
параллелограмм,
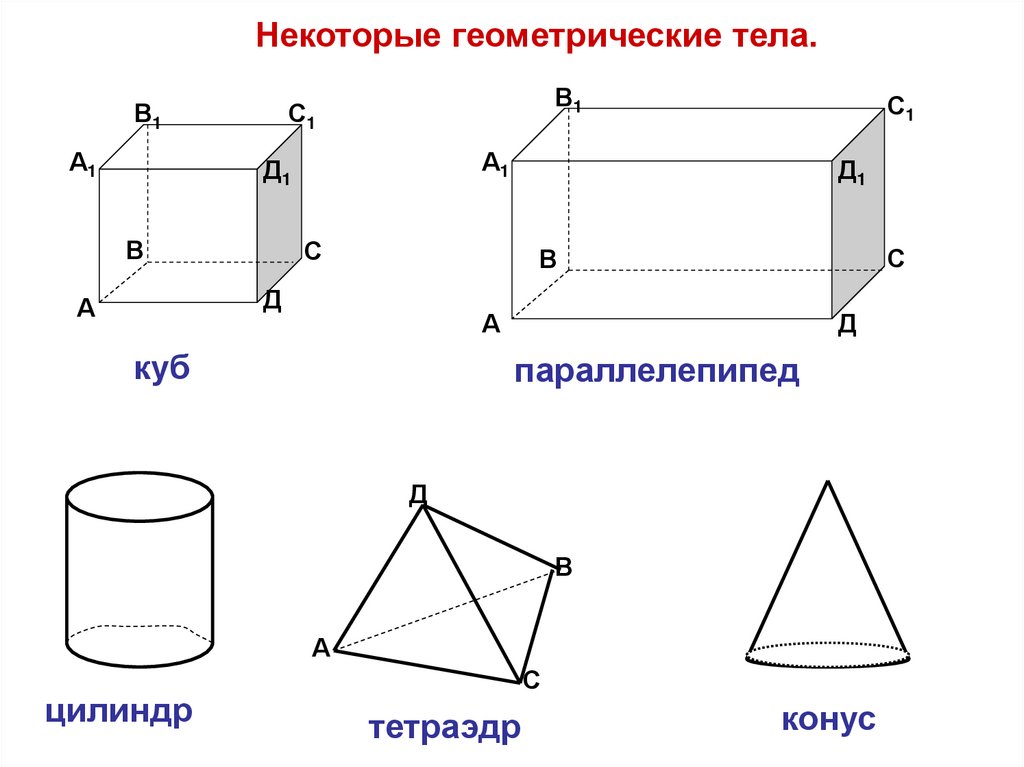
трапеция, прямоугольник, Например, многогранники.
выпуклые и невыпуклые Куб, параллелепипед,
призма, пирамида.
n-угольники, круг,
Тела вращения.
окружность, дуга и др.
Шар, сфера, цилиндр,
конус.

6.

Некоторые геометрические тела.
В1
А1
В1
С1
А1
Д1
В
Д1
С
С
В
Д
А
С1
А
куб
Д
параллелепипед
Д
В
А
цилиндр
С
тетраэдр
конус

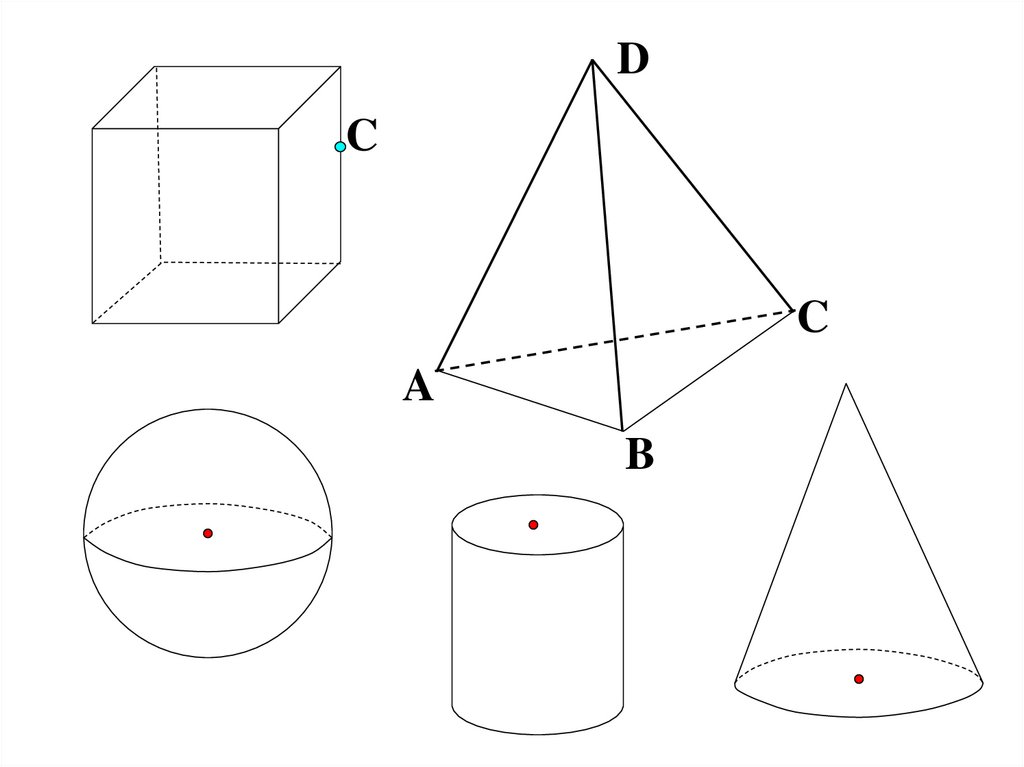
7.

D
C
C
A
B

8.

Назовите какие геометрические тела вам напоминают предметы,
изображенные на этих рисунках:
Назовите предметы из окружающей вас обстановки ( нашей классной
комнаты) напоминающие вам геометрические тела.

9.

- раздел геометрии,
в котором
изучаются свойства
фигур в
пространстве

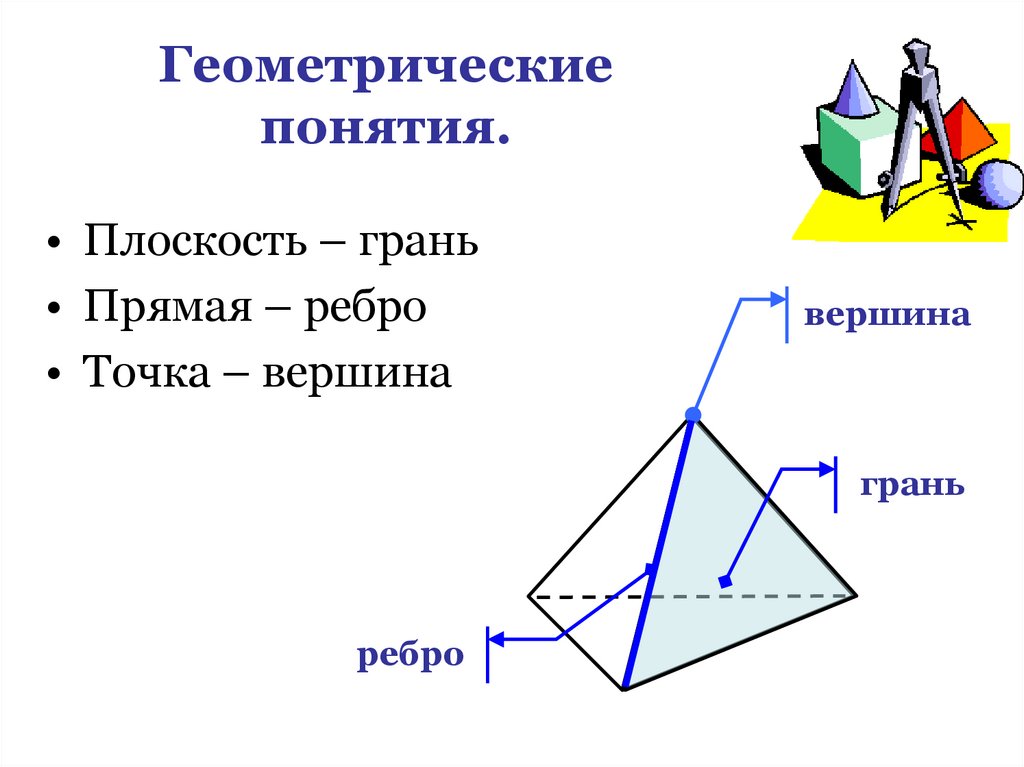
10. Геометрические понятия.

• Плоскость – грань
• Прямая – ребро
• Точка – вершина
вершина
грань
ребро

11.

A, B, C, …
a, b, c, …
или
AВ, BС, CD, …
, , ,

12.

Плоскости будем обозначать греческими буквами.
На рисунках плоскости обозначаются в виде
параллелограммов. Плоскость как геометрическую
фигуру следует представлять себе простирающейся
неограниченно во все стороны.

13.

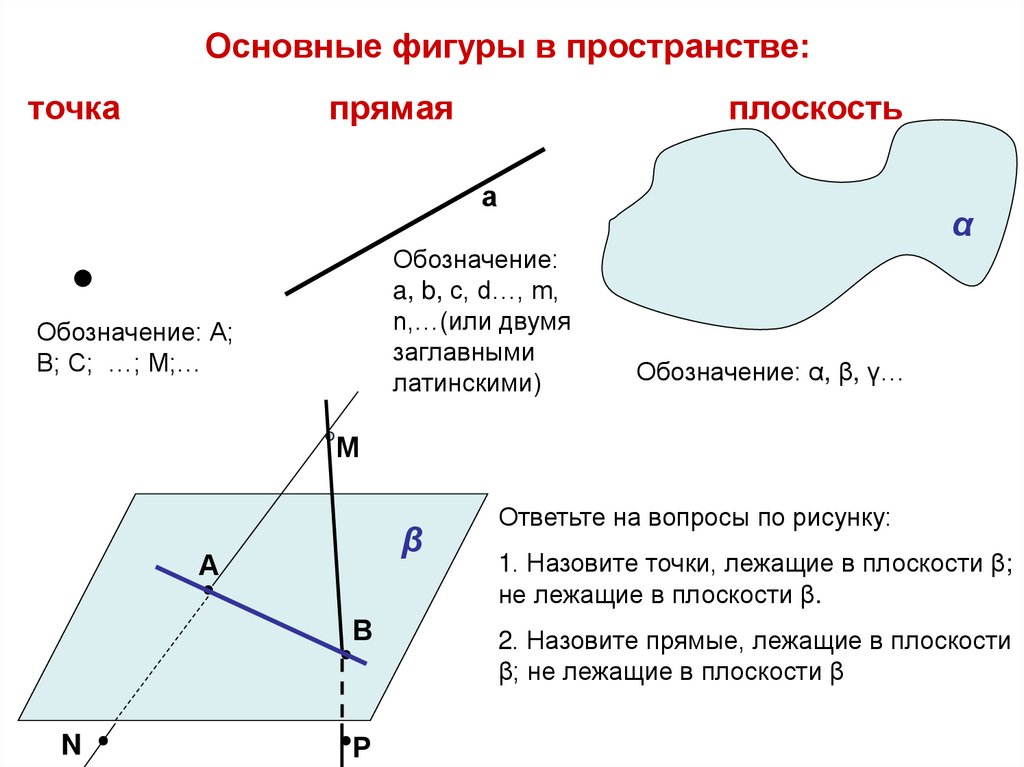
Основные фигуры в пространстве:
точка
прямая
плоскость
а
α
Обозначение:
a, b, с, d…, m,
n,…(или двумя
заглавными
латинскими)
Обозначение: А;
В; С; …; М;…
Обозначение: α, β, γ…
М
β
А
В
N
Р
Ответьте на вопросы по рисунку:
1. Назовите точки, лежащие в плоскости β;
не лежащие в плоскости β.
2. Назовите прямые, лежащие в плоскости
β; не лежащие в плоскости β

14.

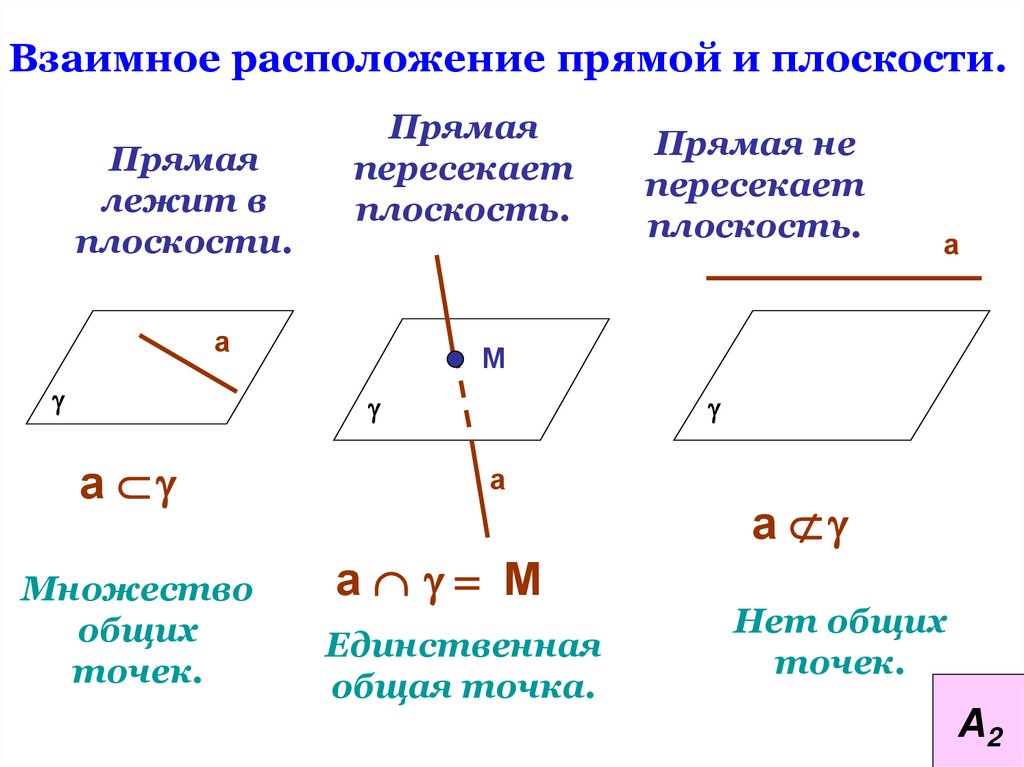
Взаимное расположение прямой и плоскости.
Прямая
лежит в
плоскости.
Прямая
пересекает
плоскость.
а
Множество
общих
точек.
а
М
а
Прямая не
пересекает
плоскость.
а
а М
Единственная
общая точка.
а
Нет общих
точек.
А2

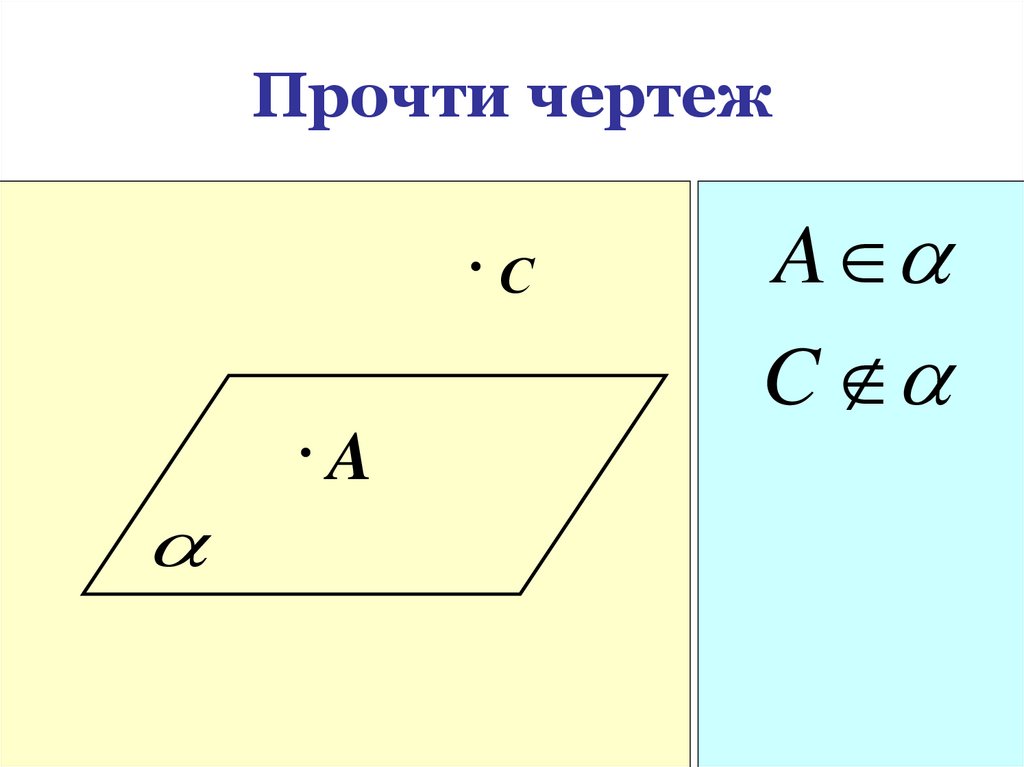
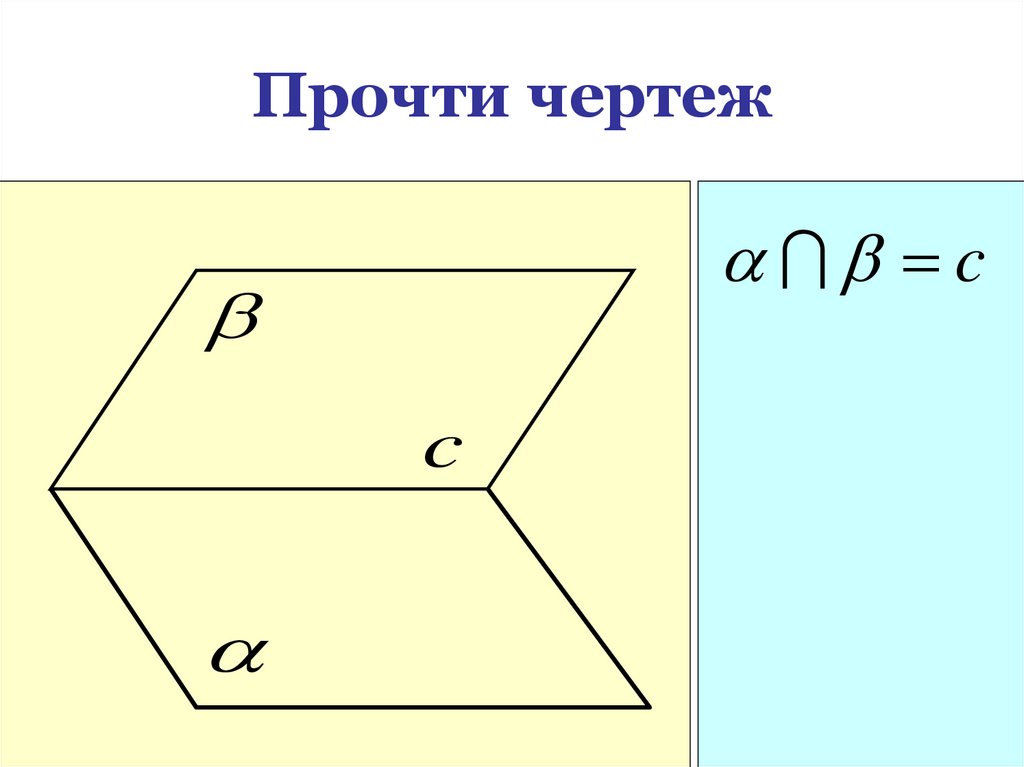
15. Прочти чертеж

С
A
A
C

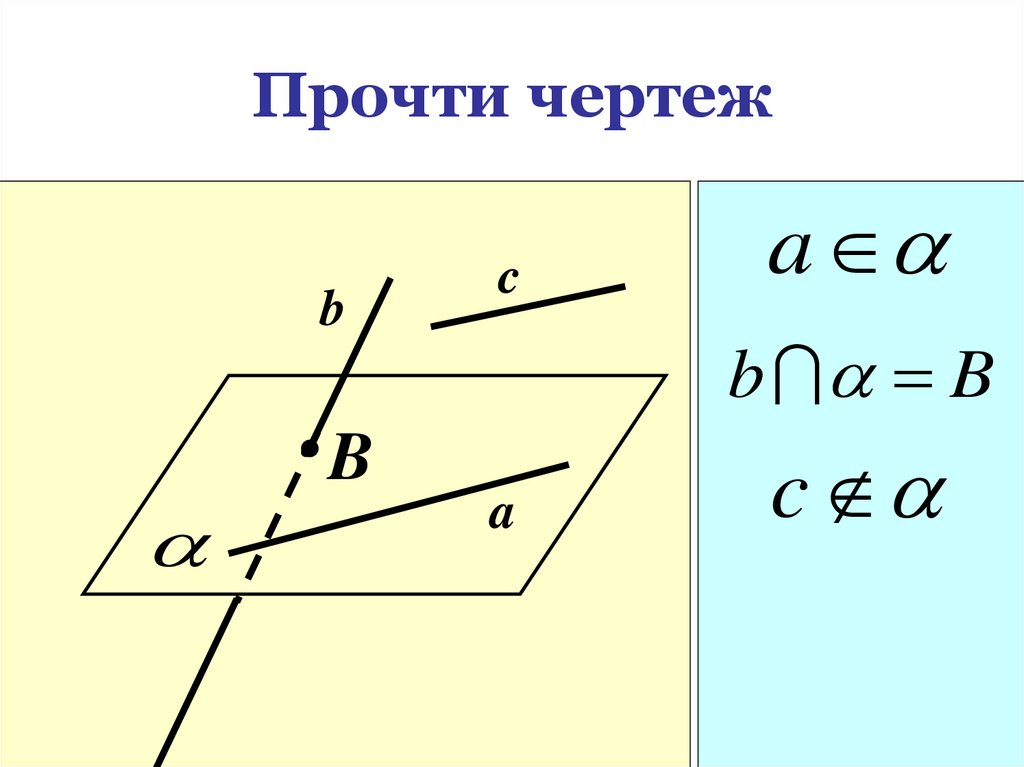
16. Прочти чертеж

b
B
c
a
b B
a
c

17. Прочти чертеж

c
c

18.

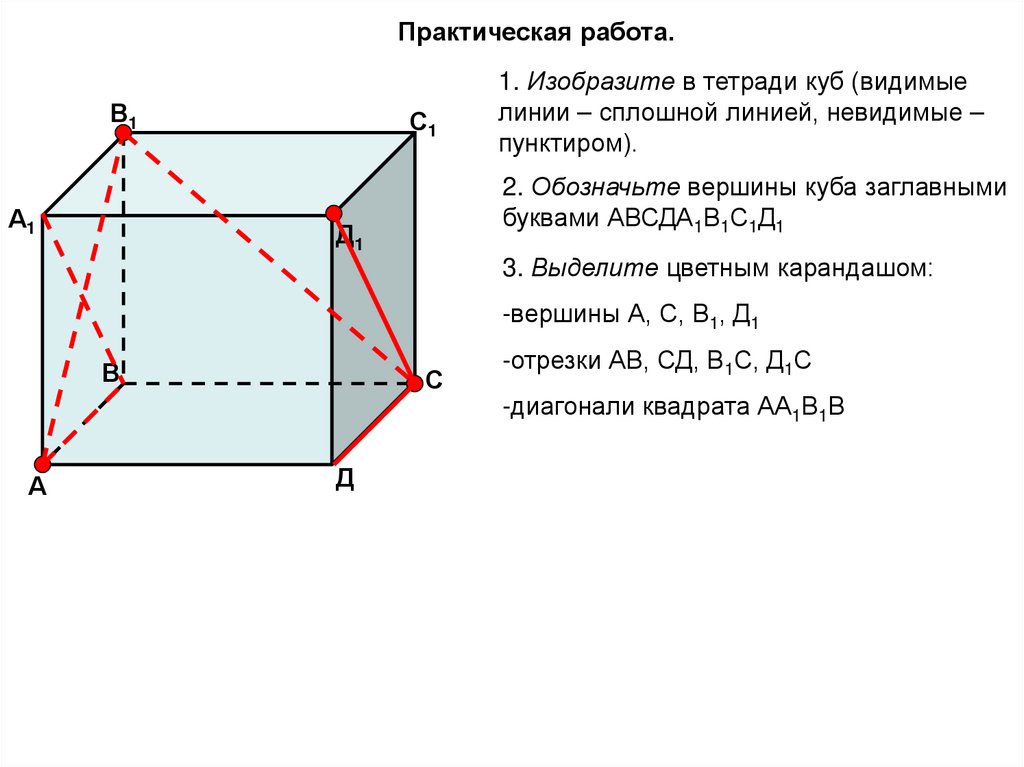
Практическая работа.
В1
А1
С1
1. Изобразите в тетради куб (видимые
линии – сплошной линией, невидимые –
пунктиром).
2. Обозначьте вершины куба заглавными
буквами АВСДА1В1С1Д1
Д1
3. Выделите цветным карандашом:
-вершины А, С, В1, Д1
В
А
С
Д
-отрезки АВ, СД, В1С, Д1С
-диагонали квадрата АА1В1В

19. Аксиома

(от греч. axíõma – принятие положения)
исходное положение
научной теории,
принимаемое без
доказательства

20. Аксиомы стереометрии

А1. Для любой плоскости существует точка,
ей не принадлежащая
А2. Для любой плоскости существует точка,
ей не принадлежащая

21.

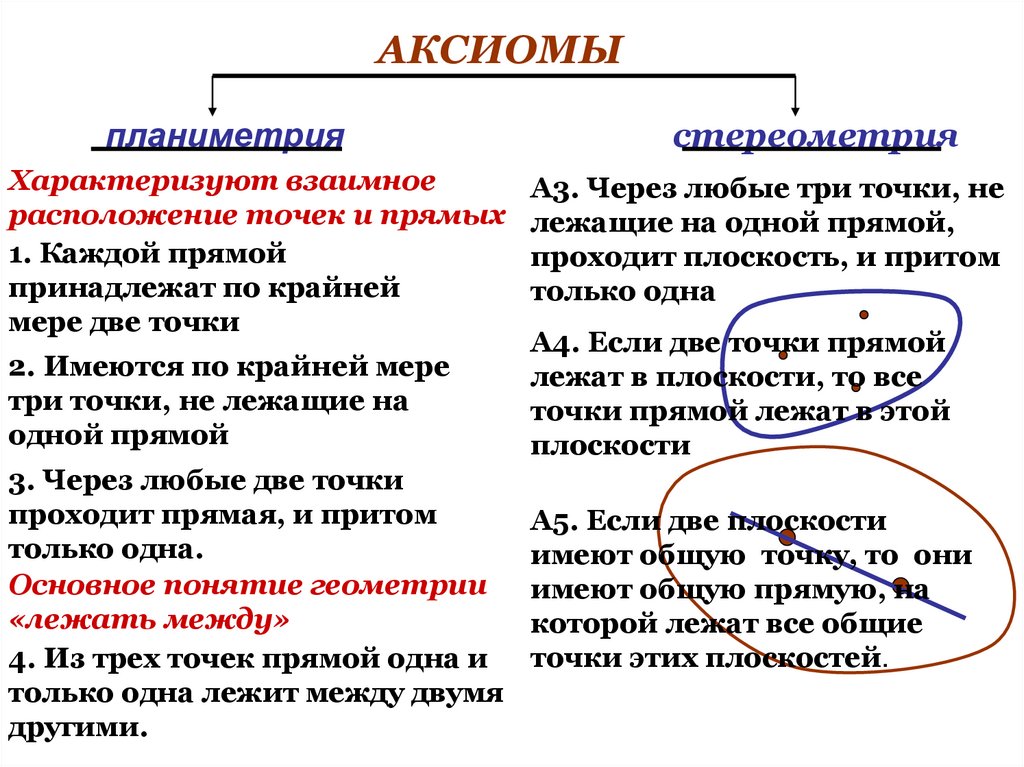
АКСИОМЫ
планиметрия
Характеризуют взаимное
расположение точек и прямых
1. Каждой прямой
принадлежат по крайней
мере две точки
стереометрия
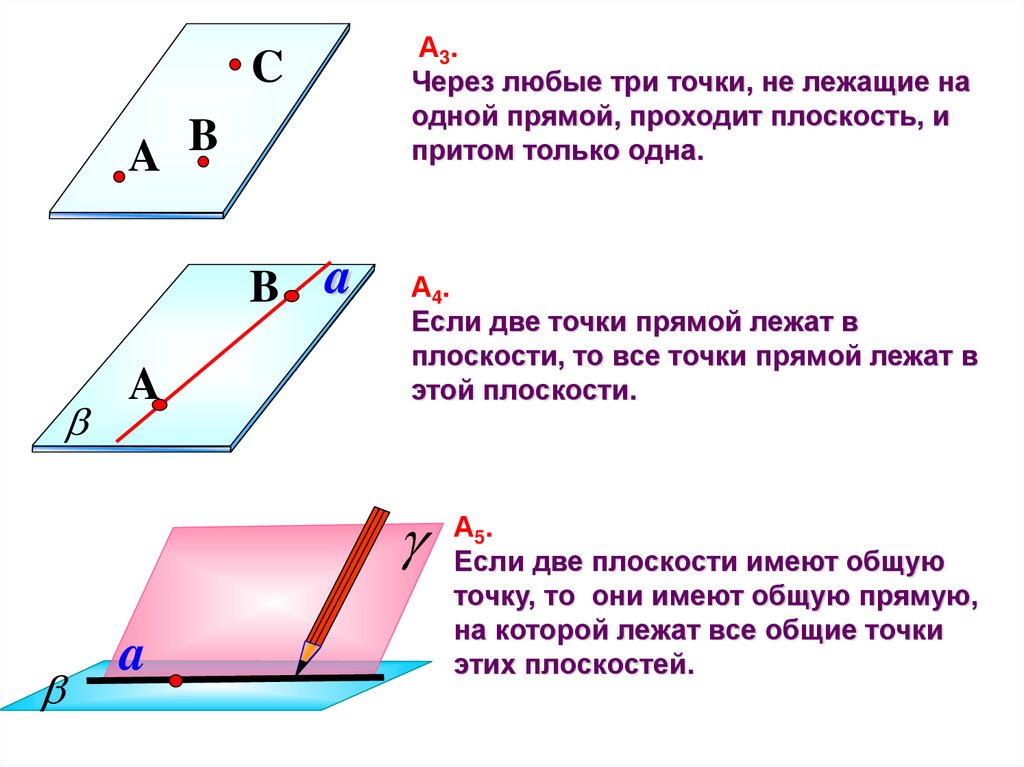
А3. Через любые три точки, не
лежащие на одной прямой,
проходит плоскость, и притом
только одна
2. Имеются по крайней мере
три точки, не лежащие на
одной прямой
А4. Если две точки прямой
лежат в плоскости, то все
точки прямой лежат в этой
плоскости
3. Через любые две точки
проходит прямая, и притом
только одна.
Основное понятие геометрии
«лежать между»
4. Из трех точек прямой одна и
только одна лежит между двумя
другими.
А5. Если две плоскости
имеют общую точку, то они
имеют общую прямую, на
которой лежат все общие
точки этих плоскостей.

22.

- Что такое аксиома?
Аксиома – это утверждение о свойствах
геометрических фигур, принимается в качестве
исходных положений, на основе которых доказываются
далее теоремы и вообще строится вся геометрия.
Активные аксиомы планиметрии
- через любые две точки можно провести прямую и
притом только одну.
-из трех точек прямой одна, и только одна, лежит
между двумя другими.
-имеются по крайней мере три точки, не лежащие на
одной прямой…

23.

C
B
A
B a
A
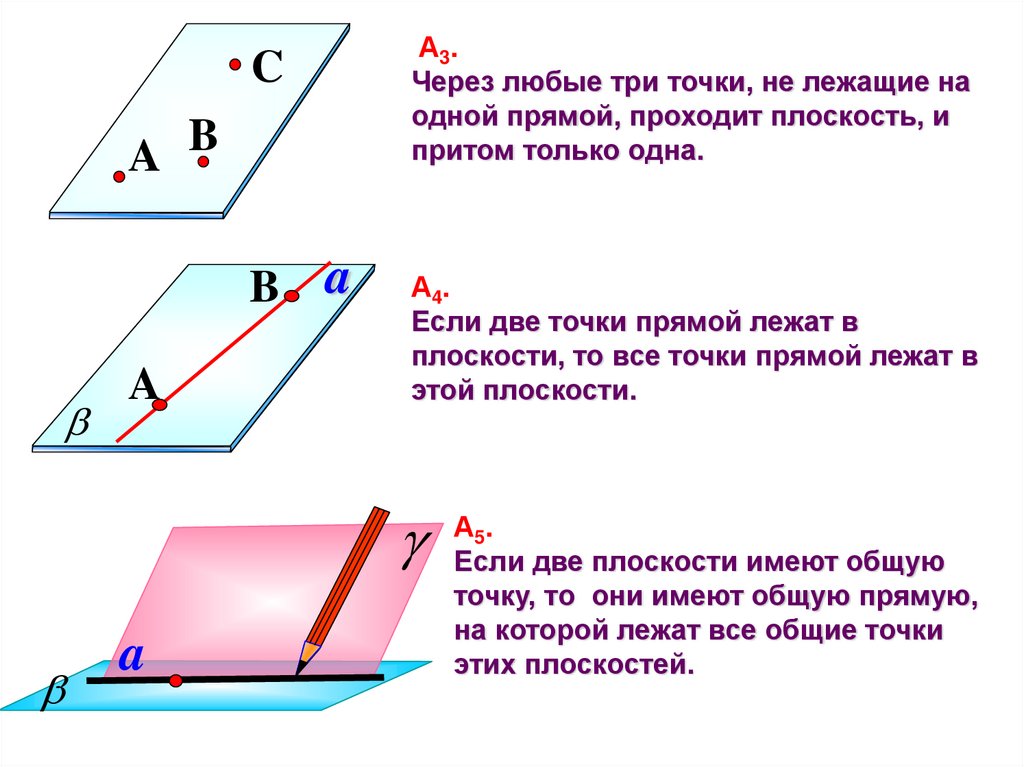
А 3.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
А 4.
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости.
a
А 5.
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки
этих плоскостей.

24.

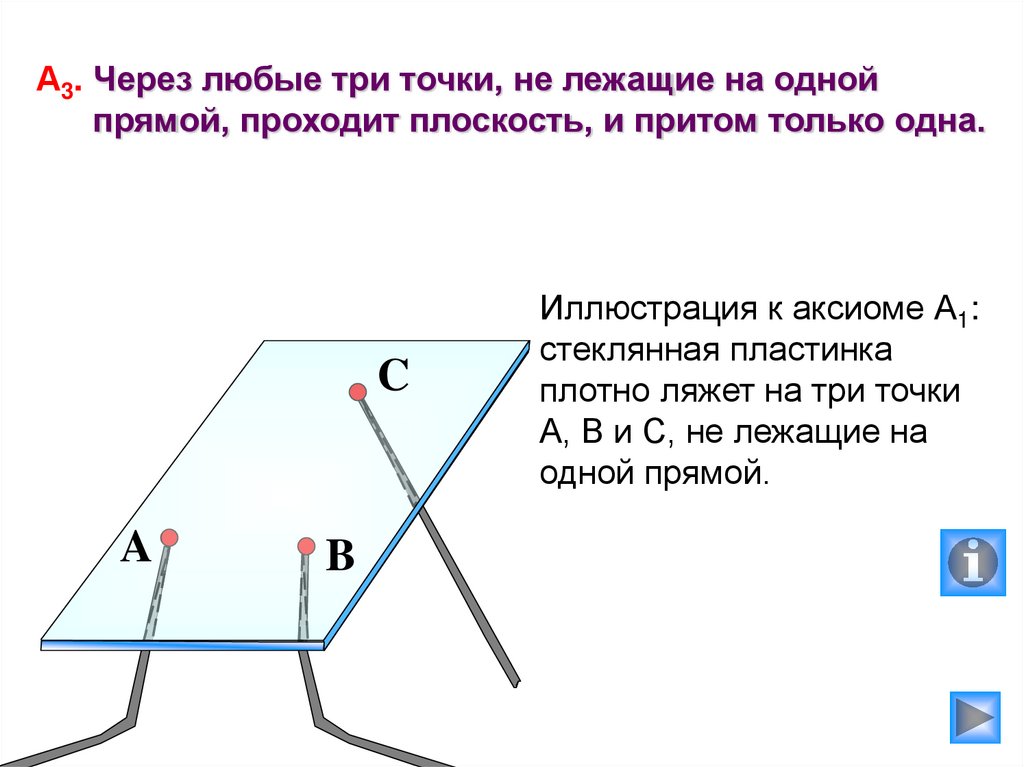
А3. Через любые три точки, не лежащие на одной
прямой, проходит плоскость, и притом только одна.
C
A
B
Иллюстрация к аксиоме А1:
стеклянная пластинка
плотно ляжет на три точки
А, В и С, не лежащие на
одной прямой.

25.

Иллюстрации к аксиоме А3 из жизни.
Для
видеокамеры,
фотосъемки
для других
приборов
часто
Табурет
с тремя ножками
всегдаиидеально
встанет
на пол
и
используют
штативУ–табурета
треногу. Три
ножки штатива
устойчиво
не будет качаться.
с четырьмя
ножками
бывают
расположатся
на любом полуесли
в помещениях,
проблемы с устойчивостью,
ножки стулана
неасфальте
одинаковые
или
прямоТабурет
на газоне
на улице,
наопирается
песке на пляже
в а
по длине.
качается,
т. е.
на триили
ножки,
траве
в лесу.
Три(четвертая
ножки штатива
всегда
четвертая
ножка
«точка»)
не найдут
лежит вплоскость.
плоскости
пола, а висит в воздухе.

26.

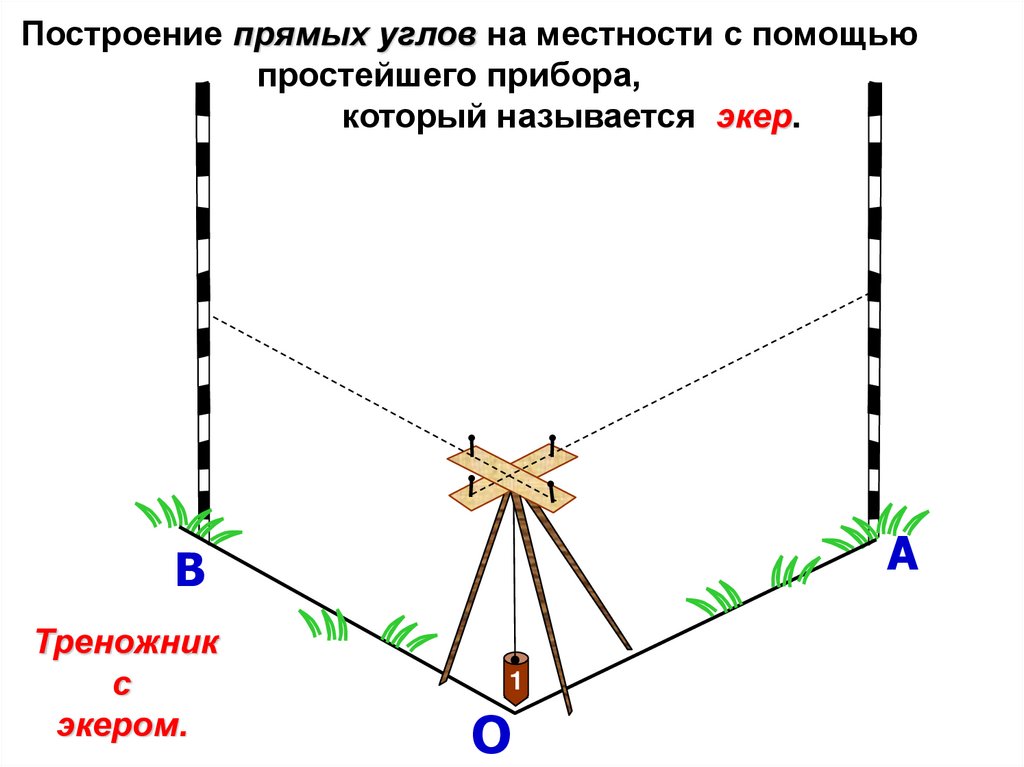
Построение прямых углов на местности с помощью
простейшего прибора,
который называется экер.
А
В
Треножник
с
экером.
1
О

27.

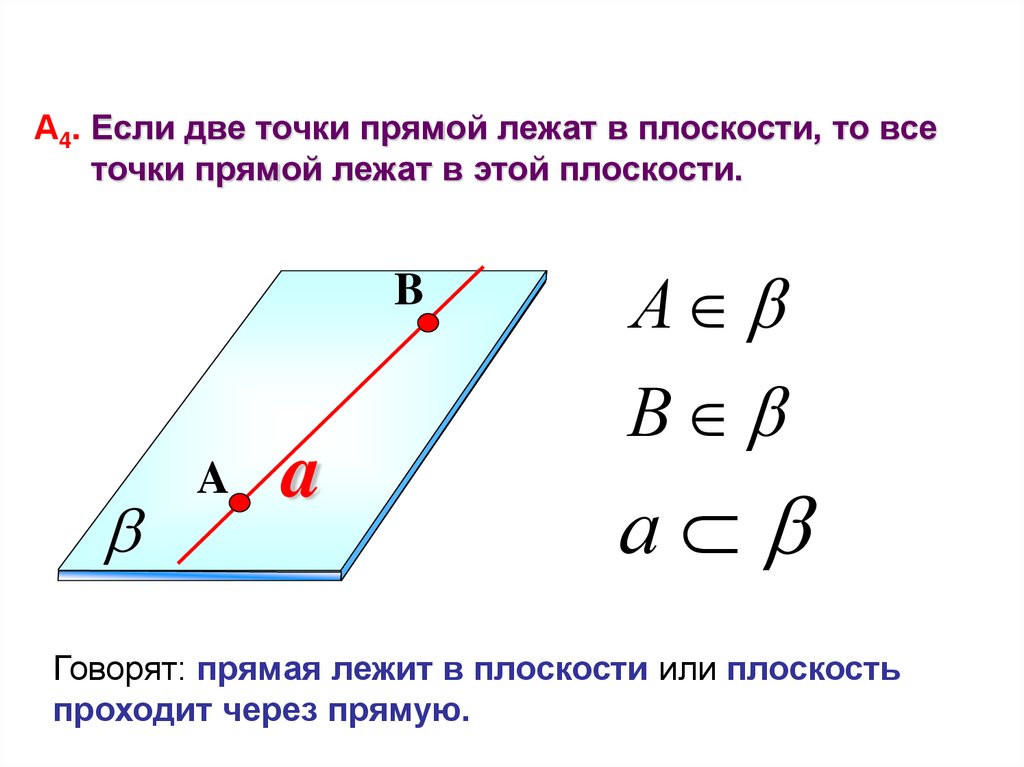
А4. Если две точки прямой лежат в плоскости, то все
точки прямой лежат в этой плоскости.
B
A
a
А
В
а
Говорят: прямая лежит в плоскости или плоскость
проходит через прямую.

28.

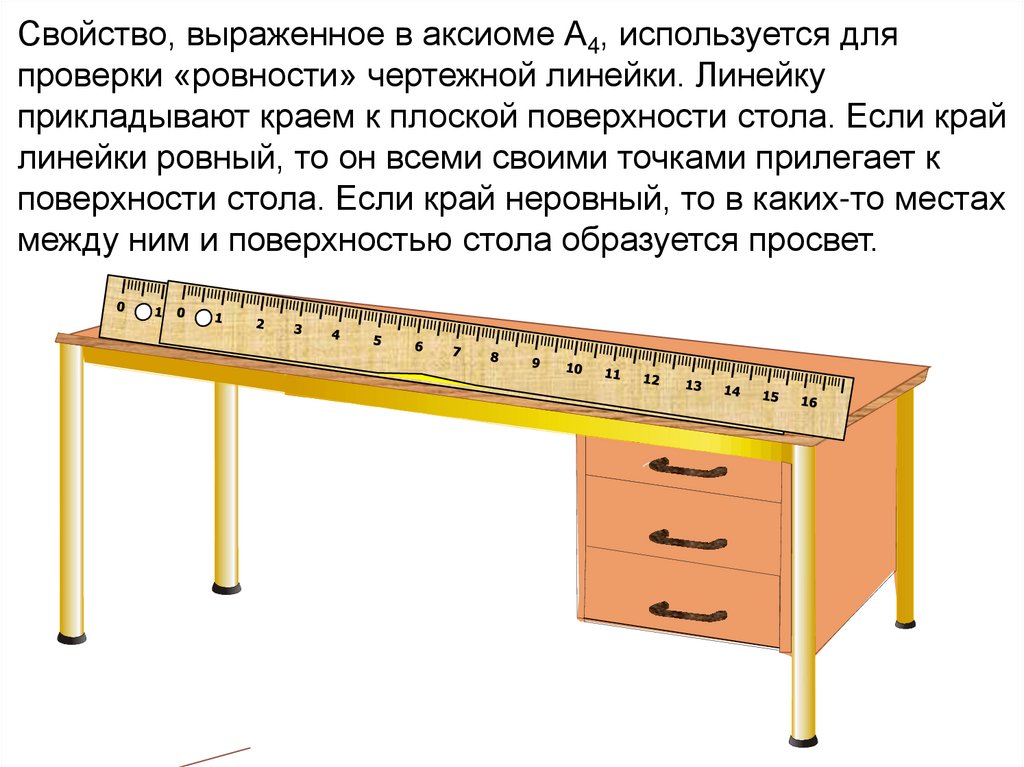
Свойство, выраженное в аксиоме А4, используется для
проверки «ровности» чертежной линейки. Линейку
прикладывают краем к плоской поверхности стола. Если край
линейки ровный, то он всеми своими точками прилегает к
поверхности стола. Если край неровный, то в каких-то местах
между ним и поверхностью стола образуется просвет.

29.

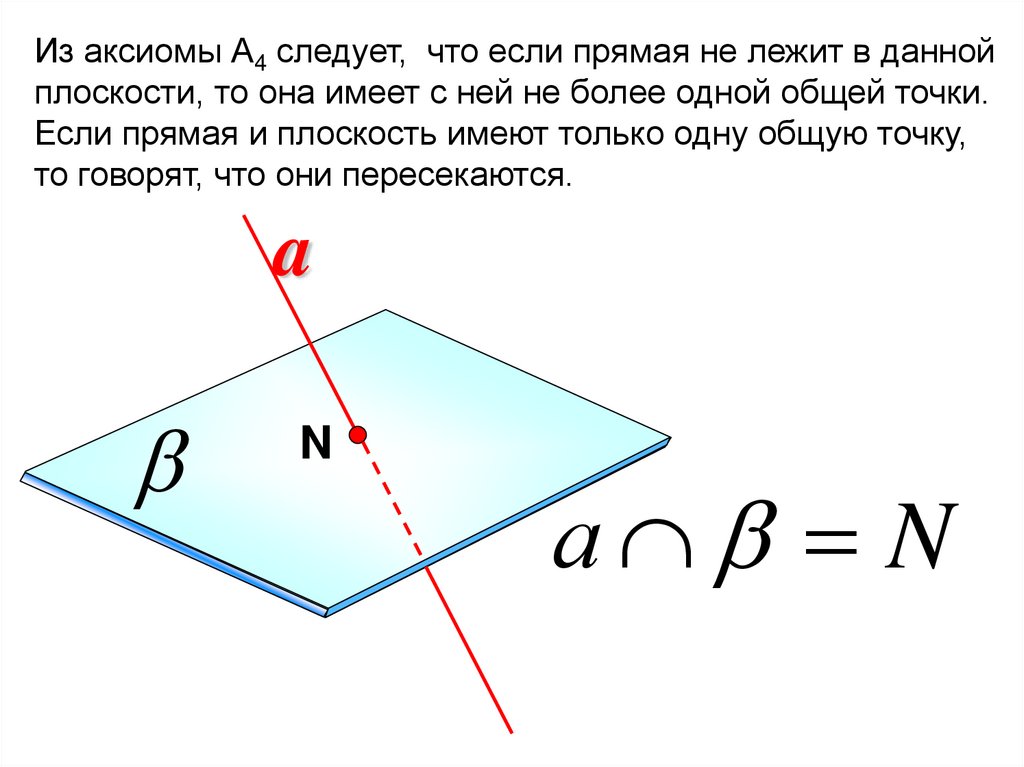
Из аксиомы А4 следует, что если прямая не лежит в данной
плоскости, то она имеет с ней не более одной общей точки.
Если прямая и плоскость имеют только одну общую точку,
то говорят, что они пересекаются.
a
N
а N

30.

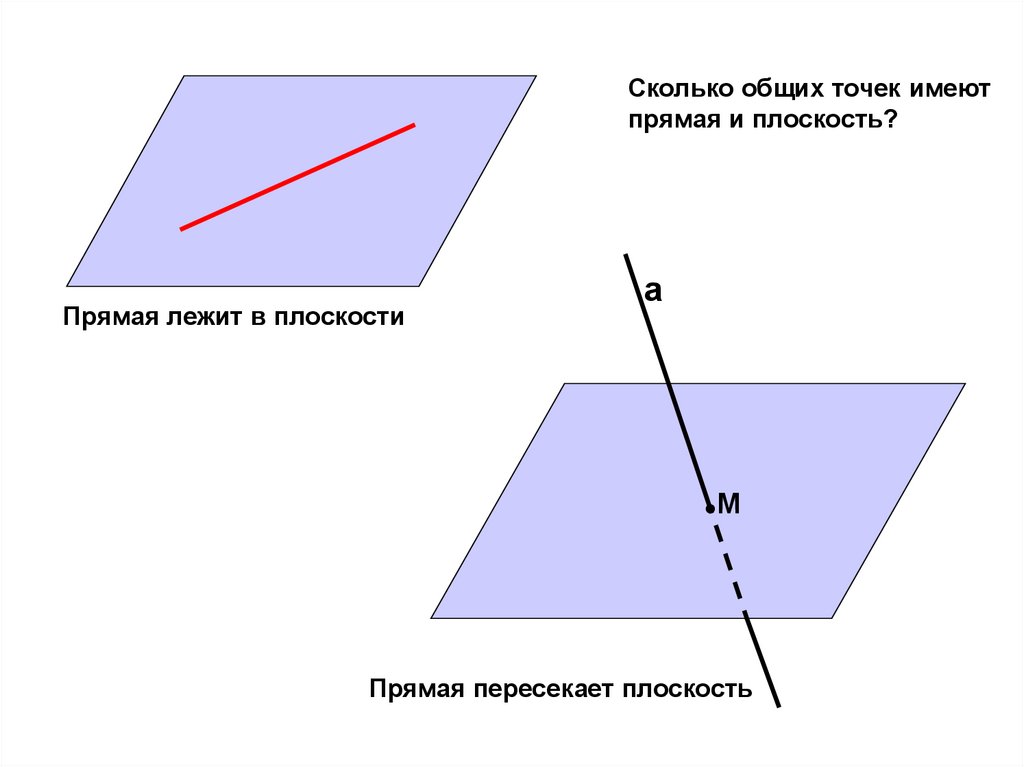
Сколько общих точек имеют
прямая и плоскость?
Прямая лежит в плоскости
а
М
Прямая пересекает плоскость

31.

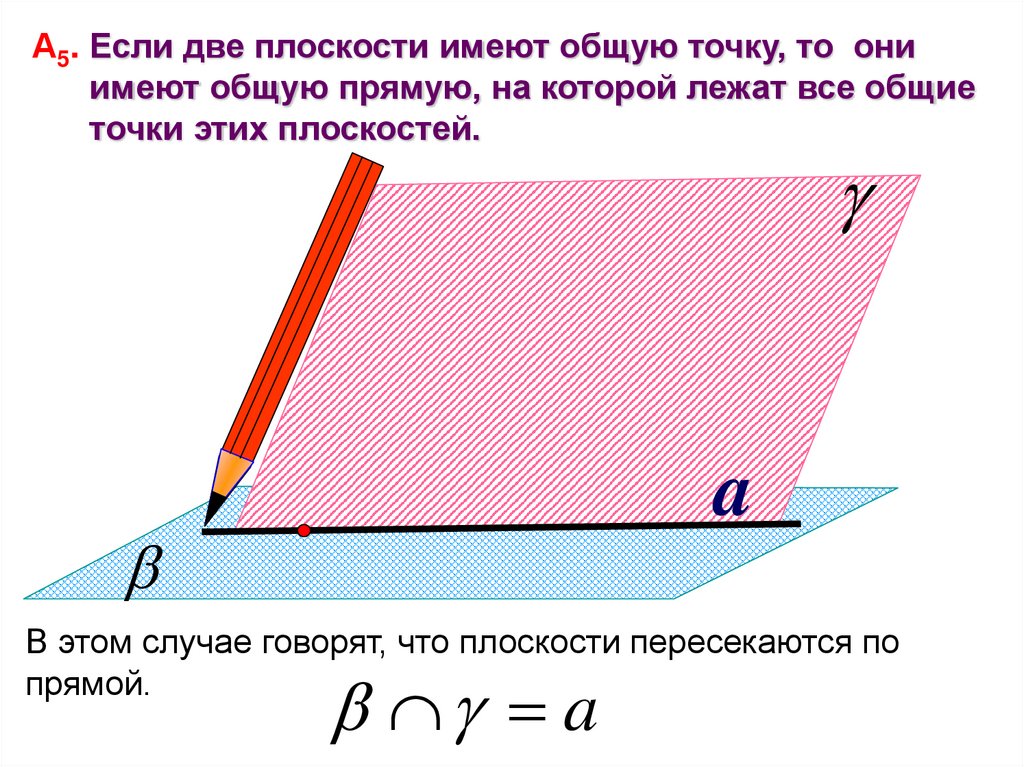
А5. Если две плоскости имеют общую точку, то они
имеют общую прямую, на которой лежат все общие
точки этих плоскостей.
a
В этом случае говорят, что плоскости пересекаются по
прямой.
a

32.

33.

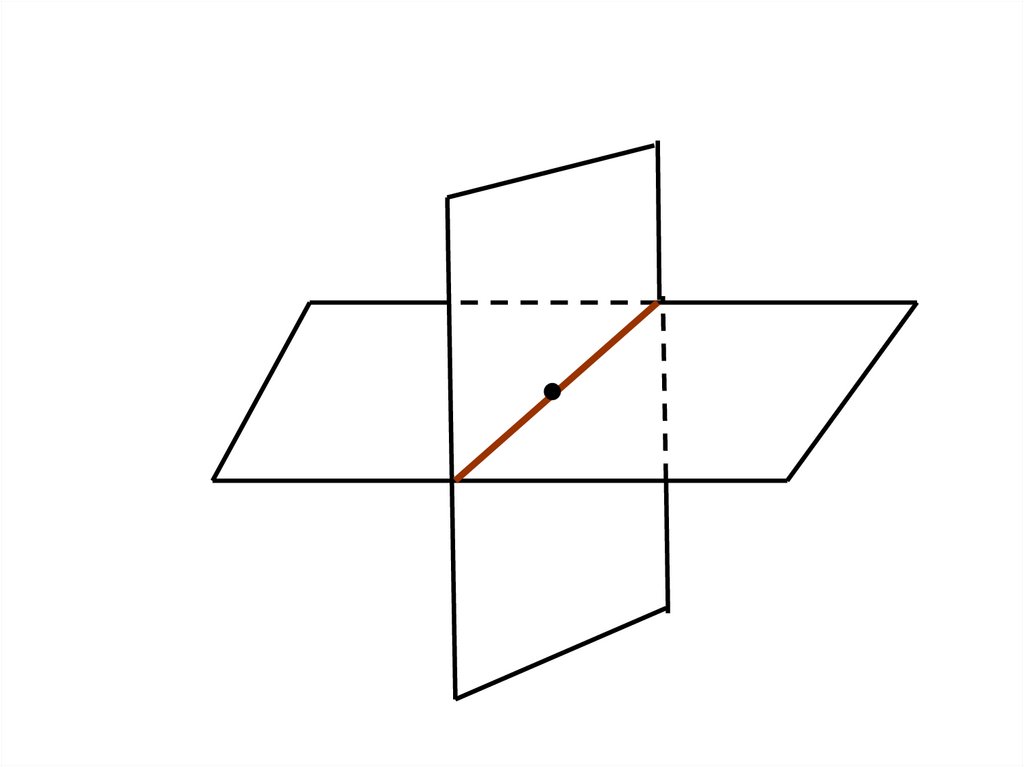
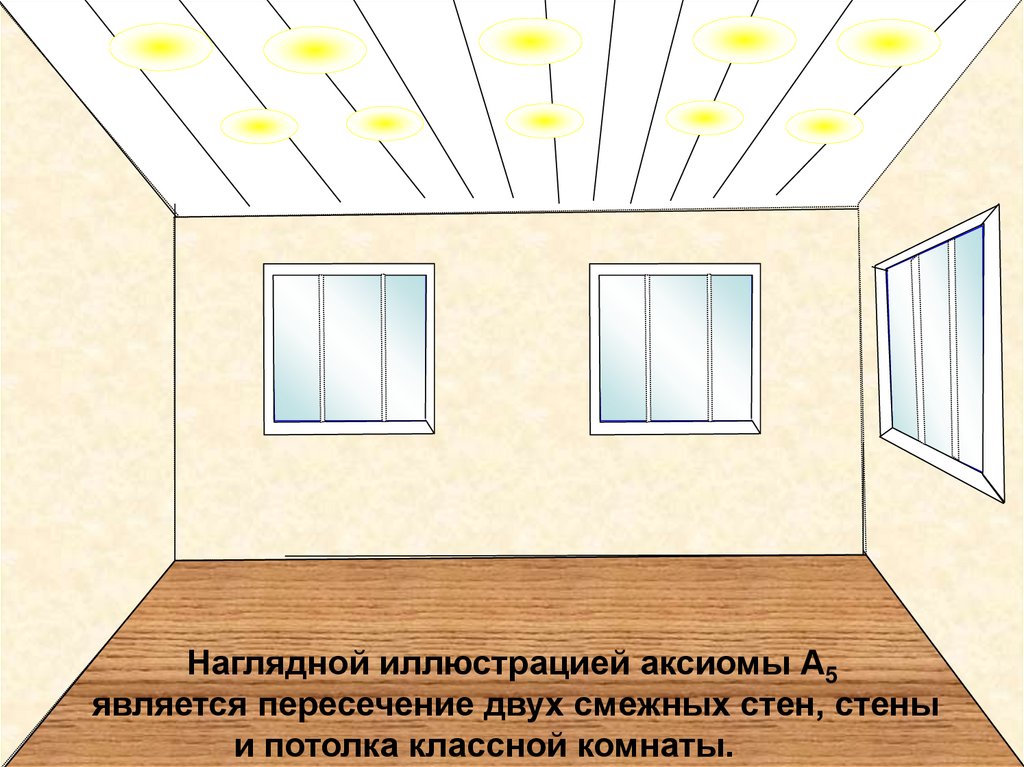
Наглядной иллюстрацией аксиомы А5
является пересечение двух смежных стен, стены
и потолка классной комнаты.

34.

C
B
A
B a
A
А 3.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и
притом только одна.
А 4.
Если две точки прямой лежат в
плоскости, то все точки прямой лежат в
этой плоскости.
a
А 5.
Если две плоскости имеют общую
точку, то они имеют общую прямую,
на которой лежат все общие точки
этих плоскостей.

35.

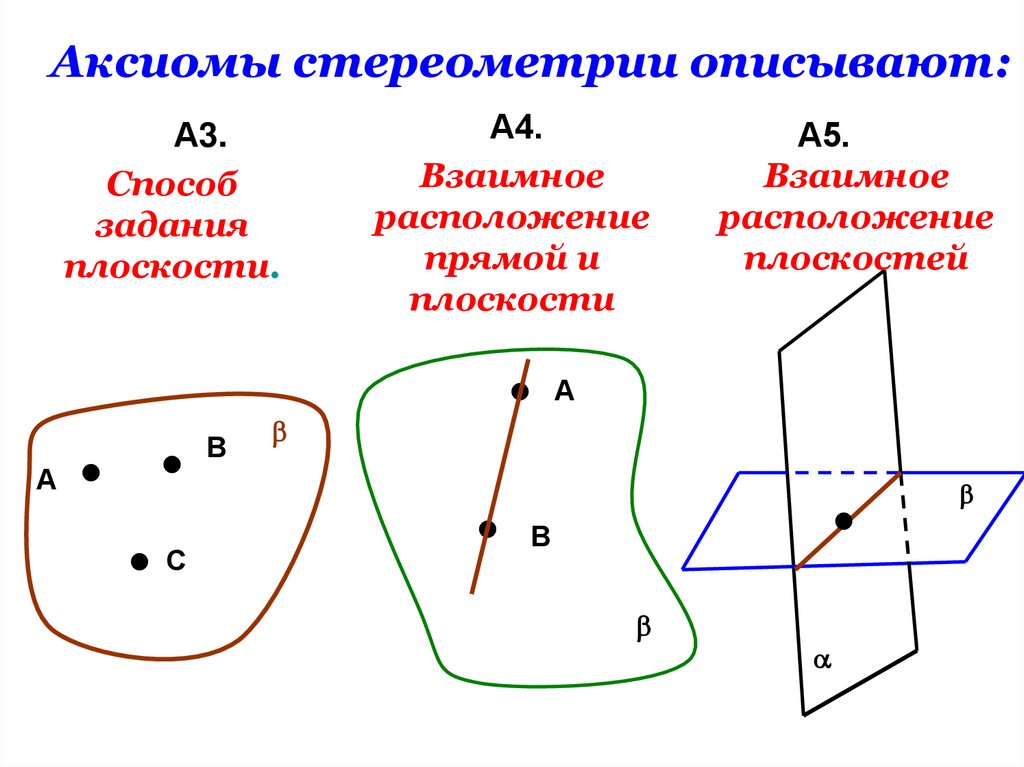
Аксиомы стереометрии описывают:
А3.
Способ
задания
плоскости.
А4.
Взаимное
расположение
прямой и
плоскости
А5.
Взаимное
расположение
плоскостей
А
В
А
С
В

36.

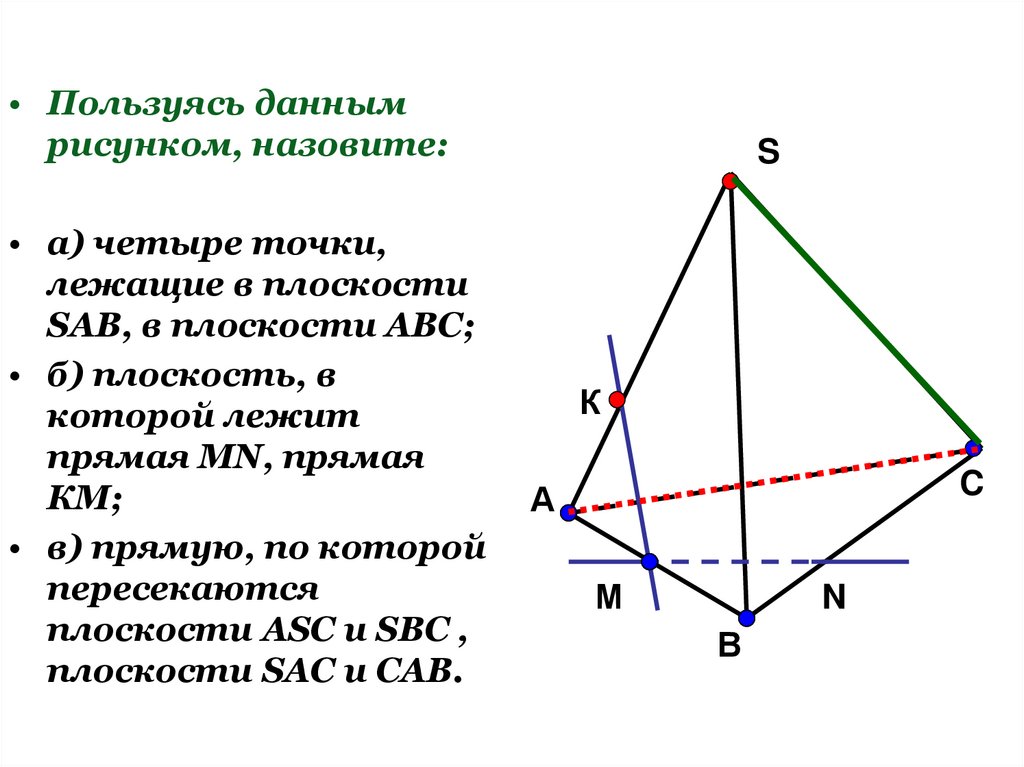
• Пользуясь данным
рисунком, назовите:
• а) четыре точки,
лежащие в плоскости
SAB, в плоскости АВС;
• б) плоскость, в
которой лежит
прямая MN, прямая
КМ;
• в) прямую, по которой
пересекаются
плоскости ASC и SBC ,
плоскости SAC и CAB.
S
К
C
А
М
N
В

37.

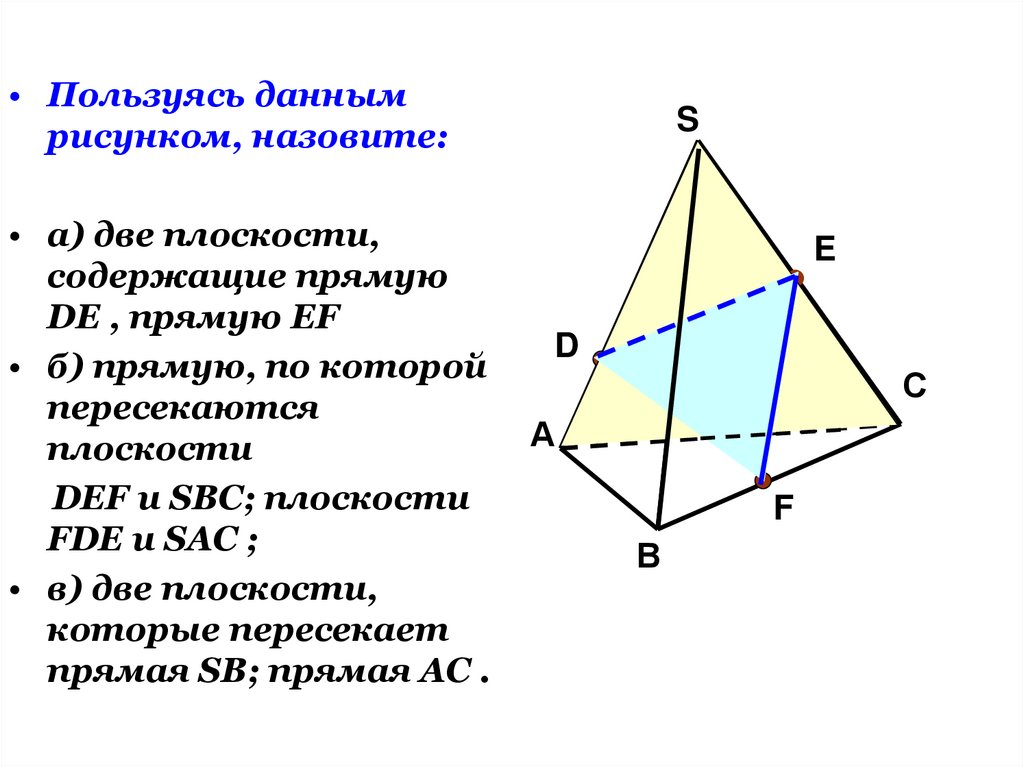
• Пользуясь данным
рисунком, назовите:
• а) две плоскости,
содержащие прямую
DE , прямую EF
• б) прямую, по которой
пересекаются
плоскости
DEF и SBC; плоскости
FDE и SAC ;
• в) две плоскости,
которые пересекает
прямая SB; прямая AC .
S
E
D
С
А
F
В

38.

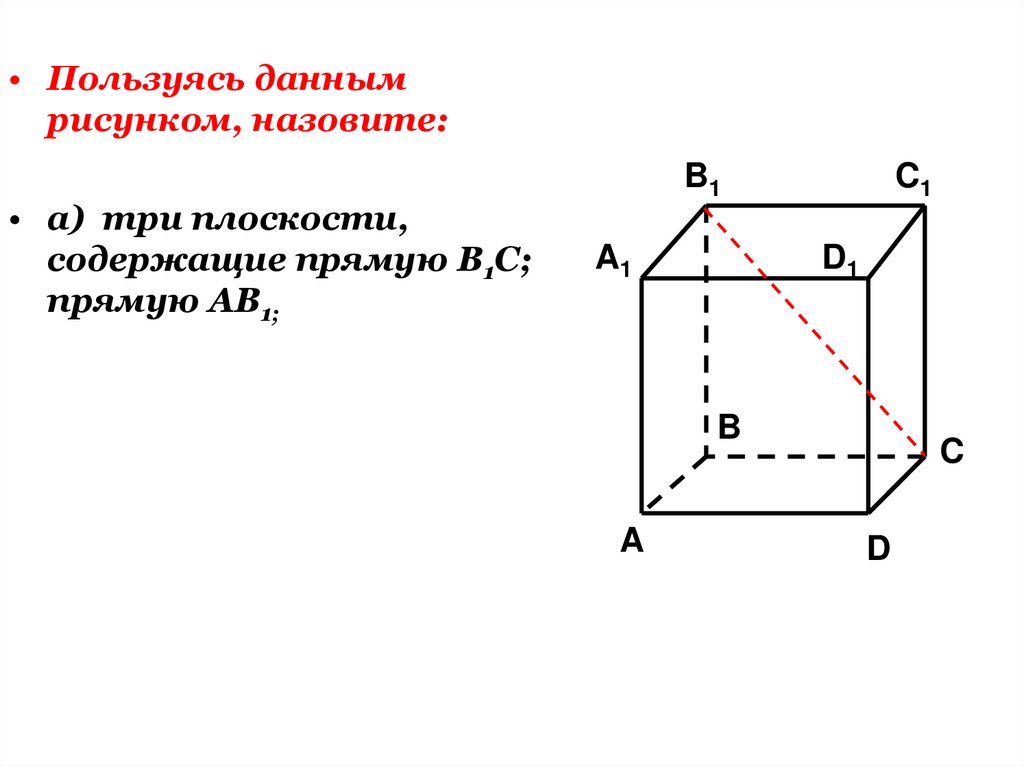
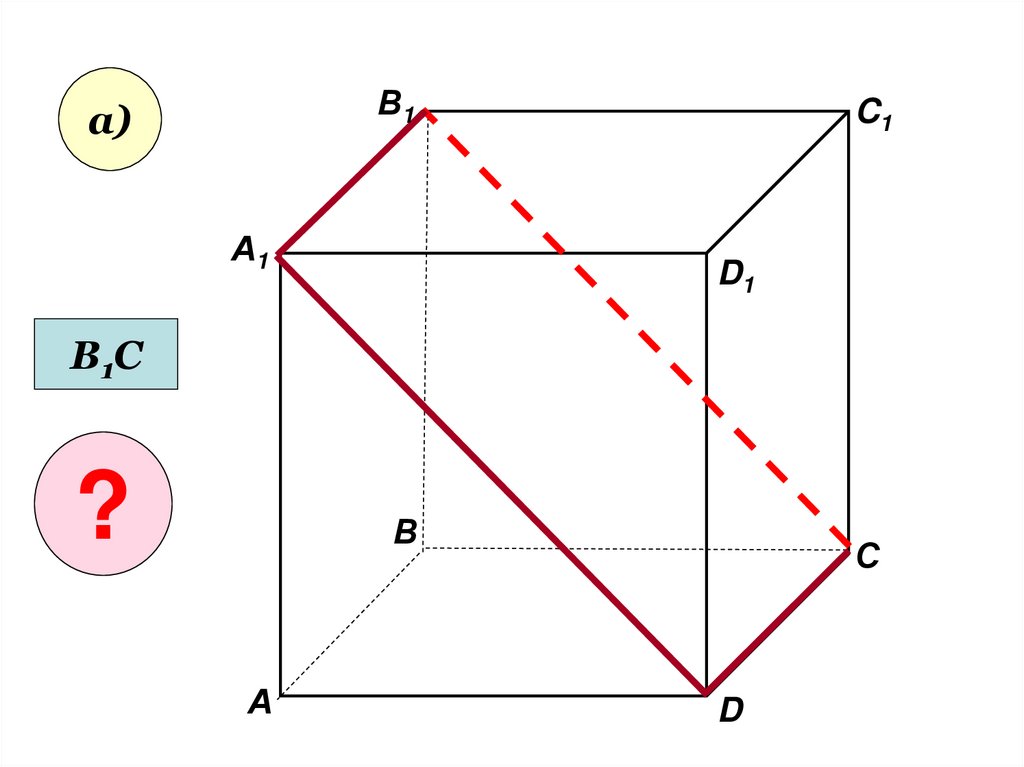
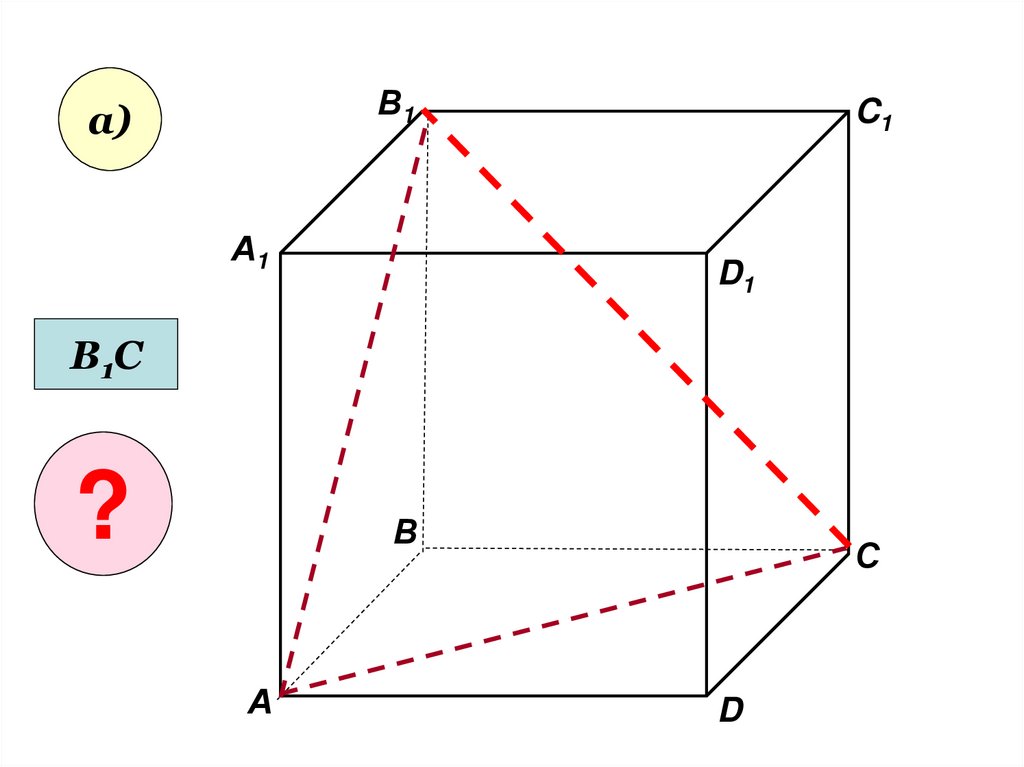
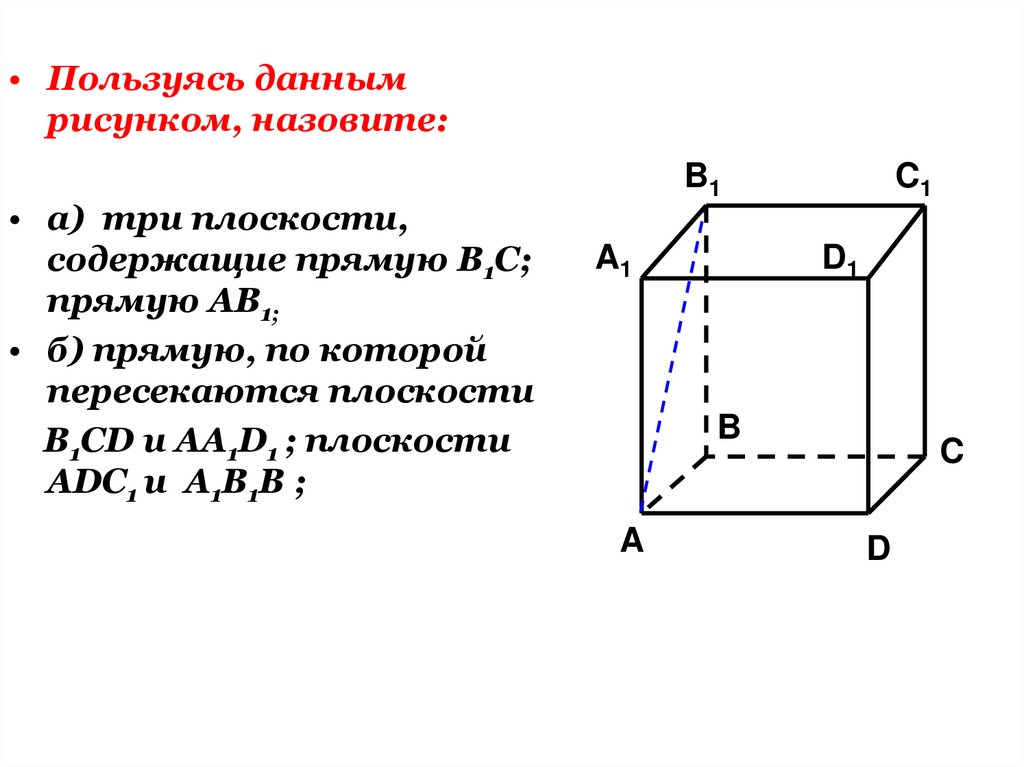
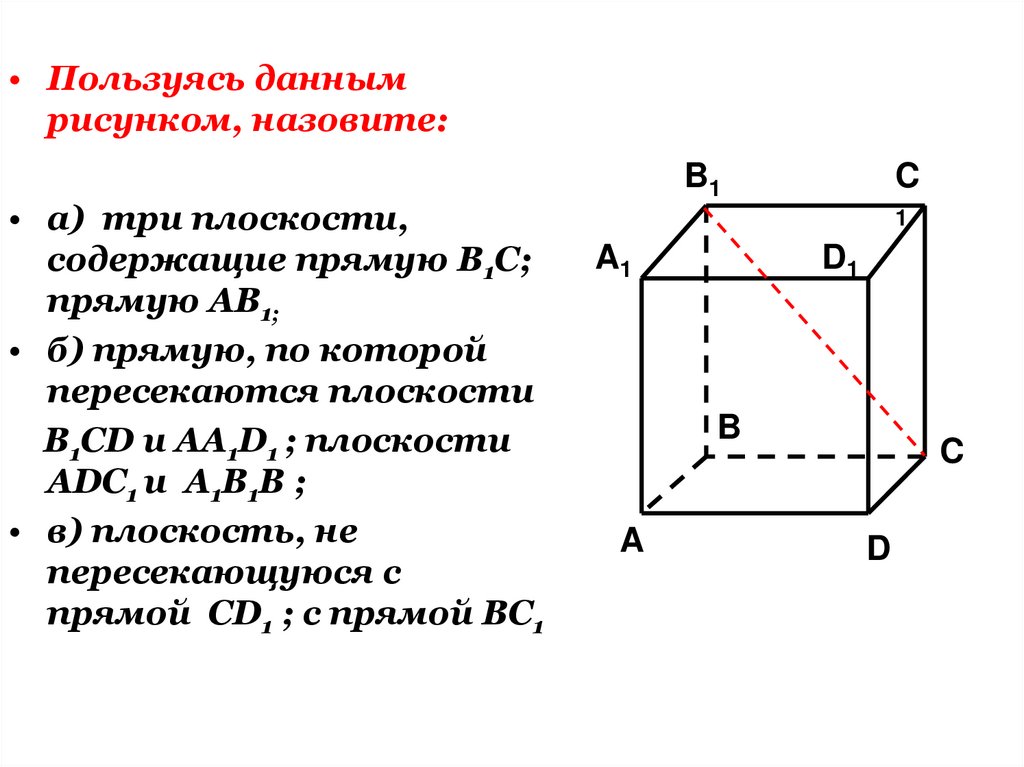
• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
B1
A1
C1
D1
B
A
C
D

39.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

40.

В1
а)
А1
C1
D1
В1С
?
В
А
С
D

41.

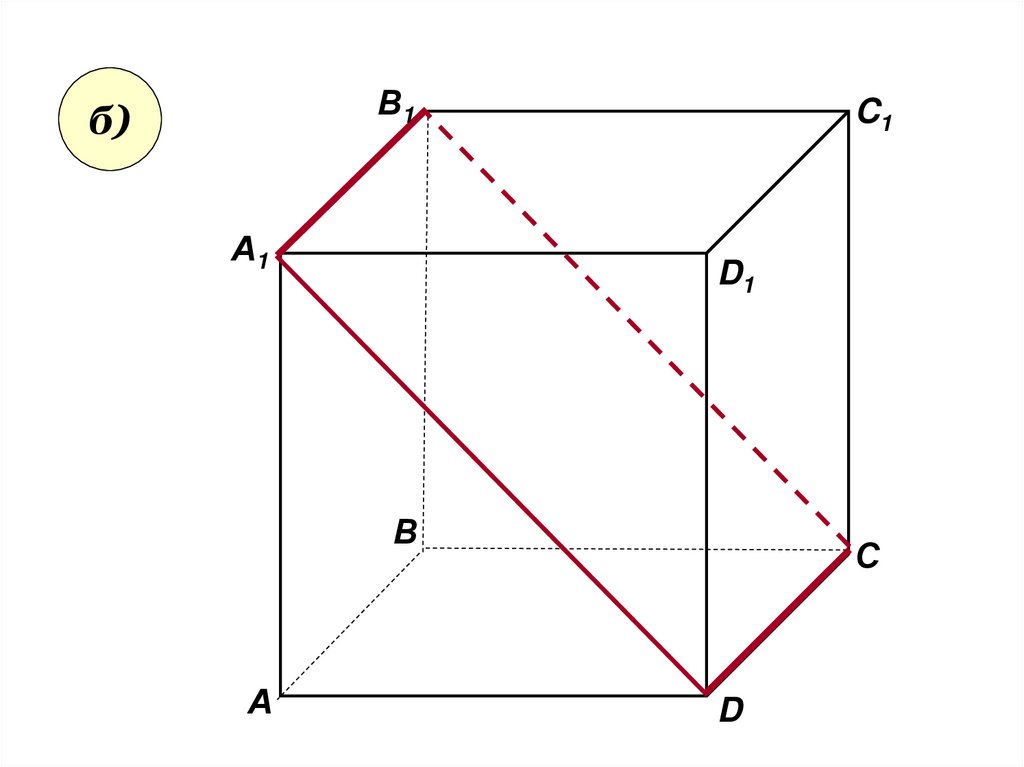
• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
B1
A1
C1
D1
B
A
C
D

42.

В1
б)
А1
C1
D1
В
А
С
D

43.

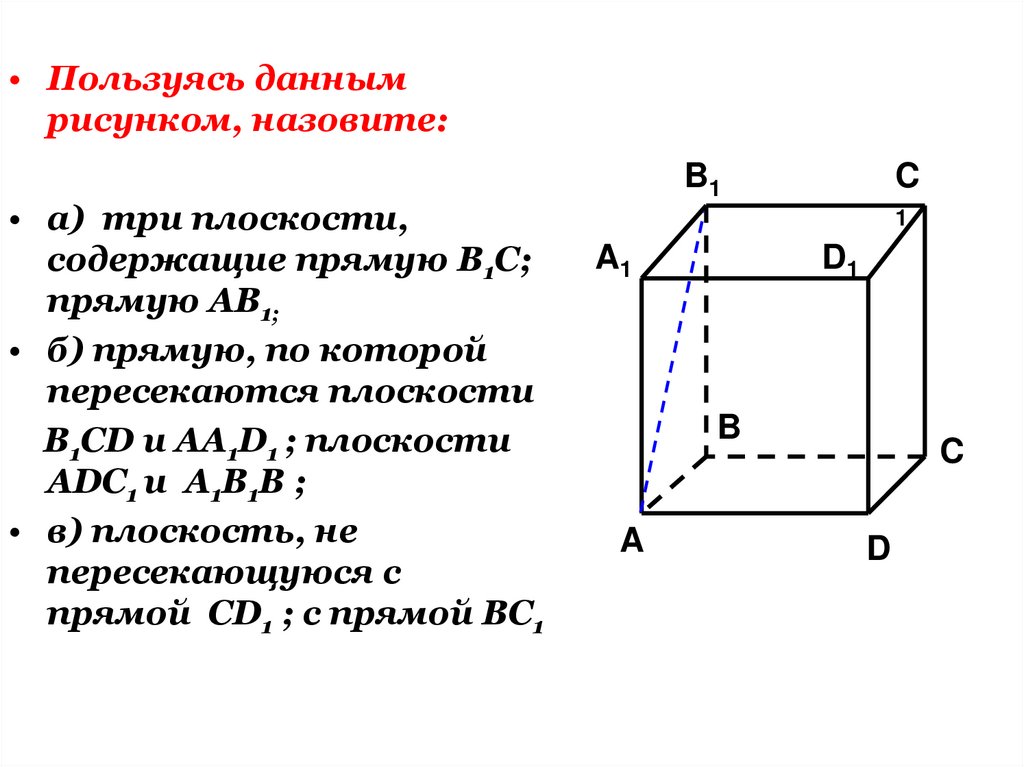
• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой BC1
B1
C
1
A1
D1
B
A
C
D

44.

В1
в)
А1
C1
D1
В
А
С
D

45.

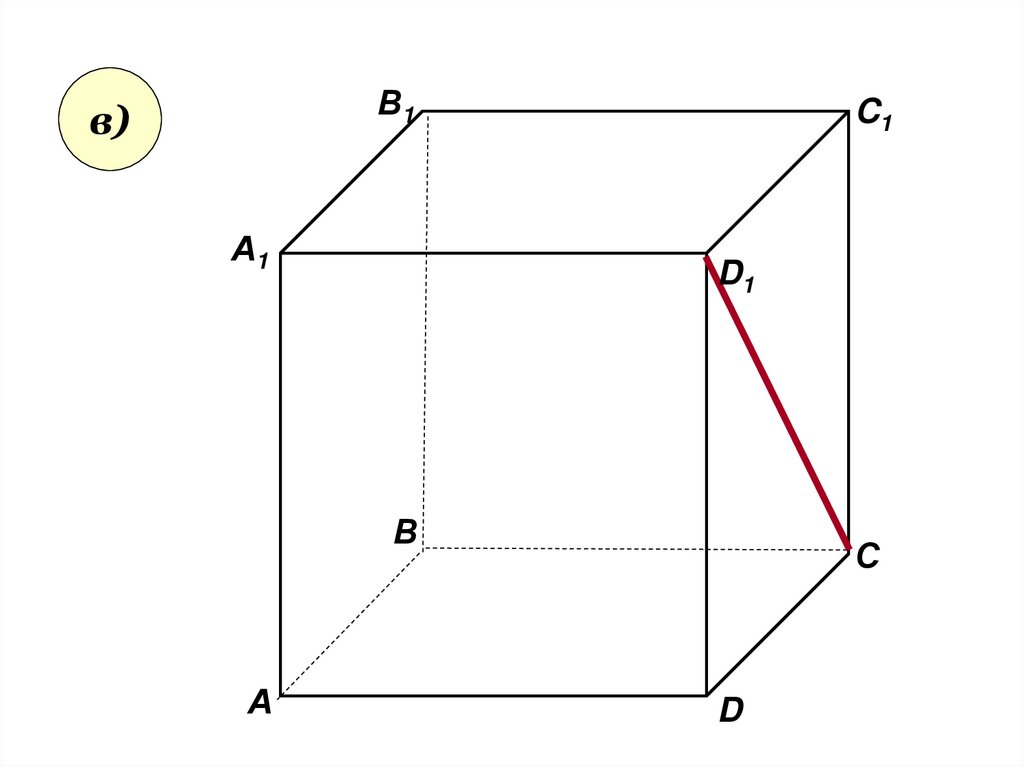
• Пользуясь данным
рисунком, назовите:
• а) три плоскости,
содержащие прямую В1С;
прямую АВ1;
• б) прямую, по которой
пересекаются плоскости
B1CD и AA1D1 ; плоскости
ADC1 и A1B1B ;
• в) плоскость, не
пересекающуюся с
прямой CD1 ; с прямой BC1
B1
C
1
A1
D1
B
A
C
D

46.

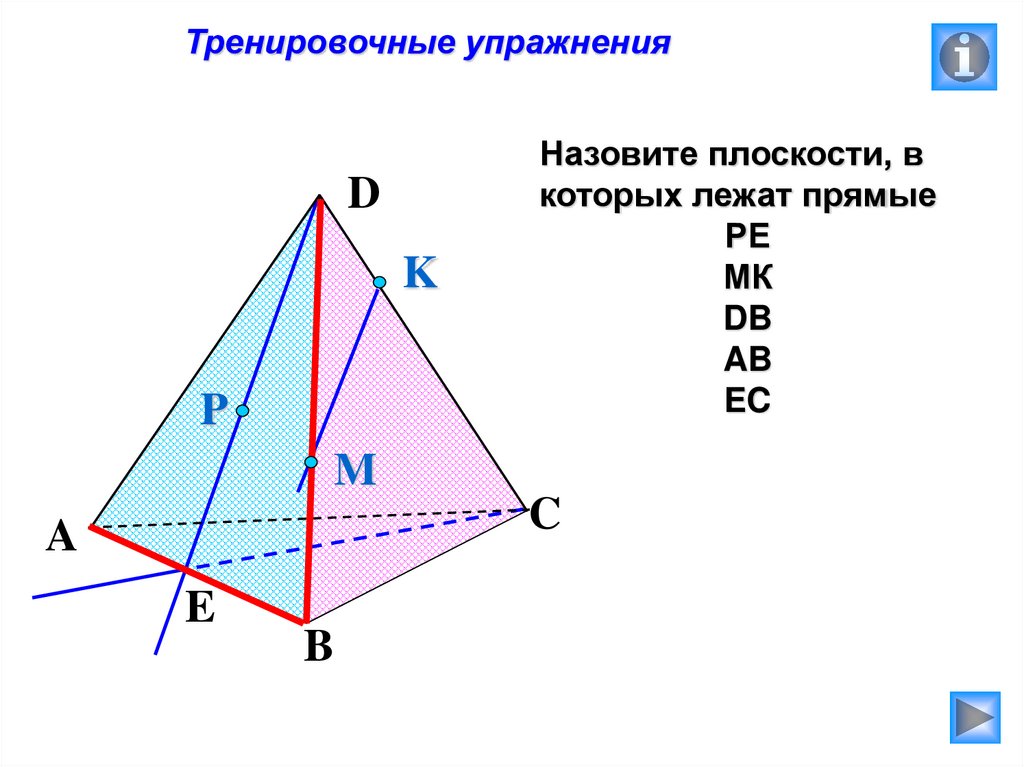
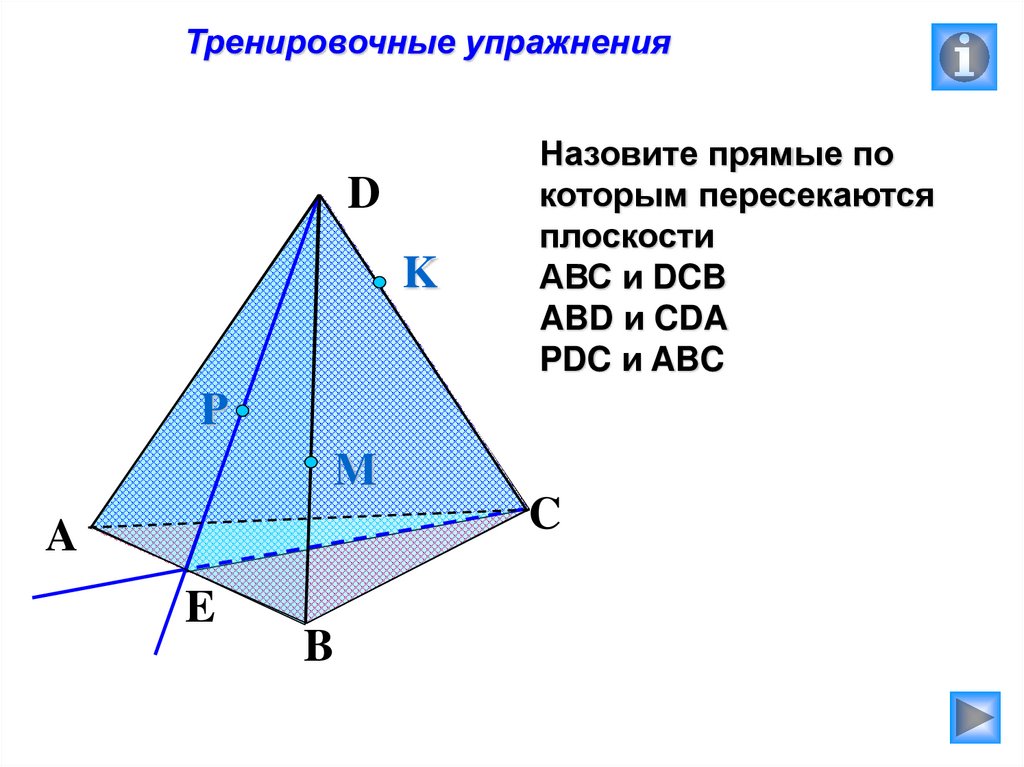
Тренировочные упражнения
D
K
P
Назовите плоскости, в
которых лежат прямые
РЕ
МК
DB
AB
EC
M
C
A
E
B

47.

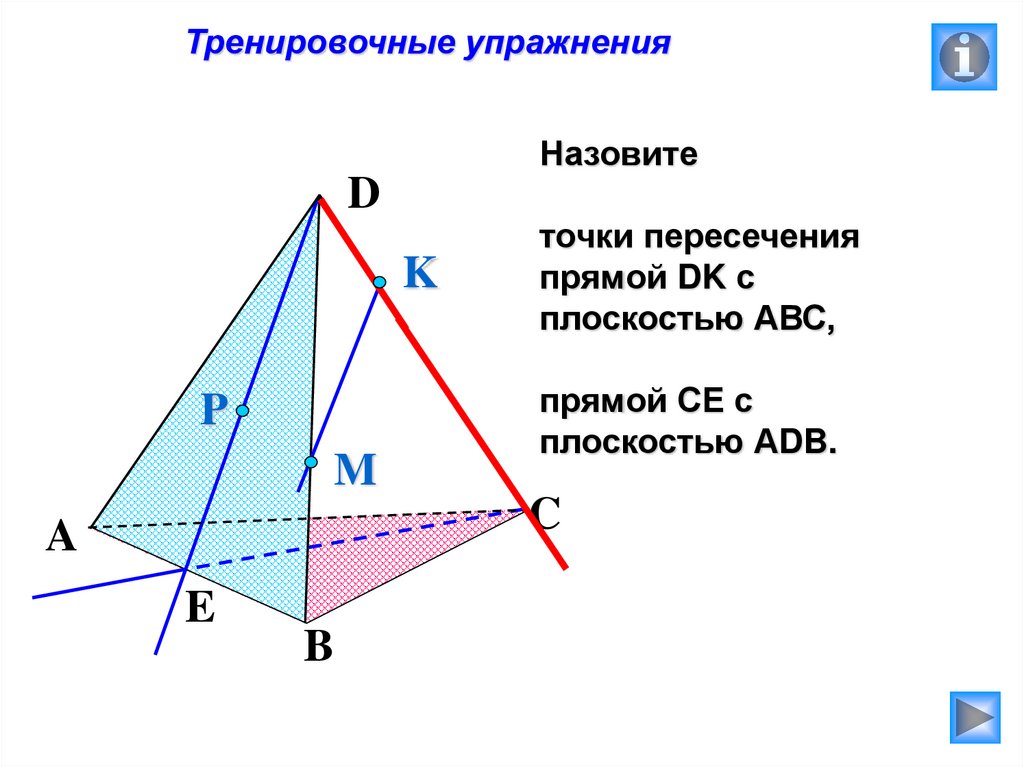
Тренировочные упражнения
Назовите
D
K
P
M
точки пересечения
прямой DK с
плоскостью АВС,
прямой СЕ с
плоскостью АDB.
C
A
E
B

48.

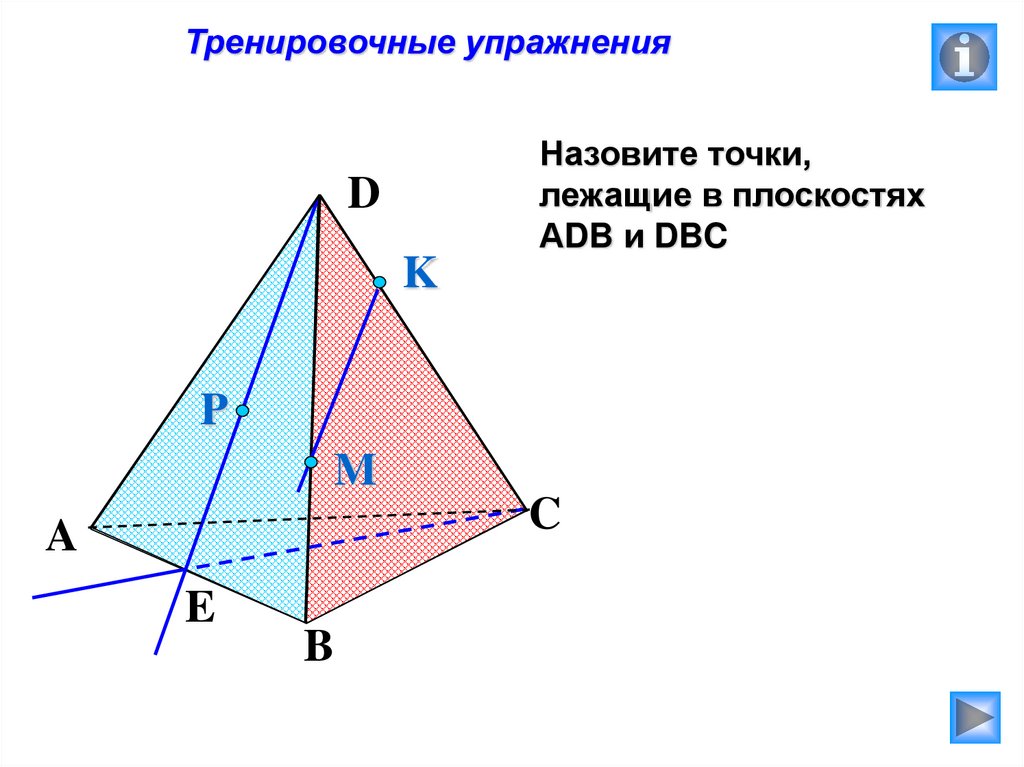
Тренировочные упражнения
Назовите точки,
лежащие в плоскостях
АDB и DBC
D
K
P
M
C
A
E
B

49.

Тренировочные упражнения
D
K
Назовите прямые по
которым пересекаются
плоскости
АВС и DCB
ABD и CDA
PDC и ABC
P
M
C
A
E
B

50.

Тренировочные упражнения
B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
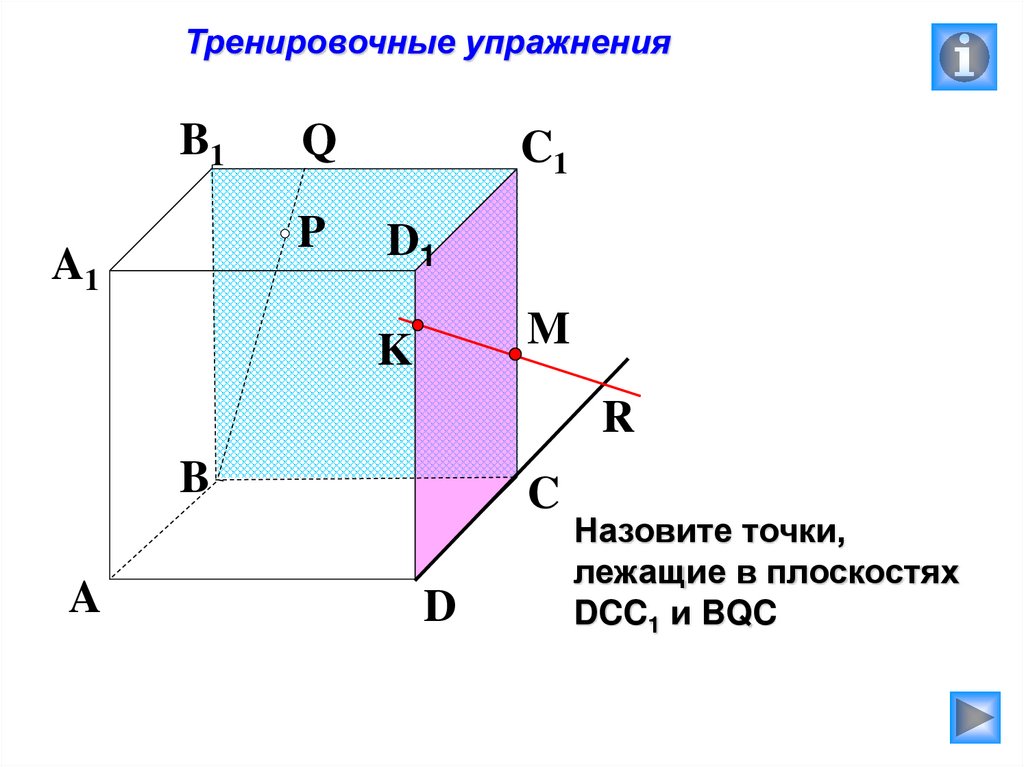
Назовите точки,
лежащие в плоскостях
DCC1 и BQC

51.

Тренировочные упражнения
B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
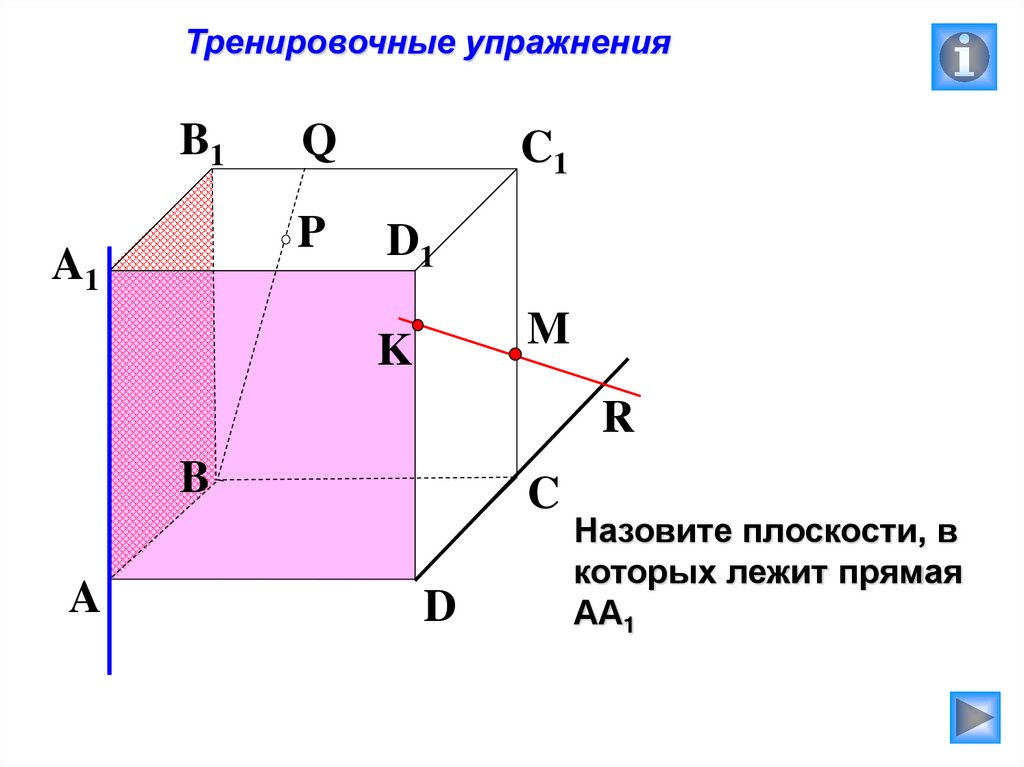
Назовите плоскости, в
которых лежит прямая
АА1

52.

Тренировочные упражнения
B1
Q
P
A1
C1
D1
M
K
B
A
C
D
R
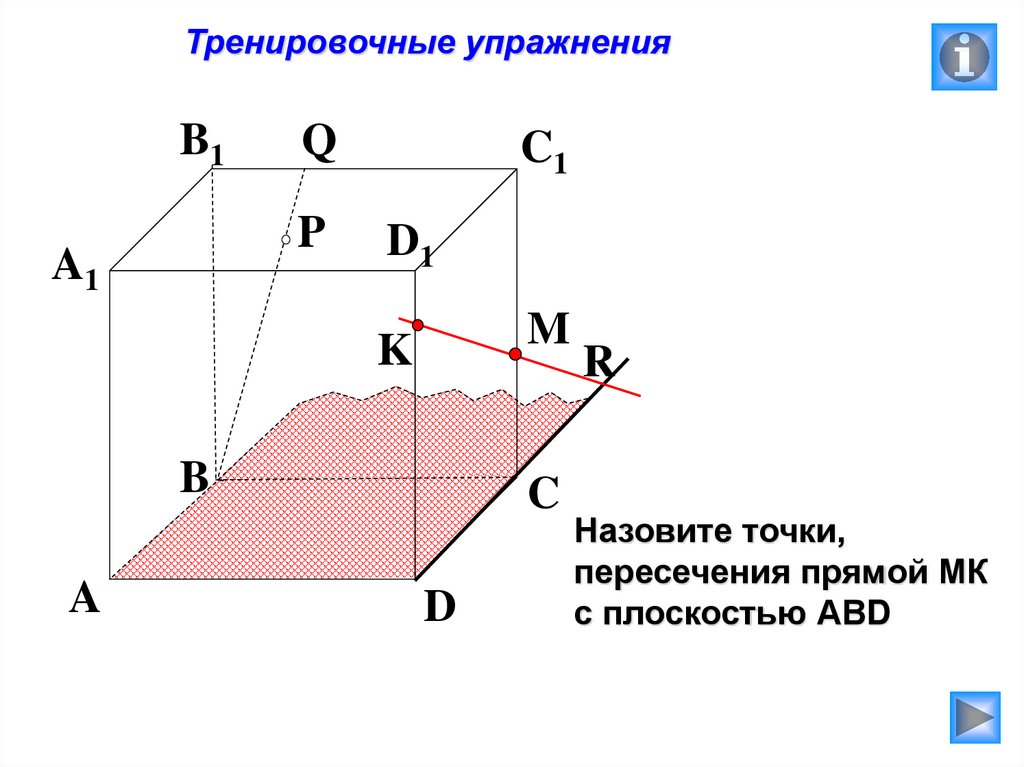
Назовите точки,
пересечения прямой МК
с плоскостью АВD

53.

Тренировочные упражнения
B1
Q
C1
P
A1
D1
K
M
R
B
A
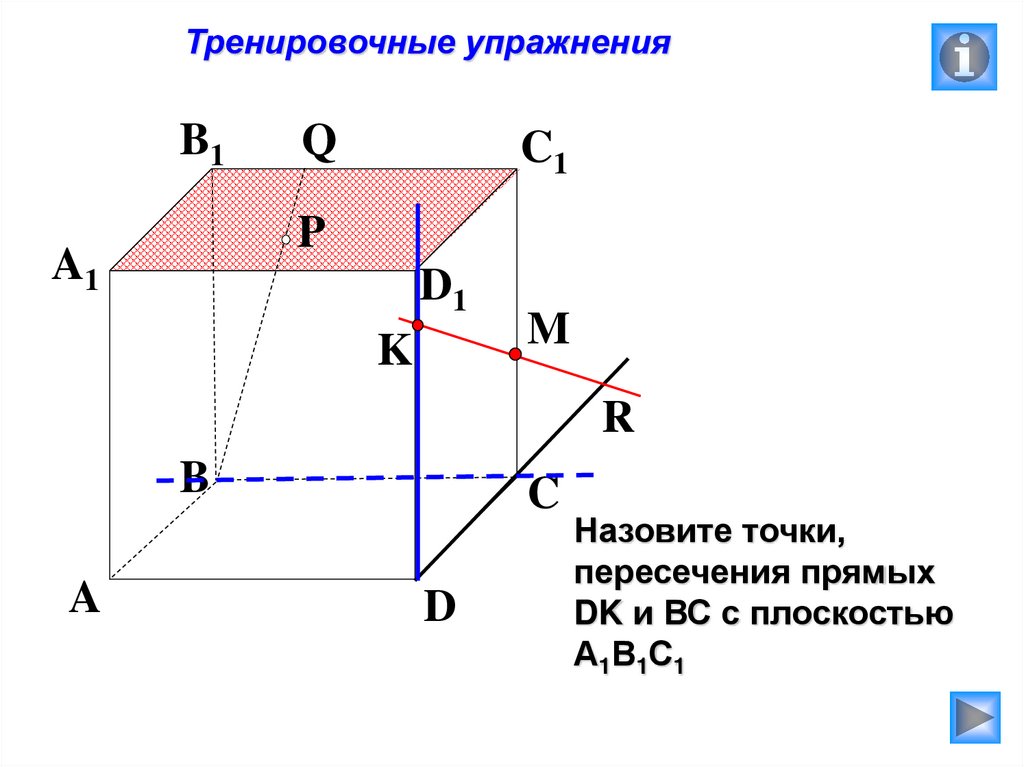
C
D
Назовите точки,
пересечения прямых
DK и ВС с плоскостью
А1В1С1

54.

Тренировочные упражнения
B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
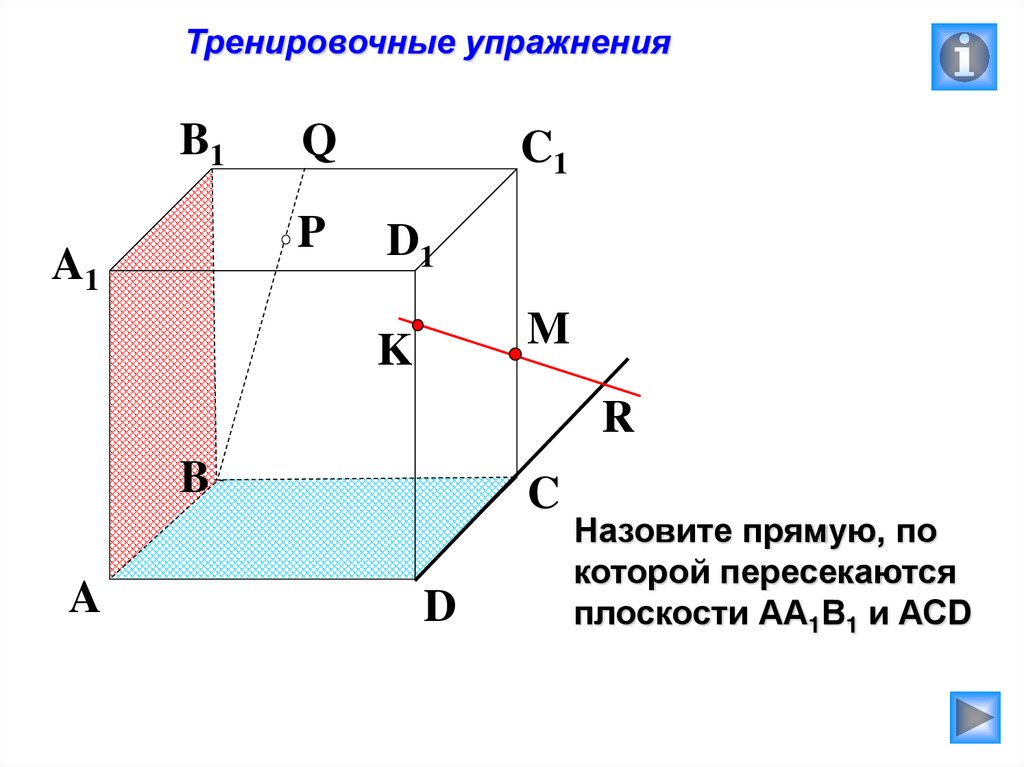
Назовите прямую, по
которой пересекаются
плоскости АА1В1 и АСD

55.

Тренировочные упражнения
B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
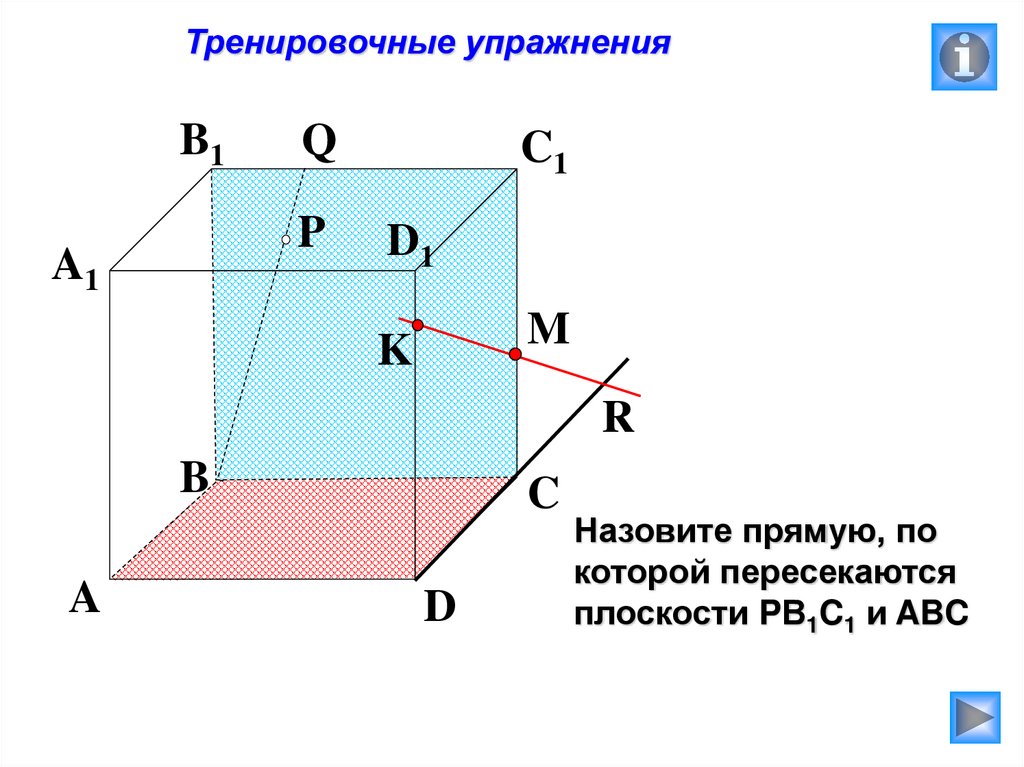
Назовите прямую, по
которой пересекаются
плоскости PВ1C1 и ABC

56.

Тренировочные упражнения
B1
Q
P
A1
C1
D1
M
K
R
B
A
C
D
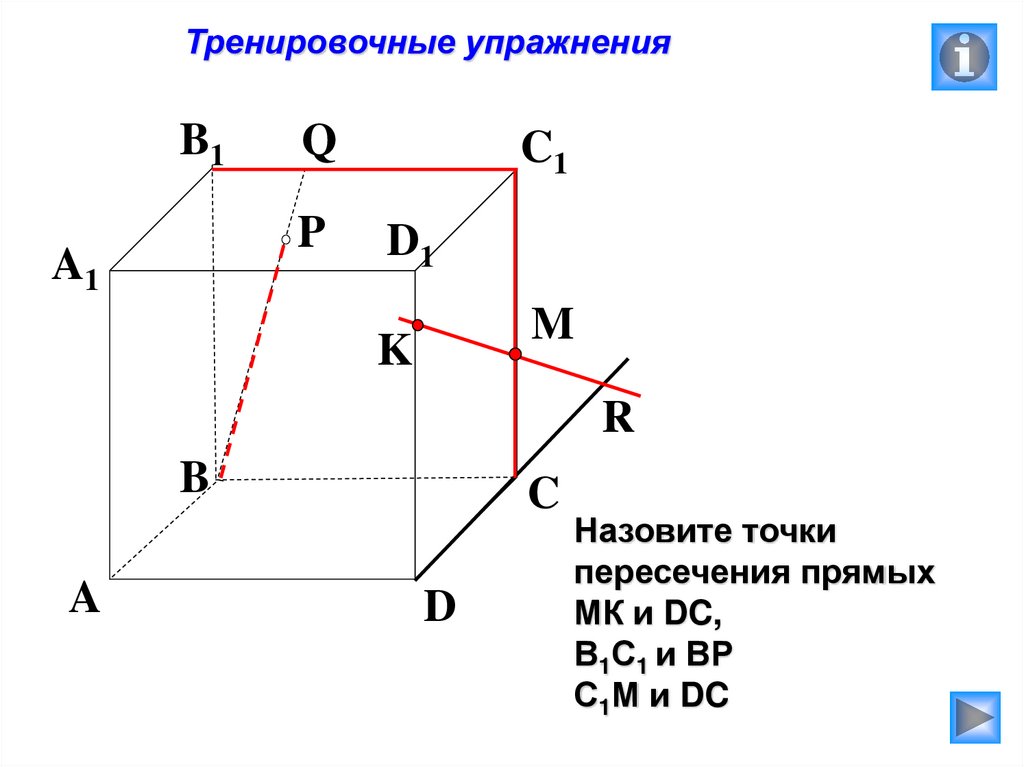
Назовите точки
пересечения прямых
МК и DC,
В1С1 и ВР
С1М и DC

57.

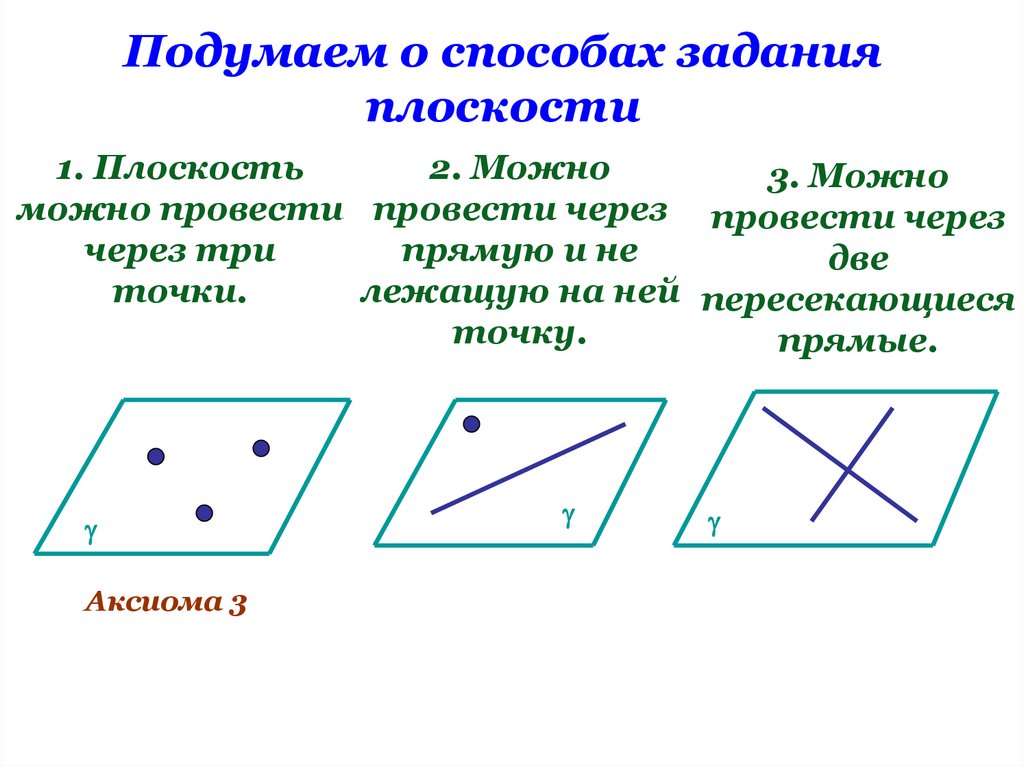
Подумаем о способах задания
плоскости
1. Плоскость
2. Можно
3. Можно
можно провести провести через провести через
через три
прямую и не
две
точки.
лежащую на ней пересекающиеся
точку.
прямые.
Аксиома 3

58.

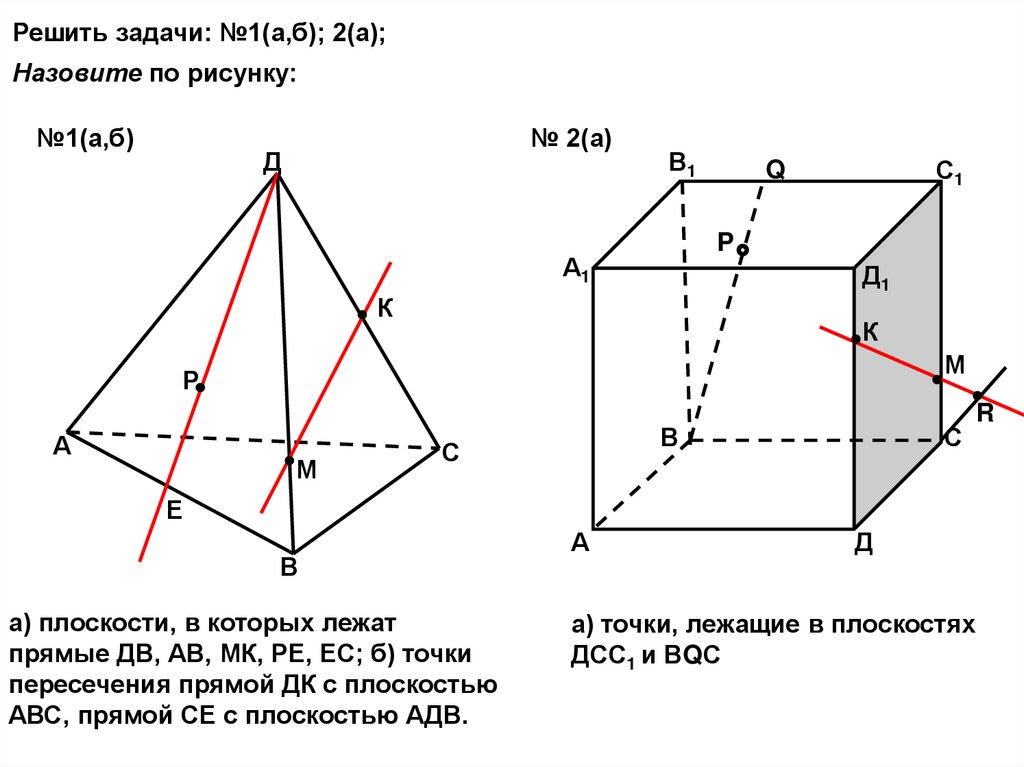
Решить задачи: №1(а,б); 2(а);
Назовите по рисунку:
№1(а,б)
№ 2(а)
Д
В1
С1
Q
P
А1
Д1
К
К
М
Р
А
М
В
С
С
Е
В
а) плоскости, в которых лежат
прямые ДВ, АВ, МК, РЕ, ЕС; б) точки
пересечения прямой ДК с плоскостью
АВС, прямой СЕ с плоскостью АДВ.
А
Д
а) точки, лежащие в плоскостях
ДСС1 и ВQС
R

59.

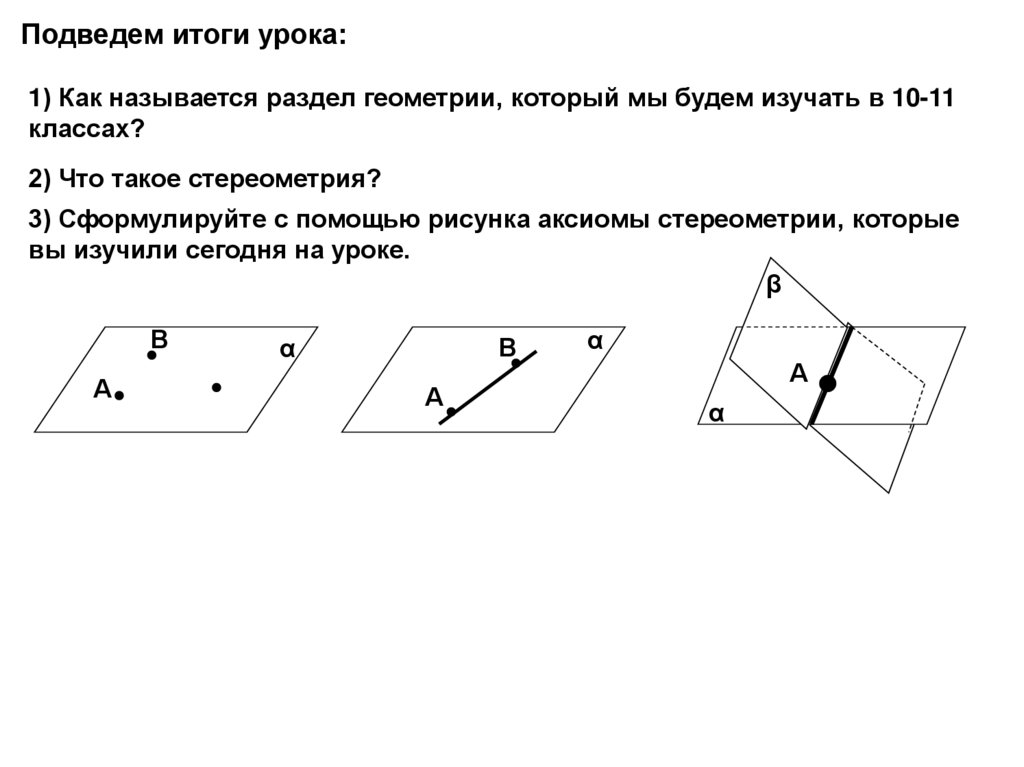
Подведем итоги урока:
1) Как называется раздел геометрии, который мы будем изучать в 10-11
классах?
2) Что такое стереометрия?
3) Сформулируйте с помощью рисунка аксиомы стереометрии, которые
вы изучили сегодня на уроке.
β
В
А
В
α
А
α
А
α