Лекция №2.1 Построение эпюр

1. Построение эпюр поперечной силы Qу и изгибающего момента Мx

ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНОЙ СИЛЫ QУ И
ИЗГИБАЮЩЕГО МОМЕНТА МX
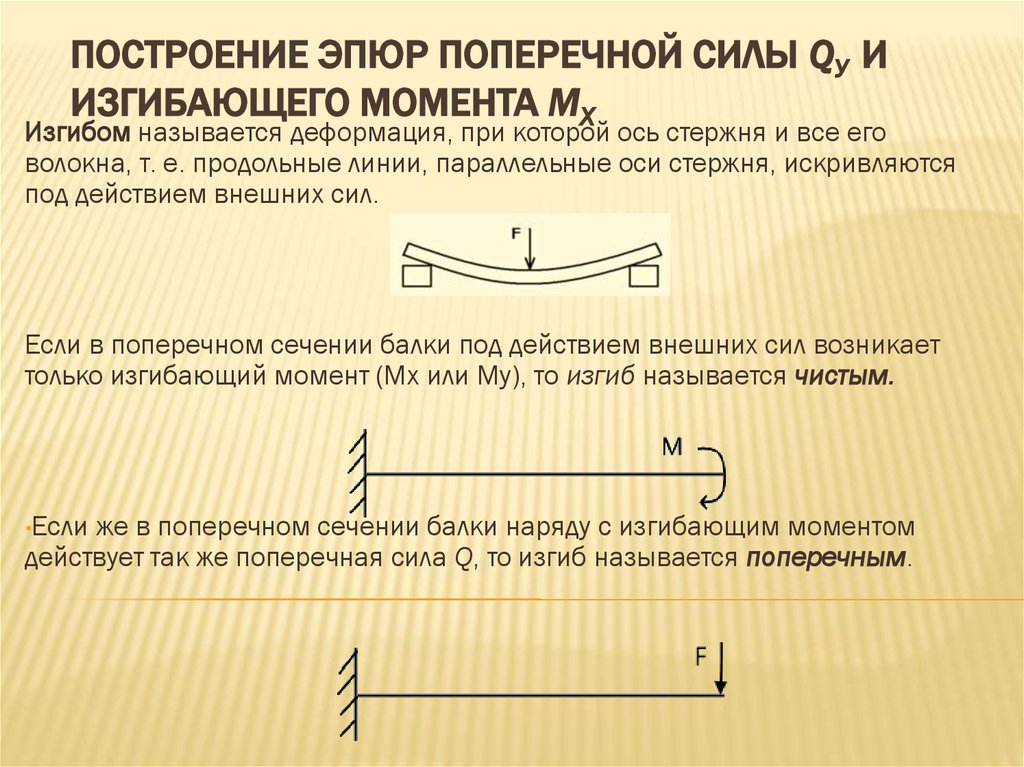
Изгибом называется деформация, при которой ось стержня и все его
волокна, т. е. продольные линии, параллельные оси стержня, искривляются
под действием внешних сил.
Если в поперечном сечении балки под действием внешних сил возникает
только изгибающий момент (Мx или My), то изгиб называется чистым.
•Если же в поперечном сечении балки наряду с изгибающим моментом
действует так же поперечная сила Q, то изгиб называется поперечным.

2. Построение эпюр поперечной силы Qу и изгибающего момента Мx

ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНОЙ СИЛЫ QУ
И ИЗГИБАЮЩЕГО МОМЕНТА МX
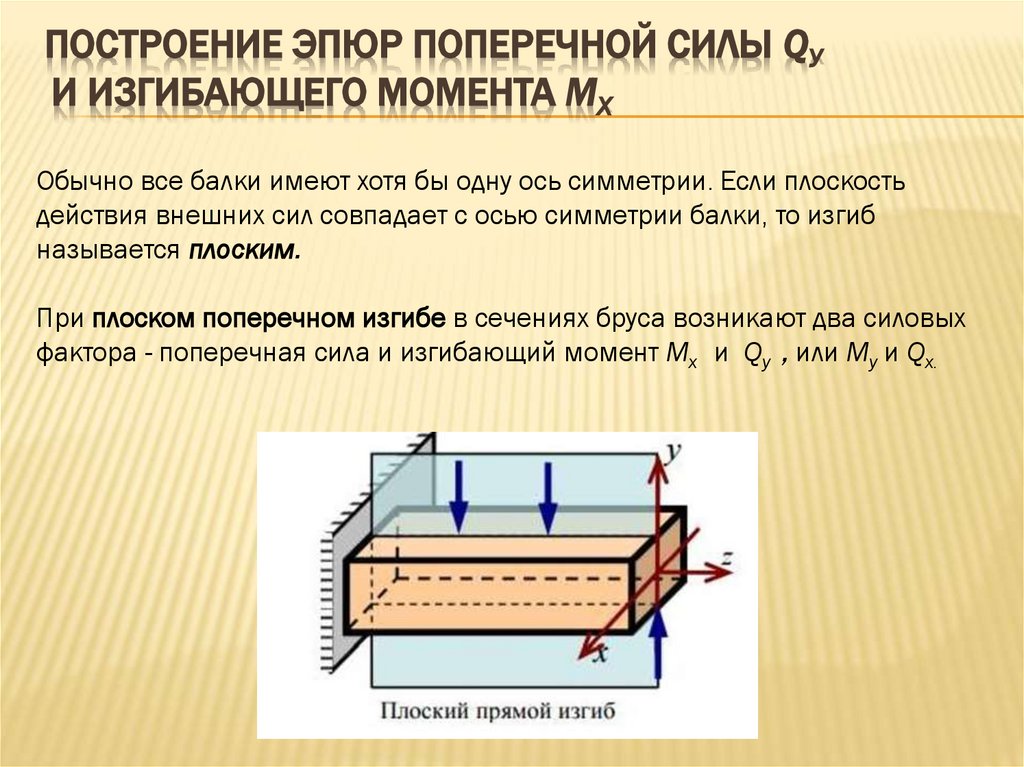
Обычно все балки имеют хотя бы одну ось симметрии. Если плоскость
действия внешних сил совпадает с осью симметрии балки, то изгиб
называется плоским.
При плоском поперечном изгибе в сечениях бруса возникают два силовых
фактора - поперечная сила и изгибающий момент Mx и Qy , или My и Qx.

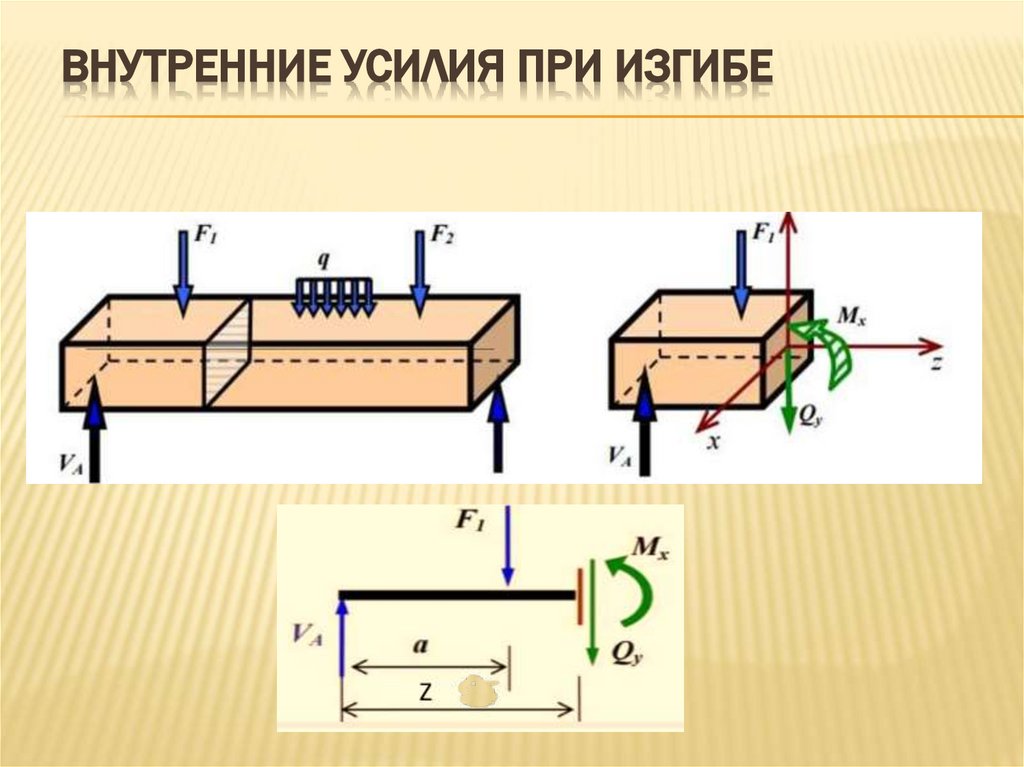
3. Внутренние усилия при изгибе

ВНУТРЕННИЕ УСИЛИЯ ПРИ ИЗГИБЕ

4. Балки и их опоры

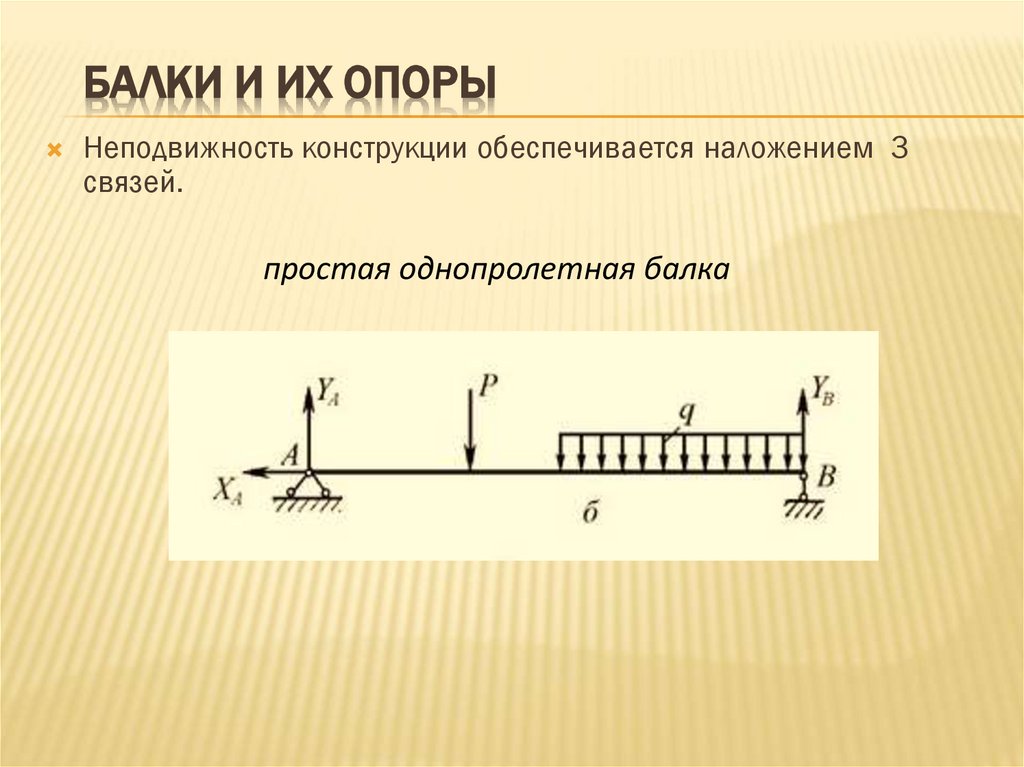
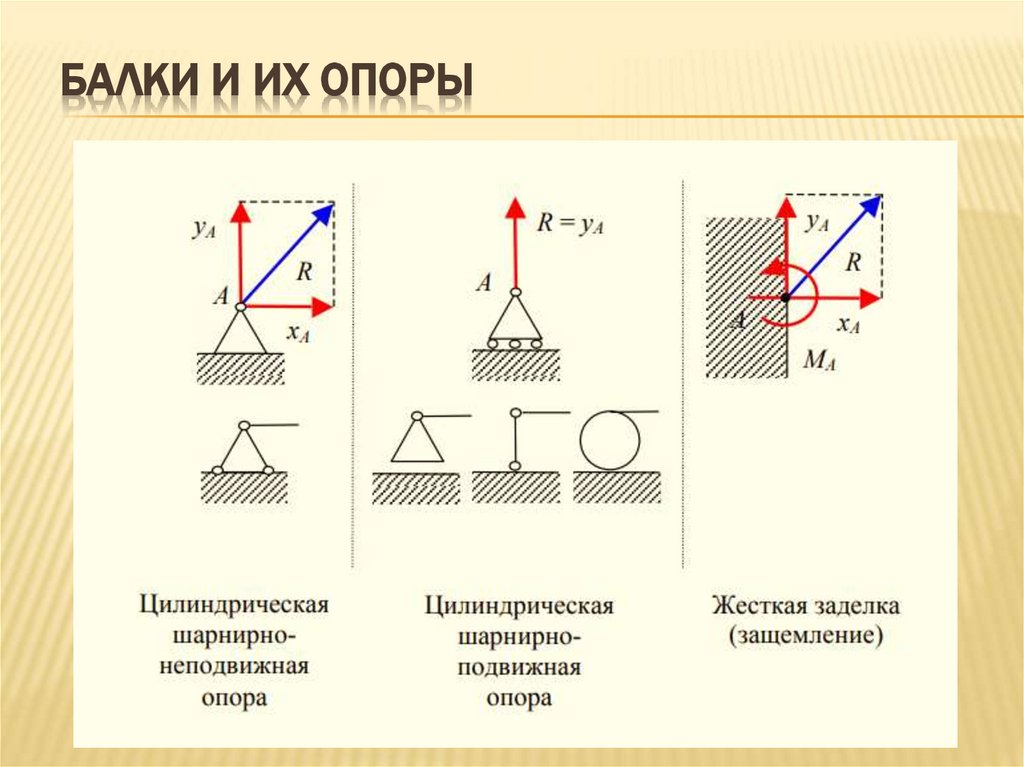
БАЛКИ И ИХ ОПОРЫ
Неподвижность конструкции обеспечивается наложением 3
связей.
простая однопролетная балка

5. Балки и их опоры

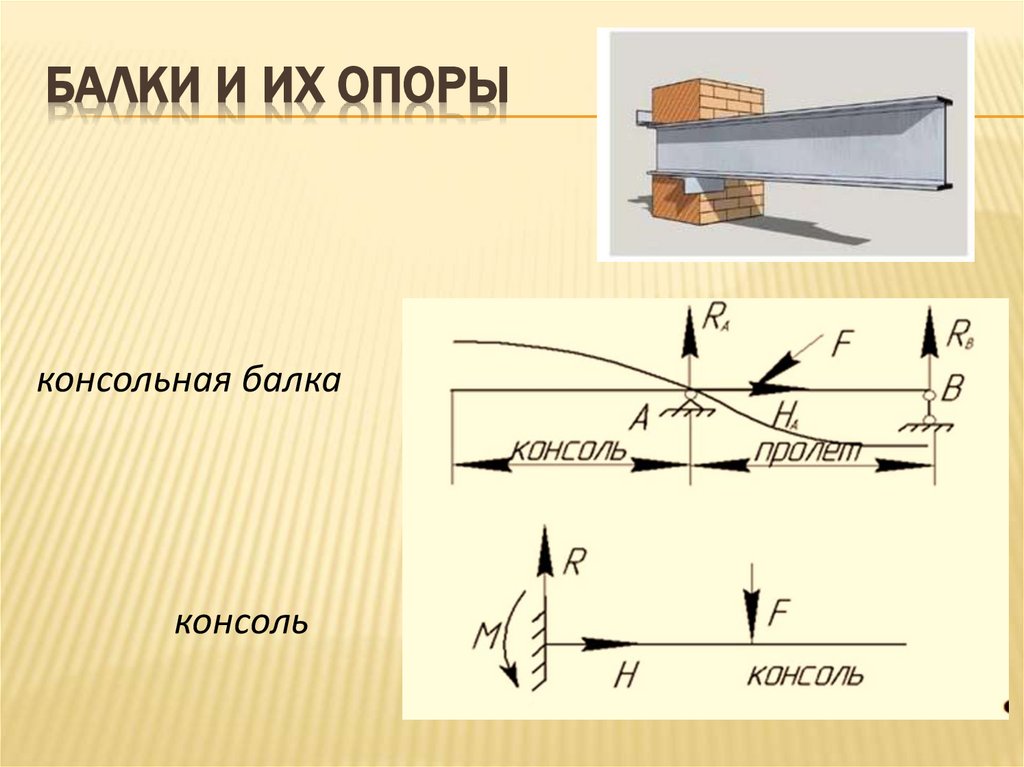
БАЛКИ И ИХ ОПОРЫ
консольная балка
консоль

6. Балки и их опоры

БАЛКИ И ИХ ОПОРЫ

7. Определение реакций в опорах

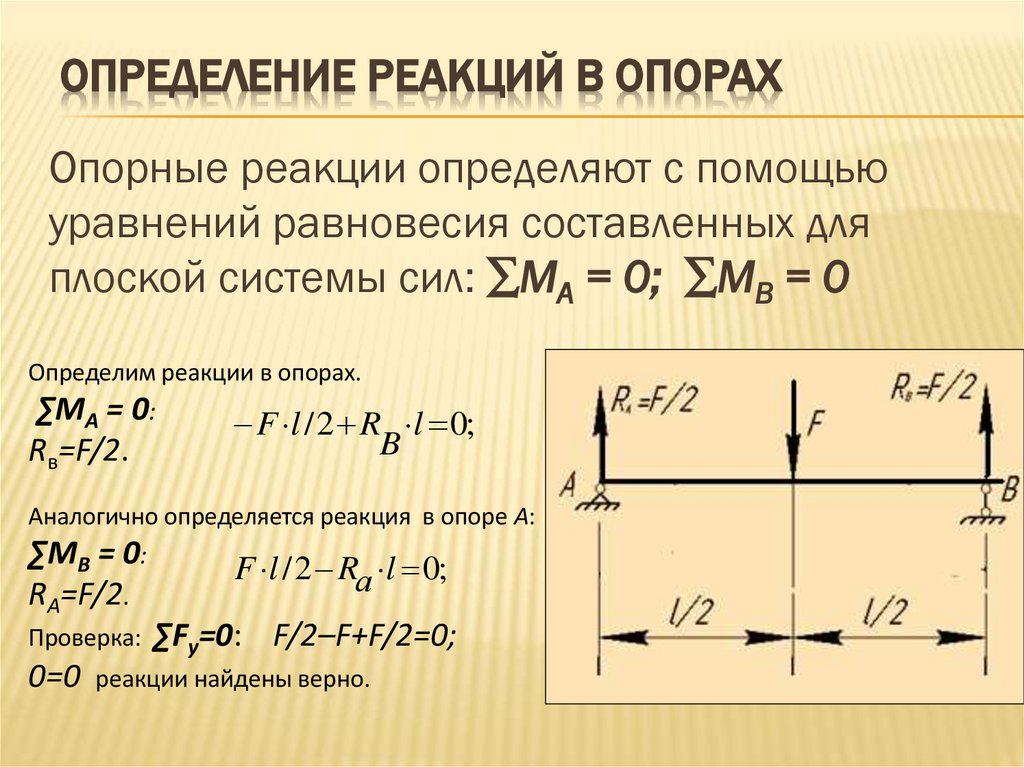
ОПРЕДЕЛЕНИЕ РЕАКЦИЙ В ОПОРАХ
Опорные реакции определяют с помощью
уравнений равновесия составленных для
плоской системы сил: ∑МА = 0; ∑МВ = 0
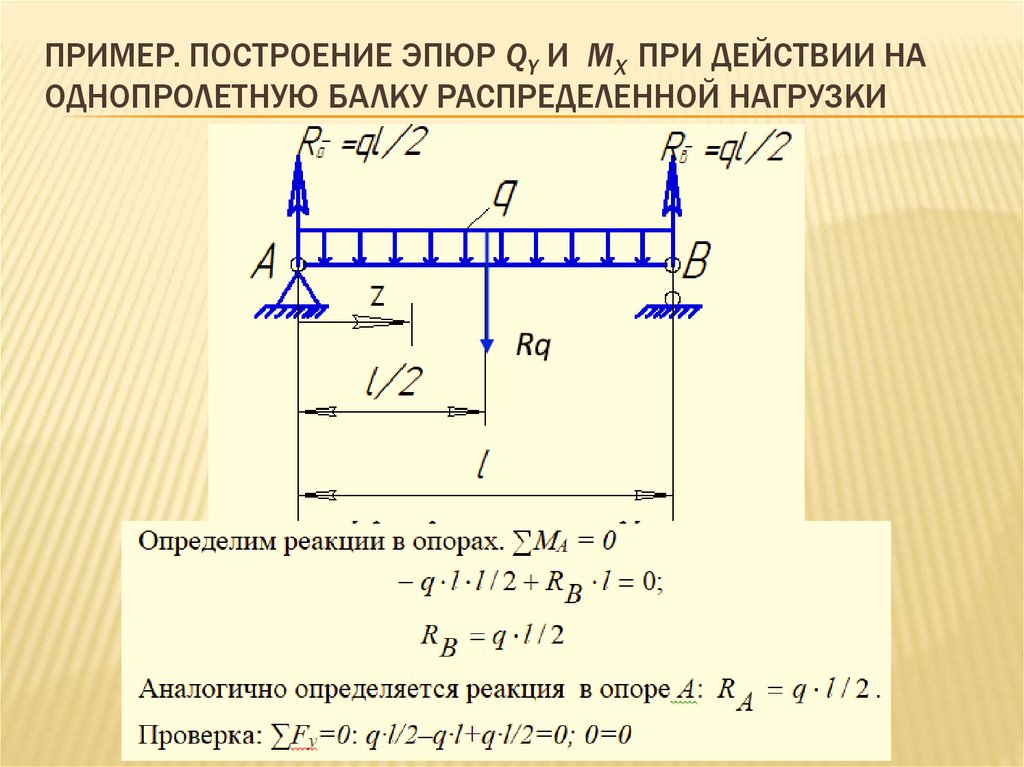
Определим реакции в опорах.
∑МА = 0:
Rв=F/2.
F l / 2 R l 0;
B
Аналогично определяется реакция в опоре А:
∑МВ = 0:
RA=F/2.
F l / 2 Rа l 0;
Проверка: ∑Fy=0:
F/2–F+F/2=0;
0=0 реакции найдены верно.

8. Правило знаков

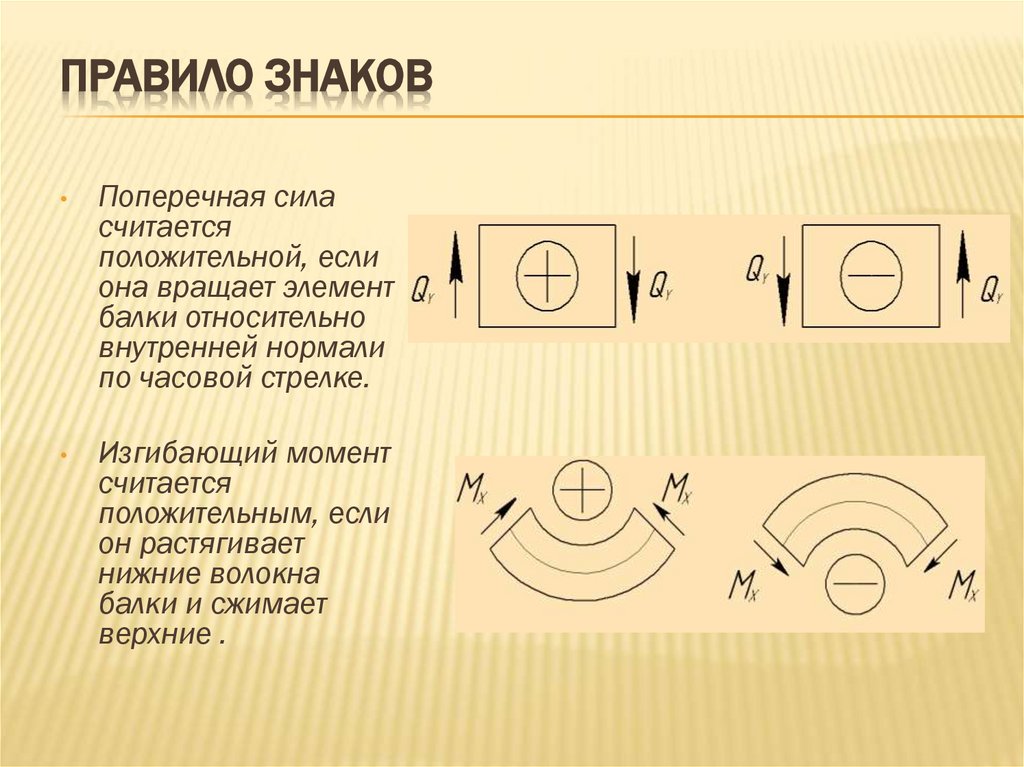
ПРАВИЛО ЗНАКОВ
Поперечная сила
считается
положительной, если
она вращает элемент
балки относительно
внутренней нормали
по часовой стрелке.
Изгибающий момент
считается
положительным, если
он растягивает
нижние волокна
балки и сжимает
верхние .

9. Определение величины внутренних усилий Qy и Мx

ОПРЕДЕЛЕНИЕ ВЕЛИЧИНЫ ВНУТРЕННИХ УСИЛИЙ
QY И МX
Поперечная сила и изгибающий момент в сечении
балки определяются с помощью метода сечений в
соответствии с выражениями:
Мx = Σ Mx; Qy = Σ Fy.
dQy
2
dM x
d Mx
Qy
;q
2
dz
dz
dz

10. Порядок построения эпюр Qу и МХ

ПОРЯДОК ПОСТРОЕНИЯ ЭПЮР QУ И МХ
1. Изображается расчетная схема балки с указанием численных
значений приложенных нагрузок и геометрических размеров
бруса.
2. Составляются уравнения равновесия балки и определяются
опорные реакции.
3. Балка разбивается на участки, границами которых являются
точки приложения сосредоточенных сил и моментов, а так же
начало и конец распределенной нагрузки.
4. Для каждого участка записываются аналитические выражения
Qу и МХ и вычисляются все их значения, необходимые для
построения эпюр.
5. Определяются точки, в которых Qу = 0. В этих точках
изгибающий момент МХ принимает экстремальные значения,
которые необходимо вычислить.
6. По полученным значениям строятся эпюры Qу и МХ.
7. Проводится проверка правильности построения эпюр.

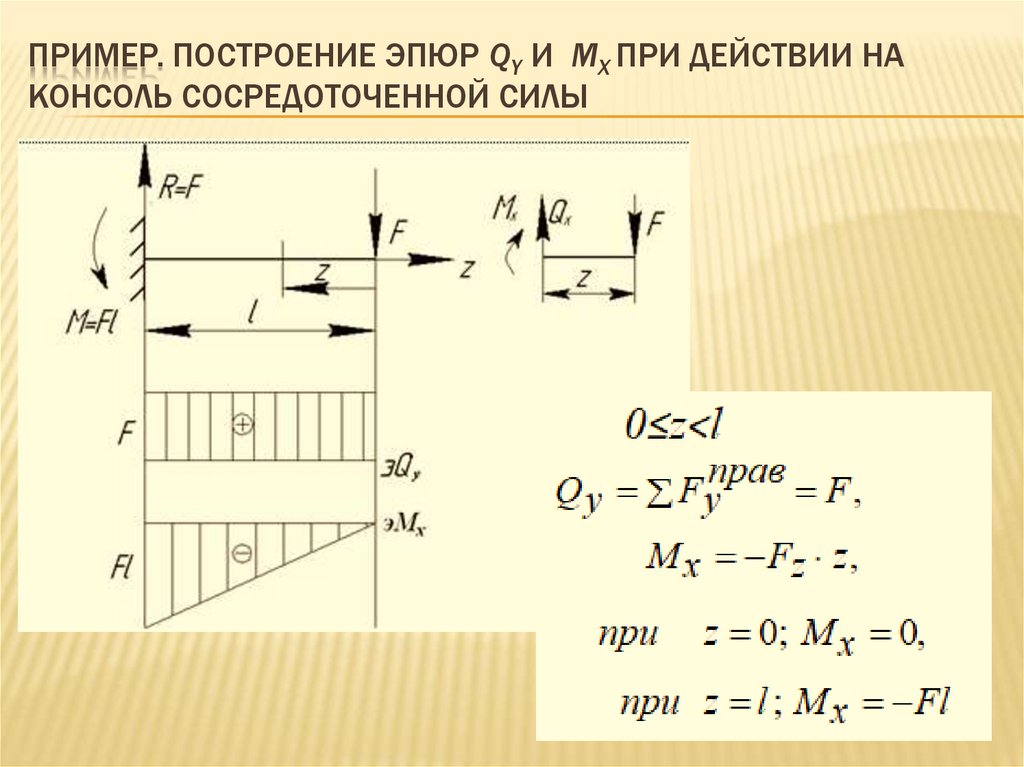
11. Пример. Построение эпюр Qy и Mx при действии на консоль сосредоточенной силы

ПРИМЕР. ПОСТРОЕНИЕ ЭПЮР QY И MX ПРИ ДЕЙСТВИИ НА
КОНСОЛЬ СОСРЕДОТОЧЕННОЙ СИЛЫ

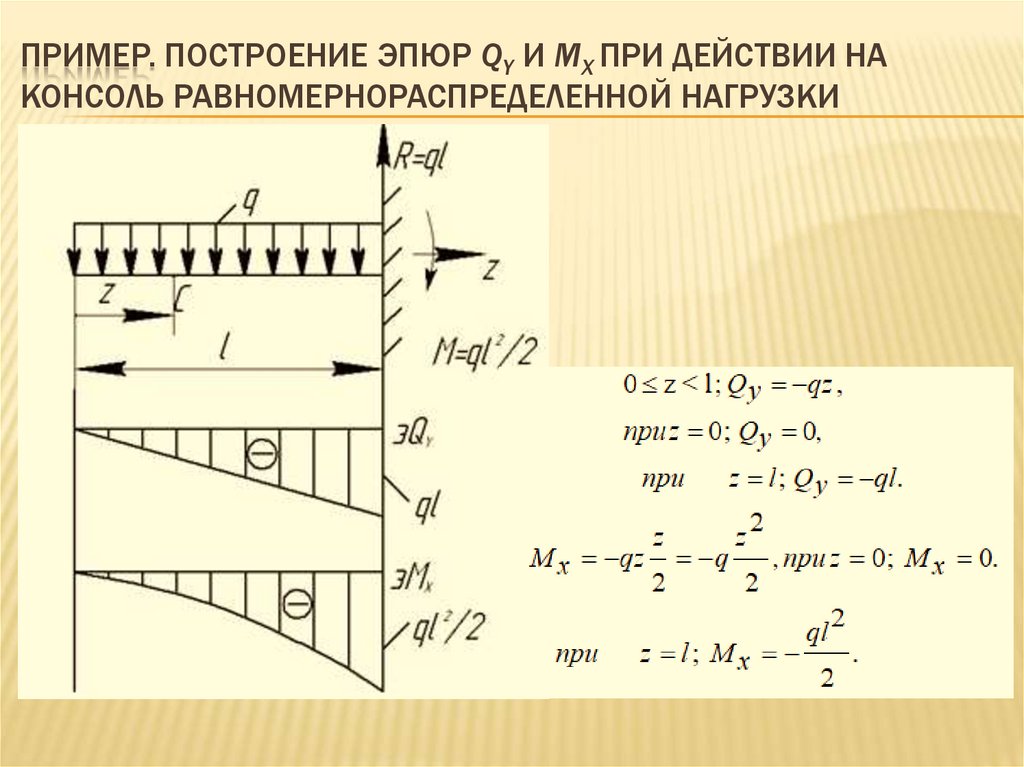
12. Пример. Построение эпюр Qy и Mx при действии на консоль Равномернораспределенной нагрузки

ПРИМЕР. ПОСТРОЕНИЕ ЭПЮР QY И MX ПРИ ДЕЙСТВИИ НА
КОНСОЛЬ РАВНОМЕРНОРАСПРЕДЕЛЕННОЙ НАГРУЗКИ

13. Пример. Построение эпюр Qy и Mx при действии на однопролетную балку сосредоточенной силы

ПРИМЕР. ПОСТРОЕНИЕ ЭПЮР QY И MX ПРИ ДЕЙСТВИИ НА
ОДНОПРОЛЕТНУЮ БАЛКУ СОСРЕДОТОЧЕННОЙ СИЛЫ

14. Пример. Построение эпюр Qy и Mx при действии на однопролетную балку распределенной нагрузки

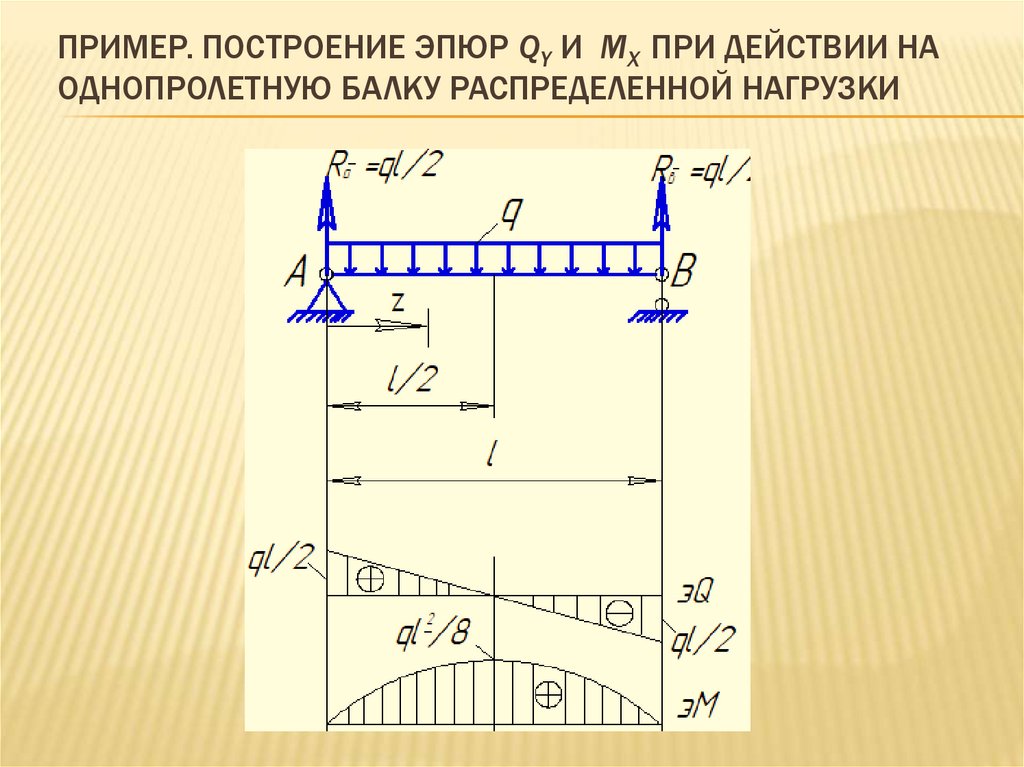
ПРИМЕР. ПОСТРОЕНИЕ ЭПЮР QY И MX ПРИ ДЕЙСТВИИ НА
ОДНОПРОЛЕТНУЮ БАЛКУ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ

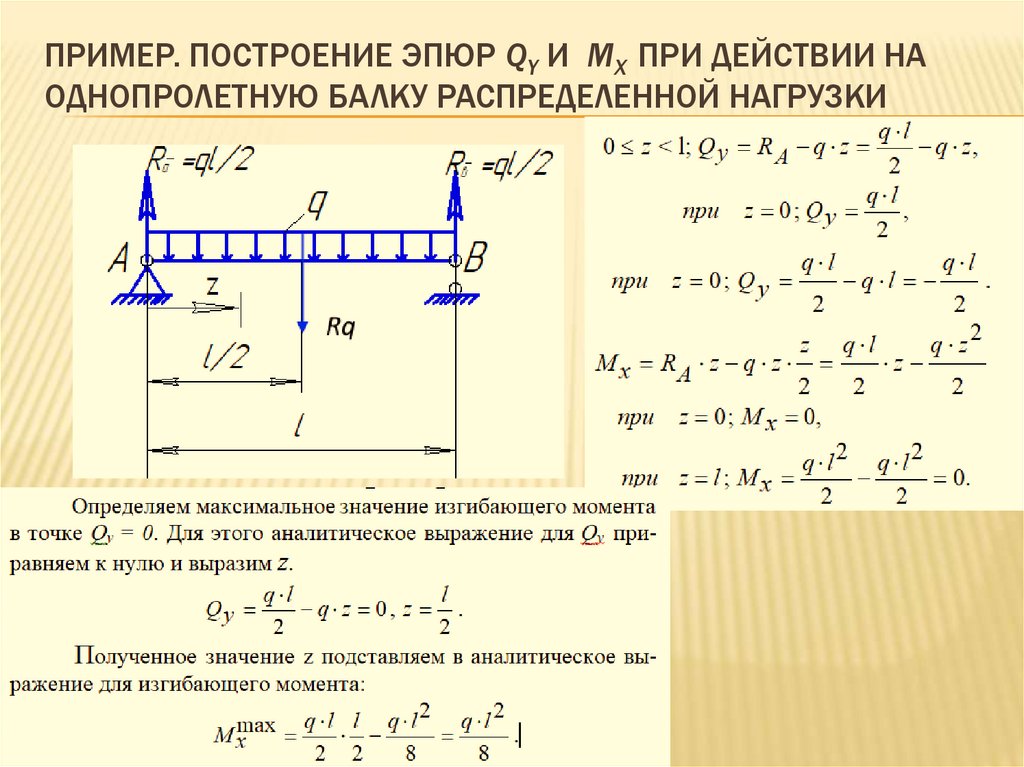
15. Пример. Построение эпюр Qy и Mx при действии на однопролетную балку распределенной нагрузки

ПРИМЕР. ПОСТРОЕНИЕ ЭПЮР QY И MX ПРИ ДЕЙСТВИИ НА
ОДНОПРОЛЕТНУЮ БАЛКУ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ

16. Пример. Построение эпюр Qy и Mx при действии на однопролетную балку распределенной нагрузки

ПРИМЕР. ПОСТРОЕНИЕ ЭПЮР QY И MX ПРИ ДЕЙСТВИИ НА
ОДНОПРОЛЕТНУЮ БАЛКУ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ

17. Проверка правильности построения эпюр Qу и МХ

ПРОВЕРКА ПРАВИЛЬНОСТИ ПОСТРОЕНИЯ
ЭПЮР QУ И МХ
1. В точке приложения сосредоточенной силы на эпюре Qу
будет скачок на величину этой силы.
2. В точке приложения сосредоточенного момента на эпюре МХ
будет скачок на величину этого момента.
3. Если на участке действуют только сосредоточенные силы, то
эпюра Qу очерчивается прямой линией параллельной оси, а
эпюра МХ прямой наклонной линией.
4. Если на участке действует равномерно распределенная
нагрузка, то эпюра QУ очерчивается прямой наклонной
линией, а эпюра МХ – параболой, выпуклостью навстречу
действия силы.
5. На участке, где Qу > 0, МХ – функция возрастающая, QУ<0, МХ
– функция убывающая. В точке Qу = 0, МХ принимает
экстремальное значение.