Похожие презентации:
Плоский изгиб. Расчет на прочность
1.
ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»Инженерно-технический институт
Кафедра прикладной механики
Лекции
по дисциплине «Техническая механика»
270800 - Строительство
2. Плоский изгиб Расчет на прочность
3.
Общие понятия и определенияИзгиб – деформация, при
которой под
действием внешних сил ось стержня изменяет
свою кривизну.
Стержень, работающий на
изгиб, называется балкой.
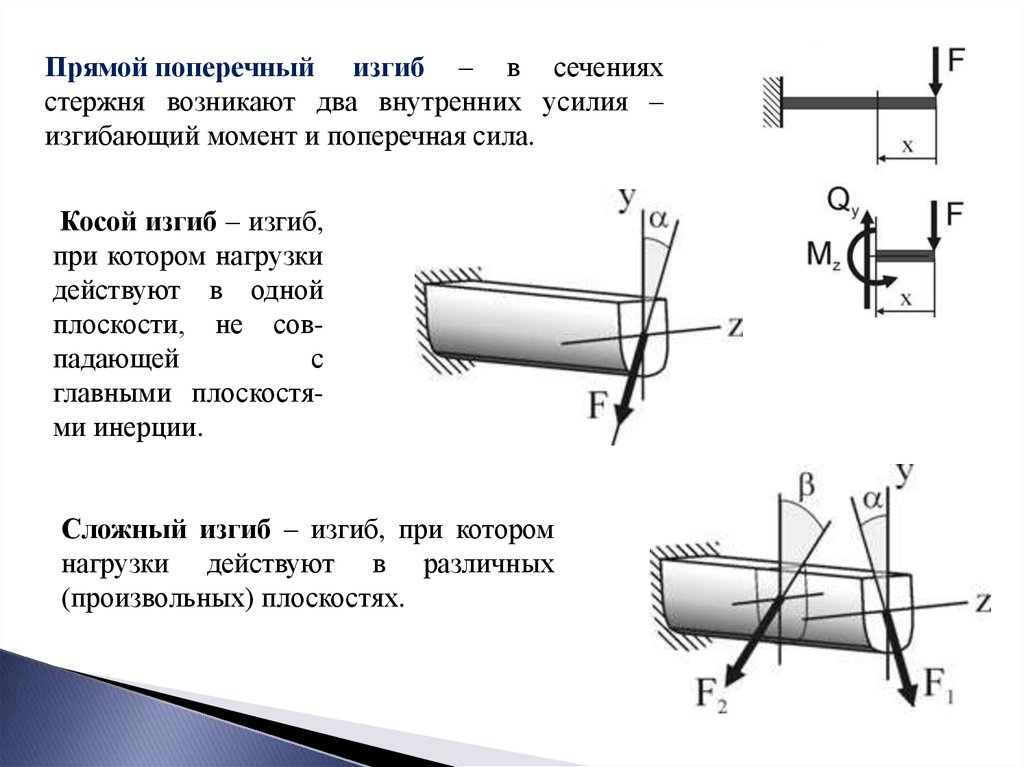
Различают изгиб плоский (чистый, прямой поперечный),
косой и сложный.
Плоский изгиб – изгиб, при котором все усилия, изгибающие балку, лежат
в одной из плоскостей симметрии балки (в одной из главных плоскостей).
Чистый изгиб – в сечениях
стержня возникает только –
изгибающий момент.
4.
Прямой поперечный изгиб – в сеченияхстержня возникают два внутренних усилия –
изгибающий момент и поперечная сила.
Косой изгиб – изгиб,
при котором нагрузки
действуют в одной
плоскости, не совпадающей
с
главными плоскостями инерции.
Сложный изгиб – изгиб, при котором
нагрузки действуют в различных
(произвольных) плоскостях.
5.
Плоский изгиб балок симметричного поперечного сечения1) Поперечное сечение балки должно иметь хотя бы одну ось симметрии;
2) Внешние силы направлены перпендикулярно к оси стержня и лежат в
плоскости, проходящей через ось симметрии, при этом деформированная ось
балки представляет плоскую кривую;
3) При этом в поперечном сечении бруса будут возникать изгибающий
момент – Мx и поперечная сила – Qy, действующие в той же плоскости
симметрии балки, продольные силы равны нулю (N=0).
6.
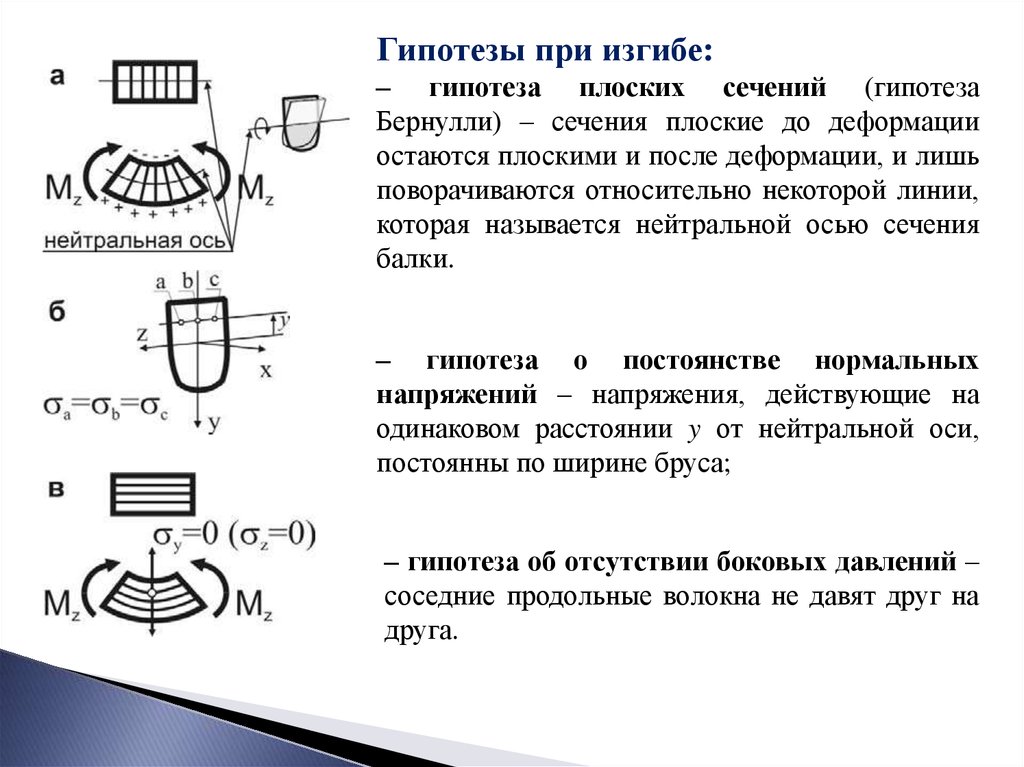
Гипотезы при изгибе:– гипотеза плоских сечений (гипотеза
Бернулли) – сечения плоские до деформации
остаются плоскими и после деформации, и лишь
поворачиваются относительно некоторой линии,
которая называется нейтральной осью сечения
балки.
– гипотеза о постоянстве нормальных
напряжений – напряжения, действующие на
одинаковом расстоянии y от нейтральной оси,
постоянны по ширине бруса;
– гипотеза об отсутствии боковых давлений –
соседние продольные волокна не давят друг на
друга.
7.
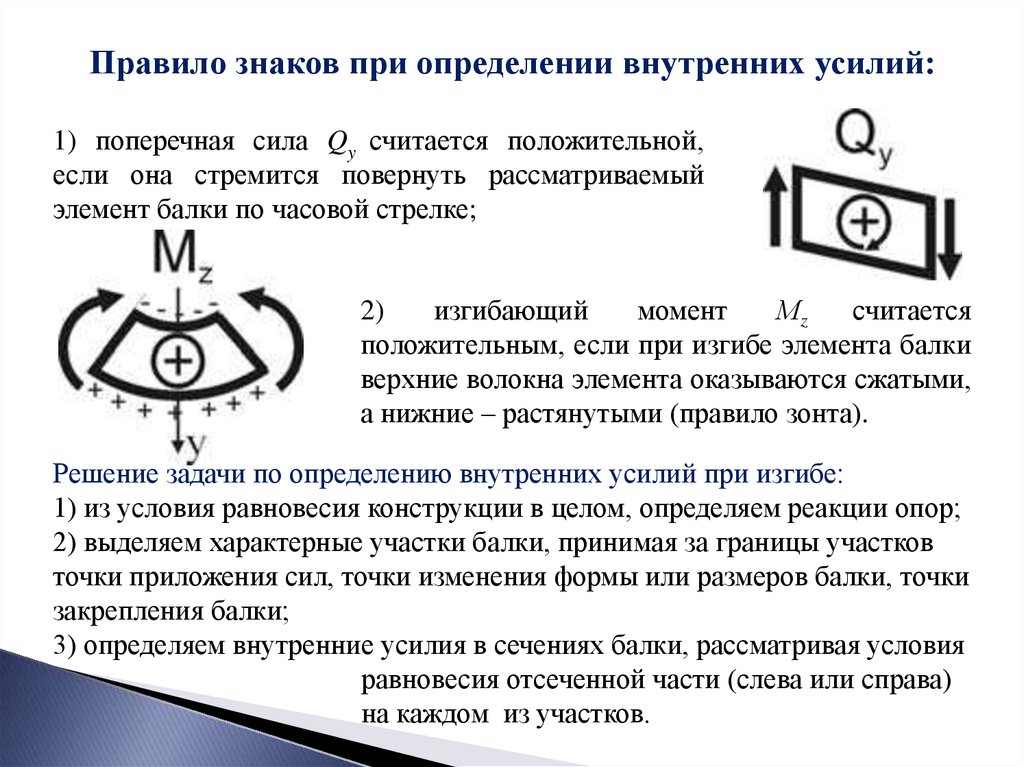
Правило знаков при определении внутренних усилий:1) поперечная сила Qy считается положительной,
если она стремится повернуть рассматриваемый
элемент балки по часовой стрелке;
2)
изгибающий
момент
Мz
считается
положительным, если при изгибе элемента балки
верхние волокна элемента оказываются сжатыми,
а нижние – растянутыми (правило зонта).
Решение задачи по определению внутренних усилий при изгибе:
1) из условия равновесия конструкции в целом, определяем реакции опор;
2) выделяем характерные участки балки, принимая за границы участков
точки приложения сил, точки изменения формы или размеров балки, точки
закрепления балки;
3) определяем внутренние усилия в сечениях балки, рассматривая условия
равновесия отсеченной части (слева или справа)
на каждом из участков.
8.
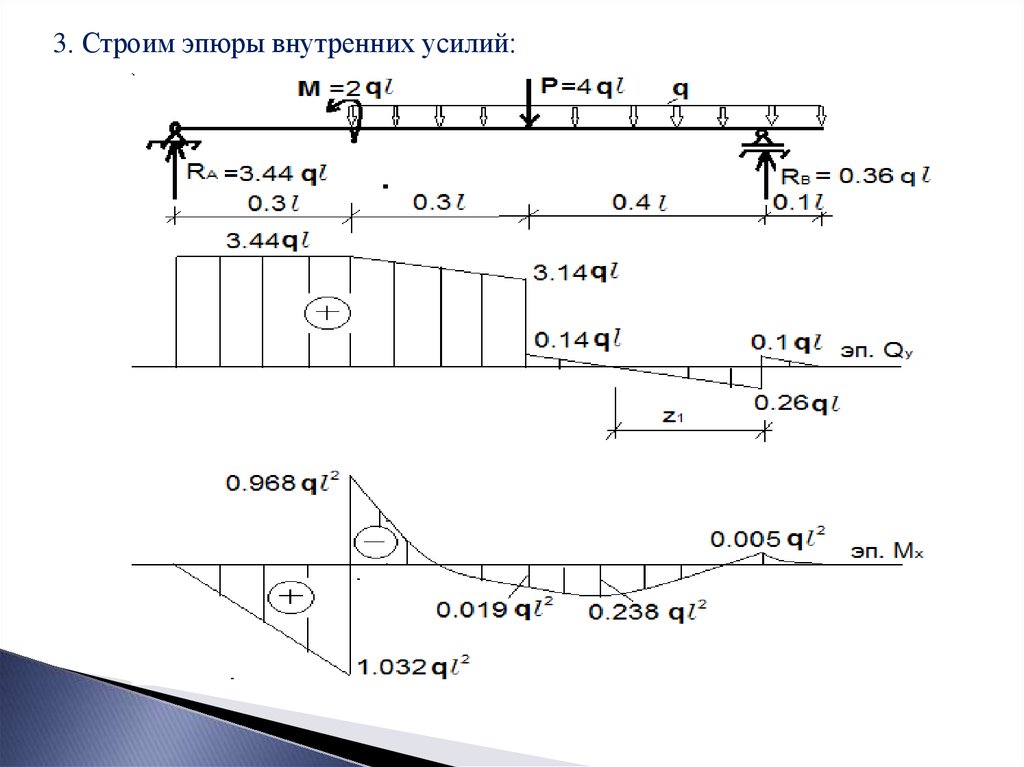
Пример построения эпюры внутренних усилий поперечных сил и изгибающих моментов1. Определяем опорные реакции:
9.
2. Определяем внутренние усилия:1-й участок: 0 ≤ z ≤ 0,3l
При
2-й участок: 0 ≤ z ≤ 0,3l
z=0,
z=0.3
Mx=0,
Mx=1.032ql
10.
3-й участок: 0 ≤ z ≤ 0,4lПоложение точки перехода эпюры
определяем из:
4-й участок: 0 ≤ z ≤ 0,1l
Qy
через ноль (особая
y Qy q z 0
z2
mo M x q
0
2
точка)
Q y q z / 00,1l / 00,1q l
z2
M x q
/ 00,1l / 0
0.005ql2
2
11.
3. Строим эпюры внутренних усилий:12.
Дифференциальные зависимостимежду интенсивностью внешней нагрузки q(Z),
поперечной силой Qy и изгибающим моментом Мx
a)
б)
q(z)
q(z)
Мx
z
Из условия
зависимости:
dz
равновесия
Qy
элемента,
d 2 M X dQy
q( z )
2
dz
dz
М x+dМ x
dz
получаем
Q y +dQ y
дифференциальные
dQY
q(Z )
dz
d 2M X
q( Z )
2
dZ
dM x
Qy
dz
Дифференциальные зависимости
Д.И.Журавского при изгибе
13.
Правила проверки правильностипостроенных эпюр Qy и Мx
Так как первая производная
от функции есть тангенс угла
наклона касательной к графику
рассматриваемой функции, то
эпюра Qy показывает изменение
тангенса
угла
наклона
касательной к эпюре Мx.
•если на участке эпюра Qy положительная, то эпюра Мx возрастает;
•если на участке эпюра Qy отрицательная, то эпюра Мx убывает;
•если на участке нет распределенной нагрузки q(Z)=0, то эпюра Qy имеет
постоянное значение, а эпюра Мx изменяется по линейному закону;
•если на участке балки действует равномерно распределенная нагрузка
q(Z)=q, то эпюра Qy изменяется по линейному закону, а эпюра Мx –
квадратная функция;
14.
•если на участке эпюра Qy переходит через нуль, то эпюра Мx в этомсечении имеет экстремальное значение. При этом, если эпюра Qy переходит
от положительного к отрицательному значению, то эпюра Mx имеет
максимальное значение, если от отрицательного к положительному
значению, то эпюра Mx имеет минимальное значение;
- так как вторая производная от функции изгибающего момента имеет
d 2M X
отрицательную величину
q( Z )
dZ 2
то выпуклость эпюры Мx направлена по направлению распределенной
нагрузки (правило «паруса»);
•в том сечении, где действует сосредоточенная сила, эпюра Qy имеет
скачок, равный по величине и по направлению силе P, а эпюра Mx имеет
излом по направлению силы;
•в том сечении, где приложен сосредоточенный момент М, эпюра Mx имеет
скачок, равный по величине и по направлению момента М, а эпюра Qy не
меняется;
15.
•на защемленном конце балки эпюра Qy равна величине опорной реакции,а эпюра Mx опорному моменту;
•на шарнирной концевой опоре эпюра Qy равна опорной реакции, а эпюра
Mx равна нулю, если на опоре не приложен сосредоточенный момент;
•на свободном конце консольной балки эпюра Qy равна нулю, если
отсутствует сосредоточенная сила, а эпюра Mx равна нулю, если нет
сосредоточенного момента;
•на промежуточной опоре эпюра Qy имеет скачок, равный по величине и
по направлению опорной реакции, а эпюра Mx имеет излом по
направлению опорной реакции;
•в промежуточном шарнирном соединении эпюра Mx равна нулю, если нет
сосредоточенного момента, а эпюра Qy равна внутренним усилиям в
шарнире.
•на участке, где эпюра поперечных сил Qy равна нулю, а эпюра
изгибающих моментов постоянная балка испытывает деформацию чистого
изгиба.
16.
Простейшие балки: реакции опор и эпюры Qy и Мx17.
Определение нормальных напряжений в балкепри чистом изгибе
Если в пределах рассматриваемого участка
балки действуют только изгибающие моменты,
а поперечные силы равны нулю, балка на этом
участке испытывает деформацию чистого
изгиба.
Рассматривая равновесие
балки получим:
вырезанного
элемента
18.
Для получения функции распределениянормальных напряжений по поперечному
сечению балки рассмотрим деформированную
схему бесконечно малого элемента длиной dz.
Волокна А-В длиной dz при деформировании
принимают положение дуги А1-В1 длиной
Относительное линейное удлинение волокна А-В равно
19.
Поставляя значение напряжения в уравнениях равновесия получаем:отсюда видно, что статической момент инерции относительно оси х равен
нулю
, следовательно ось х проходит через центр тяжести поперечного сечения балки.
отсюда видно, что центробежный момент инерции относительно осей x, y
равен нулю
, следовательно оси х и y являются главными осями
инерции поперечного сечения балки.
отсюда имеем:
MX y
IX
20.
Из формулы видно, что нормальные напряжения по высоте сечениябалки меняются линейно и наибольших значений достигают в крайних
верхних и нижних волокнах:
M X ymax / min
max / min
следовательно:
IX
Wx
y max / min
MX
WX
Осевой момент сопротивления сечения балки равен
IX
W
ymax
'
x
IX
W
ymin
"
x
max/ min
IX
21.
Условие прочности балкис сечением с двумя осями симметрии:
max
.
M xmax
min
Wx
Типовые задачи:
1.Проверочный расчет:
max
M xmax
min
Wx
2.Проектировочный (конструкционный) расчет (подбор сечения):
W
тр
X
MX
3.Проектный расчет (несущая способность):
M Xдоп WX
22.
Плоский поперечный изгиб балкиПри плоском изгибе балки, в общем случае, в поперечном сечении балки
возникают поперечные силы Qу и изгибающие моменты Mx, следовательно в
этих сечениях будут действовать нормальные и касательные напряжения.
эп.σ
Если отношение высоты балки к её длине
тогда нормальные напряжения могут с достаточной точностью могут быть
определены по формуле полученной при чистом изгибе
MX y
IX
23.
Условие прочности балки по нормальным напряжениямmax
.
M xmax
min
Wx
Типовые задачи:
1.Проверочный расчет:
max
M xmax
min
Wx
2.Проектировочный (конструкционный) расчет (подбор сечения):
W
тр
X
MX
3.Проектный расчет (несущая способность):
M Xдоп WX
24.
Определение касательных напряжений в сечении балкиКогда в балке действуют и изгибающий момент и поперечная сила, в
сечении балки возникают и нормальные – σ и касательные – τ напряжения.
a)
б)
Мx
М
z
z
М
dA
x
Qy
Aотс
x
dA
y
y
dA
Aотс
( d ) dA
Aотс
Z
Aотс
dA
( d ) dA by dz 0
Aотс
25.
Отсюда получаемAотс
Aотс
dM x y
dA
dz I x by
max
Qy
I x by
Qy S
заменяем
заменяем
y dA
Aотс
пол
x
I x by
d dA
by dz
Qy S xотс
I x by
dM x y
d
Ix
dM x
Qy
dz
- формула Журавского
S xотс – статический момент площади
отсеченной
части
сечения
относительно нейтральной оси X;
S xпол – статический момент половины
площади сечения
нейтральной оси X.
относительно
26.
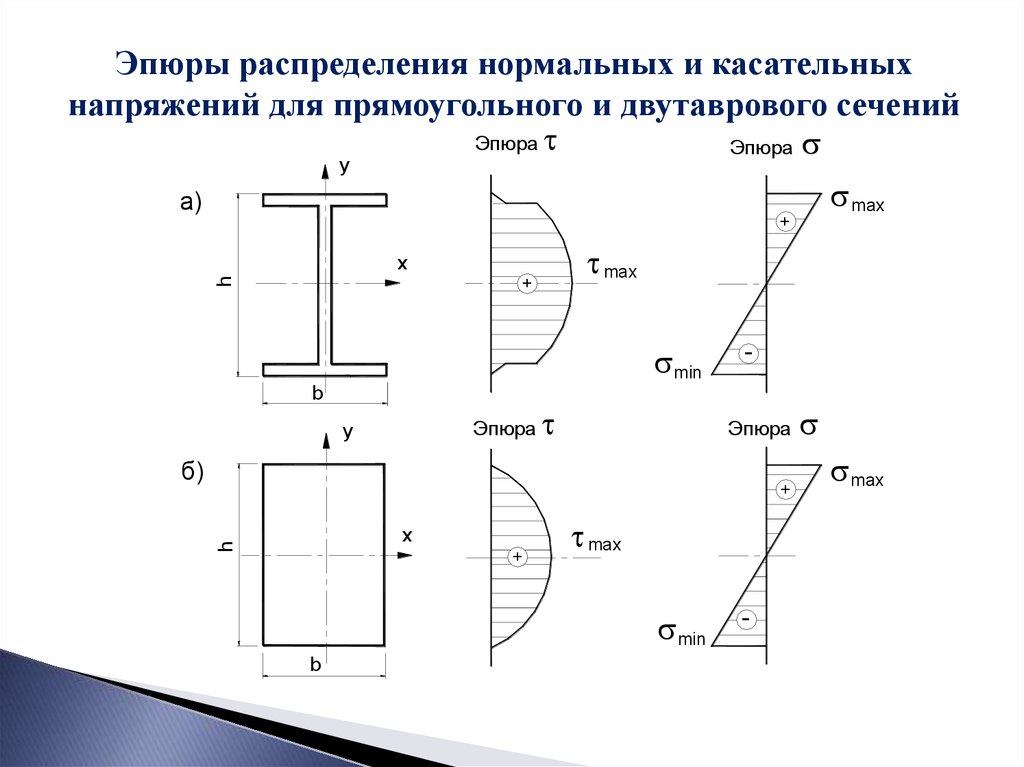
Эпюры распределения нормальных и касательныхнапряжений для прямоугольного и двутаврового сечений
Эпюра
y
Эпюра
max
+
a)
+
h
x
max
min
b
Эпюра
y
Эпюра
+
б)
+
h
x
max
min
b
-
max
27.
Полная проверка прочностиОпасные сечения и опасные точки
Для проверки на прочность при изгибе
строят эпюры изменения внутренних
усилий (Mх, Qy) по ее длине и
определяют опасные сечения балки. При
полной проверке прочности таких
сечений будет, как минимум, три (иногда
они совпадают):
1) сечение, в котором изгибающий
момент Mz достигает своего максимального по модулю значения, – именно по
этому сечению подбирают сечение всей
балки;
2) сечение, в котором поперечная сила Qy
достигает своего максимального по
модулю значения;
3) сечение, в котором и изгибающий
момент Mz и поперечная сила Qy достигают по модулю достаточно больших
величин.
В каждом из опасных сечений
необходимо,
построив
эпюры
напряжений, найти опасные точки
(проверка прочности проводится для
каждой из них), которых также будет,
как минимум, три:
1) точка, в которой нормальные
напряжения σx достигают своего максимального значения, – то есть точка на
наружной поверхности балки наиболее
удаленная от нейтральной оси сечения;
2) точка, в которой касательные
напряжения τxy достигают своего максимального значения, – точка, лежащая на
нейтральной оси сечения;
3) точка, в которой и нормальные
напряжения σx и касательные напряжения τxy достигают достаточно больших
величин (эта проверка имеет смысл для
сечений типа тавра или двутавра, где
ширина резко изменяет свое значение).
28.
Проверка прочности элементов, работающих на прямойпоперечный изгиб по различным теориям прочности
При плоском поперечном изгибе балки в том сечении, где одновременно
действуют большие значения изгибающего момента и поперечной силы,
главные напряжения в особых точках сечения балки, где одновременно
возникают достаточно большие значения и , будут иметь большие
значения. Тогда возникает необходимость проверки прочности материала
балки по различным теориям.
В любой точке сечения балки главные напряжения будут определены по:
1
1
2 4 2
2 2
1
3
2 4 2
2 2
где
– главные растягивающие напряжения,
– главные сжимающие напряжения,
Q y S xотс
Mx y
,
.
Ix
I x by
Направления главных
напряжений определяются:
tg 2 0
2
,
29.
а)A
2
k
1
:
RA=20 кН
б)
Нормальные напряжения
P=60 кН
1
4м
2м
20
B
2
RB=40 кН
Эпюра Q y (кН)
20
+
40
Mx y
Ix
Касательные напряжения
Q y S xотс
40
Эпюра М x (кНм)
в)
+
80
I x ву
Главные напряжения в окрестности
соответствующих точек:
1,3
2
1
2 4 2
2
эп.
эп
30.
Проверка прочности балкипо третьей и четвертой теориям:
По теории наибольших касательных напряжений:
экв 2 4 2
3
По теории Мора:
где
p
M
экв 3
1 p
1 p
2 4 2 ,
2
2
p
сж
По энергетической теории:
экв 3
2
4
2

























 Механика
Механика








