Лекция SVM часть 3

1. Машинное обучение и нейросетевые технологии

2.

Кол-во
Кол-во
аудиторных часов лекционных часов
92
50
Кол-во часов
практических
занятий
42
Формы
промежуточной
аттестации
Контрольная,
экзамен

3. Содержание

Линейная машина опорных векторов
Алгоритм двойственного обучения
Опорный вектор
Функция потерь шарнира
Нелинейная задача классификации
Функция ядра
Применение метода ядра в SVM
Функция полиномиального ядра, ядра Гаусса
Функция ядра строки
Нелинейный классификатор опорных векторов
Последовательный алгоритм минимальной оптимизации
Метод решения квадратичного программирования с двумя переменными

4. Нелинейный SVM

Метод ядра позволяет применить обучение линейной классификации к
нелинейным задачам классификации. Расширение линейного SVM до нелинейного
SVM требует замены внутреннего произведения в линейном SVM на функцию ядра.
Определение. (Нелинейная машина опорных векторов) Функция принятия решения
для задачи классификации, полученная из обучающего набора нелинейной
классификации и обученная с помощью функции ядра и мягкого максимизирования
границы или выпуклого квадратичного программирования
называется нелинейной машиной опорных векторов, а K(x, xi) является
положительно определенной функцией ядра.

5. Нелинейный алгоритм опорных векторов

Алгоритм
Входные данные: обучающий набор данных T = {(x1, y1), (x2, y2), · · · , (xN,
yN)}, где xi ∈X = Rn, yi ∈ Y = {− 1, + 1}, i = 1, 2, …, N.
Выходные данные: функция принятия решения для классификации.
1)
Необходимо выбрать ‘правильную’ функцию ядра K(x, z) и параметр C,
построим и решим задачу оптимизации
Решение обозначим как α∗ = (α1∗, α2∗, · · · , αN*)T .

6. Нелинейный классификатор опорных векторов

2) Выберем положительный компонент α∗, 0 < αj*< C, и вычислим
3) Построим функцию решения
Если K(x, z) — положительно определенная функция ядра, задача шага (1) —
это выпуклая задача квадратичного программирования с существующим
решением.

7. Последовательный алгоритм минимальной оптимизации

Рассмотрим задачу реализации обучения SVM. Существует множество алгоритмов
оптимизации для решения этой задачи. Однако, когда размер обучающей выборки велик,
эти алгоритмы часто становятся настолько неэффективными, что их невозможно
использовать. Поэтому эффективная реализация обучения SVM становится важной
проблемой. В настоящее время предложено много быстрых алгоритмов. Остановимся на
алгоритме последовательной минимальной оптимизации (SMO), предложенный Платтом в
1998 году. Алгоритм SMO решает двойственную задачу выпуклого квадратичного
программирования следующим образом (*):

8. Последовательный алгоритм минимальной оптимизации

Здесь переменные — это множители Лагранжа, а одна единственная переменная αi
соответствует одной точке выборки (xi, xj) . Общее количество переменных равно размеру
обучающей выборки N.
Алгоритм SMO — это эвристический алгоритм, основанный на идее, что решение задачи
оптимизации получается, если решения всех переменных удовлетворяют условиям Каруша–
Куна–Таккера (KKT) этой задачи оптимизации. Потому, что условия KKT являются
необходимыми и достаточными условиями для этой задачи оптимизации.
В противном случае выберите две переменные, зафиксируйте другие переменные и
постройте задачу квадратичного программирования для этих двух переменных. Решение задачи
квадратичного программирования относительно этих двух переменных должно быть ближе к
решению исходной задачи квадратичного программирования, поскольку это уменьшит
значение целевой функции исходной задачи квадратичного программирования.

9. Последовательный алгоритм минимальной оптимизации

Подзадачу можно решить аналитическими методами, что может значительно повысить
скорость вычислений всего алгоритма. Подзадача имеет две переменные, одна из которых
больше всего нарушает условие KKT, а другая определяется автоматически
ограничениями. Алгоритм SMO непрерывно разлагает исходную задачу на подзадачи и
решает их, чтобы решить исходную. Только одна из двух переменных подзадачи является
свободной переменной. Предположим, что α1, α2 — две переменные, а α3,α4,…, αN
фиксированы, тогда из равенства
мы знаем, что
Если α2 определено, то и α1 также определено. Таким образом, обе переменные
обновляются одновременно в подзадаче. Весь алгоритм SMO состоит из двух частей:
аналитического метода решения квадратичного программирования с двумя переменными и
эвристического метода выбора переменных.

10. Решение задачи с двумя переменными

Предположим, что выбраны две переменные α1, α2, а другие переменные αi
(i=3,4,…,N) фиксированы. Тогда подзадача задачи оптимизации SMO ​(*) может быть
записана (**):
где Kij = K(xi, xj), i, j = 1, 2,…, N, ς — константа, а постоянные члены без α1, α2
опущены в целевой функции minW(α1, α2).

11. Решение задачи с двумя переменными

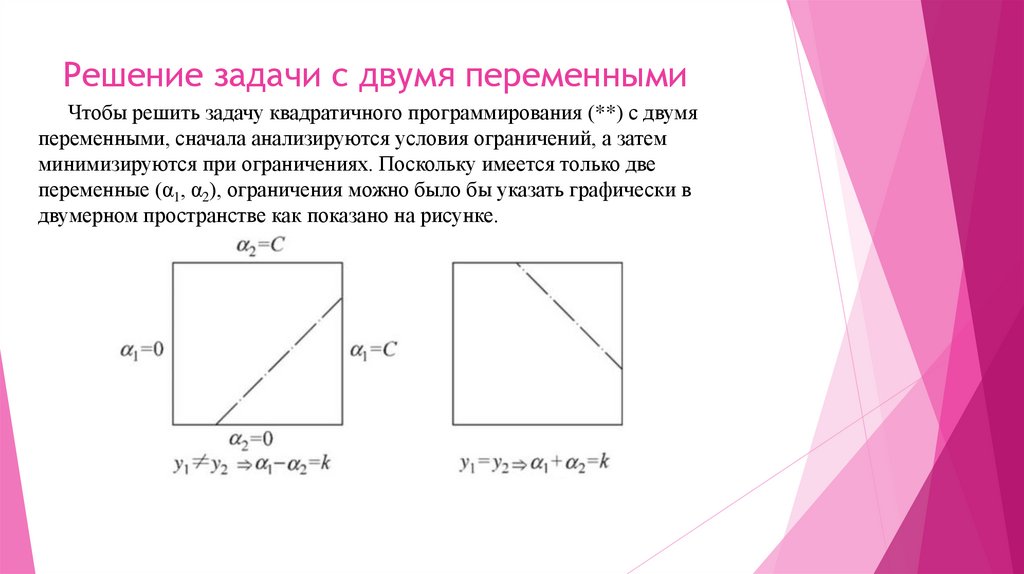
Чтобы решить задачу квадратичного программирования (**) с двумя
переменными, сначала анализируются условия ограничений, а затем
минимизируются при ограничениях. Поскольку имеется только две
переменные (α1, α2), ограничения можно было бы указать графически в
двумерном пространстве как показано на рисунке.

12. Решение задачи с двумя переменными

Неравенство αi заставляет (α1, α2) находиться в поле [0, C] × [0, C], а
равенство для ς заставляет (α1, α2) находиться на прямой, параллельной
диагонали поля [0, C] × [0, C]. Таким образом, необходимо найти оптимальное
значение целевой функции на отрезке прямой, параллельном диагонали, что
делает задачу оптимизации двух переменных задачей одномерной
оптимизации. Тогда ее можно было бы рассматривать как задачу оптимизации
переменной α2.

13. Решение задачи с двумя переменными

Предположим, что начальное допустимое решение задач (**) — это