Похожие презентации:
Многочлены от одного переменного. Глава III, §1
1.
Многочленыот одного переменного.
Глава III, §1.
2. Многочлены.
Из курса алгебры основной школы, мы знаем чтосуществуют различные виды многочленов.
1. Одночлен: 2а³, 3a²b, 7…
2. Двучлен: 3х+4, 2а³ – 4с² …
3. Трёхчлен (включая квадратный трёхчлен): 3х+4b+c,
2x²+3x–7…
И так далее
Особое место
переменной.
занимают
многочлены
от
одной
3.
БУДЕМ ЗНАТЬ!!!4.
Многочлен от одной переменной.Определение
•Любой многочлен P(x), содержащий только переменную х и её натуральные
степени, можно записать в стандартном виде
P(x) = a0xn +a1xn – 1 +…+ an – 1 x + an
где a0,a1……an – 1 ,an – некоторые действительные числа.
•Если а0 0, то многочлен P(x) называют многочленом n – ой степени, член a0xn
старшим членом, an – свободным членом.
•Если P(x) = а0, где а0 0, называют многочленом нулевой степени. Число 0
называют нулевым многочленом.
5.
БУДЕМ ЗНАТЬ!!!6.
Чтобы показать, что степень многочленаравна n, пишут (см индекс):
Рп ( х) а0 х а1 х
п
п 1
... ап 1 х ап
… – п степени
7.
УСТНО ПОВТОРИМ ЗАДАНИЕ!!!8.
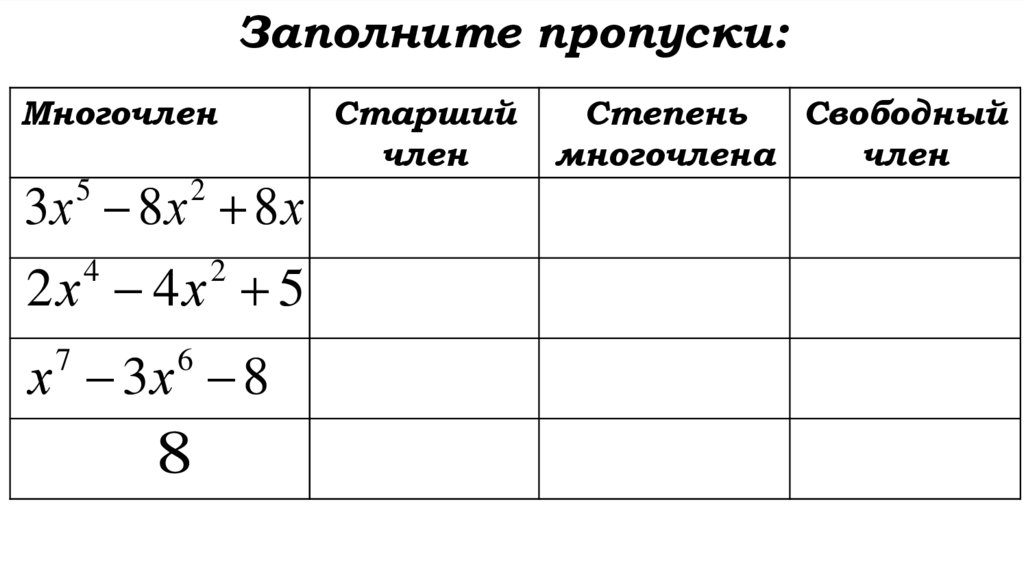
Заполните пропуски:Многочлен
3х 8 х 8 х
5
2
2х 4х 5
4
2
х 3х 8
7
6
8
Старший
член
Степень
Свободный
многочлена
член
9.
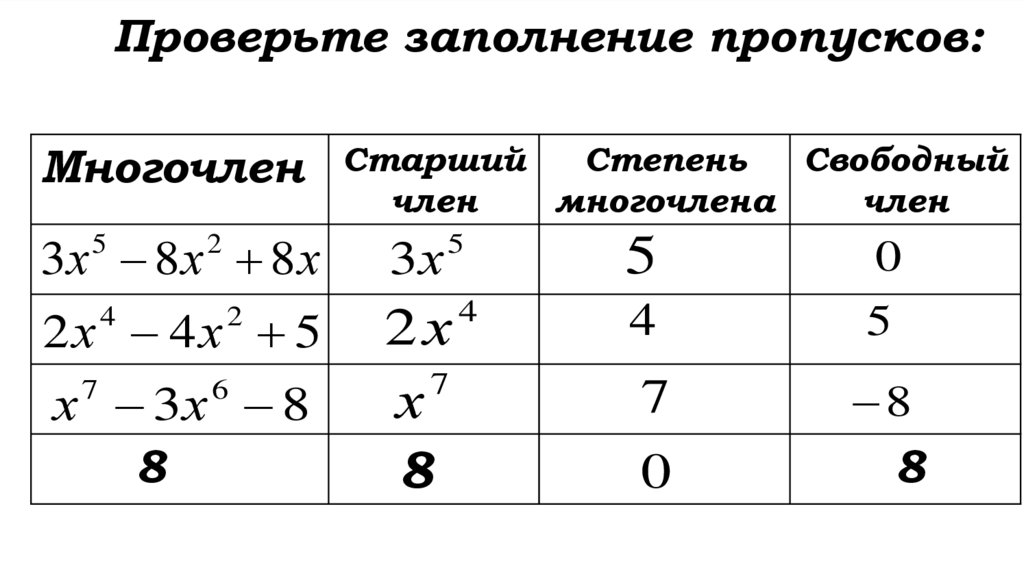
Проверьте заполнение пропусков:Многочлен
Старший
Степень
Свободный
член
многочлена
член
3х 8 х 8 х
3х
5
5
2х 4х 5
2х
7
х
8
4
0
5
7
8
0
8
5
4
2
2
х 7 3х 6 8
8
4
10.
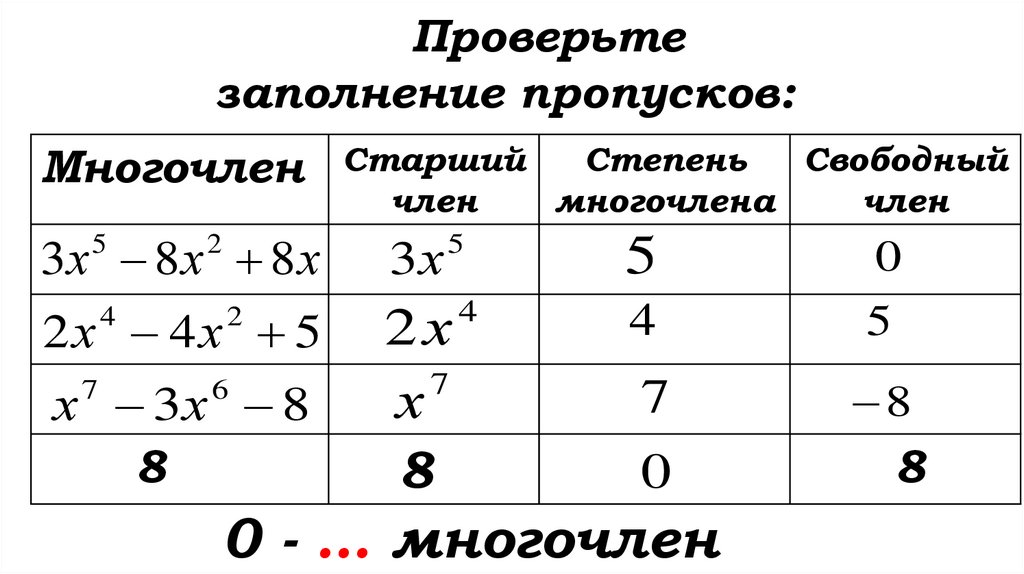
Проверьтезаполнение пропусков:
Многочлен
Старший
Степень
Свободный
член
многочлена
член
3х 8 х 8 х
3х
5
5
2х 4х 5
2х
7
х
8
4
0
5
7
8
0
8
5
4
2
2
х 7 3х 6 8
8
4
0 - … многочлен
11.
БУДЕМ ЗНАТЬ!!!12. Определение
Два многочлена Р(х) и S(х) тождественноравны, если равны их степени и равны
коэффициенты при одинаковых степенях
переменной в обоих многочленах.
13.
УСТНО ПОВТОРИМ ЗАДАНИЕ!!!14.
Укажите числа a,b и c многочленов,если они тождественно равны
а)3х 8 х 8 х ах bх cх
5
5
2
2
б ) х 3х 5х 8x 1 aх bх cх dx p
9
7
5
2
9
7
5
2
15.
1)2 х 4 х 5х 3 ( x 1)(2 x ax bx 2 x 3)5
2
4
3
2
Можно ли сразу назвать числа
a и b?
Что нужно сделать, чтобы
назвать числа
a и b?
16.
1)2 х 4 х 5х 3 ( x 1)(2 x ax bx 2 x 3)5
2
4
3
2
Сколько слагаемых получится в
правой части равенства после
умножения?
Выполняем умножение в правой
части равенства и приводим
подобные.
17.
1)2 х 4 х 5х 3 ( x 1)(2 x ax bx 2 x 3)5
2
4
3
2
( x 1)(2 x ax bx 2 x 3)
4
3
2
2 х ах bх 2 х 3x 2 x ax bx 2 x 3
5
4
3
2
4
3
2
Укажите подобные слагаемые
18.
1)2 х 4 х 5х 3 ( x 1)(2 x ax bx 2 x 3)5
2
4
3
2
( x 1)(2 x ax bx 2 x 3)
4
3
2
2 х ах bх 2 х 3x 2 x ax bx 2 x 3
5
4
3
2
4
3
2
19.
1)2 х 4 х 5х 3 ( x 1)(2 x ax bx 2 x 3)5
2
4
3
2
( x 1)( 2 x ax bx 2 x 3)
4
3
2
2 х ах bх 2 х 3x 2 x ax bx 2 x 3
5
4
3
2
4
3
2
2 х (а 2) х (b а) х (2 b) x 5х - 3
5
4
3
2
Назовите значения выделенных
выражений
20.
1)2 х 4 х 5 х 3 ( x 1)( 2 x ax bx 2 x 3)5
2
4
3
2
( x 1)( 2 x 4 ax 3 bx 2 2 x 3)
2 х 5 ах 4 bх 3 2 х 2 3 x 2 x 4 ax 3 bx 2 2 x 3
2 х 5 (а 2) х 4 (b а ) х 3 (2 b) x 2 5х - 3
а 2 0,
b а 0,
2 b 4
Найдите значения
а,b и с
21.
1)2 х 5 4 х 2 5 х 3 ( x 1)( 2 x 4 ax 3 bx 2 2 x 3)4
3
2
( x 1)( 2 x ax bx 2 x 3)
2 х ах bх 2 х 3 x 2 x ax bx 2 x 3
5
4
3
2
4
3
2
2 х (а 2) х (b а ) х (2 b) x 5х - 3
5
а 2 0,
b а 0,
2 b 4
4
3
2
а 2, b 2
Ответ : а 2, b 2
22. Свойства многочленов от одной переменной
Многочлены имеют много свойств,аналогичных свойствам целых чисел. Саму
запись многочлена в указанном виде можно
считать аналогом записи чисел в десят
системе счисления
Рп ( х) а0 х п а1 х п 1 ... ап 1 х ап
23. Свойства многочленов от одной переменной
Теорема 1.Степень произведения двух
многочленов равна сумме
степеней многочленов
множителей.
24.
УСТНО!!!25.
Степень произведения двухмногочленов равна:
а)Qk ( х) Рп ( х) М ... ( х)
б )Q3 ( х) Р4 ( х) М ... ( х)
в)Q5 ( х) Р1 ( х) М ... ( х)
г )Q3 ( х) Р0 ( х) М ... ( х)
Проверка
26.
Степень произведения двухмногочленов равна:
а)Qk ( х) Рп ( х) М k n ( х)
б )Q3 ( х) Р4 ( х) М 7 ( х)
в)Q5 ( х) Р1 ( х) М 6 ( х)
г )Q3 ( х) Р0 ( х) М 3 ( х)
27. Свойства многочленов от одной переменной
Теорема 2. (О делении многочленов уголком)28.
Выполните деление уголком1)( x 2 x 35) : ( х 7)
2
Выполняем деление уголком пошагово
29.
х 2 х 35 х 72
30.
х 2 х 35 х 72
х
31.
х 2 х 35 х 72
х ...
2
х
32.
х 2 2 х 35 х 72
х
х 7х
33.
х 2 2 х 35 х 72
х
х 7х
5х
34.
х 2 2 х 35 х 72
х
х 7х
5х 35
35.
х 2 2 х 35 х 72
х 7х
х 5
5х 35
36.
х 2 2 х 35 х 72
х 7х
х 5
5х 35
5х 35
0
x 2 x 35 ( х 7)( х 5)
2
Формула деления
37.
Определение (уточните этот факт втетради, обратив внимание на
индексы!!!)
38. Свойства многочленов от одной переменной
Теорема 3. (О делении многочленов уголком)АЛГОРИТМ! СМ НИЖЕ! ЗАПИШИ И
ВЫУЧИ!
39.
Чтобы разделить многочлен P(x) на многочлен Q(x)нужно:
1. Расположить делимое и делитель по убывающим
степеням х;
2. Разделить старший член делимого на старший член
делителя; полученный одночлен сделать первым
членом частного;
3. Первый член частного умножить на делитель; результат
вычесть из делимого; полученная разность является
первым остатком;
4. Чтобы получить следующий член частного, нужно с
первым остатком поступить так, как поступали с
делимым и делителем в пунктах 2 и 3.
40.
УСТНО РАЗБЕРЕМ РЕШЕНИЕЗАДАНИЯ!!!
41.
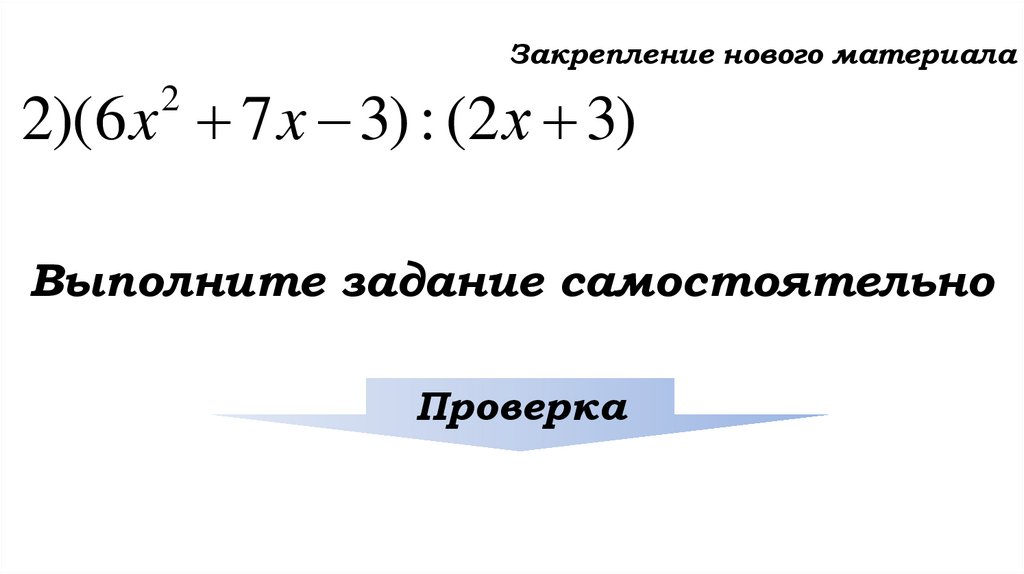
Закрепление нового материала2)(6 x 7 x 3) : (2 х 3)
2
Выполните задание самостоятельно
Проверка
42.
6 х 2 7 х 3 2х 33х 1
6х2 9х
2х 3
2х 3
0
делитель
6 x 7 x 3 (2 х 3)(3х 1)
2
делимое
частное
43.
Закрепление нового материала3)(6 x 11x 1) : (2 х 3х 1)
3
2
2
Поясните выполнение
деления
44.
6 х 11х 13
2
2 х 3х 1
2
45.
6 х 11х 13
2
2 х 3х 1
3х
2
46.
6 х 11х 13
6х
3
2
2 х 3х 1
3х
2
47.
6 х 11х 16 х3 9 х 2
3
2
2 х 3х 1
3х
2
48.
2 х 3х 16 х 11х 1
3
2
6 х 9 х 3 х 3х
3
2
2
49.
6 х 11х 1 2 х 3 х 13
2
6 х 9 х 3 х 3х
2
2 х 3х 1
3
2
2
50.
6 х 11х 1 2 х 3 х 13
2
6 х 9 х 3 х 3х 1
2
2 х 3х 1
3
2
2
51.
6 х 11х 1 2 х 3 х 13
2
6 х 9 х 3 х 3х 1
2
2 х 3х 1
2
2 х 3х 1
3
2
2
52.
6 х 11х 1 2 х 3 х 13
2
6 х 9 х 3 х 3х 1
2
2 х 3х 1
2
2 х 3х 1
0
3
2
2
6 x 3 11x 2 1 (2 х 2 3х 1) (3х 1)
Формула деления
53.
ВЫУЧИМ! ЗАПИШЕМ!!!(Формулировки свойств с
примерами)
54.
Изучение нового материалаСвойства делимости многочленов
55.
Изучение нового материалаСвойства делимости многочленов
56.
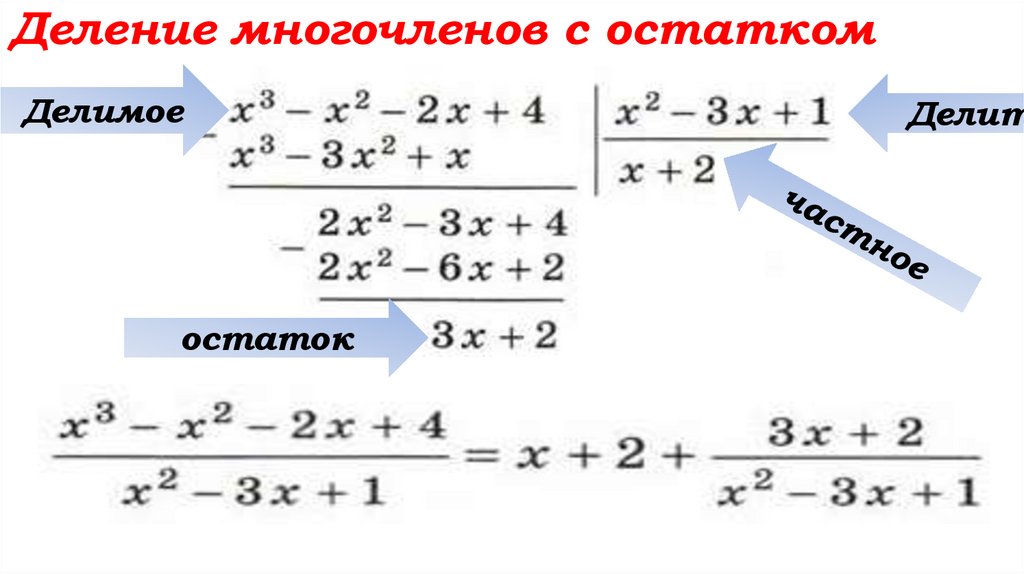
Пример : Разделить многочлен P(x) = 3x4 + 2x2 – 1 на многочленQ(x) = x2 + x.
3x4 + 0х3 + 2x2 + 0х – 1
3x4 + 3x3
– 3x3 + 2х2 + 0х – 1
– 3x3 – 3x2
x2 + x
3x2 – 3х + 5
5x2 + 0х – 1
2
5x +
5x – 5x – 1
Степень остатка – 5x – 1 меньше степени делителя x2 + x,
деление закончено.
Ответ: 3x2 – 3х + 5 частное, – 5x – 1 остаток.
57.
Деление многочленов c остатком58.
РАЗБЕРЕМ! ЗАПИШЕМ!!!59.
Деление многочленов c остаткомДелимое
остаток
Делит
60.
x x 2 х 4 ( х 3х 1) ( х 2) 3х 23
2
делимое
2
делитель частное
Формула деления с остатком
остаток













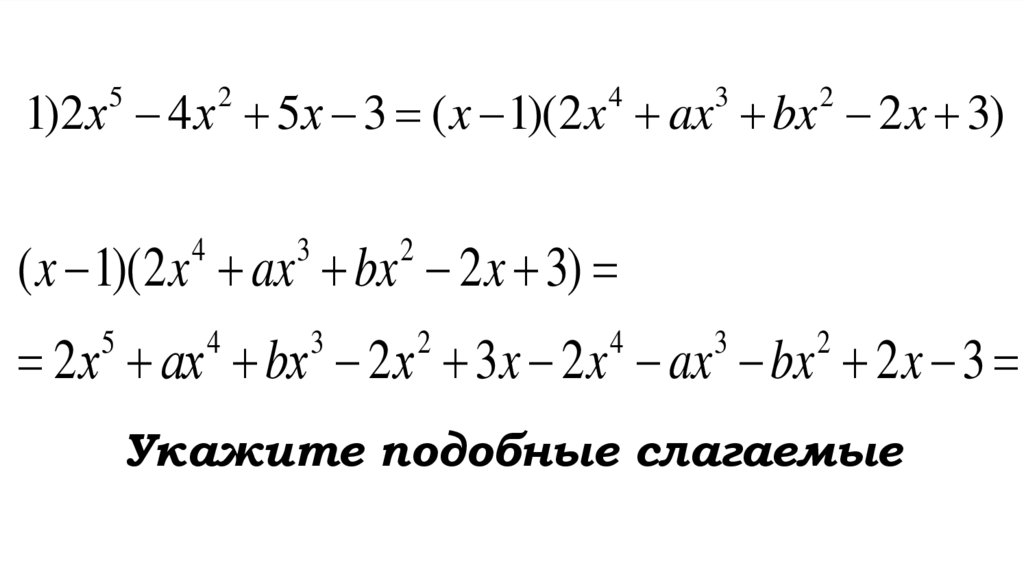
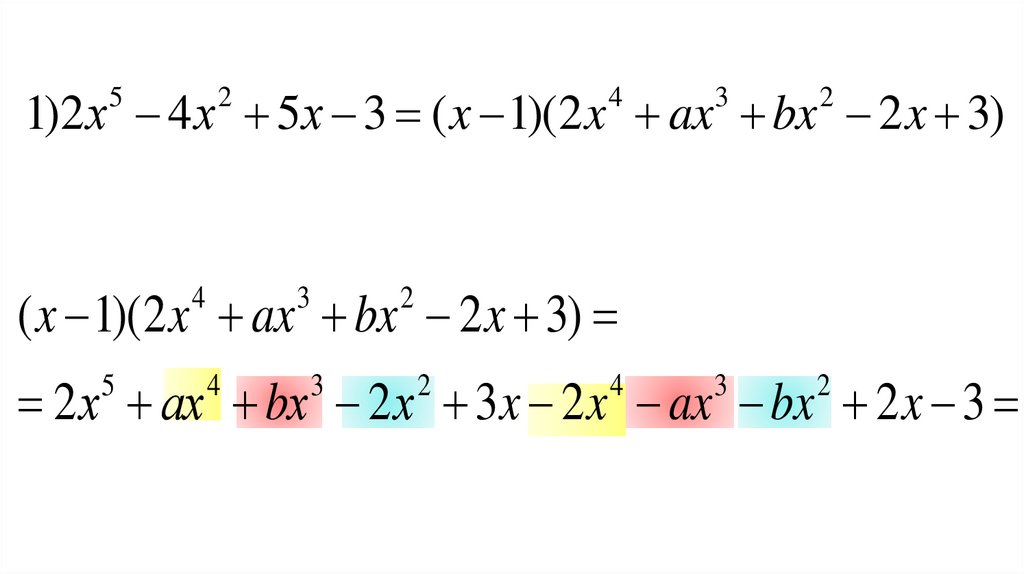


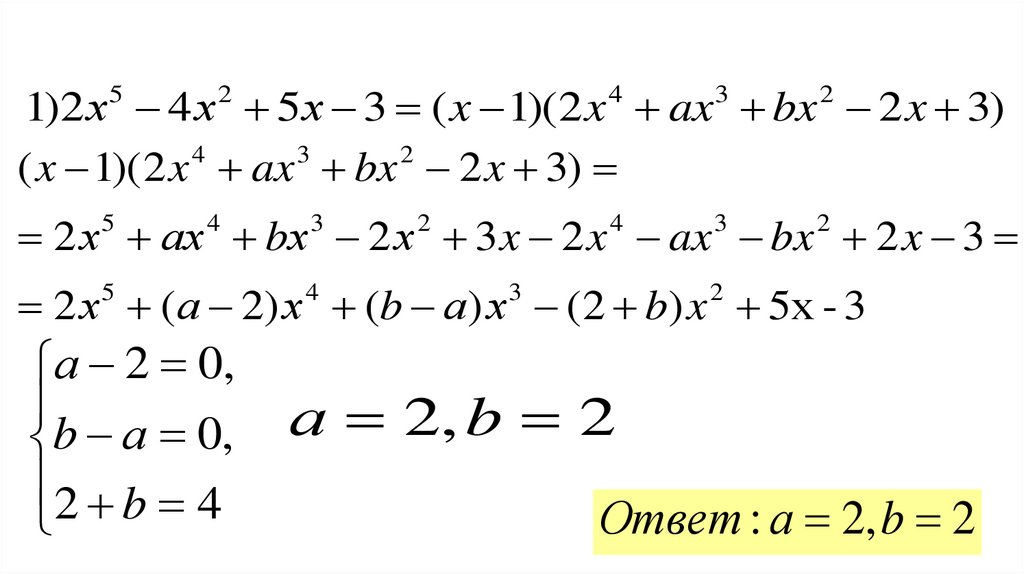







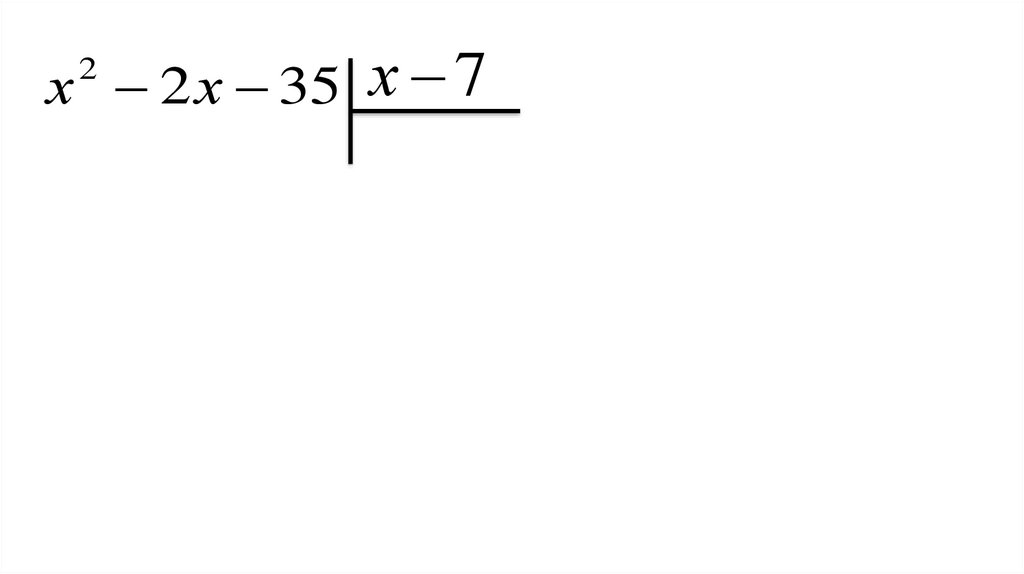
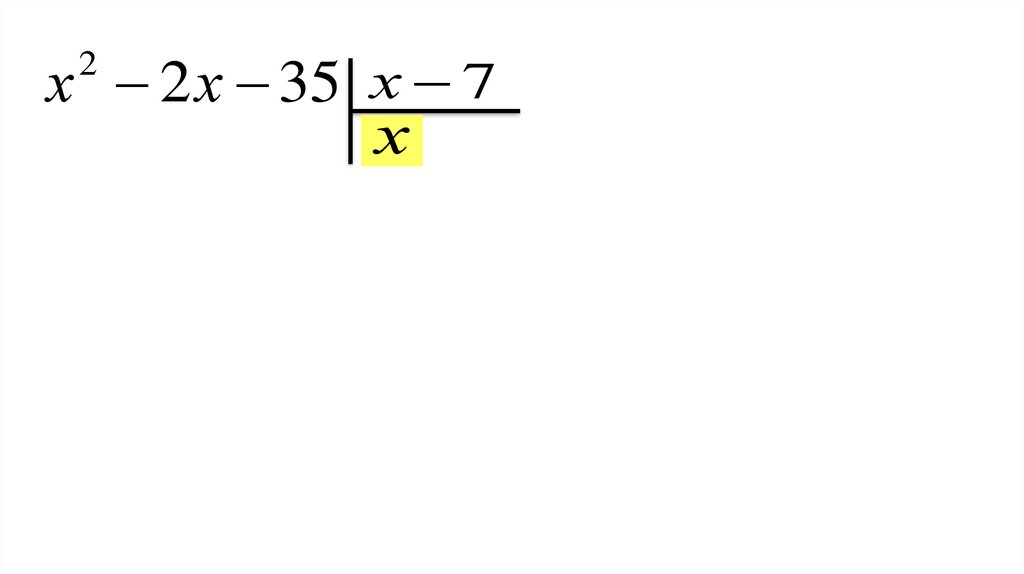
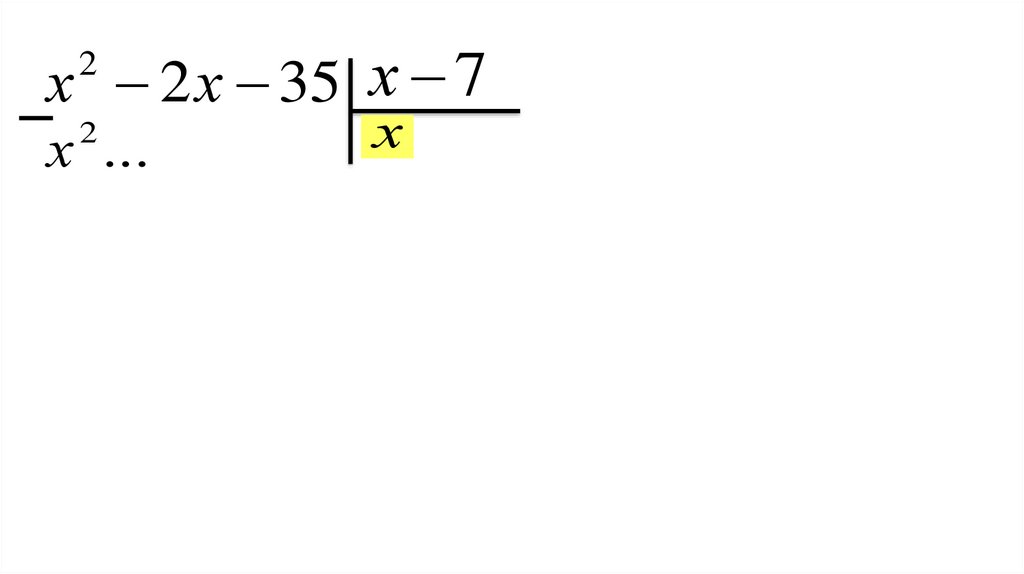
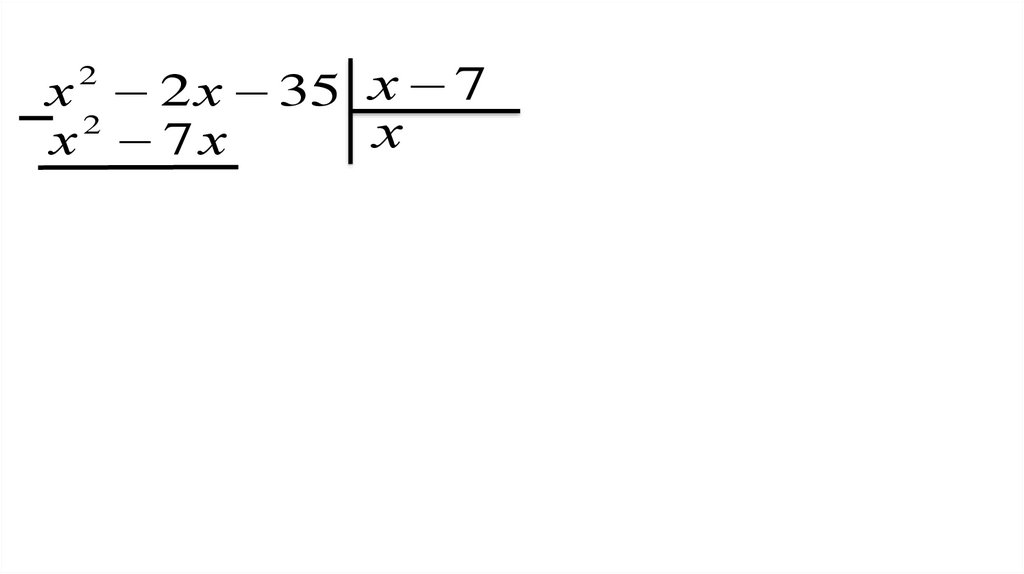
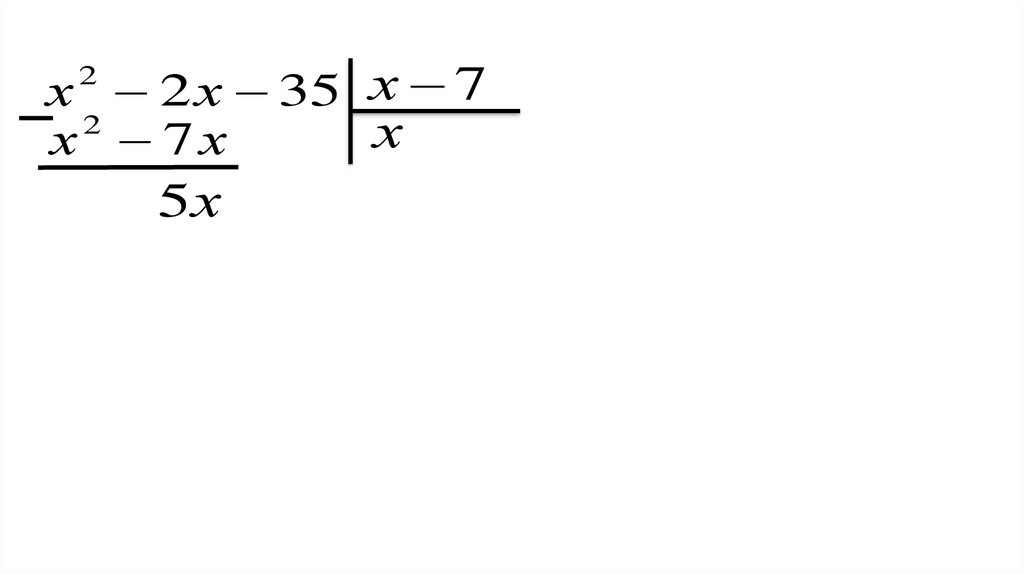
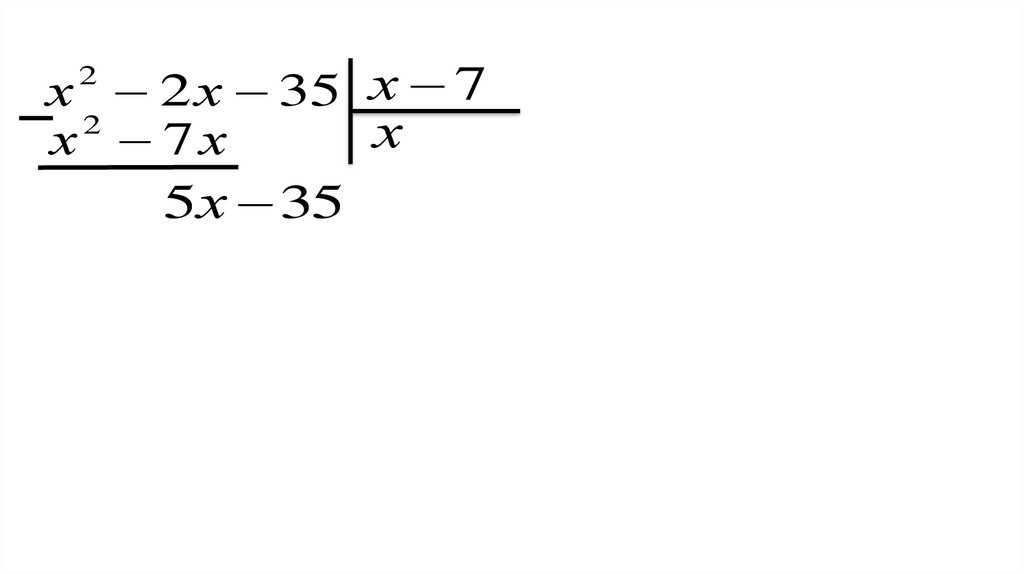
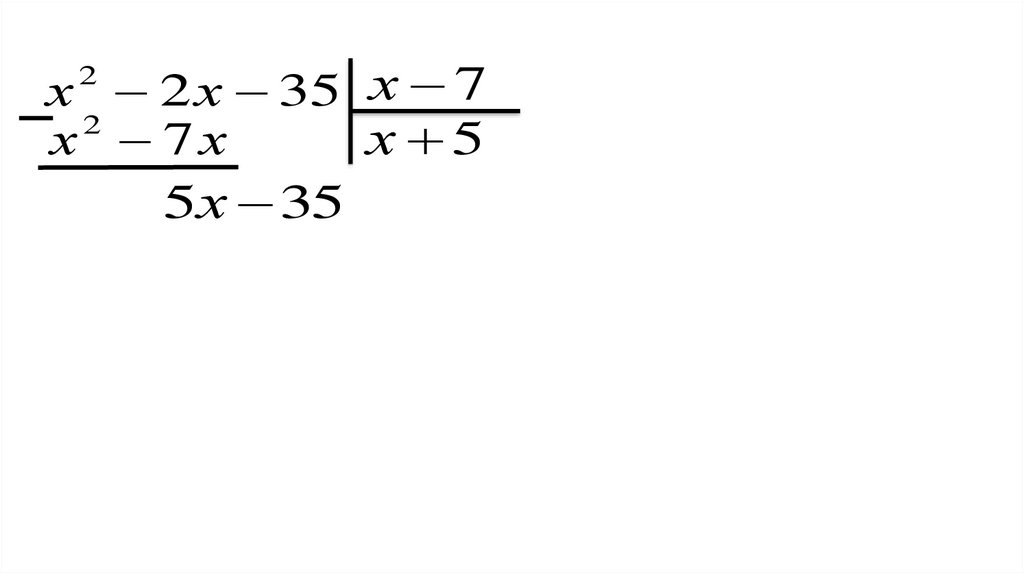







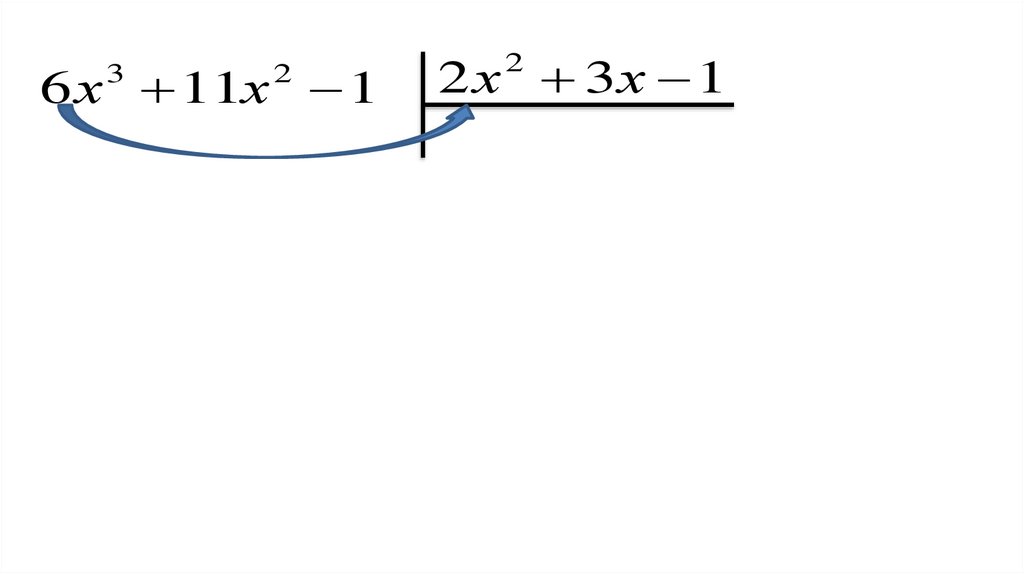
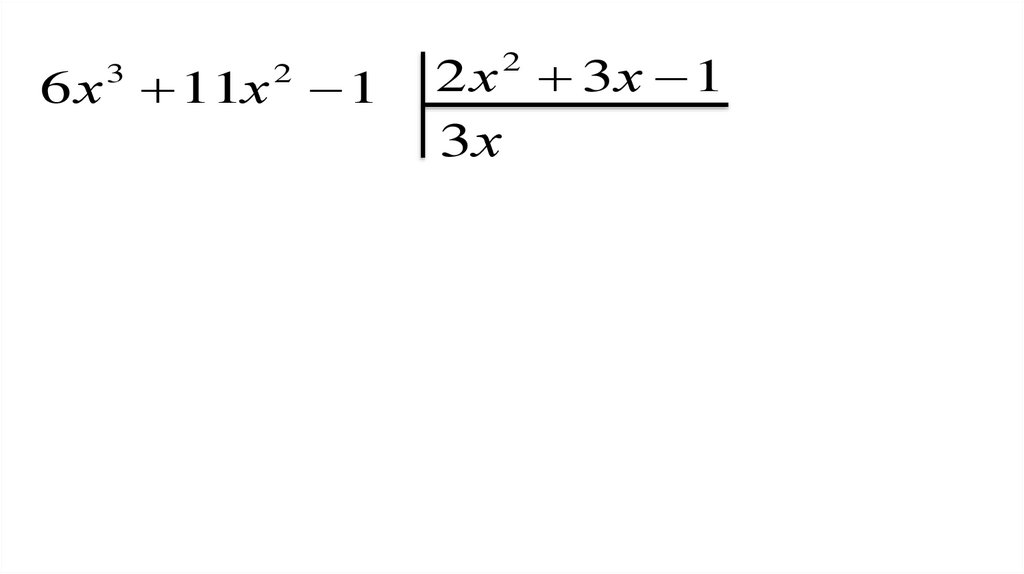
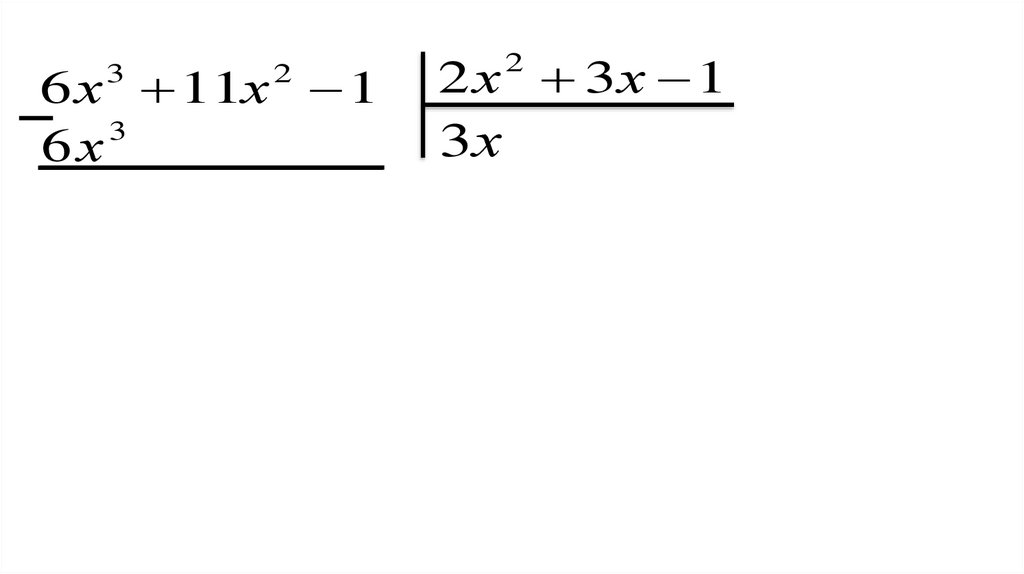
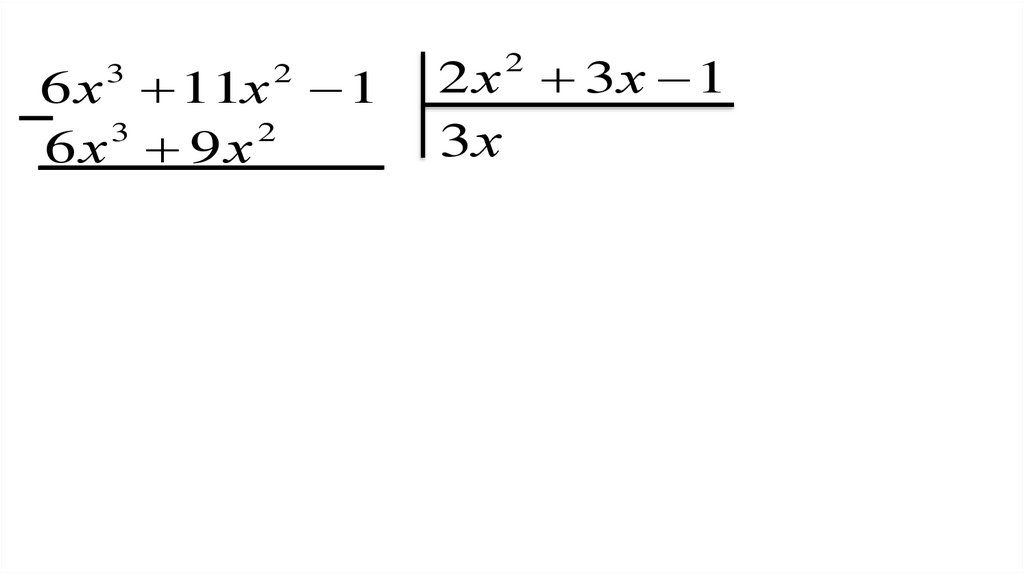
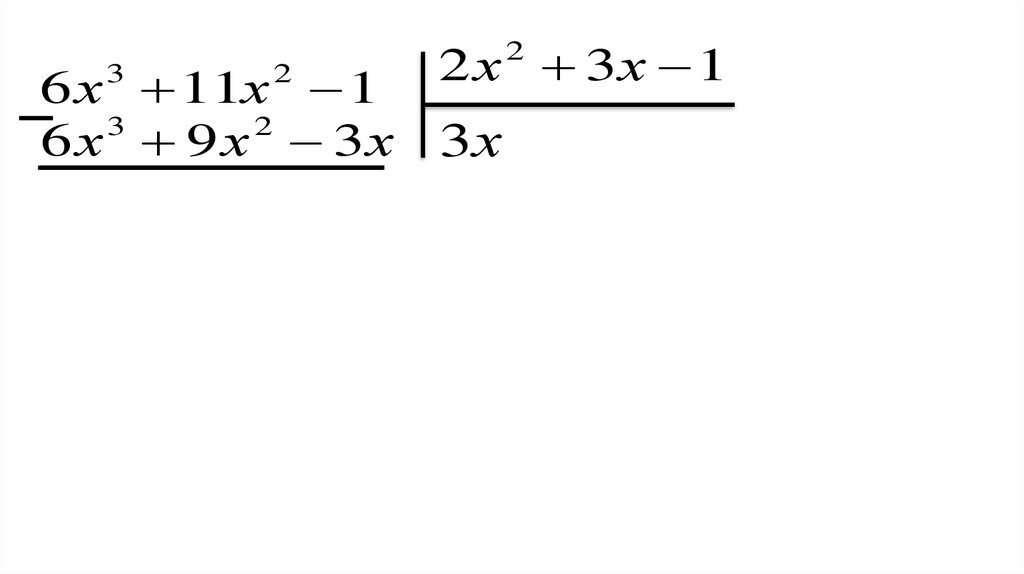
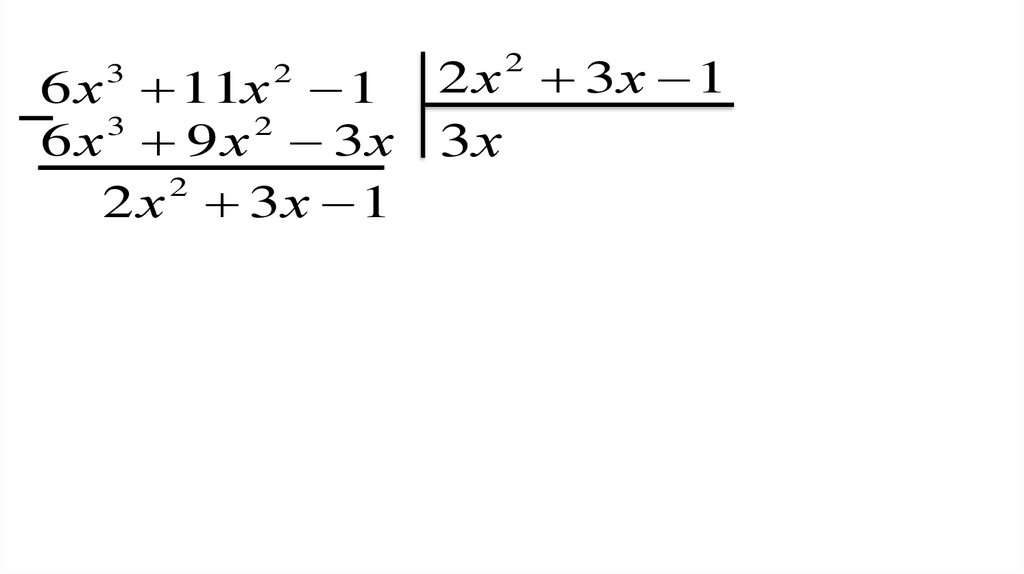
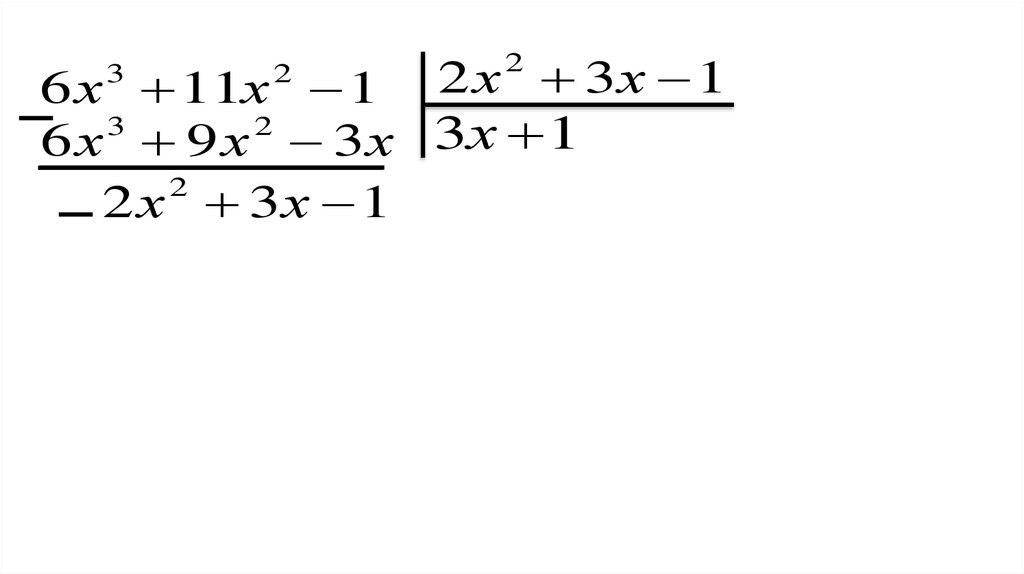
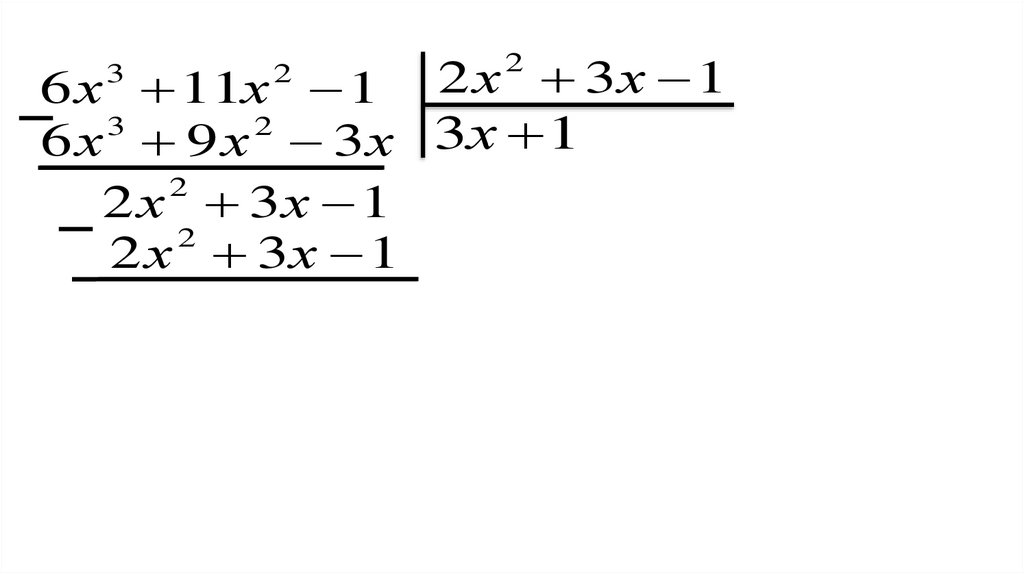








 Математика
Математика








