Derevya_i_ostov_grafov_lektsia_8

1. Деревья. Остовные графы

Лекция 8

2. ОСНОВНЫЕ ПОНЯТИЯ

1. Дерево - это связный граф без циклов.
2. Дерево - это связный граф, в котором при N вершинах всегда ровно N-1 ребро.
3. Дерево - это граф, между любыми двумя вершинами которого существует
4.
5.
ровно один путь
Дерево — это связный ациклический граф. Связность означает наличие
путей между любой парой вершин, ацикличность — отсутствие циклов и
то, что между парами вершин имеется только по одному пути.
Ориентированное дерево - орграф, в котором между любыми
двумя вершинами существует не более одного пути.

3. ОСНОВНЫЕ ПОНЯТИЯ

• Путь от узла 1 к узлу 2- это
последовательность узлов
начинаются с 1 и заканчивается
на 2
• Лист- это узел, у которого нет
поддеревьев
• Высота дерева- количество
ветвей между корнем и самым
отдаленным узлом.
• Объединение деревьев называют
лесом
• Уровень узла- это число которое
на 1 больше уровня родителя

4. ВИДЫ ДЕРЕВЬЕВ

• Корневое дерево — дерево, в котором выделена одна
вершина (корень дерева).
• Высота корневого дерева - это максимальное количество
дуг, отделяющих листья от корня. Если дерево не
взвешенное, то его высота - это просто расстояние от корня
до самого удаленного листа.

5.

6. Если добавить ребро, то добавляется и вершина.

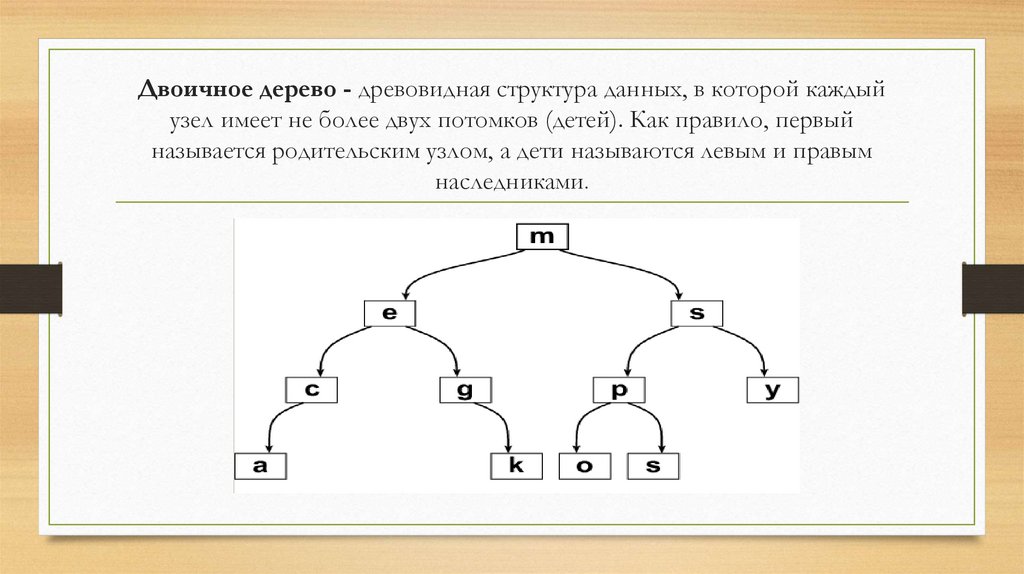
Ребра графа, принадлежащие дереву, называют ветвями

7. Двоичное дерево - древовидная структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый

называется родительским узлом, а дети называются левым и правым
наследниками.

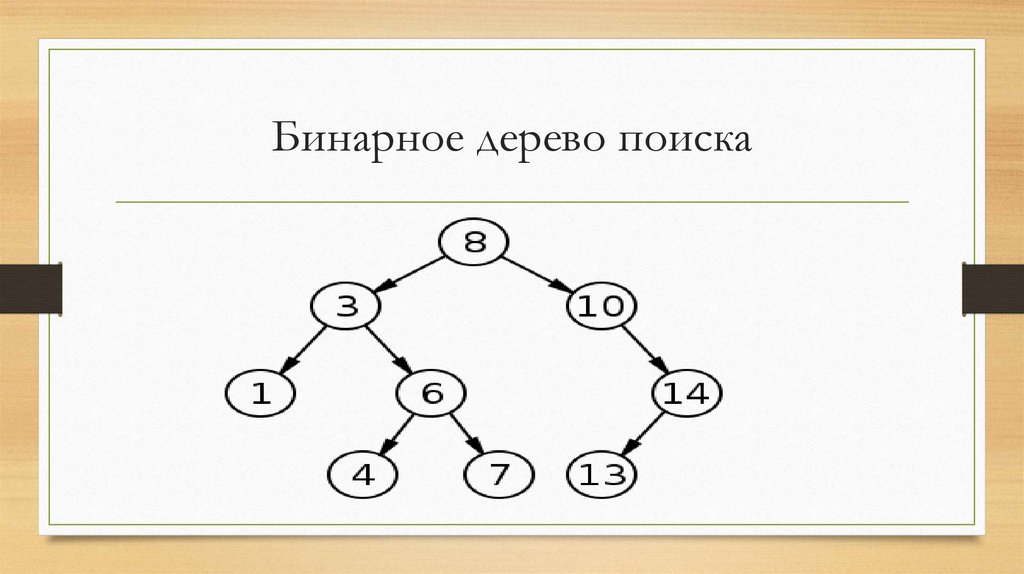
8. Бинарное дерево поиска

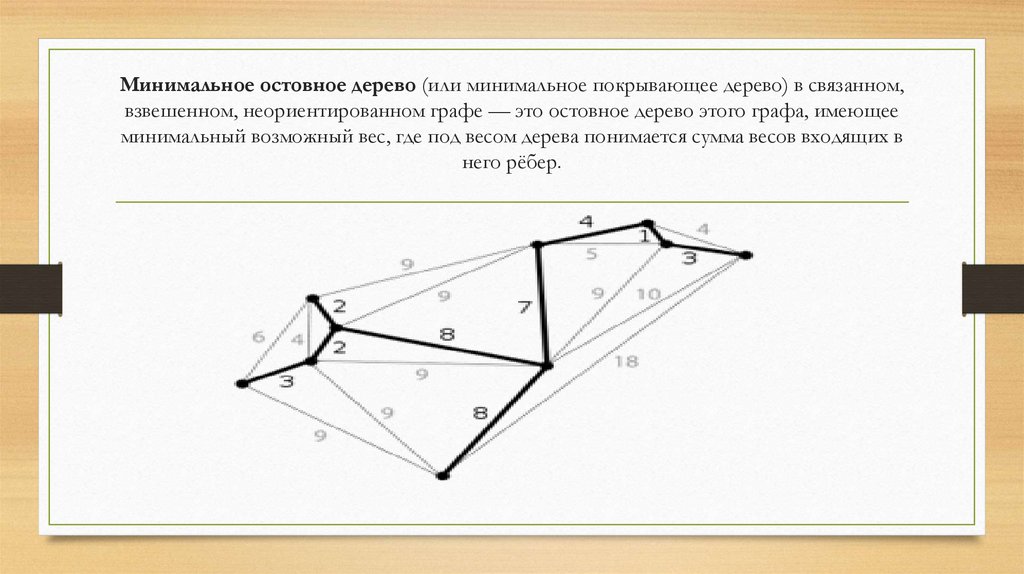
9. Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это

остовное дерево этого графа, имеющее
минимальный возможный вес, где под весом дерева понимается сумма весов входящих в
него рёбер.

10. БИНАРНОЕ ДЕРЕВО ВЫРАЖЕНИЙ

• (a+b)*(c-d/e) можно представить дерево в корневом узле которого будет
находиться операция *.
*
-
+
a
b
/
c
d
e

11. СВОЙСТВА

• Дерево не имеет кратных рёбер и петель.
• Граф является деревом тогда и только тогда, когда любые две
различные его вершины можно соединить единственной простой
цепью.
• Любое дерево однозначно определяется расстояниями (длиной
наименьшей цепи) между его концевыми (степени 1) вершинами.
• Любое дерево является двудольным. Любое дерево, множество вершин
которого не более чем счётное, является планарным графом.
• Для любых трёх вершин дерева, пути между парами этих вершин
имеют ровно одну общую вершину.

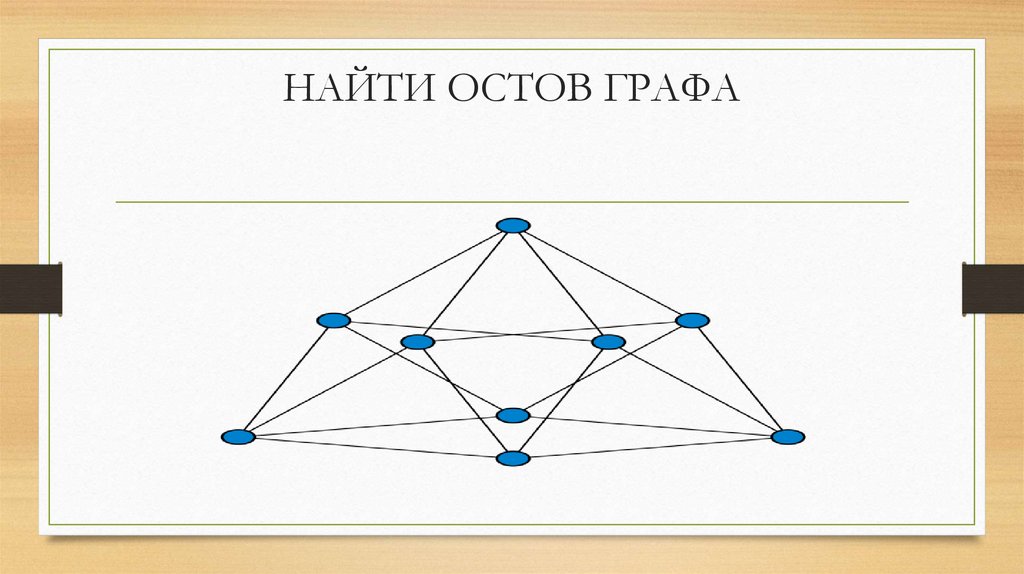
12. НАЙТИ ОСТОВ ГРАФА

13. АЛГОРИТМ НАХОЖДЕНИЯ ОСТОВА

• 1.Методом поиска в ширину ставим метки и доказываем связность.
• Далее начиная от первой вершины отмечаем все ребра при условии
отсутствия циклов
• Далее подвешиваем остов за любую вершину и получаем дерево
• Описываем дерево и все его компоненты