44069332ba6b4206ac15f894efcea053

1. ПАРАЛЛЕЛЬНОСТЬ В ПРОСТРАНСТВЕ

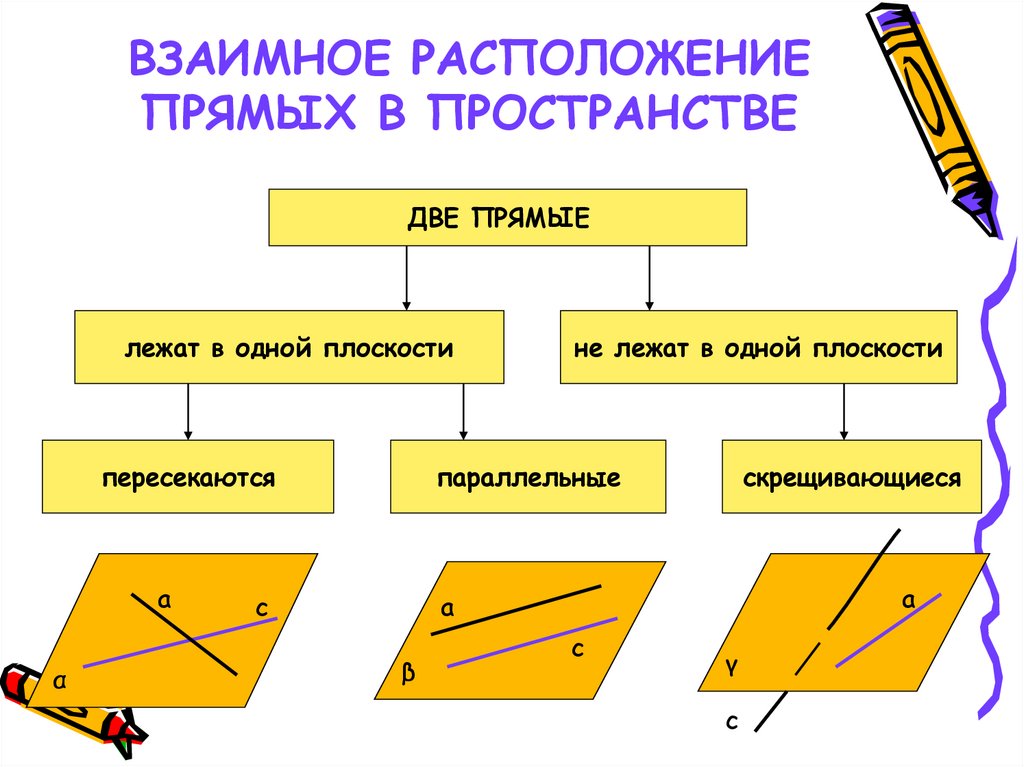
2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ В ПРОСТРАНСТВЕ

ДВЕ ПРЯМЫЕ
лежат в одной плоскости
пересекаются
а
α
не лежат в одной плоскости
параллельные
с
скрещивающиеся
а
а
β
с
γ
с

3. ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ

Две прямые в пространстве называются
параллельными, если они лежат в одной
плоскости и не пересекаются.
a в =
в
a
α
a α, в α
а || в

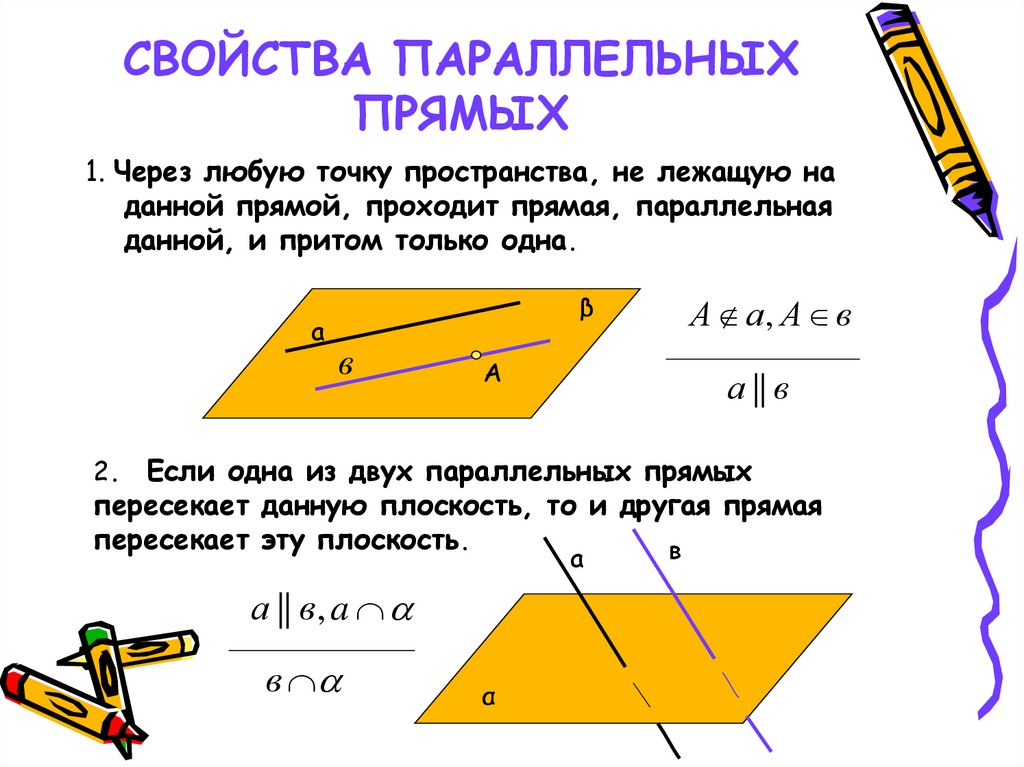
4. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПРЯМЫХ

1. Через любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная
данной, и притом только одна.
a
β
в
А
А а, А в
а || в
2. Если одна из двух параллельных прямых
пересекает данную плоскость, то и другая прямая
пересекает эту плоскость.
в
a
а || в, a
в
α

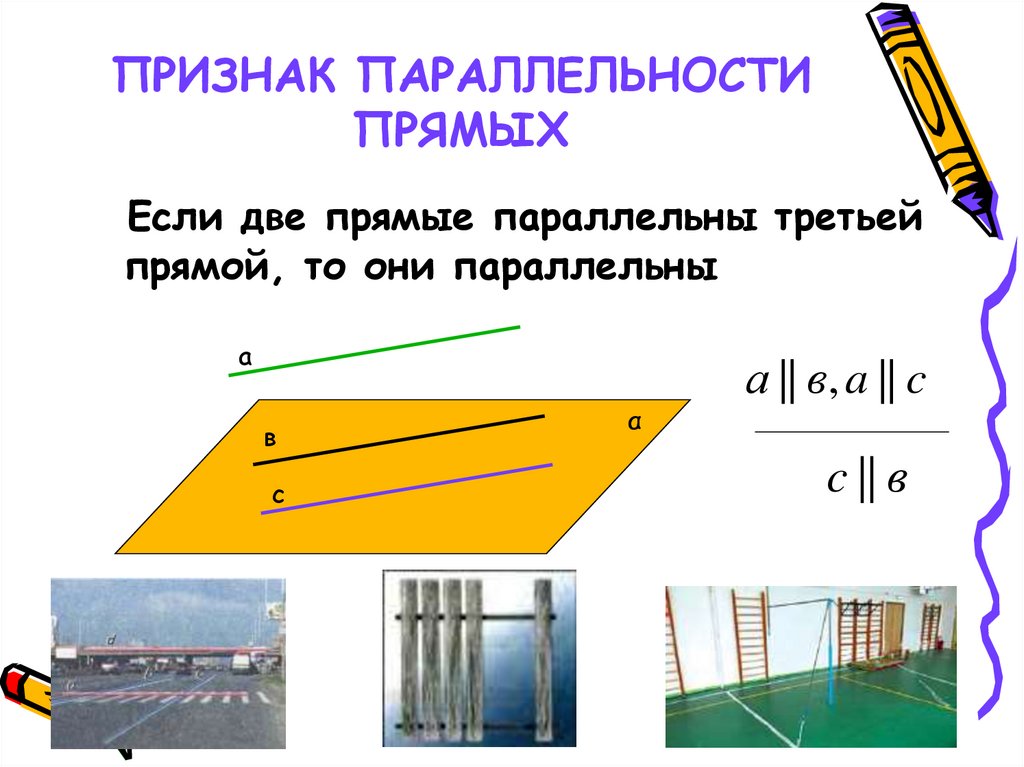
5. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМЫХ

Если две прямые параллельны третьей
прямой, то они параллельны
a
в
с
α
а || в, a || c
c || в

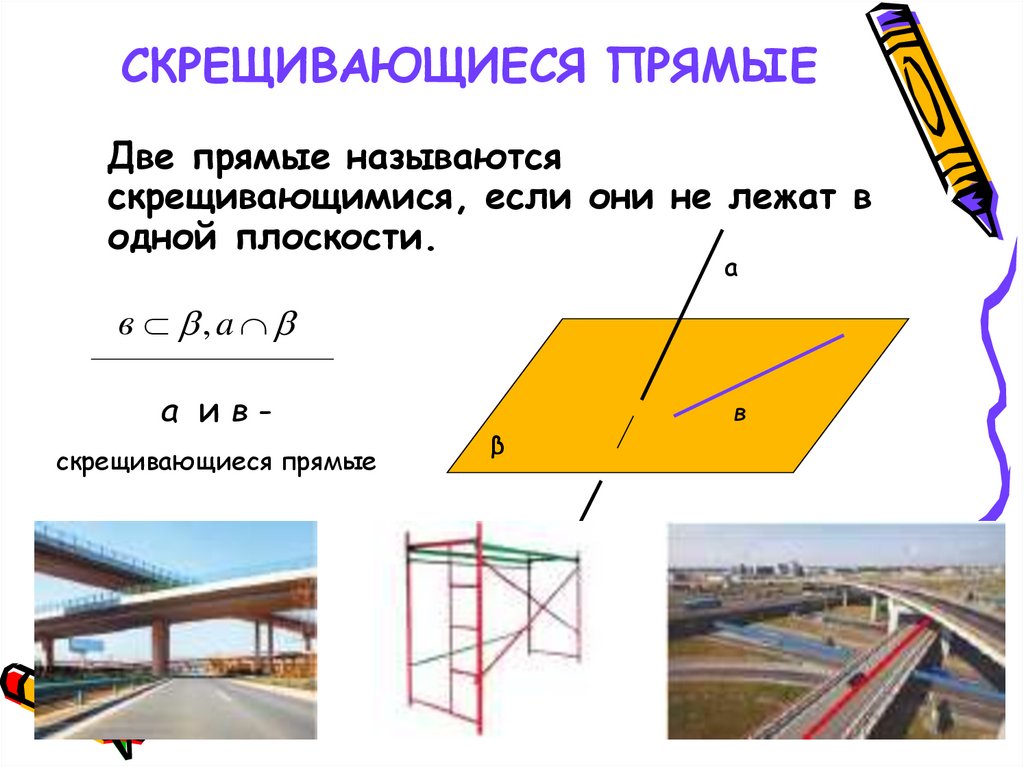
6. СКРЕЩИВАЮЩИЕСЯ ПРЯМЫЕ

Две прямые называются
скрещивающимися, если они не лежат в
одной плоскости.
a
в ,a
a ивскрещивающиеся прямые
β
в

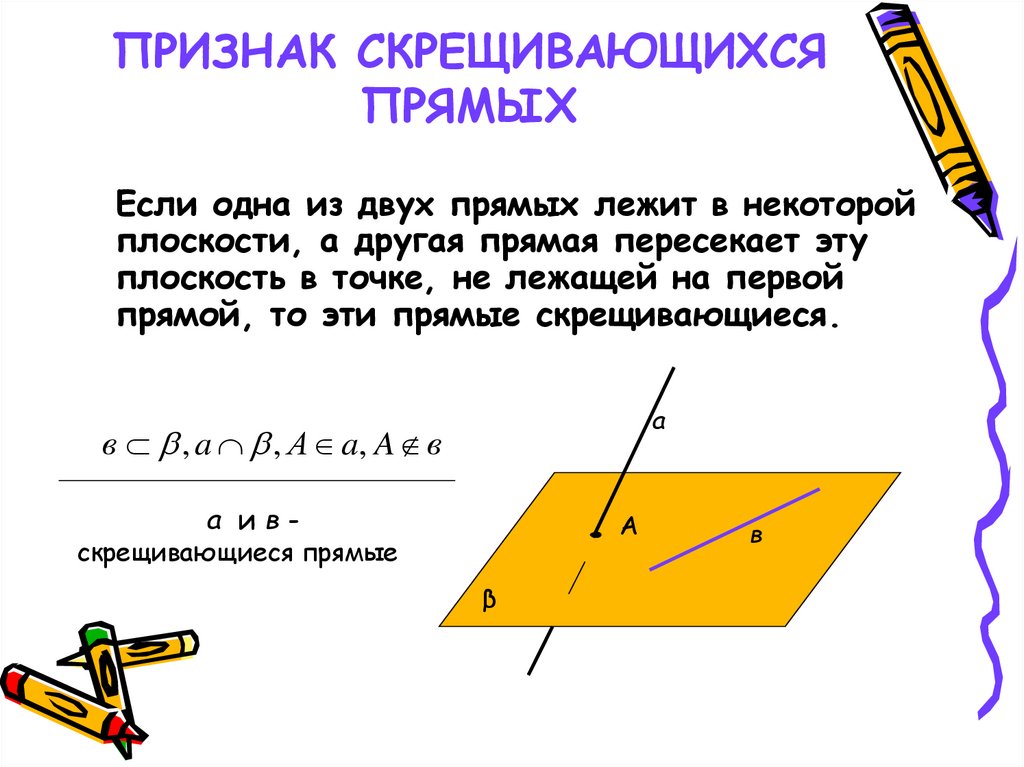
7. ПРИЗНАК СКРЕЩИВАЮЩИХСЯ ПРЯМЫХ

Если одна из двух прямых лежит в некоторой
плоскости, а другая прямая пересекает эту
плоскость в точке, не лежащей на первой
прямой, то эти прямые скрещивающиеся.
a
в , a , А a, A в
a ив-
А
скрещивающиеся прямые
β
в

8. ВЫПОЛНИТЬ ЗАДАНИЕ

Рассмотрите рисунок. Найдите на нем
материальные модели частей прямых:
А) параллельных;
В) скрещивающихся;
С) что пересекаются.

9. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ

ПРЯМАЯ И ПЛОСКОСТЬ
имеют общие точки
пересекаются
не имеют общих точек
прямая лежит в плоскости
параллельные
a
a
a
А
α
β
γ

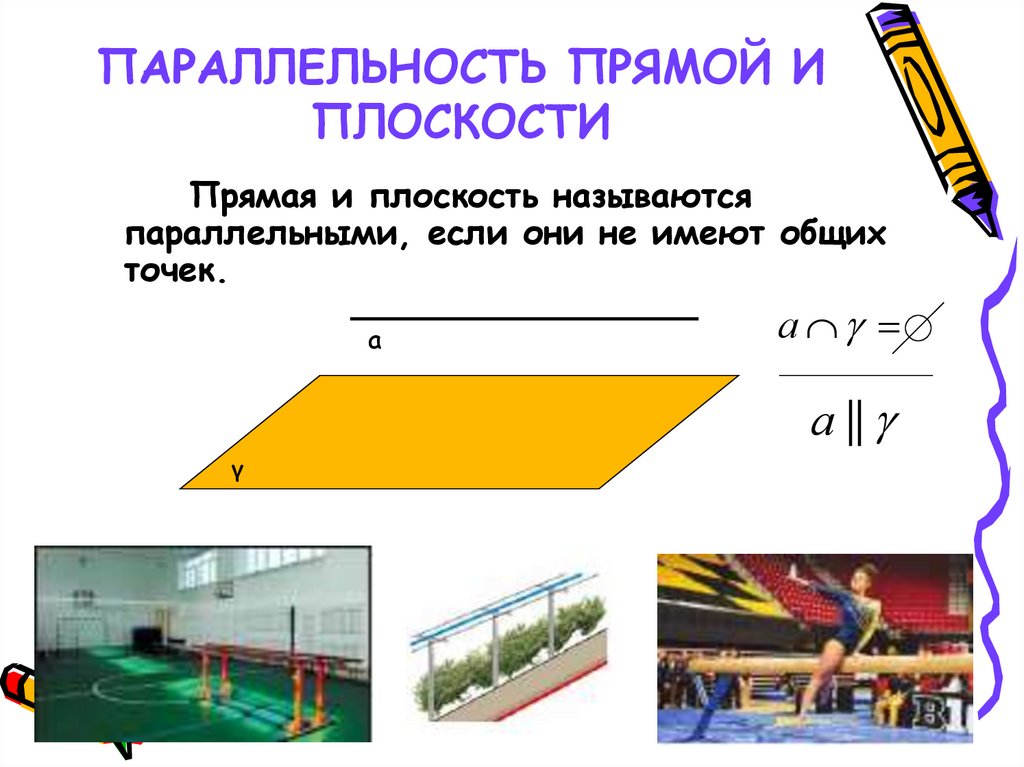
10. ПАРАЛЛЕЛЬНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ

Прямая и плоскость называются
параллельными, если они не имеют общих
точек.
а
а
а ||
γ

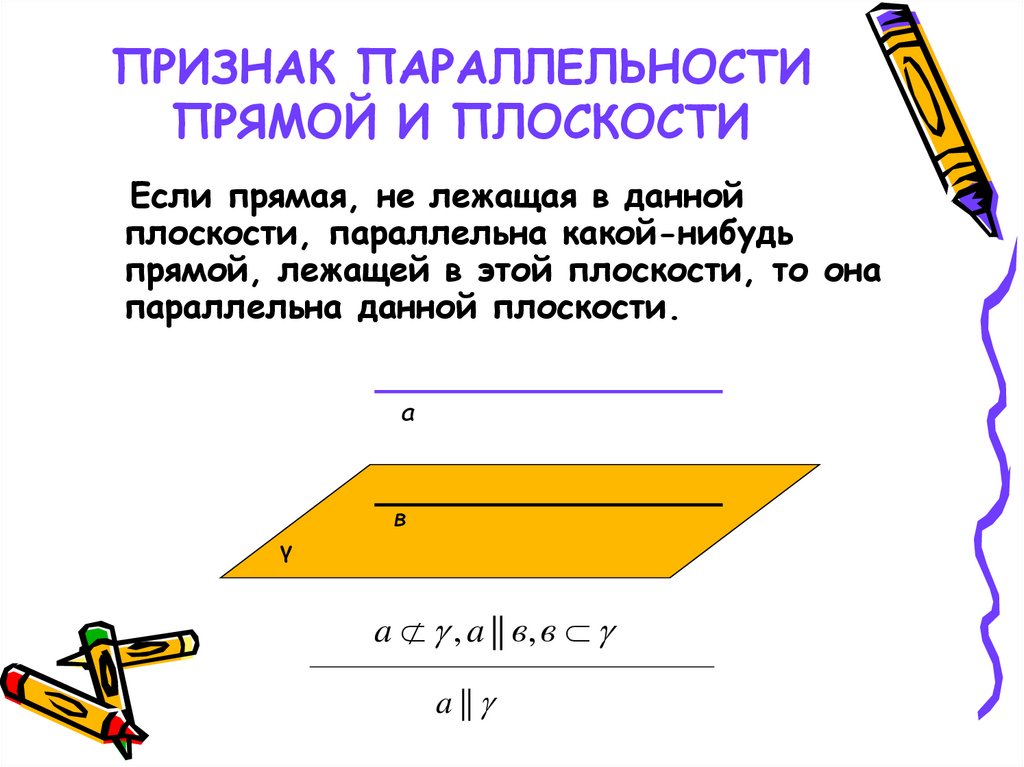
11. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ

Если прямая, не лежащая в данной
плоскости, параллельна какой-нибудь
прямой, лежащей в этой плоскости, то она
параллельна данной плоскости.
a
γ
в
a , a || в, в
a ||

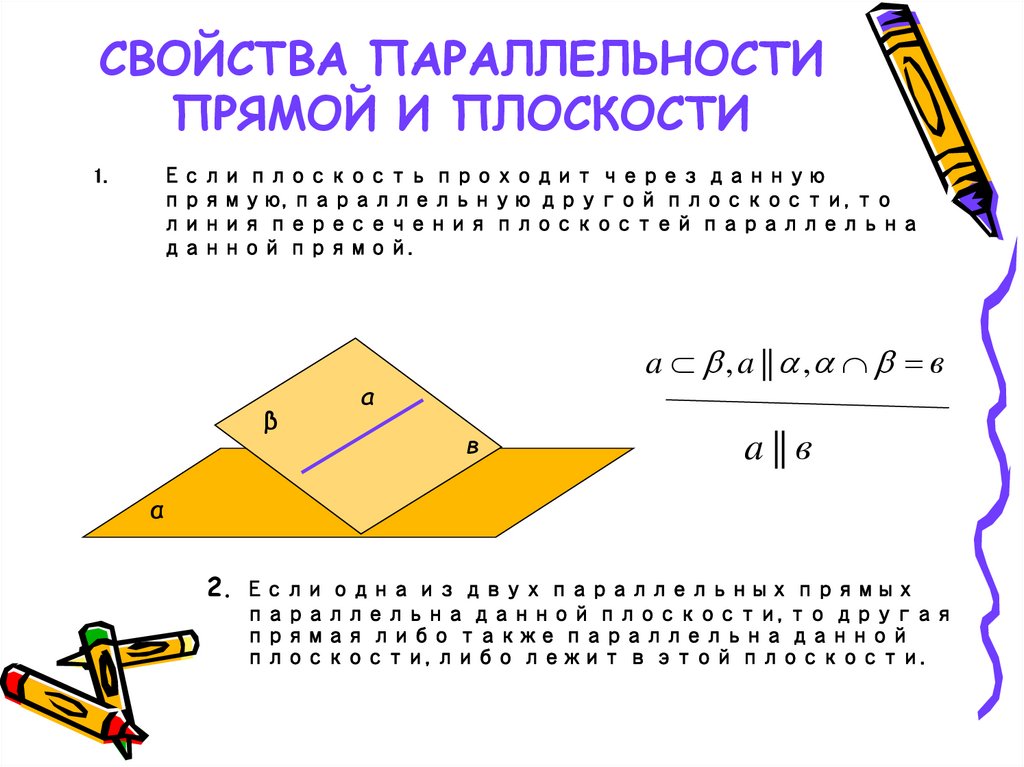
12. СВОЙСТВА ПАРАЛЛЕЛЬНОСТИ ПРЯМОЙ И ПЛОСКОСТИ

1.
Если плоскость проходит через данную
прямую, параллельную другой плоскости, то
линия пересечения плоскостей параллельна
данной прямой.
β
a , a || , в
a
в
a || в
α
2. Если одна из двух параллельных прямых
параллельна данной плоскости, то другая
прямая либо также параллельна данной
плоскости, либо лежит в этой плоскости.

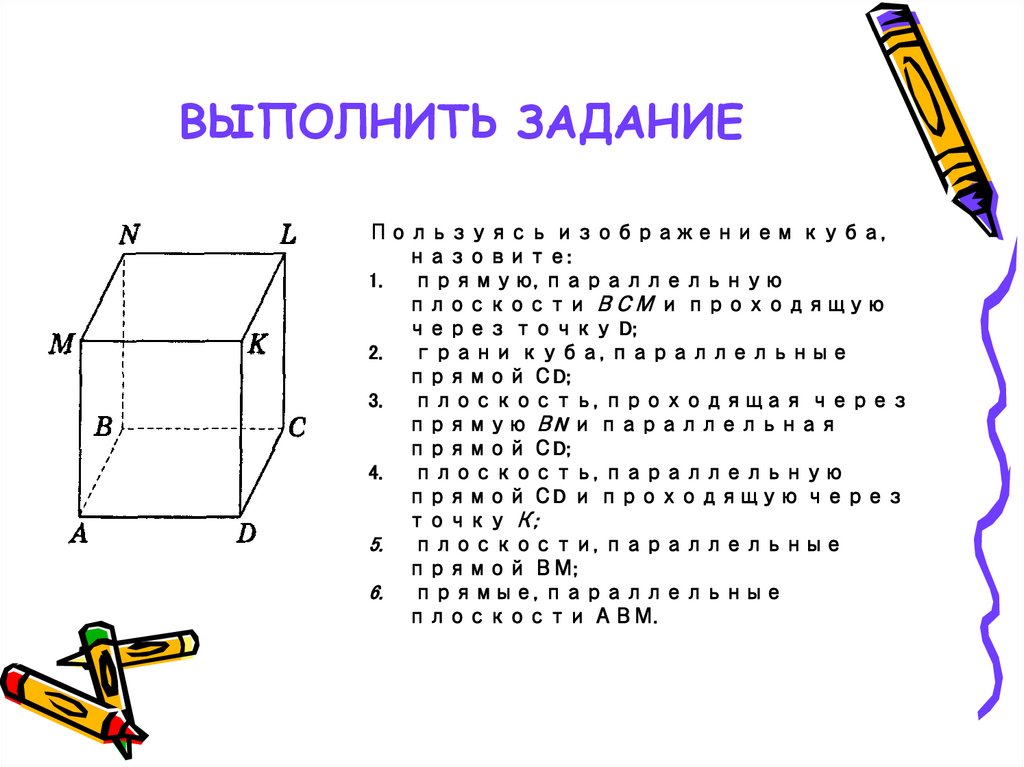
13. ВЫПОЛНИТЬ ЗАДАНИЕ

Пользуясь изображением куба,
назовите:
1.
прямую, параллельную
плоскости ВСМ и проходящую
через точку D;
2.
грани куба, параллельные
прямой СD;
3.
плоскость, проходящая через
прямую ВN и параллельная
прямой СD;
4.
плоскость, параллельную
прямой СD и проходящую через
точку К;
5. плоскости, параллельные
прямой ВМ;
6. прямые, параллельные
плоскости АВМ.

14. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ

ДВЕ ПЛОСКОСТИ
имеют общие точки
не имеют общих точек
пересекаются
параллельные
β
β
a
α
γ

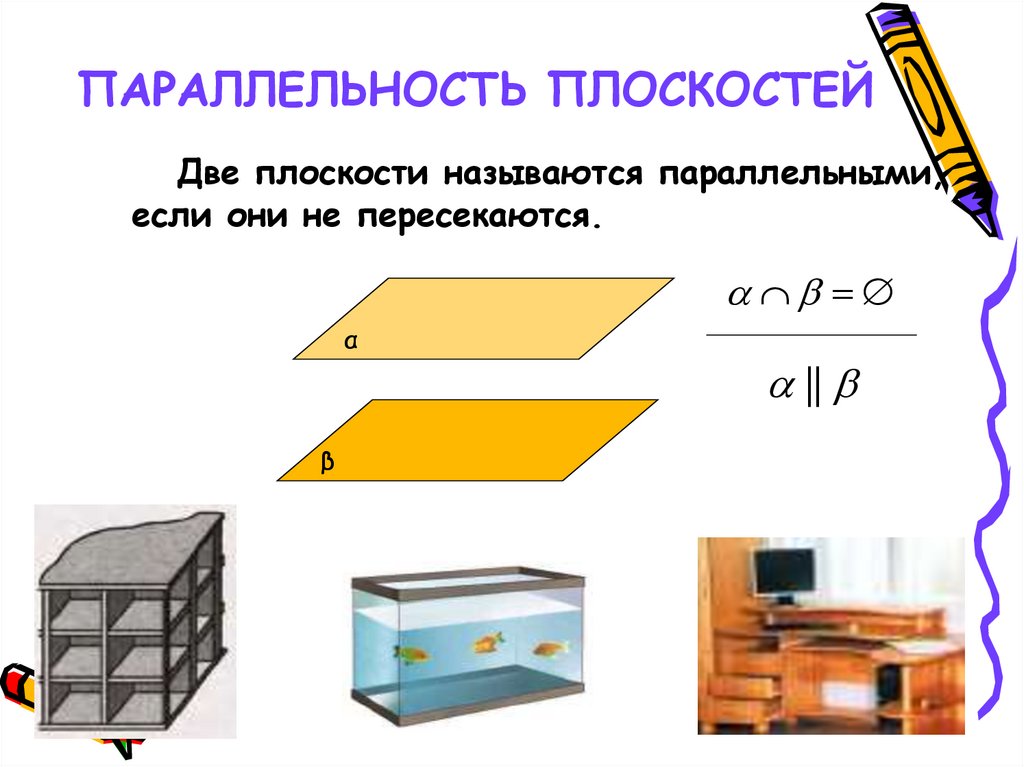
15. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ

Две плоскости называются параллельными,
если они не пересекаются.
α
β
||

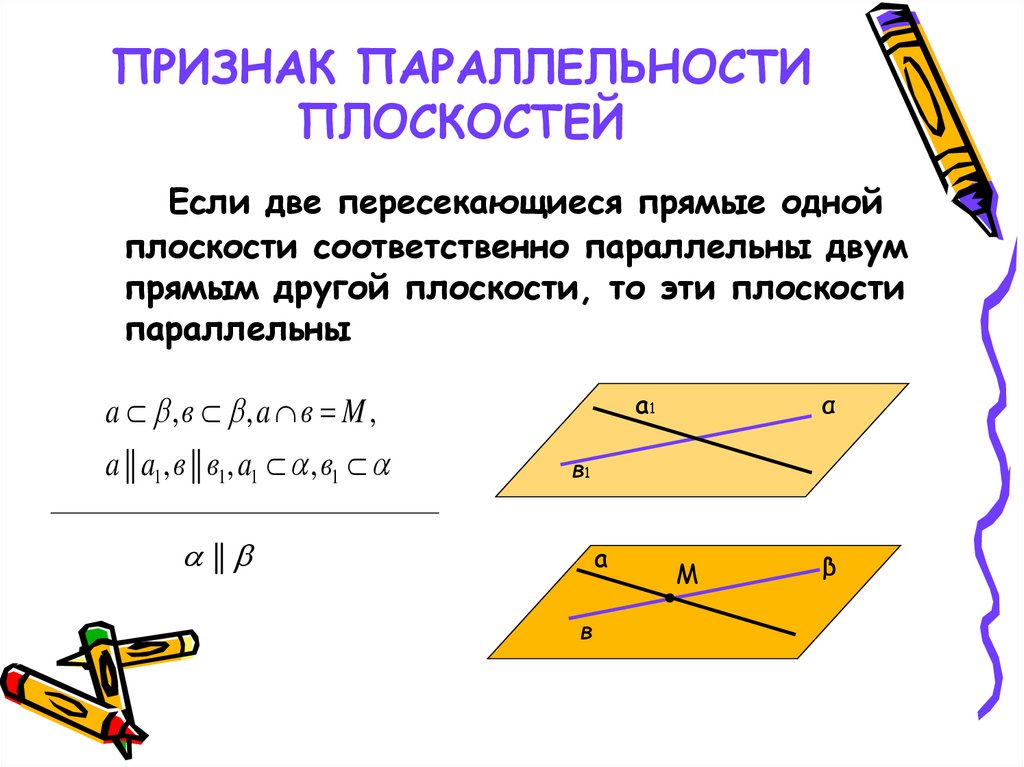
16. ПРИЗНАК ПАРАЛЛЕЛЬНОСТИ ПЛОСКОСТЕЙ

Если две пересекающиеся прямые одной
плоскости соответственно параллельны двум
прямым другой плоскости, то эти плоскости
параллельны
a ,в ,a в M ,
a || a1 , в || в1 , a1 , в1
a1
α
в1
||
a
в
М
β

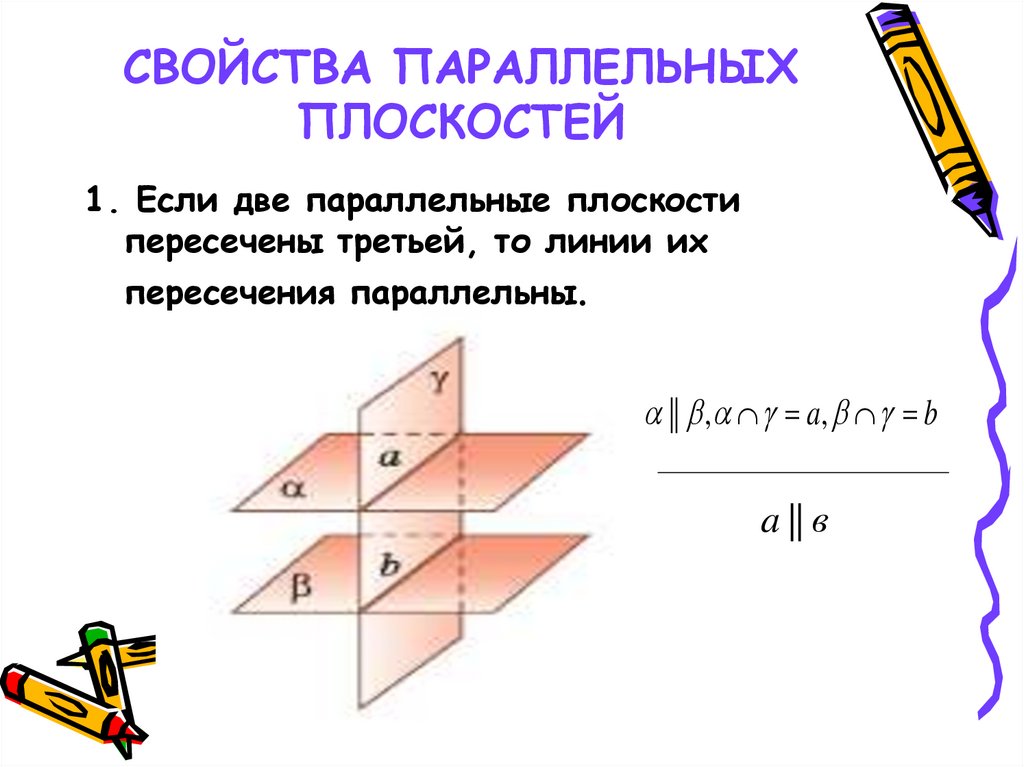
17. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ

1. Если две параллельные плоскости
пересечены третьей, то линии их
пересечения параллельны.
|| , a, b
a || в

18. СВОЙСТВА ПАРАЛЛЕЛЬНЫХ ПЛОСКОСТЕЙ

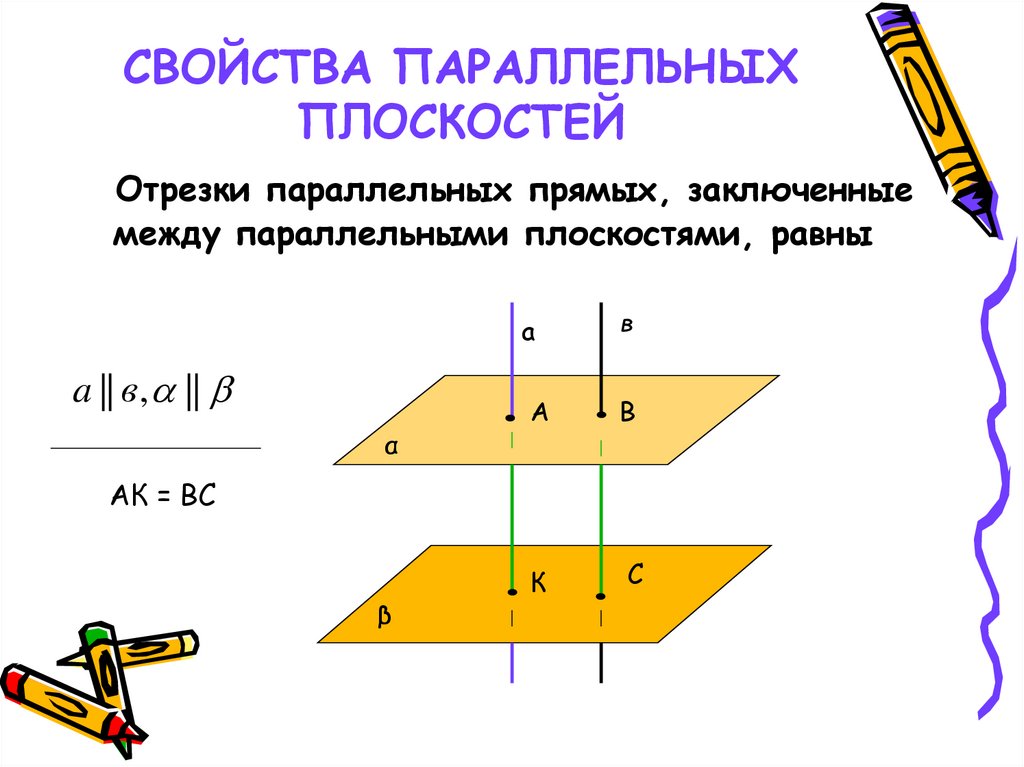
Отрезки параллельных прямых, заключенные
между параллельными плоскостями, равны
a || в, ||
α
a
в
А
В
К
С
АК = ВС
β

19. ВЫПОЛНИТЬ ЗАДАНИЕ

Пользуясь изображением
куба, назовите:
1. плоскость,
параллельную
плоскости АВС;
2. плоскость, параллельную
плоскости МКD;
3. плоскость, параллельную
плоскости СNL;
4. параллельные
плоскости, которые
проходят через
скрещивающиеся
прямые МК и АВ;
5. параллельные плоскости,
которые проходят через
скрещивающиеся прямые