Лекция. Производная (часть 1)

1.

Лекция
Производная функции. Геометрический и
механический смысл. Правила
дифференцирования. Производная сложной
и неявной функции
ст арший преподават ель Грипп Е.А.

2. Определение производной

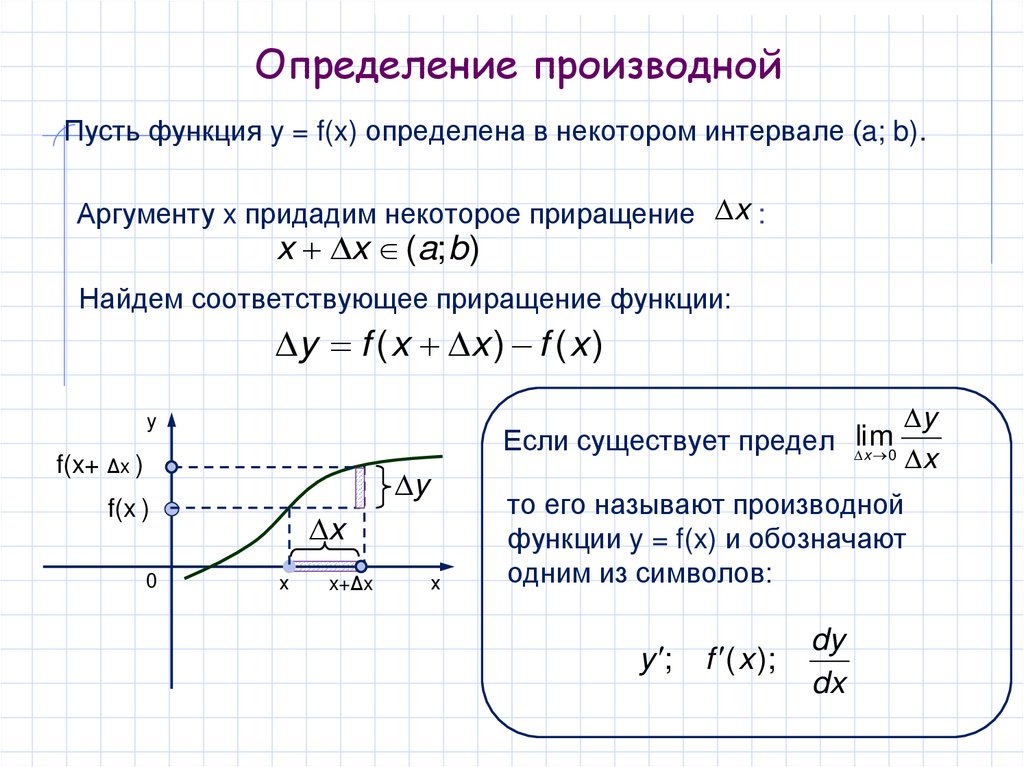
Пусть функция y = f(x) определена в некотором интервале (a; b).
Аргументу x придадим некоторое приращение x :
x x (a; b )
Найдем соответствующее приращение функции:
y f ( x x ) f ( x )
y
Если существует предел lim
x 0
f(x+ Δx )
y
f(x )
0
x
х
x+Δx
х
y
x
то его называют производной
функции y = f(x) и обозначают
одним из символов:
y ;
f ( x );
dy
dx

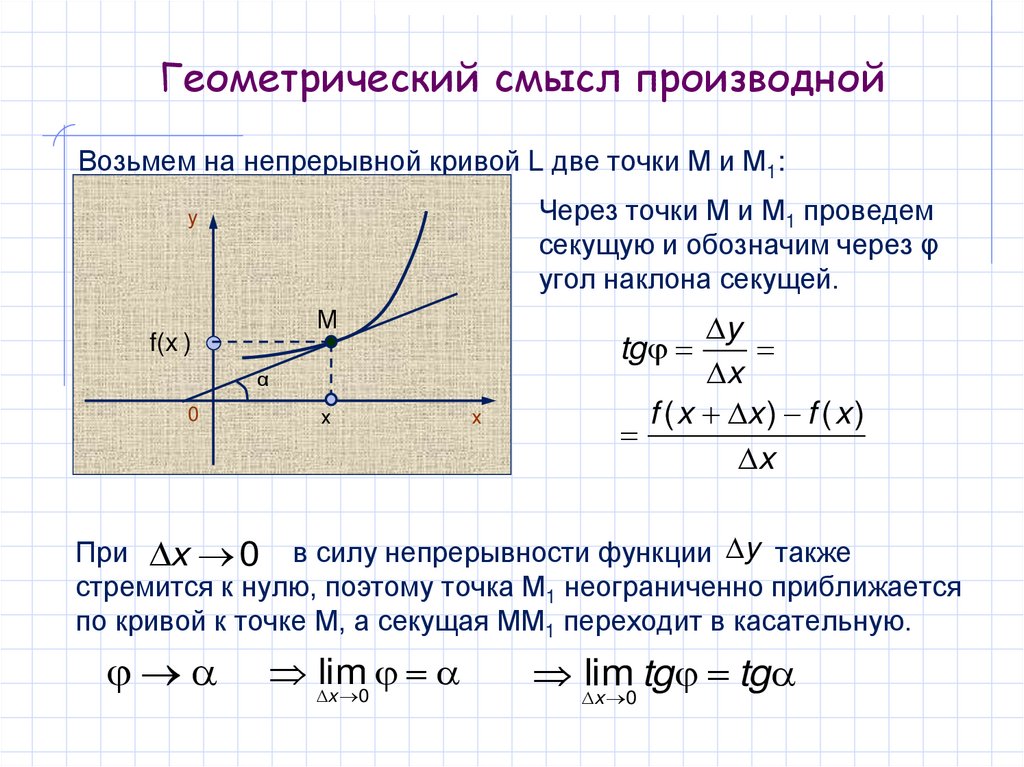
3. Определение производной

Итак, по определению:
y lim
x 0
f ( x x ) f ( x )
x
Функция y = f(x) , имеющая производную в каждой точке интервала
(a; b), называется дифференцируемой в этом интервале; операция
нахождения производной функции называется
дифференцированием.
Значение производно функции y = f(x) в точке x0 обозначается
одним из символов:
y ( x0 );
f ( x0 );
y x
0
Если функция y = f(x) описывает какой – либо физический процесс,
то f ’(x) есть скорость протекания этого процесса – физический
смысл производной.

4. Определение производной

Пример: Найти производную функции