Производная функции

1. Урок № 24 Производная функции

ПЛАН УРОКА:
1 Средняя и мгновенная скорость тела
2 Скорость изменения функции
3 Производные функций
y=C; y=x; y=x²; y=x³
4 Производная степенной функции
5 Решение задач
6 Исторический экскурс
7 Домашнее задание

2.

У каждого человека есть
определенный
кругозор. Когда
этот кругозор
сужается до
бесконечности
малого, то он
обращается в
точку. Тогда
человек и говорит,
что это есть его
точка зрения.
Давид Гильберт

3.

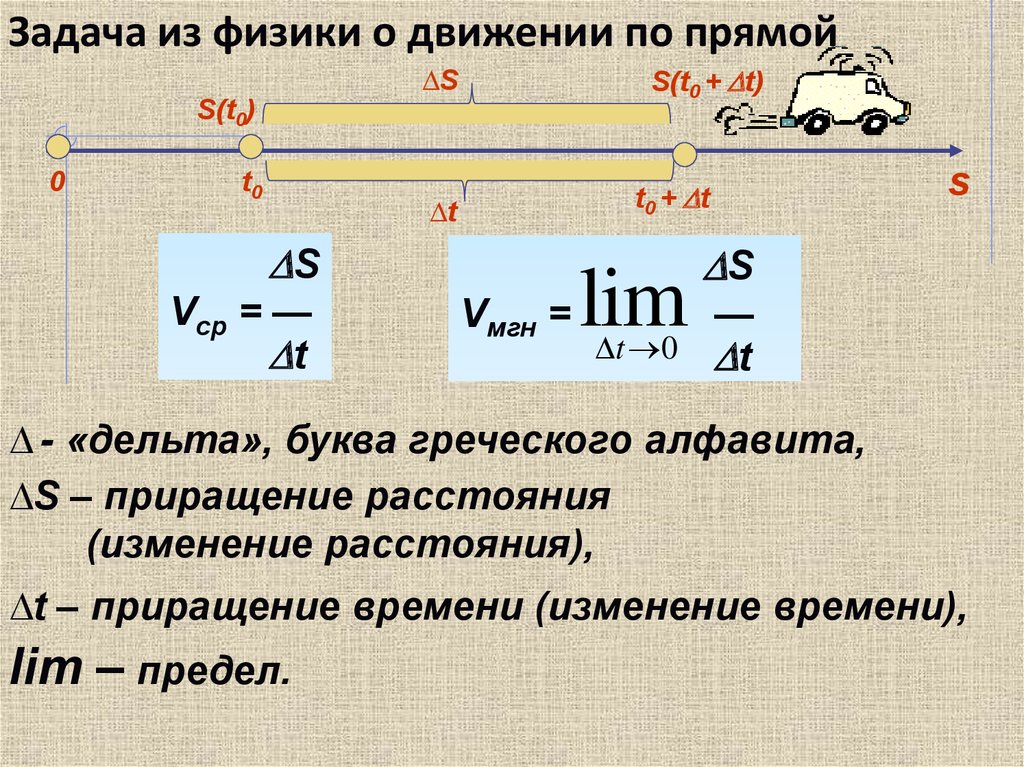
Задача из физики о движении по прямой
S(t0 + t)
∆S
S(t0)
0
t0
t0 + t
∆t
S
Vср = —
t
Vмгн =
lim
s
S
—
t 0 t
∆ - «дельта», буква греческого алфавита,
∆S – приращение расстояния
(изменение расстояния),
∆t – приращение времени (изменение времени),
lim – предел.

4. Определение производной

Пусть функция y = f(x) определена в некотором
интервале (a; b).
Аргументу x придадим некоторое приращение
x x (a; b )
: x
Найдем соответствующее приращение
функции: y f ( x x ) f ( x )
y=f(x)
y
f(x+ Δx )
y
f(x )
0
x
х
x+Δx
х
Если существует
lim
предел
x 0
то его называют
производной функции
y = f(x) и обозначают
одним из символов:
y ;
f ( x );
y
x
dy
dx

5. Определение производной

f ( x x ) f ( x )
Итак, по определению:
y lim
x 0
x
Функция y = f(x) , имеющая производную в каждой
точке интервала (a; b), называется
дифференцируемой в этом интервале;
операция нахождения производной функции
называется дифференцированием.
Значение производной функции y = f(x) в точке x0
обозначается одним из символов:
y ( x0 );
f ( x0 );
Если функция y = f(x) описывает какой – либо
физический процесс, то f ’(x) есть скорость
протекания этого процесса – физический смысл
производной.
y x
0

6. Производные функций y=C; y=x; y=x²; y=x³

Алгоритм нахождения производной
по определению:
f ( x x ) f ( x )
y lim
x 0
x
1 Придадим приращение аргументу и
вычислим: f(x+∆x).
2 Найдем разность:
f(x+∆x)-f(x).
3 Запишем отношение: f ( x x) f ( x)
x
4 Найдем предел данного отношения:
f ( x x ) f ( x )
y lim
x 0
x

7. Производная степенной функции

Степенная функция: y x
n Z
Придадим аргументу x приращение x , тогда
функция получит приращение:
n
y x x x n
n
Формула бинома Ньютона:
n(n 1) n 2 2
a b a na b
a b
2!
n(n 1) (n k 1) n k k
a b bn
k!
n
n
n 1
K – факториал
k! 1 2 3 k

8. Производная степенной функции

По формуле бинома Ньютона имеем:
y x x x n
n
n(n 1) n 2 2
n
n
( x nx x
x x x ) x
2!
y
n(n 1) n 2
n 1
n 1
nx
x
x
x
Тогда:
x
2!
y
n 1 n(n 1) n 2
n 1
lim
lim nx
x x x
x 0
x x 0
2!
n
nx n 1
n 1
x ' nx
n
n 1

9.

Найдите производные данных функций № 1-7
Найдите производные данных функций № 1-7

10.

Общее понятие
производной
было сделано
независимо
друг от друга
почти
одновременно
английским
физиком и
математиком
И.Ньютоном
немецким
философом и
математиком
Г.Лейбницем.

11.

ДОМАШНЕЕ ЗАДАНИЕ № 24
Учебник Алгебра 10-11 кл. Алимов
§ 44, стр. 229, § 45, стр. 236,
№ 787, 788, 789