Похожие презентации:
ОКТех-Лекция 2.1 Двоичная арифметика
1. Раздел 1. Арифметические основы компьютера
Тема 2:Двоичная арифметика с
положительными числами
Дисциплина:
ОКТ
Преподаватель:
Савенко А.Г.
2. Вопросы:
1. Операции сложения положительных чисел2. Методы выполнения умножения и деления
3. Особенности сложения и вычитания
двоично-десятичных чисел
3. Сложение двоичных чисел:
+0
1
• В
0
0
1
1
1
0*
таблице представлены результаты сложения для
различных слагаемых для двоичной СС.
• * -- в текущем разряде результата получен ноль и имеет
место перенос в ближайший старший разряд
4. Сложение двоичных чисел:
Пример:1
+
1
1
1
1
1
1
0
1
1
0
1
0
0
0
0
1
1
1
0
0
1
1
0
1
1
0
1
1
0
1
1
0
1
0
0
1
1
5. Вычитание двоичных чисел:
01
• В
0
0
1*
1
1
0
таблице представлены результаты вычитания для
различных слагаемых для двоичной СС.
• * -- в текущем разряде результата получена единица при
займе из ближнего старшего разряда
6. Сложение двоичных чисел:
Пример:-
1
1
-1
-
-
1
0
0
0
0
1
0
0
0
1
-1
-1
1
1
1
0
0
1
1
1
0
1
1
0
1
1
0
0
1
1
0
0
7. Умножение двоичных чисел:
*0
1
•В
0
0
0
1
0
1
таблице представлены результаты
умножения для различных множимых для
двоичной СС.
8. Умножение двоичных чисел:
• Частичноепроизведение
для
разряда
множителя равняется нулю, если разряд равен
нулю;
• Частичное
произведение
для
разряда
множителя равняется множимому , взятому с
соответствующим
весом,
если
разряд
множителя равен единице;
9. Умножение двоичных чисел:
• При последовательном способе формированиячастичных произведений, последние могут
рассчитываться поочередно для отдельных
разрядов множителя, начиная с младшего или
старшего разряда. При десятичном основании,
как
правило,
формирование
частичных
произведений осуществляется, начиная с
младшего разряда множителя.
10. Умножение двоичных чисел:
Пример:Найти произведение двоичных чисел:
1011 и 1101, начиная формирование
частичных произведений со старшего
разряда множителя.
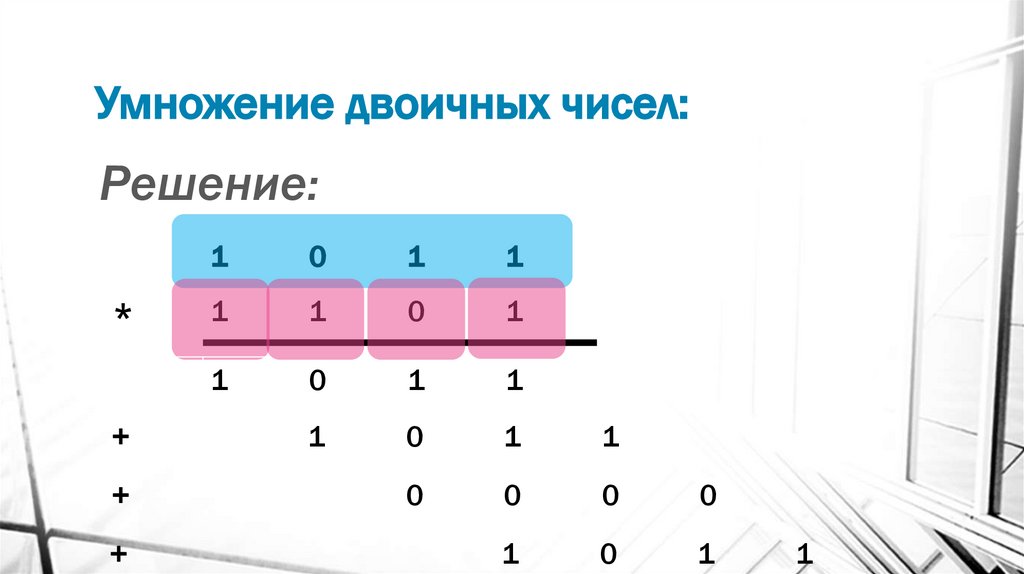
11. Умножение двоичных чисел:
Решение:*
+
+
+
1
0
1
1
1
1
0
1
1
0
1
1
1
0
1
1
0
0
0
0
1
0
1
1
12. Умножение двоичных чисел:
Решение:1
+
0
1
1
1
0
1
1
0
0
0
0
1
0
1
1
1
1
1
1
+
+
1
0
0
0
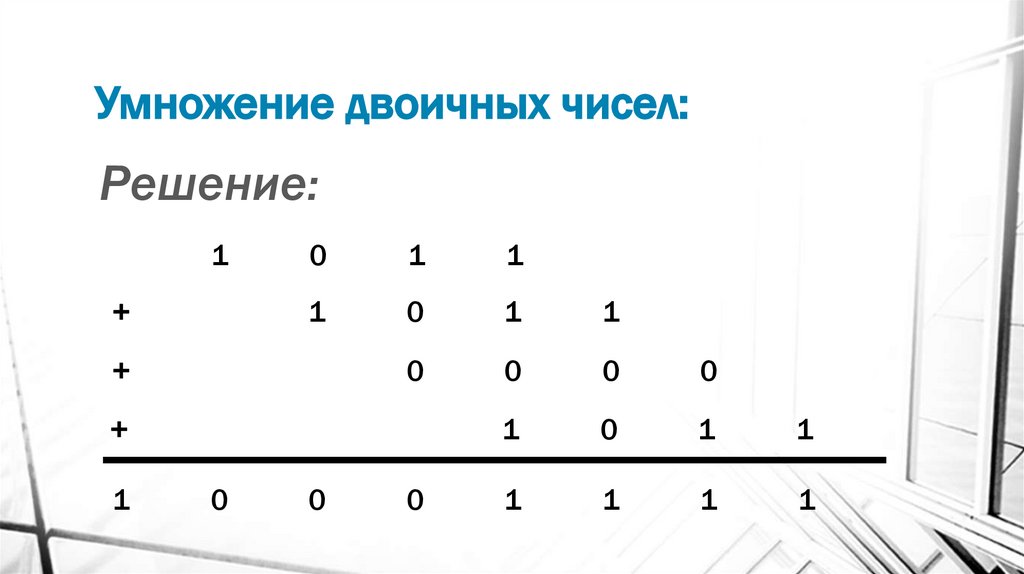
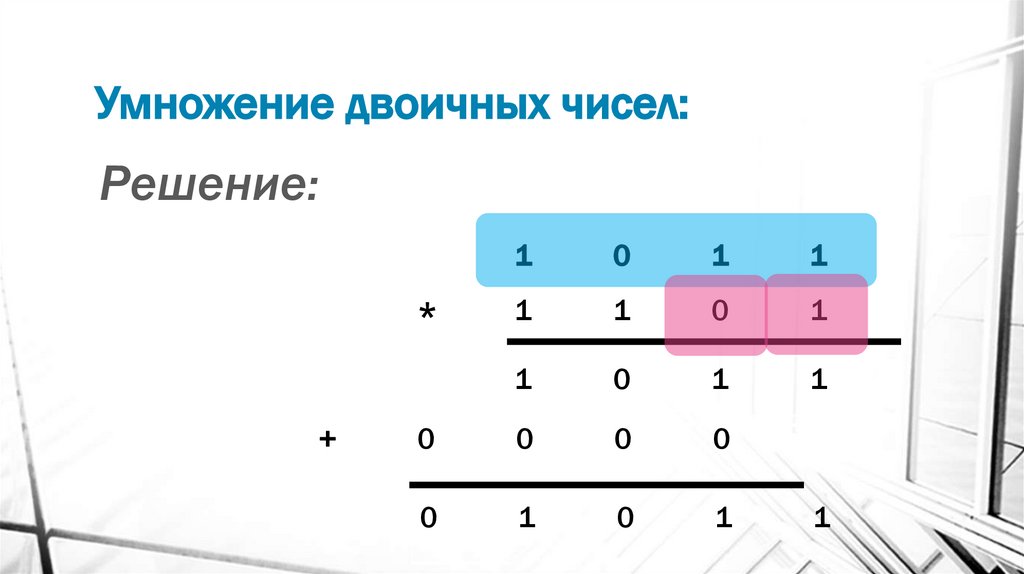
13. Умножение двоичных чисел:
Решение:1
1
1
*
+
+
+
+
1
0
0
1
0
1
0
1
0
1
0
0
0
1
1
1
1
0
1
1
1
0
0
1
0
1
1
1
1
14. Умножение двоичных чисел:
Пример:Найти произведение двоичных чисел:
1011 и 1101, начиная формирование
частичных произведений с младшего
разряда множителя и применяя учет
сформированных частичных произведений
по мере их формирования.
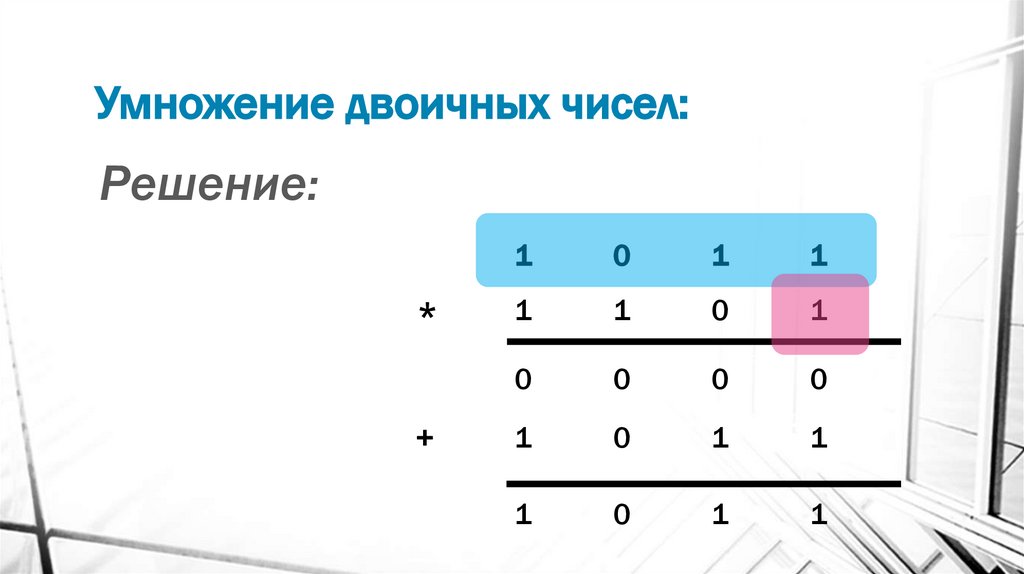
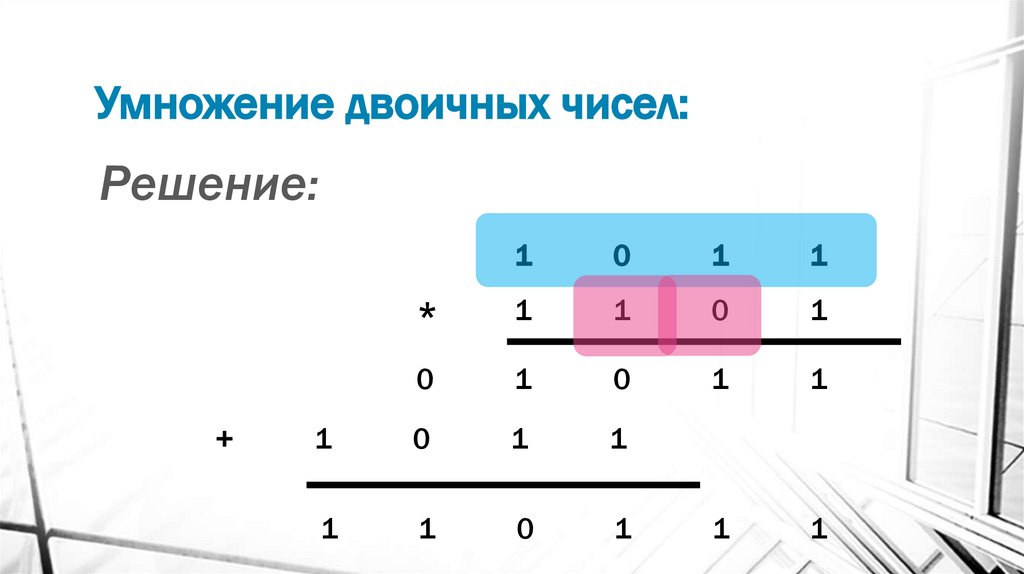
15. Умножение двоичных чисел:
Решение:*
+
1
0
1
1
1
1
0
1
0
0
0
0
1
0
1
1
1
0
1
1
16. Умножение двоичных чисел:
Решение:1
0
1
1
1
1
0
1
1
0
1
1
0
0
0
0
0
1
0
1
*
+
1
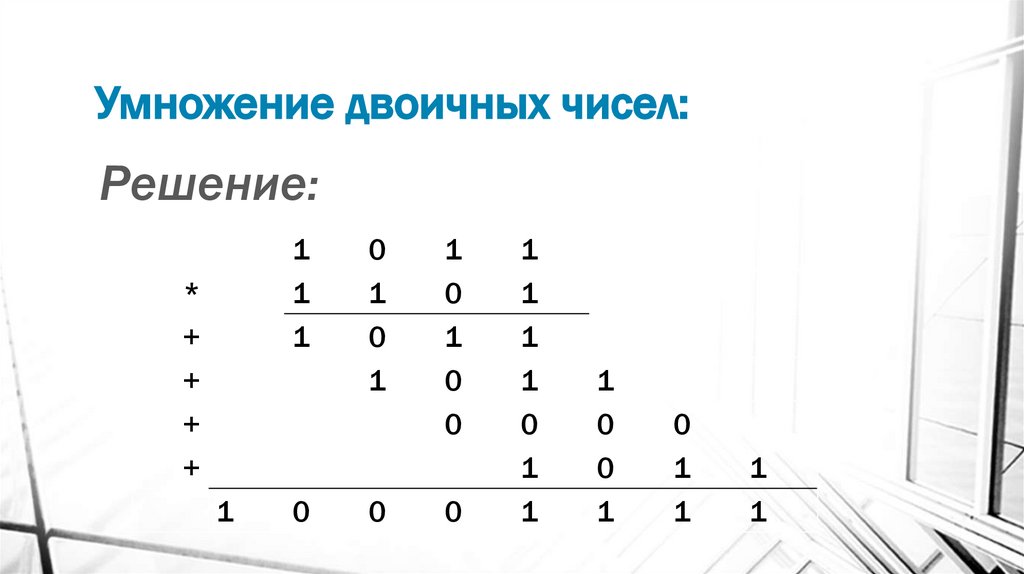
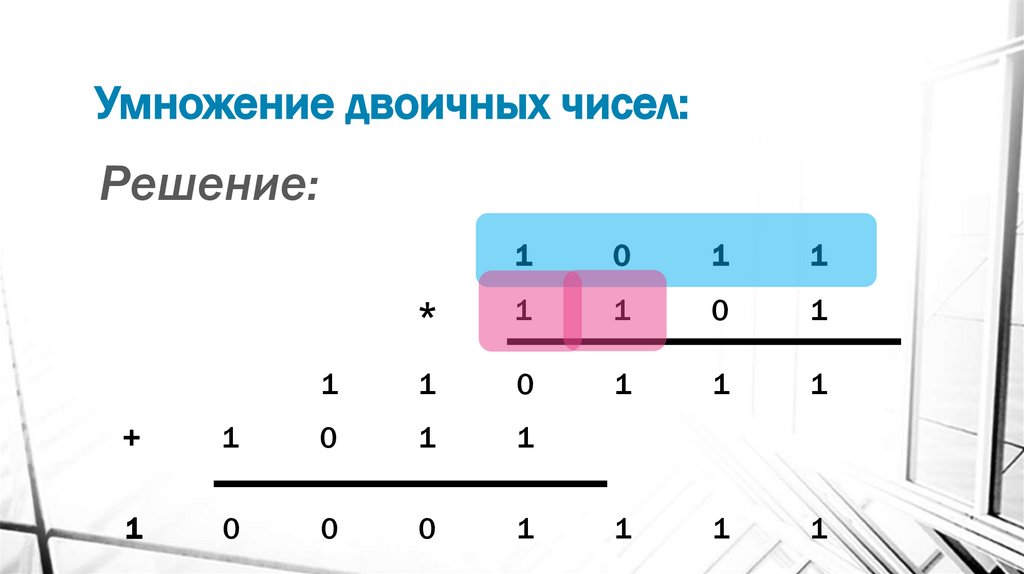
17. Умножение двоичных чисел:
Решение:+
1
0
1
1
*
1
1
0
1
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
18. Умножение двоичных чисел:
Решение:1
0
1
1
*
1
1
0
1
1
1
0
1
1
1
1
1
1
+
1
0
1
1
1
0
0
0
1
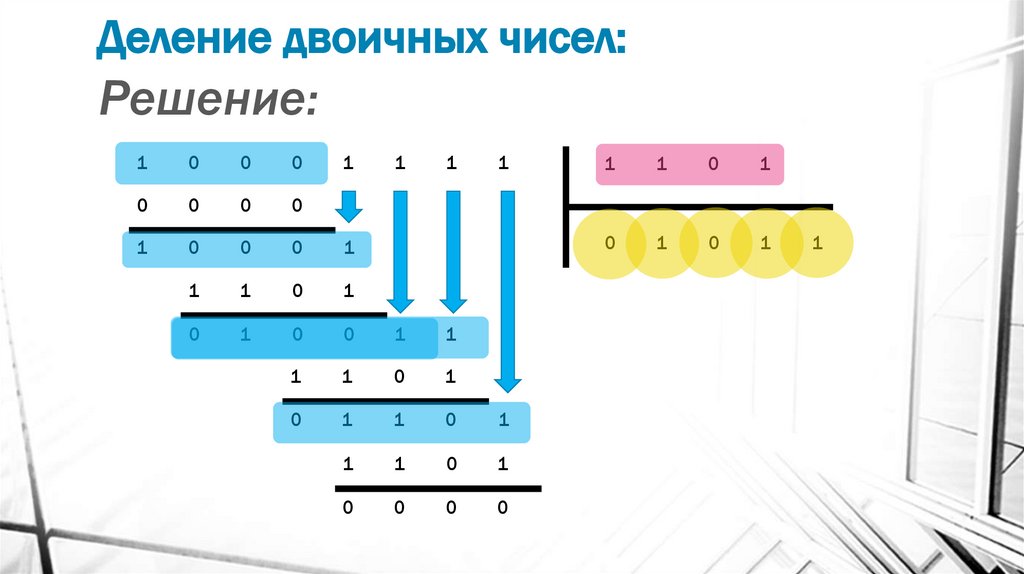
19. Деление двоичных чисел:
Пример:Найти
частное
10001111 на 1101.
двоичных
чисел:
20. Деление двоичных чисел:
Решение:1
0
0
0
1
1
1
1
0
0
0
0
1
0
0
0
1
1
1
0
1
0
1
0
0
1
1
1
1
0
1
0
1
1
0
1
1
1
0
1
0
0
0
0
1
1
0
1
0
1
0
1
1
21. Сложение двоично-десятичных чисел:
A=B+C;где
B=3927; C= 4856;
B=3927=0011 1001 0010 0111;
C=4856=0100 1000 0101 0110;
22. Сложение двоично-десятичных чисел:
***
0011
1001 0010 0111 ( B )
+ 0100
1000 0101 0110 ( C )
1000
+
0001 0111 1101 ( Двоичная сумма )
0110
1000
0110 ( Коррекция )
0111 1000 0011 ( Двоично-десятичная сумма )
23.
Сложение двоично-десятичных чисел:• * -- Добавить шестерку (0110) в те тетрады где
был перенос;
• ** -- Добавить шестерку (0110) в те тетрады, в
которых получено значение больше 9 (1001);
24. Разность двоично-десятичных чисел:
A=C-B;где
B=3927; C= 4856;
B=3927=0011 1001 0010 0111;
C=4856=0100 1000 0101 0110;
25. Разность двоично-десятичных чисел:
***
0100
1000 0101 0110 ( C )
- 0011
1001 0010 0111 ( B )
0000
-
1111 0010 1111 ( Двоичная сумма )
0110
0000
0110 ( Коррекция )
1001 0010 1001 ( Двоично-десятичная сумма )
26.
Разность двоично-десятичных чисел:• * -- Вычесть шестерку (0110) из тех тетрад в
которые пришел заем;



















 Информатика
Информатика








