Лекция_8_Теоремы_о_среднем_Правило_Лопиталя_Формула_Тейлора

1. Основные теоремы и применения дифференциального исчисления

Некоторые теоремы о дифференцируемых
функциях (теоремы о среднем значении)
Правило Лопиталя раскрытия неопределенностей
Формула Тейлора

2. Некоторые теоремы о дифференцируемых функциях

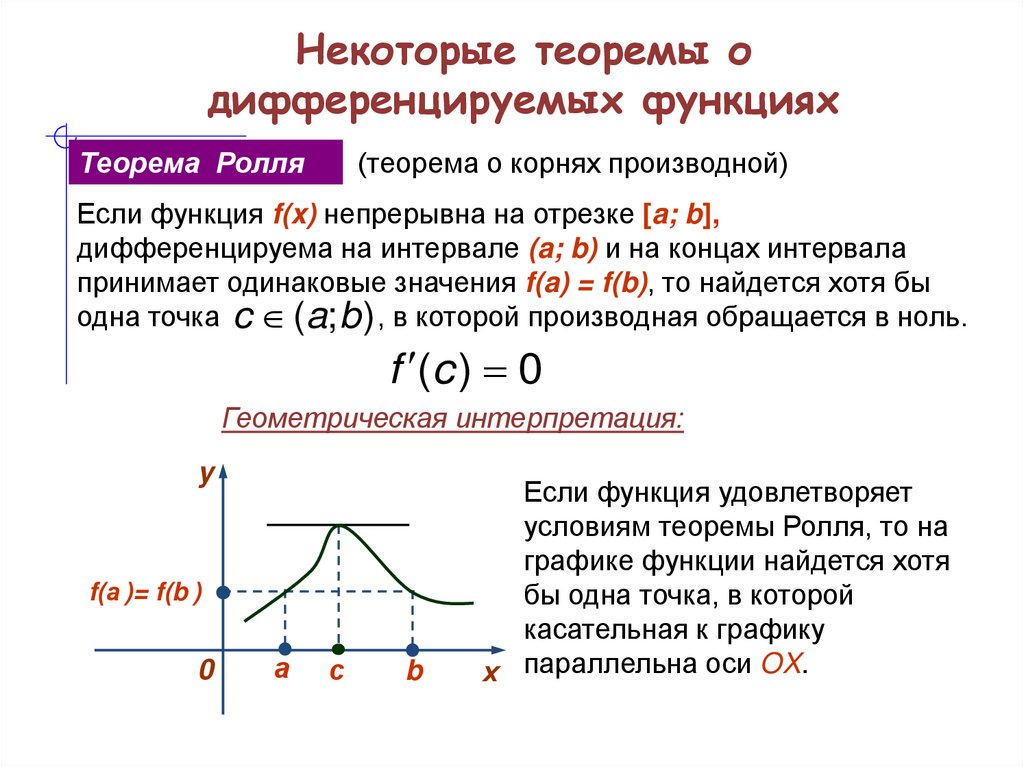
Теорема Ролля
(теорема о корнях производной)
Если функция f(x) непрерывна на отрезке [a; b],
дифференцируема на интервале (a; b) и на концах интервала
принимает одинаковые значения f(a) = f(b), то найдется хотя бы
одна точка c (a; b ) , в которой производная обращается в ноль.
f (c ) 0
Геометрическая интерпретация:
y
f(а )= f(b )
0
а
с
b
Если функция удовлетворяет
условиям теоремы Ролля, то на
графике функции найдется хотя
бы одна точка, в которой
касательная к графику
х параллельна оси OX.

3. Некоторые теоремы о дифференцируемых функциях

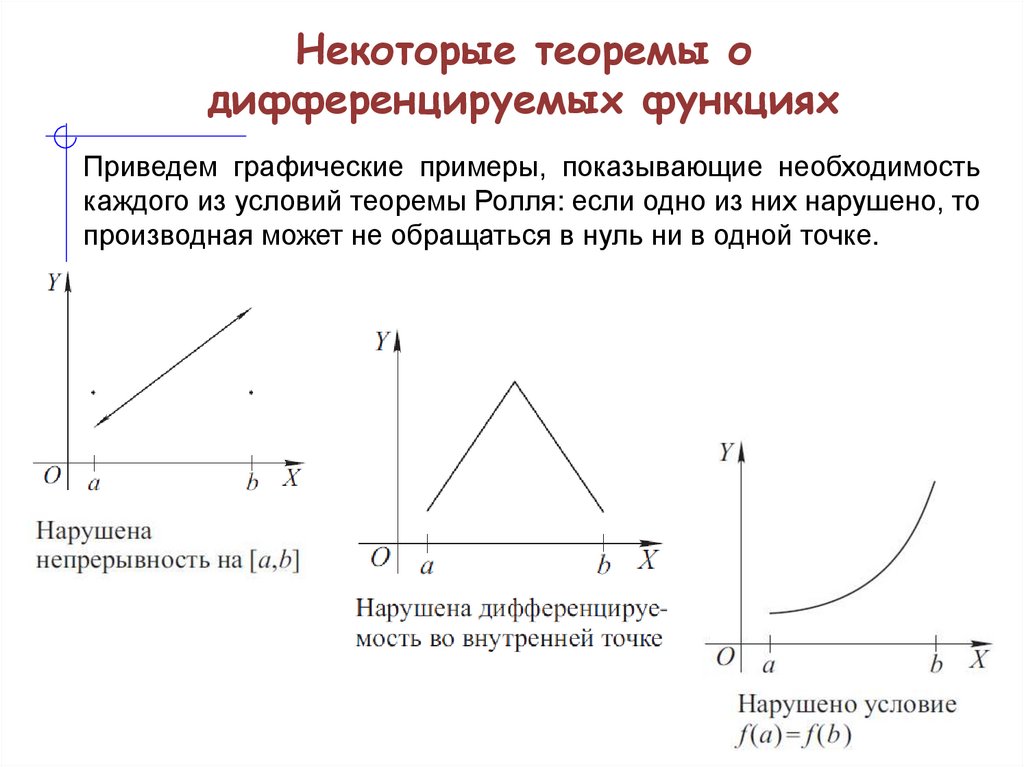
Приведем графические примеры, показывающие необходимость
каждого из условий теоремы Ролля: если одно из них нарушено, то
производная может не обращаться в нуль ни в одной точке.

4. Некоторые теоремы о дифференцируемых функциях

Теорема Коши
(теорема об отношении приращений)
Если функции f(x) и g(x) непрерывны на отрезке [a; b],
дифференцируемы на интервале (a; b), причем g ( x ) 0 для
x (a; b ) ,то найдется холя бы одна точка c (a; b ) , такая,
что выполняется равенство:
f ( b ) f (a )
f (c )
g (b ) g (a ) g (c )
На графике функции найдется
хотя бы одна точка, в которой
касательная параллельна хорде
AB
Теорема Лагранжа (теорема о конечных приращениях)
y
Если функция f(x) непрерывна на
В
отрезке [a; b], дифференцируема
f ( b ) f (a )
на интервале (a; b) ,то найдется
А
хотя бы одна точка c (a; b ), в
которой выполняется равенство:
b a
f (b ) f (a ) f (c ) (b a )
0
а
с
b
х

5. Правило Лопиталя

Рассмотрим способ раскрытия неопределенностей вида
0
и
, который основан на применении производной.
0
Теорема

6. Правило Лопиталя

Доказательство

7. Правило Лопиталя

8. Правило Лопиталя

9. Правило Лопиталя

10. Правило Лопиталя

11. Правило Лопиталя

tg 3 x
3 cos 2 5 x
(tg 3 x )
lim
lim
lim
2
tg 5 x
x
x cos 3 x 5
x (tg 5 x )
2
2
2
2
3
cos 5 x 0
3
cos 5 x
lim
lim
2
5 x cos 3 x 0
5 x cos 3 x
2
2
2
2
3
cos 5 x 3
(cos
5
x
)
lim
lim
x (cos 3 x )
5 x cos 3 x
5
2
2
2
2
2
3 5 5
3
5 sin 5 x
lim
5 x 3 sin 3 x
5 3 3
2

12. Правило Лопиталя

Правило Лопиталя дает
неопределенности типа
также
возможность
раскрывать
00 , 0 , 1 , 0 ,
Действительно, неопределенности типа 00 , , 1
можно свести к неопределенности 0 , предварительно
прологарифмировав соответствующее выражение или
воспользовавшись тождеством
0
f e
g
ln f g
e g ln f
f 0

13. Правило Лопиталя

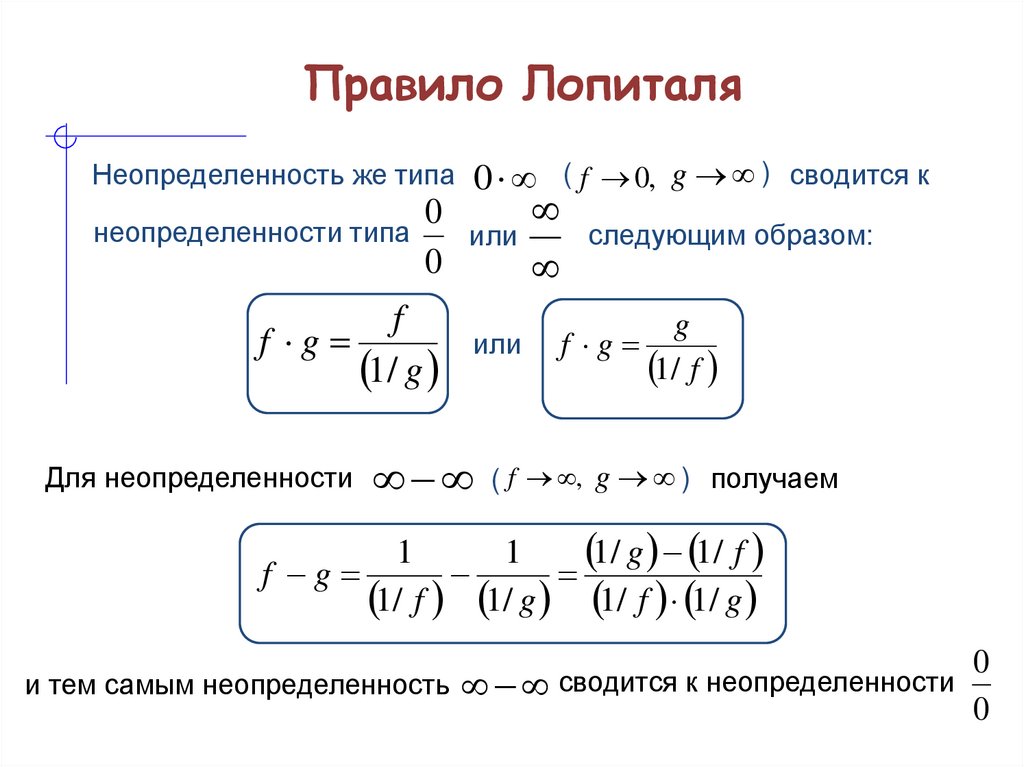
Неопределенность же типа 0 ( f 0, g ) сводится к
неопределенности типа
0
0
f
f g
1/ g
следующим образом:
или
или
g
f g
1/ f
Для неопределенности ( f , g ) получаем
1
1
1/ g 1/ f
f g
1/ f 1/ g 1/ f 1/ g
и тем самым неопределенность сводится к неопределенности
0
0

14. Правило Лопиталя

lim cos 2x x 2 1
1
x 0
Обозначим:
Прологарифмируем равенство:
A lim cos 2x x 2
1
x 0
ln A ln lim cos 2x x 2
x 0
1
ln cos 2 x
0
ln A lim ln cos 2x x lim
2
x 0
x 0
x
0
2 sin 2 x
(ln cos 2 x )
tg 2 x
cos
2
x
lim
lim
2 lim
2
2
x 0
x 0 2 x
x 0
( x )
2x
1
2
ln A 2 A e 2

15. Правило Лопиталя

1
lim
x 0 x
e
tgx
0 e
1
lim tgx ln
x 0
x
0 e
ln x
lim
x 0 ctgx
e
e
e
sin x
lim sin x
x 0 x x 0
lim
1
ln lim
x 0 x
tgx
lim tgx ln x
x 0
1
x
lim
1
x 0
2
sin x
1 0
e 1
e
e
1
lim ln
x 0 x
e
tgx
ln x
lim
x 0 ctgx
sin 2 x
lim
x 0 x

16. Правило Лопиталя

17. Правило Лопиталя

18. Правило Лопиталя

Предостережем также от невнимательного применения правила
Лопиталя к тем случаям, когда неопределенность отсутствует
Неверное применение правила Лопиталя дает нам
В то же время предел числителя равен 2, а знаменателя – 0,
поэтому искомый предел равен .

19. Формула Тейлора

20. Формула Тейлора

Теорема

21. Формула Тейлора

Доказательство

22. Формула Тейлора

Определение

23. Формула Тейлора

Теорема
Доказательство

24. Формула Тейлора

Замечание

25. Формула Тейлора

Теорема

26. Формула Тейлора

27. Формула Тейлора

Пример

28. Формула Тейлора

29. Формула Тейлора

Пример
Пример