Похожие презентации:
Дифференциальное исчисление функции одной переменной
1.
Дифференциальноеисчисление
функции одной
переменной
2.
ОПРЕДЕЛЕНИЕ Производной функции y f xв точке x называется предел отношения приращения
функции к приращению аргумента, когда приращение
аргумента стремится к нулю.
f x x f x
f x lim
.
x 0
x
Производная функции f x , вычисленная
некоторой фиксированной точке x 0 , равна
f x 0 x f x 0
f x 0 lim
.
x 0
x
в
3.
ПРИМЕР Найти производную функции y x .Возьмем произвольное x D y R и дадим
ей приращение x . Функция получит приращение
2
y x x x
2
2
2
2
x 2x x x x 2x x x .
2
2
y 2x x x
2x x .
x
x
2
4.
yy lim
lim 2 x x
x 0 x
x 0
lim 2x lim x 2x 0 2x .
x 0
x 0
Таким образом,
x 2 x
2
.
5.
ПРИМЕР Найти производную функции y sin xИмеем
x
x
2 sin
cos x
y sin x x sin x
2
2
x
x
x
x
sin
x
2
cos x
.
x
2
2
6.
xsin
y
x
2
lim
lim
lim cos x
x 0 x
x 0
x x 0
2
2
,
1 cos x cos x
то есть или sin x cos x .
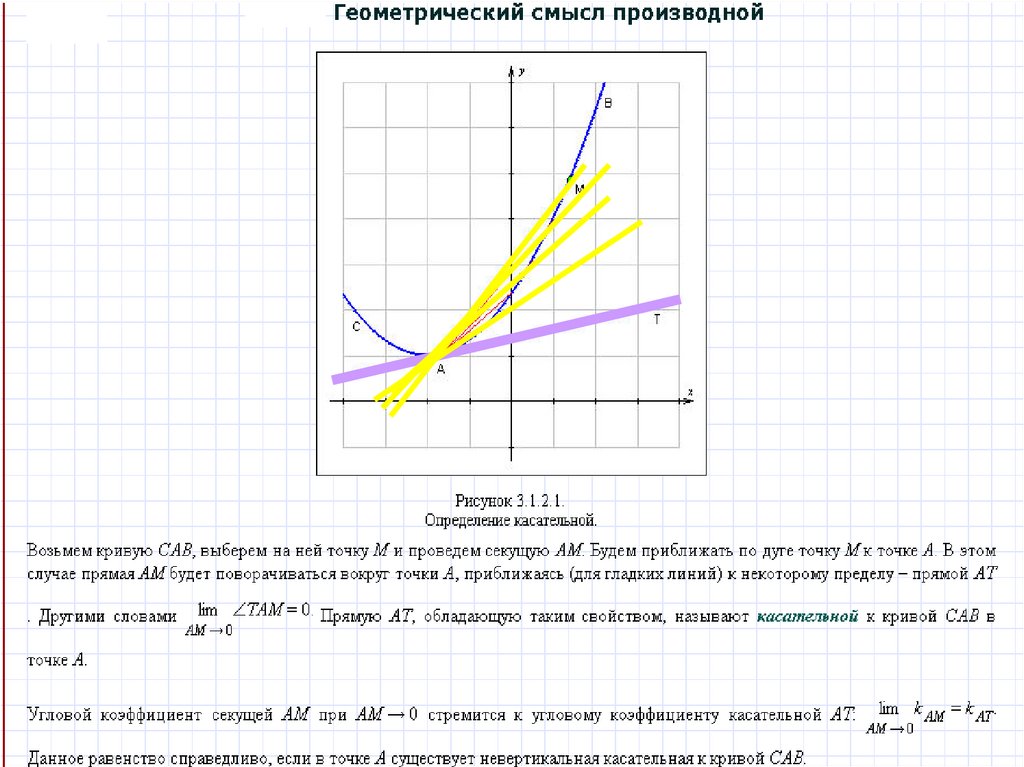
7.
8.
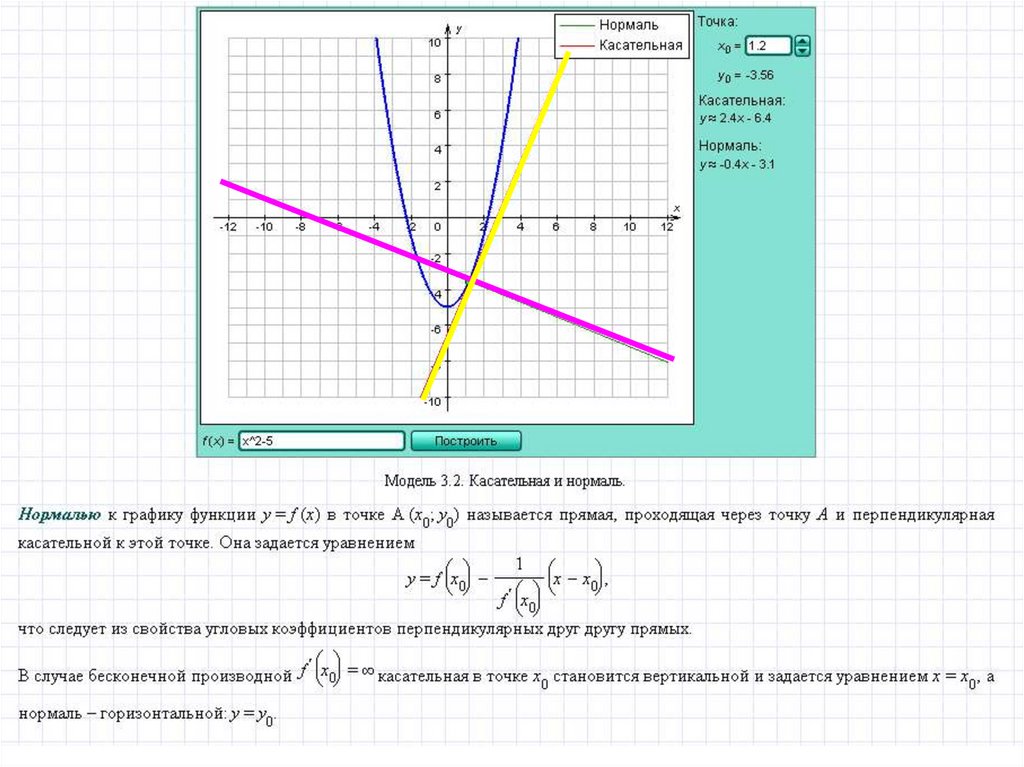
Пользуясьуравнением
прямой,
проходящей через точку M 0 x 0 , y 0 с
заданным
угловым
коэффициентом
k f x 0 , можно записать уравнение
касательной:
y y 0 f x 0 x x 0 .
9.
10.
ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИЕсли функция y f x в точке x x 0 имеет
производную, то говорят, что в этой точке функция
дифференцируема.
y f x ,
ОПРЕДЕЛЕНИЕ.
Функция
имеющая производную в каждой точке некоторого
интервала a , b , называется дифференцируемой в
этом интервале.
Операцию нахождения производной функции
называют дифференцированием функции.
11.
Теорема Если функция y f xдифференцируема в некоторой точке x x 0 ,
то она в этой точке непрерывна.
Обратное утверждение теоремы неверно, то
есть из того, что функция y f x в какойнибудь точке x x 0 непрерывна, еще не
следует,
что
в
этой
точке
она
дифференцируема.
12.
13.
ОСНОВНЫЕ ПРАВИЛАДИФФЕРЕНЦИРОВАНИЯ
Теорема Пусть функции u u x и v v x
дифференцируемы в точке x . Тогда:
1. Производная суммы (разности) двух функций
равна сумме (разности) производных этих функций:
u v u v .
2. Производная произведения двух функций
равна:
u v u v u v
3. Производная частного двух функций равна:
u v uv
u
, если v x 0 .
2
v
v
14.
ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИОПРЕДЕЛЕНИЕ. Пусть y f u и u x ,
тогда
y f x является сложной функцией
переменной
x , а переменную u называют
промежуточным аргументом.
Теорема Если функция u x имеет в
некоторой точке x производную u x x , а функция
y f u имеет в соответствующей точке u x
y u f u , то сложная функция
производную
y f x в указанной точке
также имеет
производную, которая находится по формуле
y f u x
или,
коротко,
y y u u x .
x
15.
ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИПусть функция y f x строго монотонна в
интервале a , b , тогда для нее существует обратная
функция x y .
Теорема Если функция y f x в некоторой
точке x имеет отличную от нуля производную f x ,
то обратная ей функция x y в соответствующей
точке y также имеет производную y , равную
1
y
.
f x
16.
ПРИМЕР Найти производную для y arcsin x .Обратная ей функция имеет вид x sin y , где
y ; . В интервале
2 2
x cos y 0 . Тогда по правилу
;
2 2
имеем
дифференцирования
обратной функции
arcsin x
1
1
1
1
2
2
cos
y
1
sin
y
1
x
sin y
, где перед корнем взят знак +, так как cos y 0 при
y ; .
2 2
17.
Найдем производную функции y arctg x .Она является обратной к функции x tg y , где
y ; . Тогда
2 2
1
1
1
2
,
arctg x
cos y
2
2
1
tg
y
1
x
tg y
то есть
arctg x
1
1 x
2
.
Аналогичным образом находим
arcctg x
1
1 x2
.
18.
ФОРМУЛЫ ДИФФЕРЕНЦИРОВАНИЯ ОСНОВНЫХЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
n x
3. e e
1. x
n
x
a
n 1
ln a
1
4. log a x
x ln a
6. sin x cos x
2. a
x
5. ln x
1
x
7. cos x sin x
1
2
cos
ec
x
sin 2 x
1
11. arcctg x
1 x2
1
13. arccos x
1 x2
2
e x e x
sh x
15. ch x
2
1
ch x
17. cth x
2
sh x sh x
x
1
sec 2 x
2
cos x
1
10. arctg x
1 x2
1
12. arcsin x
1 x2
x
x
e e
14. sh x
ch x
2
sh
x
1
2
16. th x
ch x ch x
8. tg x
9. ctg x
x
19.
ПРОИЗВОДНАЯ НЕЯВНО ЗАДАННОЙФУНКЦИИ.
Если функция задана неявным уравнением F x, y 0 , т.е. не разрешенным
относительно y , то для нахождения производной y x надо продифференцировать по
x обе части этого уравнения, учитывая, что
y есть функция от x , и затем разрешить
полученное уравнение относительно y x .
20.
ПРИМЕР x y 9 0 .2
2
2
Решение. Так как y является функцией x , то y сложная функ-
ция. Следовательно y
2 y y x . Продифференцировав по x обе
части данного уравнения, получим
2
x
2
y
y 9 0 x
x
таким образом y .
y
2
2
2
0 2x 2 y y 0 ,
21.
ПРИМЕР sin x y cos x y tg x y .Решение. Продифференцируем обе части данного уравнения по x , получим
sin xy cos xy tg x y
cos x y x y sin xy xy
1
x
y
cos xy y xy sin xy y xy
2
cos x y
1
1
1 y cos xy y sin xy y 2
cos 2 x y
cos x y
1
. Отсюда
y x cos xy x sin xy
2
cos x y
cos 2 x y cos xy y sin xy y 1
y
.
2
cos x y cos xy x sin xy x 1
22.
ЛОГАРИФМИЧЕСКАЯПРОИЗВОДНАЯ
функции f x 0 есть производная от логарифма
данной функции ln f x :
ln f x
f x
.
f x
Вычисление логарифмической производной называется логарифмическим дифференцированием. Логарифмическое дифференцирование применяется при
вычислении производной показательно-степенной
функции
y f x ,
где f x и x имеют производные в точке x 0 и
f x 0 , а также при нахождении производной произ x
ведения и частного нескольких функций.
23.
ПРИМЕР y sin 3xx
.
Решение. Найдем логарифм данной функции ln y ln sin 3x
x
или
ln y x ln sin 3x . Дифференцируя обе части этого равенства, получим
3 cos 3x
y
1
.
Отсюда
ln y x ln sin 3x
ln sin 3x x
y 2 x
sin 3x
ln sin 3x
x ln sin 3x
y y
3 x ctg 3x y sin 3x
3 x ctg 3x
2 x
2 x
24.
ПРИМЕР y3
6x 1 2x 1
.
5
15x 4
Решение. Прологарифмируем данное равенство
1
1
1
1
6x 1 3 2x 1 2
ln y ln 6x 1 3 ln 2x 1 2
ln y ln
1
5
4
x
15
1
1
1
1
ln 15x 4 5 ln y ln 6x 1 ln 2x 1 ln 15x 4 .
5
2
3
Дифференцируя обе части последнего равенства, получим
15
2
6
y
y 3 6x 1 2 2x 1 5 15x 4
3
1
2
y y
6x 1 2x 1 15x 4
3
6x 1 2x 1 2
3
1
y
.
5
15x 4
6x 1 2x 1 15x 4
25.
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙЗАДАННЫХ ПАРАМЕТРИЧЕСКИ
Если функция y аргумента x задана параметрическими уравнениями
x x t ,
y y t
то производная функции y по переменной
x , т.е. y x вычисляется по формуле:
y t
y x .
x t
26.
x 1 t 2 ,ПРИМЕР
y t t 3 .
2
Решение. Найдем x t 2 t и y t 1 3t .
1 3t 2
Следовательно y x
.
2t
x a cos t ,
ПРИМЕР
y a sin t.
Решение. Найдем x t a sin t; y t a cos t.
a cos t
ctgt .
Тогда y x
a sin t
27.
ДИФФЕРЕНЦИАЛ ФУНКЦИИДифференциалом 1-го порядка dy функции
y y x называется главная часть ее приращения,
пропорциональная приращению x независимой
переменной x .
Дифференциал независимой переменной
dx равен ее приращению x .
Дифференциал любой дифференцируемой
функции y y x равен произведению ее производной на дифференциал независимой переменной.
dy y x dx
28.
Если x достаточно мало по абсолютной величине, то с точностью до бесконечно малых более высокого порядка малости, чем x , имеет место приближенноеравенство:
y dy
или
y x x y x y x x .
29.
Основные свойства дифференциалаdc 0, где C const ;
d C U C dU;
d U dU d ;
d U U d dU ;
U dU U d
5) d
, где 0;
2
6) d f U f U dU.
1)
2)
3)
4)
30.
ПРИМЕРНайти
дифференциал
x2
функции y e .
Решение.
dx e
dy e
x
2
x
2x dx .
31.
ПРИМЕР Вычислить приближенное значение arcsin0,51.Решение. Рассмотрим функцию y arcsin x ,
полагая x 0 0,5; x 0,01
и применяя формулу
y dy f x 0 x f x 0 f x 0 x
f x 0 x f x 0 f x 0 x ,
получим
arcsin 0,5 0,01
arcsin 0,5 arcsin x
1
1 0,5
2
x 0 0,5
0,01 arcsin 0,51 arcsin 0,5
0,01 0,01 0,513 .
6
32.
ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХПОРЯДКОВ
Производной второго порядка функции y f x на-
зывается производная от ее производной, т.е. y .
Вторая производная обозначается y или f x . Если
существует производная от второй производной, то ее называют третьей производной и обозначают f x или y
f x f x .
Производной n порядка называют производную от
производной n 1 го порядка. Производную n го по n
n
рядка обозначают f x или y
n
n 1
x .
f x f
33.
Если функция задана параметрически, то производные y x x ; y x x x ; вычисляются по формуламy x t y t t x t x t t y t
y x x
3
x t
x t
y x x t
y x x x
и т.д.
x t
34.
Дифференциалом второго порядка функцииy f x называется дифференциал от дифференциа-
ла первого порядка: d y d dy .
Аналогично определяется дифференциал третье3
2
го порядка: d y d d y и в общем виде
2
d y dd
n
n 1
y.
Если y f x , где x - независимая переменная,
то дифференциалы высших порядков вычисляются по
d y y dx ;
n
n
n
d y y dx .
формулам
2
2
d y y dx , … ,
3
3
35.
ПРИМЕР Найти дифференциалы первого, второго итретьего порядков функции y 2x 3 .
3
Решение. dy 3 2x 3 2dx 6 2x 3 dx ;
2
2
d 2 y 12 2x 3 2dx 2 24 2x 3 dx 2 ;
d 3 y 24 2dx 3 48dx 3 .
ПРИМЕР Найти f 1 , если f x x .
5
f x 20 x
3
60 x
Решение. f x 5 x ; f x 5 x
4
2
4
20 x 3 ;
2
f 1 60 1 60 .
36.
ПРИМЕР Найти y x x , если x a cos t; y a sin t .3
Решение. y x
a sin t
a cos t
3
3
tg t t
t
t
3
3 a sin 2 t cos t
tg t
2
3 a cos t sin t
sec 2 t
1
y x x
2
4
a cos 3 t t 3 a cos t sin t 3 a sin t cos t
37.
ПРИМЕР Найти дифференциалы второго итретьего порядков функции y x ln x 1 .
Решение. dy x ln x 1 x ln x 1 dx
1
dy ln x 1 x dx
x
dy ln x 1 1 dx dy ln xdx .
1 2
2
2
d y d ln xdx d y dx ;
x
1 2
2
3
3
d y d d y d y d dx
x
1
3
d y 2 dx 3 .
x
38.
ПРАВИЛО ЛОПИТАЛЯПусть функции f x и x дифференцируемы в окрестности точки x 0 и x 0 при всех x из этой окрестности, тогда, если
lim f x lim x 0
x x 0
или
x x 0
lim f x lim x ,
x x 0
x x 0
f x
т.е. частное
принимает в точке x x 0 неопределенную
x
0
форму или , то
0
f x
f x
lim
lim
x x 0 x
x x 0 x
при условии, что существует предел отношения производных.
39.
f xЕсли частное
в точке x x 0 будет
x
0
также неопределенностью вида или
и
0
f x и x удовлетворяют соответствующим условиям, то следует перейти к отношению вторых производных и т.д.
40.
В случае неопределенности 0или необходимо алгебраически преобразовать данную
функцию так, чтобы привести к
0
неопределенности вида или
0
и далее воспользоваться правилом
Лопиталя.
41.
В случае неопределенности0
0
вида 0 или или 1 следует прологарифмировать
данную функцию и найти
предел ее логарифма.
42.
16
ПРИМЕР lim
.
2
x 3 9 x
x 3
Решение. В данном случае имеем неопределенность вида . Приведя выражение в
скобках к общему знаменателю, получим
6 3 x
x 3
.
В
результате
lim
lim
x 3 9 x 2
x 3 9 x 2
0
имеем неопределенность вида . Применив пра0
вило
Лопиталя,
x 3
1
1
.
lim
lim
x 3 9 x 2
x 3 2x
6
находим
43.
ln xПРИМЕР lim
.
x 0 ctg x
Решение. Здесь имеет место неопределенность
.
Применим правило Лопиталя, т.е. рассмотрим предел отношения производных заданных функций
1
2
ln x
sin
x
x
.
lim
lim
lim
x 0 ctg x
x 0
x 0 x
1
sin 2 x
0
Последний предел дает неопределенность
. Снова
0
применим
правило
Лопиталя
и
ln x
sin 2 x
2 sin x cos x
lim
lim
lim
0.
x 0 ctg x
x 0
x 0
x
1
получим
44.
ПРИМЕР limx 1
1
x 1 x .
Решение. В данном случае имеем неопределенность вида
1 . Обозначим данную функцию через y , т.е. y x
1
1
1
x
ln x .
гарифмируем ее ln y ln x
1 x
1
1 x ,
и проло-
Вычислим предел логарифма данной функции, применяя
0
правило Лопиталя (имеем здесь неопределенность вида ).
0
1
ln x
lim ln y lim
lim x 1,
так
x 1
x 1 1 x
x 1 1
lim ln y ln lim y , то
x 1
x 1
ln lim y 1 . Отсюда окончательно получаем lim y e 1 .
x 1
x 1
как
45.
1 cos axПРИМЕР lim
x 0 1 cos bx
Решение.
1 cos ax 0
a sin ax 0
a 2 cos ax a 2
lim
lim
lim 2
2
x 0 1 cos bx
0 x 0 b sin bx 0 x 0 b cos bx b
.
46. Теоремы Ролля, Лагранжа и Коши
• Теорема 1. (Теорема Ролля) Пустьфункция f(x)
• непрерывна на отрезке [a, b];
• дифференцируема в интервале (a, b);
• на концах отрезка [a, b] принимает
равные значения.
• Тогда существует точка c О (a, b) такая,
что f'(c) = 0.
47.
48.
• Теорема 2. (Теорема Лагранжа) Пустьфункция f(x)
• непрерывна на отрезке [a, b];
• дифференцируема в интервале (a, b).
• Тогда существует точка с О (a, b) такая,
что
f(b) − f(a) = f '(c) · (b − a) .
(1)
• Формула (1) называется формулой
Лагранжа, или формулой конечных
приращений
49.
50.
Теорема Коши. Если функции f x и g x1) непрерывны на отрезке a , b ,
2) дифференцируемы в интервале a , b , причем g x 0 для
всех x a , b , то найдется хотя бы одна точка c a, b такая, что
f b f a f c
.
g b g a g c
Теорема доказывается аналогично теореме Лагранжа. Для этого
достаточно рассмотреть вспомогательную функцию
f b f a
g x g a .
F x f x f a
g b g a
51.
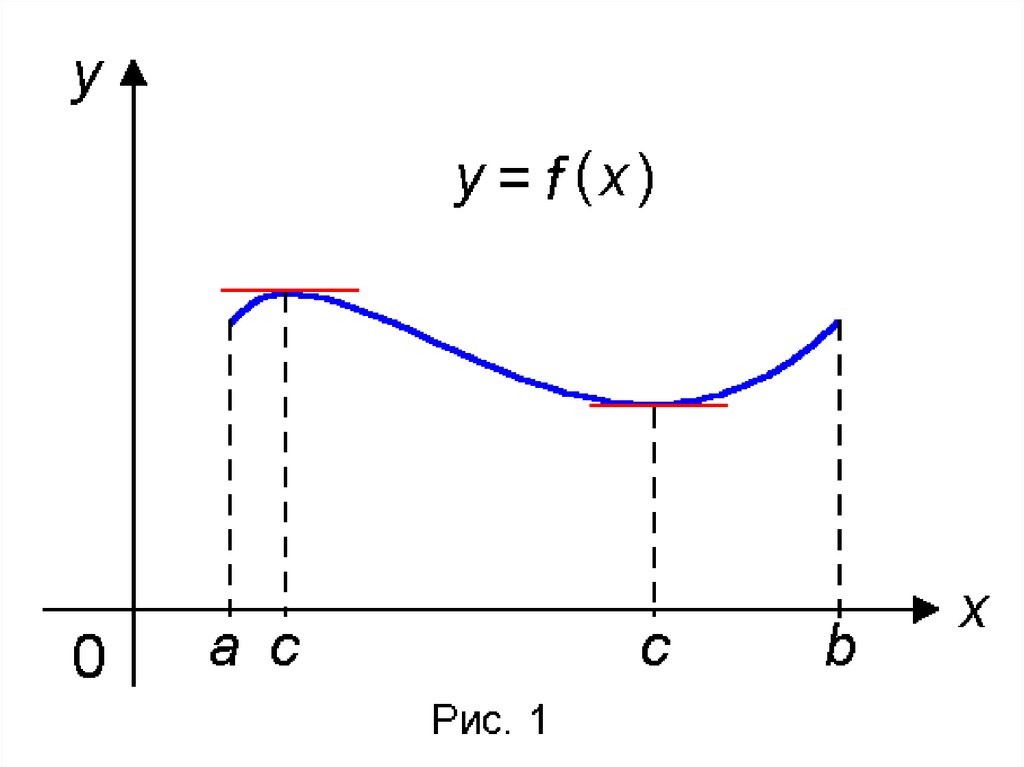
Теорема Ферма. Пустьфункция f x определена на
интервале a; b и некоторой
точке x 0 этого интервала имеет
наибольшее или наименьшее
значение. Тогда, если в точке x 0
существует производная, то она
равна 0, то есть f x 0 0 .
52.
МОНОТОННОСТЬ ФУНКЦИИ(ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ)
Теорема 1 (необходимые условия)
Если дифференцируемая в интервале a , b
функция y f x возрастает (убывает), то f x 0
f x 0 для x a, b .
Теорема 2 (достаточные условия). Если
функция y f x дифференцируема в интервале
a , b и f x 0 f x 0 для x a, b , то
эта функция возрастает (убывает) в интервале
a , b .
53.
ЭКСТРЕМУМ ФУНКЦИИОПРЕДЕЛЕНИЕ.
Точка
x0
называется
точкой
максимума функции y f x , если существует окрестность
точки x 0 , такая, что для всех x x 0 из этой окрестности
выполняется неравенство f x f x 0
Аналогично в точке x 0 функция y f x имеет минимум,
если существует окрестность этой точки, такая, что для всех
x x 0 из этой окрестности выполняется
неравенство
f x f x 0 .
54.
ОПРЕДЕЛЕНИЕ. Значение функции в точкемаксимума
(минимума)
называют
максимумом
(минимумом) функции.
ОПРЕДЕЛЕНИЕ. Максимумом и минимум
функции называют экстремумами функции.
Теорема 3 (необходимое условие экстремума).
Если дифференцируемая функция y f x в точке x 0
имеет экстремум, то ее производная в этой точке равна
нулю, то есть f x 0 0 .
55.
ОПРЕДЕЛЕНИЕ. Точки, в которых производнаяf x равна нулю или не существует, называются
критическими точками функции.
Теорема 4 (достаточное условие экстремума).
Если функция y f x дифференцируема в некоторой
окрестности критической точки x 0 (кроме, быть может,
самой точки x 0 ) и при переходе аргумента x через нее
слева направо производная f x меняет знак с плюса на
минус, то x 0 точка максимума; если f x меняет знак
с минуса на плюс, то x 0 точка минимума.
56.
Теорема 5. Пусть в точке x 0 перваяпроизводная функции равна нулю f x 0 0 ,
а вторая производная существует и отлична от
нуля f x 0 0 . Тогда, если f x 0 0 в
точке x 0 функция имеет максимум и если
f x 0 0 в точке x 0 функция имеет
минимум.
57.
НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ НАОТРЕЗКЕ
Пусть функция y f x непрерывна на отрезке a , b . Как
известно, такая функция на этом отрезке достигает наибольшего и
наименьшего значений. Эти значения функция может принять либо во
внутренней точке отрезка a , b , либо на границе отрезка.
Для нахождения наибольшего и наименьшего значений функции
на отрезке a , b необходимо:
1) найти критические точки функции в интервале a , b ;
2) вычислить значения функции в найденных критических
точках;
3) вычислить значения функции на концах отрезка, то есть при
x a и x b;
4) из всех вычисленных значений функции выбрать наибольшее и
наименьшее.
58.
ВЫПУКЛОСТЬ И ВОГНУТОСТЬ ГРАФИКАФУНКЦИИ.
ТОЧКИ ПЕРЕГИБА
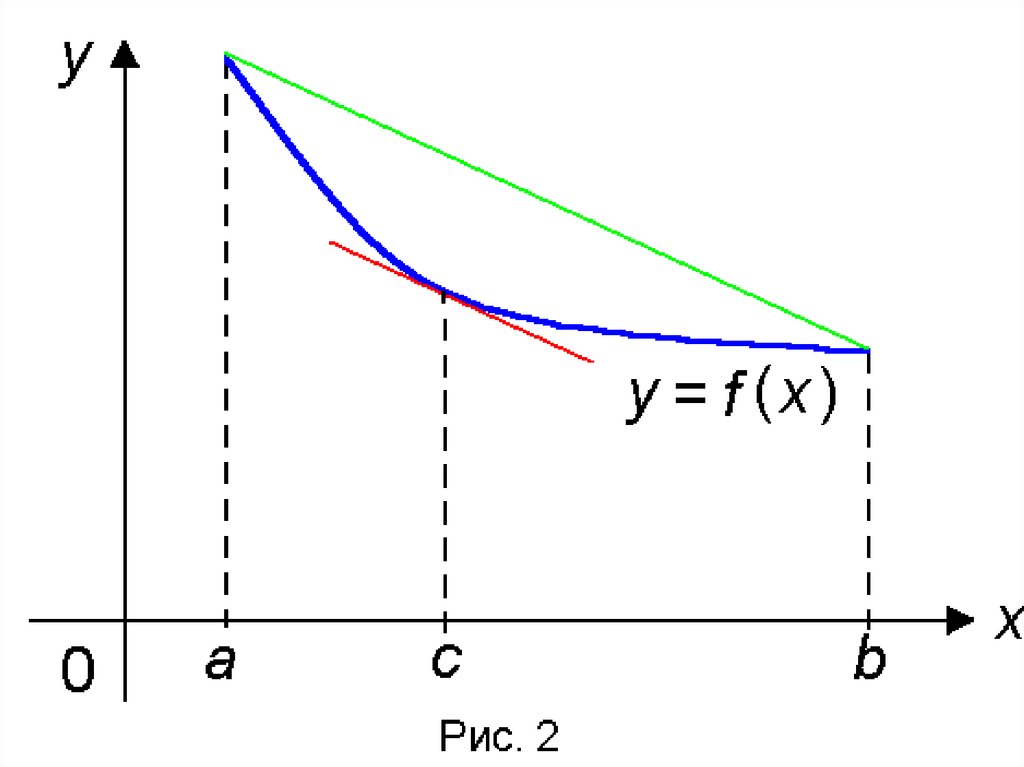
ОПРЕДЕЛЕНИЕ. График дифференцируемой
функции y f x называется выпуклым (или
вогнутым вверх) в интервале a , b , если он
расположен ниже любой ее касательной на этом
интервале.
ОПРЕДЕЛЕНИЕ. График функции y f x
называется вогнутым (или выпуклым вниз) в
интервале a , b , если он расположен выше любой ее
касательной на этом интервале.
59.
yM
0
a
c
b
x
60.
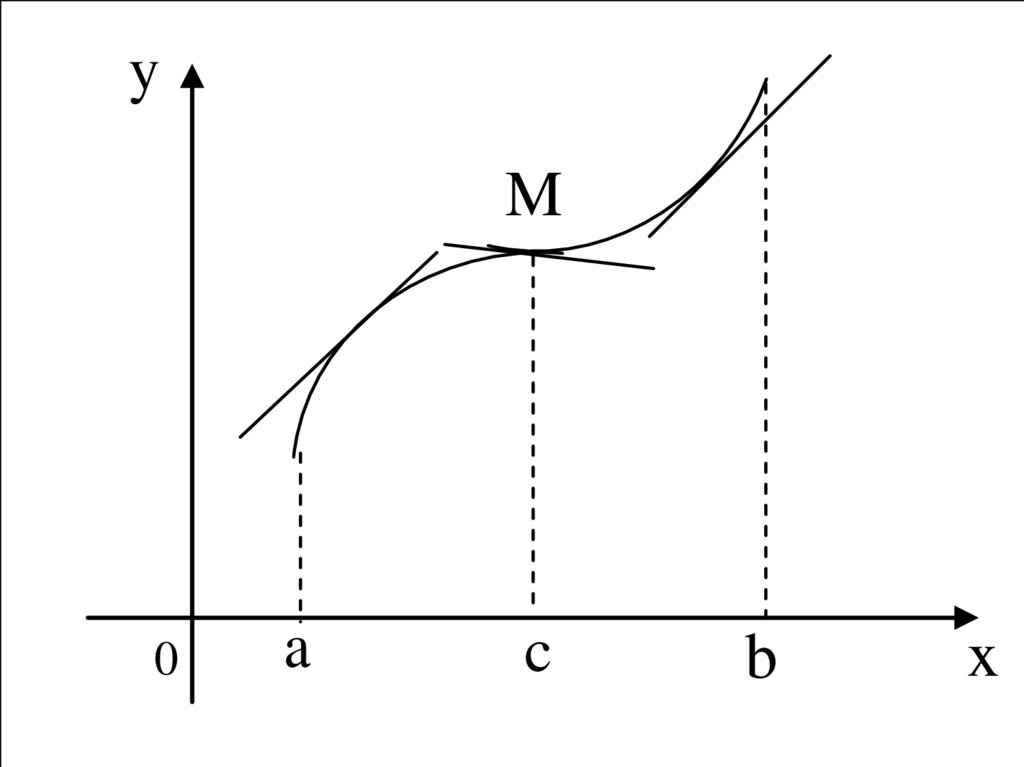
ОПРЕДЕЛЕНИЕ.Точка
графика
непрерывной функции y f x , отделяющая его
выпуклую часть от вогнутой части, называется
точкой перегиба. В интервале a , c кривая
y f x выпукла, в интервале c, b вогнута;
точка M c, f c точка перегиба.
Теорема 6. Если функция y f x во всех
точках интервала a , b имеет отрицательную вторую
производную, то есть f x 0 x a , b , то
график функции в этом интервале выпуклый. Если
f x 0 x a , b , то график функции вогнутый.
61.
Теорема 7 (достаточное условиесуществования точки перегиба). Пусть в
f x 0 0 или f x 0 не
точке x 0
существует. Если при переходе через точку
x 0 вторая производная f x 0 меняет знак,
то точка графика функции с абсциссой x 0
есть точка перегиба.
62.
ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ ИПОСТРОЕНИЯ ГРАФИКОВ
Исследование функции y f x целесообразно вести в
следующей последовательности.
1. Найти область определения функции.
2. Найти (если это можно) точки пересечения графика с осями
координат.
3. Выяснить четность и нечетность функции.
4. Найти асимптоты графика функции.
5. Найти интервалы монотонности функции.
6. Найти экстремумы функции.
7. Найти интервалы выпуклости (вогнутости) и точки перегиба
графика функции.
8. На основании проведенных исследований построить график функции.
63.
ФОРМУЛА ТЕЙЛОРАФормула Тейлора для многочлена
Рассмотрим многочлен степени n :
Pn x a 0 a 1 x a 2 x 2 a n x n . (1.28)
Дифференцируя последовательно n раз, получим
Pn x a 1 2a 2 x 3a 3 x 2 na n x n 1 ,
n 2
Pn x 1 2a 2 2 3a 3 x n 1 n a n x ,
Pn x 1 2 3 a 3 n 2 n 1 n a n x n 3 ,
,
Pn n x 1 2 3 n a n .
64.
Положим во всех равенствах x 0 , тогда найдемPn 0
Pn 0
Pn n 0
a 0 Pn 0 , a 1
, a2
, , a n
.
(1.29)
1!
2!
n!
Подставив найденные значения коэффициентов a 0 , a 1 , , a n в равенство
(1.28), получим
Pn 0
Pn 0 2
Pn n 0 n
Pn x Pn 0
x
x
x .
1!
2!
n!
(1.30)
Формула (1.30) называется формулой Маклорена для многочлена.
65.
Получим теперь разложение многочлена по степеням x x 0 , где x 0произвольное число. Пусть
Pn x b 0 b1 x x 0 b 2 x x 0 2 b 3 x x 0 3
b n x x 0 .
Обозначим x x 0 t x x 0 t . Тогда
n
Pn x Pn x 0 t P n t и
P n t b 0 b1 t b 2 t 2 b 3 t 3 b n t n .
(1.32)
(1.31)
66.
С учетом формул (1.29) получимb 0 P n 0 , b1
P
Но P n t Pn x 0 t , P
Следовательно,
n
0 ,
1!
n
b2
P
n
0 , ,
2!
t Pn x 0 t , ,
n
P n 0
bn
.
n!
n
P n t Pn n x 0 t
P n x 0
P n x 0
Pn n x 0
b 0 Pn x 0 , b1
, b2
, , b n
. (1.33)
1!
2!
n!
67.
Подставив коэффициенты (1.33) в разложении (1.31), получимPn x 0
Pn x 0
2
x x 0
x x 0
Pn x Pn x 0
1!
2!
Pn n x 0
x x 0 n .
n!
(1.34)
Формула (1.34) называется формулой Тейлора для многочлена.
При x 0 0 получаем частный случай формулы Тейлора –
формулу Маклорена.
68.
Разложение по формуле Тейлора некоторых элементарных функций1. Разложение функции f x e .
x
f x e x , f 0 1,
f x e x , f 0 1,
f x e x , f 0 1,
,
f n x e x , f n 0 1 .
Подставляя полученные выражения в формулу (1.38), получаем
x x2 x3
xn
e 1
R n x ,
1! 2! 3!
n!
x n 1 x
e , 0 1.
где R n x
n 1 !
x
69.
Разложение функций f x sin x, cos x .f x sin x, f 0 0 ,
f x cos x sin x , f 0 1,
2
f x sin x sin x 2 , f 0 0 ,
2
f x cos x sin x 3 , f 0 1,
2
f IV x sin x sin x 4 , f IV 0 0 ,
2
,
n
n 0, при n 2k,
n
f x sin x n , f 0 sin
2
2 1 k , при n 2k 1.
2 n 1
2 n 3
x3 x5
n x
n 1 x
sin x x
1
1
cos x .
2n 1 !
2n 3 !
3! 5!
Аналогичным образом получается разложение функции f x cos x :
2n
2n 2
x2 x4
n x
n 1 x
cos x 1
1
1
cos x .
2n !
2n 2 !
2! 4!



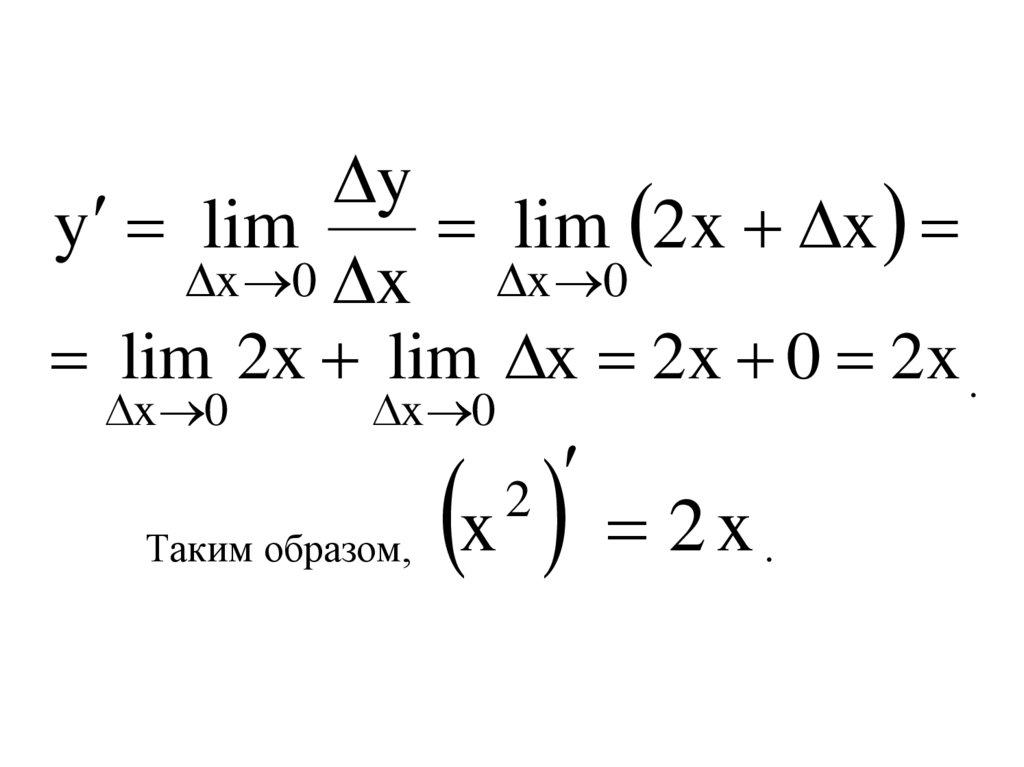

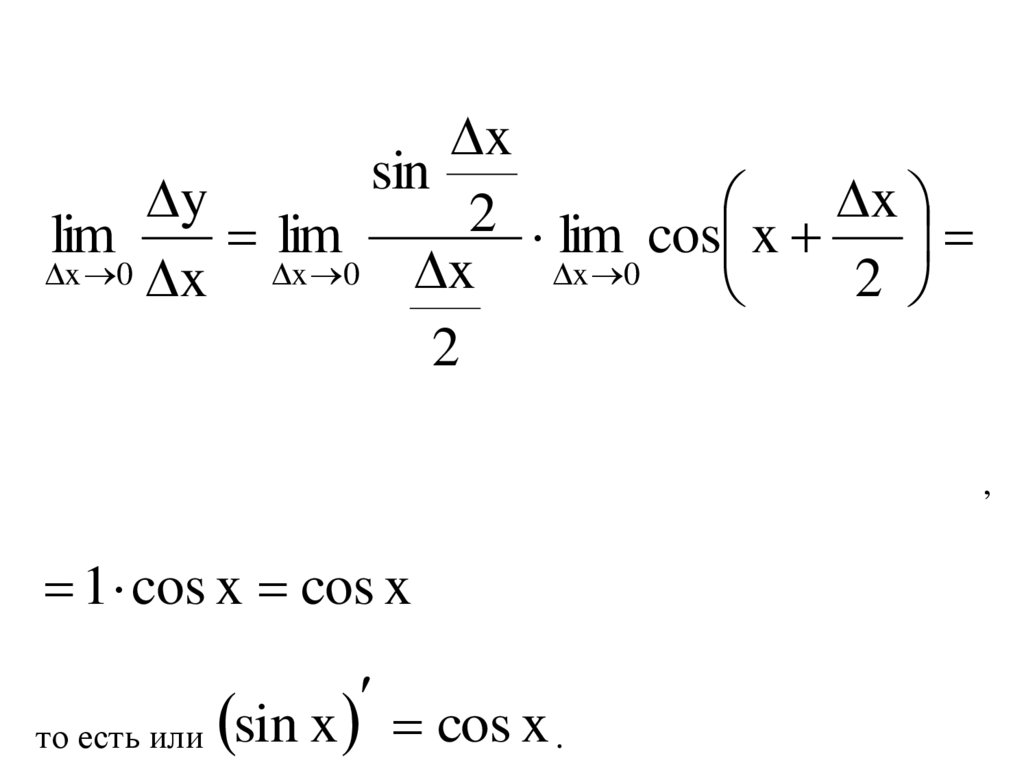
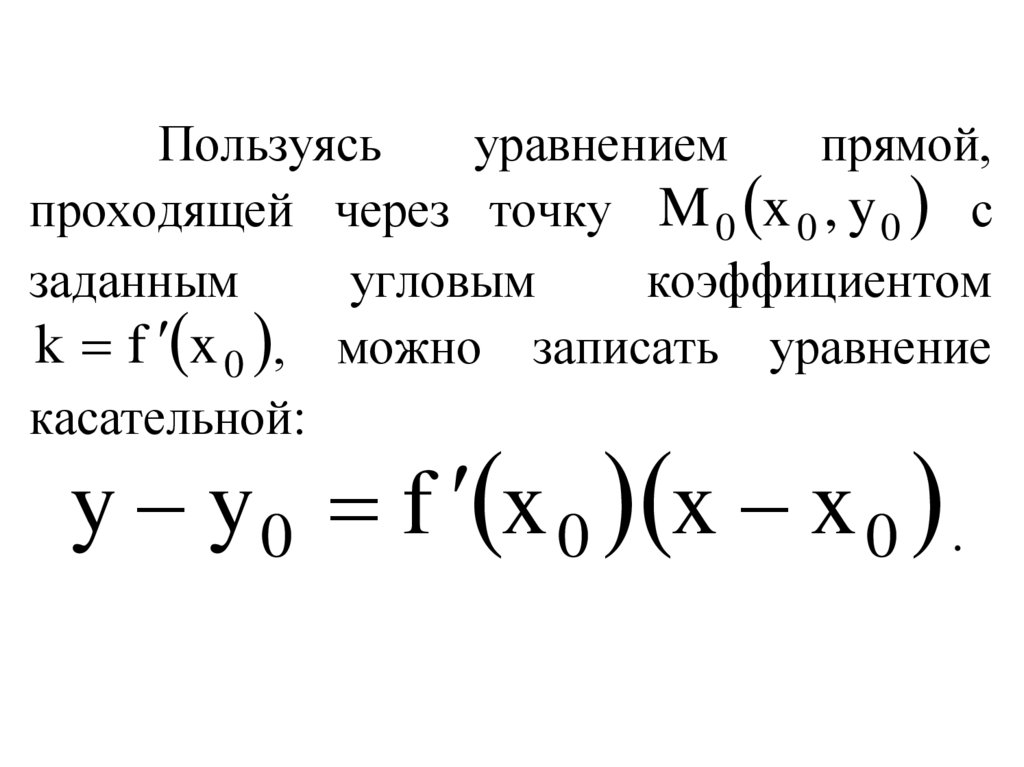










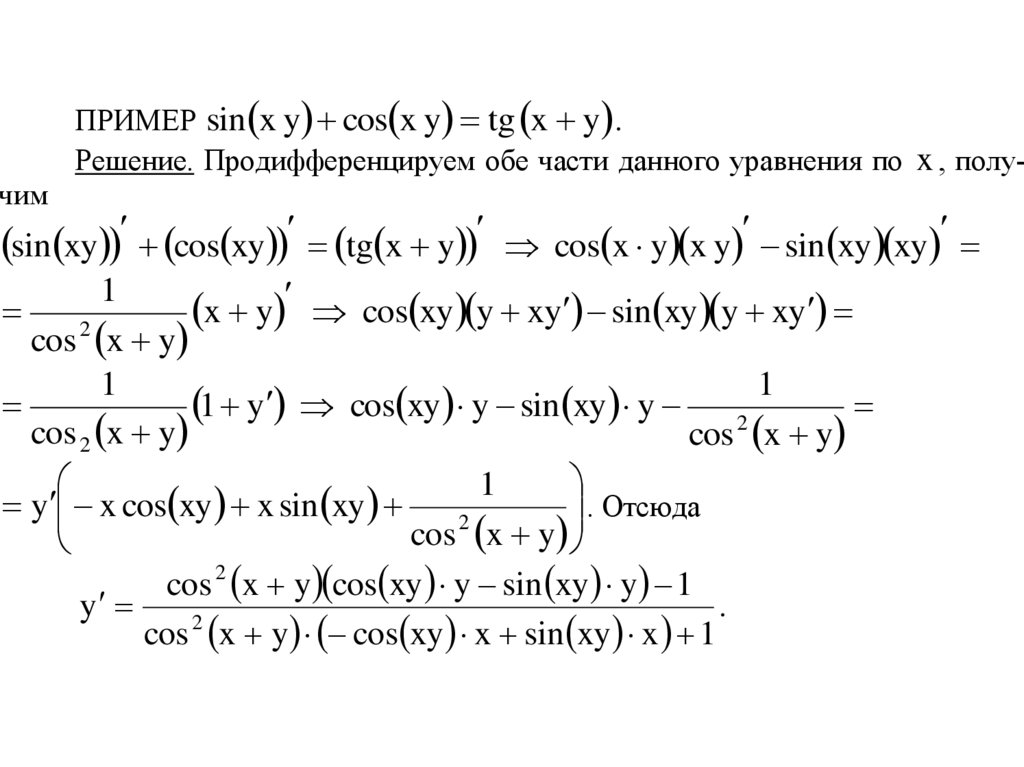














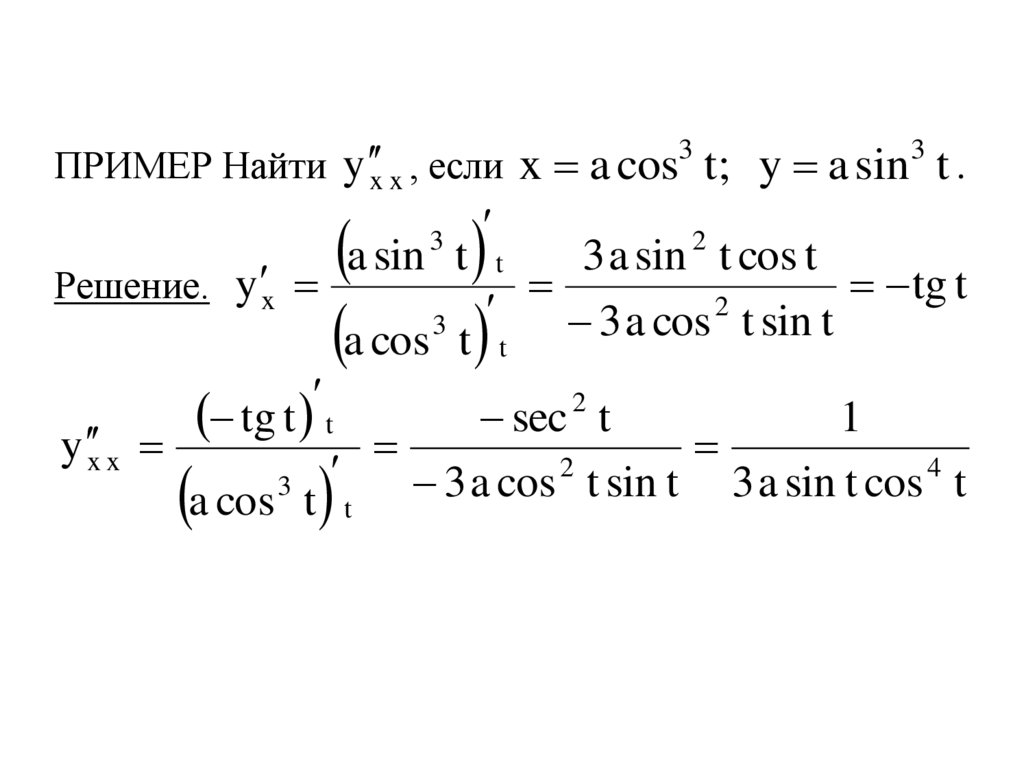






























 Математика
Математика








