СДНФ и СКНФ 2

1. Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма

1

2.

Простой конъюнкцией (элементарной)
называется конъюнкция одной или
нескольких переменных, при этом каждая
переменная встречается не более одного
раза (либо сама, либо ее отрицание).
X X
X Z
X Y X
X Y Z
Не соответствует
правилу
X Y X
2

3.

Дизъюнктивной нормальной
формой (ДНФ) называется
дизъюнкция простых конъюнкций.
X Y Y Z
X X X Y Z
X Z Y X Z
ДНФ можно построить для всякой
формулы
(путем преобразования).
3

4.

Простой дизъюнкцией (элементарной)
называется дизъюнкция одной или
нескольких переменных, при этом каждая
переменная входит не более одного раза
(либо сама, либо ее отрицание).
X X;
X Z;
X Y Z
Не соответствует
правилу
X Y X
4

5.

Конъюнктивной нормальной
формой (КНФ) называется
конъюнкция простых дизъюнкций.
( X Y Z )( X Y )
( X X Y) (Y Z )
X (Z Y ) (X Z)
КНФ можно построить для всякой
формулы
(путем преобразования).
5

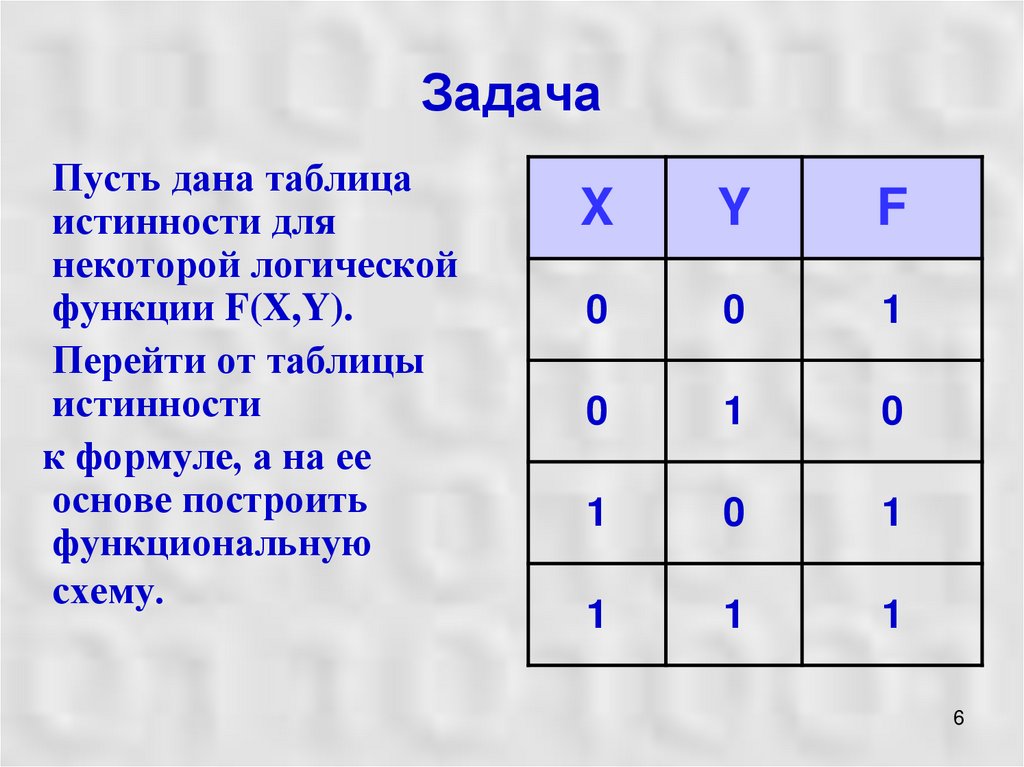
6. Задача

Пусть дана таблица
истинности для
некоторой логической
функции F(X,Y).
Перейти от таблицы
истинности
к формуле, а на ее
основе построить
функциональную
схему.
X
Y
F
0
0
1
0
1
0
1
0
1
1
1
1
6

7.

Логическая функция
ТАБЛИЦА ИСТИННОСТИ
ФОРМУЛА
СХЕМА
ПРОБЛЕМА
Как от таблицы истинности
перейти к формуле, чтобы построить
функциональную схему?
7

8.

Совершенной дизъюнктивной
нормальной формой (СДНФ) называется
такая дизъюнктивная нормальная форма, у
которой в каждую конъюнкцию входят все
переменные данного списка (либо сами,
либо их отрицания), причем в одном и том
же порядке.
(X Y Z) (X Y Z)
Не соответствует
правилу
( X X ) (Y X Y )
8

9.

Совершенной конъюнктивной
нормальной формой (СКНФ) называется
такая конъюнктивная форма, у которой в
каждую дизъюнкцию входят все
переменные данного списка (либо сами,
либо их отрицания), причем в одном и том
же порядке.
( X Z Y) (X Z Y)
Не соответствует
правилу
( X X Y) (Z X)
9

10.

Теорема алгебры логики
Любую функцию можно представить в
виде СДНФ, так и СКНФ, кроме
константы 0
X X 0
и константы 1
X X 1
10

11. Алгоритм получения СДНФ по таблице истинности

1.
Отметить те строки таблицы
истинности, в последнем
столбце которых стоят 1:
X
Y
F(X,Y)
0
0
1*
0
1
0
1
0
1*
1
1
1*
2. Выписать для каждой отмеченной строки конъюнкцию всех
переменных следующим образом: если значение в данной строке
равно 1, то в конъюнкцию включать саму эту переменную, если
равно 0, то ее отрицание :
для 1-й строки
X Y, для 3-строки
X Y, для 4-строки
X Y
3. Все полученные конъюнкции связать в дизъюнкцию:
F (X Y) (X Y) (X Y)
11

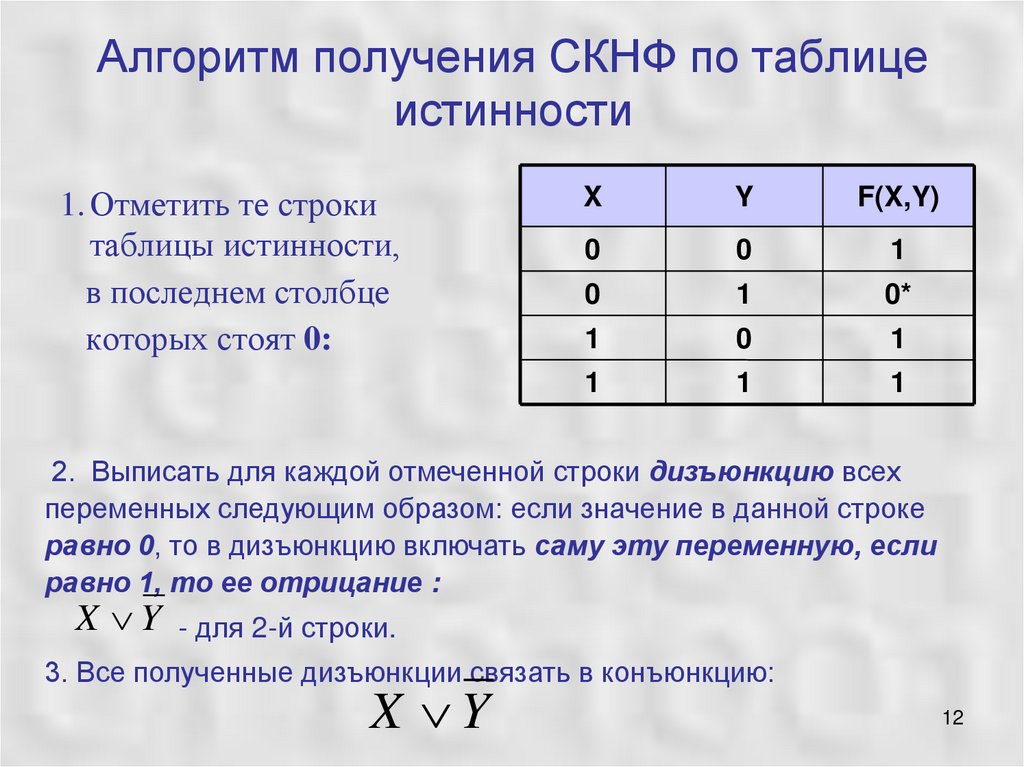
12. Алгоритм получения СКНФ по таблице истинности

1. Отметить те строки
таблицы истинности,
в последнем столбце
которых стоят 0:
X
Y
F(X,Y)
0
0
1
0
1
0*
1
0
1
1
1
1
2. Выписать для каждой отмеченной строки дизъюнкцию всех
переменных следующим образом: если значение в данной строке
равно 0, то в дизъюнкцию включать саму эту переменную, если
равно 1, то ее отрицание :
X Y - для 2-й строки.
3. Все полученные дизъюнкции связать в конъюнкцию:
X Y
12

13. Решение

Полученные по двум алгоритмам СДНФ и СКНФ
эквивалентны. Преобразуем СКНФ по правилам
алгебры логики:
СДНФ =
СКНФ =
F (X Y) (X Y) (X Y)
X Y X Y X Y X Y
X Y
Примечание: Для нахождения формулы по таблице истинности
рекомендуется использовать тот из двух алгоритмов, в котором в
таблице помечается меньше строк.
13

14. Проверка

Покажем, что полученные по двум алгоритмам
СДНФ и СКНФ эквивалентны.
СДНФ F ( X Y ) и СКНФ F ( X Y )
Можем проверить, построив таблицу истинности по
найденной формуле.
X
Y
Y
F (X Y)
0
0
1
1
0
1
0
1
1
0
1
0
1
0
1
1
14

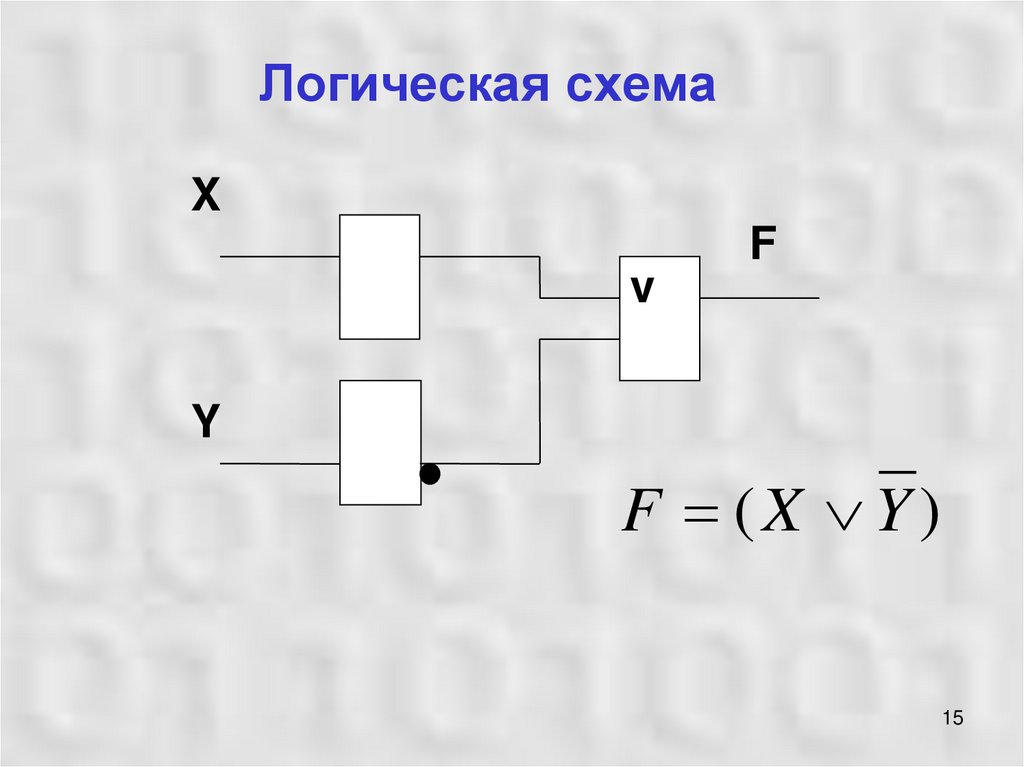
15. Логическая схема

X
F
v
Y
F (X Y)
15

16. Задача уровня В

Представить функцию в
виде СДНФ,
построить логическую
схему этой функции
( a b) c
( a b) c =
= abc abc
abc abc abc
Задача уровня В
a
0
0
0
0
1
1
1
1
b
0
0
1
1
0
0
1
1
c
0
1
0
1
0
1
0
1
( a b) c
0
1
0
1
1
1
0
1
16