Урок№26_ЧИСЛОВАЯ_ФУНКЦИЯ_Свойства_

1. ЧИСЛОВАЯ ФУНКЦИЯ.

График.
Свойства функции.
Обратная функция.

2. История создания названия функции

Г.В.Лейбниц
Термин функция впервые появился в 1692 году у
Лейбница и употреблялся в узком смысле
(различные отрезки, связанные с кривой –
например, абсциссы её точки). Современное
понятие функции, как выражения зависимости
одних переменных величин от других
сформировалось в первой половине 19 века
благодаря исследованиям таких крупных
математиков, как Лобачевский, Дирихле, Фурье.
Одним из важнейших достижений в области
математического анализа в 19 веке стало
рождение теории аналитических функций
(Огюсте Коши) и функции комплексного
переменного.

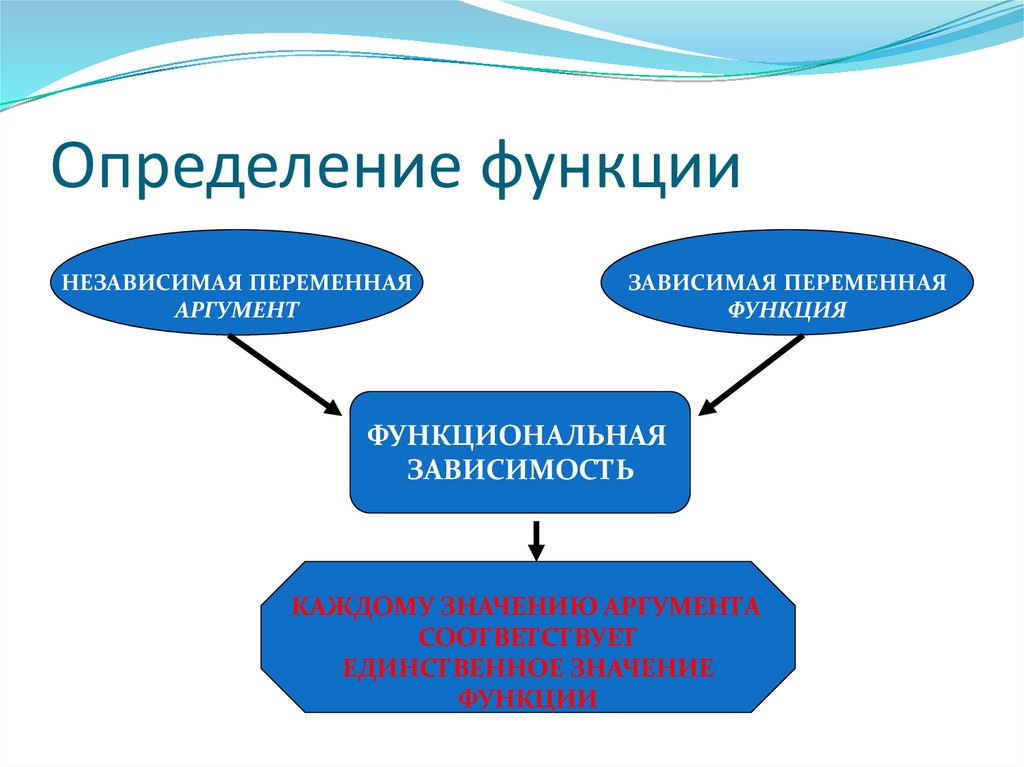
3. Определение функции

НЕЗАВИСИМАЯ ПЕРЕМЕННАЯ
АРГУМЕНТ
ЗАВИСИМАЯ ПЕРЕМЕННАЯ
ФУНКЦИЯ
ФУНКЦИОНАЛЬНАЯ
ЗАВИСИМОСТЬ
КАЖДОМУ ЗНАЧЕНИЮ АРГУМЕНТА
СООТВЕТСТВУЕТ
ЕДИНСТВЕННОЕ ЗНАЧЕНИЕ
ФУНКЦИИ

4. Определение числовой функции: Если даны числовое множество Х и правило f, позволяющее поставить в соответствие каждому элементу

х из
множества Х определенное число у, то
говорят задана функция у = f (x) с
областью определения Х;
пишут у = f (x) , х Х
Переменную х называют независимой
переменной или аргументом, а переменную
у – зависимой переменной или функцией

5. Определение. Множество всех значений функции у = f (x) , х Х, называют областью значений функции и обозначают Е(f)

Определение.
Множество всех значений х
называют областью
определения
функции и обозначают D(f)
(англ. Define – определять).
Определение.
Множество всех значений функции
у = f (x) , х Х, называют
областью
значений
функции и обозначают Е(f)
(англ.exist-существовать).

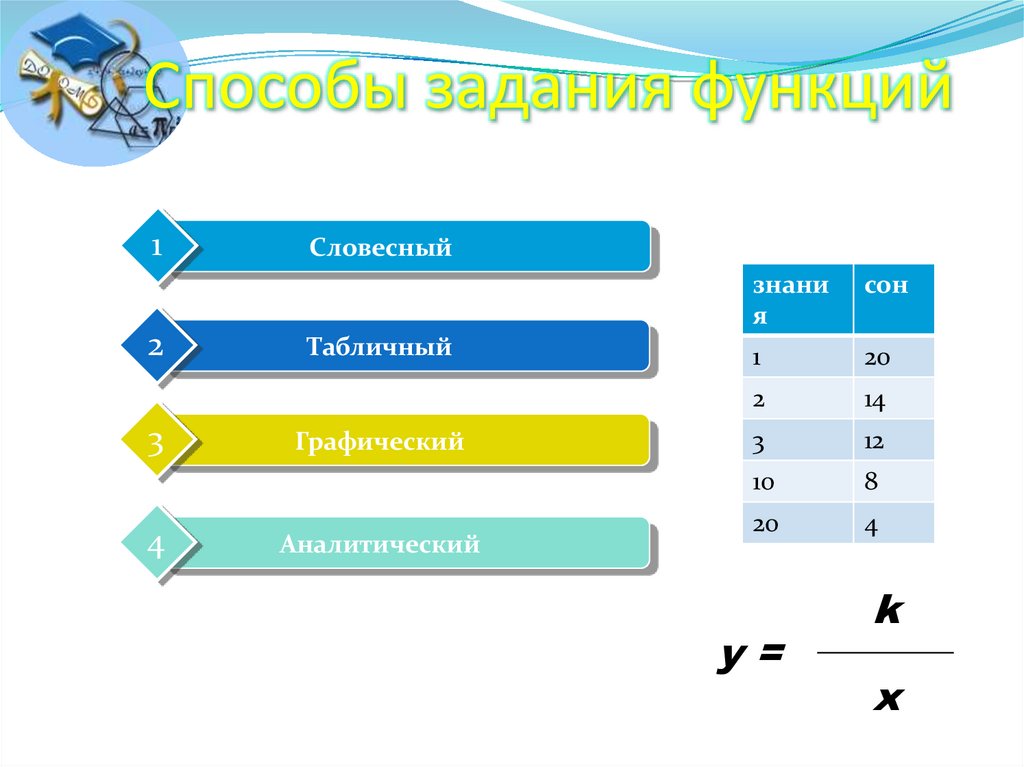
6. Способы задания функций

1
2
3
4
Словесный
Табличный
Графический
Аналитический
знани
я
сон
1
20
2
14
3
12
10
8
20
4
y=
k
x

7. График функции

Графиком функции f
называют множество
всех точек (х, у)
координатной
плоскости, где у = f(x),
а x «пробегает» всю
область определения
функции f.
4
3
2
1
0
-4
-2
-1 0
2
4
-2
-3
y=f(x)
4
3
2
1
0
-4
-2
-1 0
-2
-3
-4
2
4

8. Свойства функции

Область определения функции D(у)
Множество значений функции Е(у)
Четность функции
Промежутки монотонности (промежутки
возрастания и убывания функции)
Промежутки знакопостоянства
Нули функции
Периодичность функции
Ограниченность функции

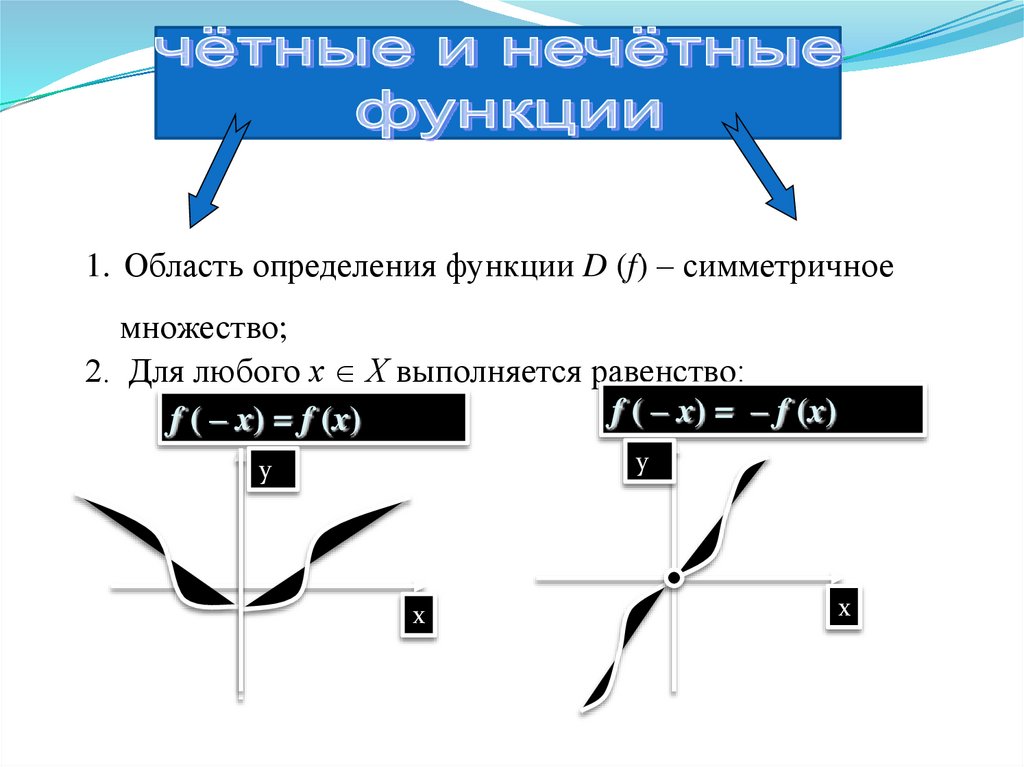
9.

1. Область определения функции D (f) – симметричное
множество;
2. Для любого х Х выполняется равенство:
f ( – x) = – f (x)
f ( – x) = f (x)
у
у
х
х

10.

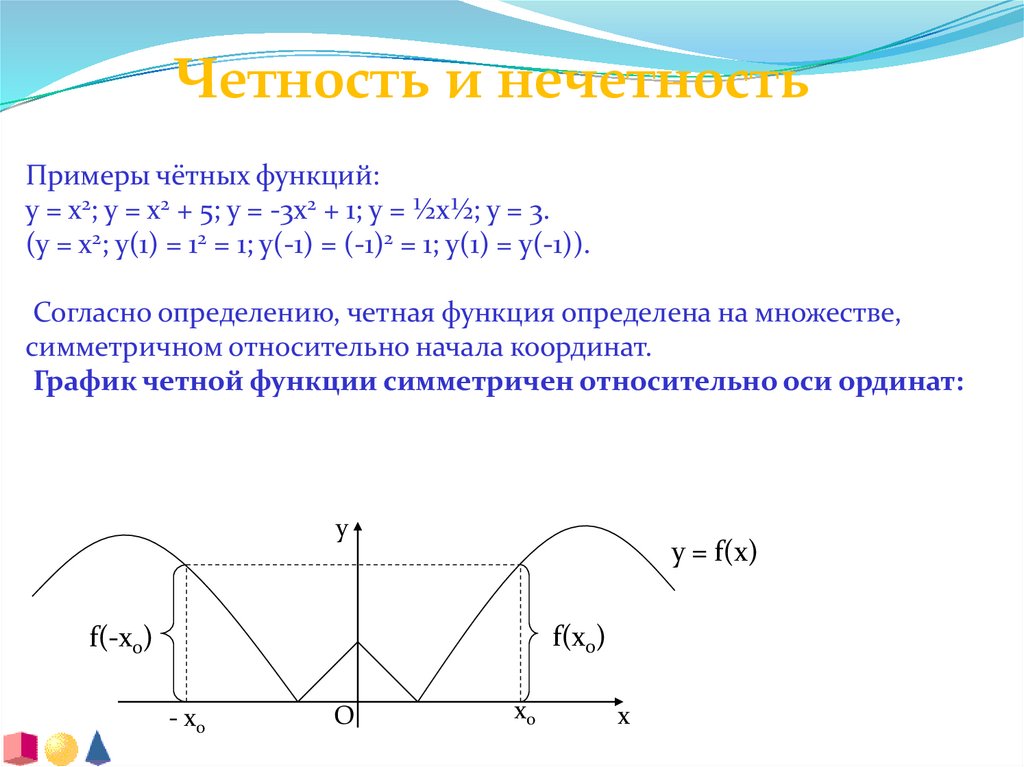
Четность и нечетность
Примеры чётных функций:
y = x2; y = x2 + 5; y = -3x2 + 1; y = ½x½; y = 3.
(y = x2; y(1) = 12 = 1; y(-1) = (-1)2 = 1; y(1) = y(-1)).
Согласно определению, четная функция определена на множестве,
симметричном относительно начала координат.
График четной функции симметричен относительно оси ординат:
y
y = f(x)
f(x0)
f(-x0)
- x0
O
x0
x

11.

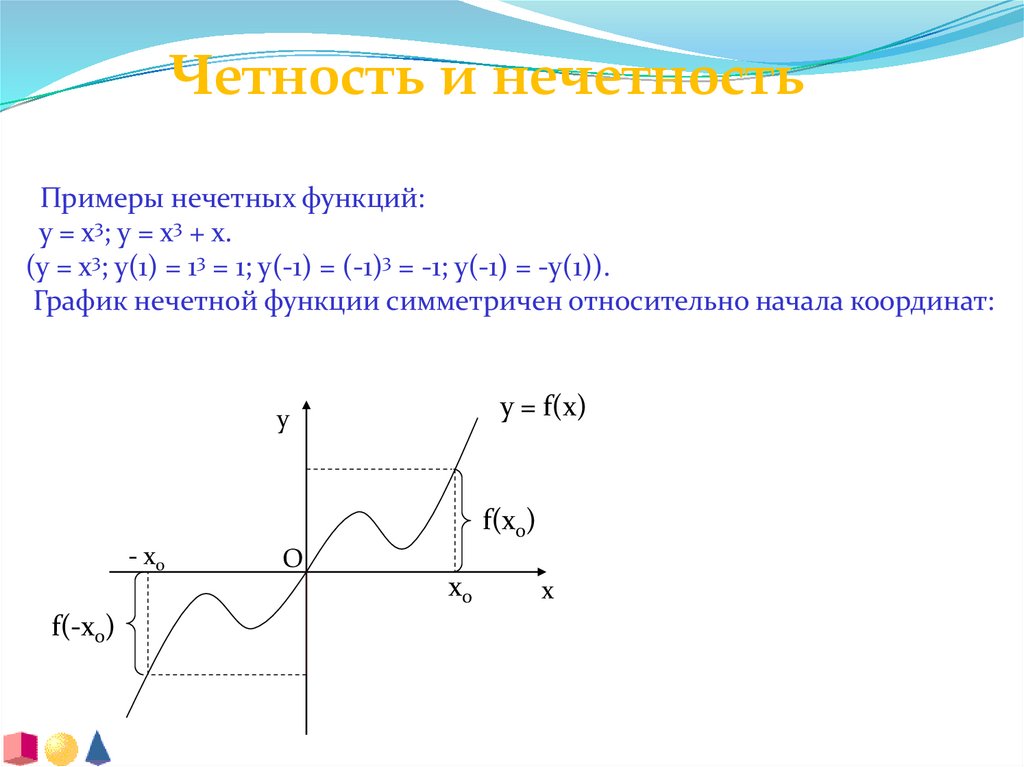
Четность и нечетность
Примеры нечетных функций:
y = x3; y = x3 + x.
(y = x3; y(1) = 13 = 1; y(-1) = (-1)3 = -1; y(-1) = -y(1)).
График нечетной функции симметричен относительно начала координат:
y = f(x)
y
f(x0)
- x0
f(-x0)
O
x0
x

12.

При построении графиков четной и нечетной функции достаточно
построить только правую ветвь графика для положительных значений
аргумента. Левая ветвь достраивается симметрично относительно начала
координат для нечетной функции и относительно оси ординат для четной
функции.
Конечно, большинство функций не являются ни четными, ни нечетными.
Пример:
y = x3 + x2
y(-1) = (-1)3 + (-1)2 = -1 + 1 = 0
y(1) = (1)3 + (1)2 = 1 + 1 = 2
назад

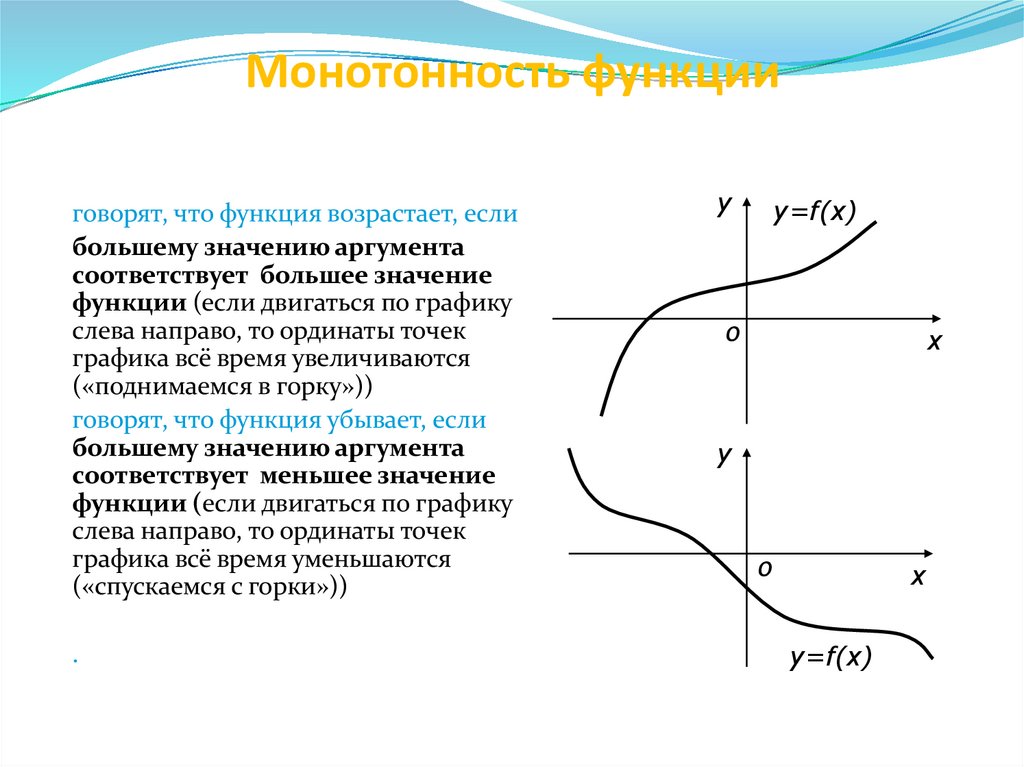
13. Монотонность функции

говорят, что функция возрастает, если
большему значению аргумента
соответствует большее значение
функции (если двигаться по графику
слева направо, то ординаты точек
графика всё время увеличиваются
(«поднимаемся в горку»))
говорят, что функция убывает, если
большему значению аргумента
соответствует меньшее значение
функции (если двигаться по графику
слева направо, то ординаты точек
графика всё время уменьшаются
(«спускаемся с горки»))
.
у
y=f(x)
о
х
y
o
x
y=f(x)

14.

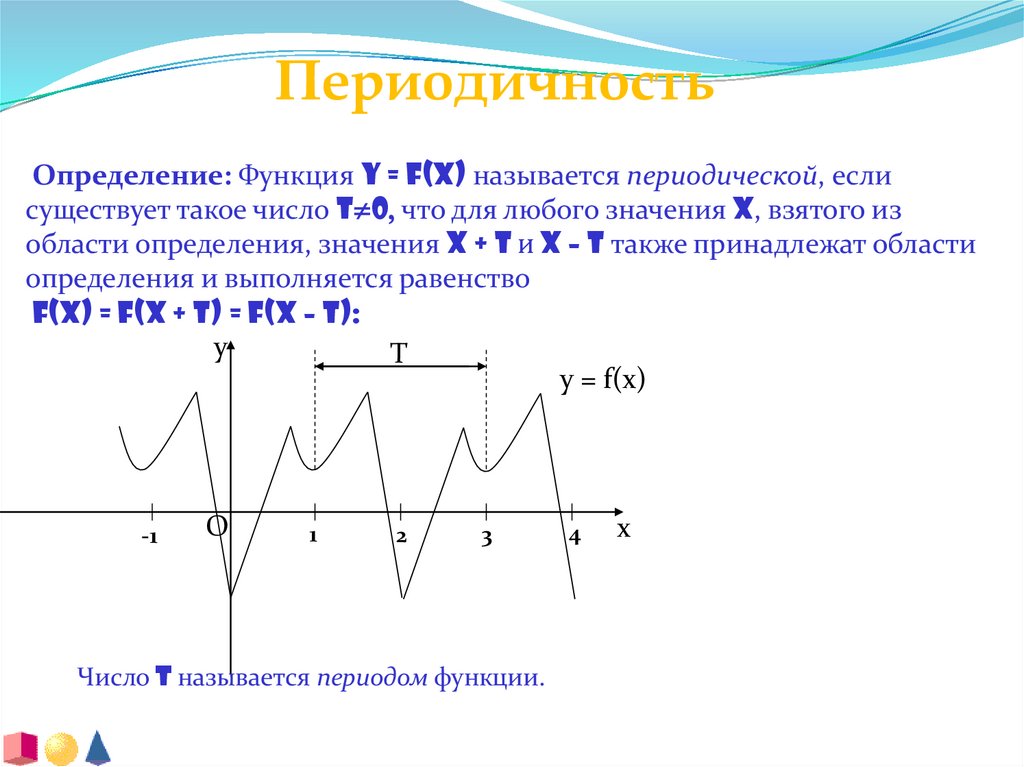
Периодичность
Определение: Функция y = f(x) называется периодической, если
существует такое число T 0, что для любого значения x, взятого из
области определения, значения x + T и x – T также принадлежат области
определения и выполняется равенство
f(x) = f(x + T) = f(x – T):
y
T
y = f(x)
-1
O
1
2
3
Число T называется периодом функции.
4
x

15.

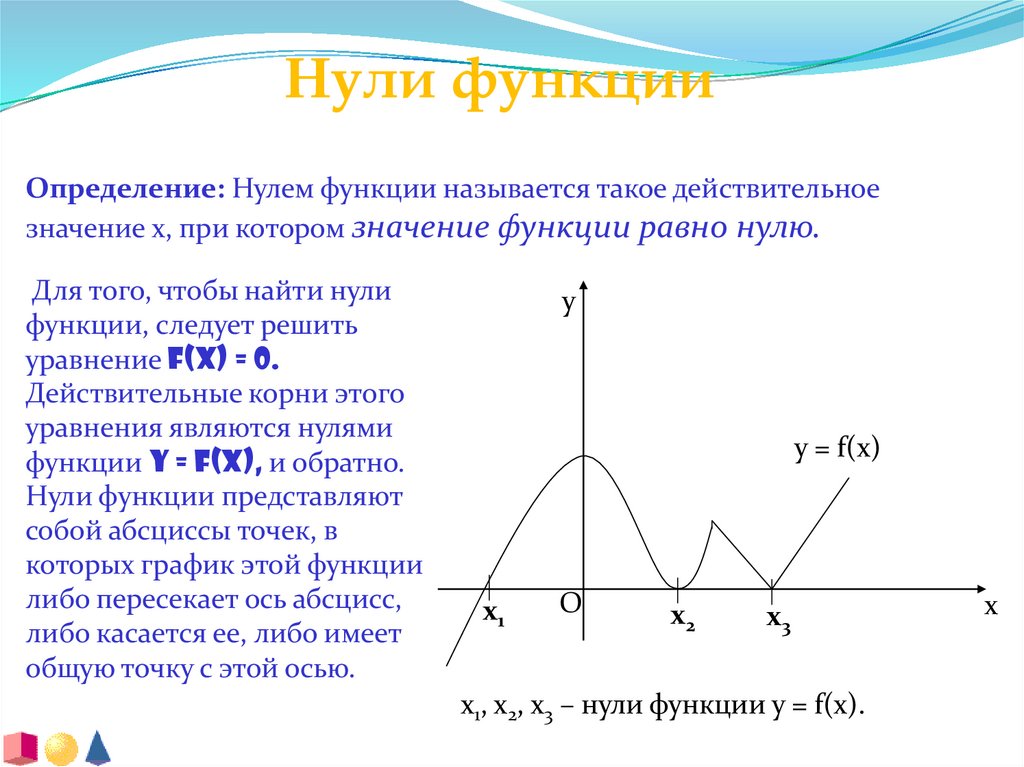
Нули функции
Определение: Нулем функции называется такое действительное
значение x, при котором значение функции равно нулю.
Для того, чтобы найти нули
функции, следует решить
уравнение f(x) = 0.
Действительные корни этого
уравнения являются нулями
функции y = f(x), и обратно.
Нули функции представляют
собой абсциссы точек, в
которых график этой функции
либо пересекает ось абсцисс,
либо касается ее, либо имеет
общую точку с этой осью.
y
y = f(x)
x1
O
x2
x3
х1, х2, х3 – нули функции у = f(x).
x

16.

Промежутки знакопостоянства
Определение: Числовые промежутки, на которых
непрерывная функция сохраняет свой знак и не
обращается в нуль, называются промежутками
знакопостоянства.
Над этими промежутками график функции лежит выше оси абсцисс, если
f(x) > 0, и ниже оси абсцисс, если f(x) < 0.
y = f(x)
y
f(x) > 0 при x > a
a
O
x
f(x) < 0 при x < a

17.

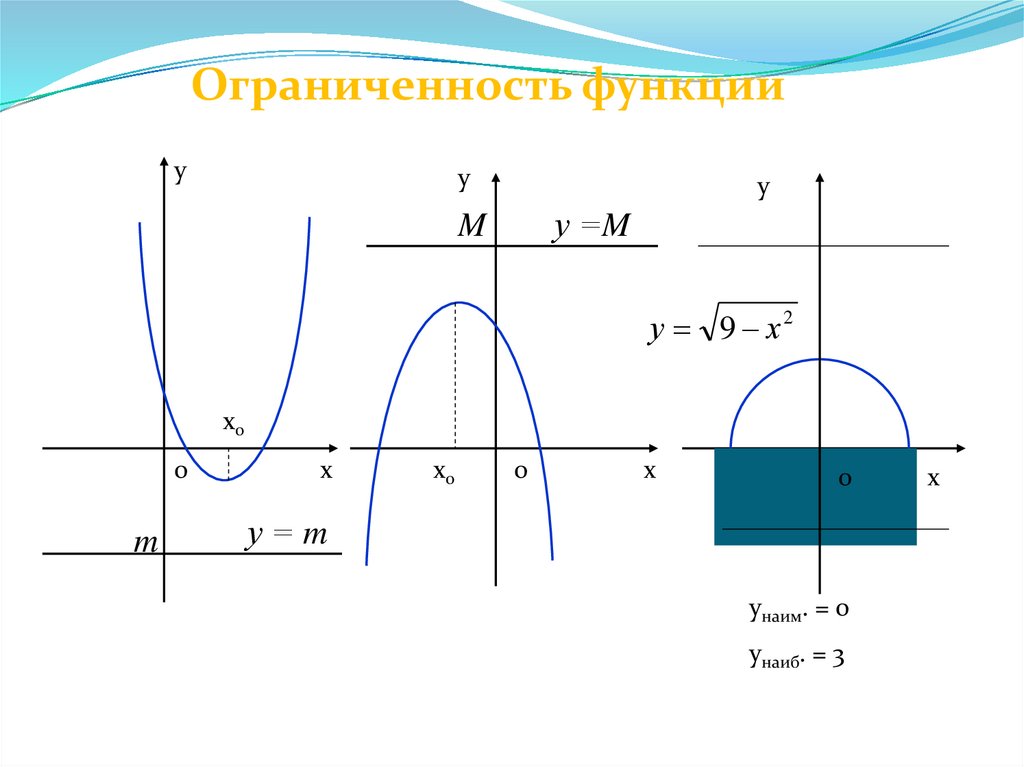
Ограниченность функции
Функция у = f (x) называют ограниченной
снизу на множестве Х D (f),
если все значения функции на множестве Х
больше некоторого числа.
если существует число m такое, что для
любого значения х Х выполняется
неравенство f (x) > m.

18.

Ограниченность функции
у
у
у
у =M
M
у 9 х2
x0
0
m
х
x0
0
х
0
у=m
унаим. = 0
унаиб. = 3
х