55-56_Многогранники и их элементы

1. Многогранники

* Многогранники
11.3.1.1 распознавать многогранники и их
элементы (призма, пирамида, правильные
многогранники);
11.3.1.2 распознавать развёртки многогранников
(n-угольная пирамида, n-угольная призма при n≤4);

2.

3.

Многогранник - геометрическое тело, ограниченное
плоскими многоугольниками.
Плоские многоугольники
называются гранями (faces)
многогранника
стороны многоугольника –
Ребрами(edges) многогранника
вершины многоугольника –
Вершинами(vertexes) многогранника.
С

4.

convex polyhedron
Невыпуклые многогранники
nonconvex polyhedron

5.

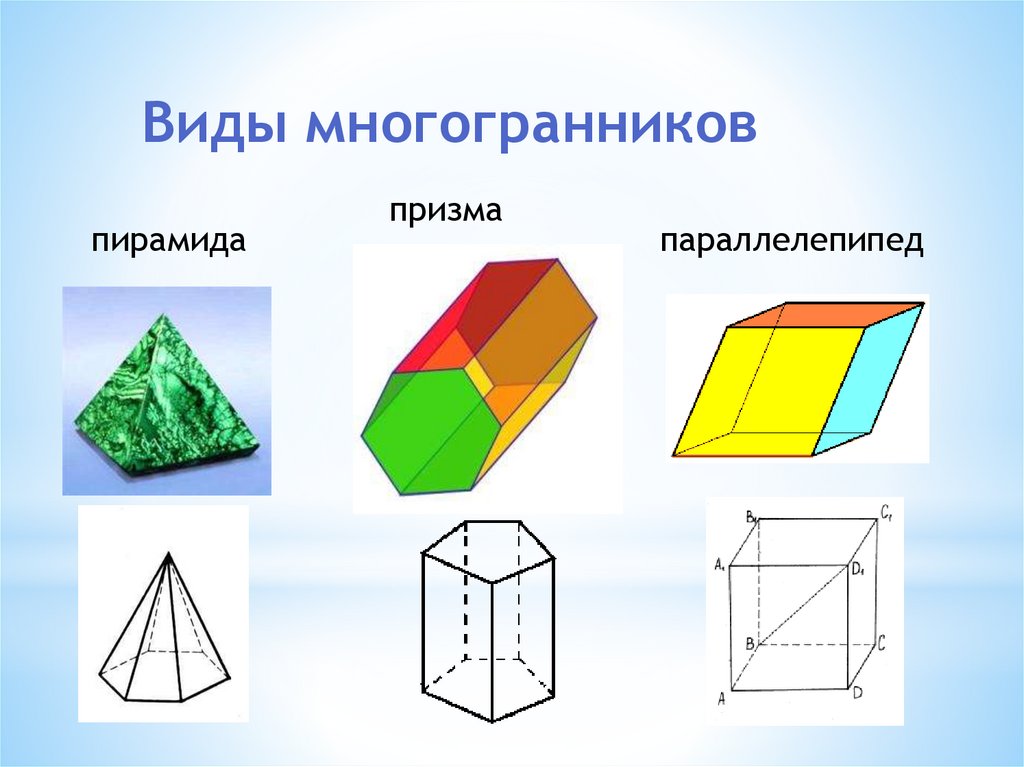
Виды многогранников
пирамида
призма
параллелепипед

6.

Призмой называется многогранник, у которого две грани
(основания) лежат в параллельных плоскостях, а все ребра
вне этих граней параллельны между собой.
Грани призмы, отличные от оснований, называются
боковыми гранями , а их ребра называются
боковыми ребрами . Все боковые ребра равны
между собой как параллельные отрезки,
ограниченные двумя параллельными плоскостями.
Все боковые грани призмы являются
параллелограммами. Соответствующие стороны
оснований призмы равны и параллельны. Поэтому в
основаниях лежат равные многоугольники.
Поверхность призмы состоит из двух оснований и
боковой поверхности.
Высотой призмы называется отрезок, являющийся
общим перпендикуляром плоскостей, в которых
лежат основания призмы.
Высота призмы равна расстоянию h между
плоскостями оснований.

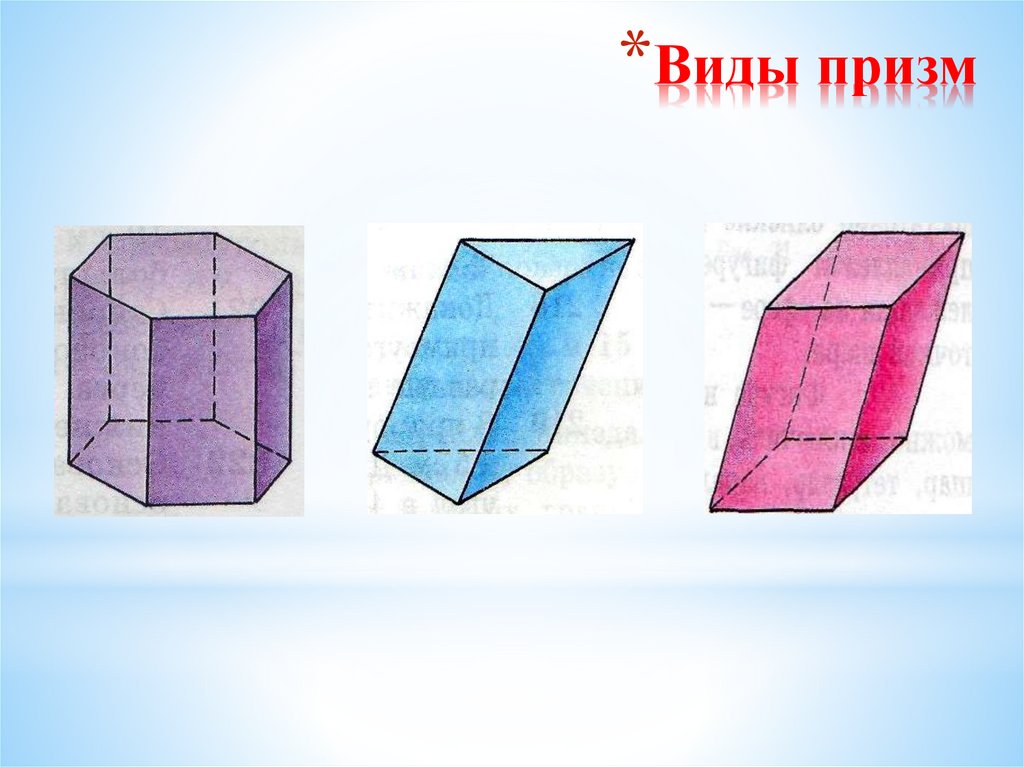
7. Виды призм

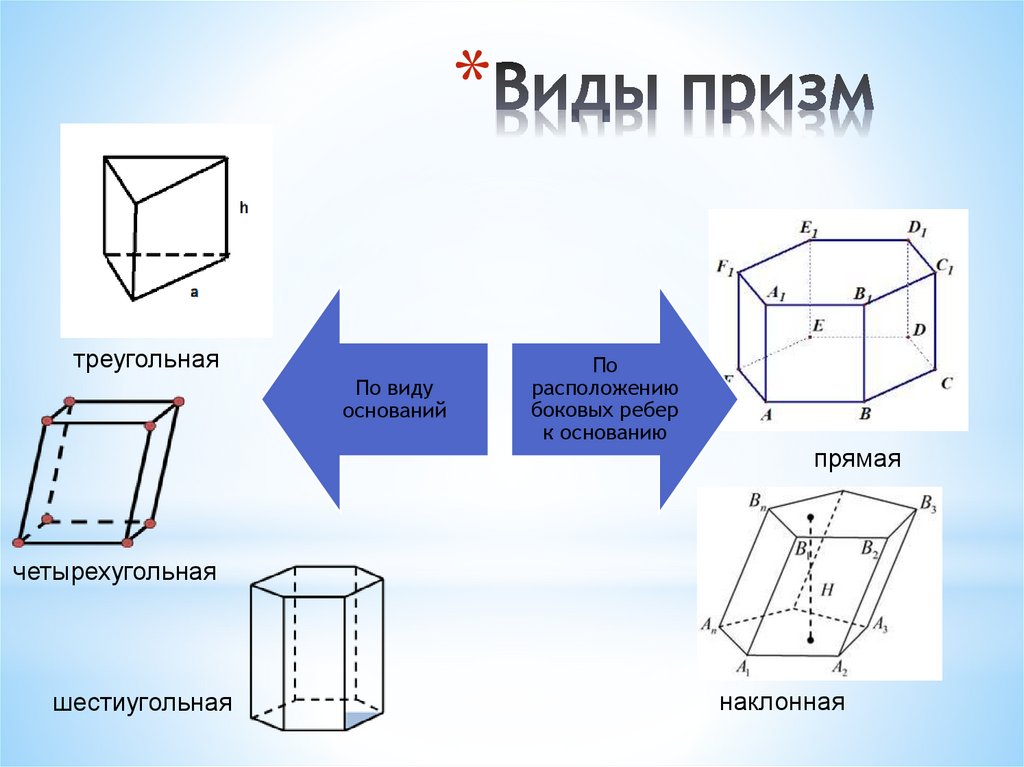
*Виды призм

8. Виды призм

*
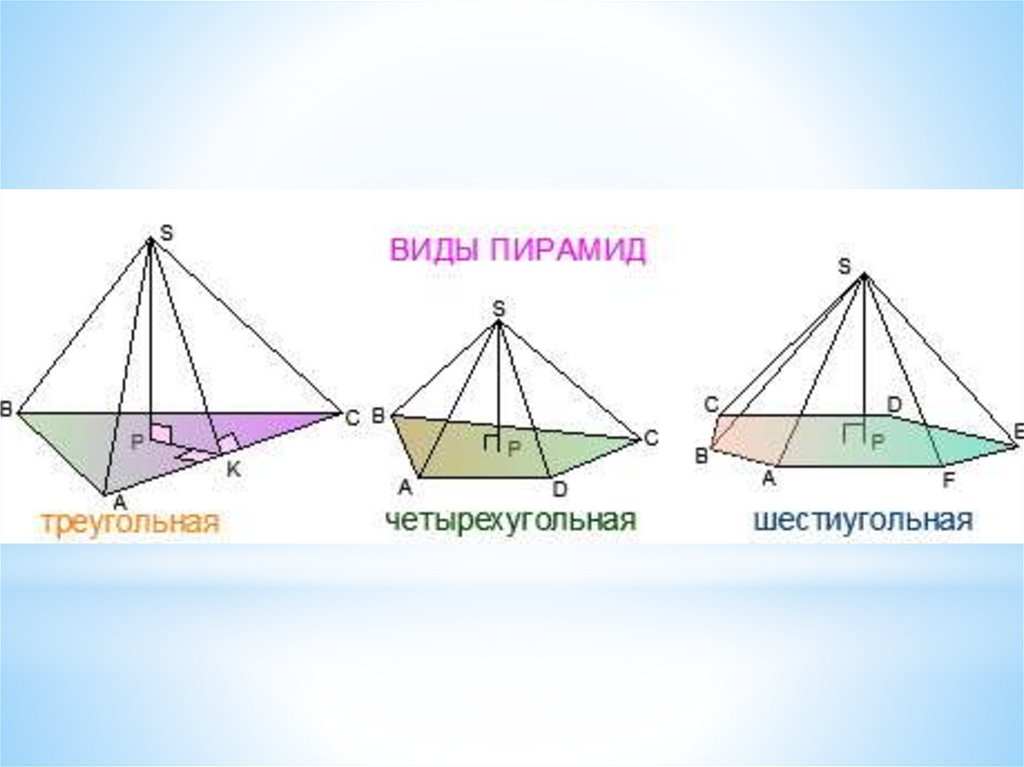
треугольная
По виду
оснований
По
расположению
боковых ребер
к основанию
прямая
четырехугольная
шестиугольная
наклонная

9. Правильная призма

*Правильная призма
Призма называется
правильной, если она
прямая и ее основания правильные
многоугольники.

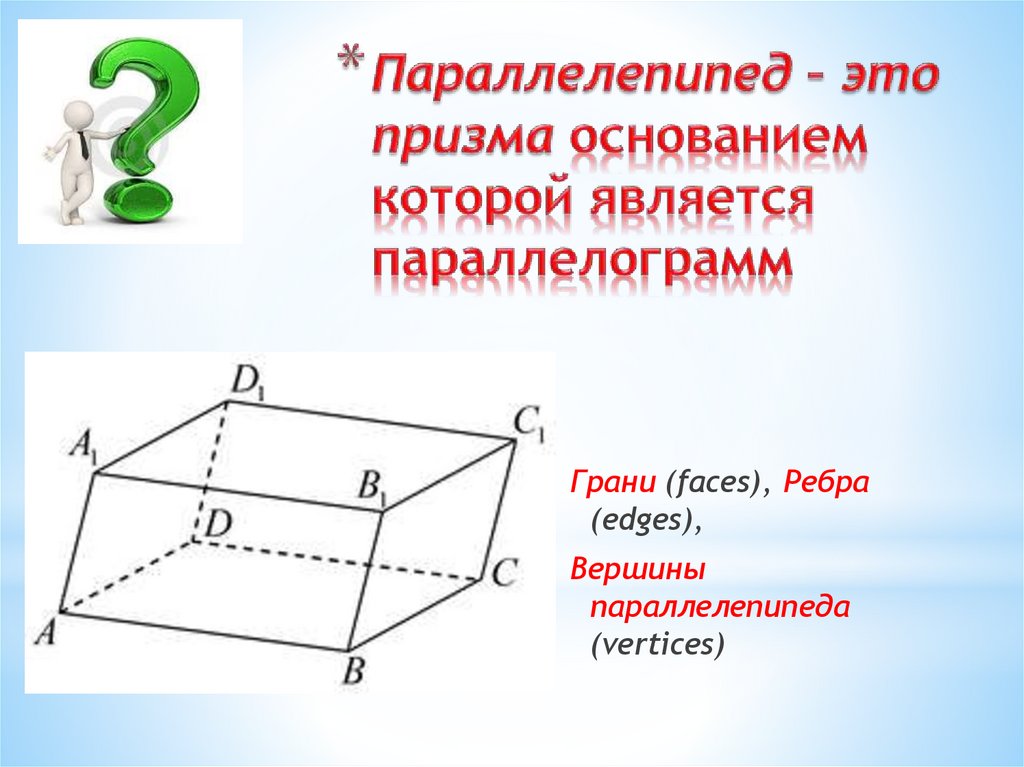
10. Параллелепипед – это призма основанием которой является параллелограмм

Грани (faces), Ребра
(edges),
Вершины
параллелепипеда
(vertices)

11.

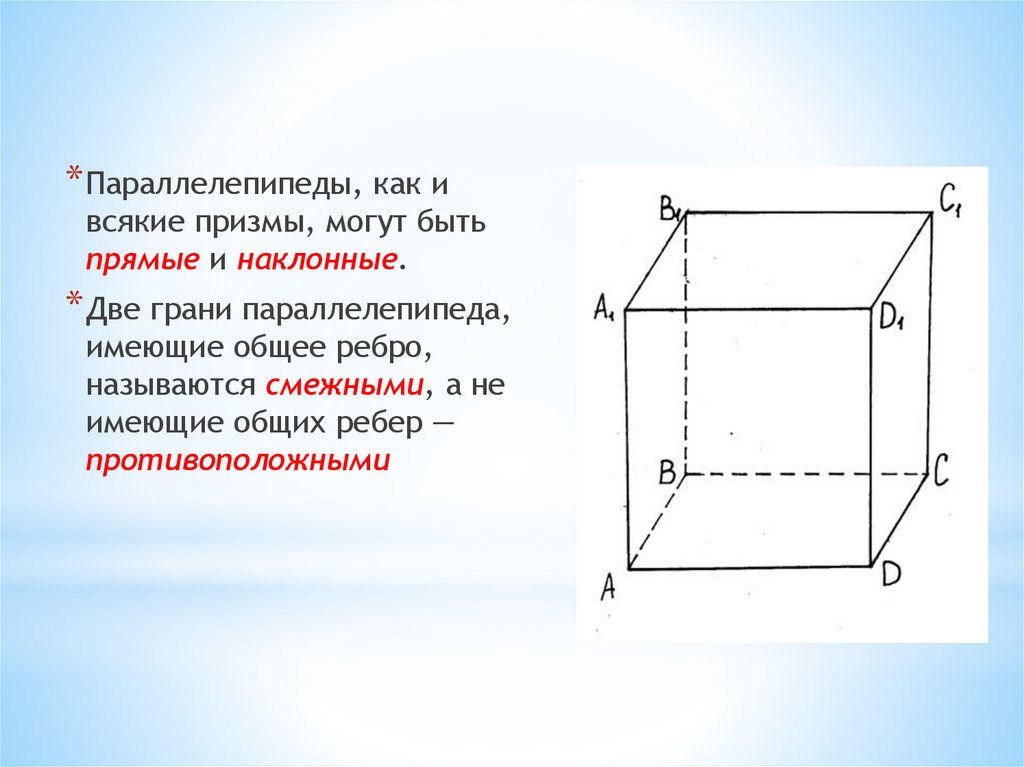
* Параллелепипеды, как и
всякие призмы, могут быть
прямые и наклонные.
* Две грани параллелепипеда,
имеющие общее ребро,
называются смежными, а не
имеющие общих ребер —
противоположными

12.

* Отрезок, соединяющий две вершины, не принадлежащие
одной грани, называется диагональю параллелепипеда.
* Длины не параллельных ребер прямоугольного
параллелепипеда называются его линейными размерами
(измерениями). У прямоугольного параллелепипеда три
линейных размера.

13. Свойства параллелепипеда:

*
Противоположные грани параллелепипеда равны и
параллельны.
Все четыре диагонали параллелепипеда пересекаются в одной
точке и делятся этой точкой пополам.
Боковые грани прямого параллелепипеда — прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме
квадратов трех его измерений.

14.

1)Какая фигура лежит в основании правильной
призмы?
2)Какая фигура является боковой гранью прямой
призмы?
3)Будет ли верным утверждение "Параллелепипед
является частным случаем призмы"?
4)При каком условии параллелепипед является
кубом?
5)Если в параллелепипеде две грани
параллелограммы, то он является прямым или
наклонным? …

15. Пирамида

*Пирамида
Пирамидой называется многогранник, который состоит из
ОСНОВАНИЯ пирамиды (плоского многоугольника),
ВЕРШИНЫ пирамиды и всех отрезков, соединяющих их.

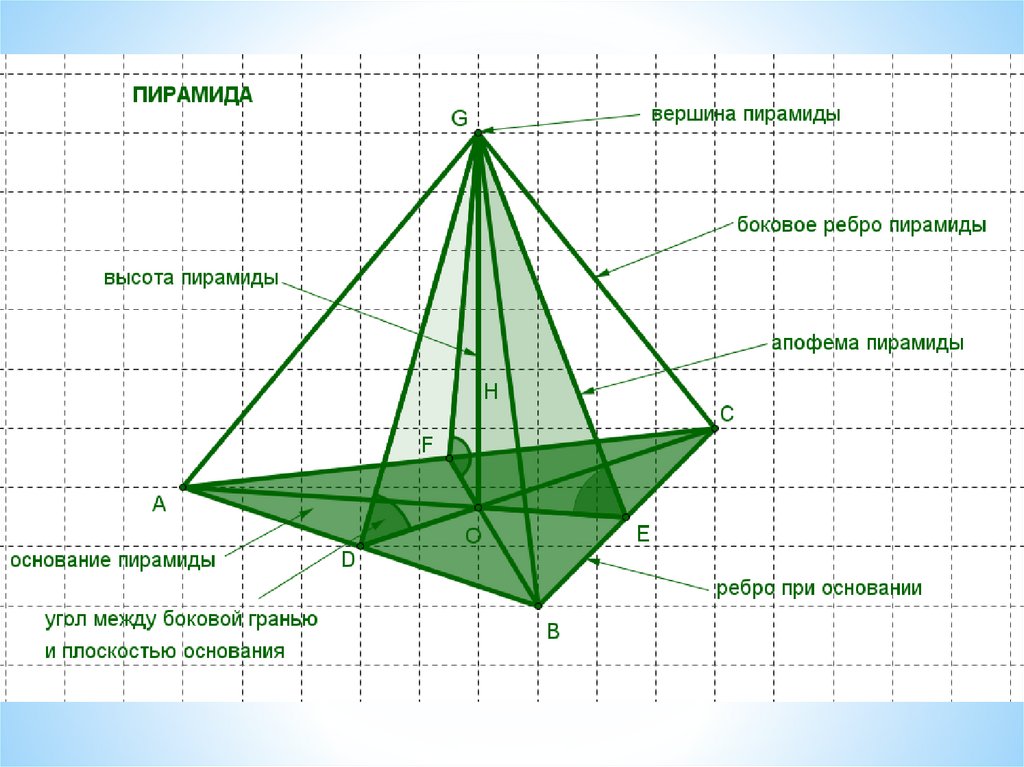
16. Элементы

* Основание- многоугольник, которому не
принадлежит вершина пирамиды
* Боковые ребра- общие стороны боковых граней;
* Вершина-точка, соединяющая боковые рёбра и
не лежащая в плоскости основания
* Высота-отрезок, перпендикулярно проведённый
через вершину пирамиды к плоскости её
основания
* Боковые грани- треугольники, сходящиеся в
вершине пирамиды
*Элементы

17.

18.

19.

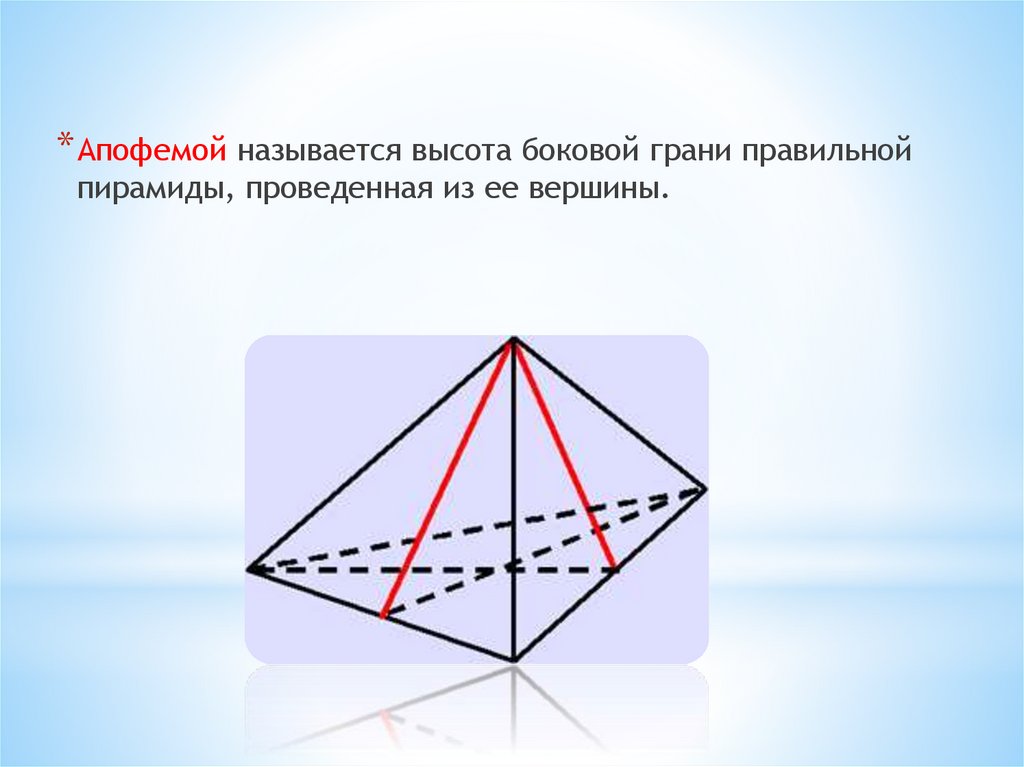
* Апофемой называется высота боковой грани правильной
пирамиды, проведенная из ее вершины.

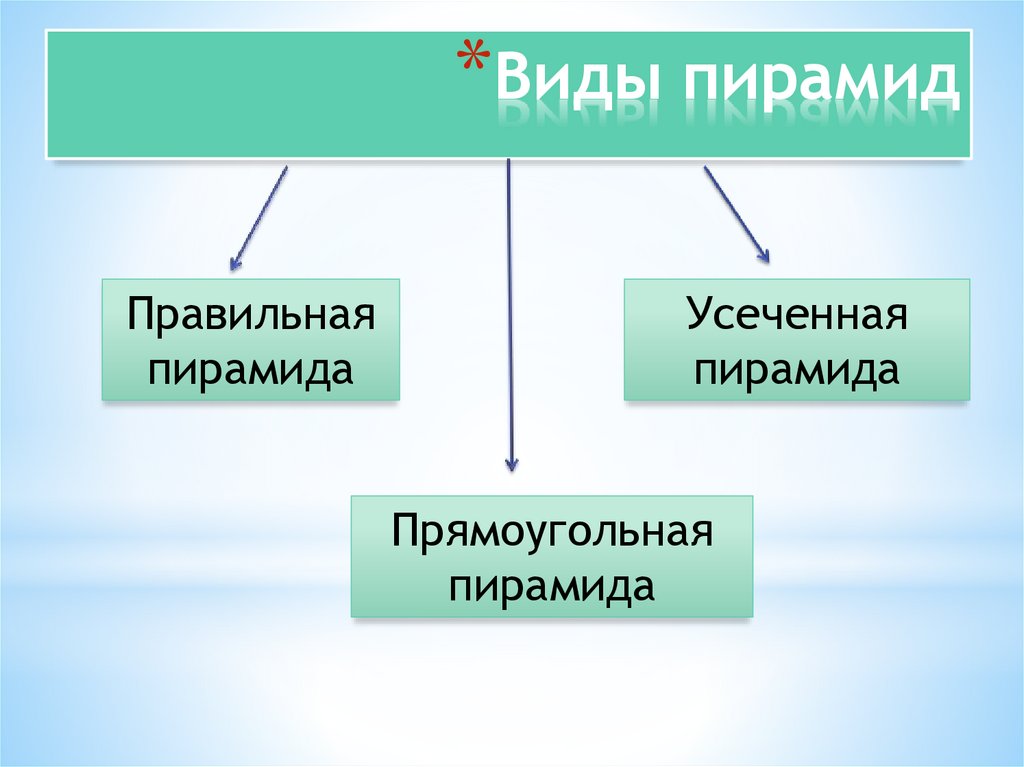
20. Виды пирамид

*Виды пирамид
Правильная
пирамида
Усеченная
пирамида
Прямоугольная
пирамида

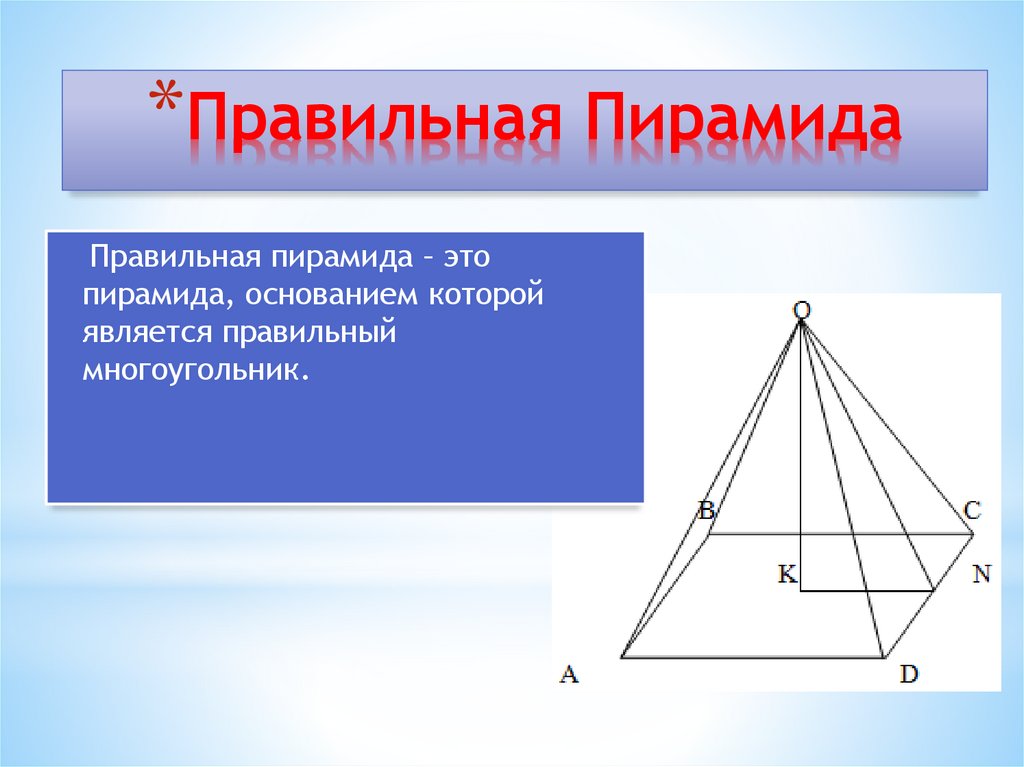
21. Правильная Пирамида

*Правильная Пирамида
Правильная пирамида – это
пирамида, основанием которой
является правильный
многоугольник.

22. Свойства

*Свойства
Боковые ребра
равны.
Двугранные углы при
боковых ребрах равны.
Боковые грани - равные
равнобедренные
треугольники.
Боковые ребра образуют с
плоскостью основания
равные углы.
Двугранные углы при
основании равны.

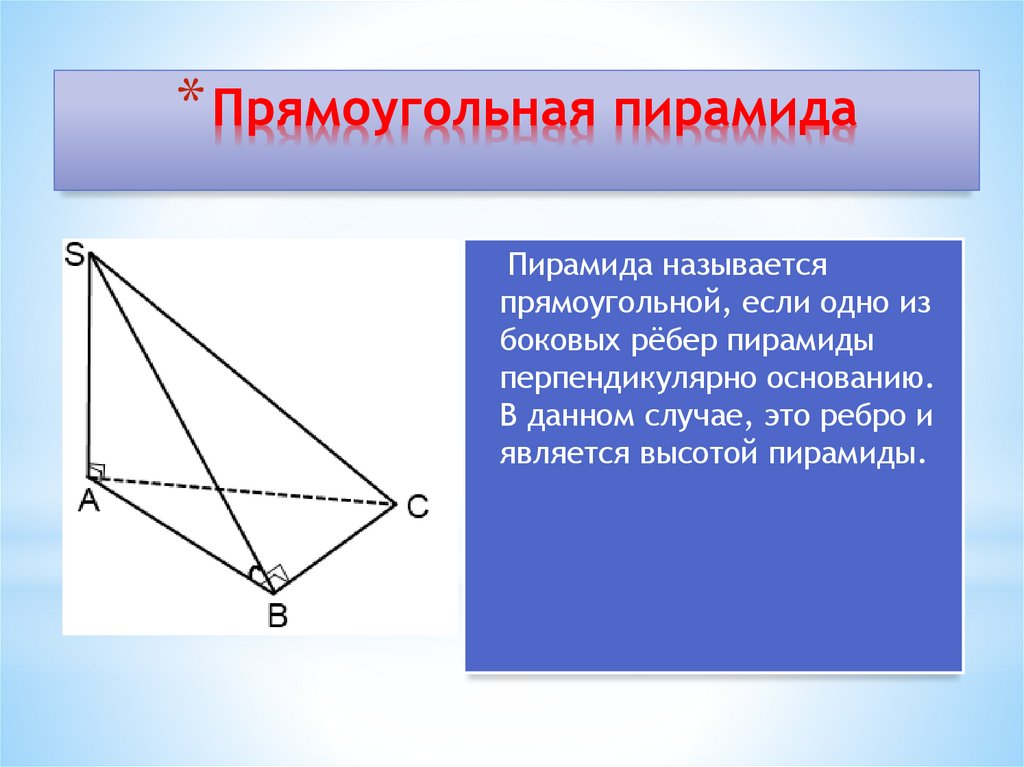
23. Прямоугольная пирамида

* Прямоугольная пирамида
Пирамида называется
прямоугольной, если одно из
боковых рёбер пирамиды
перпендикулярно основанию.
В данном случае, это ребро и
является высотой пирамиды.

24. Применение

*Примене
ние

25.

1)Апофема правильной пирамиды, является
медианой его боковой грани.
2)Пирамида является правильной, если в
основании лежит правильный многоугольник.
3)Если все грани треугольной пирамиды
прямоугольные треугольники, то высота
пирамиды проецируется в вершину прямого
угла.

26.

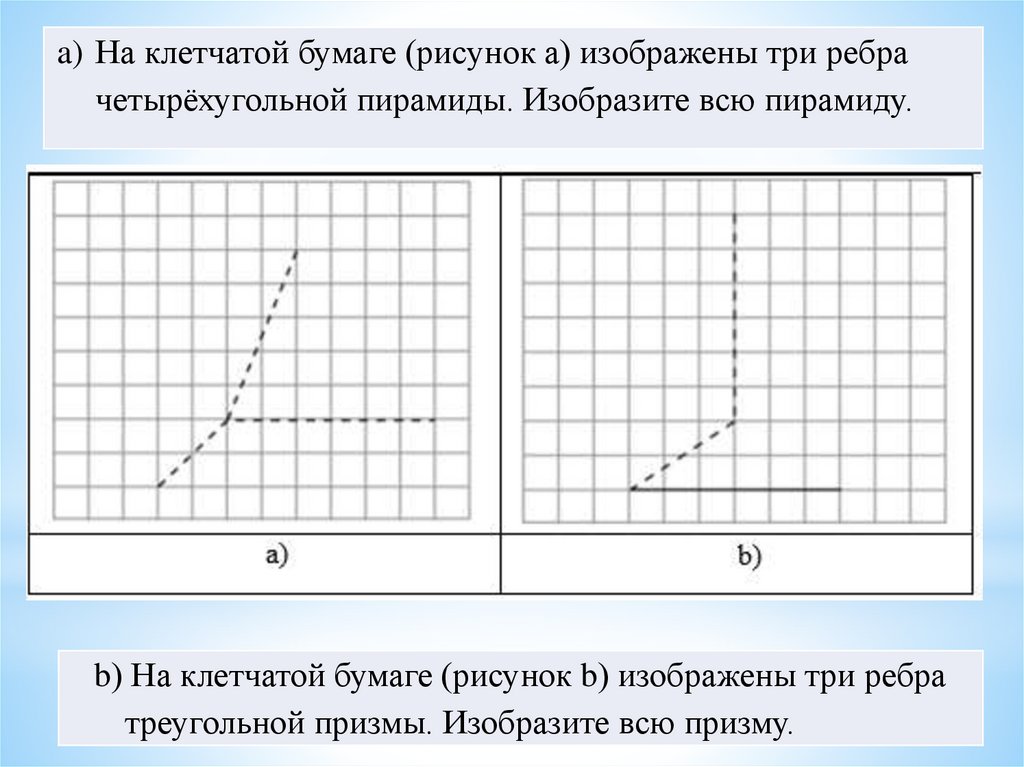
a) На клетчатой бумаге (рисунок а) изображены три ребра
четырёхугольной пирамиды. Изобразите всю пирамиду.
b) На клетчатой бумаге (рисунок b) изображены три ребра
треугольной призмы. Изобразите всю призму.

27.

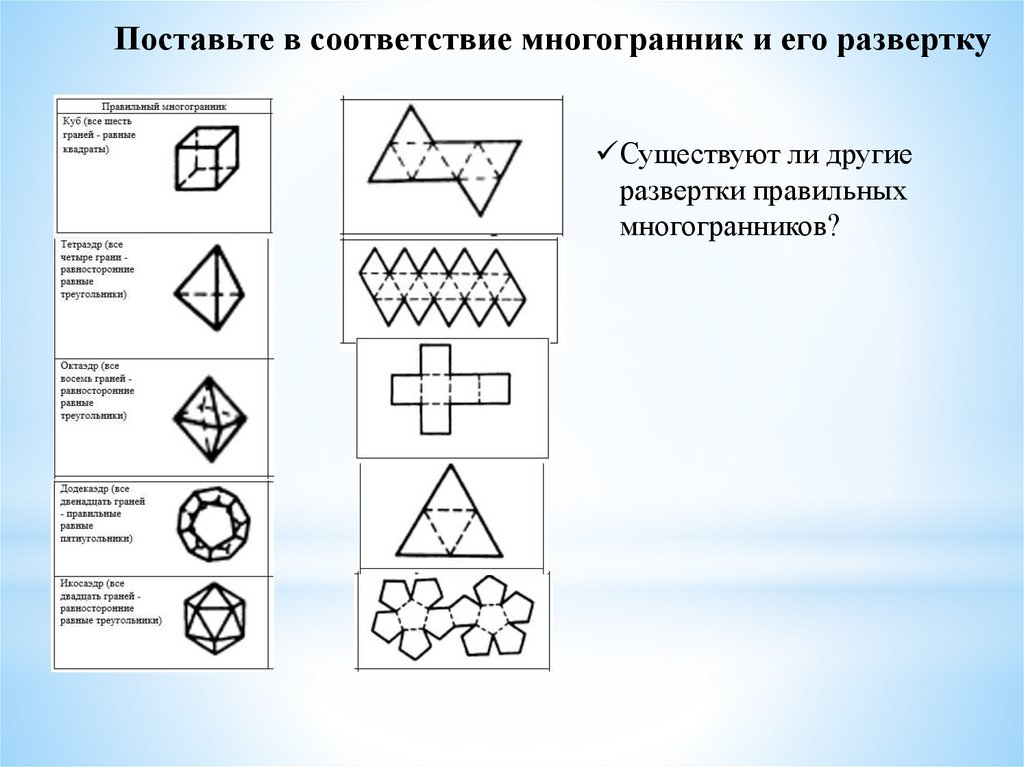
Поставьте в соответствие многогранник и его развертку
Существуют ли другие
развертки правильных
многогранников?

28.

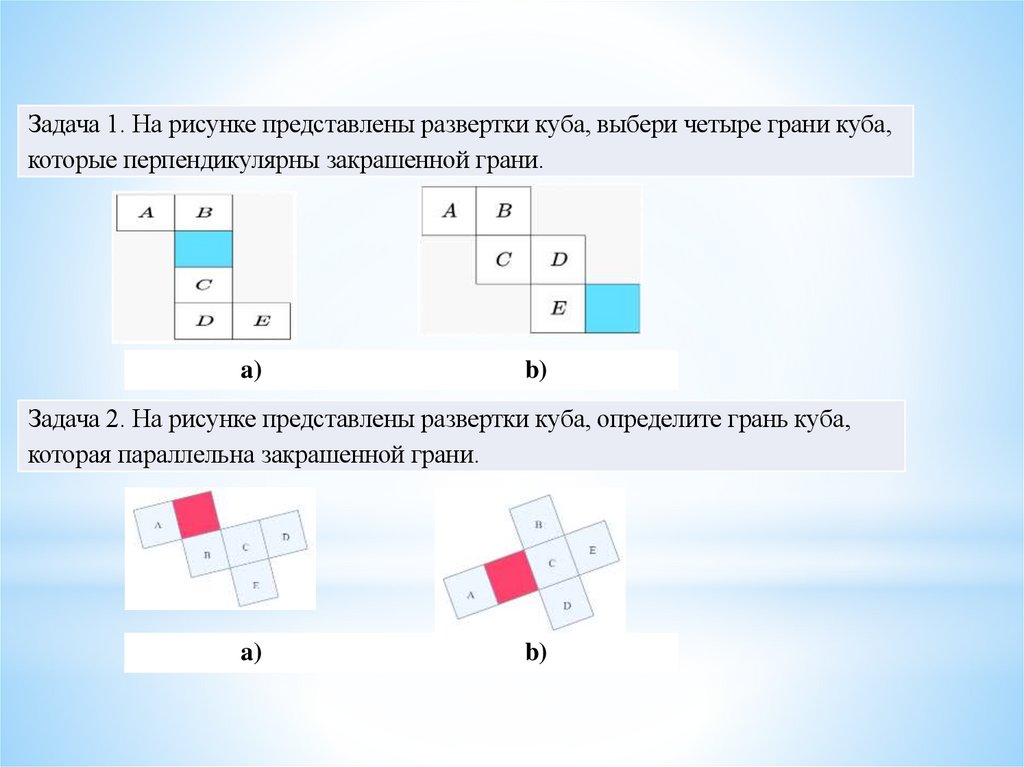
Задача 1. На рисунке представлены развертки куба, выбери четыре грани куба,
которые перпендикулярны закрашенной грани.
a)
b)
Задача 2. На рисунке представлены развертки куба, определите грань куба,
которая параллельна закрашенной грани.
a)
b)

29.

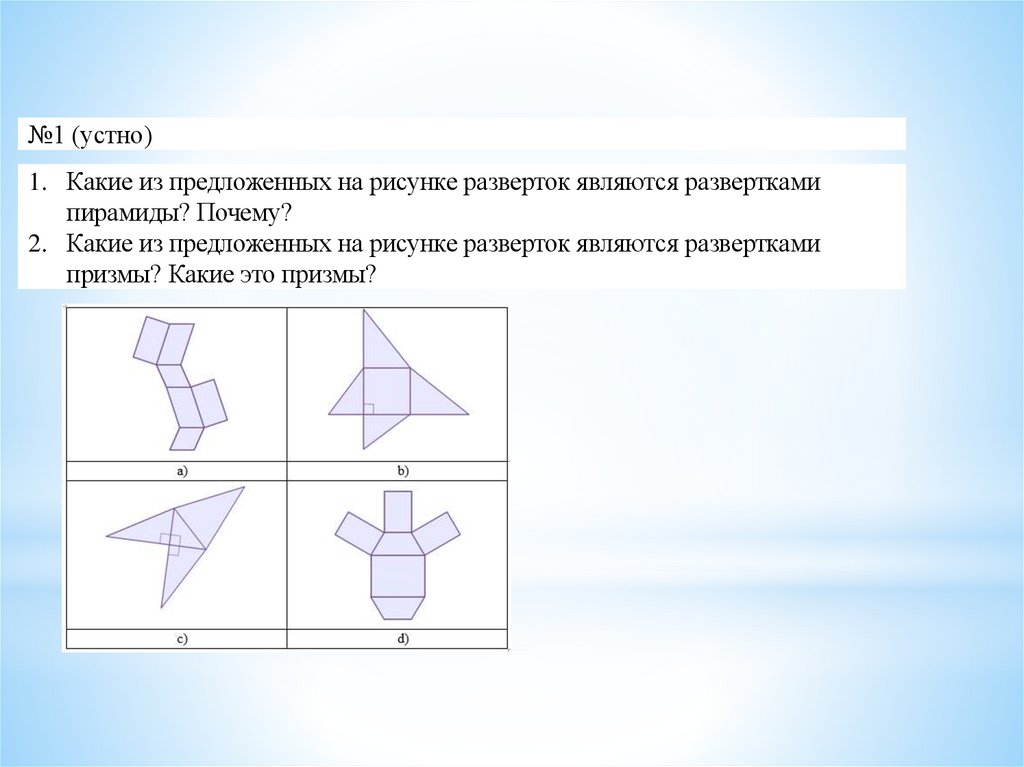
№1 (устно)
1. Какие из предложенных на рисунке разверток являются развертками
пирамиды? Почему?
2. Какие из предложенных на рисунке разверток являются развертками
призмы? Какие это призмы?

30.

№2 (задачи из книги "Геометрия Астаны":)
Какие из данных многоугольников являются развертками правильной четырехугольной
пирамиды, в форме которой построен Дворец мира и согласия в Астане? При выборе
учитывайте правильное расположение треугольников на каждой грани пирамиды.
Ответ: рис 2 и 3

31.

№3. Ер Тостик и волшебное яблоко находятся в противоположных (наиболее
удаленных) вершинах куба (см.рисунок). Как кратчайшим путем Ер Тостик может
добраться до яблока по поверхности куба? Какова длина маршрута Ер Тостика,
если ребро куба равно а?
Ответ: задачу решить с помощью
развертки куба, на ней отметить точками
свое местонахождение и
местонахождение яблока, а затем
соединить эти точки отрезком

32.

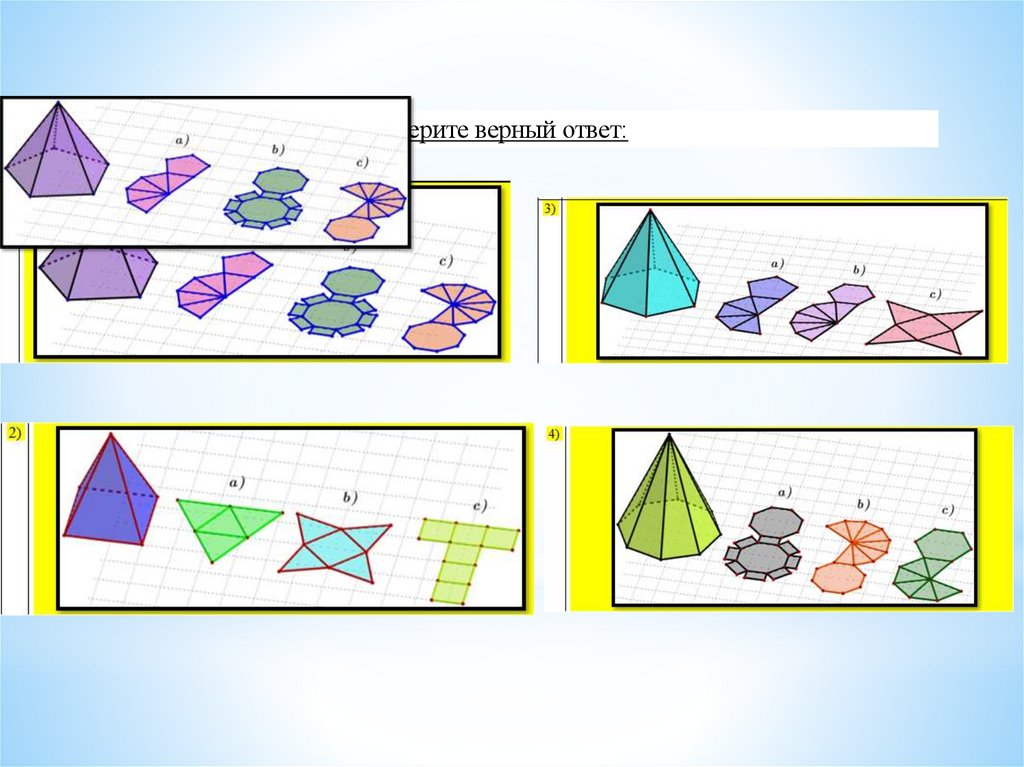
Выберите верный ответ:

33. Рефлексия

*
*что узнал, чему научился?
* что осталось непонятным?
* над чем необходимо работать?

34.

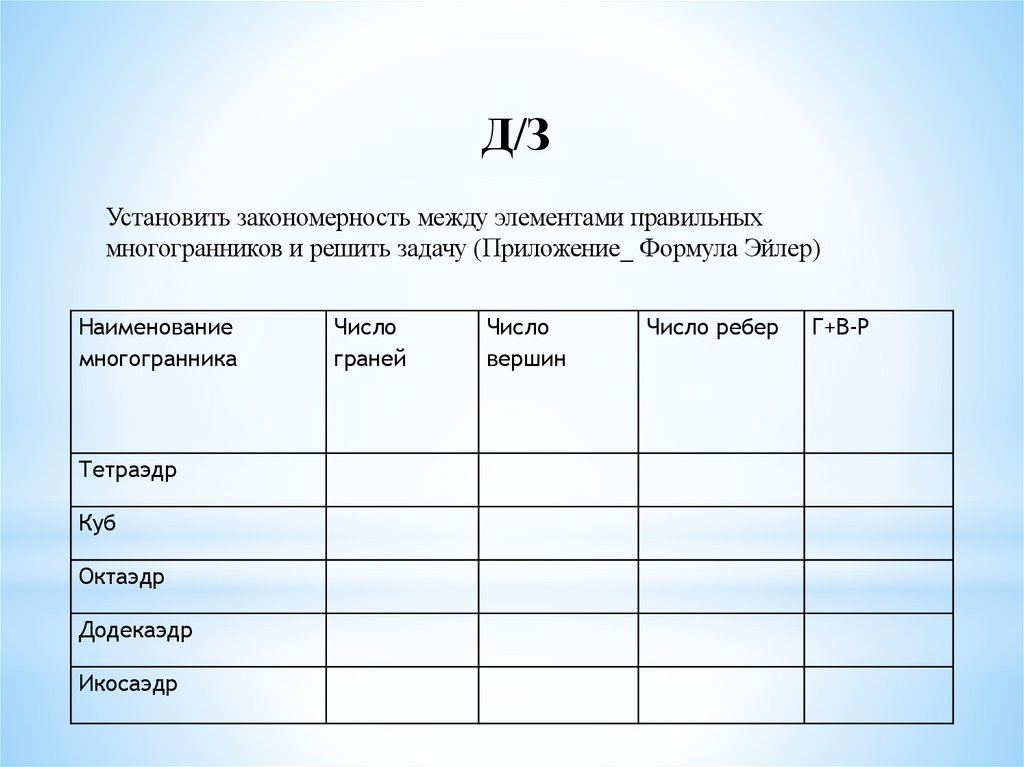
Д/З
Установить закономерность между элементами правильных
многогранников и решить задачу (Приложение_ Формула Эйлер)
Наименование
многогранника
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
Число
граней
Число
вершин
Число ребер
Г+В-Р