Лекция 4. Решение СЛАУ

1.

ЛЕКЦИЯ №4
1

2. Вспоминаем изученный материал

Матрица
Эквивалентные матрицы
Ранг матрицы
3-й тип элементарных
преобразований
Транспонирование матрицы
Теорема Кронекера-Капелли
Вырожденная матрица
Обращение матрицы
Метод Саррюса
Треугольная матрица
Согласованность матриц
Единичная матрица
Матрица системы
Трапециевидная матрица
Равные матрицы
СЛАУ
2

3.

3

4.

Метод решения хорош, если с самого начала мы можем предвидеть - и далее
подтвердить то, - что, следуя этому методу, мы достигнем цели.
Г. Лейбниц
Прямые методы:
метод Крамера;
метод обратной матрицы;
метод Гаусса.
4

5. швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры

Габриэль Крамер родился 31 июля 1704 года в Женеве
(Швейцария), в семье врача. Уже в детстве он
опережал своих сверстников в интеллектуальном
развитии и демонстрировал завидные способности в
области математики. В 18 лет он успешно защитил
диссертацию. Через 2 года Крамер выставил свою
кандидатуру на должность преподавателя в
Женевском университете. Юноша так понравился
магистрату, что специально для него и ещё одного
кандидата на место преподавателя была учреждена
отдельная кафедра математики, где Крамер и
работал в последующие годы.
Талантливый учёный написал множество статей на
самые разные темы: геометрия, история,
математика, философия. В 1730 году он
опубликовал труд по небесной механике.
5

6.

ПРАВИЛО КРАМЕРА:
Если определитель матрицы системы n линейных уравнений с n
неизвестными отличен от нуля, то система имеет единственное
решение, которое находится по формулам:
6

7.

При решении систем линейных уравнений по методу Крамера
выполняется следующий алгоритм:
- систему записывают в матричном виде;
- вычисляют главный определитель системы:
- вычисляют дополнительные определители системы:
- если главный определитель системы не равен нулю, то находят
значения всех неизвестных по формулам:
7

8.

Пример 1. Решить СЛАУ по формулам Крамера
Решение: Решим систему по формулам Крамера
значит, система имеет единственное
решение.
8

9.

9

10.

Ответ:
10

11.

Трудность решения в какой-то мере входит в само понятие задачи: там, где
нет трудности, нет и задачи.
Д. Пойа
Из-за высокой вычислительной сложности метода
(требуется вычисление n + 1 определителя размерности n
x n), он не применяется для машинного решения больших
СЛАУ. Время, необходимое на вычисление одного
определителя примерно такое же, как и время на решение
одной системы уравнений при использовании метода
Гаусса. Однако он иногда используется при ручном счёте
и в теоретических выкладках.
11

12. РЕШИТЬ СЛАУ методом Крамера

2x - y - 2z 1
2y z 3
- 2x - 2y 2z 2
12

13.

a11 x1 a12 x2 a13 x3 ... a1n xn b1
a x a x a x ... a x b
21 2
22 2
23 3
2n n
2
.......................................................
an1 x1 an 2 x2 an 3 x3 ... ann xn bn
x1
x2
X
...
xn
b1
b2
B
...
bn
Систему можно записать в виде
A X B
где
a11
a21
A
...
an1
a12 a13
a22 a23
... ...
an 2 an 3
...
...
...
...
a1n
a2 n
...
ann
13

14.

Если матрица A невырожденная
(то есть, это квадратная матрица,
определитель которой отличен
от нуля) , то верна формула
X A B
1
14

15.

Пример 2. Решить СЛАУ матричным методом (методом
обратной матрицы)
Решение: Запишем систему в матричной форме:
, где
Решение системы найдем по формуле
15

16.

Внимание! Если
, то обратной матрицы не существует, и решить
систему матричным методом невозможно. В этом случае система
решается методом исключения неизвестных (методом Гаусса)
Матрица алгебраических дополнений:
Транспонированная матрица алгебраических дополнений:
16

17.

ОБРАТНАЯ МАТРИЦА
РЕШЕНИЕ СЛАУ:
17

18. немецкий математик, астроном и физик

Дата рождения: 30 апреля 1777 года
Место рождения: Брауншвейг
Дата смерти: 23 февраля 1855 года
Место смерти: Гёттинген
Герцогство: Брауншвейг-Люнебург
Научная сфера: математика, физика,
астрономия
Альма-матер: Гёттингенский университет
Карл Фридрих Гаусс
18

19.

Метод Гаусса является более универсальным и
пригоден для систем с любым числом уравнений.
Он заключается в последовательном исключении
неизвестных из уравнений системы.
Алгоритм состоит из двух этапов.
На первом этапе осуществляется так называемый
прямой
ход,
когда
путём
элементарных
преобразований над строками систему приводят к
ступенчатой или треугольной форме.
На втором этапе осуществляется так называемый обратный ход, суть
которого заключается в том, чтобы выразить все получившиеся базисные
переменные через небазисные и построить фундаментальную систему
решений.
19

20.

менее трудоёмкий по сравнению с другими методами;
применим к любой системе линейных уравнений;
в силу простоты и однотипности выполняемых операций
пригоден для счета на электронно-вычислительных
машинах.
20

21.

Пример 3. Решить СЛАУ методом Гаусса
РЕШЕНИЕ
Запишем расширенную матрицу системы:
Наша цель – с помощью элементарных
преобразований привести матрицу к
ступенчатому виду.
21

22.

РЕЗУЛЬТАТ ЭЛЕМЕНТАРНЫХ ПРЕОБРАЗОВАНИЙ
(ПРЯМОЙ ХОД)
ОБРАТНЫЙ ХОД
22

23.

ПРОВЕРКА
Подставляем значения
неизвестных в любое из
уравнений
3*3+2*5-5*4=-1
23

24. Решить СЛАУ методом Гаусса

24

25. Решить СЛАУ с применением всех известных методов

25

26. Несовместные системы. Системы с общим решением. Частные решения

СЛАУ С ДВУМЯ И БОЛЕЕ
РЕШЕНИЯМИ
Несовместные системы.
Системы с общим
решением. Частные
решения

27. Исследование СЛАУ на совместность

1.
2.
Если ранг матрицы системы равен рангу расширенной
матрицы системы, то система совместна, причём, если данное
число (РАНГ) совпадает с количеством неизвестных, то
решение единственно.
Если РАНГ при этом меньше числа неизвестных, то СЛАУ
имеет бесконечное число решений.
3. Если ранг расширенной матрицы больше ранга
матрицы системы, система несовместна.

28. ПРИМЕР 2.

29. ПРИМЕР 3.

Тут 4 уравнения и 4 неизвестных,
таким образом, система может
иметь либо единственное
решение, либо не иметь решений,
либо иметь бесконечно много
решений.

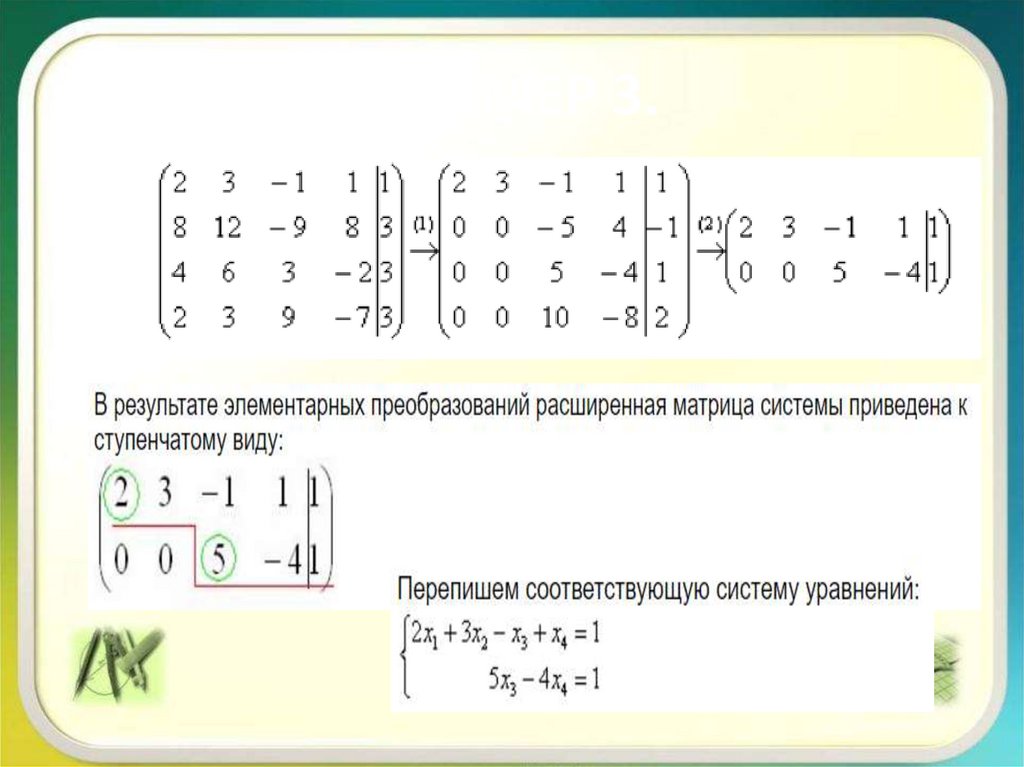
30. ПРИМЕР 3.

31. ПРИМЕР 3.

Бесконечное множество решений системы коротко
записывают в виде так называемого общего решения
системы.
Сначала нужно определить, какие переменные у нас
являются базисными, а какие переменные
свободными.

32. ПРИМЕР 3.

33. ПРИМЕР 3.

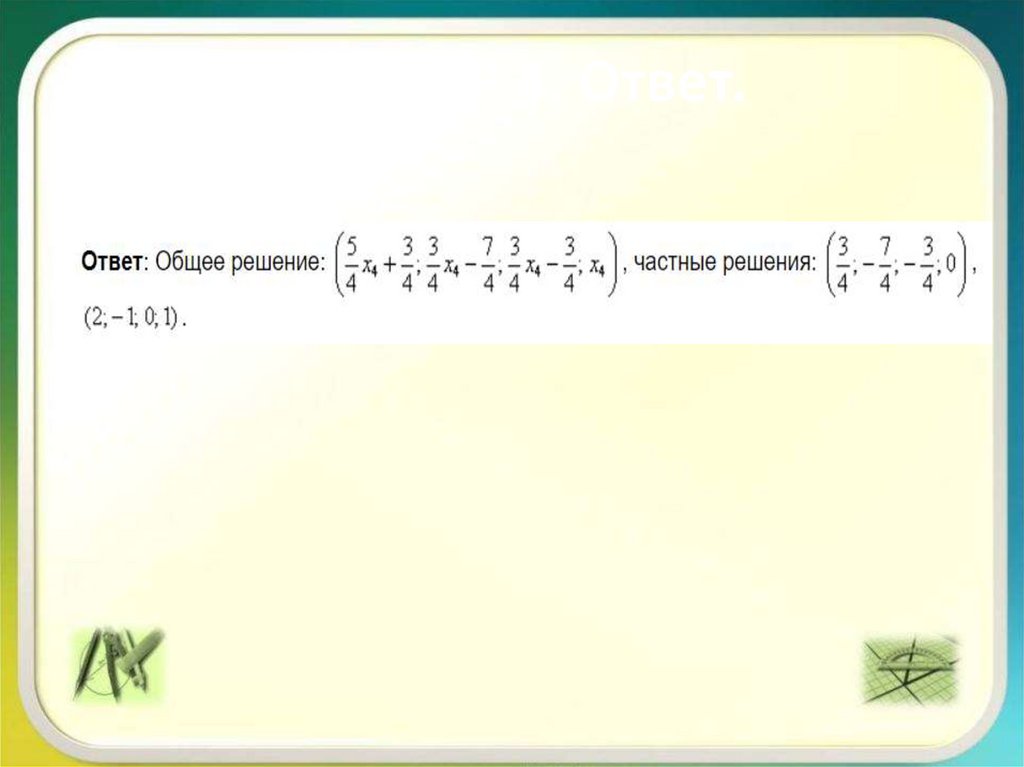
34. ПРИМЕР 3. Как правильно записать общее решение?

35. Частные решения

ТАКЖЕ МОЖНО ПРИСВОИТЬ СВОБОДНЫМ ПЕРЕМЕННЫМ
И ДРУГИЕ ЗНАЧЕНИЯ. НАПРИМЕР, ЕДИНИЦЫ
Легко заметить, что система уравнений имеет
бесконечно много решений (так как свободным
переменным мы можем придать любые
значения)

36. ПРИМЕР 4.

37. ПРИМЕР 4. Ответ.

38. НАЙТИ РЕШЕНИЕ СЛАУ

38