Происхождение геометрии пример

1.

Студент(ка) курса группы «группа»
Фамилия Имя Отчество
Тема презентации
Руководитель проекта.
Преподаватель.

2.

От практической нужды к науке
Геометрия возникла из практических
потребностей древних людей:
строительство, земледелие, навигация.
Необходимость в точности
стимулировала поиск закономерностей
в пространстве.
Ранние цивилизации (Египет,
Месопотамия) заложили основы
систематических геометрических
знаний.

3.

Геометрия без инструментов
В доисторических культурах геометрия обеспечивала
выживание и развитие общества.
Древние люди интуитивно использовали
геометрические принципы, опираясь на наблюдения и
опыт.
Примеры:
Строительство жилищ (прямые углы, окружности,
пропорции).
Мегалитические сооружения (Стоунхендж):
выравнивание камней, угловые измерения.
Орнаменты на керамике и бытовых предметах: линии,
треугольники, круги, симметрия.
Изготовление каменных орудий: симметрия, углы
заточки.

4.

Геометрия Нила и пирамид
Геометрия играла ключевую роль в
теоретических и практических аспектах жизни
египетского общества.
Применение:
Земледелие: Точное измерение полей после
разливов Нила с помощью веревок и
колышков.
Строительство пирамид: Точные расчеты
высоты, углов наклона, пропорций;
использование нивелиров и отвесов.
Папирусы Ахмеса содержат задачи по
вычислению площадей и объемов.

5.

Клинопись и вавилонская математика
Геометрия развивалась на основе нужд
сельского хозяйства, строительства и
астрономии.
Использовалась шестидесятичная система
счисления.
Применение:
Измерение земли: Определение площадей
полей после разливов рек.
Строительство/Хранение: Расчет объемов
цилиндров и конусов.
Астрономия: Предсказание явлений, расчет
углов и расстояний на небесной сфере.
Клинописные таблички (например, «Таблица
Пифагора») свидетельствуют о глубоком
понимании чисел

6.

Различные подходы к геометрии
Сходства: Обе культуры использовали
геометрию для землемерия и строительства.
Различия:
Египет: Акцент на практических
применениях (пирамиды, измерение Нила);
простые инструменты.
Месопотамия: Более теоретический подход,
разработка формул и теорем;
шестидесятичная система счисления;
абстрактное мышление.

7.

Зарождение дедуктивной геометрии
Фалес (около 624 — около 546 гг. до н.э.) — «отец
геометрии».
Первым начал применять дедуктивный подход, пе
реходя от эмпирических измерений к абстрактном
у доказательству.
Известные теоремы:
Треугольник, вписанный в окружность, с прямым
углом — равнобедренный.
При пересечении двух прямых вертикальные угл
ы равны.
Применял знания для измерения высоты объекто
в с помощью теней.

8.

Числа, гармония и Теорема Пифагора
Теорема Пифагора: В прямоугольном
треугольнике квадрат гипотенузы равен
сумме квадратов катетов.
Исследовали свойства многоугольников и
кругов, понимая их философское значение
(порядок и гармония во Вселенной).
Практическое применение:
Архитектура (например, Парфенон): расчет
высоты и пропорций зданий.
Астрономия: вычисление расстояний до
небесных тел, описание орбит планет.
Музыка: исследование соотношений
звуковых частот.
Измерение высоты недоступных объектов.

9.

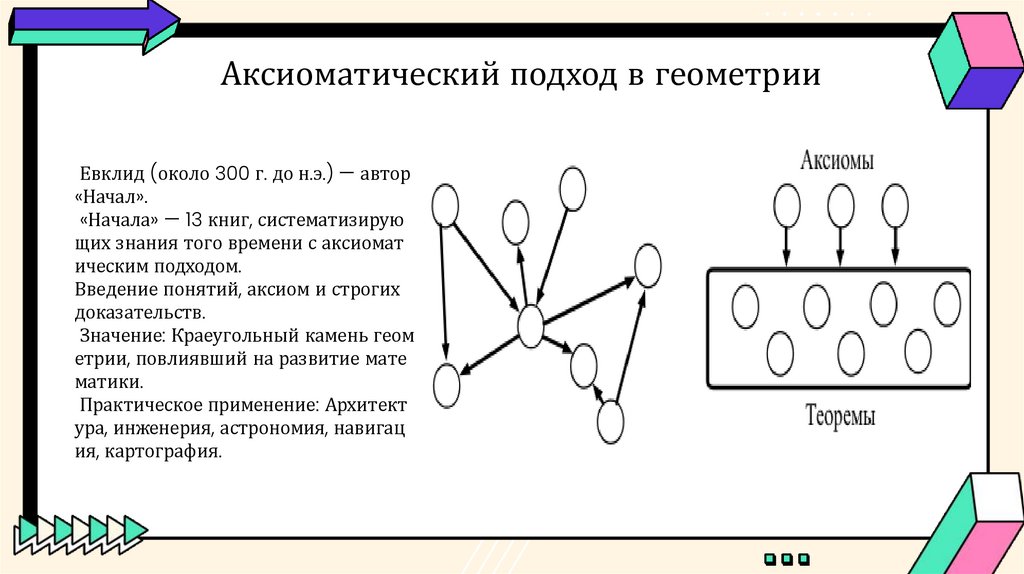
Аксиоматический подход в геометрии
Евклид (около 300 г. до н.э.) — автор
«Начал».
«Начала» — 13 книг, систематизирую
щих знания того времени с аксиомат
ическим подходом.
Введение понятий, аксиом и строгих
доказательств.
Значение: Краеугольный камень геом
етрии, повлиявший на развитие мате
матики.
Практическое применение: Архитект
ура, инженерия, астрономия, навигац
ия, картография.

10.

Архимед и Аполлоний
Архимед (287–212 гг. до н.э.):
Методы вычисления площадей и объемов (сфе
ры, цилиндры).
Теорема о центре тяжести; предвосхитил инте
гральное исчисление.
Практика: проектирование механизмов (винт
Архимеда).
Аполлоний Пергский (около 262–190 гг. до н.э.):
Работа «Конические сечения» — систематизаци
я знаний о параболах, гиперболах, эллипсах.
Основа для аналитической геометрии; примен
ение в астрономии (орбиты планет).

11.

Изменение понимания пространства
Возникла в начале XIX века (Николай
Лобачевский, Янош Бойяи).
Ключевое отличие: Отказ от аксиомы
параллельности (через точку можно
провести бесконечное количество
параллельных прямых —
гиперболическая геометрия).
Работы Гаусса о кривизне
пространства.
Влияние:
Физика: Основа общей теории
относительности А. Эйнштейна
(кривизна пространства-времени).
Применение в архитектуре,
компьютерной графике.

12.

Объединение алгебры и геометрии
Возникла в XVII веке благодаря Рене Декарту и
Пьеру Ферма.
Декарт: Использование координатной систем
ы для описания геометрических объектов (точ
ки как (x,y), прямые как y=mx+b).
Ферма: Методы анализа кривых и решения за
дач оптимизации через алгебраические уравне
ния.
Влияние: Значительно упростило решение зад
ач, стало основой для дифференциального исч
исления.
Практика: Архитектура (чертежи зданий), ком
пьютерная графика (моделирование объектов)
.

13.

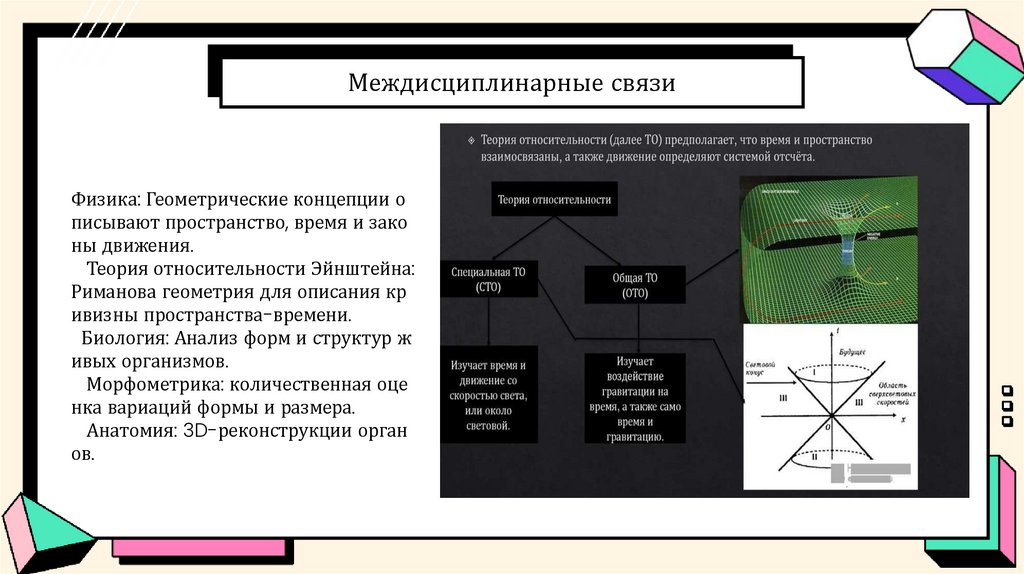
Междисциплинарные связи
Физика: Геометрические концепции о
писывают пространство, время и зако
ны движения.
Теория относительности Эйнштейна:
Риманова геометрия для описания кр
ивизны пространства-времени.
Биология: Анализ форм и структур ж
ивых организмов.
Морфометрика: количественная оце
нка вариаций формы и размера.
Анатомия: 3D-реконструкции орган
ов.

14.

Архитектура и инженер
ия: Ключевая роль в про
ектировании и строител
ьстве.
Использование принц
ипов симметрии и проп
орций для эстетики и ф
ункциональности.
Геометрические расче
ты для устойчивости и
безопасности (мосты, зд
ания).
Прикладное значение
Информатика: Компьют
ерная графика и визуал
изация данных.
Алгоритмы для реали
стичных изображений, а
нимаций.
Обработка пространст
венных данных в ГИС

15.

Эволюция и значение геометрии
Геометрия развивалась от практических нужд
(земледелие, строительство) до абстрактной на
уки.
Древние греки (Евклид) совершили революци
ю, создав дедуктивную систему.
Проект показывает эволюцию геометрических
знаний от эмпирического к дедуктивному подх
оду.
Геометрия – универсальный язык, описывающ
ий и анализирующий сложные явления в мире.