33618de45c144018a4ed861f5925bfec

1.

Геометрическая
вероятность

2.

Определение
Геометрическая вероятность события A,
являющегося подмножеством
множества Ω точек на прямой или
плоскости — это отношение площади
фигуры A к площади всего множества
Ω:
S(A)
P(A)
S(
)

3.

Свойства определения
геометрической вероятности:
1)
2)
3)
4)
Геометрическая вероятность любого
события заключена между нулем и
единицей, т.е. 0≤P(A)≤1;
Геометрическая вероятность невозможного
события равна 0;
Геометрическая вероятность достоверного
события равна 1, P(F) = 1;
Геометрическая вероятность суммы
несовместимых событий равна сумме
вероятностей этих событий, т.е. A*B = ø, то
P(A+B) = P(A)+P(B)

4.

5.

6. Задача 1. В квадрат со стороной 4 см «бросают» точку. Какова вероятность, что расстояние от этой точки до ближайшей стороны

квадрата будет меньше
1 см?
Закрасим в квадрате множество точек,
удаленных от ближайшей стороны меньше, чем
на 1 см.
Площадь закрашенной части квадрата
16см2 – 4см2 = 12см2.
Значит, P ( A) 12 3 0,75
16 4

7.

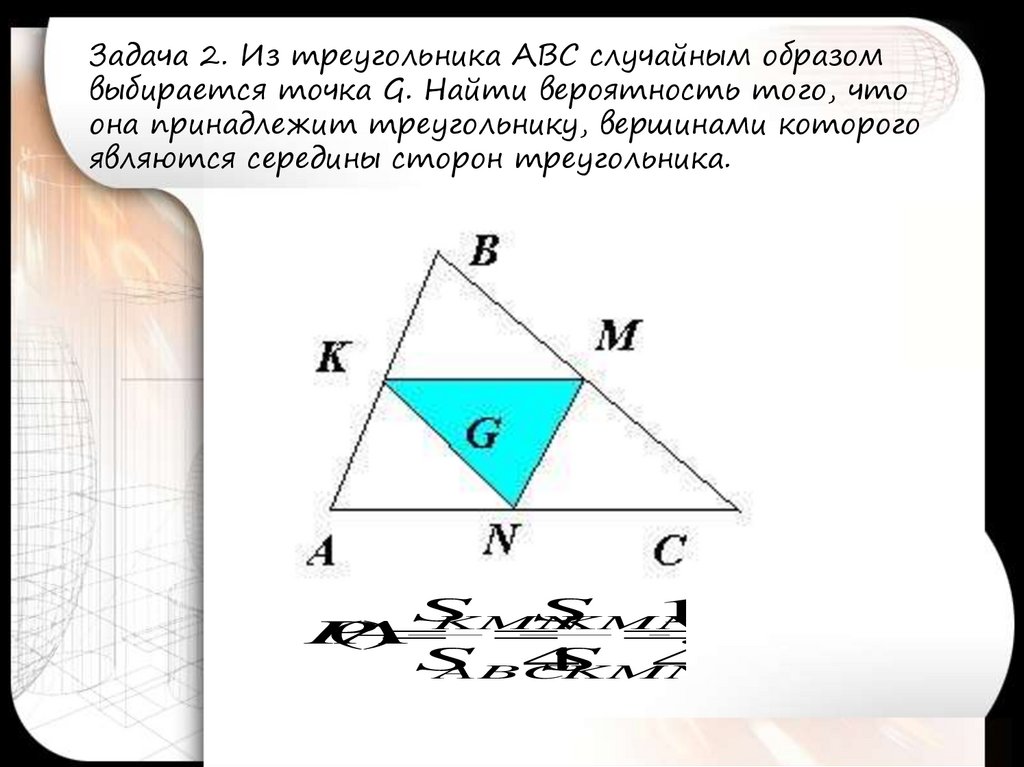
Задача 2. Из треугольника АВС случайным образом
выбирается точка G. Найти вероятность того, что
она принадлежит треугольнику, вершинами которого
являются середины сторон треугольника.
S
S
1
KMN
KMN
P
(
A
)
.
S
4
S
4
ABC
KMN

8.

Задача 3 (на оценку)
Середины сторон ромба MNPK являются
вершинами четырехугольника АВСD. Из
ромба случайным образом выбирается
точка. Найдите вероятность того, что
она не принадлежит четырехугольнику
АВСD.