Лекция_11

1.

§ 8. Формула Тейлора
Рассмотрим многочлен n-й степени
Pn x a0 a1 x a2 x 2 ... an x n ,
где x – переменная, ai – коэффициенты. Найдем значения многочлена и
его производных в точке x 0 :
Pn x a0 a1 x a2 x 2 ... an x n Pn 0 a0
a0 Pn 0 ,
Pn x a1 2a2 x ... na n x n 1 Pn 0 a1
P 0
a1 n ,
1!
Pn x 2a2 ... n n 1 an x n 2 Pn 0 2 1 a2
Pn 0
a2
2!
…
Pn n x n n 1 ... 2 1 an Pn n 0 n n 1 ... 2 1 an
Pn n 0
.
an
n!

2.

Подставляя значения коэффициентов ai в выражение для многочлена
Pn x , получим формулу Маклорена для многочлена Pn x степени n
Pn 0
Pn 0 2
Pn n 0 n
Pn x Pn 0
x
x ...
x .
1!
2!
n!
Разлагая многочлен Pn x по степеням разности x x 0 , где x0 –
число, получим формулу Тейлора для многочлена Pn x степени n
n
x
Pn x 0
Pn x 0
P
x x0
x x0 2 ... n 0 x x0 n .
Pn x Pn x 0
1!
2!
n!
Пример. Разложить в ряд Тейлора функцию y x x 2 4 x 1 в
точке x 0 2 .
Имеем: y 2 11 , y x 2 x 4, y 2 8, y x 2, y 2 2,
y n 2 0 при n 3 . Следовательно
8
2
2
2
y x 11 x 2 x 2 11 8 x 2 x 2 .
1!
2!

3.

Теорема. Если функция f x определена в некоторой окрестности
точки x0 и имеет в ней производные до n 1 -го порядка включительно,
то для любого x из этой окрестности найдется точка c x 0 ; x такая, что
справедлива формула Тейлора для функции f x ;
n
x0
f x 0
f x 0
f
x x0
x x0 2 ...
x x0 n
f x f x0
1!
2!
n!
f n 1 c
x x0 n 1 , c x0 x x0 , 0 1.
n 1 !
Тогда формулу Тейлора для функции f x можно записать в виде
f x Pn x Rn 1 x ,
n
x0
f x 0
f x 0
f
x x0
x x0 2 ...
x x0 n
Pn x f x 0
1!
2!
n!
многочлен Тейлора,
f n 1 c
x x0 n 1 –
Rn 1 x
n 1 !
остаточный член формулы Тейлора в форме Лагранжа.
–

4.

В случае x 0 0 получим формулу Маклорена для функции f x :
f 0
f 0 2
f n 0 n f n 1 x n 1
f x f 0
x
x ...
x
x , 0 1.
1!
2!
n!
n 1 !
Пример. Вычислить число e с абсолютной погрешностью, не
превосходящей 0,001.
Применяя формулу Маклорена для функции f x e x , получим
1
1 2
1 n
e n 1
e f 1 1 1 1 ... 1
1 , 0 1.
1! 2!
n!
n 1 !
e
Из условия
0,001 находим n 1 ! 1000e1 n 6 ( 7! 5040 ),
n 1 !
1 1 1 1 1 1
e 1
1! 2! 3! 4! 5! 6!
2 0,5 0,1667 0,0417 0,0083 0,0014 2,718 .

5.

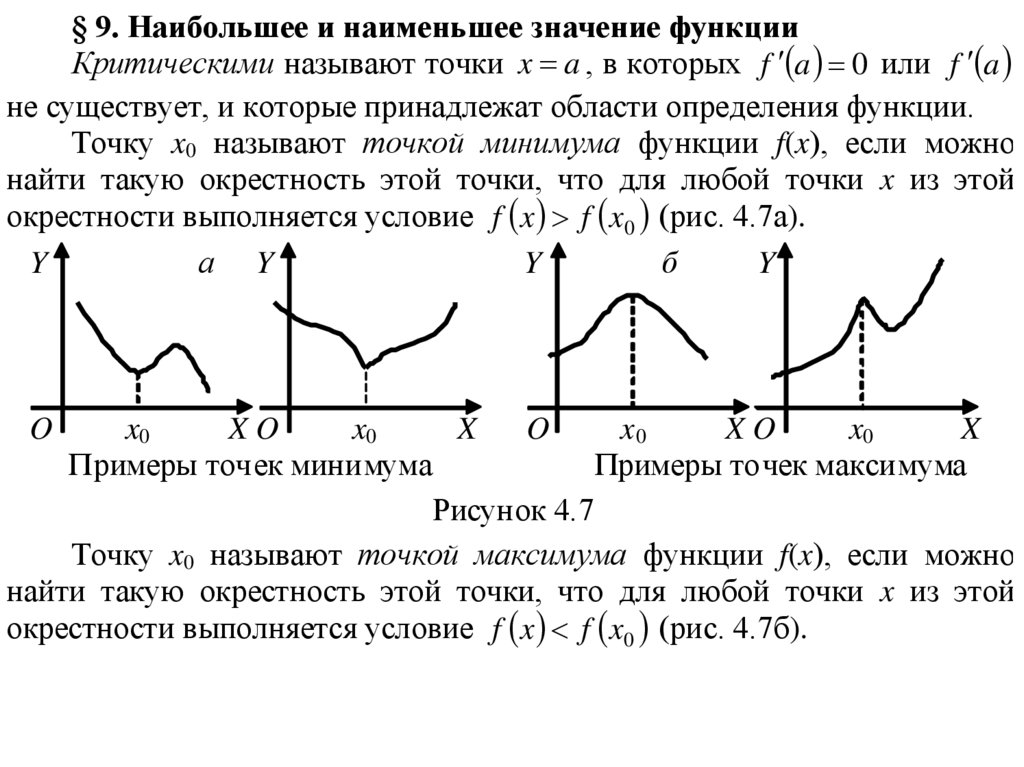
§ 9. Наибольшее и наименьшее значение функции
Критическими называют точки x a , в которых f a 0 или f a
не существует, и которые принадлежат области определения функции.
Точку x0 называют точкой минимума функции f(x), если можно
найти такую окрестность этой точки, что для любой точки x из этой
окрестности выполняется условие f x f x0 (рис. 4.7а).
Y
а Y
Y
б
Y
O
x0
XO
x0
X
O
x0
XO
x0
X
Примеры точек минимума
Примеры точек максимума
Рисунок 4.7
Точку x0 называют точкой максимума функции f(x), если можно
найти такую окрестность этой точки, что для любой точки x из этой
окрестности выполняется условие f x f x0 (рис. 4.7б).

6.

Точки минимума и максимума функции называют точками
экстремума.
Необходимое условие экстремума функции: если функция y f x
имеет экстремум в точке x a , то либо f a 0 , либо f a не
существует.
Достаточное условие экстремума функции: пусть x a –
критическая точка функции y f x , и пусть существует интервал b, c ,
содержащий точку a внутри себя и такой, что на каждом из интервалов
b, a и a, c производная f x существует и сохраняет постоянный
знак. Тогда:
1) если на интервале b, a производная f x 0 , а на интервале
a, c производная f x 0 , то x a точка максимума функции
y f x ;
2) если на интервале b, a производная f x 0 , а на интервале
a, c производная f x 0 , то x a точка минимума функции
y f x ;
3) если на интервалах b, a и a, c производная f x 0 или
f x 0 , то x a не является точкой экстремума функции y f x .

7.

Пример. Исследовать функцию f x x 3 3 x 10 на возрастание и
убывание.
Область
определения
функции
; .
f x 0 при x ; 1 и x 1; ;
f x 3x 2 3 3 x 1 x 1 ;
f x 0 при x 1;1 . Функция возрастает на интервалах ; 1 и
1; , и убывает на интервале 1;1 .
Если функция y f x непрерывна на отрезке a; b , то для
нахождения наибольшего и наименьшего значений функции на отрезке
a; b необходимо:
1) найти критические точки функции на интервале a; b ;
2) вычислить значение функции в критических точках;
3) вычислить значение функции на концах отрезка a; b ;
4) среди вычисленных значений функции выбрать наибольшее и
наименьшее значения.

8.

Если функция y f x на отрезке a; b имеет лишь одну
критическую точку, и она является точкой максимума (минимума), то в
этой точке функция принимает наибольшее (наименьшее) значение.
Если функция y f x на отрезке a; b не имеет критических
точек, то наибольшее значение функция принимает на одном конце
отрезка, а наименьшее – на другом.
Пример. Найти наибольшее и наименьшее значения функции
f x 3 x 4 4 x 3 2 на отрезке 2;1 .
Имеем f x 12 x 3 12 x 2 12 x 2 x 1 . Следовательно, f x 0
при x1 0 и x2 1 , в обоих случаях x 2;1 . Находим: f 0 2 ,
f 1 1 , f 2 18 , f 1 9 . Следовательно f max 18 в точке x 2 ,
f min 1 в точке x 1 .
§ 10. Точки перегиба. Общая схема исследования функции и
построения ее графика
График функции y f x называют выпуклым вверх на интервале
a; b , если он расположен ниже любой касательной на этом интервале и
выпуклым вниз, если он расположен выше любой касательной на этом
интервале.

9.

Пример. На рис. 4.8 кривая y f x Y
y=f(x)
B
выпукла вверх на интервале a; c и
K
M
T
выпукла вниз на интервале c; b . Точку
A
M c; f c , в которой кривая лежит по
разные стороны от касательной MT,
O a
c
b
X
называют точкой перегиба.
Рисунок 4.8
Теорема. Если функция y f x во
всех точках интервала a; b имеет отрицательную вторую производную,
то график функции в этом интервале выпуклый вверх (вогнутый вниз), а
если имеет положительную вторую производную, то график функции в
этом интервале выпуклый вниз (вогнутый вверх).
Теорема (достаточное условие существования точек перегиба).
Если вторая производная при переходе через точку x0, в которой она
равна нулю или не существует, меняет знак, то точка графика с
абсциссой x0 – точка перегиба.

10.

Пример. Исследовать на выпуклость и точки перегиба график
функции y x 5 x 10 .
Находим: y 5 x 4 1, y 20 x 3 .
Вторая производная существует на всей числовой оси, y 0 при
x 0 , y 0 при x 0 , y 0 при x 0 . Следовательно, в точке x=0
вторая производная меняет знак и график функции y x 5 x 10
выпуклый вверх в интервале ;0 , выпуклый вниз в интервале 0; ,
точка 0;10 – точка перегиба.