Презентация к уроку геометрии _Теорема о произведении отрезков хорд, теорема о произведении отрезков секущих, теорема о квадрате касатель

1. Теорема о произведении отрезков хорд. теорема о произведении отрезков секущих. теорема о квадрате касательной.

ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ ХОРД.
ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ СЕКУЩИХ.
ТЕОРЕМА О КВАДРАТЕ КАСАТЕЛЬНОЙ.

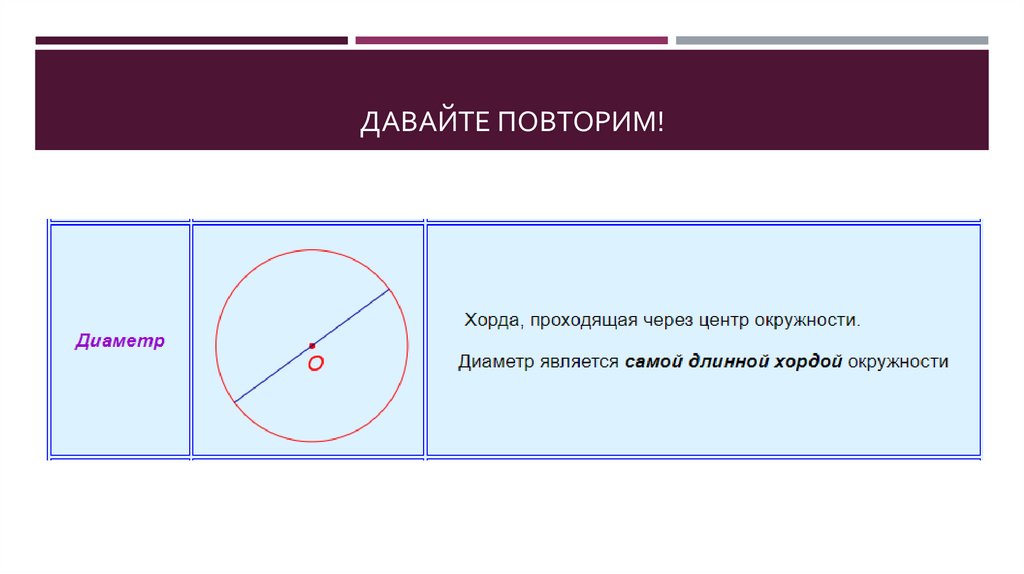
2. ДАВАЙТЕ ПОВТОРИМ!

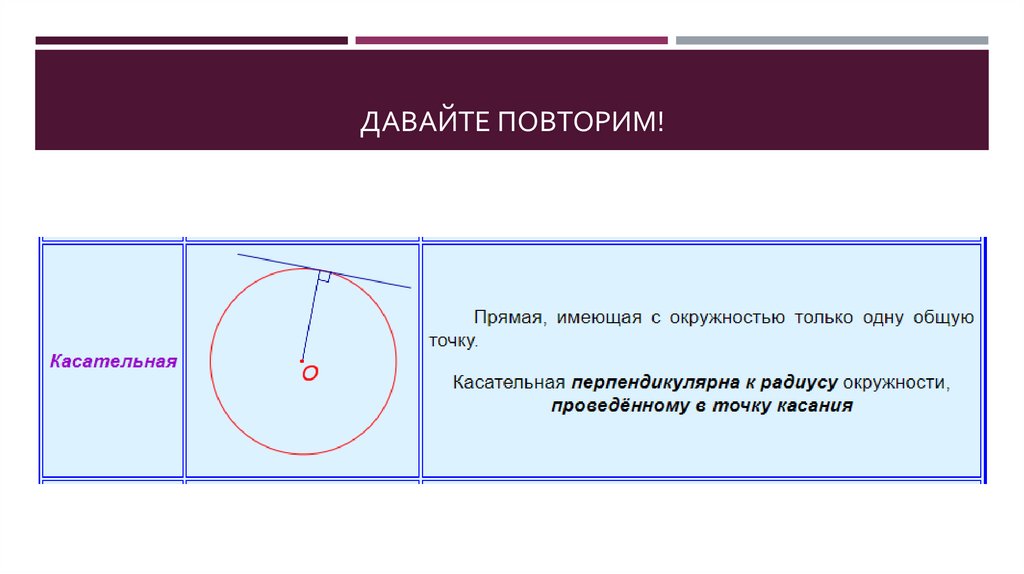
3. ДАВАЙТЕ ПОВТОРИМ!

4. ДАВАЙТЕ ПОВТОРИМ!

5. ДАВАЙТЕ ПОВТОРИМ!

6. ДАВАЙТЕ ПОВТОРИМ!

7. ДАВАЙТЕ ПОВТОРИМ!

8. Теорема о произведении отрезков хорд

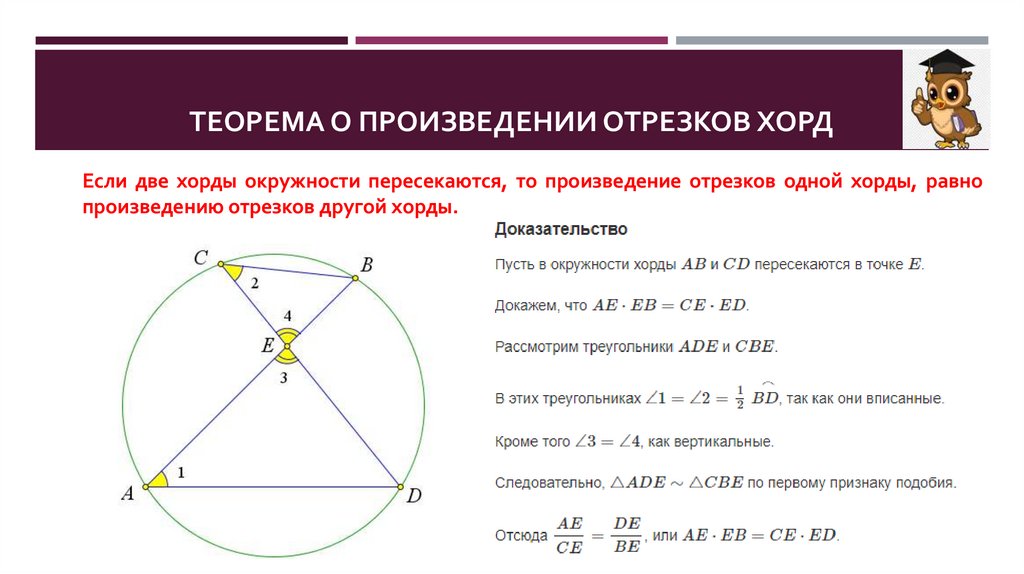
ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ ХОРД
Если две хорды окружности пересекаются, то произведение отрезков одной хорды, равно
произведению отрезков другой хорды.

9. Теорема о квадрате касательной

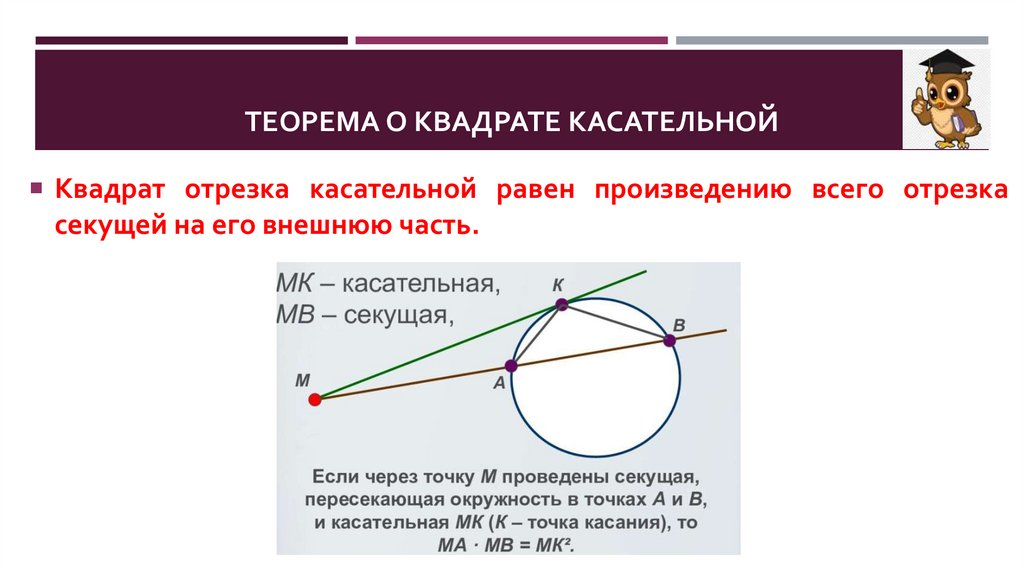
ТЕОРЕМА О КВАДРАТЕ КАСАТЕЛЬНОЙ
Квадрат отрезка касательной равен произведению всего отрезка
секущей на его внешнюю часть.

10. Теорема о произведении отрезков секущих

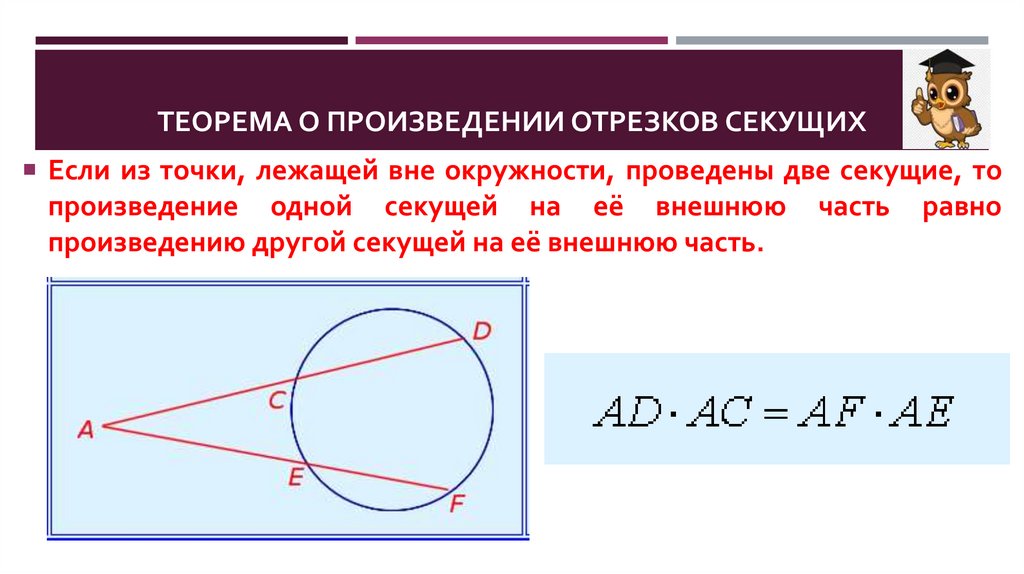
ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ СЕКУЩИХ
Если из точки, лежащей вне окружности, проведены две секущие, то
произведение одной секущей на её внешнюю
произведению другой секущей на её внешнюю часть.
часть
равно

11. ЗАДАЧА 1

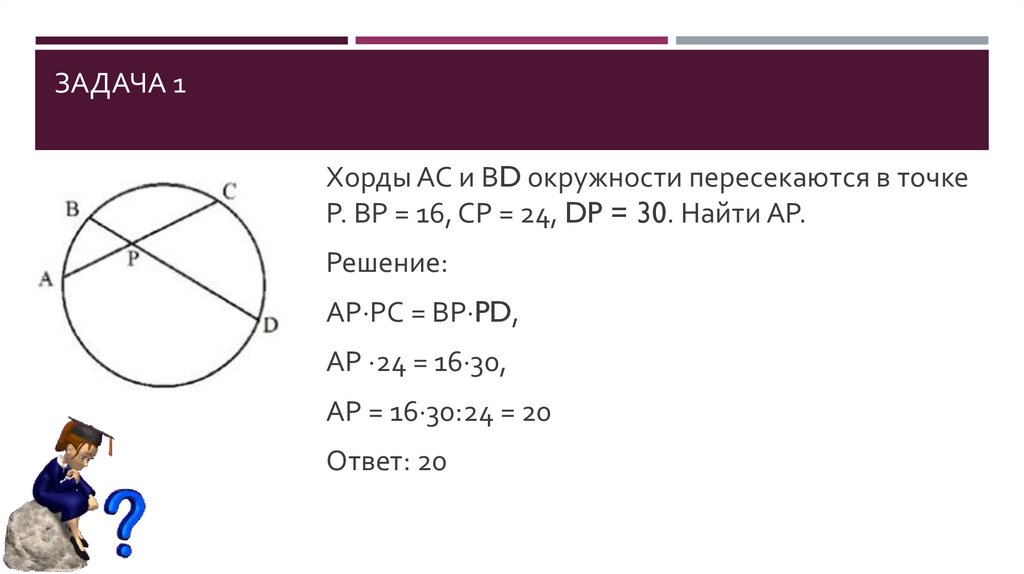
Хорды АС и ВD окружности пересекаются в точке
Р. ВР = 16, СР = 24, DP = 30. Найти АР.
Решение:
АР РС = ВР PD,
АР 24 = 16 30,
АР = 16 30:24 = 20
Ответ: 20

12. ЗАДАЧА 2

Через точку A, лежащую вне окружности,
проведены две прямые. Одна прямая касается
окружности в точке K. Другая прямая пересекает
окружность в точках B и C, причём AB = 5, AC = 20.
Найдите AK.
Решение:
АК2 = АВ АС,
АК2 = 5 20 = 100,
АК = 10
Ответ: 10

13. ЗАДАЧА 3

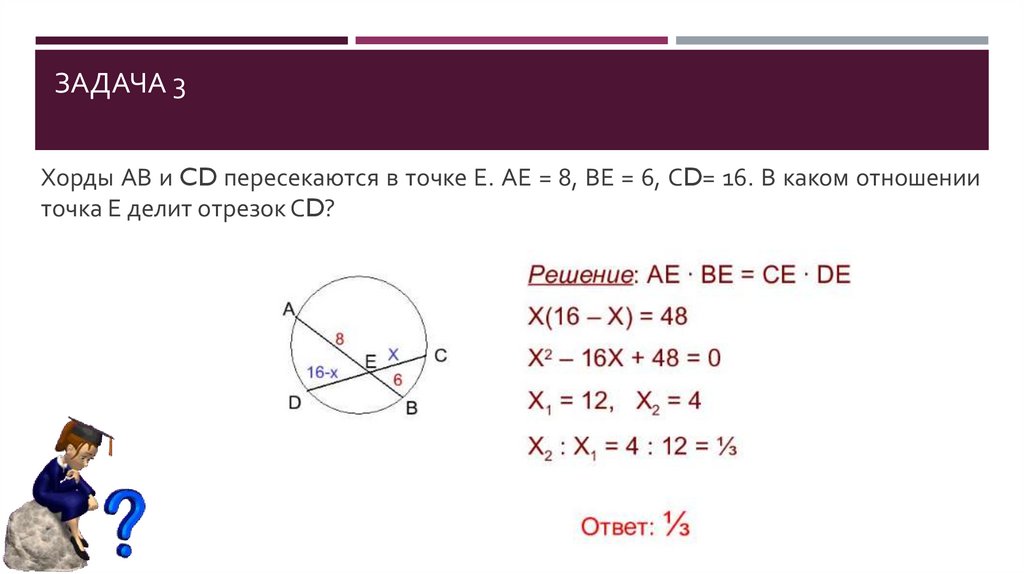
Хорды АВ и CD пересекаются в точке Е. АЕ = 8, ВЕ = 6, СD= 16. В каком отношении
точка Е делит отрезок СD?

14. ЗАДАЧА 4

Из точки вне окружности проведена секущая, пересекающая окружность в
точках, удаленных от данной на 12 и 20. Расстояние от данной точки до
центра окружности 17. Найдите радиус окружности.
Дано: АВ = 12, АС = 20, АО = 17.
Найти: ДО = ОЕ.
Решение.
АВ АС = АD AE
АВ АС = (AO – DO)(AO + EO), АВ АС = (AO – r)(AO + r)
АВ АС = AO2 – r2
12 20 = 172 - r2
r2 = 289 – 240, r2 = 47
r1 = 7, r2 = -7 – не уд.
Ответ: 7

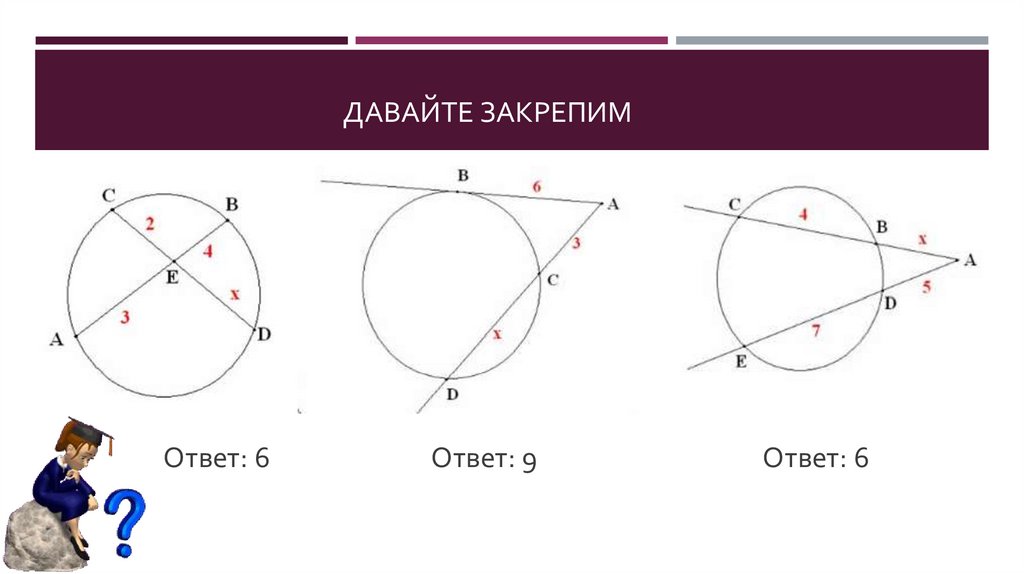
15. ДАВАЙТЕ ЗАКРЕПИМ

Ответ: 6
Ответ: 9
Ответ: 6

16. рефлексия

РЕФЛЕКСИЯ

17. Домашнее задание

ДОМАШНЕЕ ЗАДАНИЕ
Повторить § 2, п. 73 (теорему)
Выполнить в тетради № 666 (а, б, в)

18. Использованные источники:

ИСПОЛЬЗОВАННЫЕ ИСТОЧНИКИ:
https://wiki.sch239.net/math-public/proporcionalnye_otrezki_v_kruge
https://resh.edu.ru/subject/lesson/2504/main/
https://uchitel.pro/опорный-конспект-1-окружности/
https://www.resolventa.ru/demo/training.htm