14 SAF Сбалансированные деревья

1. Лекция

А.Ф. ЗУБАИРОВ

2. Сбалансированные деревья поиска

При построении деревьев из случайного набора
данных существует вероятность построения
вырожденного дерева, близкого по структуре к
линейному списку.
Поддержание бинарного дерева в оптимальном
состоянии после каждого удаления и добавления
записи сложная (ресурсоемкая) задача.
Решение проблемы поддержания дерева в
«хорошем» состоянии предложено Г.М.
Адельсоном-Вельским и Е.М. Ландисом.

3. Сбалансированные деревья поиска

Критерий сбалансированности по высоте: дерево
является сбалансированным тогда и только
тогда, когда для каждого узла высота его двух
поддеревьев различается не более, чем на 1.
Такие деревья называют АВЛ-деревьями (по
фамилиям создателей).
Теорема Адельсона-Вельского и Ландиса: путь
поиска по сбалансированному дереву не
превышает пути поиска по оптимальному дереву
более, чем на 45%.

4. Сбалансированные деревья поиска

Георгий Максимович
Адельсон-Вельский
Евгений Михайлович
Ландис

5. Сбалансированные деревья поиска

Красно-черные деревья(Red-black-trees)
АВЛ-деревья(AVL-trees)
2-3-деревья(2-3-trees)
B-деревья(B-trees)

6. Сбалансированные деревья поиска

Основная идея: если вставка или удаление
элемента приводит к нарушению
сбалансированности дерева, то необходимо
выполнить его балансировку
Коэффициент сбалансированности узла (balance
factor) – это разность высот его левого и правого
поддеревьев
В АВЛ-дереве коэффициент сбалансированности
любого узла принимает значения из множества
{-1, 0, 1}

7. Вставка узла

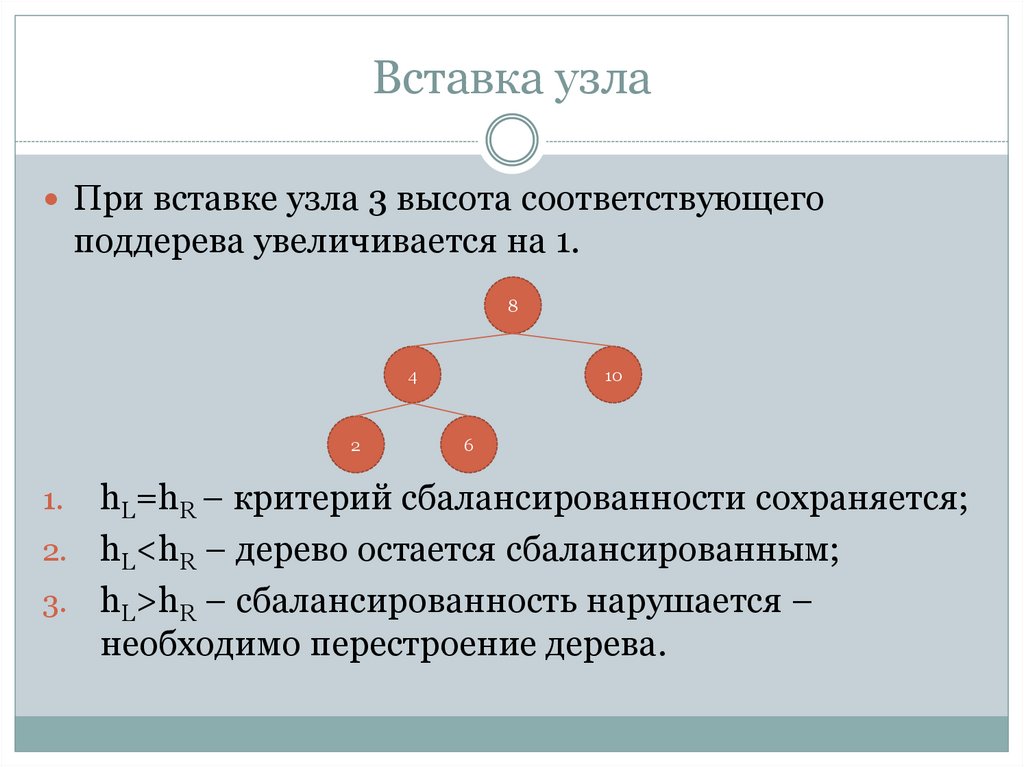
При вставке узла 3 высота соответствующего
поддерева увеличивается на 1.
8
4
2
10
6
hL=hR – критерий сбалансированности сохраняется;
2. hL<hR – дерево остается сбалансированным;
3. hL>hR – сбалансированность нарушается –
необходимо перестроение дерева.
1.

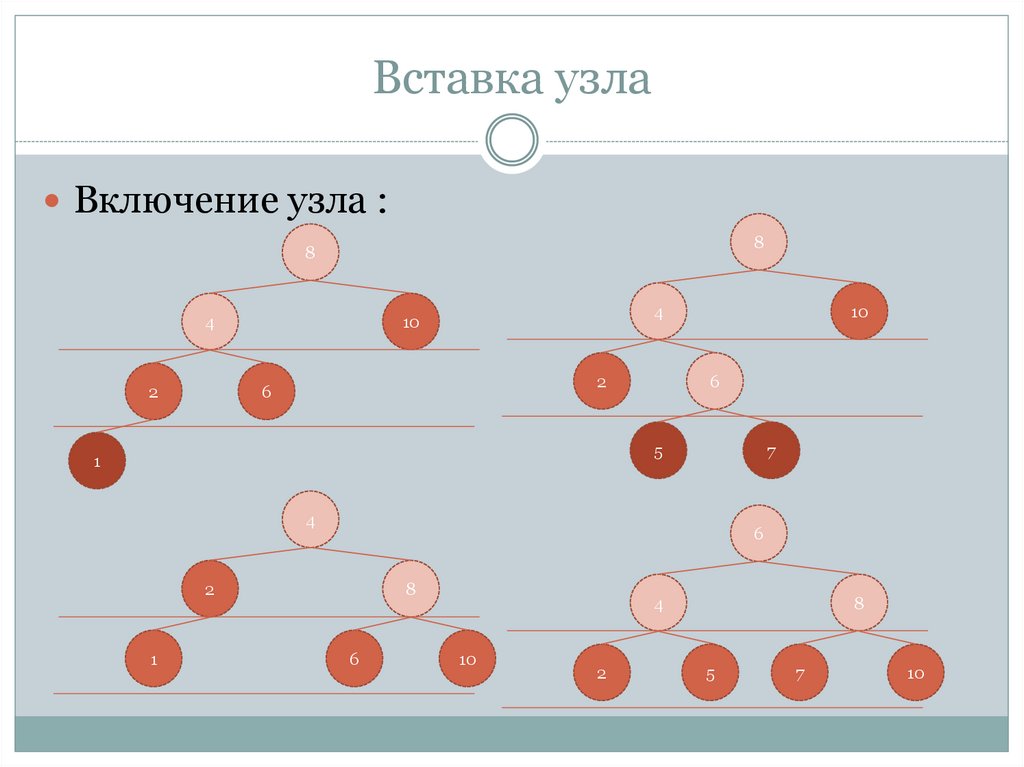
8. Вставка узла

Включение узла :
8
8
4
2
4
10
2
6
10
6
5
1
7
4
6
2
1
8
6
4
10
2
8
5
7
10

9. Вставка узла

После добавления нового элемента необходимо
обновить коэффициенты сбалансированности
родительских узлов
Если любой родительский узел принял значение -2 или 2,
то необходимо выполнить балансировку поддерева путем
поворота (rotation)
Повороты:
Одиночный правый поворот (R-rotation, single right rotation)
Одиночный левый поворот (L-rotation, single left rotation)
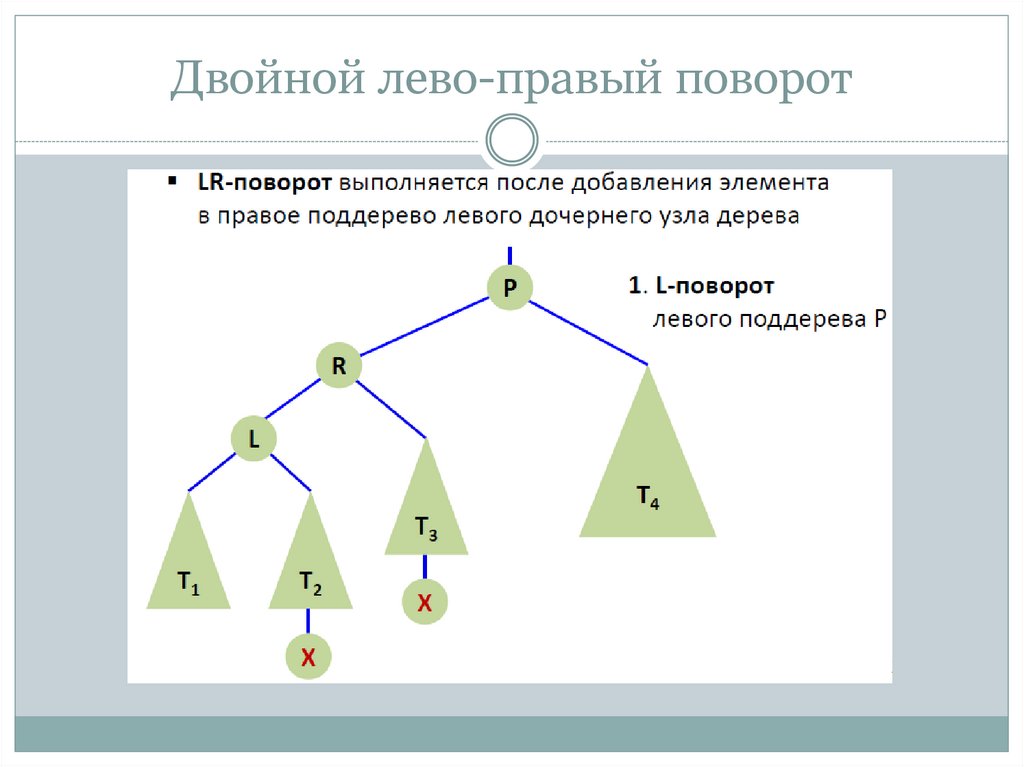
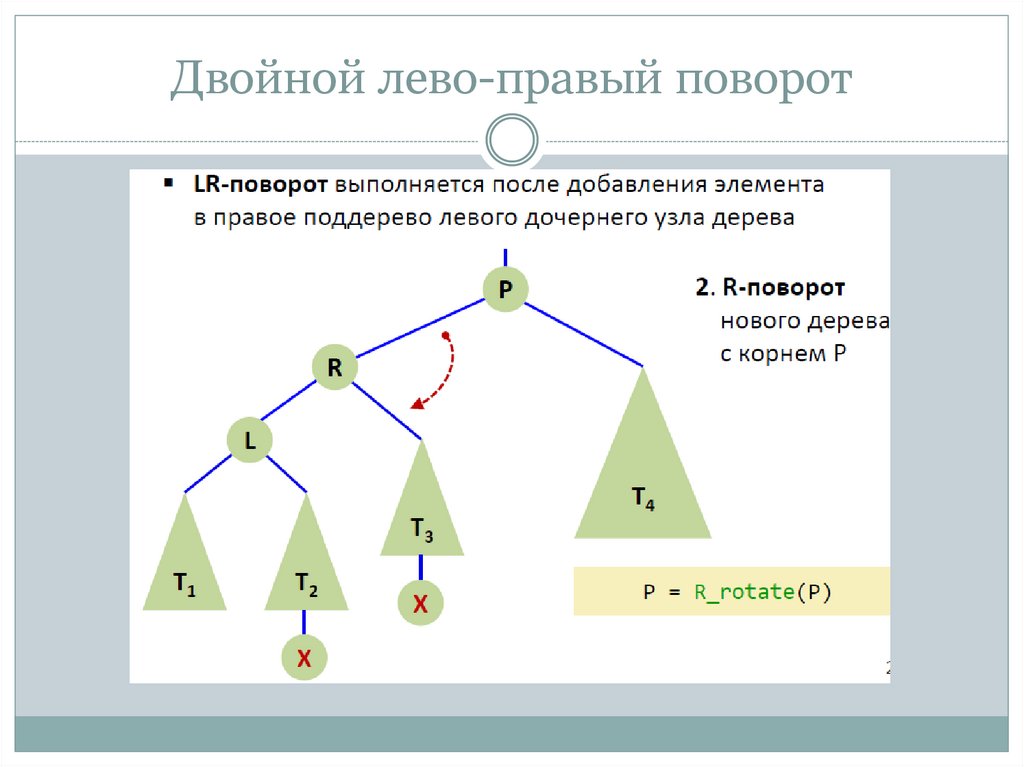
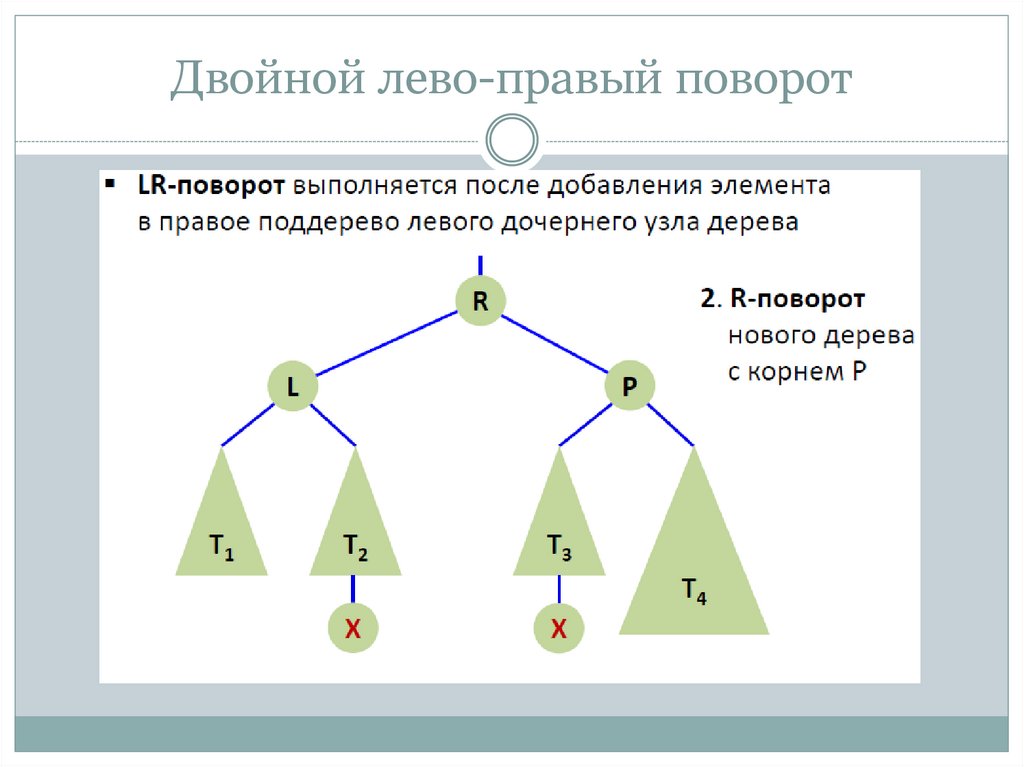
Двойной лево-правый поворот (LR-rotation, double left-right
rotation)
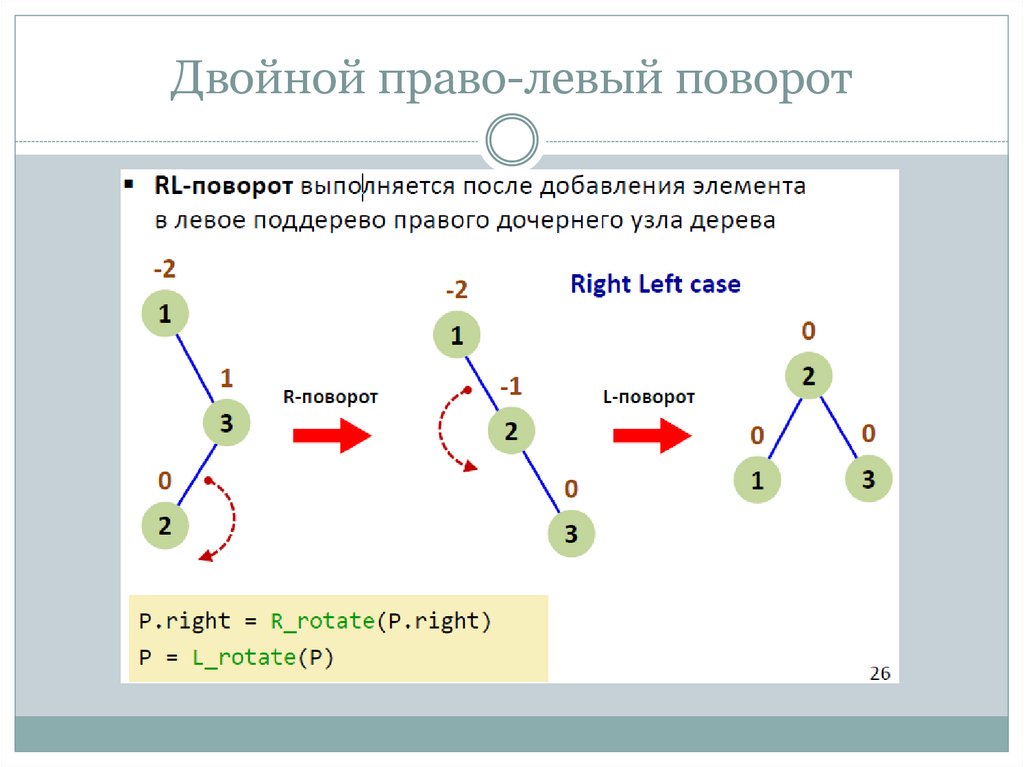
Двойной право-левый поворот (RL-rotation, double right-left
rotation)

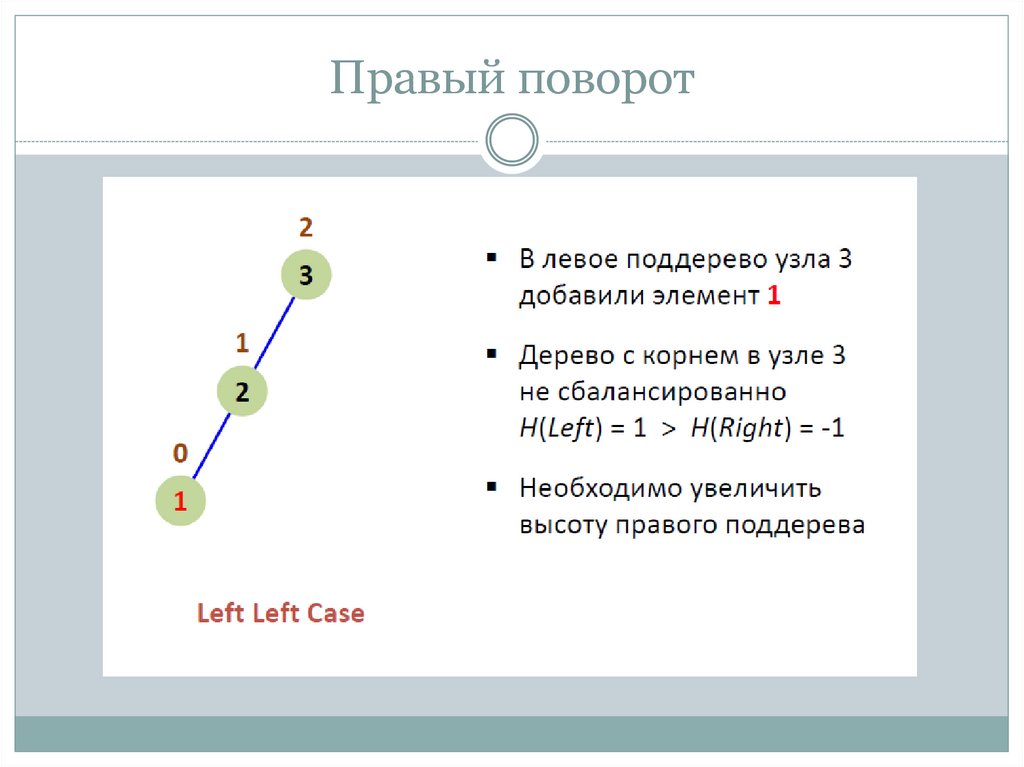
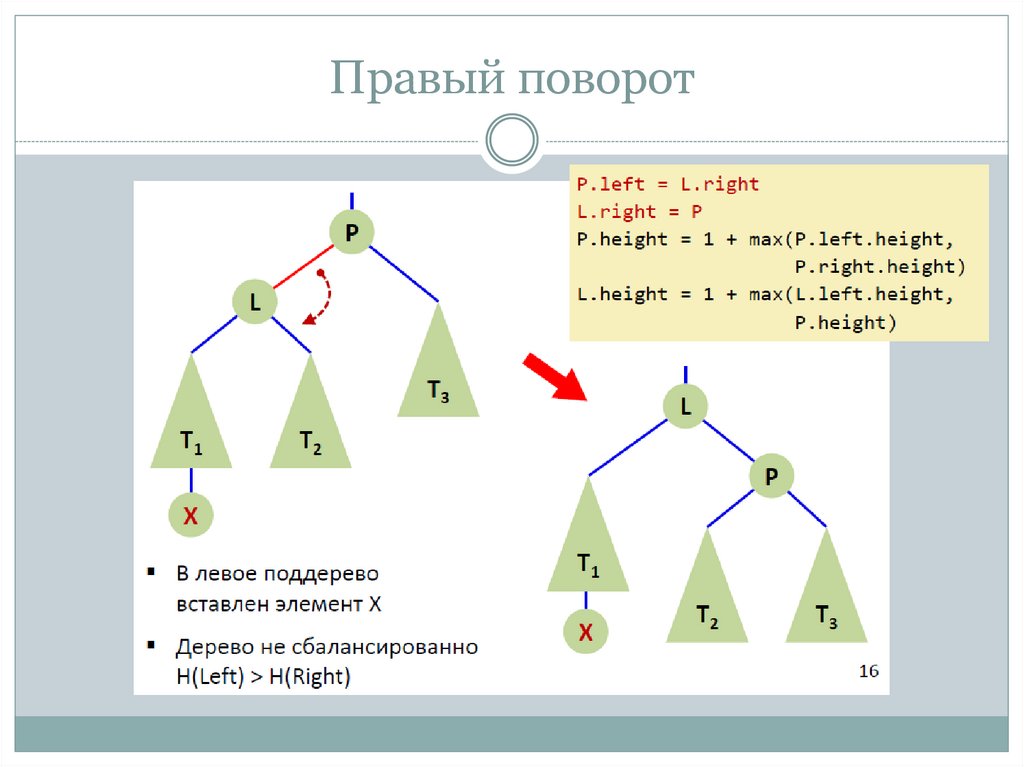
10. Правый поворот

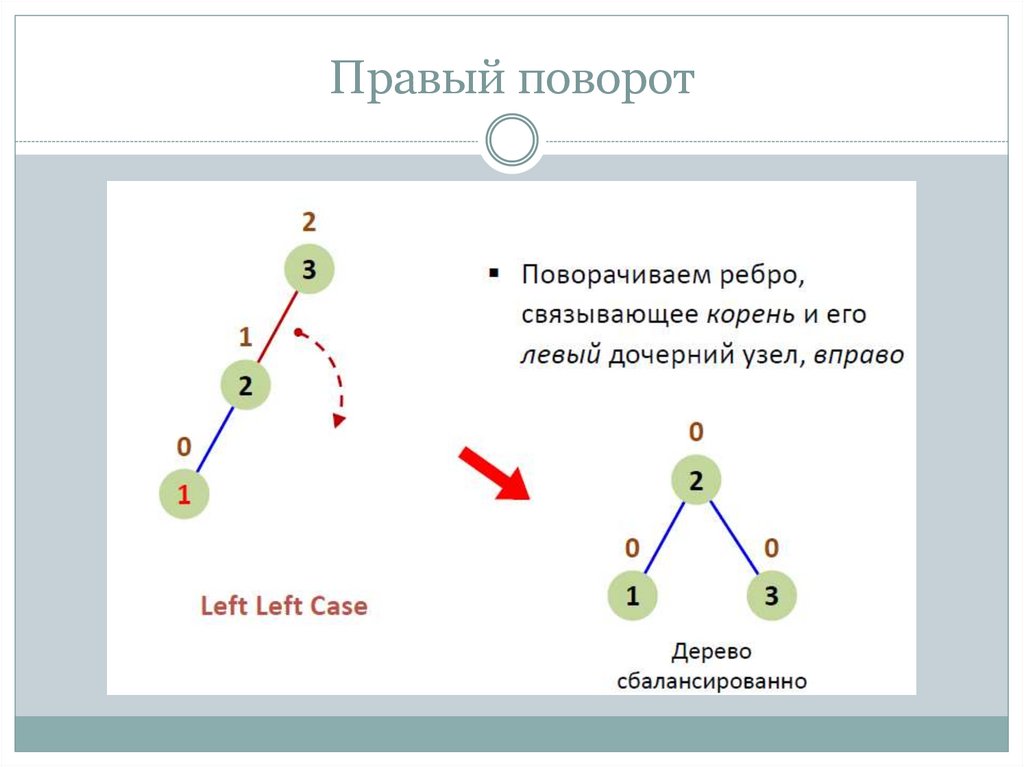
11. Правый поворот

12. Правый поворот

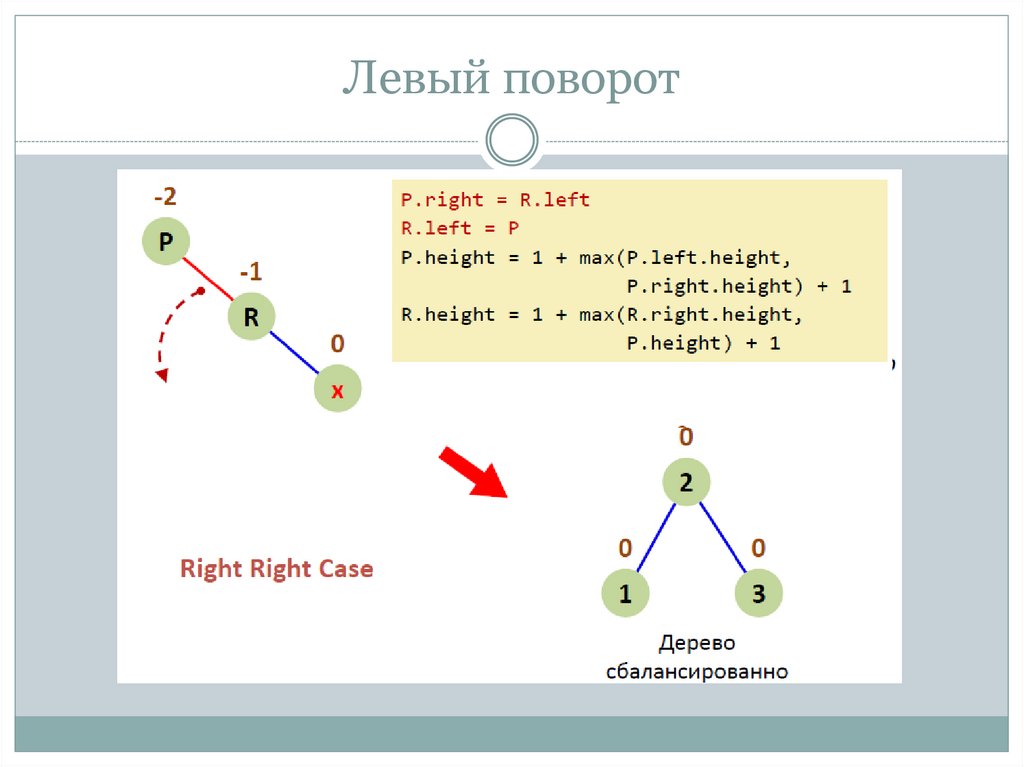
13. Левый поворот

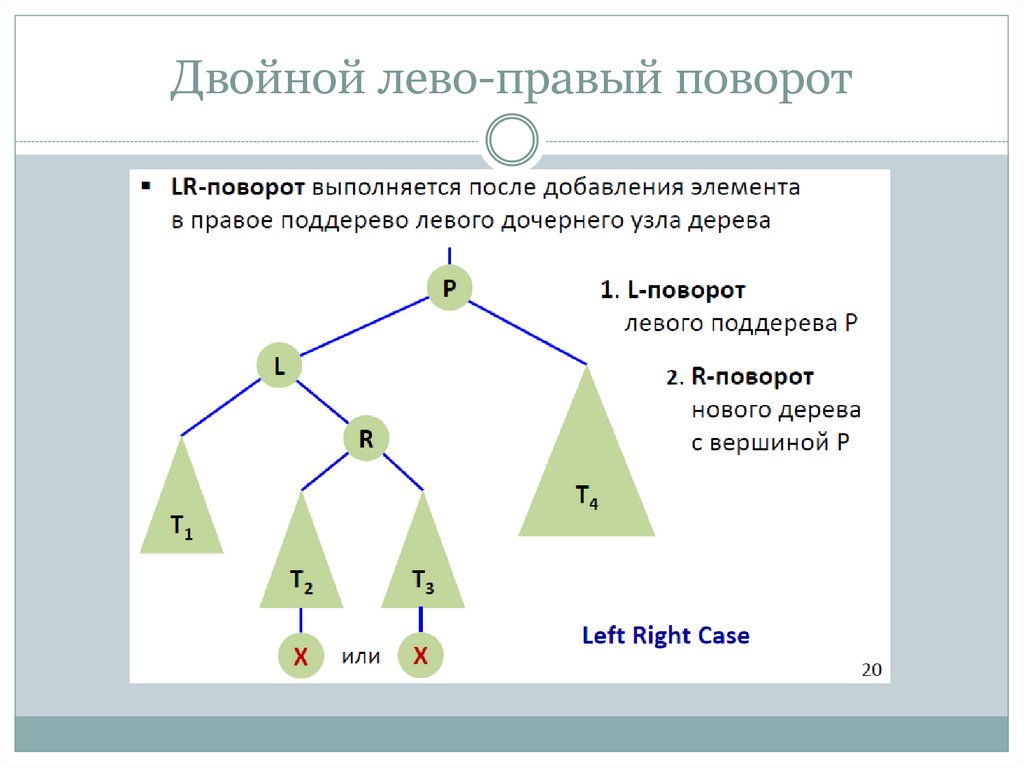
14. Двойной лево-правый поворот

15. Двойной лево-правый поворот

16. Двойной лево-правый поворот

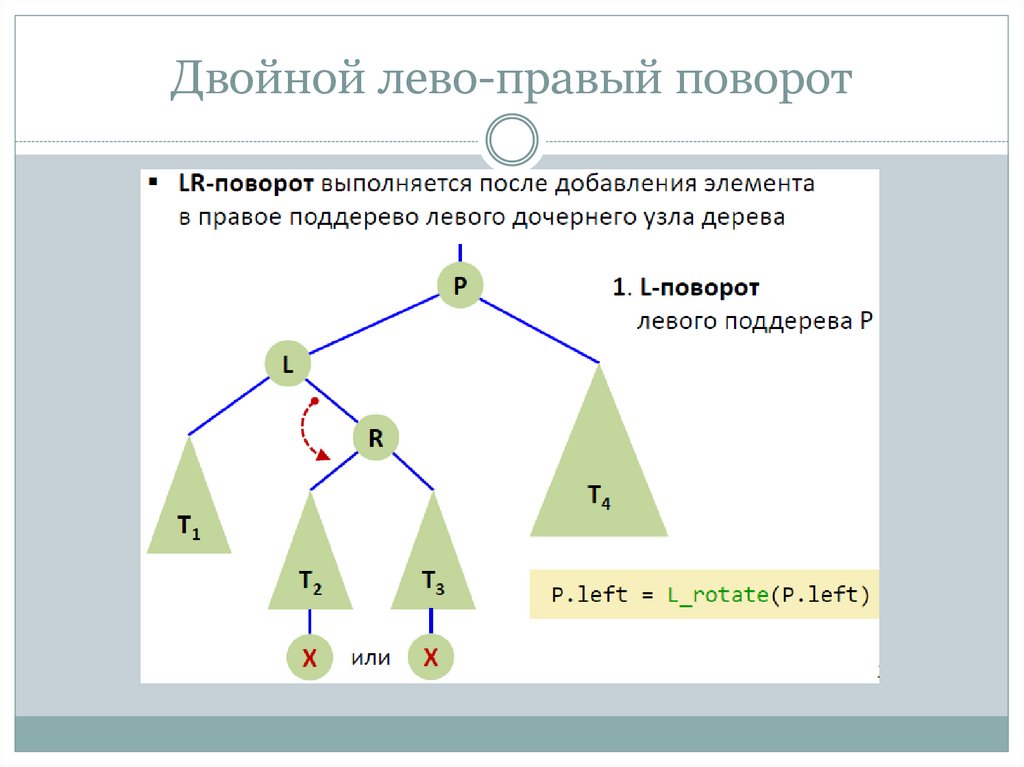
17. Двойной лево-правый поворот

18. Двойной лево-правый поворот

19. Двойной право-левый поворот

20. Вставка узла

Для хранения информации об узле следует
добавить либо а) в узел новое поле balance (b)
равное высоте правого поддерева минус высота
левого поддерева: значения -1, 0, 1; либо б) поле
height – высоту дерева.
Процесс включения узла:
1. Следовать по пути поиска до NULL.
2. Включить новый узел и определить показатель
сбалансированности.
3. Пройти обратно по пути поиска и проверить
показатель сбалансированности.

21. AVL Tree

22. Сбалансированные по высоте деревья поиска

В случае, если ограничить разность высот
деревьев величиной k, получаются
сбалансированные по высоте бинарные деревья
(К.К. Форстер) – HB(k)-деревья.
Сбалансированные деревья – частный случай
HB-деревьев – HB(1).