ЛЕКЦИЯ №5. Спорт 2

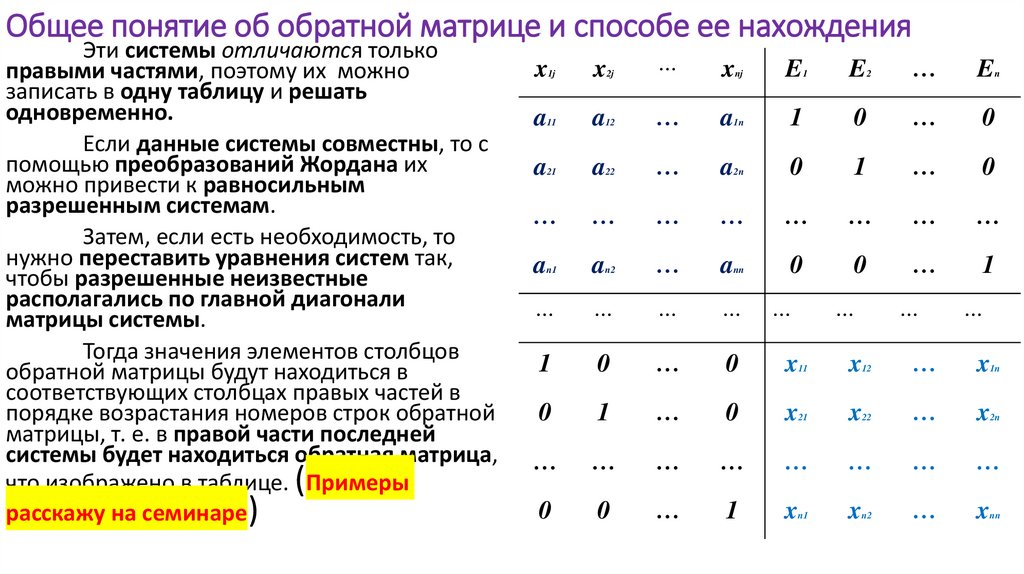
1. ОБЩАЯ ТЕОРИЯ СИСТЕМ УРАВНЕНИЙ. ОБРАТНАЯ МАТРИЦА. Матричные уравнения. ОПРЕДЕЛИТЕЛИ МАТРИЦ

Лекция 4

2. Фундаментальная система решений однородной системы уравнений

Определение. Фундаментальной системой
решений однородной системы уравнений
называется линейно независимая система
векторов-решений F1; F2; …; Fn, по которой
раскладывается любое решение системы, т. е.
любое решение системы уравнений равно
X = t1·F1 + t2·F2 + …+ tn·Fn , где t1;t2;…;tn
действительные числа.

3. Фундаментальная система решений однородной системы уравнений

Теорема. Если ранг матрицы системы однородных уравнений r меньше числа неизвестных n, то система
уравнений имеет фундаментальную систему решений, состоящую
из (n r) векторов-решений.

4. Векторная форма записи общего решения неоднородной системы уравнений

Теорема. Общее решение неоднородной системы
уравнений А·Х = В равно сумме частного решения этой
системы K и линейной комбинации решений
фундаментальной системы решений соответствующей
однородной системы уравнений А·Х = , т. е.
X = K + t1·F1 + t2·F2 + …+ tk·Fk,
где K – какое-либо решение неоднородной системы
уравнений А·Х = В; F1; F2; …; Fn – фундаментальная
система решений однородной системы уравнений А·Х = ;
t1;t2;…;tk – произвольно заданные числа.

5. Общее понятие об обратной матрице и способе ее нахождения

Пусть имеется квадратная матрица n-го порядка