Проекция силы на ось и на плоскость

1. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ

• Проекция силы на ось есть скалярная величина, равная взятой с
соответствующим знаком длине отрезка, заключенного между проекциями
начала и конца силы на данную ось.
• Проекция на ось имеет знак «+» если перемещение от ее начала к
концу совпадает с положительным направлением оси и знак « » в
противном случае.
• Проекцию силы на ось можно вычислить аналитически как произведение модуля силы на косинус угла между направлением силы и положительным направлением оси.
B4
5
F5
F4
А5
B2
А4
5
F5x = - F5
a5
a4
F4x= F4 cos =
4
F3
90
a3 , 3
F3x = 0
F2
0
А2
А1
F1
B1
X
a2
a1
2
F1x = F1
F2x= F2 cos
1
= - F4 cos
1

2. ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ

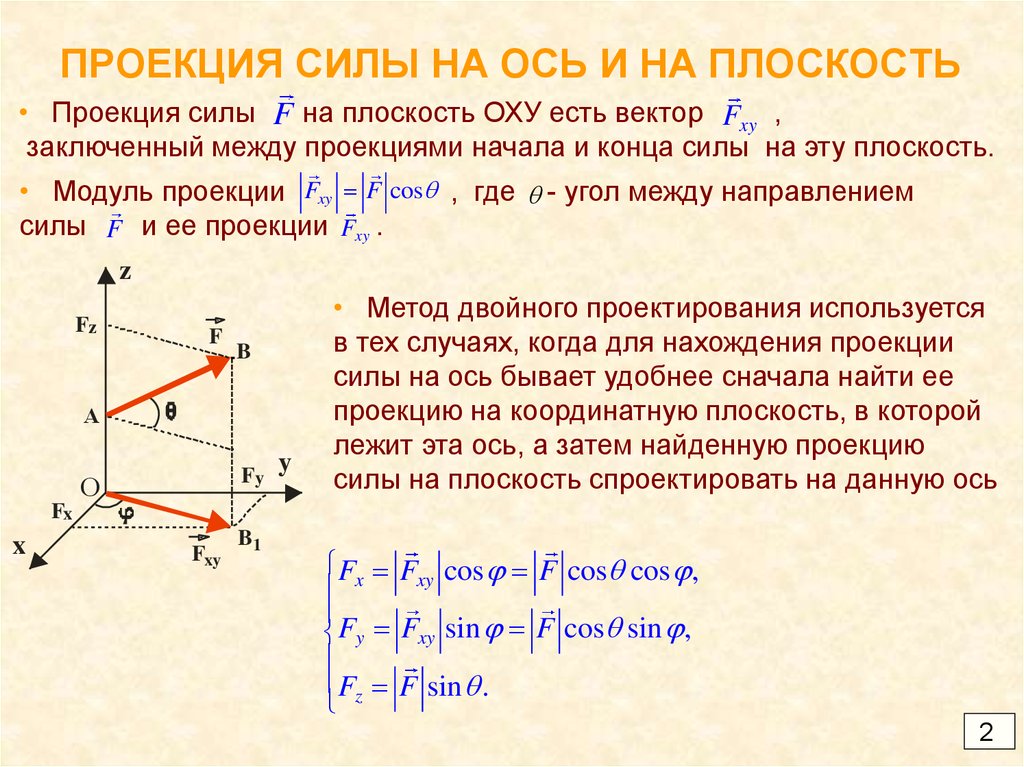
• Проекция силы F на плоскость ОХУ есть вектор Fxy ,
заключенный между проекциями начала и конца силы на эту плоскость.
• Модуль проекции Fxy F cos , где - угол между направлением
силы F и ее проекции Fxy .
z
Fz
F
B
А
Fy
О
y
• Метод двойного проектирования используется
в тех случаях, когда для нахождения проекции
силы на ось бывает удобнее сначала найти ее
проекцию на координатную плоскость, в которой
лежит эта ось, а затем найденную проекцию
силы на плоскость спроектировать на данную ось
Fx
x
Fxy
B1
F F cos F cos cos ,
xy
x
Fy Fxy sin F cos sin ,
Fz F sin .
2

3. АНАЛИТИЧЕСКИЙ СПОСОБ ЗАДАНИЯ СИЛЫ

Аналитический способ задания силы F состоит в задании
трех чисел: Fx, Fy, Fz - проекций силы на прямоугольные декартовы оси
координат, при этом модуль силы и ее направление определяются
z
по формулам:
Fz
F F2 F2 F2,
x
y
z
cos F / F ,
x
cos Fy / F ,
cos F / F .
z
О
x
Fx
y
F
Fy
Составляющие силы по осям координат XУZ выражаются формулами:
Fx Fxi , Fy Fy j , Fz Fz k .
Следовательно, вектор силы
параллелограмма:
можно строить геометрически по правилу
F Fxi Fy j Fz k .
3

4. СИСТЕМА СХОДЯЩИХСЯ СИЛ

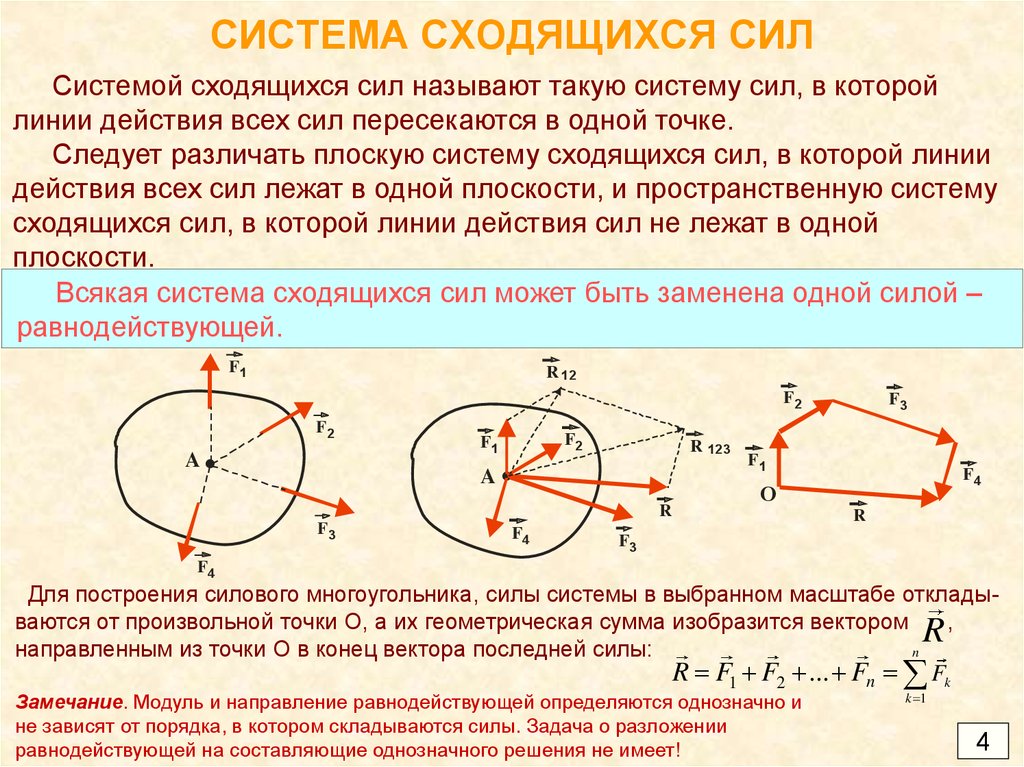
Системой сходящихся сил называют такую систему сил, в которой
линии действия всех сил пересекаются в одной точке.
Следует различать плоскую систему сходящихся сил, в которой линии
действия всех сил лежат в одной плоскости, и пространственную систему
сходящихся сил, в которой линии действия сил не лежат в одной
плоскости.
Всякая система сходящихся сил может быть заменена одной силой –
равнодействующей.
F1
R 12
F2
F2
A
F2
F1
A
R 123
R
F3
F4
F3
F1
F4
О
R
F3
F4
Для построения силового многоугольника, силы системы в выбранном масштабе откладываются от произвольной точки О, а их геометрическая сумма изобразится вектором
,
R
n
направленным из точки О в конец вектора последней силы:
R F1 F2 ... Fn Fk
Замечание. Модуль и направление равнодействующей определяются однозначно и
не зависят от порядка, в котором складываются силы. Задача о разложении
равнодействующей на составляющие однозначного решения не имеет!
k 1
4

5. СИСТЕМА СХОДЯЩИХСЯ СИЛ

Аналитический способ сложения сил состоит в нахождении проекций
вектора суммы сил R (главного вектора) на оси координат по заданным
проекциям слагаемых векторов на те же оси:
Rx Fkx , Ry Fky , Rz Fkz , R Rx2 Ry2 Rz2 ,
cos
R
Rx
R
, cos y , cos z .
R
R
R
Условия равновесия системы сходящихся сил:
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы
равнодействующая данной системы сил была равна нулю.
Геометрически это означает, что силовой многоугольник, построенный на
силах системы, должен быть замкнут!
геометрическая форма
F2
F3
F1
O
R =0
F4
F5
Fn
Fk
аналитическая форма
Fkx 0,
Fky 0,
Fkz 0.
5

6. ТЕОРЕМА О ТРЕХ СИЛАХ

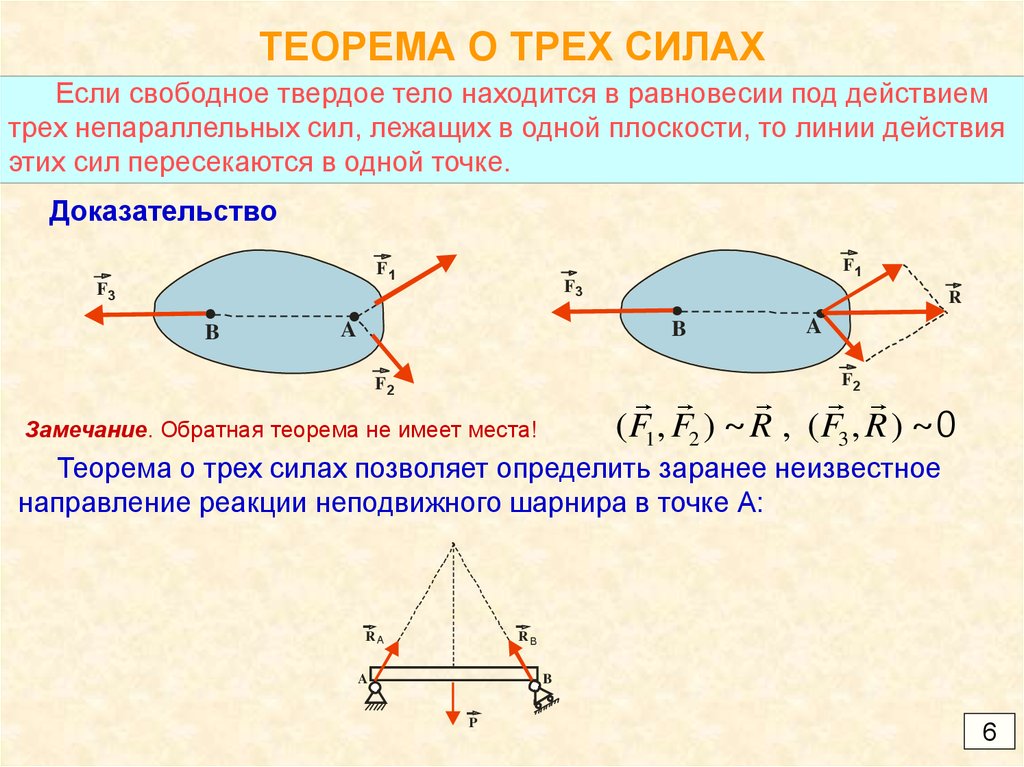
Если свободное твердое тело находится в равновесии под действием
трех непараллельных сил, лежащих в одной плоскости, то линии действия
этих сил пересекаются в одной точке.
Доказательство
F1
F1
F3
•B
F3
A
•B
R
A
F2
F2
( F1 , F2 ) ~ R , ( F3 , R ) ~0
Замечание. Обратная теорема не имеет места!
Теорема о трех силах позволяет определить заранее неизвестное
направление реакции неподвижного шарнира в точке А:
RA
RB
A
B
P
6

7. ЗАДАЧИ СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ И СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ

Задачу называют статически определимой если число неизвестных
задачи не превышает числа уравнений равновесия, даваемых статикой
твердого тела для данного вида системы сил.
В противном случае задачу называют статически неопределимой.
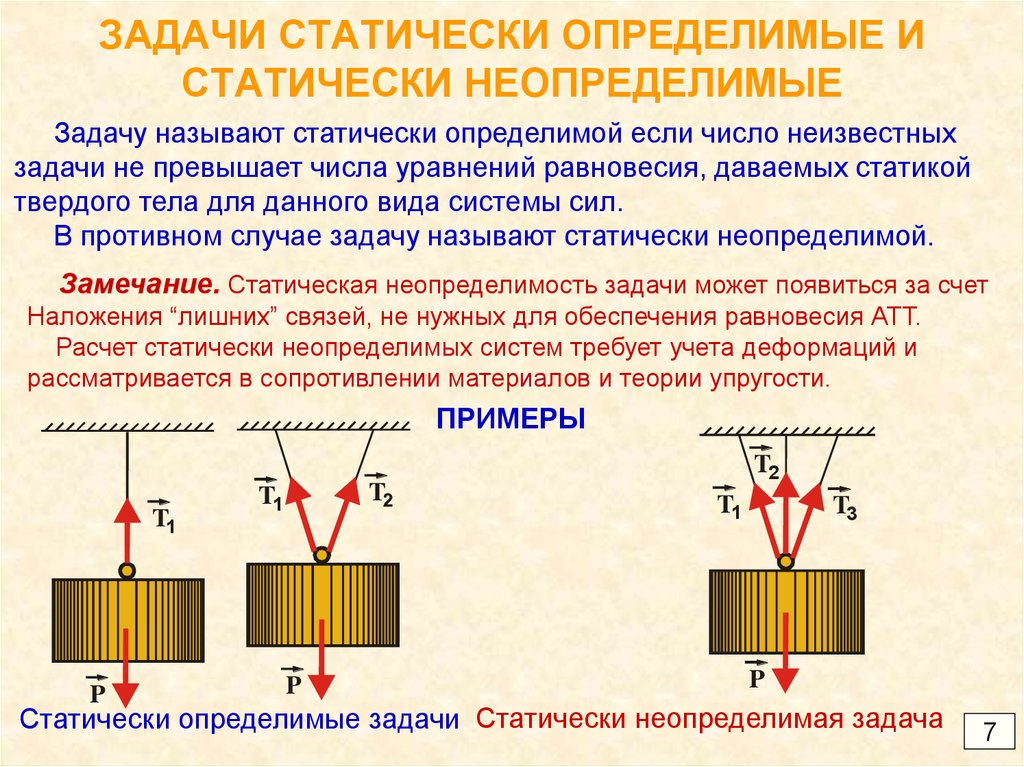
Замечание. Статическая неопределимость задачи может появиться за счет
Наложения “лишних” связей, не нужных для обеспечения равновесия АТТ.
Расчет статически неопределимых систем требует учета деформаций и
рассматривается в сопротивлении материалов и теории упругости.
ПРИМЕРЫ
T1
P
T
T1
P
T2
T1
T3
P
Статически определимые задачи Статически неопределимая задача
7

8. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ

Момент силы характеризует вращательный эффект действия силы на
твердое тело.
Различают:
• момент силы относительно точки на плоскости;
• момент силы относительно центра в пространстве;
• момент силы относительно оси.
Моментом силы относительно точки на плоскости (алгебраическим
моментом) называют скалярную величину, равную взятому со знаком «+»
или « » произведению модуля силы на плечо - кратчайшее расстояние от
точки до линии действия силы.
M 0 (F ) F h
Правило знаков: в теоретической механике момент силы считают положительным, если сила стремится повернуть тело вокруг точки против хода
часовой стрелки и отрицательным, если по часовой стрелке
8

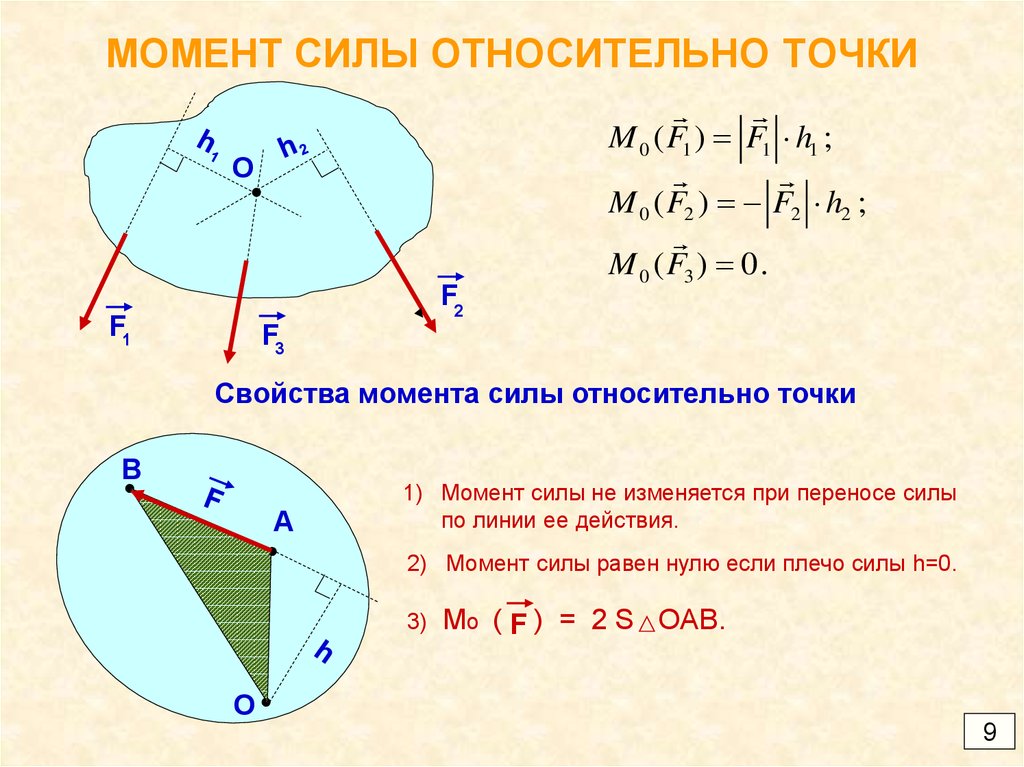
9. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ

M 0 ( F1 ) F1 h1 ;
O
M 0 ( F2 ) F2 h2 ;
F2
F1
M 0 ( F3 ) 0.
F3
Свойства момента силы относительно точки
B
A
1) Момент силы не изменяется при переносе силы
по линии ее действия.
2) Момент силы равен нулю если плечо силы h=0.
3)
O
Mo ( F ) = 2 S OAB.
9

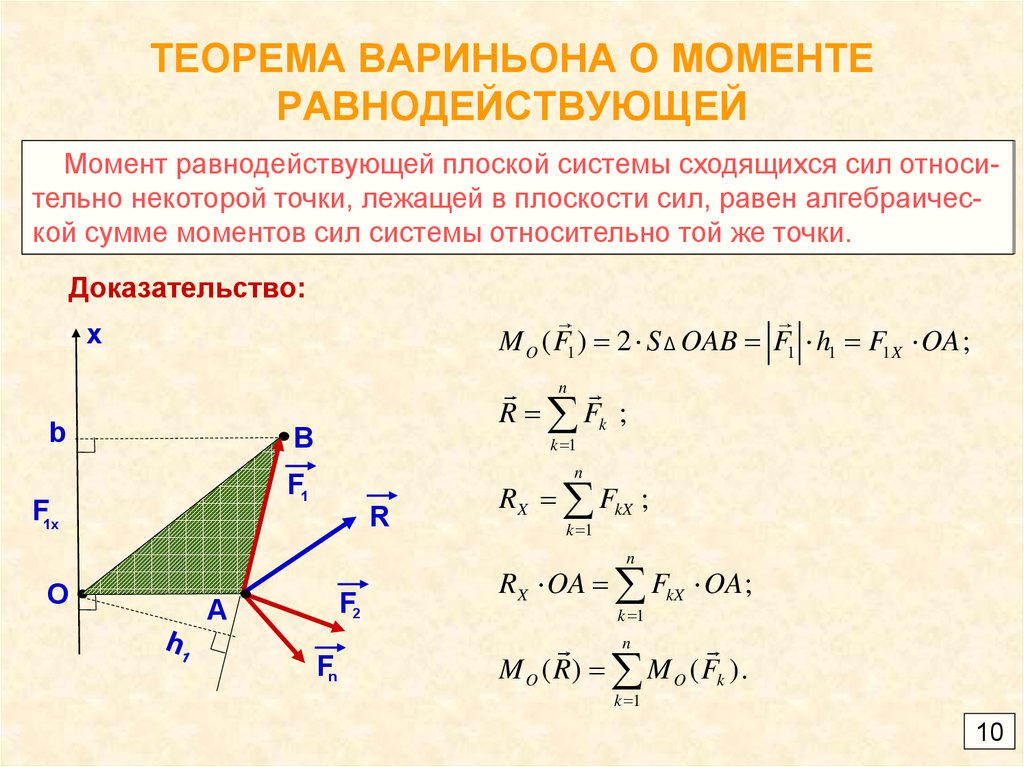
10. ТЕОРЕМА ВАРИНЬОНА О МОМЕНТЕ РАВНОДЕЙСТВУЮЩЕЙ

Момент равнодействующей плоской системы сходящихся сил относительно некоторой точки, лежащей в плоскости сил, равен алгебраической сумме моментов сил системы относительно той же точки.
Доказательство:
M O ( F1 ) 2 S Δ OAB F1 h1 F1 X OA ;
x
b
F1x
O
n
R Fk ;
B
k 1
n
F1
A
R
RX FkX ;
k 1
n
F2
RX OA FkX OA ;
k 1
n
Fn
M O ( R ) M O ( Fk ).
k 1
10

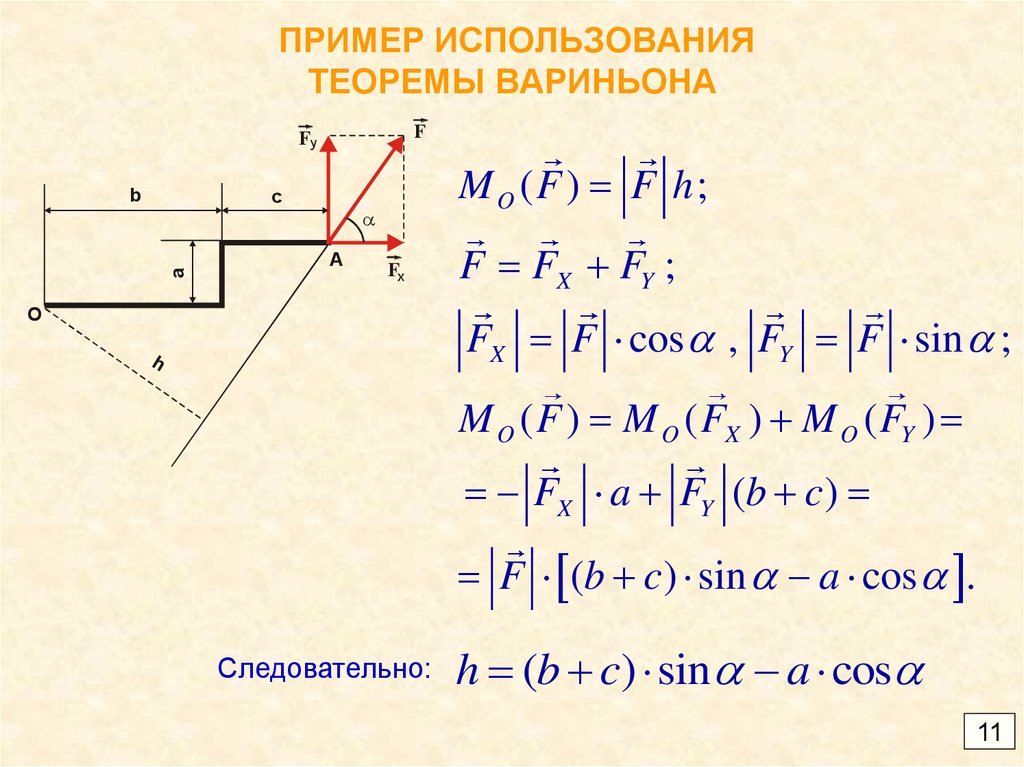
11. ПРИМЕР ИСПОЛЬЗОВАНИЯ ТЕОРЕМЫ ВАРИНЬОНА

F
Fy
b
a
c
M O (F ) F h;
A
Fx
O
F FX FY ;
FX F cos , FY F sin ;
h
M O ( F ) M O ( FX ) M O ( FY )
FX a FY (b c)
F (b c) sin a cos .
Следовательно:
h (b c) sin a cos
11