Похожие презентации:
Лекция 8 Условная оптимизация
1. Нелинейное программирование
Условная оптимизация2. Тема занятия
Общая задача условной оптимизацииГрафический метод решения
Метод множителей Лагранжа
3. Общая задача условной оптимизации
4. Общая задача условной оптимизации
Примерыz f ( x1 , x2 ) 15 x1 18 x2 max (min)
2
2
( x1 13) ( x2 3) 169
z f ( x1 , x2 ) ( x1 15) 2 ( x1 15)( x2 18) ( x2 18) 2 min
10
x
16
0
5. Графический метод решения
Алгоритм метода.– Строим на графике линии условий
– Строим одну из линий уровня целевой функции
– Определяем направление максимума и
минимума
– На графике находим координаты точек
пересечения линии условия с одной из линий
уровня целевой функции, в которой она
принимает минимальное(максимальное)
значение
6. Графический метод решения
Задача: решить следующий пример графическимметодом.
z f ( x1 , x2 ) 15 x1 18 x2 max (min)
2
2
( x1 13) ( x2 3) 169
7. Графический метод решения
1414
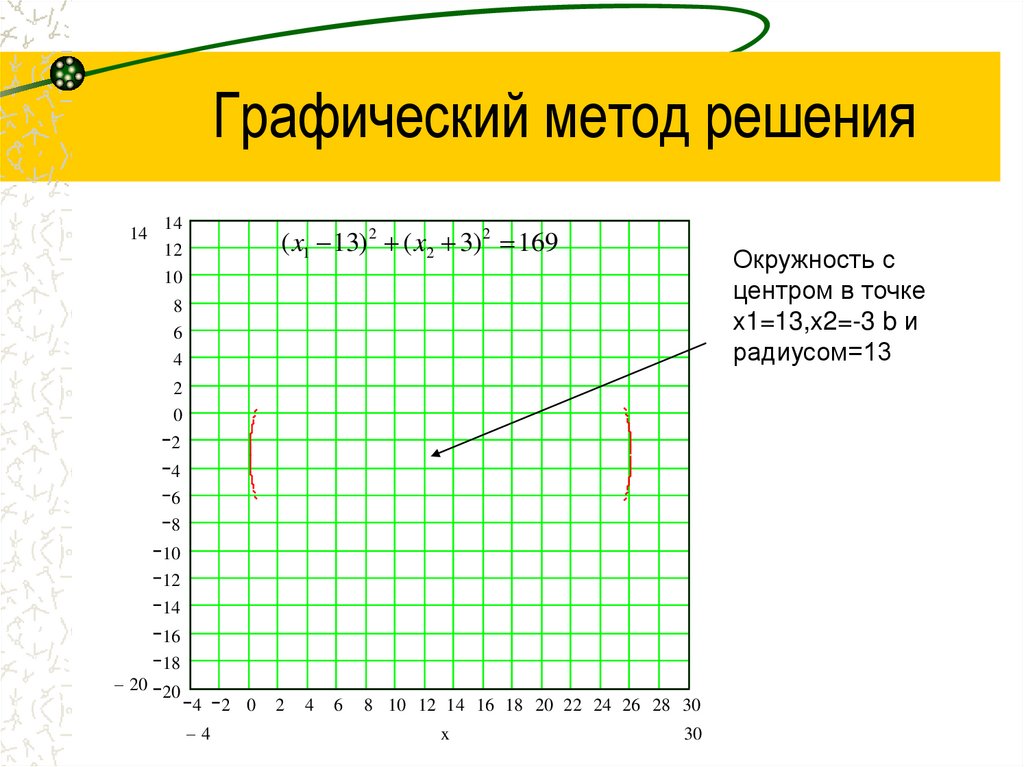
( x1 13) 2 ( x2 3) 2 169
12
10
Окружность с
центром в точке
x1=13,x2=-3 b и
радиусом=13
8
6
4
f1( x)
f2( x)
f ( x)
2
0
2
4
6
8
10
12
14
16
18
20 20
4
4
2 0
2
4
6
8 10 12 14 16 18 20 22 24 26 28 30
x
30
8. Графический метод решения
1414
12
10
8
6
4
f1( x)
f2( x)
f ( x)
2
0
2
4
6
8
10
12
14
16
18
20 20
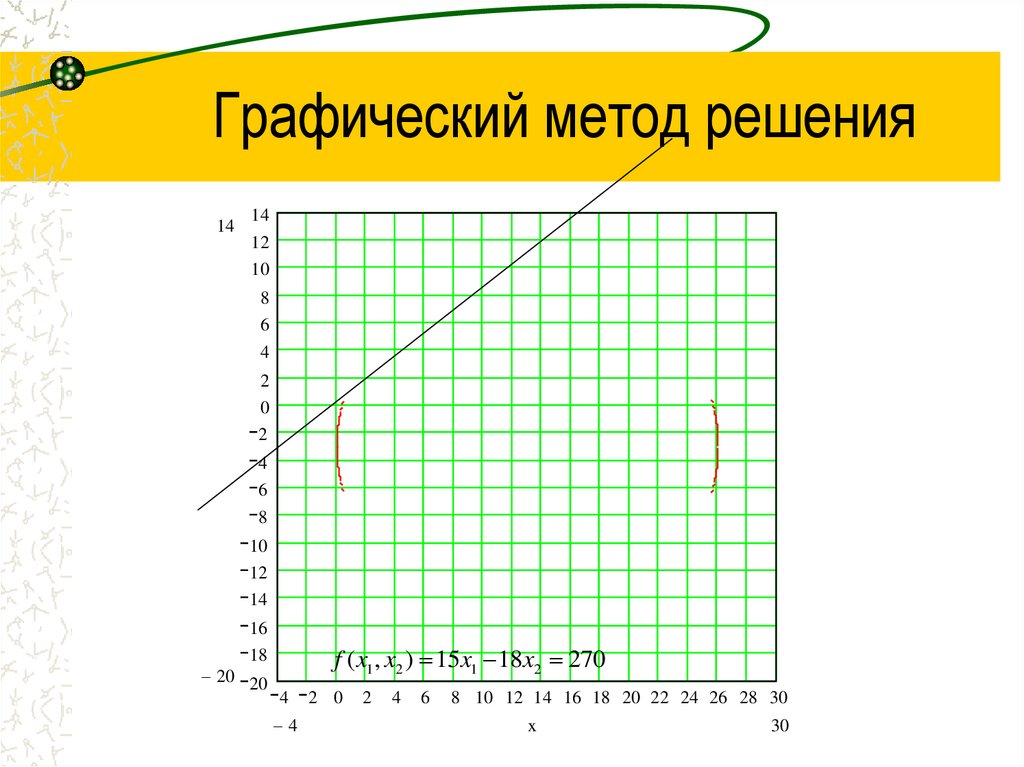
f ( x1 , x2 ) 15x1 18x2 270
4
4
2 0
2
4
6
8 10 12 14 16 18 20 22 24 26 28 30
x
30
9. Графический метод решения
1414
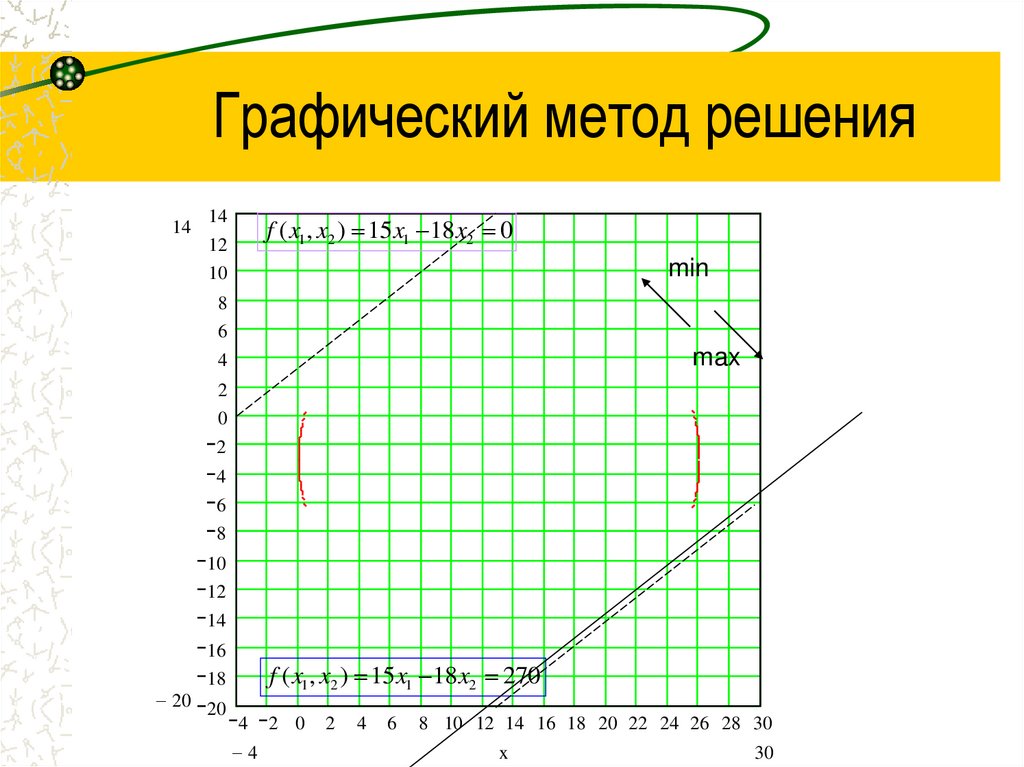
f ( x1 , x2 ) 15x1 18x2 0
12
10
min
8
6
max
4
f1( x)
f2( x)
f ( x)
ff ( x)
2
0
2
4
6
8
10
12
14
16
f ( x1 , x2 ) 15x1 18x2 270
18
20 20
4
4
2 0
2
4
6
8 10 12 14 16 18 20 22 24 26 28 30
x
30
10. Графический метод решения
1414
12
10
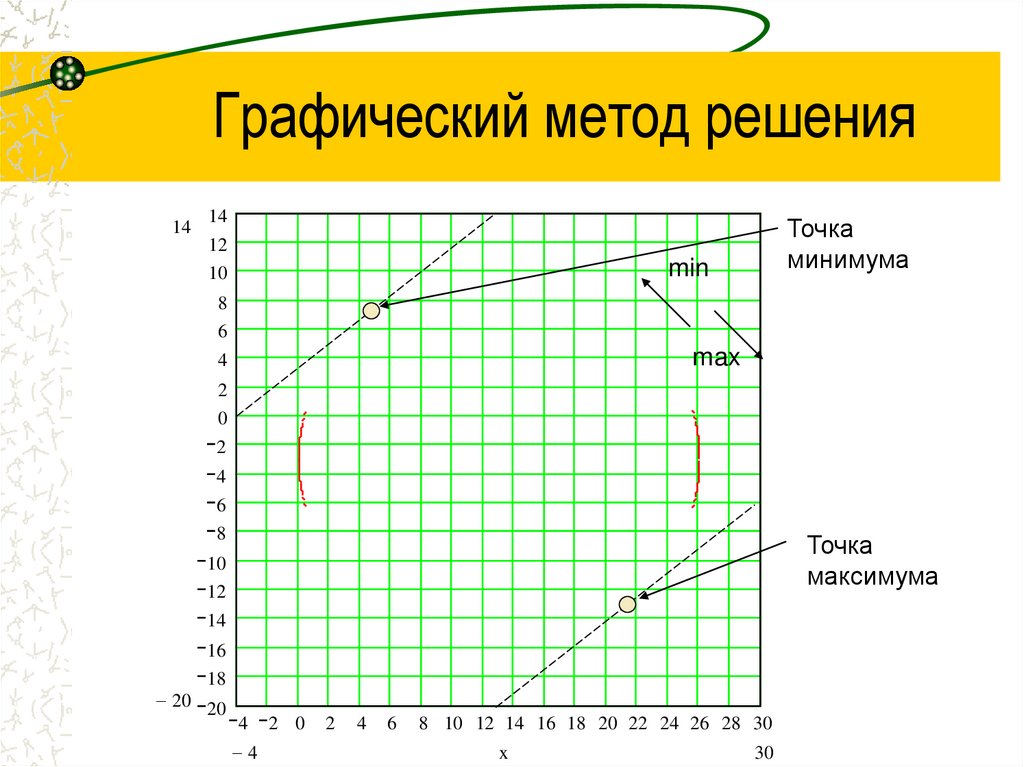
Точка
минимума
min
8
6
max
4
f1( x)
f2( x)
f ( x)
ff ( x)
2
0
2
4
6
8
Точка
максимума
10
12
14
16
18
20 20
4
4
2 0
2
4
6
8 10 12 14 16 18 20 22 24 26 28 30
x
30
11. Графический метод решения
Ответ.x min (4, 7;7); f ( x min ) 55,5
*
*
x max (21; 13); f ( x min ) 549
*
*
12. Метод множителей Лагранжа
13. Метод множителей Лагранжа
14. Метод множителей Лагранжа
15. Метод множителей Лагранжа
16. Алгоритм метода множителей Лагранжа
17. Алгоритм метода множителей Лагранжа
18. Алгоритм метода множителей Лагранжа
19. Метод множителей Лагранжа
Задача: найти стационарные точки методоммножителей Лагранжа.
z f ( x1 , x2 ) 15 x1 18 x2 max (min)
2
2
( x1 13) ( x2 3) 169
20. Метод множителей Лагранжа
22
L( x1 , x2 , ) 15 x1 18 x2 ( x1 13) ( x2 3) 169
15 2 x1 26
L 18 2 x2 6
( x 13) 2 ( x 3) 2 169
1
2
L 0
21. Метод множителей Лагранжа
15 2 x1 26 018 2 x2 6 0
2
2
(
x
13)
(
x
3)
169 0
1
2
1 0,9; x1 21,3; x2 13
2 0,9; x1 4, 67; x2 7