Детерминированные нелинейные модели с непрерывными переменными

1. Теория принятия решений

Лекция 2.2:
Детерминированные нелинейные модели с
непрерывными переменными

2. содержание

1.
2.
Текущий контроль знаний
Технологии исследования
нелинейных математических
моделей:
аналитическое исследование
методом множителей Лагранжа;
численное исследование.

3. Текущий контроль знаний

Решить графически задачу:
2 x1 4 x2 max;
5 x x 6;
1 2
3 x1 11x2 15;
i : xi 0.
Перейти к двойственной задаче и
решить ее графически:
7 x1 4 x2 5 x3 max;
9 x1 5 x2 2 x3 5;
3 x 7 x 0 x 20.
2
3
1

4. Исследование моделей

Два класса технологий исследования
нелинейных моделей с непрерывными
переменными:
1. Аналитическое исследование
моделей.
2. Численное исследование:
рандомизированное;
детерминированное.

5. Метод множителей Лагранжа

Используется для решения
однокритериальных задач на
условный экстремум вида:
f ( x ) min (max);
j : j ( x ) b j ;
(1)
x {x1 , x2 ,...., xn };
1 i n : ai xi bi .

6. Создание и исследование функции Лагранжа

Идея заключается в замене решения
системы (1) поиском экстремума
функции Лагранжа L вида:
L f ( x ) j (b j j ( x )).
(2)
j
Экстремум L отвечает решению
L
системы:
i :
0;
xi
j : L 0.
j
(3)

7. Пример: задача о консервной банке

Содержательная постановка: требуется
выбрать такое соотношение между
высотой и диаметром консервной
банки, чтобы ее поверхность была
минимальной при заданном объеме.
Формальная постановка:
2 r (h r ) min;
2
( 4)
r h V ;
r 0; h 0.

8. Функция Лагранжа и ее исследование на экстремум

1. Функция Лагранжа:
L 2 r (h r ) (V r 2 h).
(5)
2. Условия экстремума:
L
r h 2r rh 0;
L
2
2
r
r
0;
h
L
2
V
r
h 0.
V
r 3
;
(6)
2
2
; (7)
3. Результат решения системы (6):
r
h 2 r .

9. Исследование экстремума

Пусть новое значение радиуса банки
равно r+Ɛ, где Ɛ>0, тогда из системы (4)
следует, что площадь банки равна S*:
V
2
S * 2 (r )
.
2
(r )
S *
Так как производная 0, то
определяемые (7) значения r и h
отвечают минимуму S.

10. САМОСТОЯТЕЛЬНО 1

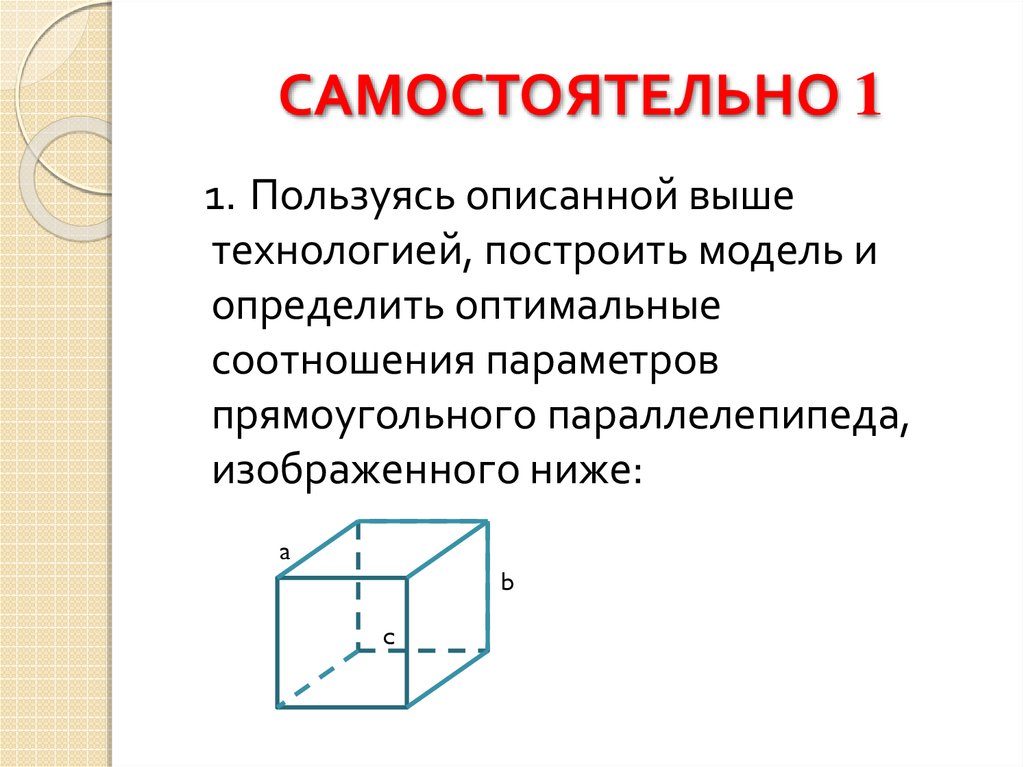
1. Пользуясь описанной выше
технологией, построить модель и
определить оптимальные
соотношения параметров
прямоугольного параллелепипеда,
изображенного ниже:
a
b
c

11. Достоинства и недостатки метода множителей Лагранжа

1. Достоинства:
Глобально оптимальное решение.
Ответ получается аналитически, т.е.
не требует для определения
численных значений больших
ресурсов компьютера.
2. Недостатки:
Возможность исследовать модель
таким образом зависит от свойств
полученной системы уравнений.